| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Корень (кубический, квадратный) в степени: решения, таблицы, примеры
Оглавление:
- org/ListItem»>
Степень с натуральным показателем
- Степень с целым показателем
- Кубический корень
- Корень -ной степени
- Сравнение арифметических корней
- Как избавиться от иррациональности в знаменателе
- Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, .
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
к оглавлению ▴
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как то
Так как то
Сравним и для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при ?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней11. Какое из чисел больше: или ?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателеЕсли дана дробь вида то нужно умножить числитель и знаменатель дроби на :
Тогда знаменатель станет рациональным.
Если дана дробь вида или то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и и — сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умноженияПокажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 07.02.2023
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2 /3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
читать далее математические задачи »
|

 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Что из этого: A.98/99 B.73/179 C.1/250 D.81/729
Что из этого: A.98/99 B.73/179 C.1/250 D.81/729 1 4 в дробях?
1 4 в дробях? Сделаем деление 1 ÷ 4 . Следовательно, десятичная форма дроби равна 0,25.
Сделаем деление 1 ÷ 4 . Следовательно, десятичная форма дроби равна 0,25. Каждый раз дробь в ее простейшей форме равна «половине».
Каждый раз дробь в ее простейшей форме равна «половине».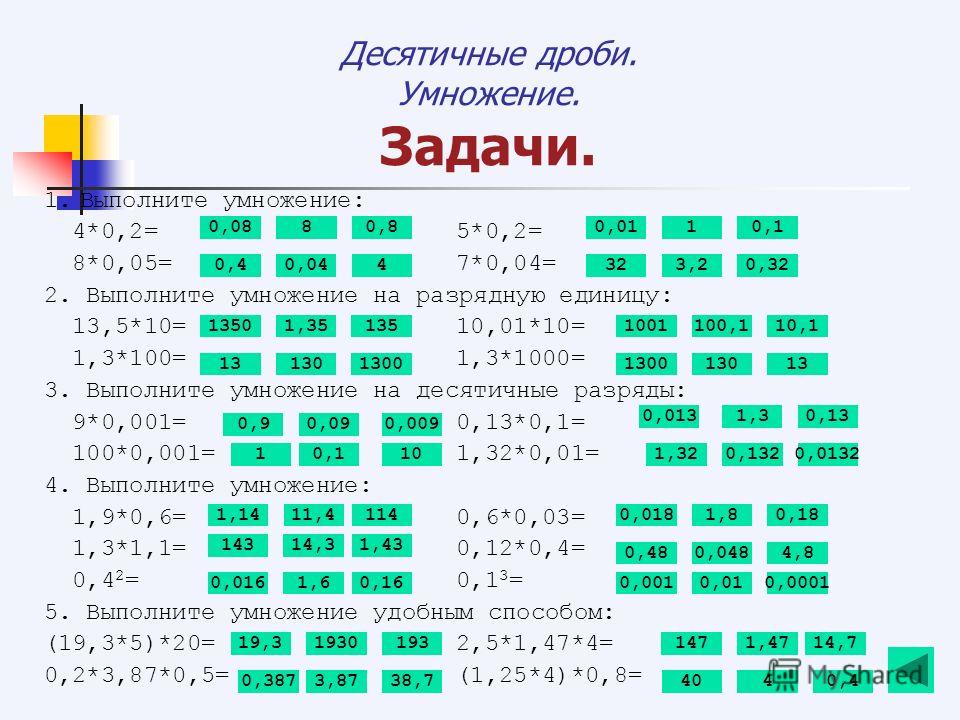

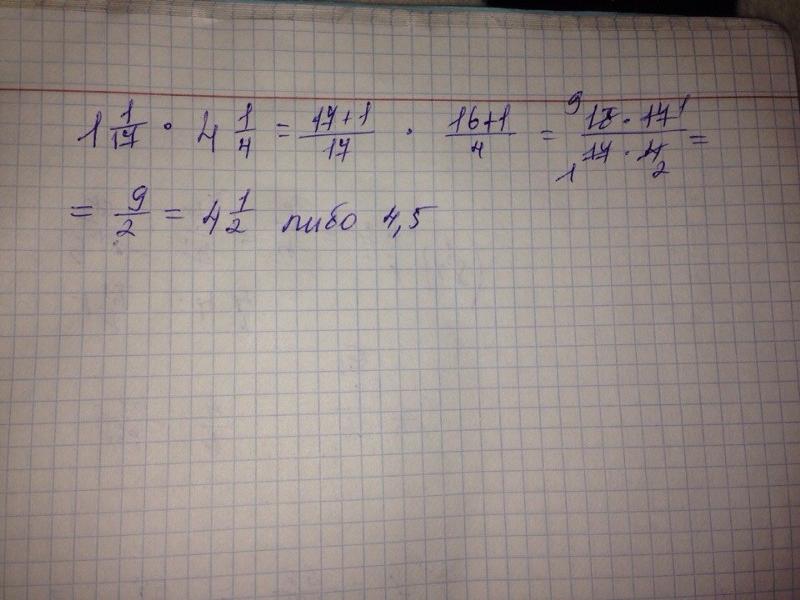 com
com 