Сколько метров в кубе посчитать онлайн калькулятор
Очень часто нужно быстро рассчитать количество необходимых пиломатериалов. Формулы расчета просты, но не всегда под рукой есть калькулятор. Наш онлайн-калькулятор призван помочь решить эту проблему. Вопросы о том, сколько метров в кубе и другие подобные им решаются путем перетаскивания ползунков нижеприведенной формы. Приведенная форма помогает легко рассчитать количество досок в 1 м.кв. зная их ширину и длину. А если добавить толщину доски, то легко можно вычислить такие величины, как количество квадратных метров или досок в 1 м.куб. Просто перетаскивайте ползунки и нажимайте кнопку «Посчитать».
Онлайн-калькулятор расчета количества пиломатериалов
Некоторые результаты расчета для самопроверки приводим в следующих таблицах.
Расчет количества доски в 1 м.куб.
| толщина, мм | ширина, мм | длина, м | кол-во, шт | м.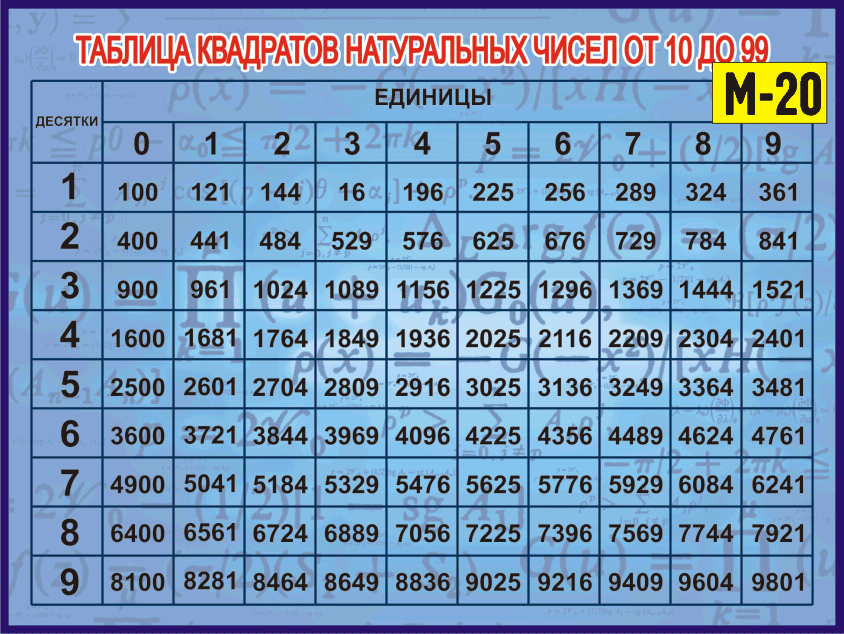 | м.куб | шт в м.кв. | шт в м.куб. | кв.м. в кубе |
| 18 | 100 | 1,5 | 1 | 0,15 | 0,003 | 6,67 | 370,37 | 55,56 |
| 20 | 120 | 2,0 | 1 | 0,24 | 0,005 | 4,17 | 208,33 | 50,00 |
| 20 | 140 | 3,0 | 1 | 0,42 | 0,008 | 2,38 | 119,05 | 50,00 |
| 35 | 70 | 3,0 | 1 | 0,21 | 0,007 | 4,76 | 136,05 | 28,57 |
| 40 | 70 | 3,0 | 1 | 0,21 | 0,008 | 4,76 | 119,05 | 25,00 |
| 27 | 120 | 4,0 | 1 | 0,48 | 0,013 | 2,08 | 77,16 | 37,04 |
| 35 | 140 | 6,0 | 1 | 0,84 | 0,029 | 1,19 | 34,01 | 28,57 |
Расчет количества бруса в 1 м.
 куб.
куб.Количество доски на забор можно рассчитать в нашем калькуляторе расчета заборной доски
Для более точного расчета количества пиломатериалов исходя из их наличия и ассортимента лучше связаться с нашими представителями по телефонам, указанным в шапке сайта.
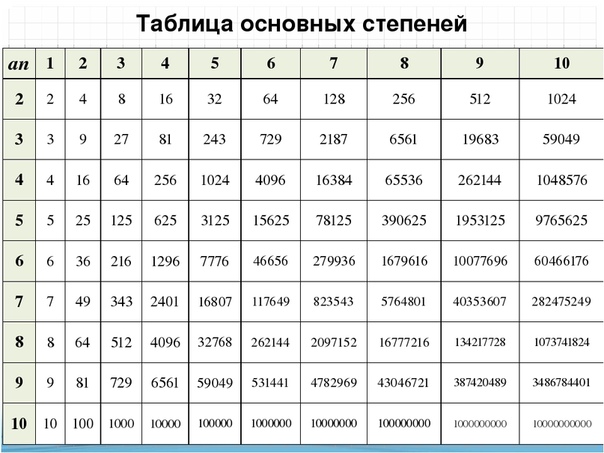
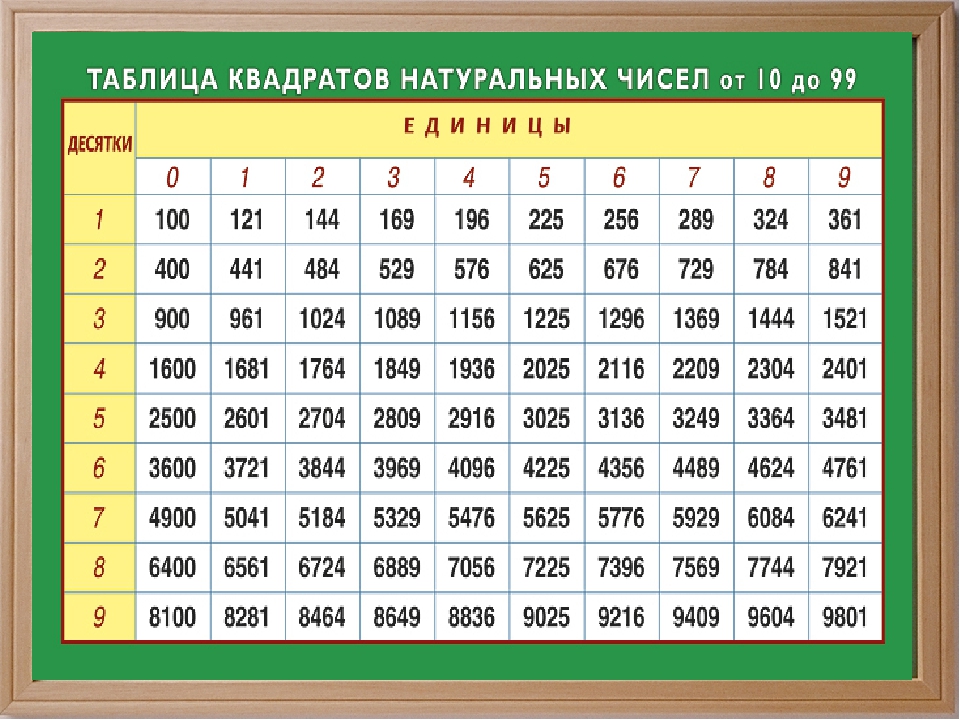
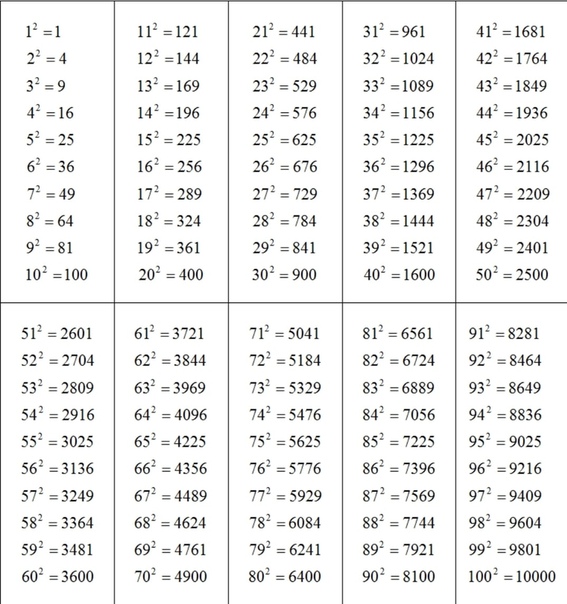
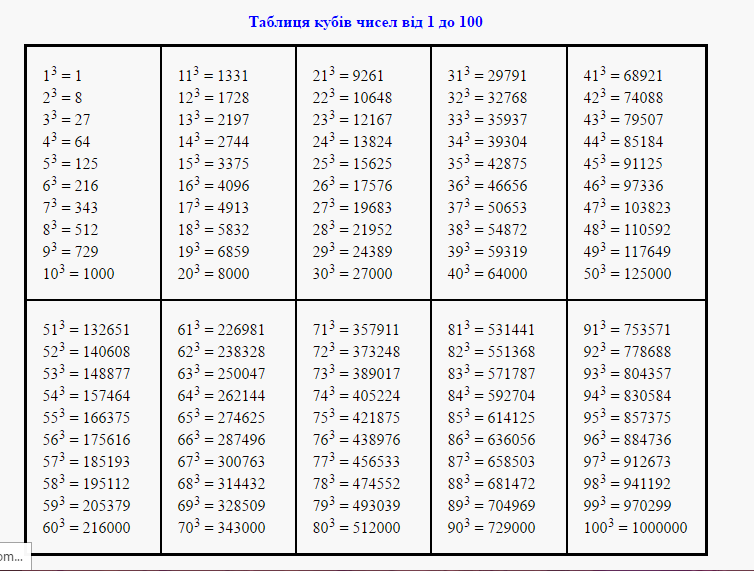
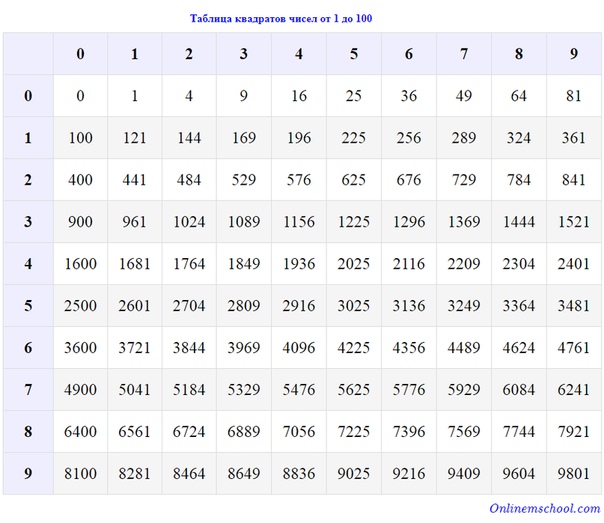
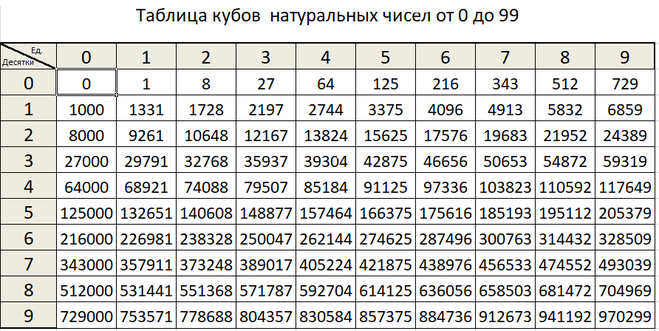
Таблица квадратов целых чисел от 1 до 30. Полезна для заучивания наизусть.
Таблица кубов Таблица квадратов натуральных чисел от 1 до 100.
таблица квадратов, таблица квадратов от 1 до 10, таблица квадратов от 1 до 30, таблица квадратов от 1,00 до 9,99, таблица квадратов натуральных чисел, таблица степеней, таблица квадратов чисел, таблица квадратов натуральных, квадраты чисел |
Раздел: Таблицы численных значений + Таблицы Брадиса:
|
|||||||||||||||
Металл листовой — сколько весит 1 металлический лист, 1 м2, предельные отклонения
Теоретическая масса металлического листа
Зная стоимость тонны, легко подсчитать цену 1 металлического листа. Для этого необходимо знать вес единицы продукции. В таблице ниже приводится теоретический вес для листов толщиной 0,5 — 60 мм наиболее популярного и востребованного раскроя — 1250х2500, 1500х6000 и 2000х6000 мм (в зависимости от толщины металла).
Для этого необходимо знать вес единицы продукции. В таблице ниже приводится теоретический вес для листов толщиной 0,5 — 60 мм наиболее популярного и востребованного раскроя — 1250х2500, 1500х6000 и 2000х6000 мм (в зависимости от толщины металла).
Следует учесть, что данной таблицей можно воспользоваться для определения приблизительной стоимости металлического листа, так как вес проката определяется для стандартной плотности стали 7,85 кг/м3 и может незначительно отличаться в зависимости от марки стали и технических условий завода — изготовителя.
| Толщина листа | Вес 1 м2 | Вес 1 листа, кг | Толщина листа | Вес 1 м2 | Вес 1 листа, кг | ||
|---|---|---|---|---|---|---|---|
| мм | кг | 1250 x 2500 мм | 1500 x 6000 мм | мм | кг | 1250 x 2500 мм | 1500 x 6000 мм |
| 0,5 | 3,93 | 12,28 | - | 5,0 | 39,3 | 353,25 | 471,00 |
| 0,55 | 4,32 | 13,50 | - | 6,0 | 47,1 | 423,90 | 565,20 |
| 0,6 | 4,72 | 14,75 | - | 7,0 | 55,0 | 494,55 | 659,40 |
0. 7 7
|
5,50 | 17,19 | - | 8,0 | 62,8 | 565,20 | 753,60 |
| 0,8 | 6,28 | 19,63 | - | 9,0 | 70,7 | 635,85 | 847,80 |
| 0,9 | 7,06 | 22,06 | - | 10,0 | 78,5 | 706,50 | 942,00 |
| 1,0 | 7,85 | 24,53 | - | 12,0 | 94,2 | 847,80 | 1130,4 |
| 1,2 | 9,49 | 29,66 | - | 14,0 | 109,9 | 989,10 | 1318,8 |
| 1,4 | 10,99 | 34,34 | - | 16,0 | 125,9 | 1133,1 | 1510,8 |
| 1,5 | 11,77 | 36,78 | - | 18,0 | 141,3 | 1271,7 | 1695,6 |
| 1,7 | 13,34 | 41,69 | - | 20,0 | 157,0 | 1413,0 | 1884,0 |
| 1,8 | 14,13 | 44,16 | - | 22,0 | 172,7 | 1554,3 | 2072,4 |
| 1,9 | 14,91 | 46,59 | - | 25,0 | 196,3 | 1766,3 | 2355,0 |
| 2,0 | 15,70 | 49,06 | - | 30,0 | 235,5 | 2119,5 | 2826,0 |
| 2,5 | 19,62 | 61,31 | - | 40,0 | 314,0 | 2826,0 | 3768,0 |
| 3,0 | 23,55 | 73,59 | 211,95 | 50,0 | 392,5 | 3532,5 | 4710,0 |
| 4,0 | 31,04 | 97,00 | 279,36 | 60,0 | 471,0 | 4239,0 | 5652,0 |
Предельные отклонения при производстве листового металла
Любой листовой металл выполняется с размерными отклонениями по длине, ширине, толщине, величина которых зависит от прокатного оборудования.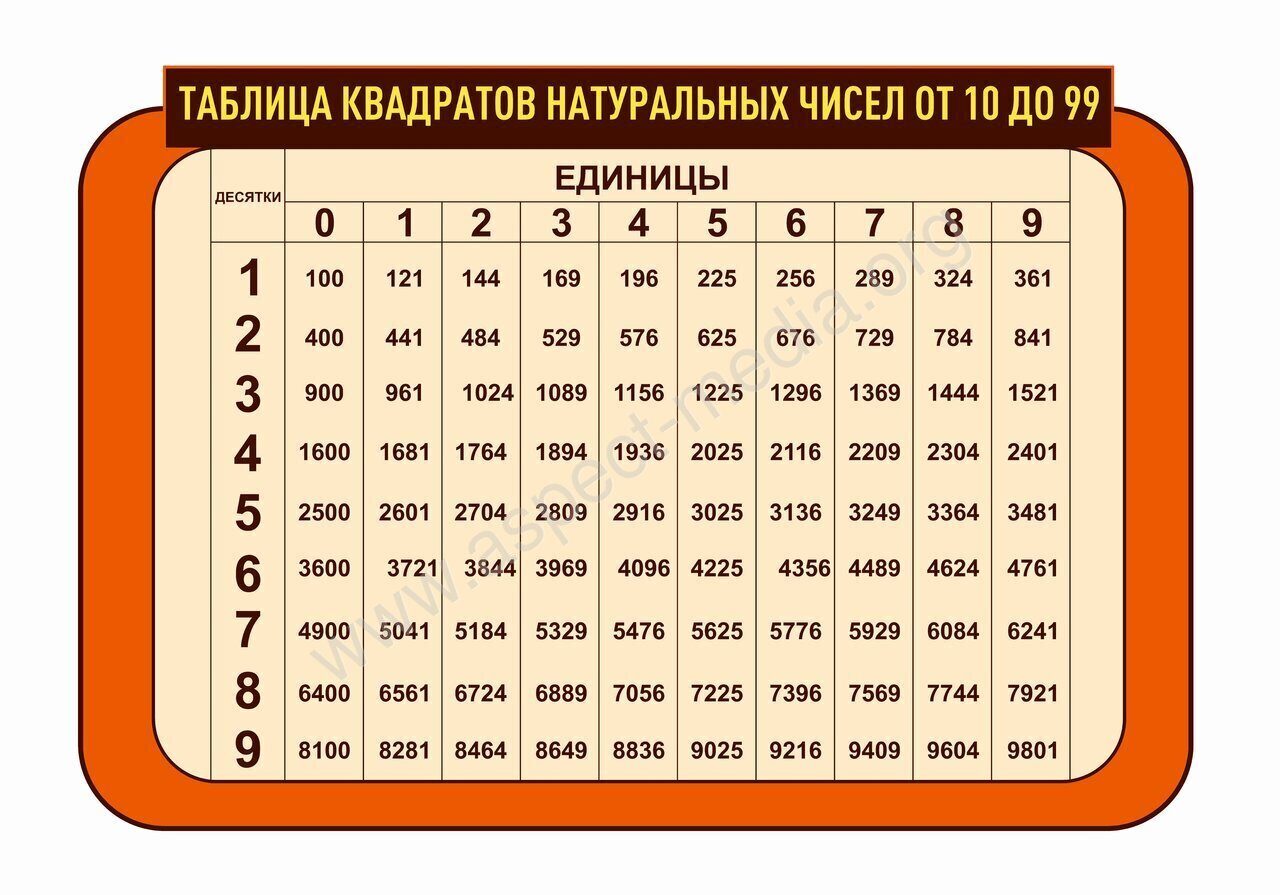 Для горячекатаной продукции по ГОСТ 19903, произведенной в листах, существуют следующие предельные отклонения:
Для горячекатаной продукции по ГОСТ 19903, произведенной в листах, существуют следующие предельные отклонения:
- по ширине составляет +10 мм (для проката с обрезной кромкой) или + 20 мм (для проката с необрезной кромкой)
- по длине может варьироваться от +10 (при длине листов до 1500 мм) и до +15 мм (при длине листов свыше 1500 мм)
Кроме того, величины допусков в размерах металлических листов зависят от:
- точности прокатки (повышенная, нормальная точность)
- назначения проката (прокат для авиационной промышленности допускается производить с минусовыми допусками)
Продажа металла с учетом возможных допусков
Изменения размерных параметров на величину предельных отклонений сказывается на увеличении веса единицы проката. В результате после взвешивания и при отгрузке продукции цена может незначительно увеличиться по сравнению с теоретически рассчитанной величиной.
APEX METAL продает листовой прокат не только в рулонах и листах стандартного раскроя, но оказывает услугу плазменной, газовой, лазерной резки, продольно -поперечной рубки.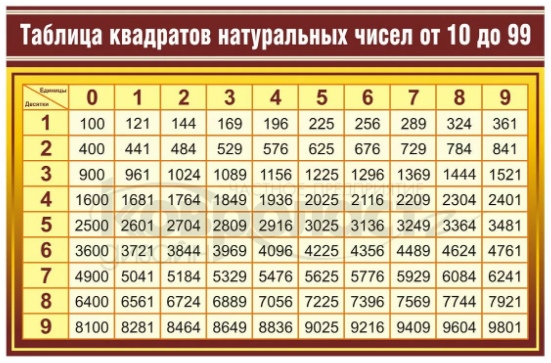 Стоимость листового металла зависит от марки стали (качественные стали, легированные стали или углеродистые стали обыкновенного качества), способа обработки поверхности и объема закупаемой продукции.
Стоимость листового металла зависит от марки стали (качественные стали, легированные стали или углеродистые стали обыкновенного качества), способа обработки поверхности и объема закупаемой продукции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица перевода сечений кабеля из стандарта AWG в систему СИ
В последнее время широкое распространение получили импортные провода и инструменты с маркировкой AWG. American Wire Gauge – американский калибр проводников.
American Wire Gauge – американский калибр проводников.
Калибр провода по стандарту AWG отражает размер токонесущей жилы. Характерной особенностью стандарта AWG является то, что чем толще провод, тем меньше его калибр.
Значение AWG характеризует количество этапов обработки проволоки. В процессе изготовления медный провод последовательно протягивается через калибровочные отверстия все меньшего и меньшего диаметра. Например, кабель 24 AWG тоньше в диаметре и меньшего сечения, чем кабель, маркированный 15 AWG. Таблица отражает перевод стандарта AWG в диаметр и площадь сечения в миллиметрах.
| AWG | приблизительный диаметр, мм | площадь, мм² | соответствие сечения по ГОСТ, мм² | удельное сопротивление, Ом/м |
|---|---|---|---|---|
| 40 | 0,08 | 0,0050 | • | 3,44 |
| 39 | 0,09 | 0,0064 | • | 2,73 |
| 38 | 0,10 | 0,0078 | • | 2,16 |
| 37 | 0,11 | 0,0095 | • | 1,72 |
| 36 | 0,13 | 0,0133 | • | 1,36 |
| 35 | 0,14 | 0,0154 | • | 1,08 |
| 34 | 0,16 | 0,0201 | • | 0,856 |
| 33 | 0,18 | 0,0254 | • | 0,679 |
| 32 | 0,20 | 0,0314 | • | 0,538 |
| 31 | 0,23 | 0,0415 | • | 0,427 |
| 30 | 0,25 | 0,0503 | 0,05 | 0,339 |
| 29 | 0,29 | 0,0646 | • | 0,268 |
| 28 | 0,32 | 0,0804 | • | 0,213 |
| 27 | 0,36 | 0,1020 | 0,1 | 0,169 |
| 26 | 0,40 | 0,1280 | 0,14 | 0,134 |
| 25 | 0,45 | 0,1630 | • | 0,106 |
| 24 | 0,51 | 0,2050 | 0,2 | 0,0842 |
| 23 | 0,57 | 0,2590 | 0,25 | 0,0668 |
| 22 | 0,64 | 0,3250 | 0,32 | 0,0530 |
| 21 | 0,72 | 0,4120 | • | 0,0420 |
| 20 | 0,81 | 0,5190 | 0,5 | 0,0333 |
| 19 | 0,91 | 0,6530 | • | 0,0264 |
| 18 | 1,02 | 0,82 | 0,75 | 0,0210 |
| 17 | 1,15 | 1,04 | 1,0 | 0,0166 |
| 16 | 1,29 | 1,31 | • | 0,0132 |
| 15 | 1,45 | 1,65 | 1,5 | 0,0104 |
| 14 | 1,63 | 2,08 | • | 0,00829 |
| 13 | 1,83 | 2,63 | 2,5 | 0,00657 |
| 12 | 2,05 | 3,31 | • | 0,00521 |
| 11 | 2,30 | 4,15 | 4 | 0,00413 |
| 10 | 2,59 | 5,27 | • | 0,00328 |
| 9 | 2,91 | 6,62 | 6 | 0,00260 |
| 8 | 3,26 | 8,35 | • | 0,00206 |
| 7 | 3,67 | 10,6 | 10 | 0,00163 |
| 6 | 4,11 | 13,3 | • | 0,00130 |
| 5 | 4,62 | 16,8 | 16 | 0,00103 |
| 4 | 5,19 | 21,2 | • | 0,000815 |
| 3 | 5,83 | 26,7 | 25 | 0,000647 |
| 2 | 6,54 | 33,6 | 35 | 0,000513 |
| 1 | 7,35 | 42,4 | • | 0,000407 |
| 0 | 8,25 | 53,5 | 50 | 0,000323 |
| 2/0 | 9,26 | 67,4 | 70 | 0,000256 |
| 3/0 | 10,4 | 85,0 | 95 | 0,000203 |
| 4/0 | 11,7 | 107,0 | 120 | 0,000161 |
Схемы укладки тротуарной плитки брусчатка и квадрат
Выбирая тротуарную плитку нужно учитывать не только ее форму, фактуру и оттенок, но и какой рисунок вы хотите видеть в течение длительного времени.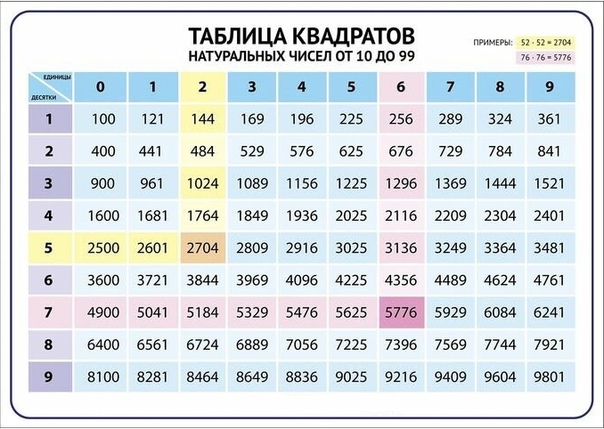 Кислотная пестрота и узоры в стиле советских ковров могут быстро перестать вам нравиться.
Кислотная пестрота и узоры в стиле советских ковров могут быстро перестать вам нравиться.
Мы уже представляли вам 50 вариантов укладки брусчатки, а в этой статье решили представить рисунки сочетания прямоугольных форм – брусчатка и квадрат. Использование нескольких прямоугольных форм значительно расширяет возможности создания индивидуального рисунка. И даже если вы не найдете подходящую схему, то с помощью любого графического редактора на компьютере, даже при минимальных знаниях, можно разложить плитку необходимых размеров создав уникальный проект мощения.
Формы тротуарной плитки для мощения:
Брусчатка
Классическая прямоугольник – брусчатка облагородит любую территорию, будь это городской тротуар или дорожка в саду. В ассортименте завода Stellard она представлена во всех цветовых вариантах и фактурах.
Размеры брусчатки – 200х100 мм по длине и ширине, толщина может быть 40, 60 или 80 мм. Выбор толщины плитки зависит от нагрузки на участок мощения. Для представленных в этой статье схем укладки используется плитка 60 мм, которую можно использовать для движения легковых автомобилей.
Для представленных в этой статье схем укладки используется плитка 60 мм, которую можно использовать для движения легковых автомобилей.
Квадрат 20х20
Квадратная плитка размером 200х200х60 мм удобна для монтажа, укладывается как самостоятельно, так и в паре с брусчаткой, за счет чего можно минимизировать подрезку крайних камней.
Квадрат 10х10
Квадратная плитка размером 100х100х60 в кладке может использоваться как самостоятельно, так и выполнять функцию связующего звена между плиткой большего размера (брусчатка, квадрат 20х20, шапка).
Схемы укладки брусчатки, квадрат 20х20, квадрат 10х10
1. Плетеный узор из Брусчатки и квадрата 10х10
В таком рисунке на каждые 1,2 м2 мощения необходимо брусчатки – 0,4 м2 серой (33,33%) и 0,6 м2 белой (50%), маленького квадрата по 0,1 м2 каждого оттенка (по 8,33%).
Плетеный узор из Брусчатки и квадрата 10х10
2. Лесенка из Брусчатки и квадрата 10х10
Необходимое количество плитки для такого решения: на каждые 1,3 м2 темно-серый прямоугольник – 0,2 м2 (15,4%), серый – 0,8 м2 (61,5%), квадратик – 0,3 м2 (23,1%).
Лесенка из Брусчатки и квадрата 10х10
3. Рисунок из квадрата 10х10
Довольно сложный рисунок из квадратиков трех оттенков. На каждый кв. метр необходимо: белых – 0,46 м 2, серых – 0,28 м 2, темно-серых – 0,26.
Рисунок из квадрата 10х10
4. Игра квадратов
Составить данный рисунок укладки тротуарной плитки несложно. В нем прослеживаются повторения квадратов из брусчатки (0,39 м2 на каждый квадратный метр), квадратика 10х10 (0,41 на 1 м2) и квадрата 20х20 (0,2 на м2).
Игра квадратов
5. Плетеный узор
Такой рисунок можно составить из двух оттенков прямоугольника (на каждый квадратный метр серой – 0,39 м2, белой – 0,5 м2), и квадрата 10х10 – 0,11м2.
Плетеный узор
6. Узор из ромбов
Здесь на м2 благоустройства вам потребуется белых квадратных камней – 0,26, темно-серых – 0,2; прямоугольных белого цвета – 0,23, темно-серых – 0,31 м2.
Узор из ромбов
7.
 Узор из уголков
Узор из уголковЗдесь при расчете количества материала нужно на каждый м2 белых квадратиков – 0,25, серых – 0,125, темно-серых – 0,125, серой брусчатки – 0,25, темно-серой – 0,25.
Узор из уголков
8. Раскладка в клетку
Раскладка в клетку
9. Елка со вставками
При расчетах учитывайте, что материал необходимо закупать из расчета 1 к 4.
Елка со вставками
10. Орнамент из квадратов
В этом рисунке плитка укладывается блоками в который входит одна квадратная плитка (0,25/м2), 4 прямоугольных (0,5/м2) и 4 маленьких квадратика (0,25/м2).
Орнамент из квадратов
Применение в рисунке укладке нескольких расцветок значительно приукрасит ваш участок. При выборе расцветки и узора тротуарной плитки следует учесть несколько нюансов:
- Чем шире дорожка (больше размер площадки мощения), тем более уместны на ней крупные рисунки;
- “Кислотная” пестрота рисунка тротуарной плитки не способствует гармоничному восприятию ландшафта и архитектуры участка.

- При выборе расцветки и рисунка мощения учитывайте стиль и цвет вашего дома.
Надеемся, что используя представленные рисунки укладки и советы, вы создадите мощение вашего участка, которое гармонично дополнит общий стиль и композицию ландшафтного дизайна.
Выбрать форму, рисунок укладки и расцветку тротуарной плитки всегда помогут наши менеджеры. Звоните по телефону +7 (4872) 70-55-55.
Перейти в каталог тротуарной плитки Stellard
Выбрать цвет тротуарной плитки
Посмотреть реализованные проекты завода Stellard
Полезные статьи по теме:
Услуги Цеха
Услуги ЦехаИндивидуальный подход к каждому клиенту
Средний срок выполнения заказа 10 дней (в зависимости от загруженности цеха)
По Вашему желанию заказ упаковывается в стрейч-пленку или картон
Наши возможности
Сообщаем Вам о том, что мы выполняем услугу «присадка изделий» на новом Сверлильно-присадочном станке с ЧПУ OPTIMAT BHX 055 (Германия).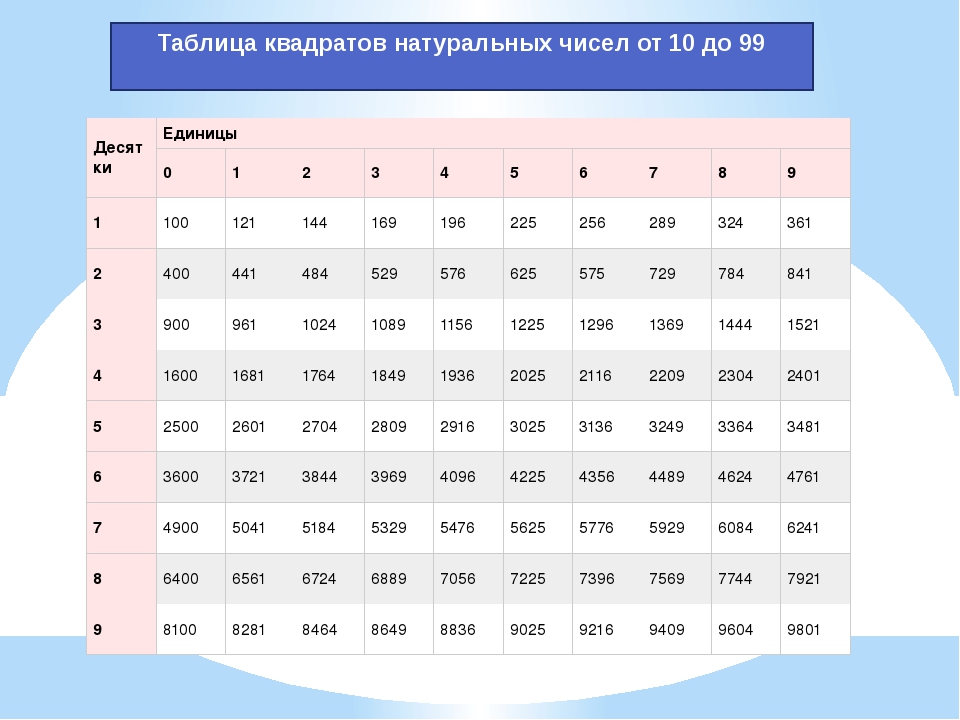 Специалисты нашей компании сделают сверловку отверстий на высокоточном специализированном сверлильном оборудовании, которое позволит без сколов и каких-либо изъянов добиться точного расположения отверстий и в нужном количестве.
Специалисты нашей компании сделают сверловку отверстий на высокоточном специализированном сверлильном оборудовании, которое позволит без сколов и каких-либо изъянов добиться точного расположения отверстий и в нужном количестве.
Мы увеличили производственные площади, закупили современное, высококачественное оборудование и рады предложить Вам услуги распила и кромления в новом качестве!
Качественный распил ЛДСП на станках с ЧПУ (HOLZ-HER, ALTENDORF), с возможностью пакетного распила материала любыми объемами.
Нанесение кромки ПВХ 0,4 и 2мм на станках BRANDT с функцией фрезеровки радиуса на углах заготовки.
Информация
Цех компании Квадрат принимает заявки на распил в виде заполненного «Бланка раскроя» и только в электронном виде.
Файл должен быть отправлен на email [email protected] заранее.
Для производителей мебели и оптовым заказчикам предусмотрены индивидуальные скидки.
Материалы БАЗИС-Мебельщик для скачивания:
СКАЧАТЬ Фурнитура Базис ( 0,5 GB )
СКАЧАТЬ База материалов Базис ( 0,9 MB )
Прайс на услуги цеха розница ( БАЗИС-Мебельщик )скачать
«Квадрат»
Челябинск, ул. Шарова 77
Шарова 77
(351) 734-97-98 (многоканальный)
Пн — Пт: 09.00 — 17.30
Сб: 09.00 — 14.00
Вс: выходной
«Галерея Квадрат»
(выставочный центр)
Челябинск, ул. Свободы 91 корпус 1
+ 7 (919) 314-49-34
Пн — Сб: 10.00 — 19.00
Вс: 10.00 — 16.00
Copyright © «Квадрат» 2021
Решение квадратных уравнений с извлечением квадратного корня
Purplemath
Давайте еще раз посмотрим на последнюю проблему на предыдущей странице:
На предыдущей странице я решил это квадратное уравнение, разложив на множители разность квадратов в левой части уравнения, а затем установив каждый коэффициент равным нулю и т.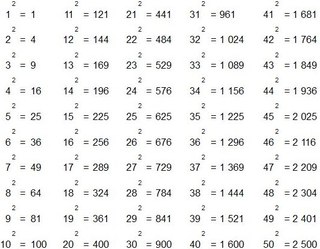 Д. И т. Д.Решение было « x = ± 2». Однако —
Д. И т. Д.Решение было « x = ± 2». Однако —
Я также могу попытаться выделить член в квадрате переменной в левой части уравнения (то есть я могу попытаться получить член x 2 сам по себе на одной стороне знака «равно»), переместив числовую часть (то есть 4) в правую часть, например:
MathHelp.com
Когда я решаю уравнение, я знаю, что могу делать все, что захочу, с этим уравнением , если я проделываю одно и то же с обеими сторонами этого уравнения . В левой части этого конкретного уравнения у меня есть x 2 , и я хочу старый добрый x . Чтобы превратить x 2 в x , я могу извлечь квадратный корень из каждой стороны уравнения, например:
Чтобы превратить x 2 в x , я могу извлечь квадратный корень из каждой стороны уравнения, например:
х = ± 2
Тогда решение будет x = ± 2, точно так же, как это было, когда я решил путем факторизации разности квадратов.
Зачем мне понадобился знак «±» (то есть «плюс-минус») на 2, когда я извлек квадратный корень из 4? Потому что я пытаюсь найти всех значений переменной, которые делают исходное утверждение истинным, и это могло быть либо положительное 2, либо отрицательное 2, возведенное в квадрат, чтобы получить 4 в исходном уравнении.
Эта двойственность похожа на то, как у меня было два фактора, один «плюс» и один «минус», когда я использовал формулу разности квадратов для решения того же уравнения на предыдущей странице.
«Поиск решения уравнения» — это процесс, очень отличающийся от «вычисления квадратного корня из числа».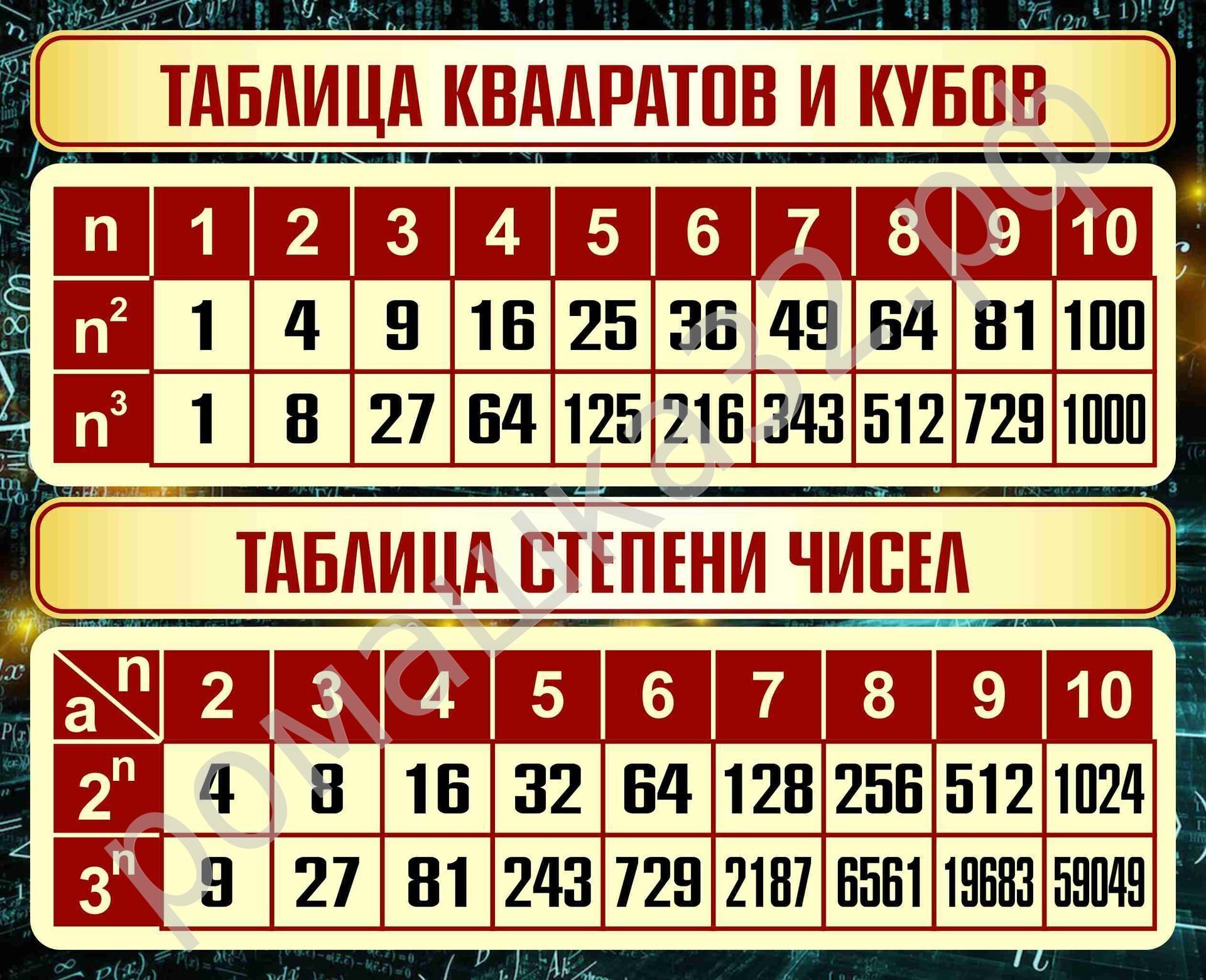 При нахождении «квадратного корня» числа мы имеем дело исключительно с положительным значением. Почему? Потому что именно так определяется квадратный корень из числа.Значение квадратного корня из числа может быть только положительным, потому что так определяется «квадратный корень из числа».
При нахождении «квадратного корня» числа мы имеем дело исключительно с положительным значением. Почему? Потому что именно так определяется квадратный корень из числа.Значение квадратного корня из числа может быть только положительным, потому что так определяется «квадратный корень из числа».
С другой стороны, решение уравнения, то есть нахождение всех возможных значений переменной, которые может работать с в уравнении, отличается от простой оценки выражения, которое уже определило как имеющее только одно значение.
Держите этих двоих прямо! Число с квадратным корнем имеет только одно значение, а уравнение с квадратным корнем имеет два из-за переменной.
В математике мы должны иметь возможность получить один и тот же ответ, независимо от того, какой действительный метод мы использовали, чтобы прийти к этому ответу. Итак, сравнение ответа, полученного мной выше, с ответом, который я получил на предыдущей странице, подтверждает, что мы должны использовать «±» при извлечении квадратного корня для решения.
(Вы можете сомневаться в моей работе выше на этапе, когда я извлекал квадратный корень из любой стороны, потому что я поставил знак «±» только на одной стороне уравнения.Разве я не должен добавить этот символ к обеим сторонам уравнения? Вроде да. Но если бы я поместил это в обе стороны уравнения, изменилось бы что-нибудь на самом деле? Нет. Попробуйте все варианты, если вы не уверены.)
Преимущество этого процесса извлечения квадратного корня состоит в том, что он позволяет нам решать некоторые квадратичные уравнения, которые мы не могли решить раньше, используя только факторинг. Например:
Эта квадратичная часть имеет квадратную и числовую части.Я начну с добавления числового члена к другой стороне уравнения (чтобы квадрат был сам по себе), а затем извлечу квадратный корень из обеих сторон. Мне нужно не забыть упростить квадратный корень:
x 2 -50 = 0
x 2 = 50
Тогда мое решение:
В то время как мы могли бы получить предыдущее целочисленное решение путем факторизации, мы никогда не смогли бы получить это радикальное решение путем факторизации. Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды техники позволяют нам находить решения дополнительных видов уравнений.
Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды техники позволяют нам находить решения дополнительных видов уравнений.
Решить (
x — 5) 2 — 100 = 0.
Эта квадратичная часть имеет квадратную и числовую части. Я начну с добавления строго числового члена в правую часть уравнения, чтобы квадрат биномиального выражения, содержащего переменную, находился в левой части.Затем я извлечу квадратный корень из обеих частей, запомнив «±» в числовой части, а затем упрощу:
( x — 5) 2 — 100 = 0
( x — 5) 2 = 100
x — 5 = ± 10
х = 5 ± 10
x = 5-10 или x = 5 + 10
x = –5 или x = 15
Это уравнение после извлечения квадратного корня из любой стороны не содержало радиальных чисел. Благодаря этому я смог упростить свои результаты вплоть до простых значений. Мой ответ:
Благодаря этому я смог упростить свои результаты вплоть до простых значений. Мой ответ:
Предыдущее уравнение является примером уравнения, в котором неосторожный ученик опускает знак «±» при решении и не понимает, как книга получила ответ « x = –5, 15».
У этих учеников есть дурная привычка не утруждать себя записью знака «±», пока они не проверит свои ответы на обратной стороне книги и внезапно «не вспомнят», что они «имели в виду» поставить там знак «±», когда они ‘ d извлекает квадратный корень из любой стороны уравнения.
Но эта «магия» работает только тогда, когда у вас есть ответ (чтобы напомнить вам) и когда раствор содержит радикалы (что не всегда происходит). В остальных случаях «напоминания» не будет. Ошибка в пропуске «±» может быть смертельной, особенно при тестировании. Не будь этим учеником. Всегда не забывайте вставлять «±».
Между прочим, поскольку решение предыдущего уравнения состояло из целых чисел, эту квадратичную можно также решить путем умножения квадрата, разложения на множители и т. Д .:
( x — 5) 2 — 100 = 0
x 2 -10 x + 25-100 = 0
x 2 — 10 x — 75 = 0
( x -15) ( x + 5) = 0
x — 15 = 0, x + 5 = 0
x = 15, –5
Решить (
x — 2) 2 — 12 = 0
Эта квадратичная часть имеет квадратную и числовую части.Я добавлю числовую часть с другой стороны, так что квадратная часть с переменной будет сама по себе. Затем я извлекаю квадратный корень из обеих сторон, не забывая добавлять «±» к числовой стороне, а затем упрощаю:
Затем я извлекаю квадратный корень из обеих сторон, не забывая добавлять «±» к числовой стороне, а затем упрощаю:
( x — 2) 2 — 12 = 0
( x — 2) 2 = 12
Я не могу больше это упрощать. В моем ответе будут радикалы.Мое решение:
Это квадратное уравнение, в отличие от предыдущего, также не могло быть решено с помощью факторизации. Но как бы я решил это, если бы у них было , а не , давая мне квадратичную, уже переведенную в форму «(часть в квадрате) минус (часть числа)»? Эта проблема приводит к следующей теме: решение путем завершения квадрата.
URL: https: // www.purplemath.com/modules/solvquad2.htm
Извлечение квадратного корня
Извлечение квадратного корня
Напомним, что квадратное уравнение имеет стандартную форму Любое квадратное уравнение в форме ax2 + bx + c = 0, где a , b и c — действительные числа и a 0. если он равен 0:
если он равен 0:
, где a , b и c — действительные числа и a 0.Решение такого уравнения называется корневым решением квадратного уравнения в стандартной форме. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Если квадратное выражение слева множители, то мы можем решить его путем факторизации. Обзор шагов, используемых для решения с помощью факторинга, следующий:
Шаг 1: Выразите квадратное уравнение в стандартной форме.
Шаг 2: Разложите квадратное выражение на множители.
Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным 0.
Шаг 4: Решите полученные линейные уравнения.
Например, мы можем решить x2−4 = 0, разложив на множители следующим образом:
Двумя решениями являются −2 и 2.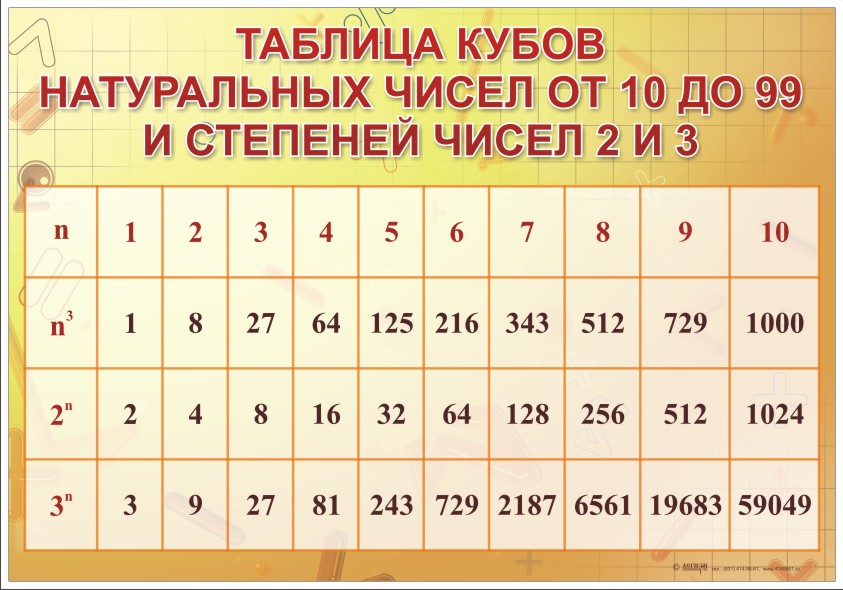 Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, давая форму
Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, давая форму
Уравнение x2−4 = 0 находится в этой форме и может быть решено путем выделения x2 вначале.
Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее:
Здесь мы видим, что x = −2 и x = 2 являются решениями полученного уравнения. В общем, это описывает свойство квадратного корня для любого действительного числа k , если x2 = k, то x = ± k .; для любого действительного числа k ,
Обозначение «±» читается как «плюс или минус» и используется как компактное обозначение, обозначающее два решения.Следовательно, утверждение x = ± k указывает, что x = −k или x = k. Применение свойства квадратного корня как средства решения квадратного уравнения называется извлечением корней Применение свойства квадратного корня как средства решения квадратного уравнения.
Пример 1: Решить: x2−25 = 0.
Решение: Начните с выделения квадрата.
Затем примените свойство квадратного корня.
Ответ: Решения — 5 и 5.Чек предоставляется читателю.
Конечно, предыдущий пример можно было бы так же легко решить с помощью факторинга. Тем не менее, он демонстрирует метод, который можно использовать для решения уравнений в этой форме, которые не учитывают факторы.
Пример 2: Решить: x2−5 = 0.
Решение: Обратите внимание, что квадратное выражение слева не множится. Мы можем извлечь корни, если сначала выделим главный член x2.
Примените свойство квадратного корня.
Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение. Как правило, проверка не является обязательной.
Как правило, проверка не является обязательной.
Ответ: Решения — 5 и 5.
Пример 3: Решить: 4×2-45 = 0.
Решение: Начните с изоляции x2.
Примените свойство квадратного корня, а затем упростите.
Ответ: Решения — 352 и 352.
Иногда квадратные уравнения не имеют реального решения.
Пример 4: Решить: x2 + 9 = 0.
Решение: Начните с изоляции x2.
После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения.
Ответ: Реального решения нет
Обратитесь к этому процессу, чтобы найти уравнения с заданными решениями вида ± k .
Пример 5: Найдите уравнение с решениями −23 и 23.
Решение: Начните с возведения в квадрат обеих частей следующего уравнения:
Наконец, вычтите 12 из обеих частей и представьте уравнение в стандартной форме.
Ответ: x2−12 = 0
Попробуй! Решить: 9×2−8 = 0.
Ответ: x = −223 или x = 223
Рассмотрите возможность решения следующего уравнения:
Чтобы решить это уравнение путем факторизации, сначала возведите в квадрат x + 2, а затем представьте его в стандартной форме, равной нулю, вычитая 25 из обеих частей.
Фактор, а затем примените свойство нулевого произведения.
Два решения: −7 и 3.
Когда уравнение имеет такую форму, мы можем получить решения за меньшее количество шагов, извлекая корни.
Пример 6: Решите: (x + 2) 2 = 25.
Решение: Решите, извлекая корни.
На этом этапе разделите «плюс или минус» на два уравнения и упростите каждое по отдельности.
Ответ: Решения −7 и 3.
В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, которые не учитывают множители.
Пример 7: Решите: (3x + 3) 2−27 = 0.
Решение: Начните с выделения квадрата.
Затем извлеките корни и упростите.
Решите относительно x .
Ответ: Решения: −1−3 и −1 + 3.
Пример 8: Решить: 9 (2x − 1) 2−8 = 0.
Решение: Начните с выделения квадратного множителя.
Примените свойство квадратного корня и решите.
Ответ: Решения 3−226 и 3 + 226.
Попробуй! Решите: 3 (x − 5) 2−2 = 0.
Ответ: 15 ± 63
Пример 9: Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
Решение:
Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы:
Решить.
Здесь мы получаем два решения, w = −25 и w = 25. Поскольку в задаче требовалась длина прямоугольника, мы игнорируем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.
Обратно подставить, чтобы найти длину.
Ответ: Длина прямоугольника составляет 455 футов, а ширина — 255 футов.
Основные выводы
- Решите уравнения вида ax2 + c = 0, извлекая корни.
- Извлечение корней включает выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все радикальные выражения и при необходимости рационализируйте знаменатель.
Тематические упражнения
Часть A: извлечение квадратного корня
Решите, разложив на множители, а затем вычислив корни.Проверить ответы.
1. x2−36 = 0
2. x2−81 = 0
3. 4y2−9 = 0
4. 9y2−25 = 0
9y2−25 = 0
5. (x − 2) 2−1 = 0
6. (x + 1) 2−4 = 0
7. 4 (y − 2) 2−9 = 0
8. 9 (y + 1) 2−4 = 0
9. −3 (t − 1) 2 + 12 = 0
10. −2 (t + 1) 2 + 8 = 0
11. (x − 5) 2−25 = 0
12. (x + 2) 2−4 = 0
Решите, извлекая корни.
13. x2 = 16
14. x2 = 1
15. y2 = 9
16. y2 = 64
17. x2 = 14
18. x2 = 19
19. y2 = 0,25
20. y2 = 0,04
21. x2 = 12
22. x2 = 18
23. 16×2 = 9
24. 4×2 = 25
25. 2t2 = 1
26.3t2 = 2
27. x2−100 = 0
28. x2−121 = 0
29. y2 + 4 = 0
30. y2 + 1 = 0
y2 + 1 = 0
31. x2−49 = 0
32. x2−925 = 0
33. y2−0.09 = 0
34. y2−0,81 = 0
35. x2−7 = 0
36. x2−2 = 0
37. x2−8 = 0
38. t2−18 = 0
39. х2 + 8 = 0
40.х2 + 125 = 0
41. 16×2−27 = 0
42. 9×2-8 = 0
43. 2y2−3 = 0
44. 5y2−2 = 0
45. 3×2−1 = 0
46. 6×2−3 = 0
47. (x + 7) 2−4 = 0
48. (x + 9) 2−36 = 0
49. (2y − 3) 2-81 = 0
50. (2у + 1) 2−25 = 0
51. (x − 5) 2−20 = 0
52. (x + 1) 2−28 = 0
53.(3t + 2) 2−6 = 0
54. (3т − 5) 2−10 = 0
55,4 (у + 2) 2−3 = 0
56. 9 (y − 7) 2−5 = 0
9 (y − 7) 2−5 = 0
57,4 (3x + 1) 2−27 = 0
58. 9 (2x − 3) 2−8 = 0
59. 2 (3x − 1) 2 + 3 = 0
60,5 (2x − 1) 2−3 = 0
61,3 (y − 23) 2−32 = 0
62. 2 (3y − 13) 2−52 = 0
Найдите квадратное уравнение стандартной формы со следующими решениями.
63. ± 7
64. ± 13
65. ± 7
66. ± 3
67. ± 35
68. ± 52
69. 1 ± 2
70,2 ± 3
Решите и округлите решения до сотых.
71. 9x (x + 2) = 18x + 1
72. x2 = 10 (x2−2) −5
73. (x + 3) (x − 7) = 11−4x
74.(x − 4) (x − 3) = 66−7x
75. (x − 2) 2 = 67−4x
76. (x + 3) 2 = 6x + 59
77. (2x + 1) (x + 3) — (x + 7) = (x + 3) 2
(2x + 1) (x + 3) — (x + 7) = (x + 3) 2
78. (3x − 1) (x + 4) = 2x (x + 6) — (x − 3)
Составьте алгебраическое уравнение и используйте его для решения следующих задач.
79. Если 9 вычесть из четырех квадратов числа, то результат будет 3. Найдите число.
80. Если из квадрата числа вычесть 20, то получится 4.Найдите номер.
81. Если 1 прибавить к троекратному квадрату числа, то получится 2. Найдите число.
82. Если 3 прибавить к двукратному квадрату числа, то получится 12. Найдите число.
83. Если квадрат имеет площадь 8 квадратных сантиметров, найдите длину каждой стороны.
84. Если круг имеет площадь 32π квадратных сантиметра, найдите длину радиуса.
85.Объем правого кругового конуса составляет 36π кубических сантиметров при высоте 6 сантиметров. Найдите радиус конуса. (Объем правого кругового конуса равен V = 13πr2h. )
)
86. Площадь поверхности сферы составляет 75π квадратных сантиметров. Найдите радиус сферы. (Площадь поверхности сферы определяется как SA = 4πr2.)
87. Длина прямоугольника в 6 раз больше его ширины. Если площадь составляет 96 квадратных дюймов, найдите размеры прямоугольника.
88. Основание треугольника вдвое больше его высоты. Если площадь составляет 16 квадратных сантиметров, то найдите длину его основания.
89. Квадрат имеет площадь 36 квадратных единиц. На какую равную величину необходимо увеличить стороны, чтобы получить квадрат с удвоенной заданной площадью?
90. Круг имеет площадь 25π квадратных единиц. На какую величину нужно увеличить радиус, чтобы создать круг с удвоенной заданной площадью?
91.Если стороны квадрата равны 1 единице, то найдите длину диагонали.
92. Если стороны квадрата равны 2 единицам, найдите длину диагонали.
93. Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны.
Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны.
94. Диагональ квадрата составляет 3 дюйма. Найдите длину каждой стороны.
95. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 10 футов, найдите размеры прямоугольника.
96. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 8 футов, найдите размеры прямоугольника.
97. Длина прямоугольника в 3 раза больше его ширины. Если диагональ 5 метров, то найдите размеры прямоугольника.
98. Длина прямоугольника в 3 раза больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
99. Высота в футах объекта, падающего с 9-футовой лестницы, определяется выражением h (t) = — 16t2 + 9, где t представляет время в секундах после падения объекта.Сколько времени нужно, чтобы объект упал на землю? (Подсказка: когда объект ударяется о землю, высота равна 0.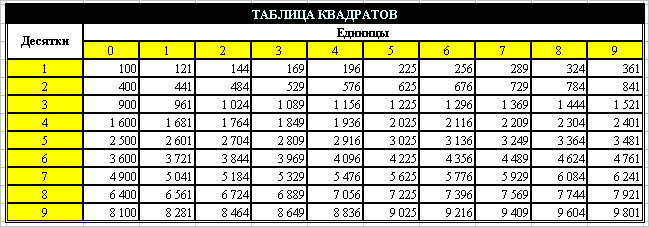 )
)
100. Высота в футах объекта, сброшенного с 20-футовой платформы, определяется выражением h (t) = — 16t2 + 20, где t представляет время в секундах после того, как объект был сброшен. Сколько времени нужно, чтобы объект упал на землю?
101. Высота в футах объекта, падающего с вершины 144-футового здания, определяется выражением h (t) = — 16t2 + 144, где t измеряется в секундах.
а. Сколько времени потребуется, чтобы достичь половины расстояния до земли, 72 фута?
г. Сколько времени потребуется, чтобы добраться до земли?
Округлите до сотых долей секунды.
102. Высота объекта в футах, сброшенного с самолета на высоте 1600 футов, определяется выражением h (t) = — 16t2 + 1,600, где t — в секундах.
а. Сколько времени потребуется, чтобы добраться до земли на половину расстояния?
г.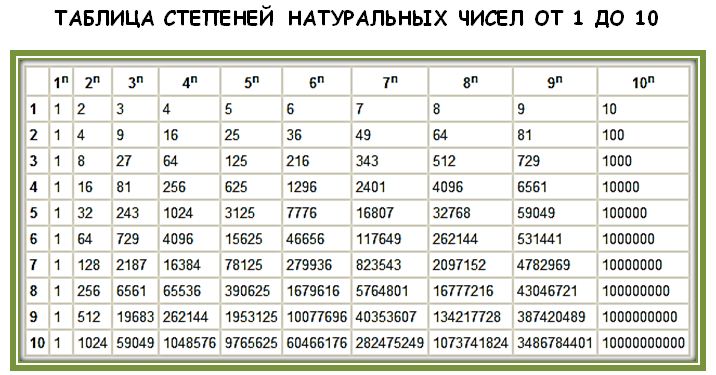 Сколько времени потребуется, чтобы добраться до земли?
Сколько времени потребуется, чтобы добраться до земли?
Округлить до сотых долей секунды .
Часть B: Обсуждение
103. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им вместе с решением на доске обсуждений.
104. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.
105. Объясните своими словами, как решить, извлекая корни.
106. Выведите формулу диагонали квадрата через его стороны.
ответов
1: −6, 6
3: −3/2, 3/2
5: 1, 3
7: 1/2, 7/2
9: -1, 3
11: 0, 10
13: ± 4
15: ± 3
17: ± 1/2
19: ± 0.5
21: ± 23
23: ± 3/4
25: ± 22
27: ± 10
29: Реального решения нет
31: ± 2/3
33: ± 0,3
35: ± 7
37: ± 22
39: Реального решения нет
41: ± 334
43: ± 62
45: ± 33
47: −9, −5
49: −3, 6
51: 5 ± 25
53: -2 ± 63
55: −4 ± 32
57: -2 ± 336
59: Реального решения нет
61: 4 ± 326
63: x2−49 = 0
65: x2−7 = 0
67: x2-45 = 0
69: x2−2x − 1 = 0
71: ± 0. 33
33
73: ± 5,66
75: ± 7,94
77: ± 3.61
79: −3 или 3
81: −33 или 33
83:22 сантиметра
85:32 сантиметра
87: Длина: 24 дюйма; ширина: 4 дюйма
89: −6 + 62≈2,49 ед.
91: 2 шт.
93: 522 дюйма
95: Длина: 45 футов; ширина: 25 футов
97: Длина: 3102 метра; ширина: 102 метра
99: 3/4 секунды
101: а.2,12 секунды; б. 0,88 секунды
Калькулятор квадратного корня. Найдите квадратный корень за один простой шаг
Как упростить квадратные корни?
Во-первых, давайте спросим себя, какие квадратные корни можно упростить. Чтобы ответить на него, вам нужно взять число, стоящее после символа квадратного корня, и найти его множители. Если какой-либо из его множителей является квадратным числом (4, 9, 16, 25, 36, 49, 64 и т. Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее.Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:
Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее.Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:
- Можете ли вы упростить √27? С помощью упомянутого выше калькулятора вы получаете множители 27: 1, 3, 9, 27. Здесь 9! Это означает, что вы можете упростить √27.
- Можете ли вы упростить √15? Факторы 15: 1, 3, 5, 15. В этих числах нет полных квадратов, поэтому этот квадратный корень нельзя упростить.(1/2) ⟺ √ (x * y) = √x * √y ,
Как вы можете использовать эти знания? Аргумент квадратного корня обычно не является точным квадратом, который можно легко вычислить, но он может содержать полный квадрат среди своих множителей.
 Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например,
Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например, 45 = 9 * 5(9 — это полный квадрат). Требование наличия по крайней мере одного множителя , который представляет собой полный квадрат, необходимо для упрощения квадратного корня.(1/2) = √9 * √5 = 3√5 .Вы успешно упростили свой первый квадратный корень! Конечно, вам не нужно записывать все эти расчеты. Если вы помните, что квадратный корень эквивалентен степени половины , вы можете сократить их. Попрактикуемся в упрощении квадратных корней на некоторых других примерах:
- Как упростить квадратный корень из 27?
√27 = √ (9 * 3) = √9 * √3 = 3√3; - Как упростить квадратный корень из 8?
√8 = √ (4 * 2) = √4 * √2 = 2√2; - Как упростить квадратный корень из 144?
√144 = √ (4 * 36) = √4 * √36 = 2 * 6 = 12.
В последнем примере вам вообще не нужно было упрощать квадратный корень, потому что 144 — это полный квадрат.
 Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .
Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .Наконец, вы можете спросить, как упростить корни более высокого порядка, например, кубические корни. Фактически, этот процесс очень похож на квадратные корни, но в случае кубических корней вы должны найти хотя бы один множитель, который представляет собой идеальный куб , а не квадрат, т.е.е., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ и так далее. Затем вы делите свое число на две части и кладете под кубический корень. Возьмем следующий пример упрощения ³√192:
∛192 = ∛ (64 * 3) = ∛64 * ∛3 = 4∛3На первый взгляд это может показаться немного сложным, но после некоторой практики вы сможете упростить корни в своей голове . Верь нам!
Завершение квадрата
Вот шаги, необходимые для решения квадратичной функции путем завершения квадрата, когда ведущий коэффициент (первое число) равен , а не a 1:
Шаг 1: Запишите квадратичный в правильной форме, поскольку ведущий коэффициент не равен 1, вы должны вычесть 2 из первых двух членов. 
Шаг 2: Заполните первый пробел, взяв коэффициент (число) из x-члена (средний член), разрезав его пополам и возведя в квадрат. Заполните второй пробел, умножив число за скобками и число в первом пробеле, в данном случае (2) (9) равно 18.
В данном случае:Шаг 3: Разложите часть в скобках на множители и объедините одинаковые термины для чисел вне скобок. Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена). В этом случае половина от –6 равна –3. Шаг 4: Теперь вы закончили заполнение квадрата, и пора решать задачу. Сначала прибавьте 11 с обеих сторон. Шаг 5: Разделите каждую сторону на 2. Шаг 6: Используйте свойство квадратного корня и извлеките квадратный корень из каждой стороны, не забывая плюс или минус. 
Шаг 7: Поскольку в знаменателе есть квадратный корень, вы должны рационализировать знаменатель.
В данном случае:Шаг 8: Добавьте по 3 с каждой стороны. Шаг 9: Проверьте, можете ли вы упростить квадратный корень, в данном случае мы не можем. Итак, окончательный ответ такой же. Шаг 1: Запишите квадратичный коэффициент в правильной форме, поскольку старший коэффициент не равен 1, вы должны вынести 2 из первых двух членов. Шаг 2: Заполните первый пробел, взяв коэффициент (число) из x-члена (средний член), разрезав его пополам и возведя в квадрат. Заполните второй пробел, умножив число за скобками и число в первом пробеле, в данном случае (3) (1) равно 3.
В данном случае:Шаг 3: Разложите часть в скобках на множители и объедините одинаковые термины для чисел вне скобок.  Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена). В этом случае половина +2 равна +1.
Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена). В этом случае половина +2 равна +1.Шаг 4: Теперь вы закончили заполнение квадрата, и пора решать задачу.Сначала прибавьте 8 с обеих сторон. Шаг 5: Разделите каждую сторону на 3. Шаг 6: Используйте свойство квадратного корня и извлеките квадратный корень из каждой стороны, не забывая плюс или минус. Шаг 7: Поскольку в знаменателе есть квадратный корень, вы должны рационализировать знаменатель.
В данном случае:Шаг 8: Вычтите по 1 с каждой стороны. Шаг 9: Проверьте, можете ли вы упростить квадратный корень, в данном случае мы можем.  Итак, окончательный ответ:
Итак, окончательный ответ:Шаг 1: Запишите квадратичный коэффициент в правильной форме, так как ведущий коэффициент не равен 1, вы должны вычесть –2 из первых двух членов. Шаг 2: Заполните первый пробел, взяв коэффициент (число) из x-члена (средний член), разрезав его пополам и возведя в квадрат.Заполните второй пробел, умножив число за скобками и число в первом пробеле, в данном случае (–2) (16) равно –32.
В данном случае:Шаг 3: Разложите часть в скобках на множители и объедините одинаковые термины для чисел вне скобок. Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена).В этом случае половина от –8 равна –4. Шаг 4: Теперь вы закончили заполнение квадрата, и пора решать задачу.  Сначала вычтите 33 с каждой стороны.
Сначала вычтите 33 с каждой стороны.Шаг 5: Разделите каждую сторону на –2. Шаг 6: Используйте свойство квадратного корня и извлеките квадратный корень из каждой стороны, не забывая плюс или минус. Шаг 7: Поскольку в знаменателе есть квадратный корень, вы должны рационализировать знаменатель.
В данном случае:Шаг 8: Добавьте по 4 с каждой стороны. Шаг 9: Проверьте, можете ли вы упростить квадратный корень, в данном случае мы не можем. Итак, окончательный ответ такой же. Функция квадратного корня Python — настоящий Python
Вы пытаетесь решить квадратное уравнение? Возможно, вам нужно рассчитать длину одной стороны прямоугольного треугольника.
 Для этих и других типов уравнений функция квадратного корня Python
Для этих и других типов уравнений функция квадратного корня Python sqrt ()может помочь вам быстро и точно вычислить решения.К концу этой статьи вы узнаете:
- Что такое квадратный корень
- Как использовать функцию квадратного корня Python,
sqrt () - Когда
sqrt ()может быть полезным в реальном мире
Давайте нырнем!
Python Pit Stop: Этот учебник представляет собой быстрый и практический способ найти нужную информацию, так что вы вернетесь к своему проекту в кратчайшие сроки!
Квадратные корни в математике
В алгебре квадрат , x , является результатом умножения числа n на само себя: x = n²
Вы можете вычислить квадраты с помощью Python:
>>>>>> п = 5 >>> х = п ** 2 >>> х 25Оператор Python
**используется для вычисления степени числа. В этом случае 5 в квадрате или 5 в степени 2 равно 25.
В этом случае 5 в квадрате или 5 в степени 2 равно 25.Таким образом, квадратный корень — это число n , которое при умножении само на себя дает квадрат x .
В этом примере n , квадратный корень, равен 5.
25 — это пример полного квадрата . Совершенные квадраты — это квадраты целых чисел:
>>>>>> 1 ** 2 1 >>> 2 ** 2 4 >>> 3 ** 2 9Возможно, вы запомнили некоторые из этих совершенных квадратов, когда выучили свои таблицы умножения на уроках элементарной алгебры.
Если вам дан маленький точный квадрат, может быть достаточно просто вычислить или запомнить его квадратный корень. Но для большинства других квадратов это вычисление может быть немного более утомительным. Часто оценки бывает достаточно, когда у вас нет калькулятора.
К счастью, у вас, как у разработчика Python, есть калькулятор, а именно интерпретатор Python!
Функция квадратного корня Python
МодульPython
mathв стандартной библиотеке может помочь вам работать с математическими проблемами в коде. Он содержит множество полезных функций, таких как
Он содержит множество полезных функций, таких как restder ()иfactorial (). Он также включает функцию извлечения квадратного корня Python,sqrt ().Вы начнете с импорта
math:Вот и все, что нужно! Теперь вы можете использовать
math.sqrt ()для вычисления квадратных корней.sqrt ()имеет простой интерфейс.Требуется один параметр,
x, который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень.В предыдущем примере это будет25.Возвращаемое значение
sqrt ()— это квадратный корень изxв виде числа с плавающей запятой. В примере это будет5,0.Давайте рассмотрим несколько примеров того, как (и как не использовать) использовать
sqrt ().Квадратный корень положительного числа
Один из типов аргументов, который вы можете передать функции
sqrt (), — это положительное число. Сюда входят типы
Сюда входят типы intиfloat.Например, вы можете найти квадратный корень из
49, используяsqrt ():Возвращаемое значение —
7,0(квадратный корень из49) в виде числа с плавающей запятой.Наряду с целыми числами вы также можете передать
>>>значений с плавающей запятой:>>> math.sqrt (70.5) 8,396427811873332Вы можете проверить точность этого квадратного корня, вычислив его обратную величину:
>>>>>> 8.396427811873332 ** 2 70,5Квадратный корень нуля
Даже
0— правильный квадрат для передачи функции квадратного корня Python:Хотя вам, вероятно, не нужно часто вычислять квадратный корень из нуля, вы можете передать переменную в
sqrt (), значение которой вы на самом деле не знаете. Итак, хорошо знать, что в таких случаях он может обрабатывать ноль.
Квадратный корень отрицательных чисел
Квадрат любого действительного числа не может быть отрицательным.Это связано с тем, что отрицательный результат возможен только в том случае, если один фактор положительный, а другой отрицательный. Квадрат по определению является произведением числа и самого себя, поэтому получить отрицательный действительный квадрат невозможно:
>>>>>> math.sqrt (-25) Отслеживание (последний вызов последний): Файл "", строка 1, в ValueError: ошибка математического домена Если вы попытаетесь передать отрицательное число в
sqrt (), вы получитеValueError, потому что отрицательные числа не входят в область возможных действительных квадратов.Вместо этого квадратный корень отрицательного числа должен быть сложным, что выходит за рамки функции квадратного корня Python.Квадратные корни в реальном мире
Чтобы увидеть практическое применение функции квадратного корня Python, давайте обратимся к теннису.

Представьте, что Рафаэль Надаль, один из самых быстрых игроков в мире, только что ударил справа из заднего угла, где базовая линия пересекается с боковой линией теннисного корта:
Теперь предположим, что его противник нанес контратакующий удар (тот, который закроет мяч с небольшим ускорением вперед) в противоположный угол, где другая боковая линия встречается с сеткой:
Как далеко Надаль должен бежать, чтобы дотянуться до мяча?
Из нормативных размеров теннисного корта можно определить, что длина базовой линии составляет 27 футов, а длина боковой линии (на одной стороне сетки) — 39 футов.Итак, по сути, это сводится к решению гипотенузы прямоугольного треугольника:
Используя ценное геометрическое уравнение, теорему Пифагора, мы знаем, что a² + b² = c² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза.
Таким образом, мы можем рассчитать расстояние, которое Надаль должен пробежать, переписав уравнение, чтобы найти c :
Вы можете решить это уравнение, используя функцию квадратного корня Python:
>>>>>> a = 27 >>> b = 39 >>> математика. sqrt (а ** 2 + b ** 2)
47.434164569
sqrt (а ** 2 + b ** 2)
47.434164569
Итак, Надаль должен пробежать около 47,4 фута (14,5 метра), чтобы дотянуться до мяча и сохранить точку.
Заключение
Поздравляем! Теперь вы знаете все о функции квадратного корня Python.
Вы покрыли:
- Краткое введение в квадратные корни
- Особенности функции квадратного корня Python,
sqrt () - Практическое применение
sqrt ()на реальном примере
Умение использовать
sqrt ()— это только половина дела.Другое дело — понять, когда его использовать. Теперь вы знаете и то, и другое, так что примените свое новое мастерство в использовании функции извлечения квадратного корня в Python!предварительных вычислений по алгебре — Почему нельзя возвести в квадрат обе части уравнения?
Основная проблема заключается в том, что когда начинающие студенты (и даже некоторые не новички) манипулируют уравнениями, у них создается ложное впечатление, что все , подразумеваемые их исходным выражением, также будут подразумевать их исходного выражения.
 2 = 1 $$
2 = 1 $$Решениями этого являются $ 1 $ и $ -1 $ (верно) и , следовательно, (неверный вывод) решения исходного уравнения — $ 1 $ и $ -1 $ (ложное заключение).2 = 1 \ подразумевает (x = 1) \ vee (x = -1)
долларов США.Итак, мы знаем, что ничего, кроме $ 1 $ и $ -1 $, не могут быть решениями, но мы все еще не знаем, какое (если оно есть) на самом деле является решением.
Это полностью аналогично рассуждению:
$$ x <1 $$
, следовательно, поскольку $ 1 <3 $ и $ <$ транзитивно:
$$ x <3 $$
Итак, $ 2 <3 $ , следовательно, (неверный вычет) $ 2 $ является решением исходного неравенства (ложный вывод). И это действительно ошибка, которую люди иногда допускают, решая проблемы неравенства.2 = -1 $, потому что это ложь. Односторонние последствия не обязательно приводят к решениям.
Проблема возникает из-за того, что вас учат различным механизмам манипулирования (не) равенствами, но при этом теряется понимание того, что на самом деле означают эти манипуляции с точки зрения правильных выводов о задействованных ценностях.
 Если операция, примененная к обеим сторонам, является инъекцией, то, конечно, она обратима, и поэтому у нас есть двусторонняя импликация, и в этом случае вывод будет действительным.
Если операция, примененная к обеим сторонам, является инъекцией, то, конечно, она обратима, и поэтому у нас есть двусторонняя импликация, и в этом случае вывод будет действительным.Вкратце: вы, , можете, конечно, возвести в квадрат с обеих сторон.Это говорит вам истинный факт о $ x $, но не все, что верно для $ x $ в уравнении в квадрате, равно , обязательно истинно для $ x $ в оригинале. В этом случае $ x = 1 \ Rightarrow x \ in \ {1, -1 \} $, но $ x \ in \ {1, -1 \} \ not \ Rightarrow x = 1 $
Решение, какой метод использовать при решении квадратных уравнений
Решение, какой метод использовать при решении квадратных уравнений Решение, какой метод использовать при решении квадратных уравненийПри решении квадратного уравнения выполните следующие действия. (в таком порядке) выбрать метод:
- Сначала попробуйте решить уравнение на множители.Быть уверенным
что ваше уравнение в стандартной форме (ax 2 + bx + c = 0) перед вами
начать попытку факторинга.
 Не тратьте много времени на попытки
факторное уравнение; если вы не можете учесть его менее чем за 60 секунд,
перейти к другому методу.
Не тратьте много времени на попытки
факторное уравнение; если вы не можете учесть его менее чем за 60 секунд,
перейти к другому методу. - Затем посмотрите на сторону уравнения, содержащую переменную. Эта сторона — идеальный квадрат? Если это так, то вы можете решить уравнение извлекая квадратный корень из обеих частей уравнения.Не забывай чтобы включить знак ± в уравнение как только вы извлечете квадратный корень.
- Далее, если коэффициент при квадрате члена равен 1 и коэффициент линейного (среднего) члена четный, завершая квадрат это хороший метод для использования.
- Наконец, квадратичная формула будет работать на любом квадратичном уравнение. Однако, если использование формулы приводит к слишком большим числа под знаком радикала, другой метод решения может быть лучше выбор.
Пример 1: Решить x 2 + 4 = 4x
Во-первых, представьте уравнение в стандартной форме, чтобы мы могли попробуйте решить это факторингом:
x 2 — 4x + 4 = 0
(х — 2) (х — 2) = 0
x — 2 = 0 | х — 2 = 0
x = 2 | х = 2
Итак, решение этого уравнения, найденное путем факторизации, это x = 2.

Пример 2: Решить (2x — 2) 2 = -4
Сторона уравнения, содержащая переменную ( левая сторона) представляет собой идеальный квадрат, поэтому мы извлечем квадратный корень из обеих сторон для решения уравнения.
(2х — 2) 2 = -4
2x — 2 = ± 2i
2x = 2 ± 2i
х = 1 ± я
Обратите внимание, что знак ± был вставлен в уравнение в точке извлечения квадратного корня.
Пример 3: Решить x 2 + 6x — 11 = 0
Это уравнение не факторизуемо, и сторона, содержащая переменная не является точным квадратом. Но поскольку коэффициент x 2 равен 1, а коэффициент при x четный, завершая квадрат будет подходящим методом. Чтобы найти номер, который нужно быть добавленным к обеим частям уравнения, чтобы получить квадрат, возьмите коэффициент при x, разделите его на 2, а затем возведите это число в квадрат.В в этой задаче 6 ¸ 2 равно 3, а 3 2 равно 9, поэтому мы добавим 9 к обеим частям уравнения, как только мы изолировали переменные условия.

х 2 + 6х — 11 = 0
x 2 + 6x = 11
x 2 + 6x +9 = 11 + 9
(х + 3) 2 = 20
Пример 4: Решить 2x 2 — x + 5 = 0
Это уравнение не факторизуемо, левая часть не учитывается. полный квадрат, а коэффициенты при x 2 и x членах не сделает завершение квадрата удобным.Остается квадратичный формула как лучший метод решения этого уравнения. Мы будем использовать a = 2, b = -1, и c = 5.
.
- Как упростить квадратный корень из 27?



 Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
 Углы с шагом в 1°. Таблица значений котангенса, ctg
Углы с шагом в 1°. Таблица значений котангенса, ctg

 Также приводятся данные допустимых отклонений теоретического веса квадратного проката – относительно фактически измеренного веса.
Также приводятся данные допустимых отклонений теоретического веса квадратного проката – относительно фактически измеренного веса.
 Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например,
Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например,  Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .
Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .

 Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена). В этом случае половина +2 равна +1.
Примечание: Часть в скобках всегда будет делиться на половину коэффициента (числа) из x-члена (среднего члена). В этом случае половина +2 равна +1. Итак, окончательный ответ:
Итак, окончательный ответ: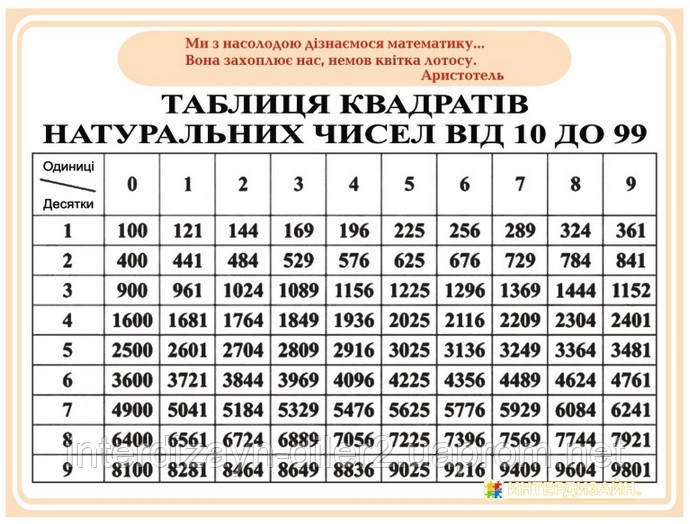 Сначала вычтите 33 с каждой стороны.
Сначала вычтите 33 с каждой стороны. Для этих и других типов уравнений функция квадратного корня Python
Для этих и других типов уравнений функция квадратного корня Python 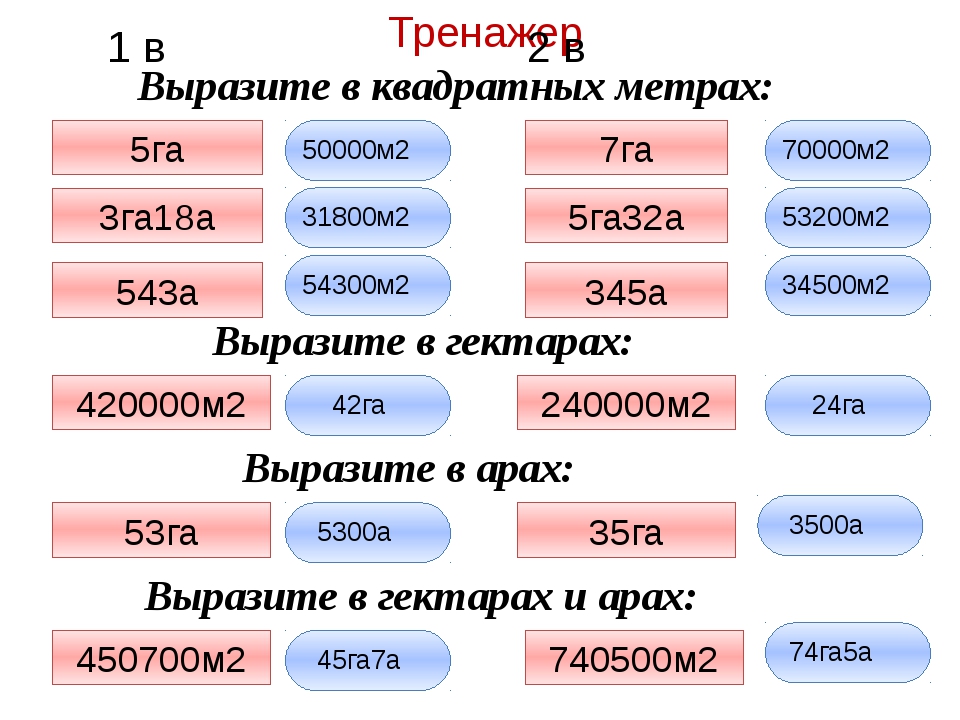 В этом случае 5 в квадрате или 5 в степени 2 равно 25.
В этом случае 5 в квадрате или 5 в степени 2 равно 25. Он содержит множество полезных функций, таких как
Он содержит множество полезных функций, таких как  Сюда входят типы
Сюда входят типы 
 sqrt (а ** 2 + b ** 2)
47.434164569
sqrt (а ** 2 + b ** 2)
47.434164569
 2 = 1 $$
2 = 1 $$ Если операция, примененная к обеим сторонам, является инъекцией, то, конечно, она обратима, и поэтому у нас есть двусторонняя импликация, и в этом случае вывод будет действительным.
Если операция, примененная к обеим сторонам, является инъекцией, то, конечно, она обратима, и поэтому у нас есть двусторонняя импликация, и в этом случае вывод будет действительным. Не тратьте много времени на попытки
факторное уравнение; если вы не можете учесть его менее чем за 60 секунд,
перейти к другому методу.
Не тратьте много времени на попытки
факторное уравнение; если вы не можете учесть его менее чем за 60 секунд,
перейти к другому методу.