Опубликовано Обыкновенные дроби и действия с ними — что это, определение и ответ
Доля – это часть от целого.
Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).
Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)
Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.
Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:
Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).
Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.
Например:
\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)
\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)
\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:
Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.
\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Например:
\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)
\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)
Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.
Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:
\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)
Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.
Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.
АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:
Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.
Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.
Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.
Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.
Например:
\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)
УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:
Обратные числа:
Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:
\(\frac{a}{1} = a : 1 = a\)
Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).
Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.
Умножение дробей:
Представим умножение дроби на число как сумму дробей:
\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)
Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:
\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)
Деление дробей:
Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе.
Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:
\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)
Таким же образом делят дроби на дроби:
\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)
3-8Сколько 1/9 разделить на 2 (Вычислить 1/9 ÷ 2?)
Итак, вы хотите разделить дробь 1/9 на целое число 2, верно? Вы находитесь в правильном месте.
В этом простом пошаговом руководстве мы покажем вам, что именно вам нужно сделать, чтобы разделить любую дробь на целое число (это очень просто). Продолжайте читать, чтобы узнать!
Если вы уже знакомились с пошаговыми руководствами наших фракций, то знаете, что мы всегда начинаем шоу с краткого обзора для детей. Число над разделительной чертой является числителем, а число под чертой — знаменателем. Простые вещи, но иногда мы все можем стать немного забывчивыми!
Чтобы визуализировать вопрос, который мы пытаемся решить, давайте поместим 1/9 и 2 рядом, чтобы было легче видеть:
1 / 9 ÷ 2
Итак, вот невероятно простой способ выяснить, чему равно 1/9, деленное на 2. Все, что нам нужно сделать здесь, это оставить числитель точно таким же (1) и умножить знаменатель на целое число:
1 / 9 х 2 «=» 1 / 18
Разве можно просто разделить дробь на целое число? Ага. Не хочу вас разочаровывать, но это может быть самая простая проблема, которую вам приходилось решать за весь день!
В некоторых случаях новую дробь, которую мы имеем после выполнения расчета, можно еще упростить до меньших членов, но в этом случае дробь уже находится в самой низкой форме.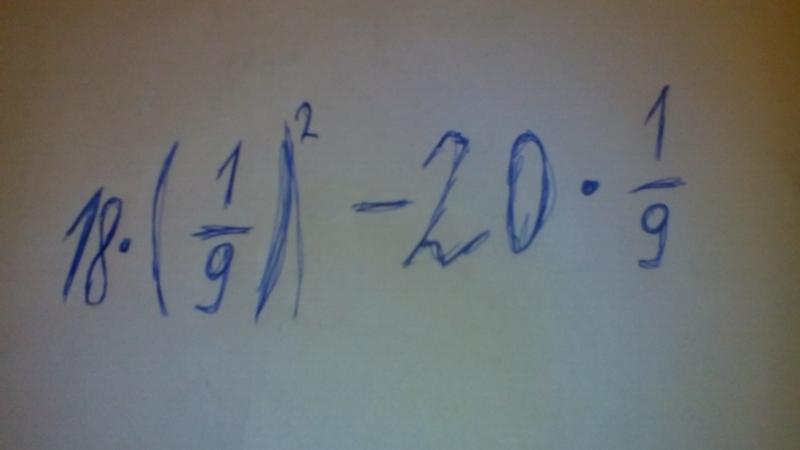
Готово! Теперь вы точно знаете, как вычислить 1/9, деленную на 2. Надеюсь, вы поняли этот процесс и можете использовать те же методы для деления других дробей на целые числа.
Хотите быстро научиться или освежить в памяти, как делить дроби на целые числа, посмотрите это быстрое и информативное видео прямо сейчас!
Преобразовать 1/9, деленную на 2, в десятичную дробь
Вот небольшой бонусный расчет, который поможет вам легко определить десятичный формат дроби, которую мы рассчитали. Получив окончательную дробь, просто разделите числитель на знаменатель, чтобы получить ответ в десятичной форме:
1 / 18 «=» 0,0556
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
