Умножение столбиком. Примеры умножения в столбик, нахождения решения онлайн.
Калькулятор
умножение чисел столбикомРассчитать Очистить
\begin{align} \end{align} |
Введите числа и калькулятор умножит числа столбиком и отобразит подробное решение.
Умножение в столбик
введениеНахождение произведения чисел
Метод умножения столбиком, позволяет упростить умножения чисел. Умножение столбиком предполагает последовательное умножения первого числа, на все цифры второго числа последующего сложения полученных произведений с учетом отступа, зависящего от положения цифры второго числа.
Рассмотрим как нужно умножать столбиком на примере нахождения произведения двух чисел 625
× 25.- 1 Запишем числа одно под другим и проведем
черту .

- 2 Число 25, состоит из 2 цифр, 2 и 5, будем умножать первое число 625, на цифры второго числа в обратном порядке. Начнем вычисление с нахождения произведения 625 × 5, запишем результат ниже черты, начинаем запись с правой стороны, получим: .
- 3 Теперь умножаем
При большем количестве цифр во втором числе, мы получим что наши произведения выстраиваются справа в виде «лесенки».

- 4 В результате умножения получаем 2 произведения, 3125 и 1250,
будем последовательно справа на лево складывать их цифры между собой, в том порядке как
они идут, и записывать результат их сложения ниже. Если сумма цифр при сложение превысит 9, то делим сумму на 10,
остаток от деления записываем под текущими цифрами, а целую часть от деления перенесем
влево.
В результате получаем .
Пример Умножить столбиком числа 687 и 253.
| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | 8^2 | |
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в упрощенную дробь | 0.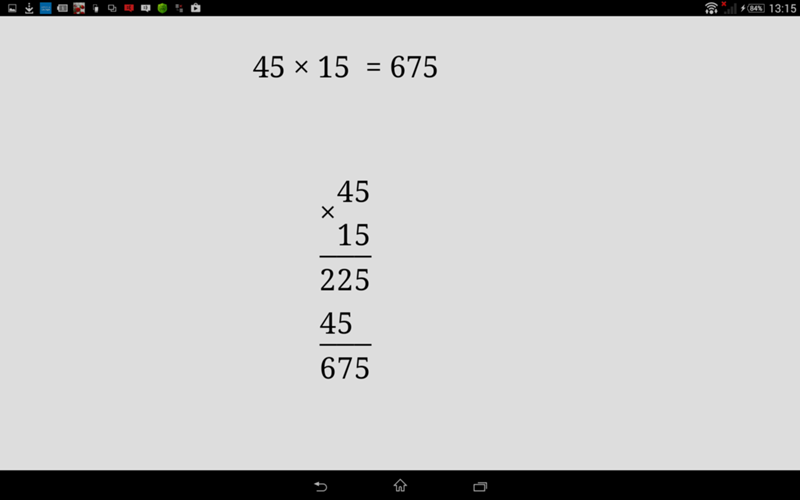 1 1 |
|
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
Умножение натуральных чисел столбиком, примеры, решения, умножение в столбик, 15 умножить на 50
Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
В этом материале мы расскажем, как считать с помощью данного способа. Все пояснения будут проиллюстрированы примерами решений задач.
Основы умножения столбиком
Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.
Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a·0=0 (a – любое натуральное число).
Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.
Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.
Как записывать множители при подсчете столбиком
Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.
Пример 1Например, чтобы вычислить и 71, 550·45 002 и 534 000·4 300, запишем такие столбики:
Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.
Как умножить столбиком многозначное число на однозначное
Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Условие: вычислить 45 027·3.
Решение
Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:
Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.
На конкретных числах процесс будет выглядеть так:
1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7·3=21. Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем.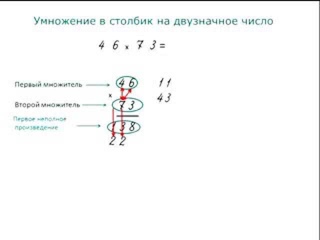
2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10, то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2·3, это будет 6. Добавляем оставшиеся с прошлого умножения десятки (от числа 21, как мы помним): 6+2=8. Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:
3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
Здесь нужно умножить 3 на 0. Согласно правилам умножения, результат будет равен 0. Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10.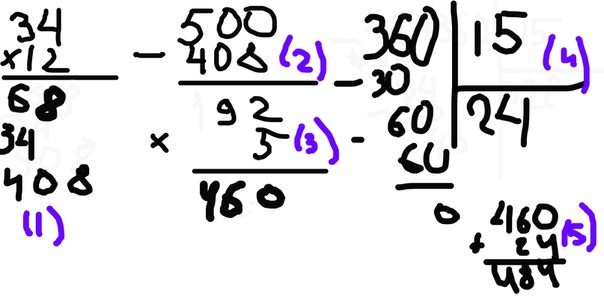 Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.
Осталось умножить 5·3 и получить 15. Результат больше 10, пишем пятерку и запоминаем десяток:
Нам осталось только перемножить 4·3, это будет 12. Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10, пишем 3 на нужное место и сохраняем единицу.
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.
Ответ: 45 027·3 = 135 081.
Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание Пример 3Условие: подсчитать, сколько будет 4 502 700·3.
Решение
Cначала запишем числа нужным способом.
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.
На этом умножение столбиком завершено.
Ответ: 4 502 700·3 =13 508 100.
Как перемножить столбиком два многозначных натуральных числа
Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.
Условие: вычислить, сколько будет 207·8 063.
Решение
Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063, а под ним 207. Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:
Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.
1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7. Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0, то сразу переходим к следующему этапу.
3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.
Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:
У нас получились все нужные нам неполные произведения.
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.
Ответ: 8 063·207 = 1 669 041.
Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:
Чтобы лучше закрепить материал, приведем решение еще одного примера.
Пример 5Условие: умножьте 297 на 321.
Решение
Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
1. Первый этап – умножаем 297 на 1, которая стоит в разряде единиц второго множителя.
2. Потом умножаем таким же образом первый множитель на 2, что стоит в десятках второго множителя. Получаем второе неполное произведение:
3. Далее умножаем на значения сотен, т.е. 297 на 3:
4. У нас получилось три неполных произведения, которые надо сложить (для этого желательно повторить, как правильно складывать столбиком три числа и более). Считаем:
Ответ: 297·321 = 95 337.
Еще один пример приведем без пояснений.
Пример 6Условие: вычислите 210 627·30 105.
Решение
Весь процесс вычислений указан в записи ниже.
Ответ: 210 627·30 105 = 6 340 925 835.
В целом можно сказать, что если вы отлично владеете способностью умножать однозначные числа и умеете складывать столбиком, то процесс умножения многозначных натуральных чисел указанным методом не будет представлять для вас никакого труда.
У нас остался еще один момент, который мы хотели бы пояснить. Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.
Пример 7Условие: вычислите 50 600·390.
Решение
Все, что нам надо сделать, – это записать множители так, чтобы друг под другом оказались цифры, отличные от нуля.
После этого мы можем просто провести все вычисления по указанному выше алгоритму, игнорируя нули. Т.е. в данном примере нам нужно просто умножить 506 на 39. Получаем два неполных произведения и складываем их:
Нам осталось все лишь дописать к результату оставшиеся нули. Мы добавляем их столько, сколько указано справа у обоих множителей. В нашем примере к готовому числу надо написать три нуля:
Это и будет корректный ответ.
Ответ: 50 600·390 = 19 734 000.
как умножать числа столбиком
Когда я вижу поисковый запросы как умножить двух, трех, четырех и т. д злачные числа столбиком, а еще когда указывают конкретные цифры – то мне становится смешно!
Просто научитесь умножать столбиком и вам будет вообще не важно сколько там цифр в каждой строчке!
Как происходит процесс умножения столбиком!?
Начнём с самого простого! Умножим 36 на 8 первое чело двузначное, втрое однозначное. Однозначное на однозначное умножают только Эйнштейны
д злачные числа столбиком, а еще когда указывают конкретные цифры – то мне становится смешно!
Просто научитесь умножать столбиком и вам будет вообще не важно сколько там цифр в каждой строчке!
Как происходит процесс умножения столбиком!?
Начнём с самого простого! Умножим 36 на 8 первое чело двузначное, втрое однозначное. Однозначное на однозначное умножают только ЭйнштейныУмножить столбиком однозначное на двузначное число.
Выравниваем числа. Которые будем умножать столбиком по правому краю. 1.(красное) Берем первый столбец , умножаем 6 * 8 = 48, 8 складываем под столбцом, 4 ставим под столбцом справа.
2.(зеленый) Умножаем 3 * 8 = 24, 4 складываем под тройкой в этот столбец.
3.Складываем цветные
8 опускаем без изменений — в этом столбце ничего больше нет…
4(красная) + 4 (зеленая) = 8 (зеленая)
2(зеленая) опускаем без изменений… на неё ничего не повлияло…
Но без первого варианта невозможно понять второй вариант.
Выравниваем числа. Которые будем умножать столбиком по правому краю.
1.(красное) Берем первый столбец , умножаем 6 * 8 = 48, 8 складываем под столбцом, 4 ставим под столбцом справа.
2.(зеленый) Умножаем 3 * 8 = 24, 4 складываем под тройкой в этот столбец.
Первые два пункта аналогично, что мы разбирали умножение однозначного и двузначного.
3.(синий)Далее умножаем 9 * 6 = 54, складываем под 9 правую цифру.
4.(желтый) Умножаем 9 * 3 = 27
Вопрос на засыпку… почему 7 не ставим в столбец по 9!? А сдвигаем в следующий столбец!?
Ответ – см. однозначное*двузначное.
5.Складываем цветные — здесь ..обычное складывание, как обычно столбиком…
8 = 8,
4 + 4 + 4 =12,
1(10) из предыдущей строки + 2 + 5 + 7 = 15,
1(10) из предыдущей строки + 2
= 3528
Все и вы должны два цветных верхних и два нижних складывать в уме….
 Т.е. умножить сперва 36 *8, а потом 36*9
Т.е. умножить сперва 36 *8, а потом 36*9 36 * 8 = 48 + 240 = 288 – складываем под 8(Посмотрите две первые строчки цветные в предыдущем варианте…)
36 * 9 = 54 + 270 = 324 – складываем под 9(Это две вторые строчки в предыдущем варианте…)
Далее как обычно складываем в столбец все цветные…
Всего 4 столбца – значит нужно произвести 4 раза сложение…
1. 8 = 8(первый столбец справа…),
2. 8 + 4 = 12,
3. 1(10) – из предыдущей строки + 2 + 2 = 5,
4. 3 = 3
= 3528
Пример умножения в столбик трехзначное и трехзначное число
1. 536 * 8 = ( 6 * 8 ) + ( 30 * 8 ) + ( 500 * 8 ) = 48 + 240 + 4000 = 4288(красный)
2. 536 * 9 = ( 6 * 9 ) + ( 30 * 9 ) + ( 500 * 9 ) = 54 + 270 + 4500 = 4824(синий)
3. 536 * 7 = ( 6 * 7 ) + ( 30 * 7 ) + ( 500 * 7 ) = 42 + 210 + 3500 = 3752(желтый)
4. 4288 + 48240 + 375200 = 427728
Написать что-нибудь.
 .. как умножать в столбик
как умножать числа столбиком
как умножать столбиком двузначные числа
умножить пример в столбик
как умножать в столбик двузначные
столбик решение умножить
как умножать столбиком трехзначные числа
25 умножить на 25 столбиком
как правильно умножать в столбик
как умножать в столбик трехзначные
как умножать в столбик десятичные
15 умножить на 15 столбиком
12 умножить на 12 столбиком
18 умножить на 18 столбиком
3 умножить на 3 в столбик
27 умножить на 27 столбиком
16 умножить на 16 столбиком
умножаем в столбик 4 класс
умножаем и делим столбиком
23 умножить на 23 столбиком
100 умножить на 100 в столбик
706 умножить на 53 столбиком
45 умножить на 45 столбиком
30 умножить на 30 столбиком
как научиться умножать столбиком
как умножать столбиком умножение
14 умножить на 14 в столбик
как умножать столбиком трехзначные числа на двузначные
научить умножать столбиком
26 умножить на 26 столбиком
как умножать в столбик с нулями
35 умножить на 35 в столбик
как умножать столбиком видео
20 умножить на 20 в столбик
28 умножить на 28 в столбик
как умножать трехзначное на двузначное в столбик
как научить ребенка умножать столбиком
17 умножить на 17 в столбик
как умножать двухзначное на двухзначное в столбик
19 умножить на 19 в столбик
36 умножить на 36 в столбик
13 умножить на 13 в столбик
.. как умножать в столбик
как умножать числа столбиком
как умножать столбиком двузначные числа
умножить пример в столбик
как умножать в столбик двузначные
столбик решение умножить
как умножать столбиком трехзначные числа
25 умножить на 25 столбиком
как правильно умножать в столбик
как умножать в столбик трехзначные
как умножать в столбик десятичные
15 умножить на 15 столбиком
12 умножить на 12 столбиком
18 умножить на 18 столбиком
3 умножить на 3 в столбик
27 умножить на 27 столбиком
16 умножить на 16 столбиком
умножаем в столбик 4 класс
умножаем и делим столбиком
23 умножить на 23 столбиком
100 умножить на 100 в столбик
706 умножить на 53 столбиком
45 умножить на 45 столбиком
30 умножить на 30 столбиком
как научиться умножать столбиком
как умножать столбиком умножение
14 умножить на 14 в столбик
как умножать столбиком трехзначные числа на двузначные
научить умножать столбиком
26 умножить на 26 столбиком
как умножать в столбик с нулями
35 умножить на 35 в столбик
как умножать столбиком видео
20 умножить на 20 в столбик
28 умножить на 28 в столбик
как умножать трехзначное на двузначное в столбик
как научить ребенка умножать столбиком
17 умножить на 17 в столбик
как умножать двухзначное на двухзначное в столбик
19 умножить на 19 в столбик
36 умножить на 36 в столбик
13 умножить на 13 в столбикУмножение в столбик | Наука делать уроки
Самое главное правило, с которого мы начинаем изучать умножение в столбик:
Умножение в столбик на двузначное число
Пример: 46 умножить на 73
Этот пример можно записать в столбик.
Под числом 46 записываем число 73 по правилу:
Единицы записываем под единицами, а десятки под десятками
1Умножать начинаем с единиц.
3 умножим на 6. Получится 18.
- 18 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами, а 1 десяток запоминаем и прибавим к десяткам.
Теперь 3 умножим на 4 десятка. Получится 12.
12 десятков, да ещё 1, всего 13 десятков.
Сотен в этом примере нет, поэтому сразу на месте сотен пишем 1.
138 — это первое неполное произведение.
2 Умножаем десятки.7 десятков умножить на 6 единиц получится 42 десятка.
- 42 десятка это 4 сотни и 2 десятка.
- 2 десятка пишем под десятками. 4 запомним и прибавим к сотням.
7 десятков умножить на 4 десятка получится 28 сотен. 28 сотен, да ещё 4 получится 32 сотни.
- 32 сотни – это 3 тысячи и 2 сотни.
- 2 сотни пишем под сотнями, а 3 тысячи запомним и прибавим к тысячам.

Тысяч в этом примере нет, поэтому сразу на месте тысяч пишу 3.
3220 – это второе неполное произведение.
3Складываем первое и второе неполные произведения по правилу сложения в столбик.138 плюс 3220 получится 3358.
Читаем ответ: 46 умножить на 73 получится 3358
Работаем в столбик
Образец записи
(Кликните по картинке)
Компоненты действия умножения
(Кликните по картинке)
Ваша Помощница
— умная и нужная
шпаргалка
Кликните, чтобы скачать и затем распечатать
Образец рассуждения
во время записи
умножения в столбик
Внимательно просмотрите и примените в своих действиях!
Какие ошибки при умножении
можно сделать и
как их избежать
[Видео]
Внимательно просмотрите,
чтобы не совершать ошибок!
Правила для других случаев умножения
Умножение в столбик на однозначное число
youtube.com/embed/1c_GI_fTGMA?autohide=2&controls=1&disablekb=0&fs=1&start=0&loop=0&rel=0&showinfo=0&theme=light&modestbranding=1&wmode=transparent» frameborder=»0″ webkitallowfullscreen=»» mozallowfullscreen=»» allowfullscreen=»»/>
34 х 2
Этот пример можно записать в столбик.
Под числом 34 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 4. Получится 8.
2х4=8
8 пишем под единицами.
Теперь 2 умножим на 3десятка. Получится 6.
2х3=6
6 пишем под десятками.
Читаем ответ: 34 умножить на 2 получится 68.
Умножение в столбик на однозначное число с переходом через десяток
38 х 2
Этот пример можно записать в столбик.
Под числом 38 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 3 десятка. Получится 6.
6 десятков да ещё 1 всего 7 десятков.
7 пишем под десятками.
Читаем ответ: 38 умножить на 2 получится 76.
Умножение в столбик на однозначное число с переходом через десятки
68 х 2
Этот пример можно записать в столбик.
Под числом 68 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 6 единиц.
- 6 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 6 десятков. Получится 12.
12 десятков да ещё 1 всего 13 десятков.
- 13 десятков – это 1 сотня да ещё 3 десятка.
- 3 десятка пишу под десятками. А 1 сотню запомним и прибавим к сотням.
Сотен в этом примере нет, поэтому сразу на месте сотен напишем 1.
Читаем ответ: 68 умножить на 2 получится 136.
Урок 12. умножение чисел столбиком — Математика — 5 класс
Математика
5 класс
Урок № 12
Умножение чисел столбиком
Перечень вопросов, рассматриваемых в теме:
— умножение натуральных чисел столбиком;
— приёмы рационального вычисления многозначных чисел.
Тезаурус
Умножение- арифметическое действие повторения данного числа слагаемым столько раз, сколько единиц находится в другом данном числе, множителе. Результат умножения- произведение.
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс.
 // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
// А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Все знакомы с таблицей умножения: её используют для умножения однозначных чисел. Следует выучить её наизусть. Кроме того, надо помнить, что для любого натурального числа а верны равенства:
а + 0 = а
а ∙ 0 = 0
а ∙ 1 = а
Вычисление произведения однозначного и многозначного чисел, и тем более двух многозначных чисел, требует применения не только таблицы умножения, но и законов сложения и умножения.
Вычислим произведение 723 ∙ 5 = ?
Можно представить число 723 в виде суммы разрядных слагаемых, и каждое из этих слагаемых умножить на 5, а затем сложить полученные результаты.
723 ∙ 5 = (700 + 20 + 3) ∙ 5 = 700 ∙ 5 + 20 ∙ 5 + 3 ∙ 5 = 3500 + 100 + 15 = 3615
А можно записать вычисление значения этого выражения столбиком:
При умножении трёх на пять получаем пятнадцать. Пять записываем в разряд единиц, единицу прибавляем в разряд десятков. При умножении двух на пять получаем десять, плюс единица, которую мы запомнили, получаем в разряде десятков единицу, единицу добавляем к разряду сотен. При умножении семи на пять получим тридцать пять, плюс один – тридцать шесть. Ответ: 3615.
При умножении двух на пять получаем десять, плюс единица, которую мы запомнили, получаем в разряде десятков единицу, единицу добавляем к разряду сотен. При умножении семи на пять получим тридцать пять, плюс один – тридцать шесть. Ответ: 3615.
Рассмотрим ещё одно выражение.
329 ∙ 34 = ?
Запишем это произведение в столбик:
Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записываем под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево.
329 ∙ 4 = 1316
Переходим к умножению числа 329 на 3. Умножаем по тем же правилам, что и в предыдущем вычислении.
329 ∙ 3 = 987
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
Полученные числа под чертой складываем по правилам сложения в столбик.
Рассмотрим такое выражение:
25 ∙ 589 ∙ 5 ∙ 125 ∙ 2 ∙ 4 ∙ 8 = ?
Чтобы найти значение этого выражения, не обязательно перемножать все числа в столбик: достаточно воспользоваться сочетательным законом умножения.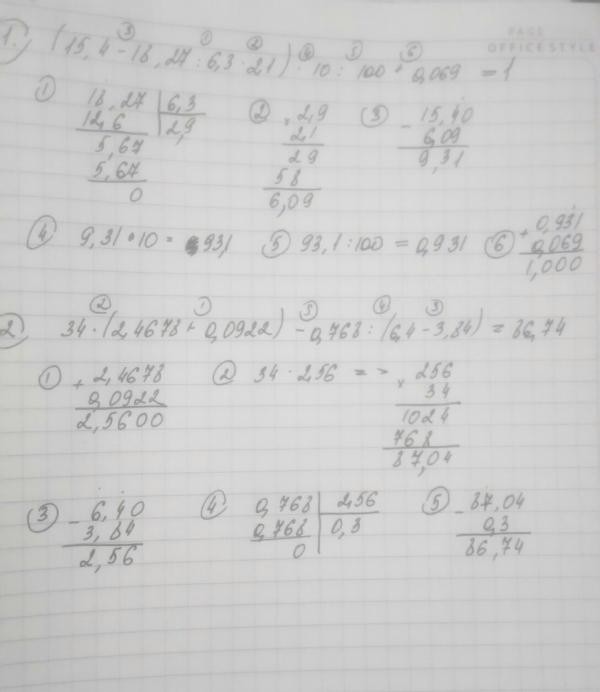 Объединим попарно некоторые множители:
Объединим попарно некоторые множители:
(25 ∙ 4) ∙ 589 ∙ (5 ∙ 2) ∙ (125 ∙ 8) = 100 ∙ 589 ∙ 10 ∙ 10000 = 589 ∙ 10000000 = 589000000
Разбор решения заданий тренировочного модуля
№ 1. Вычислите: 3256 ∙ 25 = ?
Решение: вычислим данное произведение в столбик:
Ответ: 81400.
№ 2. Пете ко Дню рождения надо было купить конфет. Он купил конфеты трёх видов: «Батончики», «Мишка на севере», «Грильяж». «Батончиков» он купил 56 штук, «Мишек на севере» – в 15 раз больше, чем «Батончиков», а «Грильяжа» на 50 конфет больше, чем «Батончиков». Сколько всего конфет купил Петя?
Варианты ответы: 1020, 1002, 1000, 992.
Решение:
- 56 ∙ 15 = 840 (шт.) – «Мишка на севере».
- 56 + 50 = 106 (шт.) – «Грильяж».
- 56 + 840 + 106 = 1002 (шт.) – всего.
Ответ: 1002 штуки.
Умножение десятичных дробей в столбик.
В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100100, 1010 и др.)
Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100100, 1010 и др.)
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.
Посмотрим, как решаются такие задачи.
Пример 1
Вычислите произведение 1,51,5 и 0,750,75.
Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 0,75 – это 75/10075/100, а 1,51,5 – это 15101510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 12510001251000 мы запишем как 1,1251,125.
Мы можем сократить дробь и произвести выделение целой части. Полученный результат 12510001251000 мы запишем как 1,1251,125.
Ответ: 1,1251,125.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Пример 2
Умножьте одну периодическую дробь 0,(3)0,(3) на другую 2,(36)2,(36).
Решение
Для начала приведем исходные дроби к обыкновенным. У нас получится:
0,(3)=0,3+0,03+0,003+0,003+…=0,31−0,1=0,39=39=132,(36)=2+(0,36+0,0036+…)=2+0,361−0,01=2+3699=2+411=2411=26110,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611
Следовательно, 0,(3)⋅2,(36)=13⋅2611=26330,(3)·2,(36)=13·2611=2633.
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
Ответ: 0,(3)⋅2,(36)=0,(78)0,(3)·2,(36)=0,(78).
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
Пример 3
Вычислите произведение 5,382…5,382… и 0,20,2.
Решение
У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,385,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38⋅0,2=538100⋅210=1 0761000=1,0765,38·0,2=538100·210=1 0761000=1,076.
Ответ: 5,382…⋅0,2≈1,0765,382…·0,2≈1,076.
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Определение 1
Умножение десятичных дробей столбиком выполняется в 22 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.
Разберем примеры таких расчетов на практике.
Пример 4
Умножьте десятичные дроби 63,3763,37 и 0,120,12 столбиком.
Решение
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 44. Дописывать нули не придется, т.к. знаков достаточно:
Ответ: 3,37⋅0,12=7,60443,37·0,12=7,6044.
Пример 5
Подсчитайте, сколько будет 3,26013,2601 умножить на 0,02540,0254.
Решение
Считаем без учета запятых. Получаем следующее число:
Мы будем ставить запятую, отделяющую 88 цифр с правой стороны, ведь исходные дроби вместе имеют 88 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Ответ: 3,2601⋅0,0254=0,082806543,2601·0,0254=0,08280654.
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Определение 2
Если мы умножим десятичную дробь на 0,1, 0,010,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.
Так, для умножения 45,3445,34 на 0,1 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,5344,534.
Пример 6
Умножьте 9,49,4 на 0,00010,0001.
Решение
Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4⋅0,0001=0,000949,4·0,0001=0,00094.
Приписываем необходимые нули и получаем, что 9,4⋅0,0001=0,000949,4·0,0001=0,00094.
Ответ: 0,000940,00094.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание
Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)⋅0,01=0,00(18)0,(18)·0,01=0,00(18) или 94,938…⋅0,1=9,4938….94,938…·0,1=9,4938…. и др.
Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Пример 7
Подсчитайте, сколько будет 15⋅2,2715·2,27.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
Ответ: 15⋅2,27=34,0515·2,27=34,05.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.
Пример 8
Вычислите произведение 0,(42)0,(42) и 2222.
Решение
Приведем периодическую дробь к виду обыкновенной.
0,(42)=0,42+0,0042+0,000042+…=0,421−0,01=0,420,99=4299=14330,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433
Далее умножаем:
0,(42)⋅22=1433⋅22=14⋅223=283=9130,42·22=1433·22=14·223=283=913
Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3)9,(3).
Ответ: 0,(42)⋅22=9,(3)0,(42)·22=9,(3).
Бесконечные дроби перед подсчетами надо предварительно округлить.
Пример 9
Вычислите, сколько будет 4⋅2,145….4·2,145….
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
4⋅2,145…≈4⋅2,15=8,60. 4·2,145…≈4·2,15=8,60.
4·2,145…≈4·2,15=8,60.
Ответ: 4⋅2,145…≈8,60.4·2,145…≈8,60.
Как умножить десятичную дробь на 1000, 100, 10 и др
Умножение десятичной дроби на 10, 10010, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:
Определение 3
Чтобы умножить десятичную дробь на 1000, 100, 101000, 100, 10 и др., нужно перенести ее запятую на 3, 2,13, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.
Покажем на примере, как именно это делать.
Пример 10
Выполните умножение 100100 и 0,07830,0783.
Решение
Для этого нам надо перенести в десятичной дроби запятую на 22 цифры в правую сторону. Мы получим в итоге 007,83007,83Нули, стоящие слева, можно отбросить и записать результат как 7,387,38.
Ответ: 0,0783⋅100=7,830,0783·100=7,83.
Пример 11
Умножьте 0,020,02 на 1010 тысяч.
Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 00. В итоге получилось 0,020000,02000,перенесем запятую и получим 00200,000200,0. Игнорируя нули слева, можем записать ответ как 200200.
Ответ: 0,02⋅10 000=2000,02·10 000=200.
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Пример 12
Вычислите произведение 5,32(672)5,32(672) на 1 0001 000.
Решение: первым делом мы запишем периодическую дробь как 5,32672672672…5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726…5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726)5 326,(726).
Ответ: 5,32(672)⋅1 000=5 326,(726)5,32(672)·1 000=5 326,(726).
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Пример 13
Умножьте 0,40,4 на 356356
Решение
Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=250,4=410=25.
Далее считаем: 0,4⋅356=25⋅236=2315=18150,4·356=25·236=2315=1815.
Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3)1,5(3).
Ответ: 1,5(3)1,5(3).
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Пример 14
Вычислите произведение 3,5678. ..⋅233,5678…·23
..⋅233,5678…·23
Решение
Второй множитель мы можем представить как 23=0,666623=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,5683,568 и 0,6670,667. Посчитаем столбиком и получим ответ:
Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,3802,379856≈2,380.
Ответ: 3,5678…⋅23≈2,380
Умножение × | Основы арифметики
На этой странице описаны основы умножения (×) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Вычитание (-) и Деление ( ÷ ).
Умножение
При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.
Чтобы выполнять вычисления умножения без калькулятора или электронной таблицы, вам нужно знать, как складывать числа. См. Нашу страницу добавления, чтобы узнать, как добавить.
Когда вы «умножаете» или «умножаете» число, вы добавляете его к самому себе несколько раз, например, умножение 4 на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Следовательно, умножение — это более быстрый способ сложения одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен выражению, если у меня есть 3 пакета по 4 яблока, сколько всего яблок у меня есть?
Основные правила умножения:
- Любое число, умноженное на 0, равно 0.200 × 0 = 0
- Любое число, умноженное на 1, остается неизменным. 200 × 1 = 200.
- Когда число умножается на два, мы удваиваем число. 200 × 2 = 400
- Когда целое число умножается на 10, мы можем просто написать 0 в конце (один ноль из 10, потому что это 1 × 10). 200 × 10 = 2000.
- При умножении на 100 мы записываем два нуля в конце, на тысячу записываем три нуля в конце и так далее.
 Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.
Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.
Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце — столбец точка пересечения двух линий и есть ответ: 24 .
Неважно, с какой стороны искать числа; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую проблему. Меган ведет трех своих братьев в кино, ей нужно купить всего 4 билета, каждый стоит 8 фунтов. Сколько будет общая стоимость поездки? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.
Меган ведет трех своих братьев в кино, ей нужно купить всего 4 билета, каждый стоит 8 фунтов. Сколько будет общая стоимость поездки? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.
Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где пересекаются две линии: 32 . Стоимость поездки в кинотеатр составит 32 фунтов стерлингов.
Часто бывает необходимо умножать числа больше 10.В этом случае приведенная выше таблица умножения не может дать немедленного ответа. Однако мы все еще можем использовать его, чтобы упростить расчет.
Лиза занимается ресторанным бизнесом. Она должна доставить бутерброды 23 предприятиям, в каждом из которых работает 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов нужно приготовить Лизе?
23 предприятиям нужно 14 бутербродов, что составляет 23 лота по 14 или, другими словами, 23, умноженные на 14. Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.
Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.
Нам нужно найти ответ на расчет 23 × 14.
Сначала запишите свои числа в столбцы, представляющие сотни, десятки и единицы (за помощью см. Нашу страницу Числа ).
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 |
Шаг 1: Начиная с правого столбца (единицы), умножьте 4 и 3.При необходимости вы можете обратиться к приведенной выше таблице умножения. Напишите ответ (12) под своими вычислениями, стараясь поставить 1 в столбце десятков и 2 в столбце единиц.
Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 |
Шаг 2: Затем мы умножаем 4 на следующее число, равное 2 (или 20, потому что оно находится в столбце десятков). Напишите свой ответ внизу в столбце десятков: мы напишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).
Напишите свой ответ внизу в столбце десятков: мы напишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 |
Шаг 3: В приведенных выше шагах мы умножили единицы нижнего числа (4) на верхнее число (23).Затем нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем описанные выше шаги. Оглядываясь на наши основные правила умножения, приведенные выше, мы знаем, что, умножая число на 10, мы пишем ноль в конце. На этом этапе, поскольку мы переместились по столбцу и работаем с десятками, мы должны не забыть записать нули в первый столбец (единицы).
Выполните 1 × 3. Как и выше, мы записываем наш ответ (3) в столбец десятков и (0) в столбец единиц.
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 |
Шаг 4: Последнее умножение, которое нам нужно выполнить, это 1 × 2.Оба числа находятся в столбце десятков, поэтому мы умножаем один лот из 10 на два лота по 10. Используя правила, которые мы узнали на предыдущих шагах, нам нужно записать ноль в столбец единиц и ноль в столбец десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 | |
| 2 | 0 | 0 |
Этап 5: На этом этапе мы закончили умножение; остается только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов. См. Нашу страницу Дополнение , если вам нужна помощь в сложении чисел.
См. Нашу страницу Дополнение , если вам нужна помощь в сложении чисел.
| Сот | Десятки | Квартир | |
| 2 | 3 | ||
| 1 | 4 | ||
| 1 | 2 | ||
| 8 | 0 | ||
| 3 | 0 | ||
| 2 | 0 | 0 | |
| Всего: | 3 | 2 | 2 |
12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать в общей сложности 322 бутербродов.
В приведенном выше примере показано, как выполнить умножение с разбиением на все возможные части, но по мере повышения уверенности можно пропустить шаги.
Мы могли бы, например, умножить 4 на 23, разбив сумму на две части:
4 × 20 = 80
4 × 3 = 12
80 + 12 = 92
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 |
Затем то же самое для второго столбца:
10 × 23 = 230
| Сот | Десятки | Квартир |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 | |
| 2 | 3 | 0 |
Наконец, мы складываем два наших ответа:
| Сот | Десятки | Квартир | |
| 2 | 3 | ||
| 1 | 4 | ||
| 9 | 2 | ||
| 2 | 3 | 0 | |
| Всего: | 3 | 2 | 2 |
92 + 230 = 322.
Умножение более двух чисел
Если вам нужно перемножить более двух элементов, обычно проще перемножить первые два элемента, получить общую сумму, а затем умножить следующее число на первую сумму. Например, если Джо хотел вычислить, сколько часов он проработал за четырехнедельный период, расчет будет выглядеть так:
Джо работает 7 часов в день 5 дней в неделю в течение четырех недель.
Шаг первый:
7 × 5 = 35 (количество часов, которые Джо работает в неделю).
Шаг второй:
Чтобы узнать, сколько часов Джо работает за четыре недели, мы можем затем умножить этот ответ (35) на 4. 35 × 4 = 140.
Если мы знаем, что Джо платят 12 фунтов в час, мы можем затем подсчитать, сколько денег он заработал за четырехнедельный период: 12 × 140.
Быстрый способ решить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножаем на 10, мы просто добавляем ноль в конец числа, на которое умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.
Мы складываем наши ответы вместе: 1400 + 280 = 1680.
Таким образом, Джо заработал 1680 фунтов стерлингов за четырехнедельный период.
Умножение отрицательных чисел
Умножение отрицательного числа на положительное всегда дает отрицательный ответ:
15 × (−4) = −60
Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:
(−15) × (−4) = 60
Массивы, умножение и деление
Массивы, умножение и деление
Дженни Пеннант с помощью Дженни Уэй и Майка Аскью исследует, как использовать массив в качестве инструмента мышления, чтобы помочь детям развить глубокое понимание умножения и деления.
Использование массивов для исследования чисел
Массивы — это полезные модели для умножения, которые можно использовать по-разному, от высоко структурированных уроков до игр и открытых исследований.
Массив формируется путем размещения набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, что и другие столбцы, и каждая строка должна иметь то же количество объектов, что и другие строки.
Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12, 4 x 3 = 12, 3 + 3 + 3 + 3 = 12 и 4 + 4 + 4 = 12.
Построение фактов и таблиц умножения
Массивы можно использовать для конструктивного построения фактов умножения. Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты выводятся. Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить для себя трехкратные таблицы. Это представление не только помогает понять процесс, но и дает визуальное изображение для детей, которых можно использовать, когда они начнут использовать и запоминать основные числовые факты.
Использование массивов для исследования больших чисел
Массивы могут быть полезны для изучения вычислений, таких как 13 x 5, где массив можно разделить на полезные части, такие как 10 и 3. Это означает, что дети могут использовать свои известные количество фактов для проведения расчетов.
Это означает, что дети могут использовать свои известные количество фактов для проведения расчетов.
Здесь 13 x 5 = (10 x 5) + (3 x 5).
Через некоторое время рисование всех точек может стать очень утомительным! Пустой массив затем становится очень полезным инструментом, помогающим детям моделировать свое мышление и разрабатывать более сложные операции умножения в неформальной обстановке.
Вот ребенок, использующий пустой массив в качестве инструмента мышления, чтобы помочь им вычислить 15 x 14.
Пустой массив помогает детям использовать другие стратегии, такие как компенсация, при выполнении умножения. Здесь, чтобы вычислить 34 x 9, ребенок решил сделать 34 x 10, а затем снять 34 x 1.
Помимо пустого массива, эта стратегия «деления умножения на простые части» может быть формализована в виде сеточный метод.Дети могут видеть, как «абстрактный» метод сетки накладывает на массив и формализует пустой массив в стандартной форме.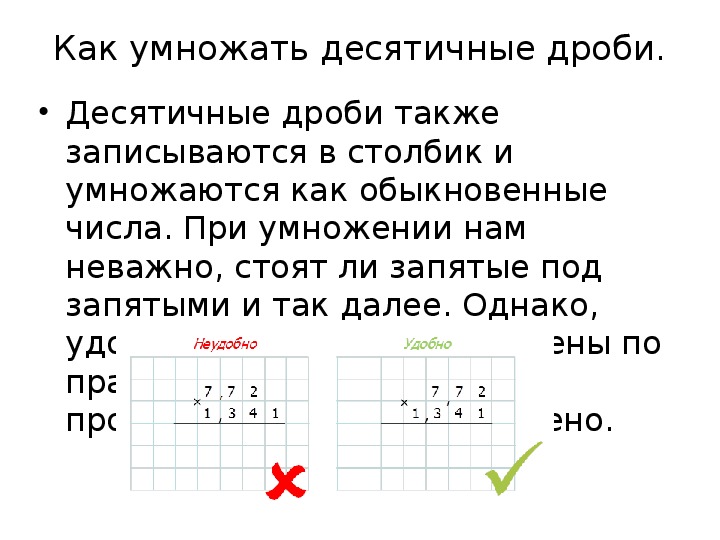
Деление как обратная операция умножения
Из четырех операций деление является наиболее сложной задачей для молодых студентов. Полное понимание деления обычно сильно отстает от других операций. Для многих детей возможности исследовать концепцию на конкретных материалах ограничиваются задолго до того, как они осознают взаимосвязь между разделением и тремя другими операциями.Одна из таких отношений, обратная связь Между делением и умножением можно эффективно проиллюстрировать использование массивов.
Например; 3 × 5 = 15 или 3 строки из 5 составляют 15, могут быть представлены следующим массивом.
Если взглянуть на массив по-другому, можно увидеть обратное:
15 ÷ 3 = 5 или 15, помещенные в 3 строки, дают 5 столбцов — или 5 в каждой строке.
Язык явно играет важную роль в способности выражать математические взаимосвязи, и физический массив поддерживает этот аспект понимания, давая детям конкретный образ для разговора.
Помещение математики в контекст реальной жизни с помощью словесных задач может облегчить как понимание взаимосвязи, так и ее выражение в словах.
Например, «Садовник посадил 3 ряда по 5 семян. Сколько семян она посадила?» представляет собой совсем другую проблему, чем «Садовник посадил 15 семян в 3 равных ряда. Сколько семян в каждом ряду?» тем не менее, обе эти проблемы со словами можно смоделировать с использованием одного и того же массива.
Дальнейшее изучение массива обнаруживает еще два способа выражения обратных отношений: 5 × 3 = 15 и 15 ÷ 3 = 5.
Слова «проблемы» могут быть адаптированы для описания этих операций и выделения сходства и различий между четырьмя выражениями, моделируемыми одним массивом.
Использование пустого массива
Предположим, вы хотите вычислить 176 ÷ 8. Мы можем настроить его как массив с отсутствующим значением одной стороны.
Используя известные факты умножения, можно построить значение отсутствующей стороны.
Итак, ребенок может видеть, что 22 лота из 8 — это то же самое, что 176.
Массив — очень мощный инструмент для поддержки развития детского мышления как в отношении умножения, так и деления.
Дополнительная литература
Чтобы прочитать об использовании массивов для иллюстрации числовых свойств, перейдите сюда, чтобы прочитать статью Дженни Уэй, озаглавленную «Иллюстрирование числовых свойств с помощью массивов».
Вот версия этой статьи в формате PDF.
Калькулятор длинного умножения
Использование калькулятора
Умножение положительных или отрицательных целых или десятичных чисел в качестве множимого и множителя для вычисления произведения с использованием длинного умножения.Решение показывает работу стандартного алгоритма.
Части длинного умножения
2
5
6
Множаемое
×
3
2
Множитель
+
5
1
2
Частичный продукт
+
7
6
8
Частичный продукт
Как сделать длинное умножение
Длинное умножение означает, что вы выполняете умножение вручную.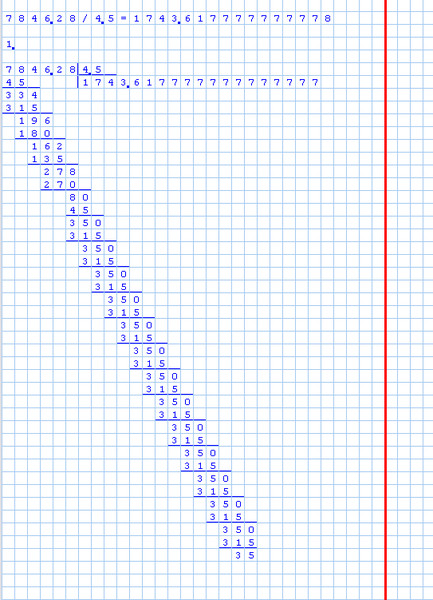 Традиционный метод, или стандартный алгоритм, включает в себя умножение чисел и выстраивание результатов в соответствии с разрядами. Вот шаги, чтобы выполнить длинное умножение вручную:
Традиционный метод, или стандартный алгоритм, включает в себя умножение чисел и выстраивание результатов в соответствии с разрядами. Вот шаги, чтобы выполнить длинное умножение вручную:
- Расположите числа одно над другим и выровняйте их по столбцам. Число с наибольшим количеством цифр обычно ставится сверху как множимое.
- Начиная с единицы нижнего числа, множителя, умножьте его на последнюю цифру верхнего числа
- Напишите ответ под строкой равно
- Если этот ответ больше девяти, запишите единицы в качестве ответа и перенесите цифру десятков
- Двигайтесь справа налево.Умножьте единицы нижнего числа на следующую цифру слева в верхнем числе. Если у вас есть цифра, добавьте ее к результату и напишите ответ под линией равенства. Если вам нужно снова нести, сделайте это.
- Когда вы умножили цифру единиц на каждую цифру верхнего числа, перейдите к цифре десятков в нижнем числе.

- Умножьте, как указано выше, но на этот раз запишите ответы в новой строке со сдвигом на одну цифру влево.
- Когда вы закончите умножение, нарисуйте еще одну линию ответов под последним рядом номеров ответов.
- Используйте длинное сложение для добавления столбцов чисел справа налево, как обычно при длинном сложении.
Длинное умножение с десятичными знаками
Длинное умножение с десятичными знаками с использованием стандартного алгоритма требует выполнения нескольких простых дополнительных правил.
- Подсчитайте общее количество десятичных знаков, содержащихся как в множимом, так и в множителе.
- Игнорировать десятичные дроби и выравнивать числа по правому краю одно над другим, как если бы они были целыми числами
- Умножайте числа, используя длинное умножение.

- Вставьте десятичную запятую в продукт, чтобы оно имело такое же количество десятичных знаков, как сумма из шага 1.
Пример длинного умножения с десятичными знаками
Умножить 45,2 на 0,21
Всего в обоих числах 3 десятичных разряда.
Игнорируйте десятичные разряды и завершите умножение, как если бы работали с двумя целыми числами.
Перепишите произведение с 3 десятичных разряда.
Ответ = 9,492
Следовательно: 45,2 × 0,21 = 9,492
Длинное умножение на отрицательные числа
При выполнении длинного умножения вы можете игнорировать знаки, пока не завершите стандартный алгоритм умножения.После завершения умножения следуйте этим двум правилам:
- Если одно число положительное, а одно отрицательное, сделайте произведение отрицательным.

- Если оба числа отрицательны или оба числа положительны, сделайте произведение положительным.
Пример длинного умножения: умножить 234 на 56
Длинные шаги умножения:
Сложите числа с большим числом наверху.Выровняйте числа по столбцам с разрядными значениями.
Умножьте единичную цифру нижнего числа на каждую цифру верхнего числа
6 × 4 = 24
Поместите 4 на место
Отнести 2 к десяткам
6 × 3 = 18
Добавьте 2, которые у вас есть, = 20
Поставьте 0 на место десятков
Отнести 2 к сотням место
6 × 2 = 12
Добавьте 2, которые у вас есть, = 14
Это последнее число, которое нужно умножать, поэтому напишите ответ целым числом. Не нужно носить с собой 1.
Не нужно носить с собой 1.
Переместитесь на одну позицию влево. Умножьте цифру десятков в нижнем числе на каждую цифру в верхнем числе.
5 × 4 = 20
Добавьте строку в свой ответ на умножение
Когда вы пишете свой ответ, сдвиньте один столбец влево
Поставьте 0 на место
Отнести 2 к десяткам
5 × 3 = 15
Добавьте 2, которые у вас есть, = 17
Поставьте 7 на место десятков
Отнести 1 к сотням место
5 × 2 = 10
Добавьте 1, что у вас есть, = 11
Это последнее число, которое нужно умножать, поэтому напишите ответ целым числом.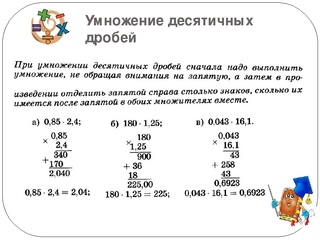 Не нужно носить с собой 1.
Не нужно носить с собой 1.
Сложите числа в столбцах, используя длинное сложение
4 + 0 = 4
0 + 0 = 0
4 + 7 = 11
написать 1 и перенести 1
1 + 1 + 1 = 3
Сложив столбцы, вы увидите результат длинного умножения: 234 × 56 = 13104.
Сопутствующие калькуляторы
Если вам нужна помощь с длинным сложением, посетите наш Калькулятор длинного сложения для сложения чисел путем длинного сложения и просмотра работы.
Для длинного деления см. Калькулятор деления чисел в столбик для деления чисел с помощью деления в столбик с остатками. Этот калькулятор тоже показывает работу.
Если вам нужно умножить дроби, посетите наш
Калькулятор дробей. Здесь вы можете выполнять умножение, сложение, вычитание и деление дробей.
Здесь вы можете выполнять умножение, сложение, вычитание и деление дробей.
Список литературы
Math is Fun показывает примеры Длинное умножение в анимационном ролике.
Длинное умножение — это алгоритм, и вы можете найти примеры алгоритмы умножения в Википедии.
Гудман, Лен.«Длинное умножение». От MathWorld — Интернет-ресурс Wolfram, созданный Эрик В. Вайсштейн. http://mathworld.wolfram.com/LongMultiplication.html
Как умножать целые числа. Как умножать десятичные дроби — Полный курс арифметики
6 × 45 = 6 × 40 + 6 × 5 = 240 + 30 = 270.
О разделении двух десятичных цифр:
6% от 45 долларов — 2 доллара. 70.
70.
В любом случае, это то, что мы сделали бы , , если бы мы изменили 6% на . 06 (Урок 4) и умножаем . 06 × 45; то есть, если мы взяли 6 сотых от 45. (Урок 27.)
Эквивалентно с
1% от 45 долларов составляет доллара. 45
(Урок 4), то 6% будет 6 умножить на 1%, то есть 6 × . 45.
Примечание : Из-за свойства порядка умножения
6% от 45 долларов = 45% от 6 долларов.
Например, поскольку 50% означает половину:
24% от 50 = 50% от 24 = 12.
Пример 7. Сколько 9% от 84 долларов?
Решение . Умножьте 9 × 84, затем разделите две десятичные цифры.
При раздаче с 9 по 80 + 4:
9 × 84 = 720 + 36 = 756.
9% от 84 долларов это 7 долларов. 56.
Пример 8. Сколько 3% от 247 долларов?
Решение . 3 ×
247 = 6 00 + 1 20 + 21 = 7 41.
3% от 247 долларов — это 7 долларов. 41.
Пример 9. Сколько составляет 11% от 76 долларов?
Решение . 11 × 76 = 7 6 0 + 7 6 = 8 3 6.(Урок 9.)
11% от 76 долларов это 8 долларов. 36.
Это простые задачи, для которых не требуется калькулятор. Дополнительные сведения о таких простых задачах см. В Уроке 29. Чтобы узнать, как решать задачи с процентами с помощью калькулятора, см. Урок 14.
Площадь прямоугольника
Что такое «1 квадратный фут»?
1 квадратный фут — это квадратная фигура, каждая сторона которой равна 1 футу.
Мы сокращаем «1 квадратный фут» как 1 фут².
1 фут (1 фут) — это единица измерения длины. Если это единица длины, то 1 квадратный фут (1 фут²) равен единице площади . И аналогично для любой единицы длины и соответствующей единицы площади.
А теперь прямоугольник с основанием 3 см и высотой 2 см.
Как мы называем маленький заштрихованный квадрат?
Так как каждая сторона равна 1 см, мы называем это «1 квадратный сантиметр».»И мы видим, что вся фигура состоит из 2х3 или 6 из них
Другими словами, площадь этого прямоугольника — пространство, ограниченное рамкой, — составляет 6 квадратных сантиметров: 6 см².
Если бы прямоугольник был 3 на 3, то есть если бы он был квадратом, то он составлял бы 9 см². Если бы было 3 на 4, то площадь была бы 12 см². И так далее. В любом случае, чтобы вычислить площадь прямоугольника, просто умножьте основание на высоту.
Если длина измеряется в сантиметрах, площадь измеряется в квадрате. сантиметры: см². И аналогично для любой единицы длины.
Мы проиллюстрировали это целыми числами, но это будет верно для любых чисел.
Если основание 12 дюймов, а высота 6,5 дюйма, то чтобы найти площадь, умножьте
12 × 6 . 5
Сейчас,
12 × 65 = 10 × 65 + 2 × 65 = 650 + 130 = 780.
Следовательно, при разделении одной десятичной цифры (6 . 5):
Площадь = 78 кв.
Задача 1. 1 ярд = 3 фута. 1 квадратный ярд теперь состоит из многих квадратных футов?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
9 квадратных футов.
Проблема 2.Цена ковра — 50 долларов за квадратный ярд. Какова приблизительная цена ковра размером 5 на 7 футов?
Примерно 200 долларов.
Площадь ковра 5 на 7 составляет 35 квадратных футов. Квадратный двор составляет 9 квадратных футов. Площадь этого ковра составляет примерно 4 квадратных ярда. Следовательно, цена составляет примерно 4 раза по 50 долларов, что составляет 200 долларов.
Порядок собственности
Вернемся к свойству порядка умножения (Урок 9):
Если два числа умножаются друг на друга, то полученные числа
будут равны друг другу.
(Евклид, VII.16)
Например, если два числа — 32 и 5, то, если мы несколько раз сложим 32 пять раз, мы получим то же число, что и при сложении 5 тридцать два раза.
32 + 32 + 32 + 32 + 32 = 5 + 5 + 5 +. . . + 5 + 5.
Мы смогли доказать это, не называя продукт.
Но чтобы взять более простой пример, пусть два числа будут 3 и 4. Тогда
Три четверки = четыре тройки.
И мы не имеем в виду, что каждому 12.
Посмотрите на эту цифру:
Первый столбец слева, скажем, составляет 4 см². Весь прямоугольник состоит из 3 таких столбцов. Состоит из
3 × 4 см².
Но соответствует каждому см² в первом столбце, один в каждом из следующих столбцов. Следовательно, если смотреть на строки, прямоугольник состоит из
4 × 3 см².
Другими словами,
4 × 3 см² = 3 × 4 см².
Если мы прибавим 3 см² четыре раза, мы получим тот же результат, что и при трехкратном добавлении 4 см² — и чтобы знать, что нам не нужно знать, что 3 × 4 = 12.
Это свойство порядка умножения.
*
Иногда вы видите
3 см × 4 см = 12 см²,
, что, честно говоря, не имеет смысла.Множитель (слева) показывает, сколько раз нужно повторно сложить множимое (справа). Следовательно, множитель всегда должен быть чистым числом.
Пожалуйста, «переверните» страницу и выполните несколько задач .
или
Переходите к следующему уроку.
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Как умножать в Excel: числа, ячейки, целые столбцы
В этом руководстве объясняется, как умножать в Excel с помощью символа и функций умножения, как создать формулу для умножения ячеек, диапазонов или целых столбцов, как умножить и суммировать и многое другое.
Хотя в Excel нет универсальной формулы умножения, существует несколько различных способов умножения чисел и ячеек. Приведенные ниже примеры научат вас, как написать формулу, наиболее подходящую для вашей конкретной задачи.
Приведенные ниже примеры научат вас, как написать формулу, наиболее подходящую для вашей конкретной задачи.
Умножение в Excel с помощью оператора умножения
Самый простой способ произвести умножение в Excel — использовать символ умножения (*). При таком подходе вы можете быстро умножать числа, ячейки, целые столбцы и строки.
Как умножать числа в Excel
Чтобы составить простейшую формулу умножения в Excel, введите знак равенства (=) в ячейку, затем введите первое число, которое вы хотите умножить, за которым следует звездочка, затем второе число и нажмите клавишу Enter, чтобы вычислить формула.
Например, чтобы умножить 2 на 5, введите это выражение в ячейку (без пробелов): = 2 * 5
Как показано на скриншоте ниже, Excel позволяет выполнять различные арифметические операции в рамках одной формулы. Просто помните о порядке вычислений (PEMDAS): скобки, возведение в степень, умножение или деление в зависимости от того, что наступит раньше, сложение или вычитание, в зависимости от того, что наступит раньше.
Как умножить ячейки в Excel
Чтобы умножить две ячейки в Excel, используйте формулу умножения, как в приведенном выше примере, но укажите ссылки на ячейки вместо чисел.Например, чтобы умножить значение в ячейке A2 на значение в B2, введите следующее выражение:
= A2 * B2
На умножить несколько ячеек , включить в формулу дополнительные ссылки на ячейки, разделенные знаком умножения. Например:
= A2 * B2 * C2
Как умножить столбцы в Excel
Чтобы умножить два столбца в Excel, напишите формулу умножения для самой верхней ячейки, например:
= A2 * B2
После того, как вы поместили формулу в первую ячейку (C2 в этом примере), дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу, до последней ячейки с данными. :
Из-за использования относительных ссылок на ячейки (без знака $) наша формула умножения Excel будет правильно настраиваться для каждой строки:
На мой взгляд, это лучший, но не единственный способ умножить один столбец на другой. Вы можете изучить другие подходы в этом руководстве: Как умножить столбцы в Excel.
Вы можете изучить другие подходы в этом руководстве: Как умножить столбцы в Excel.
Как умножить строки в Excel
Умножение строк в Excel — менее распространенная задача, но и для нее есть простое решение. Чтобы умножить две строки в Excel, просто сделайте следующее:
- Вставьте формулу умножения в первую (крайнюю левую) ячейку.
В этом примере мы умножаем значения в строке 1 на значения в строке 2, начиная со столбца B, поэтому наша формула выглядит следующим образом:
= B1 * B2 - Выберите ячейку формулы и наведите курсор мыши на маленький квадрат в правом нижнем углу, пока он не изменится на толстый черный крест.
- Перетащите черный крестик вправо по ячейкам, в которые вы хотите скопировать формулу.
Как и при умножении столбцов, относительные ссылки на ячейки в формуле меняются в зависимости от относительного положения строк и столбцов, умножая значение в строке 1 на значение в строке 2 в каждом столбце:
Функция умножения в Excel (ПРОДУКТ)
Если вам нужно умножить несколько ячеек или диапазонов, самым быстрым методом будет использование функции ПРОИЗВОДИТ:
ПРОДУКТ (номер1, [номер2],…)
Где номер1 , номер2 и т.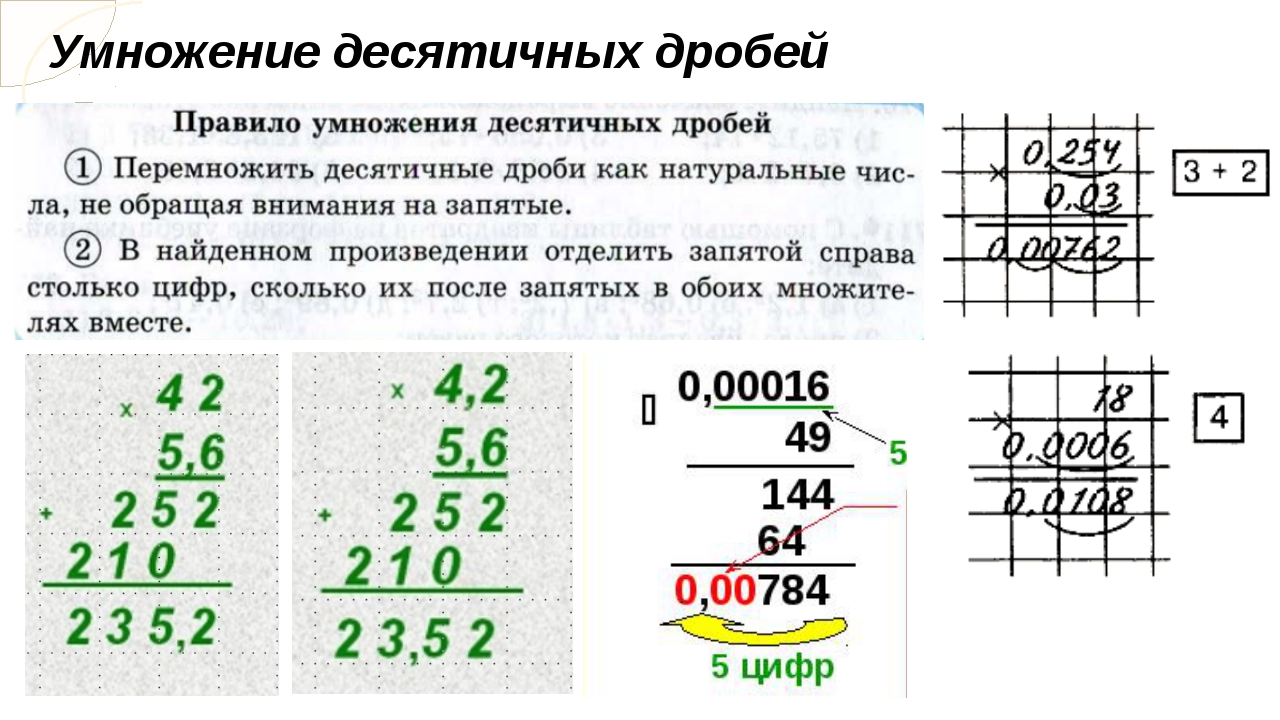 Д.числа, ячейки или диапазоны, которые вы хотите умножить.
Д.числа, ячейки или диапазоны, которые вы хотите умножить.
Например, чтобы умножить значения в ячейках A2, B2 и C2, используйте эту формулу:
= ПРОДУКТ (A2: C2)
Чтобы умножить числа в ячейках с A2 по C2, а затем умножить результат на 3, используйте это:
= ПРОДУКТ (A2: C2,3)
На снимке экрана ниже показаны эти формулы умножения в Excel:
Как умножить на процент в Excel
Чтобы умножить проценты в Excel, составьте формулу умножения следующим образом: введите знак равенства, затем число или ячейку, затем знак умножения (*), а затем процент.
Другими словами, составьте формулу, подобную этой:
- Чтобы умножить число на процентное соотношение :
= 50 * 10% - Чтобы умножить ячейку на процентное соотношение :
= A1 * 10%
Вместо процентов можно умножить на соответствующее десятичное число. Например, зная, что 10 процентов составляют 10 частей от сотни (0,1), используйте следующее выражение, чтобы умножить 50 на 10%:
Например, зная, что 10 процентов составляют 10 частей от сотни (0,1), используйте следующее выражение, чтобы умножить 50 на 10%: = 50 * 0,1
Как показано на скриншоте ниже, все три выражения дают одинаковый результат:
Как умножить столбец на число в Excel
Чтобы умножить числовой столбец на такое же число, выполните следующие действия:
- Введите число для умножения в какую-нибудь ячейку, например, в A2.
- Напишите формулу умножения для самой верхней ячейки столбца.
Предполагая, что числа для умножения находятся в столбце C, начиная со строки 2, вы помещаете следующую формулу в D2:
= C2 * 2 австралийских доллараВажно, чтобы вы заблокировали координаты столбца и строки ячейки с числом для умножения, чтобы предотвратить изменение ссылки при копировании формулы в другие ячейки. Для этого введите символ $ перед буквой столбца и номером строки, чтобы создать абсолютную ссылку ($ A $ 2).
 Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную.
Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную. - Дважды щелкните маркер заполнения в ячейке формулы (D2), чтобы скопировать формулу вниз по столбцу. Выполнено!
Как видно на скриншоте ниже, C2 (относительная ссылка) меняется на C3, когда формула копируется в строку 3, а $ A $ 2 (абсолютная ссылка) остается неизменной:
Если дизайн вашего рабочего листа не позволяет разместить число в дополнительной ячейке, вы можете указать его непосредственно в формуле, например.г .: = C2 * 3
Вы также можете использовать функцию Специальная вставка > Умножить , чтобы умножить столбец на постоянное число и получить результаты в виде значений, а не формул. Пожалуйста, ознакомьтесь с этим примером для получения подробных инструкций.
Как умножать и суммировать в Excel
В ситуациях, когда вам нужно умножить два столбца или строки чисел, а затем сложить результаты отдельных вычислений, используйте функцию СУММПРОИЗВ для умножения ячеек и суммирования произведений.
Предположим, у вас есть цены в столбце B, количество в столбце C, и вы хотите рассчитать общую стоимость продаж. На уроке математики вы умножаете каждую цену / количество. соедините индивидуально и сложите промежуточные итоги.
В Microsoft Excel все эти вычисления можно произвести с помощью одной формулы:
= СУММПРОИЗВ (B2: B5, C2: C5)
При желании вы можете проверить результат с помощью этого расчета:
= (B2 * C2) + (B3 * C3) + (B4 * C4) + (B5 * C5)
И убедитесь, что формула СУММПРОИЗВ дает точное умножение и суммирование:
Умножение в формулах массива
Если вы хотите умножить два столбца чисел, а затем выполнить дальнейшие вычисления с результатами, выполните умножение в формуле массива.
В приведенном выше наборе данных есть еще один способ вычисления общей стоимости продаж:
= СУММ (B2: B5 * C2: C5)
Эта формула умножения суммы в Excel эквивалентна СУММПРОИЗВ и возвращает точно такой же результат (см. Снимок экрана ниже).
Снимок экрана ниже).
Продолжая этот пример, давайте найдем среднее значение продаж. Для этого просто используйте функцию СРЕДНИЙ вместо СУММ:
= СРЕДНИЙ (B2: B5 * C2: C5)
Чтобы найти самую большую и самую маленькую продажу, используйте функции MAX и MIN соответственно:
= МАКС (B2: B5 * C2: C5)
= МИН (B2: B5 * C2: C5)
Чтобы правильно заполнить формулу массива, не забудьте нажать комбинацию Ctrl + Shift + Enter вместо обводки Enter.Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
Результаты могут выглядеть примерно так:
Вот как вы умножаете в Excel, чтобы понять это, не требуется ученый-ракетчик 🙂 Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, не стесняйтесь скачать наш образец книги умножения Excel.
Как быстро производить любые вычисления в Excel
Если вы новичок в Excel и еще не знакомы с формулами умножения, наш Ultimate Suite значительно упростит вам задачу. Среди более чем 60 симпатичных функций он предоставляет инструмент Calculation , который может выполнять все основные математические операции, включая умножение, одним щелчком мыши. Позвольте мне показать вам, как это сделать.
Среди более чем 60 симпатичных функций он предоставляет инструмент Calculation , который может выполнять все основные математические операции, включая умножение, одним щелчком мыши. Позвольте мне показать вам, как это сделать.
Предположим, у вас есть список цен нетто и вы хотите узнать соответствующую сумму НДС. Нет ничего страшного, если вы умеете рассчитывать проценты в Excel. Если нет, пусть Ultimate Suite сделает всю работу за вас:
- Скопируйте цены в столбец НДС. Это нужно сделать, потому что вы не хотите переопределять исходные значения в столбце Цена .
- Выберите скопированные цены (C2: C5 на скриншоте ниже).
- Перейдите на вкладку Инструменты Ablebits > Рассчитайте группу и выполните следующие действия:
- Выберите символ процента (%) в поле Operation .
- Введите желаемое число в поле Значение .
- Нажмите кнопку Рассчитать .
Вот и все! Вы получите проценты, рассчитанные за одно мгновение:
Аналогичным образом вы можете умножать и делить, складывать и вычитать, вычислять проценты и многое другое. Все, что вам нужно сделать, это выбрать соответствующий оператор, например, символ умножения (*):
Все, что вам нужно сделать, это выбрать соответствующий оператор, например, символ умножения (*):
Чтобы выполнить одно из недавних вычислений для другого диапазона или столбца, просто нажмите кнопку Применить последние и выберите операцию:
Результатом всех вычислений, выполненных с помощью Ultimate Suite, являются значений , а не формулы. Таким образом, вы можете перемещать или копировать их на другой лист или книгу, не беспокоясь об обновлении ссылок на формулы. Рассчитанные значения останутся неизменными даже при перемещении или удалении исходных чисел.
Если вам интересно узнать больше об этом и многих других инструментах для экономии времени, включенных в Ultimate Suite for Excel, вы можете загрузить 15-дневную пробную версию.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
РАЗ МОДУЛЬ M9 — Умножение целых чисел
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Предполагаемые знания
- Понимание разряда применительно к целым числам (см.
 Модуль «Подсчет и разметка»).
Модуль «Подсчет и разметка»). - Понимание того, что сложение может быть смоделировано путем комбинирования наборов объектов, а также может быть смоделировано на числовой прямой.
- Понимание и свободное владение счетом пропусков.
- Понимание и свободное владение сложением двух однозначных чисел.
- Знакомство с использованием массивов для моделирования умножения.
- Использование символа умножения для обозначения «групп».
- Знание простых фактов умножения и деления.
Мотивация
Примеры использования умножения включают расчет стоимости шести предметов
стоимостью 25 центов каждая. Намного быстрее вычислить 6 × 25 умножением
, чем повторным сложением.
Умножение отвечает на такие вопросы, как:
1 Джуди купила 15 коробок конфет. В каждой коробке было 24 шоколадных конфеты. Сколько конфет было у Джуди?
2 У Генри 16 мотков проволоки. Каждый рулон имеет длину 18 м.Какова общая длина провода у Генри?
Естественная геометрическая модель умножения в виде прямоугольной области находит применение в измерениях. Таким образом, умножение обеспечивает раннюю связь между арифметикой и геометрией.
Таким образом, умножение обеспечивает раннюю связь между арифметикой и геометрией.
Свободное владение с умножением снижает когнитивное напряжение при изучении более поздних тем, таких как
, как деление. Развитие твердого понимания арифметики необходимо для всей дальнейшей математики.
Содержимое
Введение в умножение
Для целых чисел умножение эквивалентно повторному сложению.
Моделирование умножения на массивы
Использование массивов для моделирования умножения имеет важное значение. Например, 3 × 5 изображается цифрой
.Мы называем 15 произведением 3 и 5, а 3 и 5 множителями 15.
Глядя на строки массива, мы видим, что
3 × 5 = 5 + 5 + 5
Глядя на столбцы массива, мы также видим, что
5 × 3 = 3 + 3 + 3 + 3 + 3
Это иллюстрирует 3 × 5 = 5 × 3.Мы говорим, что умножение коммутативно.
Моделирование умножения путем подсчета пропусков
Подсчет пропусков, такой как чтение 3, 6, 9, 12, 15, . .., является одним из первых введений в повторное сложение и, следовательно, умножение. Это можно проиллюстрировать числовой прямой, как показано ниже для 3 × 5 = 15.
.., является одним из первых введений в повторное сложение и, следовательно, умножение. Это можно проиллюстрировать числовой прямой, как показано ниже для 3 × 5 = 15.
3 × 5 = 15
На числовой прямой то, что 3 + 3 + 3 + 3 + 3 = 5 + 5 + 5, не так очевидно; диаграмма выше показывает 5 + 5 + 5, тогда как 3 + 3 + 3 + 3 + 3 в числовой строке выглядит совершенно иначе.
Подсчет пропусков важен, потому что он помогает детям выучить свои таблицы умножения.
Моделирование умножения по площади
Замена объектов в массиве единичными квадратами или квадратами 1 × 1 вводит площадную модель умножения. Это показано ниже для 3 × 5.
На этом этапе мы используем единичные квадраты вместо счетчиков или звездочек. Мы также можем использовать модель умножения площади для умножения дробей.
Изучение таблицы умножения
Свободное владение таблицами умножения необходимо для дальнейшего изучения математики и повседневной жизни.
Если учащиеся могут добавить однозначное число к двузначному числу, они смогут по крайней мере восстановить таблицу умножения, даже если они еще не развили беглость речи. Поэтому важно убедиться, что учащиеся могут плавно добавлять.
Мы настоятельно рекомендуем учащимся выучить факты умножения до 12 × 12.Это связано прежде всего с тем, что таблица умножения на 12 важна для расчета времени — в году 12 месяцев, 24 часа в день и 60 минут в часе. Знакомство с десятками полезно в повседневной жизни, потому что упаковка в массивы 3 × 4 намного удобнее, чем в массивы 2 × 5. Кроме того, в таблице 12 × 12 есть множество шаблонов, которые можно конструктивно использовать в упражнениях по предалгебре.
Простой подход к изучению таблиц состоит в том, чтобы читать каждую строку наизусть или путем подсчета пропусков.Однако учащимся также необходимо уметь вспоминать отдельные факты, не обращаясь ко всей таблице.
Глядя на таблицу умножения 12 × 12, создается впечатление, что необходимо усвоить 144 факта.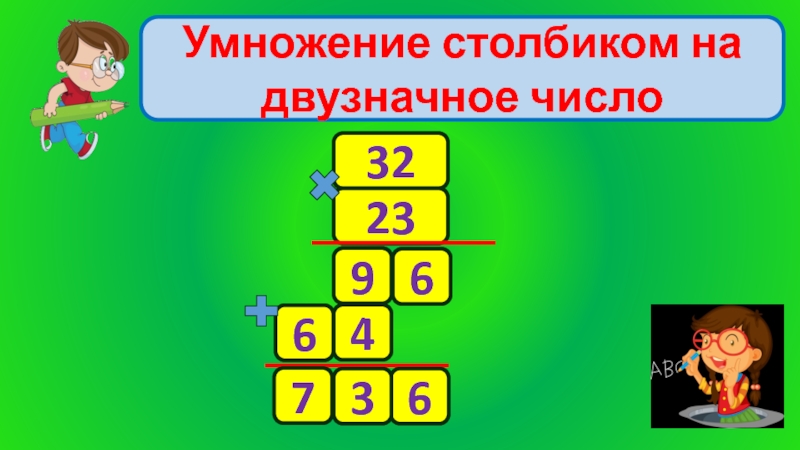
Однако есть несколько методов, которые можно использовать для уменьшения количества фактов, которые необходимо изучить.
- Коммутативность умножения немедленно сокращается с 144 до 78.
- Таблицы умножения на 1 и 10 просты, и их усвоение сокращает количество
фактов, которые необходимо выучить, до 55.
- Таблицы умножения на 2 и 5 также легко выучить, и их усвоение еще больше сокращает количество фактов, которые необходимо выучить, до 36.
- Таблицы умножения на 9 и 11 являются следующими, что легче всего пропустить, потому что 9 и 11 отличаются от 10 на 1. Это сокращает количество фактов до 21.
- Квадраты полезны, и их можно выучить так же, как выучить таблицу умножения.
Это сокращает количество выученных терминов до 15.
Какие бы техники не использовались, целью должно быть свободное владение языком.
Свойства умножения
Коммутативность
Одним из преимуществ подхода массива и площади является то, что свойства умножения более очевидны.
Как обсуждалось выше, поворот массива 3 × 5 на бок показывает, что 3 × 5 = 5 × 3, потому что площадь не изменяется.
| 3 × 5 = 5 × 3 | ||
Мы видели это раньше, рассматривая строки и столбцы по отдельности, но мы также можем сделать это, повернув прямоугольник на бок, то есть вращением.
| 3 × 5 = 5 × 3 |
Собственность произвольной формы
Еще одно важное свойство умножения — ассоциативность, согласно которой
a × (b × c) = (a × b) × c для всех чисел.
Ассоциативность умножения гарантирует, что выражение a × b × c будет однозначным. Обычно мы не учим ассоциативности умножения в 4-7 лет. Вместо этого мы обучаем свойству умножения произвольного порядка, которое является следствием коммутативных и ассоциативных свойств.
Обычно мы не учим ассоциативности умножения в 4-7 лет. Вместо этого мы обучаем свойству умножения произвольного порядка, которое является следствием коммутативных и ассоциативных свойств.
Произвольное умножение
Список чисел можно перемножить в любом порядке, чтобы получить произведение чисел.
Свойство умножения произвольного порядка аналогично свойству сложения произвольного порядка.И ассоциативность, и коммутативность — нетривиальные наблюдения; обратите внимание, что вычитание и деление не коммутативны и не ассоциативны. Когда мы знакомы с арифметическими операциями, мы склонны принимать как ассоциативность, так и коммутативность умножения как должное, как и в случае сложения. Время от времени стоит задумываться о том, что коммутативность и ассоциативность в сочетании дают важные и мощные свойства любого порядка.
Умножение трех целых чисел геометрически соответствует вычислению количества единичных кубов в (или объеме) прямоугольной призмы.Свойство умножения произвольного порядка означает, что мы можем вычислить этот объем, умножив длины сторон в любом порядке. Порядок вычисления соответствует разному увеличению громкости.
Порядок вычисления соответствует разному увеличению громкости.
Дистрибутивность умножения по сложению и вычитанию.
Уравнение 3 × (2 + 4) = (3 × 2) + (3 × 4) является примером дистрибутивности
умножения над сложением. Для массивов это соответствует следующей диаграмме
.
=
По площади соответствует диаграмме ниже.
| Площадь = 3 × 6 |
Умножение также является распределительным по сравнению с вычитанием.
Например, 7 × (10 — 2) = 7 × 10 — 7 × 2. Это можно проиллюстрировать с помощью модели площади.
Ментальные стратегии
Свойство умножения произвольного порядка и закон распределения для умножения позволяют решать некоторые задачи умножения без сложных вычислений.
Использование свойства произвольного порядка
Мы используем свойство произвольного порядка умножения, чтобы упростить вычисления,
изменив порядок, в котором мы выполняем умножение. Например,
Например,
| 1 |
| ||
| 2 | 2 × 17 × 5 = 10 × 17 | ||
| 3 | 25 × 7 × 4 = 25 × 4 × 7 = 100 × 7. |
Иногда это переупорядочивание происходит после того, как мы разложим один из факторов,
, например, когда мы дважды удваиваем, чтобы умножить на четыре, как в
17 × 4 = (17 × 2) × 2 = 34 × 2 = 68.
Этот метод перемещения множителя от одного числа к другому в порядке
для упрощения вычислений имеет применения помимо повторного удвоения, как в
36 × 5 = 18 × (2 × 5) = 180.
Иногда это называют «вдвое и вдвое».
УПРАЖНЕНИЕ 1
Используйте свойство произвольного порядка для выполнения следующих умножений.
Использование распределительного свойства
Мы используем оба дистрибутивных свойства, чтобы упростить некоторые задачи умножения. Например,
7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,
7 × 99 = 7 × (100 — 1) = 700 — 7 = 693,
7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,
и
7 × 98 = 7 × (100 — 2) = 700 — 14 = 686.
Некоторые примеры такого рода можно использовать для разработки концепций, необходимых для формального алгоритма. Такие наблюдения, как 14 × 60 = 14 × 6 × 10 и 14 × 600 = 14 × 6 × 100, являются фундаментальными для понимания алгоритма умножения.
Вычисления, такие как
21 × 7 = 20 × 7 + 1 × 7 = 140 + 7 = 147
можно сделать сначала как мысленную стратегию, а затем использовать в качестве первых примеров в формальном алгоритме. Другие умственные стратегии, связанные с алгоритмом, включают наблюдения, такие как
Другие умственные стратегии, связанные с алгоритмом, включают наблюдения, такие как
200 × 81 = 2 × 81 × 100 = 162 × 100 = 16 200
, где умножение на однозначные кратные степени десяти на самом деле не сложнее, чем умножение на однозначное число и отслеживание разряда.
УПРАЖНЕНИЕ 2
Используйте закон распределения для выполнения следующих умножений.
УПРАЖНЕНИЕ 3
Тождество (a — b) (a + b) = a2 — b2 также полезно для мысленных вычислений.
Например: 49 × 51 = (50 — 1) × (50 + 1) = 2500 — 1 = 2499
Выполните каждое из следующих умножений, используя этот идентификатор.
Письменные стратегии
Алгоритм работает наиболее эффективно, если он использует небольшое количество шагов, применимых в
во всех ситуациях. Таким образом, алгоритмы не прибегают к методам, таким как использование почти двойников, которые эффективны в некоторых случаях, но бесполезны в большинстве случаев.
Стандартный алгоритм не поможет вам умножить два однозначных числа.Важно, чтобы студенты свободно владели умножением двух однозначных чисел, прежде чем приступить к любому формальному алгоритму.
Стандартные алгоритмы
Свойство распределения лежит в основе нашего алгоритма умножения, потому что оно позволяет нам вычислять продукты по одному столбцу за раз, а затем складывать результаты вместе. Его следует усилить арифметически, геометрически и алгоритмически. Например, арифметически мы имеем 6 × 14 = 6 × 10 + 6 × 4, геометрически мы видим то же явление,
и алгоритмически реализуем это в следующем расчете.
Как только этот процесс и схема будут поняты, мы можем перейти к согласованному алгоритму.
Умножение на одну цифру
Сначала мы сокращаем вычисления, отслеживая цифры переноса и добавляя их по мере продвижения. Предыдущий расчет сокращается до
. в зависимости от того, где записаны цифры переноса.
Следует проявлять осторожность даже на этой ранней стадии из-за смеси умножения и сложения.Также обратите внимание, что точное расположение и размер цифры переноса не важны для процесса и варьируются в зависимости от культуры. Когда мы выполняем длинное умножение, в каждом столбце может появиться несколько цифр переноса, и их запись в макет может быть скорее помехой, чем помощью. Поэтому желательно развить достаточную беглость умножения на одну цифру, чтобы учащийся мог выполнять вычисления, такие как
без необходимости явно записывать цифры переноса.Если студенту действительно необходимо записать цифры переноса, мы рекомендуем разместить их над соответствующим столбцом и вычеркнуть их по мере включения в решение.
Умножение на однозначное число, кратное степени десяти
Следующее наблюдение заключается в том, что умножение на однозначное число, кратное десяти, не сложнее, чем умножение на однозначное число, при условии, что мы отслеживаем разряд. Итак, чтобы найти количество секунд в 14 минутах, мы вычисляем
Итак, чтобы найти количество секунд в 14 минутах, мы вычисляем
14 × 60 = 14 × 6 × 10 = 840
и реализовать его в макете, таком как
Точно так же мы можем отслеживать более высокие степени десяти, используя разряды в своих интересах.Итак
14 × 600 = 14 × 6 × 100 = 8400
становится
Для студентов, которые выполнили основное наблюдение в рамках своих мысленных арифметических упражнений, единственное новшество на данном этапе состоит в том, как планировать эти вычисления.
Умножение на двузначное число
Следующий когнитивный скачок происходит, когда мы используем распределимость для умножения двух двузначных чисел.Это реализовано в виде двух продуктов упомянутых выше типов. Например,
74 × 63 = 74 × (60 + 3) = 74 × 60 + 74 × 3
используется в двухэтапном расчете ниже.
Это соответствует разложению по площади, показанному ниже.
На ранних этапах стоит одновременно развивать арифметические, геометрические и алгоритмические аспекты, показанные выше.
Распаковка каждой строки при вычислении длинного умножения с явным использованием распределенности,
как в
Это 74 × 63 = (70 + 4) (60 + 3)
Это также соответствует разложению области
Это расширенное длинное умножение неэффективно, но его можно использовать, чтобы подчеркнуть многократное использование распределенности в процессе. Иллюстрация модели области, используемая в этом случае, позже появится снова как геометрическая интерпретация вычислений в алгебре.
Умножение многозначных чисел
Чем больше цифр в числах, которые мы умножаем, тем больше раз нам нужно применить свойство распределения и тем больше строк будет в нашем вычислении, как показано ниже.
Этот пример соответствует: 5974 × 3 + 5974 × 60 + 5974 × 200 + 5974 × 1000
Кроме того, умножение целых чисел никогда не станет более сложным.
Ссылки вперед
Первое применение умножения, которое скорее всего встретят учащиеся, — это деление.При вычислении деления мы постоянно вычисляем кратные делителю, и отсутствие беглости при умножении является существенным препятствием в этом процессе. Материал этого модуля закладывает основу для умножения, а затем деления дробей и десятичных знаков.
Другие приложения умножения, которые встречаются раньше, включают проценты и потребительскую арифметику. Например, мы рассчитываем цену товара с учетом GST, рассчитывая в 1,1 раза больше его стоимости до GST.
Знакомство с умножением и выражением чисел как произведений множителей открывает путь к одной из основных теорем математики.
Основная теорема арифметики: каждое целое число больше 1 может быть записано как произведение простых чисел, и такое выражение уникально до порядка, в котором написаны множители. Например, 24 = 23 × 3 и 20 = 22 × 5.
Например, 24 = 23 × 3 и 20 = 22 × 5.
Фундаментальная теорема арифметики имеет далеко идущие последствия и может применяться в информатике, кодировании и криптографии с открытым ключом.
И последнее, но не менее важное: хорошее знание арифметики готовит ученика к успеху в алгебре.
Использование таблицы умножения как источника шаблонов
Способность определять закономерности и решать открытые задачи являются важными математическими навыками. Таблицу умножения можно использовать как источник действий для обоих.
Аудиторная деятельность
Нарисуйте сетку 10 × 10 и выделите на ней числа, кратные 9.Какой геометрический узор образуют в таблице числа, кратные 9, и почему он возникает? Какова арифметическая последовательность цифр в таблице умножения на 9 и почему она возникает?
Аудиторная деятельность
Нарисуйте сетку 12 × 12 с написанными на ней числами от 1 до 144. Выберите запись, которая находится не на краю таблицы. Как числа, расположенные непосредственно над ним и непосредственно под ним, связаны с числом в выбранном вами поле? Что вы можете сказать о числах слева и справа от выбранного вами числа?
История
Произведение двух чисел одинаково, независимо от того, как вы его вычисляете или как пишете свой ответ. Подобно тому, как история числа на самом деле связана с развитием числительных, история умножения — это в основном история процессов, которые люди использовали для выполнения вычислений. Развитие индо-арабской системы обозначений разностей позволило реализовать эффективные алгоритмы арифметики и, вероятно, было основной причиной популярности и быстрого принятия этой записи.
Подобно тому, как история числа на самом деле связана с развитием числительных, история умножения — это в основном история процессов, которые люди использовали для выполнения вычислений. Развитие индо-арабской системы обозначений разностей позволило реализовать эффективные алгоритмы арифметики и, вероятно, было основной причиной популярности и быстрого принятия этой записи.
Египетское дублирование
Одним из методов, который сильно отличается от стандартного алгоритма, является египетское дублирование и датируется до 1850 года до нашей эры.Это сводит вычисления к серии удвоений с последним сложением.
Предположим, вы хотите умножить 63 на 22. Сначала напишите
, затем удвойте оба числа и запишите их ниже, чтобы получить
Продолжайте удваивать, пока число в левом столбце не станет настолько большим, насколько может быть, но не больше 22. Итак, мы пишем
| 1 | 63 | |||
| 2 | 126 | |||
| 4 | 252 | |||
| 8 | 504 | |||
| 16 | 1008 |
и остановитесь, потому что 32 больше 22.
Теперь идем в обратном направлении и начинаем с отметки 16; Традиционно это делалось, помещая линию слева от числа, как показано ниже.
Добавление 8 к 16 дает число больше 22, поэтому мы не отмечаем строку выше.
Поскольку 16 + 4 ≤ 22, мы отмечаем строку цифрой 4 в левом столбце.
Поскольку 16 + 4 + 2 = 22, мы отмечаем строку цифрой 2 в левом столбце,
, а поскольку 16 + 4 + 2 + 1> 22, мы не отмечаем верхнюю строку.Остается
| 1 | 63 | |||
| / | 2 | 126 | ||
| / | 4 | 252 | ||
| 8 | 504 | |||
| / | 16 | 1008 |
Если сложить числа в правом столбце отмеченных строк, получится
1008 + 252 + 126 = 1386,
, который является произведением 22 × 63. Это работает, потому что
Это работает, потому что
22 × 63 = (16 + 4 + 2) × 63 = 1008 + 252 + 126 = 1386.
Египетское дублирование основано на распределенности и на том факте, что каждое число может быть записано как сумма степеней 2.
УПРАЖНЕНИЕ 4
Выполните следующее, используя египетское дублирование.
| а | 34 × 56 | б 57 × 34 |
Русский крестьянский метод
Как и египетское дублирование, метод русского крестьянина работает, потому что каждое число имеет уникальное выражение в базе 2.Метод русского крестьянина сводит вычисления к последовательности удвоений и делений пополам с последним сложением.
В качестве алгоритма Русский крестьянский метод работает следующим образом.
- Поместите два числа, которые вы хотите умножить, в верхнюю часть двух столбцов.
- Создайте еще одну строку из двух чисел, удвоив число в первом столбце
и уменьшив вдвое число во втором столбце, игнорируя любые остатки в процессе деления
вдвое.
- Повторяйте предыдущий шаг, пока число в столбце деления пополам не станет равным 1.
- Вычеркните все строки, в которых число в столбце, уменьшенном вдвое, четное.
- Сложите все числа в столбце удвоения, которые не были зачеркнуты.
- Эта сумма равна произведению двух исходных чисел. Например, используя его для вычисления 63 × 22, мы пишем
| | | |
| 126 | 11 | |
| 252 | 5 | |
| | | |
| 1008 | 1 |
, затем вычислите 126 + 252 + 1008 = 1386 и сделайте вывод, что 63 × 22 = 1386.
Эта процедура работает всегда, но почему?
Предположим, мы хотим умножить 63 на 16. Мы начинаем с записи 63 и 16 в верхней части
двух столбцов, а под каждым мы записываем числа, которые мы получаем удвоением одного и
деления другого вдвое.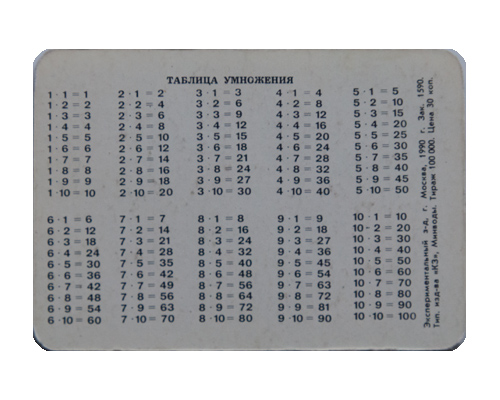
| | | |
| | | |
| | | |
| | | |
| 1008 | 1 |
В этом случае произведение двух чисел в каждой строке идентично произведению чисел непосредственно выше.Например, 126 × 8 = 63 × 16. Следуя цепочке продуктов, мы заключаем, что 63 × 16 = 1008 × 1 = 1008. Это работает особенно легко, потому что 16 — это степень 2.
Предположим, вместо этого мы хотим умножить 63 на 14.
| | | |
| 126 | 7 | |
| 252 | 3 | |
| 504 | 1 |
Поскольку в первом делении нет остатков, 126 × 7 = 63 × 14, и первым шагом было просто переформулировать произведение по-другому. Мы можем смело вычеркнуть 63 × 14 и представить, что его никогда не было. Однако на втором шаге мы проигнорировали остаток, поэтому между двумя строками есть разница; в частности, 126 × 7 = 252 × 3 + 126 × 1. Обратите внимание, что разница между продуктом в двух строках составляет 126, число в верхней строке в столбце удвоения. Так как остаток от деления на 2 может быть только 0 или 1, на каждом шаге мы либо точно переформулируем задачу, либо на одну копию числа в столбце удвоения.В этом вычислении мы проигнорировали одну копию 126 и одну копию 252, прежде чем прийти к нашему выражению 504 × 1. Таким образом, наш исходный продукт, 63 × 14, должен быть равен 504 + 252 + 126.
Мы можем смело вычеркнуть 63 × 14 и представить, что его никогда не было. Однако на втором шаге мы проигнорировали остаток, поэтому между двумя строками есть разница; в частности, 126 × 7 = 252 × 3 + 126 × 1. Обратите внимание, что разница между продуктом в двух строках составляет 126, число в верхней строке в столбце удвоения. Так как остаток от деления на 2 может быть только 0 или 1, на каждом шаге мы либо точно переформулируем задачу, либо на одну копию числа в столбце удвоения.В этом вычислении мы проигнорировали одну копию 126 и одну копию 252, прежде чем прийти к нашему выражению 504 × 1. Таким образом, наш исходный продукт, 63 × 14, должен быть равен 504 + 252 + 126.
В общем, может быть несколько строк, в которых у нас нет остатка, и несколько строк, в которых мы игнорируем остатки. Вычеркиваем те строки, для которых деление на 2 привело к точному пересчету продукта в предыдущей строке; это точно соответствует строкам с четными числами в столбце, уменьшенном вдвое.Числа, которые не были зачеркнуты в столбце удвоения, соответствуют остаткам, и их сумма равна исходному произведению.
Итальянский или решетчатый
Другой метод, известный как итальянский метод или метод решеток, по сути, является реализацией расширенной версии стандартного алгоритма, но в другой схеме. Этот метод очень старый и мог бы стать общепринятым, если бы его не было трудно печатать. Впервые он появился в Индии, но вскоре появился в работах китайцев и арабов.От арабов он попал в Италию, и его можно найти во многих итальянских рукописях XIV и XV веков.
Здесь показано умножение 34 × 27.
34 × 27 = 918
В верхнем правом прямоугольнике вычисляется 4 × 2. Цифра 8 помещается в нижний треугольник, а 0 — в верхний.
Затем вычисляется 3 × 2 и вводится результат, как показано.
В правом нижнем прямоугольнике вычислено 4 × 7.Цифра 8 помещается в нижний треугольник, а цифра 2 — в верхний. Таким же образом записывается и результат 3 × 7.
Зеленая диагональ содержит единицы.
Синяя диагональ содержит десятки.
Коричневая диагональ содержит сотни.
Теперь цифры суммируются по каждой диагонали, начиная справа, и каждый результат
записывается, как показано. Обратите внимание, что существует «перенос» от «десятков по диагонали» к «сотням по диагонали»
УПРАЖНЕНИЕ 5
Используйте метод решетки для выполнения каждого из следующих умножений
| а | 35 × 73 | б | 67 × 87 | c | 453 × 235 |
Список литературы
История математики: Введение, 3-е издание, Виктор Дж.Кац, Эддисон-Уэсли, (2008)
История математики, Д. Э. Смит, Дуврские публикации, Нью-Йорк, (1958)
https://en.wikipedia.org/wiki/Ancient_Egyptian_multiplication
Ответы к упражнениям
Упражнение 1
УПРАЖНЕНИЕ 2
УПРАЖНЕНИЕ 3
УПРАЖНЕНИЕ 4
УПРАЖНЕНИЕ 5
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений Австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Умножение на процент — Excel
Умножить весь столбец чисел на процент
Рассмотрим пример таблицы, подобной той, что на рисунке, в которой у нас есть несколько чисел, которые нужно умножить на 15 процентов. Даже если столбец содержит 100 или 1000 ячеек данных, Excel все равно может обработать их за несколько шагов.
Вот как это сделать:
Введите числа, которые вы хотите умножить на 15%, в столбец.
В пустой ячейке введите процентное значение 15% (или 0,15), а затем скопируйте это число, нажав Ctrl-C.
Выберите диапазон ячеек A1: A5 (перетащив столбец вниз).
Щелкните правой кнопкой мыши выделенную ячейку, а затем выберите Специальная вставка (не , а щелкните стрелку рядом с Специальная вставка ).

Щелкните Значения > Умножьте , затем щелкните ОК .
В результате все числа умножаются на 15%.
Совет: Вы также можете умножить столбец, чтобы вычесть процент.Чтобы вычесть 15%, добавьте знак минуса перед процентом и вычтите процент из 1, используя формулу = 1- n % , в которой n — процент. Чтобы вычесть 15%, используйте в качестве формулы = 1-15% .
Умножить весь столбец чисел на процент
В этом примере нам нужно умножить всего несколько чисел на 15 процентов. Даже если в столбце 100 или 1000 ячеек данных, Excel в Интернете все равно может обработать это за несколько шагов. Вот как:
Вот как:
Введите = A2 * $ C $ 2 в ячейке B2. (Обязательно включите в формулу символ $ перед C и перед 2.)
Символ $ делает ссылку на C2 абсолютной, что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel в Интернете изменит формулу на = A3 * C3, что не сработает, потому что в C3 нет значения.
Перетащите формулу в B2 вниз в другие ячейки в столбце B.
Совет: Вы также можете умножить столбец, чтобы вычесть процент.


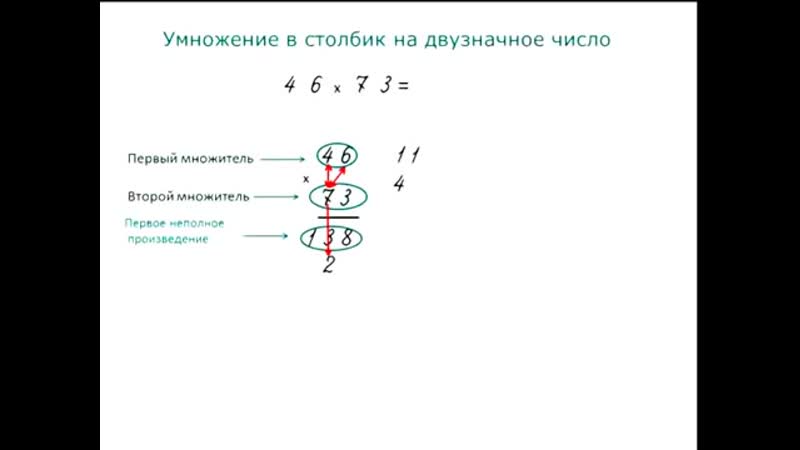

 // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
// А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с. Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.
Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.


 Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную.
Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную. Модуль «Подсчет и разметка»).
Модуль «Подсчет и разметка»).
