Опубликовано правила, примеры, решения, умножение дробей с разными знаменателями
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32).
Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.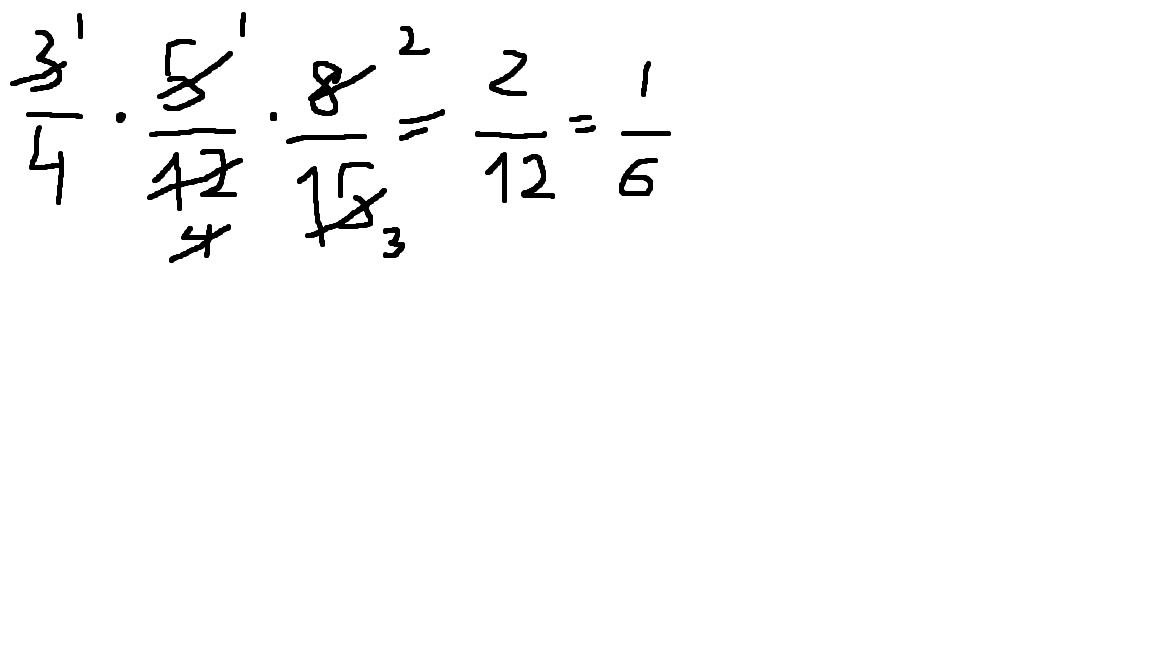
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: .
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10.
В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел.
Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения.
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Дробь 12 3/4 в виде десятичной дроби
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Как записать 12 целых 3/4 в виде десятичной дроби?
Ответ: Дробь 12 3/4 в десятичном виде это 12,75
12
=12,75
Объяснение конвертации дроби 12 3/4 в десятичную
Для того, чтобы перевести дробь 12 3/4 (12¾) в десятичный формат необходимо разделить числитель 3 на знаменатель 4. Результат деления:
3 ÷ 4 = 12,75
и прибавить целую часть (12):
0.75 + 12 = 12,75
Другой способ перевод дроби 12 целых 3/4 в десятичный формат заключается в том, чтобы перевести эту смешанную дробь в неправильную дробь.
Для этого необходимо сперва умножить целую часть (12) на знаменатель (4):
12 × 4 = 48
после чего прибавить результат к числителю (3):
48 + 3 = 51
и в конце разделить результат на числитель (4):
= 51 ÷ 4 =12,75
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/fraction-as-a-decimal/12—3—4
<a href=»https://calculat.io/ru/number/fraction-as-a-decimal/12—3—4″>Дробь 12 3/4 в виде десятичной дроби — Calculatio</a>
О калькуляторе «Конвертер обыкновенных дробей в десятичные»
Данный онлайн-конвертер обыкновенных дробей в десятичные является полезным инструментом, предназначенным для легкого преобразовывания любой дроби в ее эквивалентную десятичную форму. Например, он может помочь узнать как записать 12 целых 3/4 в виде десятичной дроби? Независимо от того, являетесь ли вы учеником, студентом или профессионалом, этот конвертер может сэкономить ваше время и усилия при выполнении ручных вычислений.
Чтобы использовать этот конвертер, просто введите дробь, которую вы хотите преобразовать, в соответствующие поля. Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 12 3/4 в его десятичный эквивалент, вы введете ’12’ как целую часть, ‘3’ как числитель и ‘4’ как знаменатель.
После того, как вы ввели дробь, нажмите кнопку ‘Конвертировать’, чтобы получить результаты. Конвертер отобразит десятичный эквивалент дроби, который в нашем случае равен 12,75. Кроме того, он предоставит пошаговое объяснение процесса преобразования, чтобы вы могли понять, как был получен десятичный эквивалент дроби. Если результат является периодической десятичной дробью, конвертер отобразит повторяющийся шаблон, используя скобки для обозначения повторяющихся цифр.
Одной из ключевых особенностей этого конвертера является его способность выводить периодические десятичные дроби. В математике периодическая десятичная дробь — это десятичная дробь, в которой есть повторяющийся шаблон цифр, например, 0,33333.
.. или 0,142857142857… Это отличает такие дроби от непериодических десятичных дробей, которые заканчиваются после определенного числа цифр, например, 0,5 или 0,75.
Использование этого онлайн-конвертера дробей в десятичные является быстрым и простым способом преобразования любой дроби в ее десятичный эквивалент. Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Таблица конвертации обыкновенных дробей в десятичные
| Дробь | Десятичная |
|---|---|
| 12 3/1 | 15 |
| 12 3/2 | 13,5 |
| 12 3/3 | 13 |
| 12 3/4 | 12,75 |
| 12 3/5 | 12,6 |
| 12 3/6 | 12,5 |
| 12 3/7 | 12,(428571) |
| 12 3/8 | 12,375 |
| 12 3/9 | 12,(3) |
| 12 3/10 | 12,3 |
| 12 3/11 | 12,(27) |
| 12 3/12 | 12,25 |
| 12 3/13 | 12,(230769) |
| 12 3/14 | 12,2(142857) |
| 12 3/15 | 12,2 |
| 12 3/16 | 12,1875 |
| 12 3/17 | 12,(1764705882352941) |
| 12 3/18 | 12,1(6) |
| 12 3/19 | 12,(157894736842105263) |
| 12 3/20 | 12,15 |
| 12 3/21 | 12,(142857) |
| 12 3/22 | 12,1(36) |
| 12 3/23 | 12,(1304347826086956521739) |
| 12 3/24 | 12,125 |
| 12 3/25 | 12,12 |
| 12 3/26 | 12,1(153846) |
| 12 3/27 | 12,(1) |
| 12 3/28 | 12,10(714285) |
| 12 3/29 | 12,(1034482758620689655172413793) |
| 12 3/30 | 12,1 |
FAQ
Как записать 12 целых 3/4 в виде десятичной дроби?
Дробь 12 3/4 в десятичном виде это 12,75
Смотрите также
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | круг (4) | | ||
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| Найти том | сфера (2) | | ||
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
Умножение дробей | Умножение дробей
Умножение дробей начинается с умножения заданных числителей, за которым следует умножение знаменателей.
Затем полученная дробь еще больше упрощается и при необходимости сокращается до наименьших членов. Давайте узнаем больше об умножении дробей, как умножать дроби на целые числа, как умножать неправильные дроби, умножать смешанные дроби и правила умножения дробей в этой статье.
| 1. | Как умножать дроби? |
| 2. | Правила умножения дробей |
| 3. | Умножение дробей с одинаковым знаменателем |
| 4. | Умножение дробей с разными знаменателями |
| 5. | Умножение дробей на целые числа |
| 6. | Умножение дробей со смешанными числами |
| 7. | Как умножать неправильные дроби? |
| 8. | Часто задаваемые вопросы об умножении дробей |
Как умножать дроби?
Умножение дробей не похоже на сложение или вычитание дробей, где знаменатель должен быть одинаковым.
Здесь можно легко перемножить любые две дроби с разными знаменателями. Единственное, что нужно иметь в виду, это то, что дроби не должны быть в смешанной форме, они должны быть либо правильными дробями, либо неправильными дробями. Давайте научимся умножать дроби, выполнив следующие шаги:
- Шаг 1: Умножьте числители.
- Шаг 2: Умножьте знаменатели.
- Шаг 3: Сократите полученную дробь до наименьшего значения.
Примечание: Другой способ умножения дробей состоит в том, чтобы упростить и сократить дроби между собой, а затем перемножить числители вместе и знаменатели вместе, чтобы получить конечный продукт.
Давайте разберем эти шаги на примере.
Пример: Умножьте следующие дроби: 1/3 × 3/5.
Решение: Начнем с умножения числителей: 1 × 3 = 3, затем умножим знаменатели: 3 × 5 = 15. Это можно записать как: (1 × 3)/(3 × 5) = 3 /15.
Теперь уменьшите это значение до самой низкой формы. 3 — это наибольший общий делитель (НОД) 3 и 15, поэтому разделите и 3, и 15 на 3, чтобы упростить дробь. Следовательно, 1/3 × 3/5 = 1/5.
Метод 2: Теперь давайте воспользуемся другим методом умножения этих дробей, где мы можем упростить дроби между собой, а затем перемножить числители вместе, затем знаменатели вместе, чтобы получить конечный продукт. Здесь будет 1/3 × 3/5→ 1/1 × 1/5 = 1/5, и мы получим тот же ответ.
Правила умножения дробей
При умножении дробей следует помнить следующие правила:
- Правило 1: Первое правило состоит в том, чтобы преобразовать смешанные дроби в неправильные дроби, если таковые имеются. Затем умножьте числители данных дробей.
- Правило 2: Умножьте знаменатели отдельно.
- Правило 3: Упростите полученное значение до наименьшего члена.
- Правило 4: Еще один простой способ умножения дробей состоит в том, чтобы упростить и сократить дроби между собой, а затем перемножить числители вместе и знаменатели вместе, чтобы получить конечный продукт.
Эти правила можно применить к любым двум дробям, чтобы найти их произведение. Теперь давайте изучим отдельные случаи умножения дробей с разными типами дробей.
Умножение дробей с одинаковым знаменателем
Умножение дробей с одинаковым знаменателем не меняет правила умножения дробей. Дроби, имеющие одинаковые знаменатели, называются дробями. Хотя сложение и вычитание одинаковых дробей отличается от сложения и вычитания разнородных дробей, в случае умножения и деления метод остается тем же. Мы умножаем числители, затем знаменатели, а затем дробь сокращается до наименьших членов.
Пример: Умножить 1/3 × 5/3
Решение: Мы можем умножить эти дроби, используя следующие шаги.
- Шаг 1: Умножьте числители, 1 × 5 = 5.
- Шаг 2: Умножьте знаменатели, 3 × 3 = 9.
- Шаг 3: Произведение, которое мы получаем, равно 5/9. Это не может быть уменьшено дальше, поэтому ответ 5/9.
Это не может быть уменьшено дальше, поэтому ответ 5/9.Умножение дробей с разными знаменателями
Умножение дробей с разными знаменателями точно такое же, как умножение одинаковых дробей. Давайте разберемся в этом на примере.
Пример: Умножьте 4/12 × 16/24.
Мы можем умножить эти дроби, используя следующие шаги:
- Шаг 1: Умножьте числители, 4 × 16 = 64.
- Шаг 2: Умножьте знаменатели, 12 × 24 = 288.
- Шаг 3: Произведение, которое мы получаем, равно 64/288. Это может быть уменьшено до 2/9. Таким образом, 2/9 является ответом.
Альтернативный метод
Те же дроби можно умножить другим методом, в котором мы упрощаем дроби между собой, а затем умножаем числители, затем знаменатели, чтобы получить конечный продукт.
Пример: Умножьте 4/12 × 16/24.
Умножим данные дроби, используя следующие шаги:
- Шаг 1: Упростим данные дроби между собой. Другими словами, эти дроби можно сократить до 1/3 × 2/3.
- Шаг 2: Умножим числители, 1 × 2 = 2.
- Шаг 3: Теперь умножим знаменатели, 3 × 3 = 9.
- Шаг 4: Следовательно, произведение, которое мы получаем, равно 2/9.
Другими словами, эти дроби можно сократить до 1/3 × 2/3.Умножение дробей на целые числа
Умножение дробей на целые числа — простая идея. Поскольку мы знаем, что умножение — это многократное сложение одного и того же числа, этот факт можно применить и к дробям.
Умножение дробей на целые числа Визуальная модель
Рассмотрим следующий пример: 4 × 2/3. Это означает, что 2/3 добавляется 4 раза. Представим этот пример с помощью визуальной модели. Четырежды две трети представлены как:
Шаги умножения дробей на целые числа
Чтобы умножать дроби с целыми числами, мы используем простое правило умножения числителей, затем умножения знаменателей, а затем сокращения их до наименьших членов.
Однако в случае целых чисел мы запишем их в дробной форме, поставив «1» в знаменателе. Давайте разберемся в этом на примере.
Пример: Умножить: 5 × 3/4
Решение: Давайте используем следующие шаги, чтобы умножить данную дробь на целое число.
- Шаг 1: Здесь 5 — это целое число, которое можно записать как 5/1, а затем его можно умножить, как мы умножаем обычные дроби.
- Шаг 2: Это означает, что нам нужно умножить 5/1 × 3/4
- Шаг 3: Умножьте числители, 5 × 3 = 15
- Шаг 4: Умножьте знаменатели, 1 × 4 = 4
- Шаг 5: Полученное произведение равно 15/4, и его нельзя уменьшить дальше.
- Шаг 6: Поскольку 15/4 — неправильная дробь, мы изменим ее на смешанную дробь, 15/4 = \(3\frac{3}{4}\)
Умножение смешанных дробей
Смешанные числа или смешанные дроби — это дроби, состоящие из целого числа и правильной дроби, например \(2\frac{3}{4}\), где 2 — целое число, а 3/4 — правильная дробь.
Для умножения смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если число равно \(2\frac{2}{3}\), нам нужно изменить его на 8/3. Давайте разберемся в этом с помощью примера.
Пример: Умножение \(2\frac{2}{3}\) и \(3\frac{1}{4}\)
Решение: Для умножения дробей с помощью смешанные числа.
- Шаг 1: Измените заданные смешанные дроби на неправильные, т. е. (8/3) × (13/4).
- Шаг 2: Умножьте числители неправильных дробей, а затем умножьте знаменатели. Это даст 104/12.
- Шаг 3: Теперь уменьшите полученную дробь до наименьшего значения, что сделает ее равной 26/3.
- Шаг 4: Далее, преобразуйте ответ обратно в смешанную дробь, которая будет \(8\frac{2}{3}\).
Как умножать неправильные дроби?
Теперь разберемся с умножением неправильных дробей.
Мы уже знаем, что неправильная дробь — это та, у которой числитель больше знаменателя. При умножении двух неправильных дробей часто получается неправильная дробь. Например, чтобы умножить 3/2 × 7/5, две неправильные дроби, нам нужно выполнить следующие шаги:
- Шаг 1: Умножьте числители и знаменатели. (3 × 7)/(2 × 5) = 21/10.
- Шаг 2: Дробь 21/10 не может быть приведена к наименьшему члену.
- Шаг 3: Следовательно, ответ равен 21/10, что можно записать как \(2\frac{1}{10}\).
Советы и приемы умножения дробей
Вот несколько важных советов и приемов, которые помогут при умножении дробей.
- Обычно учащиеся упрощают дробь после умножения. Однако, чтобы упростить расчеты, проверьте, не находятся ли две дроби, которые нужно умножить, в младших формах. Если нет, сначала упростите их, а затем умножьте. Например, 4/12 × 5/13 будет сложно умножить напрямую.
- Теперь, если мы сначала упростим дробь, мы получим 1/3 × 5/13 = 5/39
- Упрощение также можно выполнить для двух дробей. Если между числителем одной из дробей и знаменателем другой дроби есть общий множитель, можно их упростить и продолжить. Например, 5/28 × 7/9можно упростить до 5/4 × 1/9 перед умножением.
☛ Похожие темы
- Калькулятор умножения дробей
- Обратное число дробей
- Умножение десятичных дробей
- Умножение и деление целых чисел
- Сложение дробей
- Вычитание дробей
- Разделение дробей
Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Умножение дробей Примеры
Пример 1: Найдите произведение дробей: 1/4 × 5/8
Решение:
Для умножения дробей с разными знаменателями, как указано в 1/4 × 5/8, мы начинаем с умножения числители: 1 × 5 = 5. После этого умножаем знаменатели: 4 × 8 = 32. Это можно записать так: (1 × 5)/(4 × 8) = 5/32. Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32 9.0953
Пример 2: Изменяет ли правило умножения дробей умножение дробей на целые числа? Обоснуйте свой ответ и найдите произведение дробей: 4 × 6/5
Решение:
Нет, умножение дробей на целые числа не меняет правила умножения дробей. Нам просто нужно записать целое число в форме дроби. В этом случае 4 будет записано как 4/1, и тогда мы будем использовать тот же метод. Итак, мы будем умножать 4/1 × 6/5. При умножении числителей мы получаем 4 × 6 = 24. При умножении знаменателей мы получаем 1 × 5 = 5.
Следовательно, результирующее произведение равно 24/5, которое нельзя уменьшить дальше. Поэтому мы изменим эту неправильную дробь 24/5 на смешанную дробь, чтобы представить ее как ответ: 24/5 = \(4\frac{4}{5}\).Пример 3: Найдите произведение дробей: 5/4 × 5/2 × 5/3
Решение:
Для умножения трех дробей мы сначала умножим все три числителя, а затем все три знаменателя. Затем мы упростим окончательный ответ.
⇒ 5/4 × 5/2 × 5/3
⇒ (5 × 5 × 5)/(4 × 2 × 3)
⇒ 125/24
Следовательно, 5/4 × 5/2 × 5/3 = 125/24 или \(5\frac{5}{24}\)
Следовательно, результирующее произведение равно 24/5, которое нельзя уменьшить дальше. Поэтому мы изменим эту неправильную дробь 24/5 на смешанную дробь, чтобы представить ее как ответ: 24/5 = \(4\frac{4}{5}\).перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать его с помощью реального приложения.
Записаться на бесплатный пробный урок
Практические вопросы по умножению дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об умножении дробей
Как умножать дроби?
Умножение дробей означает нахождение произведения двух или более дробей.
Метод, используемый для умножения дробей, отличается от сложения и вычитания дробей. Чтобы умножить любые две дроби, мы следуем шагам, указанным ниже. Давайте умножим 7/8 × 2/6, чтобы понять шаги.
- Умножьте числители. Итак, 7 × 2 = 14, .
- Умножьте знаменатели. Это означает, что 8 × 6 = 48, .
- Полученная дробь равна 14/48. Упростите полученную дробь до наименьших членов. Упрощение дроби 14/48 дает нам 7/24. Следовательно, ответ 7/24.
- Еще один способ умножения этих дробей заключается в том, что мы можем упростить дроби между собой, а затем перемножить числители вместе, а затем вместе знаменатели, чтобы получить конечный продукт. Здесь будет 7/8 × 2/6 → 7/8 × 1/3 = 7/24 .
Каковы правила умножения дробей?
Есть четыре простых правила умножения дробей.
- Сначала умножьте числители.
- Затем перемножьте знаменатели обеих дробей, чтобы получить результирующую дробь.
- Затем нам нужно упростить полученную дробь, чтобы получить окончательный ответ. Это можно понять на простом примере → 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.
- Другой способ умножения дробей заключается в том, что мы можем сократить дроби между собой, а затем перемножить числители вместе, затем вместе знаменатели, чтобы получить конечный продукт. Более простой способ можно сделать следующим образом: → 2/6 × 4/7 = 1/3 × 4/7 = (1 × 4)/(3 × 7) = 4/21.
Это можно понять на простом примере → 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.Как умножать смешанные дроби?
Следующие шаги можно использовать для умножения смешанных дробей. Умножим 1/4 × \(3\frac{1}{2}\).
- Замените смешанную дробь на неправильную. Здесь \(3\frac{1}{2}\) станет 7/2. Итак, теперь нам нужно умножить 1/4 × 7/2.
- Умножьте числители, а затем знаменатели. Это означает, что (1 × 7)/(4 × 2) = 7/8.
- Убедитесь, что ответ указан в самом низком выражении. Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.
Как умножать дроби на целые числа?
Чтобы понять умножение дроби на целое число, мы можем взять простой числовой пример 2/7 × 3.
Начните с перезаписи целого числа (3 в этом примере) в виде дроби 3/1. Теперь мы можем применить шаги, которые мы используем для умножения дробей. Это означает, что 2/7 × 3/1 = (2 × 3)/(7 × 1) = 6/7.
Как умножать дроби с одинаковым знаменателем?
Умножение дробей с одинаковыми знаменателями аналогично умножению других правильных дробей. Давайте разберемся в этом на примере. Умножим 4/5 × 3/5. Умножаем числители, то есть 4 × 3 = 12. Затем умножаем знаменатели, то есть 5 × 5 = 25. Это даст нам произведение как 12/25. Поскольку это нельзя уменьшить дальше, ответом будет 12/25.
Как умножать дроби с разными знаменателями?
Умножение дробей с разными знаменателями не меняет правила умножения дробей. Давайте разберемся в этом на примере. Умножьте 2/6 × 3/4. Мы можем умножить эти дроби, выполнив следующие шаги:
- Умножить числители, 2 × 3 = 6.
- Умножьте знаменатели, 6 × 4 = 24.
- Продукт, который мы получаем, 6/24. Это можно уменьшить до 1/4, следовательно, ответ 1/4.
Это можно уменьшить до 1/4, следовательно, ответ 1/4.Как умножить дробь на дробь?
Умножение двух дробей — простейшая форма арифметических операций между двумя дробями. Сначала умножаются числители обеих дробей, а затем умножаются знаменатели. Затем полученная дробь при необходимости упрощается до наименьших членов.
Чем умножение дробей отличается от сложения дробей?
Сложение дробей отличается от умножения дробей. При умножении сначала умножаются числители двух дробей, затем умножаются знаменатели, чтобы получить результирующую дробь. Однако в процессе сложения дробей нам сначала нужно сделать знаменатели обеих дробей равными, а затем сложить числители, чтобы получить результирующую дробь. Кроме сложения или вычитания дробей, мы не складываем и не вычитаем знаменатели отдельно.
Как умножать десятичные дроби?
Чтобы умножить дроби на десятичные, мы преобразуем десятичное число в дробь, а затем используем те же правила умножения дробей.
Например, давайте умножим 5/7 × 0,6
- Здесь мы преобразуем 0,6 в дробную форму, что даст 6/10.
- Теперь умножим 5/7 × 6/10 обычным способом.
- Умножим числители, 5 × 6 = 30.
- Умножим знаменатели, 7 × 10 = 70.
- Таким образом, результирующая дробь будет 30/70.
- Упростив полученную дробь, мы получим произведение как 3/7.
Как научить умножению дробей?
Умножению дробей можно научиться так же, как умножению целых чисел. Важным аспектом перед умножением дробей является преобразование смешанной дроби в неправильную дробь. После этого шага мы умножаем числители обеих дробей, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Для обучения умножению дробей можно использовать следующие способы:
- Максимально используйте визуальные модели для представления концепции. Учить учащихся понимать использование и процесс умножения дробей.
- Используйте рабочие листы для умножения дробей после обучения понятию.
