Опубликовано | 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
6/2(2+1)= Как решается этот проклятый пример: demakhin — LiveJournal
?Делал по нему опросы
И сейчас попробую обосновать мою новую точку зрения, которая теперь выглядит так:
Дело в том, что между алгеброй и арифметикой есть разница в порядке действий:
Теперь понятно, почему инженерный калькулятор показывает ответ: 1.
Он не сломался. Он алгебраический.
Алгебраический калькулятор считает по правилам алгебры.
Осталось понять, алгебраический это пример или арифметический. От этого будет зависеть ответ.
Букв в примере нет, однако, в нем есть пропущенный знак умножения перед скобкой:
Случаи возможного пропуска знака умножения:
- Между буквенными множителями;
- Между числовым и буквенным множителем;
- Между множителем и скобкой;
- Между выражениями в скобках.
И получается, что если выражение (2+1) заменить на икс, то написание 6/2Х читается как «шесть, разделить на два икса».
Тогда ответ: 1.
Но почему тогда самая умная штука на Земле — Гугл-поисковик считает, что ответ 9?
Потому что и Гугл и смартфон считают по арифметическим правилам.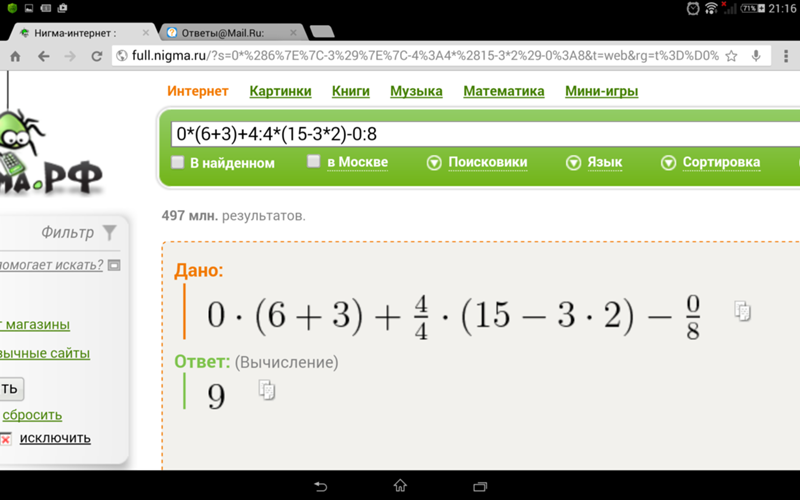
Но вот тут есть тонкий момент. Арифметические правила должны, по-правильному то, действовать при указании знака умножения. Так, как я написал здесь:
Тут уже нет оснований применять правила алгебры, в которых пропущенный знак умножения считается неразрывным. И ответ получается: 9.
Вывод:
Всё зависит от того, алгебра это или арифметика.
Еще интересные штуки:
Задачи, ломающие мозг (с ответами, спрятанными под спойлер)
Тренировка ума развивальщика предприятий
Подписывайся, мыслитель!
Subscribe
Как мой друг развивальщик развалил схему воровства в департаменте продаж
Снова мой излюбленный формат — интервьюирование друзей. Эти истории никогда бы не увидели свет, т.к. их герои никогда и не собирались ни о чем…
Проблема пожарной безопасности детских лабиринтов в торговых центрах
Вот эти детские лабиринты в торговых центрах.
Внутри сотня детей. Если в ТЦ будет пожар, такой лабиринт — это западня, из него не выбраться. Из…Как работать над профессиональным блогом
Писать я начал в 2015 году. Могу ли я что-то сказать об этом, когда у меня всего лишь 10’000 подписчиков по всем соцсетям, а у кого-то их…
Внутри сотня детей. Если в ТЦ будет пожар, такой лабиринт — это западня, из него не выбраться. Из…Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Как мой друг развивальщик развалил схему воровства в департаменте продаж
Снова мой излюбленный формат — интервьюирование друзей. Эти истории никогда бы не увидели свет, т.к. их герои никогда и не собирались ни о чем…
Проблема пожарной безопасности детских лабиринтов в торговых центрах
Вот эти детские лабиринты в торговых центрах. Внутри сотня детей. Если в ТЦ будет пожар, такой лабиринт — это западня, из него не выбраться. Из…
Как работать над профессиональным блогом
Писать я начал в 2015 году.
Могу ли я что-то сказать об этом, когда у меня всего лишь 10’000 подписчиков по всем соцсетям, а у кого-то их…
Могу ли я что-то сказать об этом, когда у меня всего лишь 10’000 подписчиков по всем соцсетям, а у кого-то их…Калькулятор комбинаций (nCr)
Калькулятор Использование
Калькулятор комбинаций найдет количество возможных комбинаций, которые можно получить, взяв выборку предметов из большего набора. По сути, он показывает, сколько различных возможных подмножеств можно составить из большего набора. Для этого калькулятора порядок элементов, выбранных в подмножестве, не имеет значения.
- Факториал
- Есть! способы расположения n различных объектов в упорядоченную последовательность, перестановки, где n = r.
- Комбинация
- Количество способов выбрать выборку из r элементов из набора n различных объектов, где порядок не имеет значения и замены не допускаются.
- Перестановка
- Количество способов выбрать выборку из r элементов из набора n различных объектов, где порядок имеет значение, а замены запрещены. Когда n = r, это сводится к n!, простому факториалу n.
- Замена комбинации
- Количество способов выбрать выборку из r элементов из набора n различных объектов, где порядок не имеет значения и разрешены замены.
- Замена замены
- Количество способов выбрать выборку из r элементов из набора n различных объектов, где порядок имеет значение и разрешены замены.
- №
- набор или популяция
- р
- подмножество n или набор образцов
Когда n = r, это сводится к n!, простому факториалу n.
Формула комбинаций:
\( C(n,r) = \dfrac{n!}{( r! (n — r)! )} \)
Для n ≥ r ≥ 0,
Формула показывает нам, сколько способов можно получить выборку из «r» элементов из большего набора «n» различимых объектов, где порядок не имеет значения и повторения не допускаются. [1] «Число способов выбрать r неупорядоченных исходов из n возможностей».
Также называется r-комбинацией или «n выберите r» или биномиальный коэффициент . В некоторых ресурсах в нотации используется k вместо r, поэтому вы можете увидеть, что это называется k-комбинацией или «n выбирает k».
Комбинированная задача 1
Выберите 2 приза из набора из 6 призов
Вы заняли первое место в конкурсе и можете выбрать 2 приза из таблицы, в которой 6 призов пронумерованы от 1 до 6. Сколько различные комбинации из 2 призов вы могли бы выбрать?
В этом примере мы берем подмножество из 2 призов (r) из большего набора из 6 призов (n). Глядя на формулу, мы должны вычислить «6 выбирают 2».
C (6,2)= 6!/(2! * (6-2)!) = 6!/(2! * 4!) = 15 возможных призовых комбинаций
15 возможных комбинаций {1 ,2}, {1,3}, {1,4}, {1,5}, {1,6}, {2,3}, {2,4}, {2,5}, {2,6 }, {3,4}, {3,5}, {3,6}, {4,5}, {4,6}, {5,6}
Комбинированная задача 2
Выберите 3 учащихся из класс 25
Учительница выбирает 3 учеников из своего класса для участия в конкурсе правописания.
Она хочет выяснить, сколько уникальных команд по 3 человека можно создать из ее класса из 25 человек.
В этом примере мы берем подмножество из 3 учеников (r) из большей группы из 25 учеников (n). Глядя на формулу, мы должны вычислить «25 выбирают 3».
C (25,3)= 25!/(3! * (25-3)!)= 2300 возможных команд
Комбинированная задача 3
Выберите 4 пункта меню из 18 пунктов меню
Ресторан просит своих постоянных клиентов выбрать из меню 4 любимых блюда. Если в меню 18 позиций на выбор, сколько разных ответов могут дать клиенты?
Здесь мы берем подмножество из 4 пунктов (r) из большего меню из 18 пунктов (n). Следовательно, мы должны просто найти «18 выбирают 4».
C (18,4)= 18!/(4! * (18-4)!)= 3060 Возможные ответы
Задача о рукопожатии
Сколько в группе из n человек возможны разные рукопожатия?
Сначала найдем всего возможных рукопожатий.
То есть, если каждый человек один раз пожал руку каждому другому человеку в группе, каково общее количество рукопожатий?
Можно предположить, что каждый человек в группе совершит в общей сложности n-1 рукопожатий. Поскольку есть n человек, всего будет n раз (n-1) рукопожатий. Другими словами, общее количество людей, умноженное на количество рукопожатий, которое может сделать каждый, и будет общим числом рукопожатий. Группа из 3 человек составит в общей сложности 3 (3-1) = 3 * 2 = 6. Каждый человек регистрирует 2 рукопожатия с двумя другими людьми в группе; 3*2.
Всего рукопожатий = n(n-1)
Однако это включает каждое рукопожатие дважды (1 с 2, 2 с 1, 1 с 3, 3 с 1, 2 с 3 и 3 с 2), и поскольку исходный вопрос хочет знать, сколько возможны разные рукопожатия мы должны разделить на 2, чтобы получить правильный ответ.
Всего разных рукопожатий = n(n-1)/2
Задача о рукопожатиях как задача о комбинациях
Мы также можем решить эту задачу о рукопожатиях как задачу о комбинациях как C(n,2).
n (объектов) = количество человек в группе
р
(выборка) = 2, количество людей, участвующих в каждом рукопожатии
Порядок элементов, выбранных в подмножестве, не имеет значения, поэтому для группы из 3 будет учитываться 1 с 2, 1 с 3 и 2 с 3, но игнорировать 2 с 1, 3 с 1 и 3 с 2, потому что эти последние 3 являются дубликатами первых 3 соответственно.
\( C(n,r) = \dfrac{n!}{( r! (n — r)! )} \)
\( C(n,2) = \dfrac{n!}{( 2! (n — 2)! )} \)
расширение факториалов,
\( = \dfrac{1\times2\times3. ..\times(n-2)\times(n-1)\times(n)}{( 2\times1\times(1\times2\times3…\times(n-2)) )} \)
отмена и упрощение,
\( = \dfrac{(n-1)\times(n)}{2} = \dfrac{n(n-1)}{2} \)
что то же самое как уравнение выше.
Задача о комбинациях бутербродов
Это классическая математическая задача.
Рассчитайте возможные комбинации бутербродов, если вы можете выбрать по одному продукту из каждой из четырех категорий:
- 1 хлеб из 8 вариантов
- 1 мясо из 5 вариантов
- 1 сыр из 5 вариантов
- 1 топпинг из 3 вариантов
Часто вы увидите ответ без какой-либо ссылки на уравнение комбинаций C(n,r) как произведение количества возможных вариантов в каждой из категорий. В этом случае мы вычисляем:
8 × 5 × 5 × 3 = 600
возможных комбинаций сэндвичей
С точки зрения приведенного ниже уравнения комбинаций, количество возможных вариантов для каждой категории равно количеству возможных комбинаций для каждой категории, поскольку мы делаем только 1 выбор; например, C(8,1) = 8, C(5,1) = 5 и C(3,1) = 3, используя следующее уравнение:
C(n,r) = n! / ( r!(n — r)! )
Мы можем использовать это уравнение комбинаций для расчета более сложной задачи сэндвича.
Задача комбинаций бутербродов с множественным выбором
Рассчитайте возможные комбинации, если вы можете выбрать несколько предметов из каждой из четырех категорий:
- 1 хлеб из 8 вариантов
- 3 вида мяса из 5 вариантов
- 2 сыра из 5 вариантов
- От 0 до 3 начинок из 3 вариантов
Применяя уравнение комбинаций, где порядок не имеет значения и замены не допускаются, мы вычисляем количество возможных комбинаций в каждой из категорий. Вы можете использовать калькулятор выше, чтобы доказать, что каждое из них верно.
- 1 хлеб из 8 вариантов равен C(8,1) = 8
- 3 вида мяса из 5 вариантов C(5,3) = 10
- 2 сыра из 5 вариантов C(5,2) = 10
- от 0 до 3 начинок из 3 вариантов; мы должны вычислить каждое возможное количество вариантов от 0 до 3 и получить C(3,0) + C(3,1) + C(3,2) + C(3,3) = 8
Умножая возможные комбинации для каждой категории, получаем:
8 × 10 × 10 × 8 = 6400
возможных комбинаций сэндвичей
Сколько возможных комбинаций существует, если вашим клиентам разрешено выбирать такие варианты, которые остаются в пределах общего разрешенного количества порций:
- 2 порции одного мяса и 1 порция другого?
- 3 порции только одного мяса?
- 2 порции только одного сыра?
В предыдущем расчете замены не допускались; клиенты должны были выбрать 3 разных мяса и 2 разных сыра.
Теперь разрешены замены, покупатели могут выбирать любой товар более одного раза при выборе своей порции. Для мяса и сыров это теперь
замена комбинаций или проблема с множественным выбором с использованием уравнения комбинаций с заменами:
C R (n,r) = C(n+r-1, r) = (n+r-1)! / (r! (n — 1)!)
Для мяса, где количество объектов n = 5 и количество вариантов выбора r = 3, мы можем вычислить либо замена комбинаций C R (5,3) = 35 или заменить члены и вычислить комбинации C(n+r-1, r) = C(5+3-1, 3) = С(7, 3) = 35 .
Подсчитав выбор сыра таким же образом, мы получили общее количество возможных вариантов для каждой категории, равное 9.0005
- хлеб 8
- мясо 35
- сыр 15
- начинки это 8
и, наконец, мы умножаем, чтобы найти общее количество
8 × 35 × 15 × 8 =; 33 600
возможных комбинаций бутербродов!
Сколько комбинаций возможно, если клиентам также разрешены замены при выборе начинки?
Ссылки
[1] Zwillinger, Daniel (главный редактор).
Стандартные математические таблицы и формулы CRC, 31-е издание New York, NY: CRC Press, p. 206, 2003.
Дополнительную информацию о комбинациях и биномиальных коэффициентах см. Wolfram MathWorld: Комбинация.
В решении 6-3 суд отменяет закон Нью-Йорка о скрытом ношении
АНАЛИЗ МНЕНИЙ
Эми Хоу
от 23 июня 2022 г.
в 10:36
Защитное ограждение Верховного суда. (Кэти Барлоу)
Эта статья была обновлена 23 июня в 16:06.
В четверг Верховный суд отменил закон Нью-Йорка о лицензировании огнестрельного оружия, который требовал от жителей Нью-Йорка, желающих носить пистолет в общественных местах, проявлять особую потребность защищать себя.
Постановление 6-3, написанное судьей Кларенсом Томасом, является первым значительным решением суда по правам на оружие более чем за десять лет.
В далеко идущем постановлении суд ясно дал понять, что гарантия Второй поправкой права «хранить и носить оружие» защищает широкое право носить пистолет вне дома в целях самообороны. В будущем, пояснил Томас, суды должны поддерживать ограничения на оружие только в том случае, если в истории США существует традиция такого регулирования.
Историческое решение, принятое в четверг, было принято менее чем через шесть недель после того, как вооруженный человек убил 10 чернокожих в супермаркете Buffalo, и менее чем через месяц после того, как 21 человек — 19 детей и два учителя — были застрелены в начальной школе в Увальде, штат Техас. В ответ на эти перестрелки Сенат на этой неделе достиг соглашения по двухпартийному закону о безопасности оружия, который, если он будет принят, станет первым федеральным законом о контроле над оружием почти за 30 лет. 80-страничный законопроект (среди прочего) потребует более жесткой проверки биографических данных покупателей оружия в возрасте до 21 года и предоставит больше средств для ресурсов, связанных с психическим здоровьем.
Закон штата, лежащий в основе дела New York State Rifle & Pistol Association v. Bruen , требует от любого, кто хочет носить скрытое огнестрельное оружие вне дома, предъявить «уважительную причину» для получения лицензии. Суды Нью-Йорка истолковали эту фразу как требующую от заявителей показать больше, чем просто желание защитить себя или свою собственность. Вместо этого заявители должны продемонстрировать особую потребность в самообороне — например, последовательность физических угроз. Несколько других штатов, включая Калифорнию, Гавайи, Мэриленд, Массачусетс и Нью-Джерси, вводят аналогичные ограничения, как и многие города.
Суды низшей инстанции поддержали закон Нью-Йорка против двух мужчин, которым было отказано в выдаче лицензии на скрытое ношение оружия. Но в четверг Верховный суд отклонил закон в идеологически разделенном мнении на 63 страницах.
Суд отклонил тест, состоящий из двух частей, который многие суды низшей инстанции использовали для рассмотрения возражений против мер контроля над оружием.
В этом тесте сначала рассматривалось, регулирует ли ограничение поведение, защищенное первоначальной сферой действия Второй поправки, а затем, если да, было ли ограничение точно настроено для продвижения значительных общественных интересов. Вместо этого, писал Томас, если «простой текст Второй поправки охватывает поведение человека», на правительстве лежит бремя доказывания того, что регулирование соответствует историческому пониманию Второй поправки.
Применив этот новый и более строгий стандарт к требованиям Нью-Йорка о наличии уважительной причины, Томас обнаружил, что желание претендентов носить пистолет в общественных местах для самообороны полностью подпадает под действие, защищаемое Второй поправкой. По словам Томаса, текст поправки не делает различий между правами на оружие дома и правами на оружие в общественных местах. Действительно, предположил он, ссылка во Второй поправке на право «носить» оружие наиболее естественно относится к праву носить оружие вне дома.
Изучив почти семь столетий исторических источников, начиная с 1200-х и заканчивая началом 1900-х годов, Томас пришел к выводу, что, хотя история США время от времени накладывала некоторые «четко определенные ограничения» на право ношения огнестрельного оружия в общественных местах, не существовало традиции широкого запрета на ношение в общественных местах широко используемого оружия для самообороны.
И, за редкими исключениями, добавил Томас, исторически не существовало требования, чтобы законопослушные граждане проявляли особую потребность в самообороне, требуемую законом Нью-Йорка для ношения оружия в общественных местах. Действительно, заключает Томас, «не существует другого конституционного права, которым человек может воспользоваться только после того, как продемонстрирует государственным служащим какую-то особую потребность».
Томас отверг попытку Нью-Йорка оправдать свое требование уважительной причины попыткой регулировать использование оружия в «чувствительных местах» — в частности, в многолюдных городских районах, таких как Манхэттен, где люди могут собираться. Томас согласился с тем, что исторически давно существуют законы, ограничивающие использование оружия в таких местах, как здания судов и избирательные участки. Более того, продолжил он, ограничения, которые применяются к современным версиям «чувствительных мест», также могут пройти конституционную проверку. Хотя Томас оставил открытым вопрос о том, что можно было бы назвать «чувствительным местом», он ясно дал понять, что городские районы не соответствуют этому определению.
«Аргумент государства фактически освободит города от Второй поправки и лишит общее право публично носить оружие для самообороны», — заключил Томас.
В совпадающем мнении, к которому присоединился председатель Верховного суда Джон Робертс, судья Бретт Кавано попытался изобразить масштаб решения, принятого в четверг, как ограниченный. По словам Кавано, постановление не запрещает штатам вводить какие-либо лицензионные требования. Он отметил, что в 43 штатах используются схемы лицензирования, которые включают такие требования, как проверка биографических данных, обучение обращению с огнестрельным оружием, проверка записей о психическом здоровье и снятие отпечатков пальцев. Такие схемы являются объективными, объяснил Кавано, а не предоставляют «неограниченную свободу действий лицензирующим органам» и требуют «проявления какой-то особой потребности помимо самообороны».
Действительно, продолжил он, Вторая поправка «допускает «разнообразие» правил обращения с оружием». Кавано подробно процитировал заключение покойного судьи Антонина Скалиа для суда по делу District of Columbia v.
Heller , заключение 2008 года, подтверждающее право хранить пистолет дома для самообороны. «Ничто, по нашему мнению, — писал Скалиа, — не должно ставить под сомнение давние запреты на владение огнестрельным оружием преступниками и психически больными или законы, запрещающие ношение огнестрельного оружия в особо важных местах, таких как школы и правительственные учреждения. зданий или законов, устанавливающих условия и ограничения на коммерческую продажу оружия».
Судья Стивен Брейер выразил несогласие с мнением, к которому присоединились судьи Соня Сотомайор и Елена Каган. Отметив, что более 45 000 американцев были убиты огнестрельным оружием в 2020 году, Брейер подчеркнул, что штаты пытались снизить вероятность насилия с применением огнестрельного оружия, «путем принятия законов, которые различными способами ограничивают тех, кто может покупать, носить или использовать огнестрельное оружие различных видов». Но решение, принятое в четверг, по словам Брейера, «серьезно обременяет усилия Штатов в этом направлении».
Утверждая, что вопрос перед судом заключался в том, «в какой степени Вторая поправка ограничивает различные штаты (и федеральное правительство) в выработке решений «насилия с применением огнестрельного оружия» посредством демократических процессов», Брейер обвинил своих коллег в том, что они отвергли Новую йоркского закона без доказательной базы, которая позволила бы ему определить, как нью-йоркская схема фактически работает на практике, «без учета настоятельной заинтересованности штата в предотвращении насилия с применением огнестрельного оружия и защите безопасности своих граждан, а также без учета потенциально смертельных последствий ее применения». решение.»
Несогласие Брейера вызвало резкую критику со стороны судьи Сэмюэля Алито, который представил совпадающее мнение, резко критикующее описание Брейером воздействия оружия на американское общество. Это обсуждение, по словам Алито, в значительной степени не имеет отношения к фактическому решению суда, которое, как подчеркнул Алито, «ничего не решает о том, кто может законно владеть огнестрельным оружием, или о требованиях, которые необходимо выполнить, чтобы купить оружие.
Он также ничего не решает о виде оружия, которым могут владеть люди».
В более широком смысле Алито выступил против утверждения Брейера и Нью-Йорка о том, что «повсеместное распространение оружия и высокий уровень насилия с применением огнестрельного оружия в нашей стране дают основания для поддержки закона Нью-Йорка». По мнению Алито, люди хотят иметь право носить оружие именно из-за этих условий. Как и во время устной дискуссии в ноябре, Алито предположил, что «многие американцы имеют веские основания опасаться, что они станут жертвами, если не смогут защитить себя. И сегодня не менее чем в 1791», — заключил Алито, — «Вторая поправка гарантирует их право на это».
В заявлении, опубликованном Белым домом, президент Джо Байден сказал, что он «глубоко разочарован» принятым в четверг постановлением, которое он назвал противоречащим «как здравому смыслу, так и Конституции». Повторяя совпадающее мнение Кавано, Байден сослался на Скалиа и подчеркнул, что Вторая поправка не является абсолютной.