определение, формула, таблица, график, свойства
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:

Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| π | 180° | |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| π/2 | 90° | |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 0 | 0° |
microexcel.ru
Арксинус, арккосинус — свойства, графики, формулы
Арксинус, arcsin
Определение и обозначения
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .
Арксинус иногда обозначают так:
.
График функции арксинус

График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .
Арккосинус иногда обозначают так:
.
График функции арккосинус

График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См. также: Вывод формулВыражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin t. Интегрируем по частям, учитывая что –π/2 ≤ t ≤ π/2, cos t ≥ 0:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| < 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
определение, формула, таблица, график, свойства
Определение
Арксинус (arcsin) – это обратная тригонометрическая функция.
Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
arcsin x = sin-1 x = y
Примечание: sin-1x означает обратный синус, а не синус в степени -1.
Например:
arcsin 1 = sin-1 1 = 90° (π/2 рад)
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel.ru
определение, формула, таблица, график, свойства
Определение
Арккотангенс (arcctg или arccot) – это обратная тригонометрическая функция.
Арккотангенс x определяется как функция, обратная к котангенсу x.
Если котангенс угла у равен х (ctg y = x), значит арккотангенс x равняется y:
arcctg x = ctg-1 x = y
Примечание: ctg-1x означает обратный котангенс, а не котангенс в степени -1.
Например:
arctg 1 = ctg-1 1 = 45° = π/4 рад
График арккотангенса
Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):

Свойства арккотангенса
Ниже в табличном виде представлены основные свойства арккотангенса с формулами.
Таблица арккотангенсов
| x (°) | x (рад) | arcctg x |
| 180° | π | -∞ |
| 150° | 5π/6 | -√3 |
| 135° | 3π/4 | -1 |
| 120° | 2π/3 | -1/√3 |
| 90 | π/2 | 0 |
| 60 | π/3 | 1/√3 |
| 45 | π/4 | 1 |
| 30 | π/6 | √3 |
| 0 | 0 | ∞ |
microexcel.ru
определение, формула, таблица, график, свойства
Определение
Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.
Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:
arctg x = tg-1 x = y, причем -π/2<y<π/2
Примечание: tg-1x означает обратный тангенс, а не тангенс в степени -1.
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
График арктангенса
Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:

Свойства арктангенса
Ниже в табличном виде представлены основные свойства арктангенса с формулами.
Таблица арктангенсов
| x (°) | x (рад) | arctg x |
| -90° | -π/2 | -∞ |
| -71.565° | -1.2490 | -3 |
| -63.435° | -1.1071 | -2 |
| -60° | -π/3 | -√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -1/√3 |
| -26.565° | -0.4636 | -0.5 |
| 0° | 0 | 0 |
| 26.565° | 0.4636 | 0.5 |
| 30° | π/6 | 1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 63.435° | 1.1071 | 2 |
| 71.565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
microexcel.ru
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
Arccos Calculator — вычисляет arccos (x)
Используйте этот калькулятор arccos, чтобы легко вычислить арккозин числа.
Арккос функция
Арккос (аркосинус, арккосин) является одной из обратных тригонометрических функций (антитригонометрических функций, аркусовых функций) и является обратной функцией косинуса. Это иногда пишется как cos -1 (x), но этого обозначения следует избегать, так как его можно спутать с обозначением показателя степени (степень, возведенная в степень).Арккос используется для получения угла из косинус-тригонометрического отношения, которое представляет собой отношение стороны, прилегающей к углу, и гипотенузы в прямоугольном треугольнике.
Функция охватывает диапазон от -1 до 1, как и результаты нашего калькулятора arccos. Диапазон значений угла обычно составляет от 0 ° до 180 °. Существует ряд правил arccos, например cos (arccos (x)) = x или arccosα + arccosβ = arccos (αβ — √ ((1-α 2 ) (1-β 2 )), а также синус арккозина: sin (arccos (x)) = √ (1-x 2 ), который может помочь вам в исчислении тригонометрии.
Как рассчитать арккозин из числа?
Самый простой способ рассчитать это — использовать наш калькулятор arccos выше, который будет выводить результаты как в градусах, так и в радианах. Другие способы включают другую заданную информацию, такую как значения других тригонометрических функций для того же угла или других углов в том же треугольнике.
Вот таблица общих значений arccos:
| x | арккос (х) (°) | арккос (х) (рад.) |
|---|---|---|
| -1 | 180 ° | № |
| -√3 / 2 | 150 ° | 5π / 6 |
| -√2 / 2 | 135 ° | 3π / 4 |
| -1/2 | 120 ° | 2π / 3 |
| 0 | 90 ° | π / 2 |
| 1/2 | 60 ° | π / 3 |
| √2 / 2 | 45 ° | π / 4 |
| √3 / 2 | 30 ° | π / 5 |
| 1 | 0 ° | π / 6 |
π, конечно, математическая константа примерно равна 3.14159.
Пример использования арккозина
Для заданного прямоугольного треугольника, как на рисунке ниже, из которого мы знаем длину стороны a = 52 и гипотенузы c = 60, а также зная, что угол в точке C составляет 90 градусов, найдите угол β в точке B, используя функция обратного косинуса.
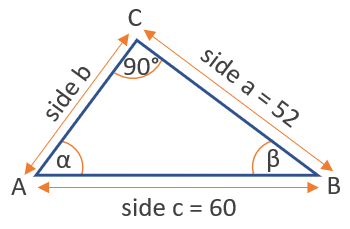
По определению косинуса мы знаем, что косинус β равен соседней стороне, деленной на гипотенузу: cos (β) = a / c = 52/60 = 0,866. Подставляя этот результат в обратную функцию, мы получаем, что β = arccos (0.866) = 30 ° (или 0,52 в радианах).
,Описание:
Функция arccos позволяет вычислить арккосинус числа. Функция арккозина является обратной функцией косинуса.
Арккос онлайнОписание:
Функция арккозин является обратной функцией функция косинуса, это вычисляет дуговой косинус числа онлайн .
Число, к которому вы хотите применить функцию fccction arccosine, должно принадлежать диапазону [-1,1].
- Расчет арккозина
Чтобы вычислить арккозин числа, просто введите число и примените Арккос функция. Таким образом, для вычисление для арккозина из числа, следующего за 0,4, ты должен войти агссоз ( `0.2) `.
Функция arccos позволяет вычислить арккосинус числа. Функция арккозина является обратной функцией косинуса.
Синтаксис:
arccos (x), где x — это число.
Иногда используются другие обозначения: acos
Примеры:
arccos (`1`) возвращает 0Производный арккозин:
Чтобы дифференцировать функцию арккозина онлайн, можно использовать калькулятор производной, который позволяет рассчитать производную функции арккозина
Производная от arccos (x) является производной (`arccos (x)`) = `-1 / sqrt (1- (x) ^ 2)`
Антидеривативный арккозин:
Антидеривативный калькулятор позволяет рассчитать антипроизводное функции арккозина.2) `
Предельный арккозин:
Калькулятор пределов позволяет вычислять пределы функции арккозина.
Ограничение arccos (x) является ограничением (`arccos (x)`)
Арккозин с обратной функцией:
Обратная функция арккозина является функцией косинуса, отмеченной как cos.
Графический арккозин:
Графический калькулятор способен отображать функцию арккозина в интервале ее определения.
Рассчитать онлайн с Arccos (арккозин) ,
Арккос (х) | функция обратного косинуса
Arccos (x), cos -1 (x), функция обратного косинуса.
Арккос, определение
Арккозин х определяется как обратная косинус-функция х, когда -1≤x≤1.
Когда косинус y равен x:
cos y = x
Тогда арккосинус x равен обратной функции косинуса x, которая равна y:
arccos x = cos -1 x = y
(Здесь cos -1 x означает обратный косинус и не означает косинус в степени -1).
Пример
arccos 1 = cos -1 1 = 0 рад = 0 °
График Арккос
Arccos правила
| Имя правила | Правило |
|---|---|
| Косинус арккозина | cos (arccos x ) = x |
| Арккозин косинус | арккос (cos x ) = x + 2 k π, когда k ∈ ( k является целым числом) |
| Арккос отрицательного аргумента | арккос (- х ) = π — арккос х = 180 ° — арккос x |
| Дополнительные углы | arccos x = π / 2 — arcsin x = 90 ° — арксинус x |
| Арккос сумма | арккос ( α ) + арккос ( β ) = arccos ( αβ — √ (1- α 2 ) (1- β 2 )) |
| разность Арккос | Арккос ( α ) — Арккос ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 )) |
| Арккос греха х | арккос (грех х ) = — х — (2 к +0.5) № |
| Синус арккозина | |
| Касательный арккозина | |
| Производная арккозина | |
| Неопределенный интеграл арккозина |
Арккос стол
| х | арккос (х) (рад) | арккос (х) (°) |
|---|---|---|
| -1 | № | 180 ° |
| -√3 / 2 | 5π / 6 | 150 ° |
| -√2 / 2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √2 / 2 | π / 4 | 45 ° |
| √3 / 2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
См. Также
,Калькулятор— arccos (0.4) — Solumaths
Описание:
Функция arccos позволяет вычислить арккосинус числа. Функция арккозина является обратной функцией косинуса.
Арккос онлайнОписание:
Функция арккозин является обратной функцией функция косинуса, это вычисляет дуговой косинус числа онлайн .
Число, к которому вы хотите применить функцию fccction arccosine, должно принадлежать диапазону [-1,1].
- Расчет арккозина
Чтобы вычислить арккозин числа, просто введите число и примените Арккос функция. Таким образом, для вычисление для арккозина из числа, следующего за 0,4, ты должен войти агссоз ( `0.2) `.
Функция arccos позволяет вычислить арккосинус числа. Функция арккозина является обратной функцией косинуса.
Синтаксис:
arccos (x), где x — это число.
Иногда используются другие обозначения: acos
Примеры:
arccos (`1`) возвращает 0Производный арккозин:
Чтобы дифференцировать функцию арккозина онлайн, можно использовать калькулятор производной, который позволяет рассчитать производную функции арккозина
Производная от arccos (x) является производной (`arccos (x)`) = `-1 / sqrt (1- (x) ^ 2)`
Антидеривативный арккозин:
Антидеривативный калькулятор позволяет рассчитать антипроизводное функции арккозина.2) `
Предельный арккозин:
Калькулятор пределов позволяет вычислять пределы функции арккозина.
Ограничение arccos (x) является ограничением (`arccos (x)`)
Арккозин с обратной функцией:
Обратная функция арккозина является функцией косинуса, отмеченной как cos.
Графический арккозин:
Графический калькулятор способен отображать функцию арккозина в интервале ее определения.
Рассчитать онлайн с Arccos (арккозин) ,
