| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| Найти точное значение | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
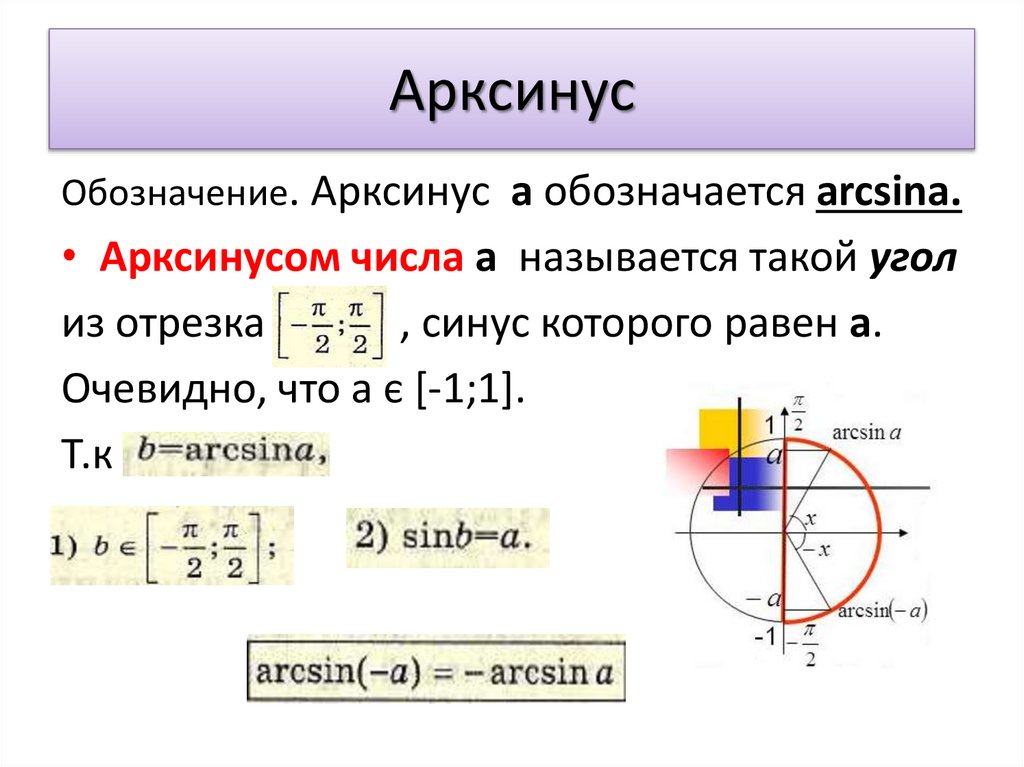
Таблица значений обратных тригонометрических функций
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Значения обратных тригонометрических функций
ru Математика Значения обратных тригонометрических функций
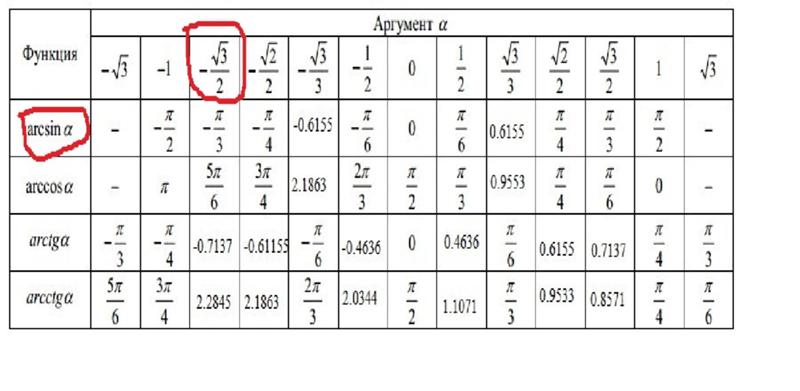
Ниже представлена таблица со значениями обратных тригонометрических функций: арксинусов (arcsin), арккосинусов (arccos), арктангенсов (arctg) и арккотангенсов (arcctg).
В радианах:
| Значение | arcsin α | arccos α | arctg a | arcctg α |
| -√3 | — | — | -π/3 | 5π/6 |
| -1 | -π/2 | π | -π/4 | 3π/4 |
| -√3/2 | -π/3 | 5π/6 | 7137″ data-order=»-0.7137″>-0.7137 | 2.2845 |
| -√2/2 | -π/4 | 3π/4 | -0.6155 | 1863″ data-order=»2.1863″>2.1863 |
| -√3/3 | -0.6155 | 2.1863 | -π/6 | 2π/3 |
| -1/2 | -π/6 | 2π/3 | 4636″ data-order=»-0.4636″>-0.4636 | 2.0344 |
| 0 | 0 | π/2 | 0 | π/2 |
| 1/2 | π/6 | π/3 | 4636″ data-order=»0.4636″>0.4636 | 1.1071 |
| √3/3 | 0.6155 | 0.9553 | π/6 | π/3 |
| √2/2 | π/4 | π/4 | 6155″ data-order=»0.6155″>0.6155 | 0.9553 |
| √3/2 | π/3 | π/6 | 0.7137 | 8571″ data-order=»0.8571″>0.8571 |
| 1 | π/2 | 0 | π/4 | π/4 |
| √3 | — | — | π/3 | π/6 |
microexcel. ru
ru
В градусах:
| Значение | arcsin α | arccos α | arctg a | arcctg α |
| -√3 | — | — | -60° | 150° |
| -1 | -90° | 180° | -45° | 135° |
| -√3/2 | -60° | 150° | 89°» data-order=»-40.89°»>-40.89° | 130.89° |
| -√2/2 | -45° | 135° | -35.26° | 26°» data-order=»125.26°»>125.26° |
| -√3/3 | -35.26° | 125.26° | -30° | 120° |
| -1/2 | -30° | 120° | 57°» data-order=»-26.57°»>-26.57° | 116.57° |
| 0 | 0° | 90° | 0° | 90° |
| 1/2 | 30° | 60° | 57°» data-order=»26.57°»>26.57° | 63.43° |
| √3/3 | 35.26° | 54.74° | 30° | 60° |
| √2/2 | 45° | 45° | 26°» data-order=»35.26°»>35.26° | 54.74° |
| √3/2 | 60° | 30° | 40.89° | 11°» data-order=»49.11°»>49.11° |
| 1 | 90° | 0° | 45° | 45° |
| √3 | — | — | 60° | 30° |
microexcel.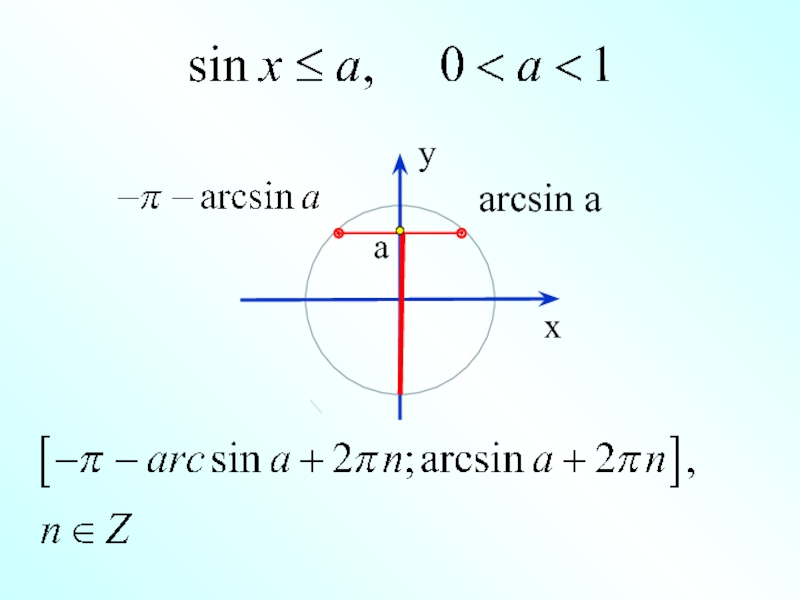 ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Обратная тригонометрическая функция: арксинус
Перед изучением этого раздела рекомендуется прочитать
Попытка «отменить» тригонометрические функции.
Чтобы функция имела обратную, каждый выход должен иметь ровно один соответствующий вход .
Таким образом, только взаимно однозначные функции имеют обратные.
Синусоидальная функция не имеет истинной обратной, потому что синусоидальная функция не является однозначной.
Итак, чтобы попытаться определить «функцию обратного синуса», мы делаем все возможное, как описано ниже.
Функция арксинуса (точное определение ниже) — это лучшее, что мы можем сделать , пытаясь получить обратную функцию
синусоидальная функция.
Функция арксинуса на самом деле обратная зеленой фигуре, показанной выше!
Вот функциональная панель того, что происходит:
| Функция синуса принимает на вход вещественное число .  Выдает результат в интервале $\,[-1,1]\,.$ Например (как показано ниже), | Когда мы пытаемся использовать поле функции синуса «назад»,
мы попадаем в беду. Результат $\,0.5\,$ мог быть | Однако,
когда мы используем зеленый кусок синусоида, проблема решена! Теперь есть только один вход , который работает. Заметим, что $\,\color{green}{x}\,$ находится в интервале $\,[-\frac{\pi}2,\frac{\pi}2]\,. |
Это немного неправильное название, но функция арксинуса (точное определение ниже) часто упоминается как
как «функция обратного синуса».
Лучшее название было бы что-то вроде «обратная функция синуса с соответствующими ограничениями».
(Неудивительно, однако, что люди не говорят что-то такое длинное и громоздкое.)
Итак, что же такое $\,\arcsin 0.5\,$?
$\,\arcsin 0,5\,$ — число из интервала $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$, синус которого равен $\ ,0.5\,$
Что такое $\,\arcsin x\,$?
В более общем случае пусть $\,x\,$ будет любым числом в интервале $\,[-1,1]\,.$
Тогда:
$\,\arcsin x\,$ — число в интервале $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$, синус которого равен $\ ,х\,$
В моем собственном уме (здесь говорит автор доктор Кэрол Бернс) я произношу следующие слова:
$\,\arcsin x\,$ — это число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$, синус которого равен $\,х\,$
Я лично знаю конечные точки включая , так что это меня не смущает.
Однако слово «между» неоднозначно — оно может включать или не включать конечные точки, в зависимости от контекста.
Это можно прояснить, сказав:
$\,\arcsin x\,$ — число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$ (включая концы), синус которого равен $\,x\,$
… но тогда он теряет свою простоту. Ах, проблемы с языком. Выберите слова, которые работают на вас!Точное определение функции арксинуса
Далее следует точное определение функции арксинуса.
Это может выглядеть немного пугающе — примечания, следующие за определением, должны помочь.
9{-1} х}\ \ \ \ \
\cssId{s67}{\text{если и только если}}\ \ \ \
\cssId{s68}{\bigl(\\sin y = x\\\text{AND}\ \ -\frac{\pi}{2} \le y\le \frac{\pi}{2}\ \ больше)}
$$
Примечания к определению функции арксинуса:
Ваш браузер не поддерживает аудио элементы.
ПРОЧТЕНИЕ, ЧАСТЬ 2
- ОФИЦИАЛЬНОЕ НАЗВАНИЕ В ОТНОШЕНИИ ФУНКЦИОНАЛЬНЫХ ОБОЗНАЧЕНИЙ СОКРАЩЕНИЯ: 9{-1}\,$’ вводит в заблуждение и дает
себя к ошибкам.
Этот автор настоятельно предпочитает обозначение ‘$\,\arcsin\,$’. - АЛЬТЕРНАТИВНОЕ ОПРЕДЕЛЕНИЕ, ИСПОЛЬЗУЮЩЕЕ ГРАДУСЫ ВМЕСТО РАДИАНОВ:
Входные данные для тригонометрических функций можно рассматривать как действительные числа (радианы) или градусы.
Например, $\,\sin \frac{\pi}{2} = 1\,$: здесь $\,\frac{\pi}{2}\,$ — мера в радианах.
Эквивалентно $\,\sin 9\circ]\,$, синус которого равен $\,x\,$ - НАВЫКИ КАЛЬКУЛЯТОРА:
Если калькулятор находится в режиме градусов, то $\,\arcsin x\,$ сообщается в градусах.
Если калькулятор работает в радианном режиме, то значение $\,\arcsin x\,$ отображается в радианах. {-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$
{-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$
Ниже этот метод используется для построения графика функции арксинуса:Вот часть синусоидальной кривой
, которая используется для определения функции арксинуса:
домен: $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$диапазон: $\,[-1,1]\,$
Вот та же кривая
вместе с ее отражением относительно линии $\,\color{red}{y = x}\,$График функции арксинуса
домен: $\,[-1,1]\,$диапазон: $\,[-\frac{\pi}{2},\frac{\pi}{2} ]\,$
Обратите внимание, что домен и область значений функции и ее обратной функции меняются местами!
Домен одного является диапазоном другого.
Диапазон одного является доменом другого. 9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции синуса и арксинуса являются , а не истинными инверсиями друг друга,
отношения между ними немного сложнее.Вот направление, в котором они делают красиво «отменяют» друг друга: начните с числа, сначала примените функцию арксинуса, затем примените функцию синуса, и в конечном итоге там, где вы начали. Подробности:
Для всех $\,x\in [-1,1]\,$ $$ \cssId{sb67}{\sin(\arcsin x) = x} $$
- начните с $\,\color{red}{x}\in [-1,1]\,$
- функция арксинуса переводит $\,\color{red}{x}\,$ в $\,\color{green}{\arcsin x}\,$ в интервале $\,[-\frac{\pi}2 ,\frac{\pi}2]\,$
- функция синуса возвращает
$\,\color{green}{\arcsin x}\,$ обратно в $\,\color{red}{x}\,$
Вот направление, где они не обязательно красиво «отменить» друг друга: начните с числа, сначала примените функцию синуса, затем примените функцию арксинуса.  Если число, с которого вы начали, находится за пределами интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится за пределами интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$
тогда вы не окажетесь там, где начали!Вот подробности:
Для всех $\,x\in [-\frac{\pi}2,\frac{\pi}2]\,$ $$ \cssId{sb77}{\arcsin(\sinx) = x} $$
(См. верхний график справа.) Для всех $\,x\not\in [-\frac{\pi}2,\frac{\pi}2]\,$ $$ \cssId{sb80}{\arcsin(\sin x) \ne x} $$
(См. нижний график справа.) Пример: Найдите точное значение $\,\arcsin(-0.
 5)\,$
5)\,$
(используйте как единичный круг, так и специальный треугольник) 9\циркуляр\,.$- Используя радианную меру, $\,\arcsin(-\frac 12) = -\frac{\pi}6\,.$
Калькулятор обратного синуса, арксинус, арксинус(х)
Калькулятор тригонометрического обратного синуса
Значение Между -1 и 1
#
Что такое арксинус?Обратный синус — это функция, обратная основному синусу.


 $
$ {-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$
{-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$ 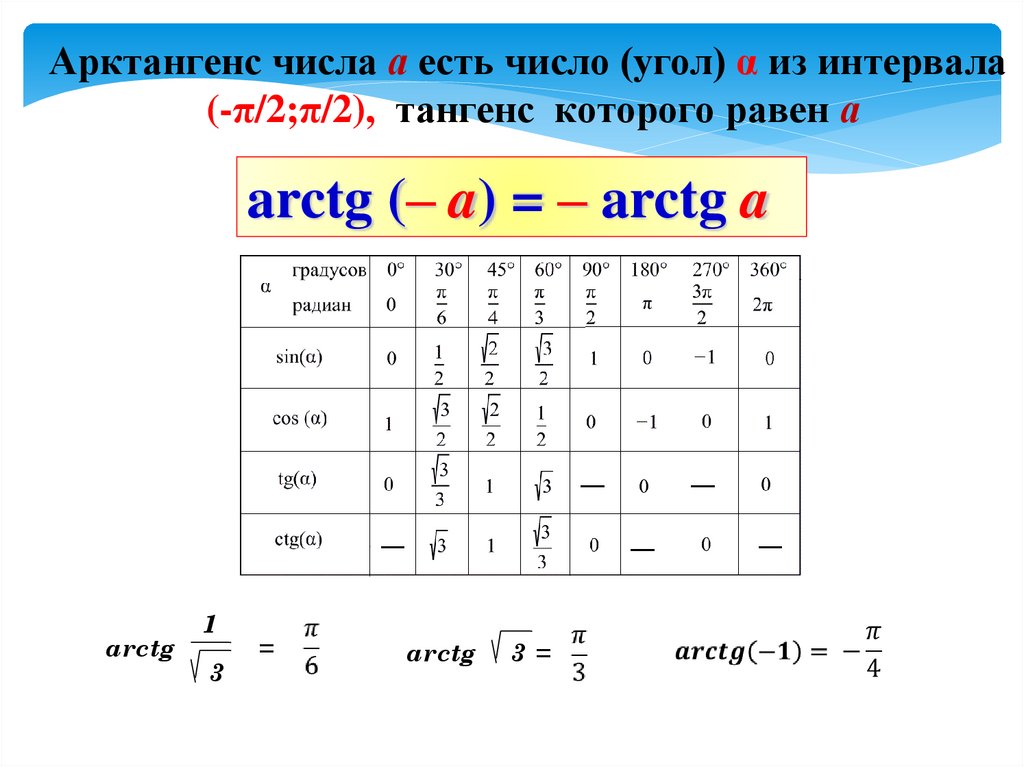
 Если число, с которого вы начали, находится за пределами интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится за пределами интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$
тогда вы не окажетесь там, где начали!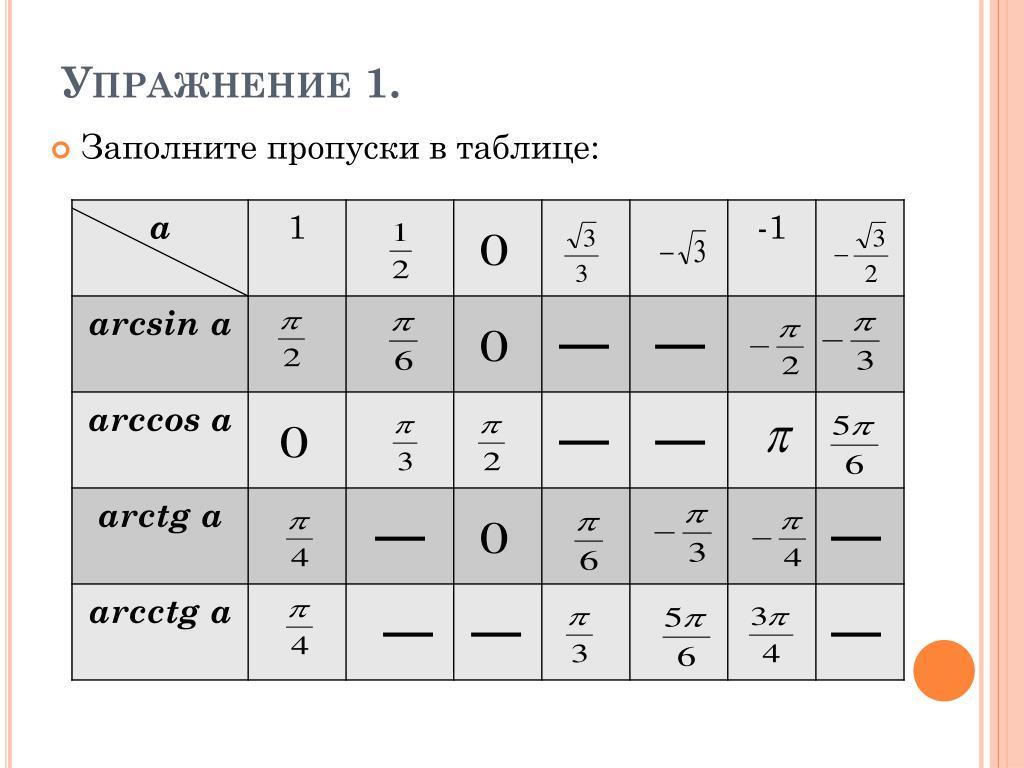 5)\,$
5)\,$