Арктангенс ℹ️ определение, свойства и функции, формулы расчета производной, график функции, таблица значений, онлайн-калькулятор
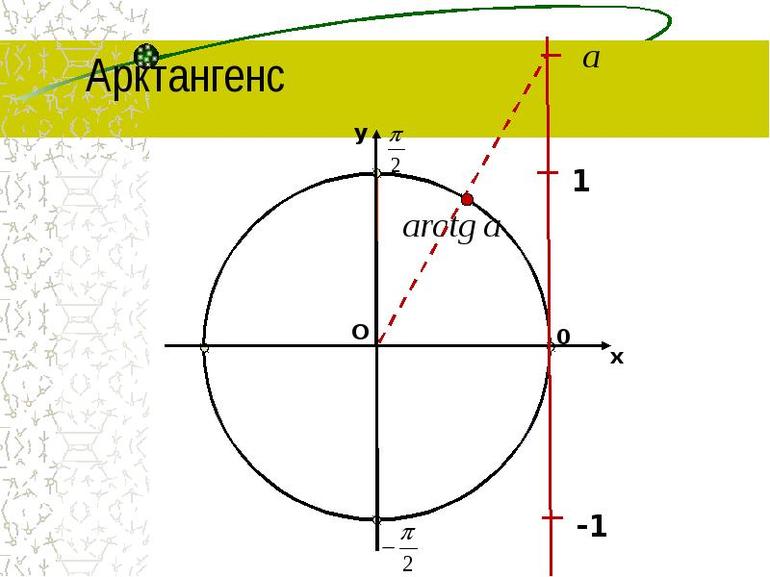
Чётность и возрастание
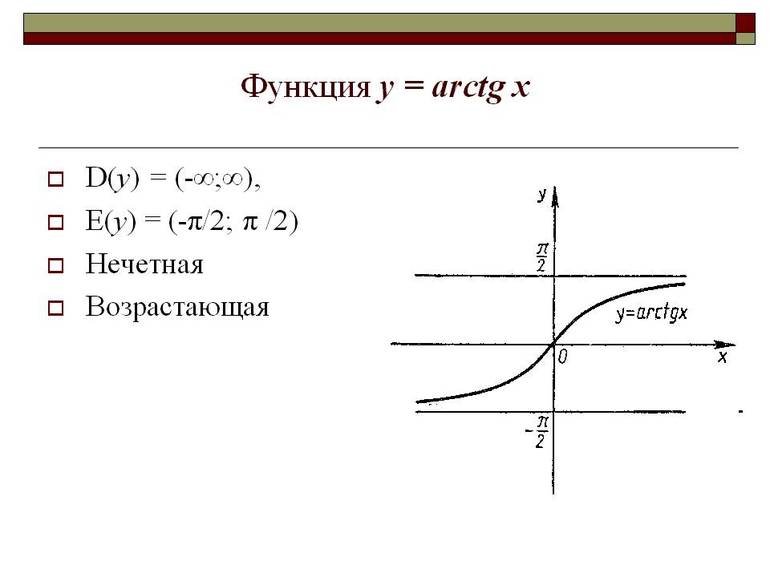
Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.
Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.
В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.
Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:
- косинус: cos (arccos a)=a;
- тангенс: tg (arctg a)=a;
- катангенс: ctg (arcctg a)=a.
В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.
Противоположные числа
Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).
Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.
На основе свойств неравенств, выполняется умножение составных частей на -а. Заменив знаки неравенств на противоположные, можно произвести умножение на -1: −π/2≤−arcsin a≤π/2.
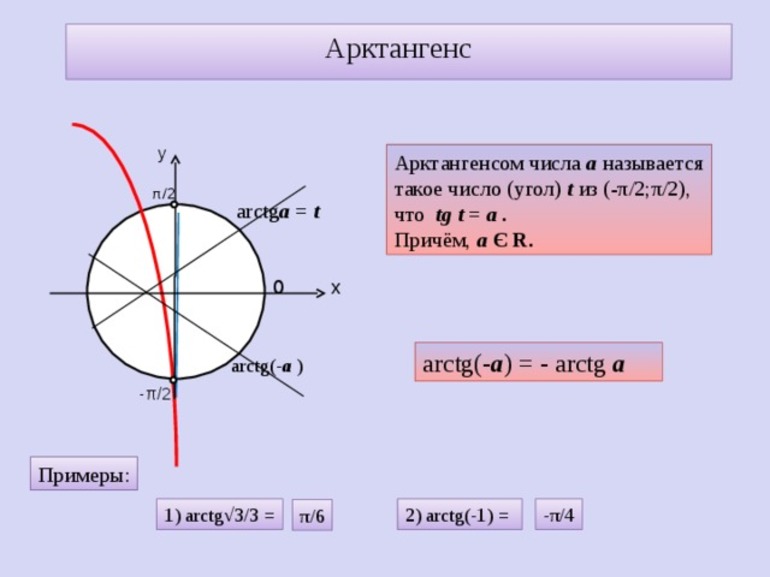
Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.
Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.
Используя свойства неравенств, перемножаются поочерёдно его части на -1, сменяются знаки. Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.
Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.
Сложение величин
Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.
Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.

С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.
Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.
Примеры и задачи
Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:
- arcsin (sinx)=x;
- arccos (cosx)=x;
- arctg (tgx)=x;
- arcctg (ctgx)=x.
Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.
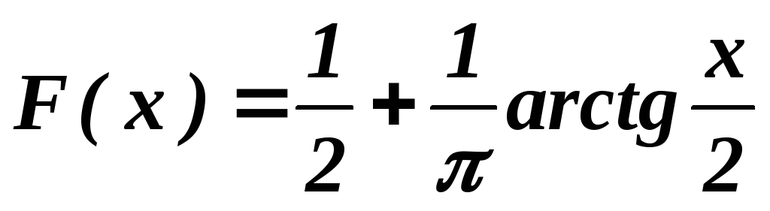
Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
Известно, аrcsin sin (-15)= -15 град., arccos (cos (2π/3))=2π/3, arctg (tg (0,2))=0,2. Нужно отметить, что выражение arcsin (sin α) справедливо на отрезке −π/2≤α≤π/2. Но равенство arcsin (sin α)=α имеет смысл только при соблюдении этого условия. Нельзя утверждать, что arcsin (sin (7π/4))=7π/4, так как 7π/4 не принадлежит указанному интервалу (−π/2-π/2).
Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).
Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.
Таблица Брадиса: арккосинус
Замечание 1
Таблица Брадиса — это таблица, позволяющая высчитывать значения арктангенсов и других тригонометрических функций с высокой точностью.
Для того чтобы воспользоваться таблицей Брадиса, ищут угол в градусах в крайнем столбце слева для синуса (для косинуса в соответствующем столбце справа), а затем в верхней строке минуты. На пересечении строки со столбцом находится искомое значение.
При необходимости найти значения обратных тригонометрических функций — таблицу Брадиса используют наоборот. Например, ищут числовое значение в таблице арктангенсов и тангенсов и для него определяют, в какой строке градусов и столбце минут оно находится.
Таким образом, Таблицу Брадиса можно использовать не только для поиска обычных тригонометрических функций, но и как таблицу арккосинуса и арксинуса, арктангенсов и арккотангенсов.
Сверху в этой статье расположена таблица значений arcsin и arccos, ближе к концу — таблица значений arctg и arcctg.
Таблица Брадиса: таблица arcsin, arccos, cos и sin
Рисунок 1. Таблица Брадиса таблица значений arcsin и arccos. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Таблица. Автор24 — интернет-биржа студенческих работ
Таблица значений арктангенсов и арккотангенсов, тангенсов и котангенсов
Рисунок 4. Таблица Брадиса: таблица значений арктангенсов arctg и арккотангенсов arctg. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 7. Таблица. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите значение $\arccos (0,2504)$.
Найдём в строке число, находящееся максимально близко к $0,2504$. В нашем случае это число $0,2588$. Так как оно больше чем $0,2504$, дальше смотрим в строки, которые находятся справа сверху от этого значения. Наконец, значение $0,2504$ найдено, оно находится на пересечении строки 75 градусов и 30 минут, значит $\arccos (0,2504)=75°30’$.
Рисунок 8. Таблица. Автор24 — интернет-биржа студенческих работ
spravochnick.ru
Арктангенс, арккотангенс — свойства, графики, формулы
Арктангенс, arctg
Определение и обозначения
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
tg(arctg x) = x ;
arctg(tg x) = x .
Арктангенс обозначается так:
.
График функции арктангенс

График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений .
ctg(arcctg x) = x ;
arcctg(ctg x) = x .
Арккотангенс обозначается так:
.
График функции арккотангенс

График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x. (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при
при
при
при
при
при
Выражения через логарифм, комплексные числа
См. также: Вывод формул ,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x) = x
ctg(arcctg x) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x) = x при
arcctg(ctg x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Онлайн вычисление обратных тригонометрических функций
- ГЛАВНАЯ
- расчеты
- мониторинг
- консалтинг
- ОБЪЕКТЫ
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
- ОНЛАЙН
- сосуды и аппараты
- трубопроводы
- прочие
- математика
- МАТЕРИАЛЫ
- статьи
- презентации
- отчеты
- log-files
- прочие
- ЛИТЕРАТУРА
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
cae-cube.ru
Чему равен арктангенс 1 и артангенс 2?
Пожелание — используй компьютерный калькулятор (группа стандартные) Используй команду Вид/Инженерный Набери 2 или 1 (твое значение) Установи флажок Inv Нажми кнопку tg Результат на экране Удачи!!!
Легче простого))))… правда для этого нужен калькулятор, но если нет под рукой… . arctag1 = 45 град arctag2 = 63,4349 град
arctg1=45 arctg2=63 с копейками..
arctg(1)=Pi/4, а аrctg(2) увы, считать надо.
arctg 1=45 градусам
Арктангенс 1 в радианах, Пи/4 (0,785398) Арктангенс 1 в градусах (45) Второе — не помню.
arctg= 1/tg отсюда arctg1=1/1=1 =45 градусам arctg2=1/2=0.5 =26 градусов 34 минуты
touch.otvet.mail.ru
как посчитать arctg 0,16. таблицы брадиса у меня нет, а на калькуляторе только tan и tan и в степени -1?
Так вот tan в степени -1 и есть арктангенс. Только учтите то, что аргумент под arctg может быть как в градусах, так и в радианах. На всех нормальных калькуляторах должна быть опция задания аргумента как в одном, так и в другом. Вы сами должны проверить, что у Вас там стоит. Делаете так: набираете -1, потом жмете кнопку tan, затем цифру 1 и давите на результат. Если на табло выскочила цифра 45, значит у Вас расчет ведется в градусах, а если 0.78539….тогда это в радианах. А arctg(0.16) = 0.15865 в радианах или 9.095 в градусах.
tan в -1 на калькуляторе — это и есть русский arctg.
блин, с такими вопросами, используя калькулятор, караул. во первых у вас в винде есть стандартный калькулятор, включаете научную форму, инвертировать тангенс и считайте сколько влезет во вторых у вас есть ёксель, тоже самое там есть функция арктангенса в довесок к ответу Игоря, Еще угол может измеряться в градах, 90 градусов = 100 градов
Верхний индекс -1 у знака операции означает обратную операцию.
В обчыном калькуляторе Виндов можно брать обратную функцию — арктангенс, экспоненту (вместо логарифма) , замысловатый корень и т. п. Для этого перед тем, как нажимать значток функции, надо поставить флажок в окошечке Inv.
touch.otvet.mail.ru
