Нет комментариев Разное

Арктангенс 0 8: Арктангенс — калькулятор онлайн

Опубликовано

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67
Найти точное значение		cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )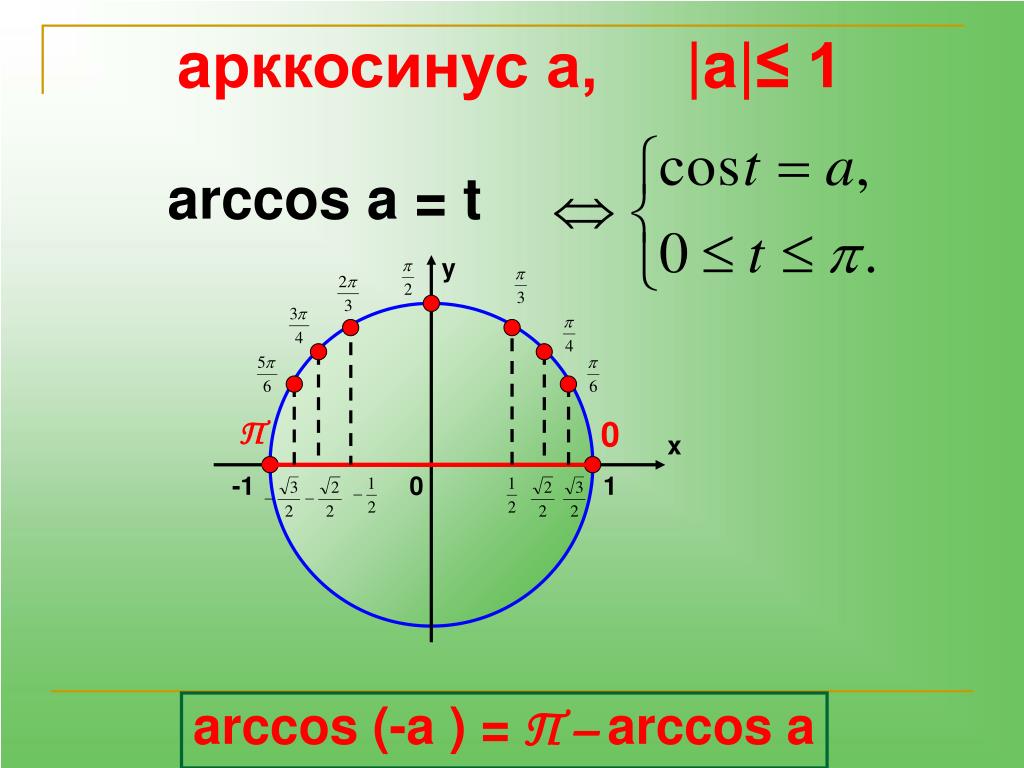
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87
Найти точное значение		sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы
88 град.

Арктангенс и решение уравнения tg x=a 10 класс онлайн-подготовка на Ростелеком Лицей

График функции y=tgt, понятие арктангенса

 

Чтобы ввести понятие арктангенс, рассмотрим функцию

 

Построим её подробный график.

На оси абсцисс будем откладывать точки кратные  На оси ординат отложим соответствующие значения функции, известные нам из таблиц (рис. 1).

Промежуток  был выбран, так как на нем функция принимает все свои значения от  и монотонно возрастает.

Напомним о прямой и обратной задаче для любой функции.

Прямая задача: по заданному значению аргумента найти соответствующее значение функции. Например, если аргумент равен  то значение функции равно 1.

Обратная задача: задано значение функции, найти соответствующее значение аргумента промежутке . Например, если

Каждое значение функции  на промежутке  достигается только при одном значении аргумента и называется арктангенсом.

 

Определение арктангенса и графическая интерпретация

 

 

Арктангенс  это такое число  тангенс которого равен

 

Значения арктангенса определяются по графику (рис. 1).

Например:

Покажем, как определять значения арктангенсов на тригонометрической окружности с помощью линии тангенсов.

Отметим на числовой окружности точки  Соединим каждую из них с  началом координат и проведем лучи до пересечения с линией тангенсов. Получим значения тангенсов для указанных углов (рис. 3).

Примеры:

 

Свойства арктангенса

 

 

Отметим важное свойство арктангенса:

 

Проиллюстрируем его на единичной окружности (рис. 4).

Если

Если  ему соответствует дуга

Например:

 

Решение задач

 

 

Задача 1. Вычислить:

 

Решение:

Значения арктангенсов определим по графику (рис. 1) или по свойству.

Ответ:

Задача 2. Расположите в порядке возрастания числа:

Решение (рис. 5).

На промежутке  функция монотонно возрастает

Задача 3. Вычислить

Решение:

Найдем  

 

Проиллюстрируем решение на прямоугольном треугольнике (рис. 6).

Дан угол  т.е. катеты равны  Гипотенузу находим по теореме Пифагора, 

Ответ:

Задача 4. Вычислить

Решение:

Проиллюстрируем решение на прямоугольном треугольнике  (рис. 7).

Ответ:

Задача 5. Вычислить

Решение:

Ответ:

 

Вывод, заключение

 

 

Мы познакомились с понятием арктангенс и решили типовые задачи. На следующем уроке мы решим уравнение  с помощью арктангенса.

 

 

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

 

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М. : Мнемозина, 2007.

№ 21.31, 21.35, 21.48 (а, г).

 

Дополнительные веб-ресурсы

1. Математика (Источник).

2. Интернет-портал Problems.ru (Источник).

3. Образовательный портал для подготовки к экзаменам (Источник).

 

Калькулятор — arctan(0.8) — Солуматы

Арктан, расчет онлайн

Резюме:

Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.

arctan онлайн

Описание:

Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .

  1. Расчет арктангенса

    2. Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.

    Например, чтобы вычислить арктангенс

    следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.

  2. Пределы арктангенса
    3. Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
  • Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
      • `lim_(x->-oo)arctan(x)=pi/2`
  • Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
      • `lim_(x->+oo)arctan(x)=-pi/2`

  • Таблица замечательных значений
    • arctan (`-sqrt(3)`)
    `
    arctan(`-1`) `3*pi/4`
    arctan(`-sqrt(3)/3`) `5*pi/6` `2*pi/3`
    arctan(`0`) `0`
    arctan(`sqrt(3)`) /3`
    arctan(`1`) `pi/4`
    arctan(`sqrt(3)/3`) `pi/6`
    Syntax :

    arctan(x) , x — число. 92)`

    Предельный арктангенс :

    Калькулятор пределов позволяет вычислить пределы функции арктангенса.

    предел арктангенса(x) is limit(`»arctan»(x)`)

    Обратная функция арктангенса :

    обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.

    Графический арктангенс :

    Графический калькулятор может строить график функции арктангенса в интервале ее определения.

    Свойство функции арктангенс :

    Функция арктангенса является нечетной функцией.

    Расчет онлайн с арктангенсом (арктангенсом)

    См. также

    Список связанных калькуляторов:

    • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
    • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
    • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
    • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
    • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
    • Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
    • Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
    • Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
    • Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
    • Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
    • Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

    Прочие ресурсы

    • Исправленные упражнения по числовым функциям
    • Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
    • Научитесь считать с помощью обычных математических функций

     

    Тригонометрические функции

    Тригонометрические функции — это периодические волновые функции, которые используются в математике и физике. Функции можно сгруппировать в три взаимосвязанные группы: основные функции: синус, косинус и тангенс. Взаимные функции: косеканс, секанс и котангенс. И дуговые функции: арксинус, арккосинус и арктангенс.

    Калькуляторы часто имеют возможность переключения между системами радиан и градус-угол, но некоторые языки программирования и калькуляторы обеспечивают реализацию функций только с использованием радианов. Это связано с тем, что радианы являются предпочтительной единицей измерения углов в математике [1] , и при использовании радианов функции наследуют полезные свойства.

    Определение круга

    Тригонометрические функции обычно вводятся с использованием геометрии прямоугольного треугольника, как показано на этой странице. Позже определения расширяются с использованием геометрии круга, как показано ниже. Этот веб-сайт называет их «круговыми определениями» тригонометрических функций.

    Каждая из функций принимает угол в радианах на вход и возвращает отношение на выходе. Геометрически определения соответствуют кругу с радиусом и точкой, образующей угол (тета). Функции можно визуализировать с помощью геометрии единичного круга. Это можно увидеть, подставив в приведенные выше определения круга.

    Основные функции

    Основные функции — это наиболее часто используемые тригонометрические функции.

    Синус

    При заданном угле в радианах функция синуса возвращает синус угла. Например, при заданном угле в радианах функция синуса возвращает значение .

    Этот пример можно визуализировать, нарисовав окружность и точку, соответствующую введенному углу. Поскольку функция возвращает соотношение, размер круга не имеет значения. Это показано ниже

    Все возможные выходы функции могут быть отображены на единичном круге. Геометрически, если в качестве входных данных задан угол, функция синуса возвращает вертикальную составляющую точки, соответствующую углу на единичной окружности. Это показано в интерактиве ниже. Нажмите и перетащите любую синюю контрольную точку.

    Косинус

    При заданном угле в радианах функция косинуса возвращает косинус угла. Например, при заданном угле функция косинуса возвращает значение .

    Этот пример можно визуализировать, нарисовав окружность и точку, соответствующую введенному углу. Размер круга не имеет значения, так как функция возвращает отношение. Этот круг показан ниже.

    Все возможные выходы функции могут быть отображены на единичном круге. Геометрически, при заданном угле функция косинуса возвращает горизонтальную составляющую точки, соответствующую углу на единичной окружности. Это показано в интерактиве ниже. Нажмите и перетащите любую синюю контрольную точку.

    Касательная

    При заданном угле в радианах функция тангенса возвращает тангенс угла. Геометрически результат функции можно изобразить линией, проведенной касательной к точке на единичной окружности, образованной из угла. Ниже показан график функции тангенса.

    Ниже представлен интерактив, который визуализирует вывод функции касательной к единичной окружности. Нажмите и перетащите любую синюю контрольную точку.

    Взаимные функции

    Функции секанс, косеканс и котангенс являются обратными функциями косинуса, синуса и тангенса. Как и основные функции, эти функции принимают угол на окружности в качестве входных данных и возвращают тригонометрическое соотношение. Каждая функция может быть выражена как величина, обратная ее аналогу.

    Примечание: Обратите внимание, что косеканс и секанс не так распространены, как котангенс, и в основном включены по историческим причинам.

    Косеканс

    Функция косеканса возвращает значение, обратное синусоидальной функции. Функция также может быть записана в терминах синуса.

    На приведенном ниже графике черным цветом показаны выходные данные функции косеканса, а зеленым — функции синуса.

    Секанс

    Функция секанса возвращает обратную величину функции косинуса. Функция также может быть записана в терминах косинуса.

    График ниже показывает выход функции секанса черным цветом и функции косинуса зеленым цветом.

    Котангенс

    Функция котангенса возвращает обратную величину функции тангенса. Функция также может быть записана в терминах тангенса.

    Функция визуализирована на графике ниже, на котором функция тангенса показана зеленым цветом, а котангенс — черным.

    Выход котангенса может быть визуализирован на единичной окружности как другая линия, касательная к точке на единичной окружности, соответствующей углу.

    Рисунок 1: Тангенс и котангенс единичной окружности.

    Функции дуги

    Функции дуги обратны косинусу, синусу и тангенсу. Учитывая отношение двух сторон прямоугольного треугольника, функции возвращают соответствующий угол. Префикс arc используется, поскольку выходной угол возвращается в радианах, что соответствует длине дуги окружности окружности.

    Примечание: При вводе действительных чисел функции дуги иногда возвращают связанный угол, а не истинный угол в координатной плоскости. Есть две стратегии возврата всех углов. 1) использовать приведенную ниже функцию ATAN2, которая принимает два числа в качестве входных данных, или 2) расширить определения функции дуги, чтобы использовать комплексные числа.

    ArcSine

    Функция ArcSine является обратной функцией синуса. Учитывая числовое значение, функция ArcSine возвращает соответствующий угол. График функции приведен ниже.

    Обратите внимание, что функция возвращает только углы в пределах первого и четвертого квадрантов системы координат. Таким образом, следующее выражение верно не для всех углов.

    Арккосинус

    Функция ArcCosine обратна функции косинуса. Учитывая значение, функция ArcCosine возвращает соответствующий угол. График функции приведен ниже.

    Обратите внимание, что функция возвращает только углы в пределах первого и второго квадрантов системы координат. Таким образом, следующее выражение верно не для всех углов.

    См. atan2 ниже для функции, которая возвращает углы во всех квадрантах.

    Арктангенс

    Функция ArcTangent обратна касательной. При заданном значении функция ArcTangent возвращает соответствующий угол. График функции приведен ниже.

    Обратите внимание, что функция возвращает только углы в пределах первого и четвертого квадрантов системы координат. Таким образом, следующее выражение верно не для всех углов.

    Однако показанная ниже улучшенная версия работает.

    Арктангенс 2

    Функция Arc Tangent 2 является улучшенной версией функций дуги и возвращает углы во всех квадрантах системы координат. Учитывая координаты точки, функция возвращает угол, соответствующий точке.

    Примечание: Будьте внимательны при вводе аргументов функции ATAN2 в калькуляторах и языках программирования, так как их порядок не соответствует.

    Leave a Reply

    Ваш адрес email не будет опубликован. Обязательные поля помечены *