Число умножить на корень: Как умножить корень на число 🚩 Корень умножить на корень 🚩 Образование 🚩 Другое

Действия с корнями.

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Деление корней с одинаковыми и разными показателями

Чтобы разделить корни с одинаковыми показателями, нужно разделить подкоренные выражения, а показатель корня оставить прежний.

^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Если показатели корней разные, то сначала нужно привести корни к общему показателю, а потом — поделить получившиеся корни с одинаковыми показателями. Можно делить (число на корень или корень на число) — для этого нужно занести под знак корня (в числитель или в знаменатель) это число, возведённое в степень с показателем, как у корня.

^∛‎(729) / _√(25) =
= ^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Возведение корней в степень

Чтобы возвести корень в степень, нужно возвести в эту степень подкоренное выражение, а показатель корня оставить тем же.
(∛‎(125))² = (∛‎(125²))

Извлечение корня из корня

Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить прежним.

Уничтожение иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.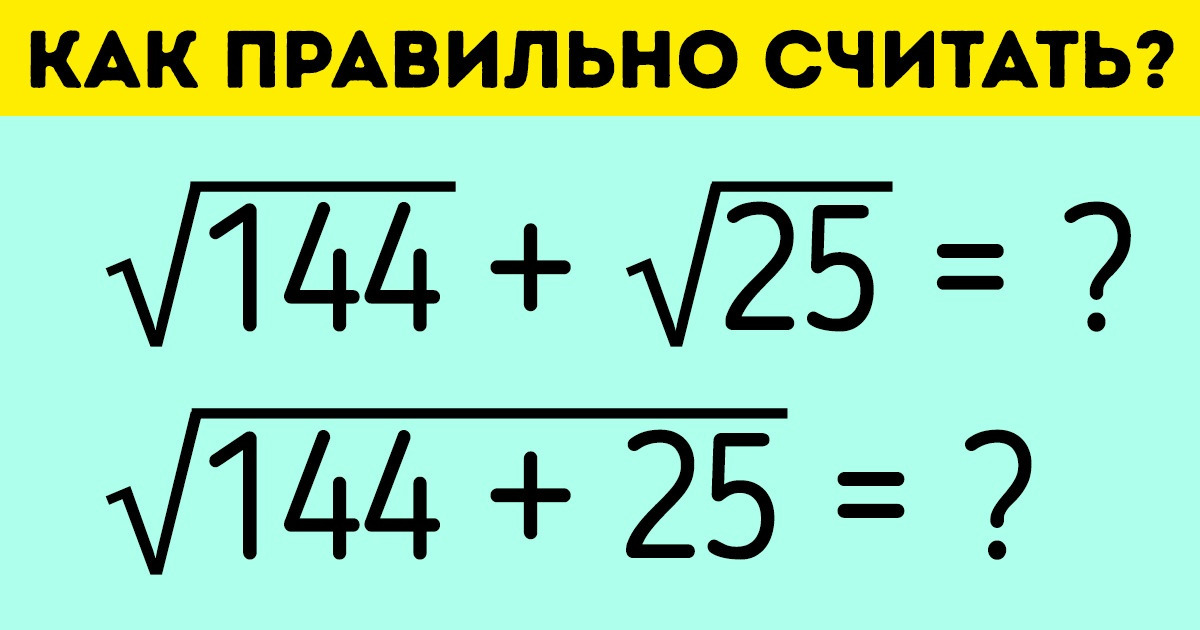

⁷ / _√(5) =
= ^{7 × √(5)} / ₅

Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.

⁷ / _{[ √(7) — √(3) ]} =
= ^{7 × [ √(7) + √(3) ]} / _{[ 7 — 3 ]} =
= ^{7 × [ √(7) + √(3) ]} / ₄

Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.

⁵ / _{[ ∛(7) + ∛(4) ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / _{[ 7 + 4 ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / ₁₁

← Предыдущий урок

Оглавление

Следующий урок →

Корень (кубический, квадратный) в степени: решения, таблицы, примеры

Степенью называется выражение вида .

Здесь  — основание степени,  — показатель степени.

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

.

Возвести число в куб — значит умножить его само на себя три раза.

.

Возвести число в натуральную степень  — значит умножить его само на себя раз:

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

.

Это верно для . Выражение 0⁰ не определено.

Определим также, что такое степень с целым отрицательным показателем.

Конечно, все это верно для , поскольку на ноль делить нельзя.

Например,

Заметим, что при возведении в минус первую степень дробь переворачивается.

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где  — целое,  — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Определение.

Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен .

Согласно определению,

В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение    для нас сейчас имеет смысл только при .

Выражение всегда неотрицательно, т. е. . Например, .

Свойства арифметического квадратного корня:

 

Запомним важное правило:

По определению, .

Кубический корень

Аналогично, кубический корень из  — это такое число, которое при возведении в третью степень дает число .

Например, , так как ;

, так как ;

, так как .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

Корень -ной степени

Корень -ной степени из числа  — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

в общем случае .

Сразу договоримся, что основание степени больше 0.

Например,

Выражение по определению равно .

При этом также выполняется условие, что больше 0.

Например,

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются;

— при делении степени на степень показатели вычитаются;

— при возведении степени в степень показатели перемножаются;

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1.

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2.

3.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при

Решение:

При получим

Ответ: -0,5.

5. Найдите значение выражения при

Решение:

При a = 12 получим

Мы воспользовались свойствами степеней.

Ответ: 144.

6. Найдите значение выражения при b = — 5.

Решение:

При b = — 5 получим:

Ответ: -125.

7. Расположите в порядке возрастания:

Решение:

Запишем выражения как степени с положительным показателем и сравним.

Так как то

Так как то

Сравним и для этого оценим их разность:

значит

Получим : поэтому

Ответ:

8. Представьте выражение в виде степени:

Решение:

Вынесем за скобку степень с меньшим показателем:

Ответ:

9. Упростите выражение:

Решение:

Приведем основания 6 и 12 к основаниям 2 и 3:

(выполним деление степеней с одинаковыми основаниями)

Ответ: 0,25.

10. Чему равно значение выражения при ?

Решение:

При получим

Ответ: 9.

Сравнение арифметических корней

11. Какое из чисел больше: или ?

Решение:

Возведем в квадрат оба числа (числа положительные):

Найдем разность полученных результатов:

так как

Значит, первое число больше второго.

Ответ:

Как избавиться от иррациональности в знаменателе

Если дана дробь вида то нужно умножить числитель и знаменатель дроби на :

Тогда знаменатель станет рациональным.

Если дана дробь вида или то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.

Сопряженные выражения — это выражения, отличающиеся только знаками. Например,

и и — сопряженные выражения.

Пример:

12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.

Пример 5.

13. Сравните и

1)

2) Сравним и 14.

то и а значит,

Ответ: меньше.

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Покажем несколько примеров.

14. Упростите: выражения:

Пример 5.

т.к.

Пример 6.

Пример 7.

так как

Следующие несколько задач решаются с помощью формулы:

Решение:

Получим уравнение

Ответ:

19. Вычислите значение выражения:

Решение:

Ответ: 1.

20. Вычислите значение выражения:

Решение:

Ответ: 1.

21. Вычислите значение выражения: если

Решение.

Если то следовательно

Ответ: — 1.

22. Вычислите:

Решение:

Ответ: 1.

Рассмотрим уравнение вида где

Это равенство выполняется, только если

Подробно об таких уравнениях — в статье «Показательные уравнения».

При решении уравнений такого вида мы пользуемся монотонностью показательной функции.

23. Решите уравнение:

а)

б)

в)

Решение.

23. Решите уравнение:

Решение:

тогда

Ответ: -1.

24. Решите уравнение:

Решение:

Ответ: 4.

25. Решите уравнение:

Решение:

Значит,

Ответ: -0,2.

Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Как умножать квадратные корни

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

SAT Math Help » Арифметика » Базовое возведение в квадрат / квадратные корни » Квадратные корни и операции » Как умножать квадратные корни

Упростить: 

Возможные ответы:

Правильный ответ:

Объяснение:

При умножении квадратных корней разрешается умножать числа внутри квадратного корня. Затем упростите, если необходимо.

Сообщить об ошибке. Объяснение:

При умножении квадратных корней разрешается умножать числа внутри квадратного корня. Затем упростите, если необходимо.

Сообщить об ошибке. Объяснение:

При умножении квадратных корней разрешается умножать числа внутри квадратного корня. Затем упростите, если необходимо.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы упростить задачу, просто распределите радикал перед каждым термином в круглых скобках.

Отчет о ошибке

Оцените и упростите:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня и можем упростить их, если это возможно.

Сообщить об ошибке

Упростить и оценить: 

Возможные ответы:

Правильный ответ:

04

04

09 Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня и можем упростить их, если это возможно.

В этом случае упростим каждый отдельный радикал и перемножим их.

 

Сообщить об ошибке

Упрощение: 

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня и можем упростить их, если это возможно.

Сообщить об ошибке. Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня.

Любые числа вне корня также умножаются. Мы можем упростить их, если это возможно.

Сообщить об ошибке. Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня.

Любые числа вне корня также умножаются.

Мы можем упростить их, если это возможно.

Сообщить об ошибке. Объяснение:

Чтобы умножить квадратные корни, мы умножаем числа внутри корня.

Любые числа вне корня также умножаются.

Мы можем упростить их, если это возможно.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все математические ресурсы SAT

16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept

Как умножать радикалы вместе — Криста Кинг Математика

Умножение радикалов с одинаковым корнем

Когда мы умножаем два радикала с одинаковым корнем (оба квадратных корня, оба кубических корня и т. д.), мы просто умножаем подкоренные (выражения под знаками радикалов) и ставим произведение под знаком корня.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Как умножать радикалы

Пройти курс

Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение произведения корней

Пример

Найдите продукт.

???\sqrt3\sqrt2???

Когда мы видим два радикала рядом друг с другом вот так, это означает, что мы должны их перемножить.

Чтобы умножить два квадратных корня, мы просто умножаем подкоренные и ставим произведение под знаком радикала. То есть произведение двух квадратных корней равно квадратному корню из произведения подкоренных.

???\sqrt{3\cdot2}???

???\sqrt{6}???

Полезно помнить, что мы можем использовать это правило для умножения радикалов и в обратном направлении. Другими словами, если нам дано ???\sqrt{6}???, мы можем разложить ???6??? как ???3\cdot2???, затем переписать ???\sqrt6??? как ???\sqrt{3\cdot2}???, и, наконец, перепишите квадратный корень из произведения (из ???3??? и ???2???) как произведение их квадратных корней.

???\sqrt{6}???

???\sqrt{3\cdot2}???

???\sqrt3\sqrt2???

Иногда переписывание радикала как произведения радикалов может помочь нам решить проблему, над которой мы работаем, поэтому полезно помнить, что с этим правилом умножения радикалов можно действовать в обоих направлениях.

Теорема о квадратных корнях говорит нам, что если ???m??? и/или ???н??? неотрицательные действительные числа, то

???\sqrt{m}\sqrt{n}=\sqrt{mn}??? и ???\sqrt{mn}=\sqrt{m}\sqrt{n}???

Давайте сделаем еще один пример, где мы умножаем два квадратных корня.

Чтобы умножить два квадратных корня, мы просто умножаем подкоренные и ставим произведение под знаком радикала.

Пример

Найдите продукт.

???\sqrt5\sqrt5???

Давайте повторим те же шаги, что и раньше, где мы перепишем произведение квадратных корней как квадратный корень из произведения подкоренных.

???\sqrt{5\cdot5}???

???\sqrt{25}???

Но теперь нам нужно понять, что ???\sqrt{25}??? просто ???5???, так как ???5??? умноженное само на себя равно ???25???. Итак, мы можем написать ???\sqrt{25}??? как раз ???5???.

Что приводит нас к тому, что при умножении двух одинаковых квадратных корней результат будет таким же, как подкоренное в каждом из квадратных корней. Итак,

Точно так же, когда у нас есть произведение трех одинаковых кубических корней, мы получаем число, равное подкоренному в каждом из них.