Как рассчитать диагональ треугольника: Рассчитать диагональ прямоугольника зная длину сторон

Диагональ треугольника – формула

4.7

Средняя оценка: 4.7

Всего получено оценок: 76.

4.7

Средняя оценка: 4.7

Всего получено оценок: 76.

Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Треугольник

Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:

• Высота;
• Медиана;
• Биссектриса.

Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.

Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной.

Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

• Делит фигуру на две равных прямоугольных треугольника.
• В полученных треугольниках диагональ будет являться гипотенузой
• Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб.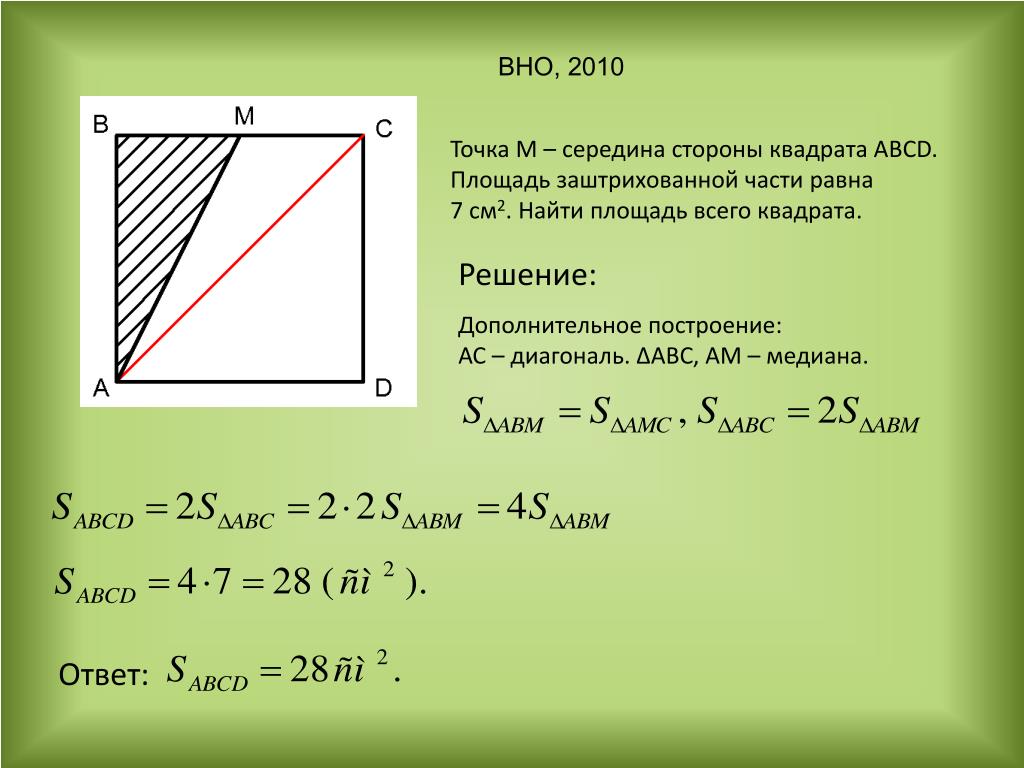

При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P={n(n-3)\over{2}}$ – где n это число сторон многоугольника.

Проверим для квадрата:

$P={4(4-3)\over{2}}={4\over2}=2$ – все верно.

Рис. 3. Диагонали квадрата.

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.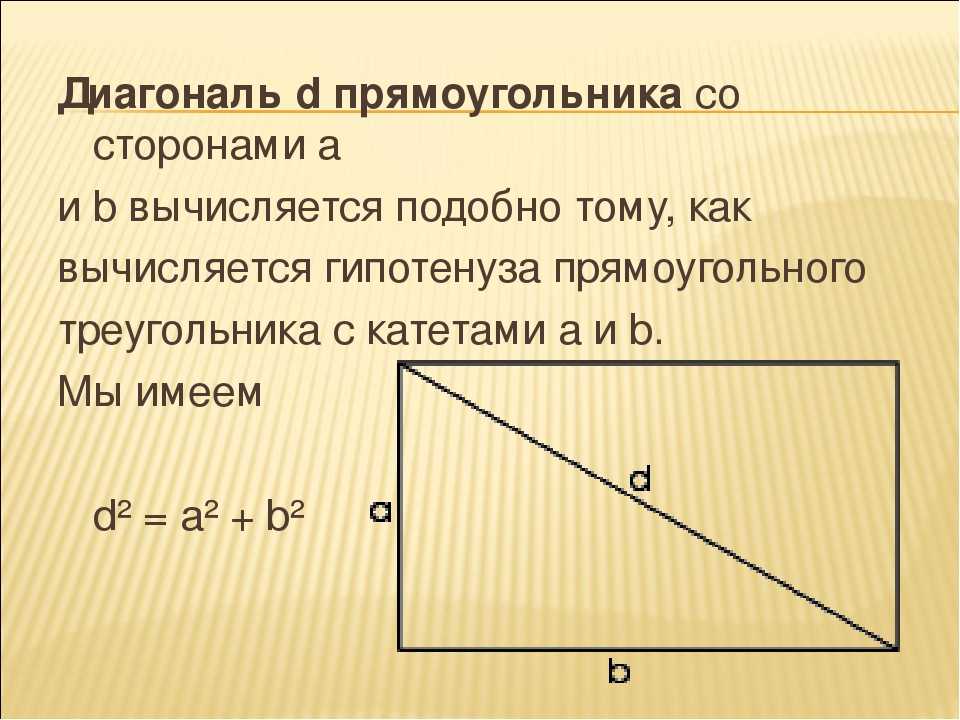

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Алексей Касюгин

  4/5

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 76.

---

А какая ваша оценка?

Как рассчитать диагональ зная длину и ширину. Геометрические фигуры

Прерывание беременности

Квадрат – самая простая фигура в геометрии. Именно с нее, прямоугольника и квадрата начинают изучать данный предмет. Умение решать задачи с квадратом помогут вам освоить более сложный материал. Данная статья расскажет о том, как найти диагональ квадрата.

Решение геометрических задач интересно тем, что решить их можно несколькими способами. Каждый способ по-своему интересен. Не исключение и диагональ квадрата, которую можно найти прямым и косвенным путями.

Как найти диагональ квадрата – формула

Существует довольно простая формула для нахождения диагонали квадрата.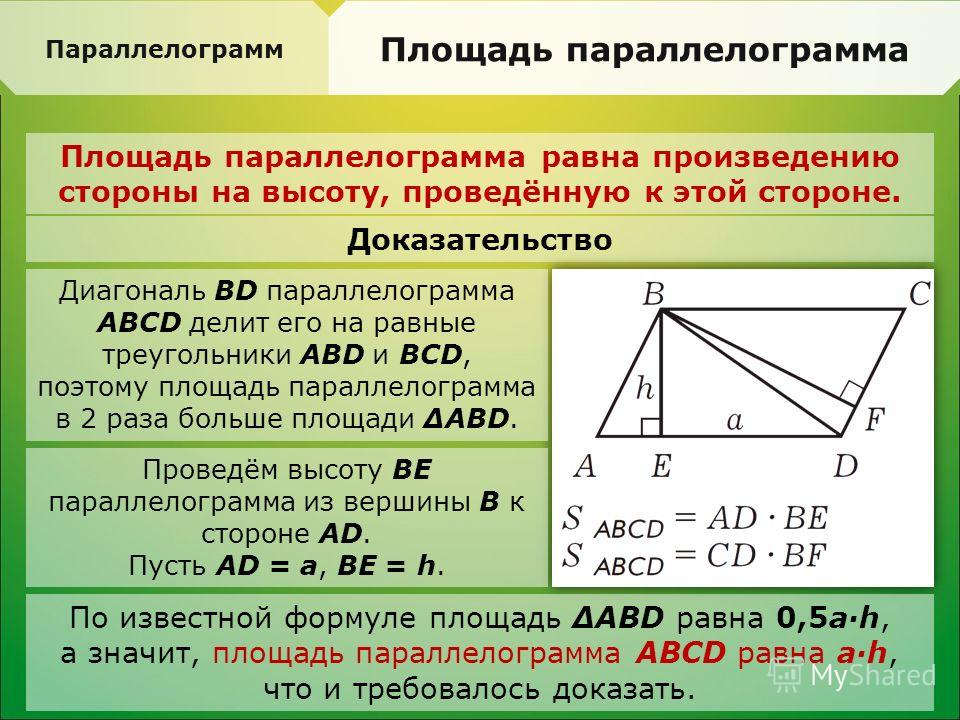 Она выглядит следующим образом: a√2. a – сторона квадрата. Вспомним, что все стороны квадрата равны. Таким образом, если вы знаете величину одной стороны, вы знаете и величину остальных трех сторон. Чтобы узнать диагональ квадрата необходимо ее сторону умножить на корень из двух.

Пример 1: Найти диагональ квадрата, если известно, что его сторона равна 5.

Решение: Подставив значение в вышеупомянутую формулу, нетрудно догадаться, что диагональ будет равна 5√2.

Пример 2: Найти сторону квадрата, если известно, что его диагональ составляет 5√2.

Решение: Диагональ обозначается маленькой латинской буквой d. d = a√2. Следовательно, чтобы найти сторону зная диагональ необходимо значение диагонали разделить на корень из двух. Проделав это действие, мы узнаем сторону квадрата, которая, в данном случае, равна 5.

Как найти диагональ квадрата через прямоугольный треугольник

Если в квадрате провести диагональ, несложно заметить, что образуются два прямоугольных треугольника. Вспомним, что у прямоугольного треугольника один угол обязательно прямой. Состоит он из двух катетов (стороны при угле в 90 градусов) и гипотенузы (противоположной 90 -градусному углу стороны). Квадрат гипотенузы равен сумме квадратов катетов. В данном случае гипотенуза и есть диагональ нашего квадрата. Так как катеты – это стороны квадрата, формула будет иметь следующий вид: d² = a² + a² = 2a². Отсюда следует, что d = √2a² = a√2.

Пример 3: Найти диагональ квадрата, если его сторона равна 3.

Решение:

1. Складываем квадраты сторон, получаем 18.
2. Считаем корень из 18 и получаем 3√2.

Несмотря на то, что последний способ более длинный и в конечном итоге мы выходи на формулу из первого примера, знать его необходимо. По сути, этот способ является доказательством формулу диагонали квадрата. Именно это доказательство может прийти на экзамене или олимпиаде. Хорошо выучите ее, ведь она может помочь вам на вышеупомянутых мероприятиях.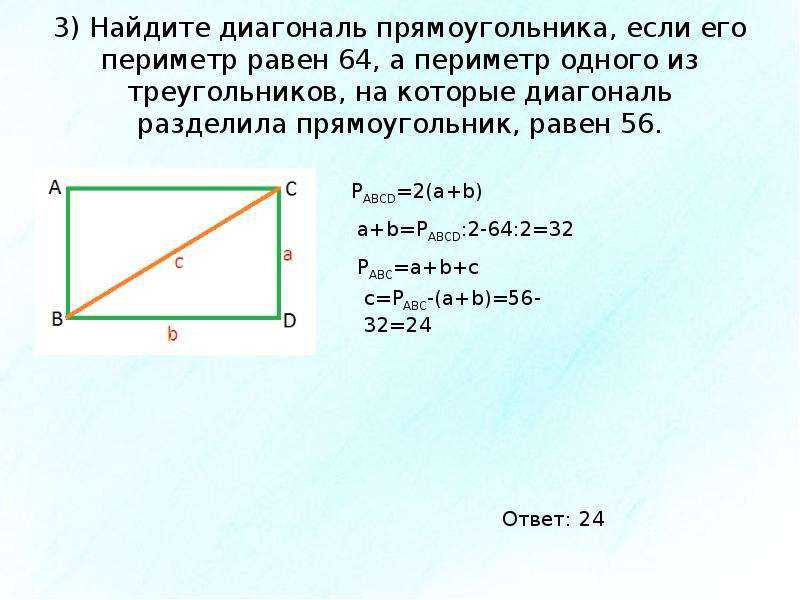

Онлайн-калькулятор

Несмотря на то, что решать такие задачи не составляет большого труда, некоторые ученики могут забыть формулу. Для таких случаев существует онлайн калькулятор, который позволяет найти правильный ответ исходя из того, что дано в задаче. Чтобы воспользоваться данным сервисом перейдите по ссылке .

1. Прокрутите страницу вниз и вы найдете подзаголовок “найти диагональ квадрата, зная сторону.
2. Ниже этого подзаголовка будет приведена формула, посмотрев на которую вам и не понадобится калькулятор.
3. Но все-таки, если вы не уверены, впишите в поле значение длины квадрата, а затем на кнопку “вычислить”.
4. Калькулятор за 1 секунду выдаст вам правильный ответ.

Теперь, зная несколько способов для решения задачи на данную тематику, вы не будете листать книгу по математике в поисках нужной формулы, а просто воспользуетесь онлайн-калькулятором или примерами, которые приведены выше.

Чтоб правильно рассчитать и выставить диагональ фундамента или опалубки фундамента — очень хорошо нанять спецов.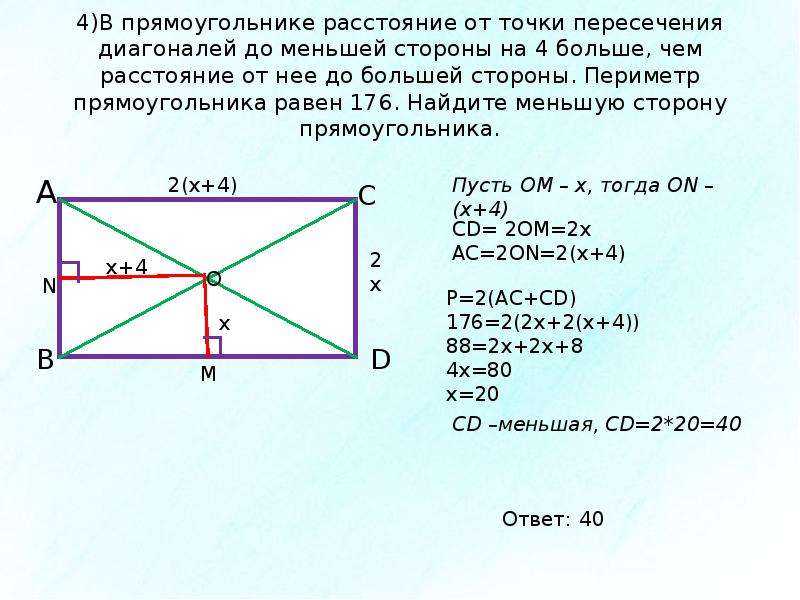 Но если вы уже несколько раз видели передачу «квадратный метр», несколько раз слышали разговор о том как надо строить, а еще кучу анекдотов о строительстве? — другое дело. Это и дает нам «полное право» предполагать, что мы сами справимся с таким простым делом, как углы и диагонали опалубки фундамента. Именно такого высокого мнения о себе каждый, кто планирует строить баню своими руками (Ха-ха!)

О начале разметки и проектирования фундамента и опалубки я писал в статье . На момент вбивания кольев и установки внешних досок опалубки я уже проверял длину диагонали. Все сходилось до миллиметра. Это самое главное условия получения прямых углов сруба бани. Но после первой разметки были манипуляции с установкой дна ростверка, монтаж внутренних щитов опалубки, доделывание опалубки столбиков от уровня земли до дна будущего фундамента. Конечно же, я очень старался чтоб ничего не сдвинуть, и колья вбивал глубоко.

Но как и во всякой стройке, случился перекосяк. Это не так страшно, как если бы я этого не заметил или я об этом не знал.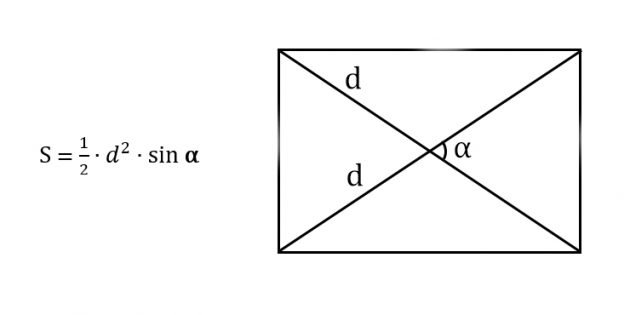 Поэтому я перед укладкой арматуры решил опять проверить диагонали. Разница получилась в 2 см. Вот и хорошо, что обнаружилось до заливки бетона.

Как вывести диагональ опалубки?

Для упрощения постройки правильной опалубки я делал длину стенок абсолютно равной. Поэтому перекос может получиться только в виде ромба. На рисунке умышлено увеличена степень перекоса опалубки для наглядности.
Для исправления ситуации поступили так:

Такое комбинированное перемещение одной из сторон опалубки (северной на рисунке) не было слишком трудном, поскольку колья и первоначальное расположение опалубки соответствовали правильному положению. Поэтому смещение диагонали было минимальным и усилия по «корректировке» положения щитов не вызывали механического напряжения и усилий.

Способ установки углов по равным диагоналям можно использовать только при условии равенства сторон. Равенства диагоналей будет достаточно!

Для сторон опалубки с большим размером возможно применить правило «золотого» треугольника.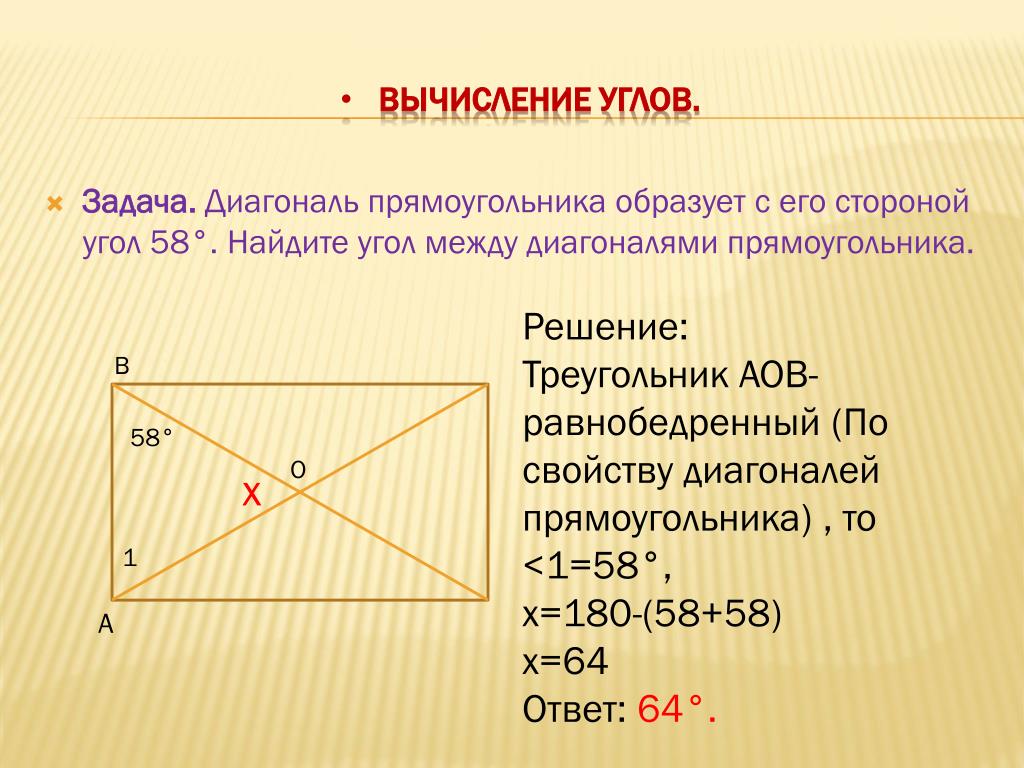 Если такой треугольник, согласно теореме Пифагора, имеет стороны 3, 4, то гипотенуза равна 5 единицам. Таким образом, достаточно отмерить на сторонах опалубки части кратные 3 и 4 у вершины прямого угла и тогда расстояние между контрольными точками будет 5 частей! Это и будет гарантией прямых углов и равенства диагоналей!

Для осуществления правильного планирования монтажа опалубки очень рекомендую использовать метод обноски, который позволяет в любое время монтажных работ производить сверку углов, снимать и повторно устанавливать шнуры периметра фундамента.

Перед заливкой фундамента не поленитесь еще раз проверить диагонали. Это лишним не будет! Бетон невозможно легко и быстро поправить. Ошибки исправлять очень дорого и долго. Фундамент для сруба имеет больше требований к качеству чем фундамент для каменного дома. Раствором уже ничего не выровнять!

Не забудьте перед заливкой для ее легкого демонтажа!

Прямоугольник — это четырехугольник, у которого каждый угол является прямым.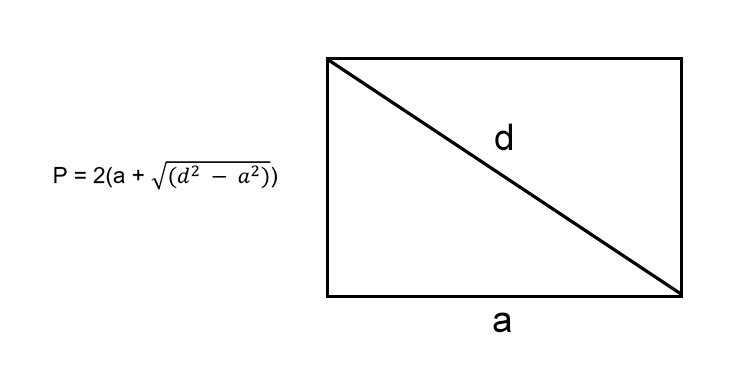

Доказательство

Свойство объясняется действием признака 3 параллелограмма (то есть \angle A = \angle C , \angle B = \angle D )

2. Противоположные стороны равны.

AB = CD,\enspace BC = AD

3. Противоположные стороны параллельны.

AB \parallel CD,\enspace BC \parallel AD

4. Прилегающие стороны перпендикулярны друг другу.

AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB

5. Диагонали прямоугольника равны.

AC = BD

Доказательство

Согласно свойству 1 прямоугольник является параллелограммом, а значит AB = CD .

Следовательно, \triangle ABD = \triangle DCA по двум катетам (AB = CD и AD — совместный).

Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.

Значит, AC = BD .

Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.

Докажем и это.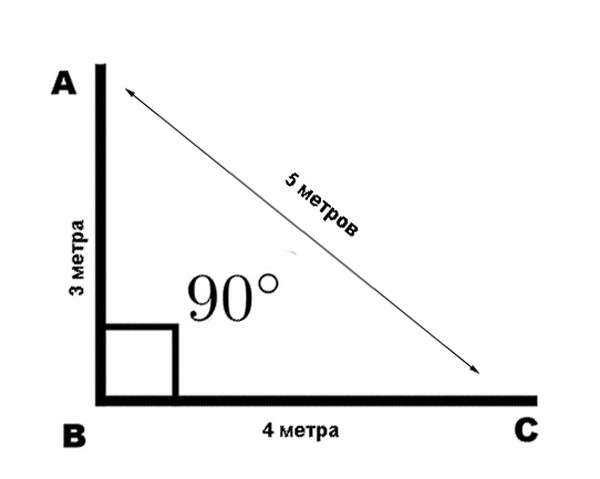 {\circ}

14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.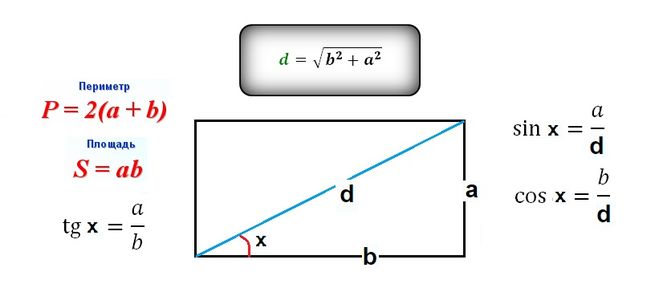

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Задача на нахождение диагонали прямоугольника может быть сформулирована тремя разными способами. Рассмотрим подробнее каждый из них. Способы зависят от известных данных, итак как найти диагональ прямоугольника?

Если известны две его стороны

В случае, когда известны две стороны прямоугольника a и b, для нахождения диагонали необходимо воспользоваться теоремой Пифагора: a 2 +b 2 =c 2 , здесь a и b — катеты прямоугольного треугольника, с – гипотенуза прямоугольного треугольника. Когда в прямоугольнике прочерчена диагональ, он делится на два прямоугольных треугольника.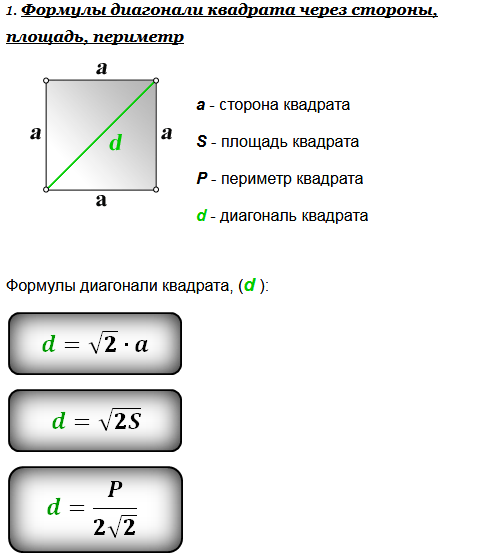 Две стороны этого прямоугольного треугольника нам известны (a и b). То есть, чтобы найти диагональ прямоугольника, формула нужна следующая: c=√(a 2 +b 2), здесь с – длина диагонали прямоугольника.

По известной стороне и углу, между стороной и диагональю

Пусть известна сторона прямоугольника a и угол, который она образует с диагональю прямоугольника α. Для начала вспомним формулу косинуса: cos α = a/c,здесь с – диагональ прямоугольника. Как рассчитать диагональ прямоугольника из этой формулы: с = a/cos α.

По известной стороне, углу между прилегающей к ней стороне прямоугольника и диагональю.

Так как диагональ прямоугольника делит сам прямоугольник на два прямоугольных треугольника, логично обратиться к определению синуса. Синус — отношение катета, лежащего против этого угла, к гипотенузе.sin α = b/c. Отсюда выводим формулу для нахождения диагонали прямоугольника, которая также является и гипотенузой прямоугольного треугольника: с = b/sin α.

Теперь вы подкованы в этом вопросе. Можете порадовать учителя геометрии уже завтра!

Как вычислить диагональ треугольника

••• doraartem/iStock/GettyImages

Обновлено 16 ноября 2020 г. вам ценная информация. Эта фраза говорит вам, что вы имеете дело с прямоугольным треугольником, две стороны которого перпендикулярны друг другу (или, говоря иначе, они образуют прямоугольный треугольник), и только одна сторона остается «диагональной» по отношению к другим. . Эта диагональ называется гипотенузой, и вы можете найти ее длину, используя теорему Пифагора.

TL;DR (слишком длинно, не читал)

Чтобы найти длину диагонали (или гипотенузы) прямоугольного треугольника, подставьте длины двух перпендикулярных сторон в формулу ​ a ² ​ + ​ b ² ​ = ​ c ² ​, где ​ a ​ и ​ b ​ длины перпендикулярных сторон и ​ c ​гипотенуза. Затем найдите ​ c ​.

Теорема Пифагора 92

В реальном мире это означает, что если вы знаете длину любых двух сторон прямоугольного треугольника, вы можете использовать эту информацию, чтобы узнать длину недостающей стороны.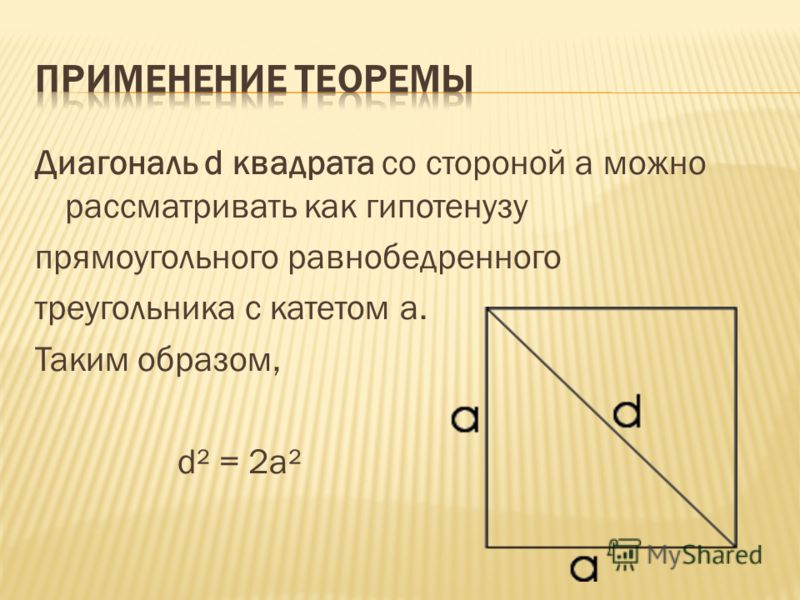 Обратите внимание, что это работает только для прямоугольных треугольников.

Нахождение гипотенузы

Предполагая, что вы знаете длины двух недиагональных сторон треугольника, вы можете подставить эту информацию в теорему Пифагора, а затем найти c. ​

Подставить известные значения ​ 92 = 25

Возьмите квадратный корень из обеих частей, последний шаг в решении для c . Это дает вам:

c = \sqrt{25}= 5

Итак, длина диагонали или гипотенузы этого треугольника равна 5 единицам.

• Что, если вы знаете длину диагонали треугольника и длины одной другой стороны? Вы можете использовать ту же формулу, чтобы найти длину неизвестной стороны. Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную с одной стороны от знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны.

Связанные статьи

Ссылки

• Purple Math: Теорема Пифагора
• Математика — это весело: Pythagoras Theoorem
• Encyclopaedia Britannica: Pythagoras
• , Artanile

  , 9008, 9008, 9008, 9008,

  , 9008, 9008, 9008,

• , а Энцикл. Анкоридже, и провел несколько лет, обучая старшеклассников и студентов университетов страшным, но веселым! — математические предметы, такие как алгебра и исчисление.

  Калькулятор прямоугольного треугольника | Определение

  Создано Альваро Диесом, Матеушем Мухой и Петром Малеком.

• Калькулятор гипотенузы
• Как найти площадь прямоугольного треугольника
• Другие соображения при работе с прямоугольным треугольником
• Особые треугольники
• Особые прямоугольные треугольники
• Прямоугольные треугольники и параллелограммы
• Пифагорейские тройки, треугольники и математика
• Тени и прямоугольные треугольники (радиус Земли)
• Часто задаваемые вопросы

Калькулятор прямоугольного треугольника поможет вам найти длины сторон прямого угла -угольный треугольник . Этот решатель треугольников также научит вас находить площадь прямоугольного треугольника, а также даст много информации о практическом использовании прямоугольного треугольника.

Что такое прямоугольный треугольник (или прямоугольный треугольник)?

Прежде всего, давайте объясним, что такое прямоугольный треугольник. Определение очень простое и может даже показаться очевидным для тех, кто его уже знает: прямоугольный треугольник — это треугольник, в котором один и только один из углов равен ровно 90° . Очевидно, что два других угла будут меньше прямого угла, потому что сумма всех углов треугольника всегда равна 180°.

В прямоугольном треугольнике стороны определяются особым образом. Сторона, противолежащая прямому углу, всегда является наибольшей в треугольнике и получает название «гипотенуза». Две другие стороны называются катетами. Связь между гипотенузой и каждым катетом прямая, как мы увидим 9.0137 когда мы говорим о теореме Пифагора .

Калькулятор гипотенузы

Если все, что вы хотите вычислить, это гипотенуза прямоугольного треугольника, эта страница и ее калькулятор прямоугольного треугольника отлично подойдут.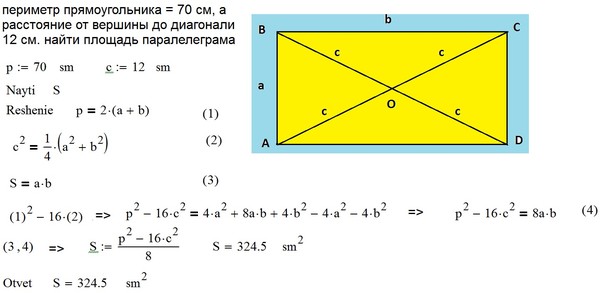 Однако мы также рекомендуем использовать специальный инструмент, разработанный нами в Omni Calculators: калькулятор гипотенузы. Гипотенуза находится напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом , и b и с гипотенузой c , теорема Пифагора утверждает, что: a² + b² = c² .

Чтобы найти c , извлеките квадратный корень из обеих частей, чтобы получить c = √(b²+a²) . Мы можем рассматривать это расширение теоремы Пифагора как «формулу гипотенузы». Калькулятор теоремы Пифагора также является отличным инструментом для вычисления гипотенузы.

Давайте теперь решим практический пример того, что потребуется, чтобы вычислить гипотенузу прямоугольного треугольника без использования каких-либо калькуляторов доступен в Omni:

1. Получите значения a и b .
2. Квадрат a и b .
3. Суммируйте оба значения: a² + b² .
4. Извлеките квадратный корень из результата.
5. Квадратный корень даст положительные и отрицательные результаты. Поскольку мы имеем дело с длиной, не обращайте внимания на отрицательную.
6. Полученное значение является значением гипотенузы c .

Теперь посмотрим каким будет процесс с использованием одного из калькуляторов Omni , например, калькулятор прямоугольного треугольника на этой веб-странице:

1. Вставьте значение a и b в калькулятор; и
2. Немедленно получить значение c ;
3. В качестве бонуса вы получите значение площади такого треугольника.

Как найти площадь прямоугольного треугольника

Мы уже видели, что вычислить площадь прямоугольного треугольника очень просто с калькулятором прямоугольного треугольника. В Omni Calculators у нас есть калькулятор, специально разработанный для этой цели: калькулятор площади прямоугольного треугольника. Давайте теперь более подробно рассмотрим, как вычислять площади прямоугольных треугольников.

Способ нахождения площади прямоугольного треугольника довольно прост. Все, что вам нужно, это 90 137 длины основания и 90 138 высоты. В прямоугольном треугольнике основание и высота – две стороны, образующие прямой угол. Поскольку умножение этих значений на значения вместе дает площадь соответствующего прямоугольника, а площадь треугольника составляет половину этой площади, формула такова:

площадь = ½ × основание × высота .

Если вы не знаете ни основания, ни высоты, вы можете найти их по теореме Пифагора. Воспользуйтесь калькулятором прямоугольного треугольника, чтобы проверить свои расчеты или вычислить площадь треугольников, стороны которых имеют большую или десятичную длину.

Другие соображения при работе с прямоугольным треугольником

Теперь мы увидим другие вещи, которые можно вычислить из прямоугольного треугольника с помощью некоторых инструментов, доступных в Omni. Стороны треугольника имеют определенный градиент или наклон. Формула наклона

наклон = (y₂ — y₁)/(x₂ — x₁) .

Итак, если координаты (1,-6) и (4,8) , наклон сегмента равен (8 + 6)/(4 — 1) = 14/3 . Простой способ определить, является ли треугольник правильным, и вы просто знаете координаты, состоит в том, чтобы посмотреть, умножаются ли наклоны любых двух линий на равные -1 .

Существует простой способ преобразования углов из радианов в градусы и градусов в радианы с использованием преобразования углов:

• Если угол в радианах – умножить на 180/π ; и
• Если угол в градусах – умножить на π/180 .

Иногда вы можете столкнуться с проблемой отсутствия двух или даже трех длин сторон. В таких случаях калькулятор прямоугольного треугольника, калькулятор гипотенузы и метод нахождения площади прямоугольного треугольника не помогут. Вы должны использовать тригонометрические функции, чтобы найти недостающие части.

Особые треугольники

Прямоугольный треугольник — это лишь один из многих существующих особых треугольников. Эти треугольники обладают одной или несколькими особыми характеристиками, которые делают их уникальными. Например, как мы видели, прямоугольный треугольник имеет прямой угол и, следовательно, гипотенузу, что делает его уникальным видом треугольника. Помимо прямоугольного треугольника, есть и другие особые треугольники с интересными свойствами.

Одним из самых известных специальных треугольников является равносторонний треугольник, у которого три равные стороны и все его углы равны 60°. Это значительно упрощает вычисление различных параметров такого треугольника с помощью калькулятора решения треугольников.

Другим особым треугольником является равнобедренный треугольник, у которого две стороны одинаковой длины , а значит, два угла одинаковой величины. В отличие от равностороннего треугольника, равнобедренные треугольники бывают разных форм.

Есть много других специальных треугольников. Однако сейчас мы рассмотрим несколько совершенно особых прямоугольных треугольников, которые, помимо прямоугольных треугольников, обладают другими уникальными свойствами, делающими их интересными.

Особые прямоугольные треугольники

Так называемый треугольник «45 45 90», вероятно, самый особенный среди всех особых прямоугольных треугольников. Это прямоугольный треугольник, который также является равнобедренным треугольником . Оба его катета имеют одинаковую длину (равнобедренные), а также он имеет ту особенность, что непрямые углы составляют ровно половину размера прямого угла, что и дало название прямоугольному треугольнику.

Этот прямоугольный треугольник можно получить, когда вы разделить квадрат на его диагональ . Вот почему обе катеты (стороны квадрата) имеют одинаковую длину.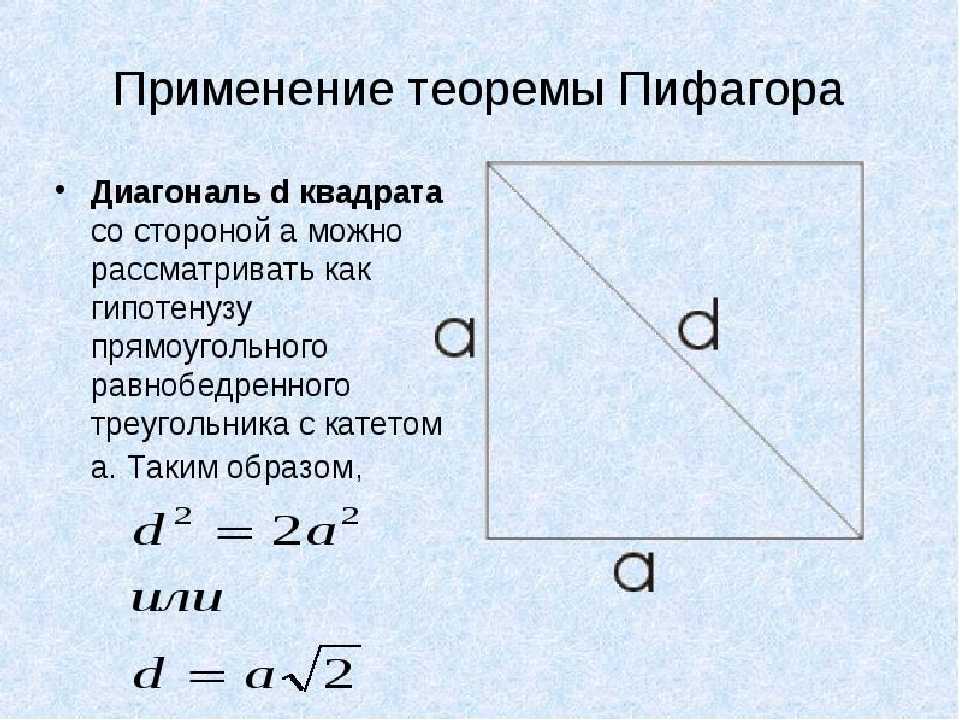 Для тех, кто хочет узнать больше о самых особенных из особых прямоугольных треугольников, мы рекомендуем проверить калькулятор треугольника 45 45 90, созданный для этой цели.

Еще один увлекательный треугольник из группы особых прямоугольных треугольников — так называемый треугольник «30 60 90». Название происходит от наличия одного прямого угла (90°), затем одного угла 30° и другого 60°. Эти углы особенные из-за значений их тригонометрических функций (косинуса, синуса, тангенса и т. д.). Последствия этого можно увидеть и понять с помощью 30 60 90 калькулятор треугольников, но для тех, кому лень переходить по ссылке, мы приведем некоторые из них здесь . Предположим, что длина меньшей стороны равна 90 153 a 90 154 , тогда треугольник выглядит следующим образом:

1. Вторая длина равна 90 153 a√3 ;
2. Гипотенуза равна 2a ;
3. Площадь равна a²√(3/2) ; и
4. Периметр равен a(3 + √3) .

Прямоугольные треугольники и параллелограммы

На первый взгляд может показаться, что прямоугольный треугольник и параллелограмм не имеют ничего общего. Как решатель треугольников может помочь вам понять параллелограмм? Реальность такова, что любой параллелограмм можно разложить на 2 или более прямоугольных треугольника . Давайте возьмем пример прямоугольника, который проще всего увидеть.

Представьте себе прямоугольник, любой прямоугольник. Теперь нарисуйте след на одной из диагоналей этого прямоугольника. Если разделить прямоугольник диагональю, то получится два прямоугольных треугольника . Глядя на треугольники, нет необходимости использовать калькулятор прямоугольного треугольника, чтобы убедиться, что оба треугольника равны, поэтому их площади будут одинаковыми. Это означает, что площадь прямоугольника вдвое больше площади каждого треугольника .

Если мы подумаем об уравнениях, это имеет смысл, поскольку площадь прямоугольника со сторонами a и b равна площади = a × b , а для прямоугольного треугольника равна площади = основание × высота / 2 , что в данном случае будет означать площадь = a × b /2 . Это именно то, что мы уже видели, просто разрезав прямоугольник по диагонали.

Это был простой пример прямоугольника, но то же самое относится и к площади квадрата. Для других параллелограммов процесс несколько усложняется (может быть задействовано до 4-х прямоугольных треугольников разных размеров). Тем не менее, при некотором навыке, вы можете использовать ту же идею и вычислить площадь параллелограмма, используя прямоугольные треугольники. Вы можете, конечно, быть еще более эффективным и просто использовать наш калькулятор.

Пифагорейские тройки, треугольники и математика

Геометрия и многоугольники, особенно треугольники, всегда идут рука об руку. Свойства некоторых треугольников, например прямоугольных, обычно интересны и шокируют даже нематематиков. Теперь мы рассмотрим интересных наборов чисел , очень тесно связанных с прямоугольными треугольниками, которые любят математики, и, возможно, вы тоже.

Эти наборы чисел называются пифагорейскими тройками и представляют собой наборы из 3 целых чисел (назовем их a , b и c ) и удовлетворяют теореме Пифагора: a² + b² = c² .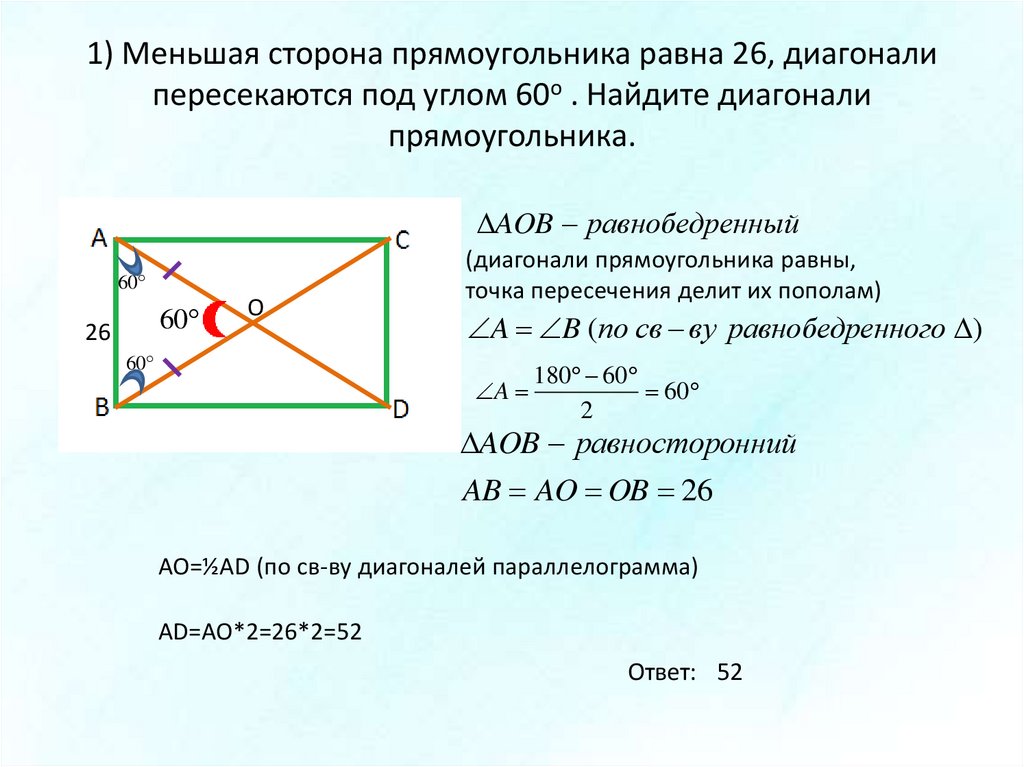 То есть они могли бы образовать прямоугольный треугольник со сторонами длиной a , b и c . Количество чисел, удовлетворяющих этому соотношению, ограничено, но математики находят удовольствие в поиске новых.

Помимо фактора любопытства в этих отношениях, в них есть несколько интересных свойства, которые используются в криптографии . Учитывая приложения, которые можно найти для таких наборов чисел, математики исследовали даже больше, используя 4, 5… и больше наборов чисел, которые удовлетворяют аналогичному соотношению, в котором сумма квадратов всех чисел, кроме одного, дает квадрат оставшегося числа.

С этими пифагорейскими тройками тесно связана также печально известная последняя теорема Ферма , в которой почти легендарный загадочный математик Пьер Ферма заявил, что не может быть набора из трех целых чисел, которые удовлетворяли бы соотношению: aⁿ + bⁿ = cⁿ для n больше 2. Эта гипотеза не была доказана математически, и она считается единицей. из важнейших математических задач века.

Тени и прямоугольные треугольники (радиус Земли)

Мы много говорили о треугольниках, особенно прямоугольных, и их применении в математике и геометрии. О чем мы еще не говорили, так это о полезность прямоугольных треугольников для расчетов в реальной жизни . Может показаться, что возможности применения вне геометрии ограничены, но давайте взглянем на тени.

Да, тени. Темный оттенок, отбрасываемый объектом при его освещении. Если бы вы посмотрели на форму, созданную тенью, объектом и землей, вы бы заметили, что на самом деле это прямоугольный треугольник! По крайней мере, когда объект совершенно вертикальный, а земля горизонтальная. В большинстве случаев это так или, по крайней мере, достаточно близко. Это означает, что мы можем использовать калькулятор прямоугольного треугольника, чтобы найти различную информацию об объектах под солнцем. Посмотрим, как.

Представьте, что у вас есть здание, высоту которого мы хотим узнать , но вы не можете измерить его напрямую, потому что оно слишком высокое, чтобы сбросить рулетку сверху. Что вы можете сделать, так это измерить длину тени на улице. Затем с помощью любого углового инструмента и листа бумаги можно узнать угол между тенью и землей. Зная, что угол между зданием и землей равен 90°, можно получить значение высоты здания.

Используя эту технику, вы можете измерить высоту многих объектов , если у вас есть яркий солнечный день или другие источники света для освещения объекта. Фактически, это был очень распространенный метод измерения в старые времена. Вероятно, самое интересное и умопомрачительное использование прямоугольных треугольников принадлежит Эратосфену, которому удалось использовать прямоугольные треугольники и тени для измерения радиуса Земли , и теперь мы объясним, как он это сделал.

Эратосфен заметил, что в день летнего солнцестояния было место на Земле, где колодцы не имели тени в полдень, т. е. солнце светило прямо на них. Заметив это, он поставил столб известной высоты на известном расстоянии от этого колодца и измерил величину тени в одно и то же время дня и в один и тот же день года в обоих местах. Затем, используя прямоугольные треугольники и тригонометрию, он смог измерить угол между двумя городами, а также радиус Земли так как знал расстояние между городами.

Это был поразительный подвиг, который теперь можно сделать гораздо проще, просто используя калькуляторы Omni, которые мы создали для вас .

Часто задаваемые вопросы

Длины каких сторон образуют прямоугольный треугольник?

Длины сторон a , b , c образуют прямоугольный треугольник тогда и только тогда, когда они удовлетворяют a² + b² = c² . Мы говорим, что эти числа образуют Тройка Пифагора .