Как рассчитать прямой угол: Как найти прямой угол

Три варианта построения прямого угла на местности | Как проверить угол уже построенного дома, когда замер диагоналей невозможен? | Строю для себя

20.02.2021

В данной статье описываются три распространенных варианта построения прямых углов при разметке участка для будущего дома, а также описываются методы проверки углов уже возведенных зданий и сооружений без доступа к замеру их диагоналей.

На самом же деле, вариантов существует множество и большинство из них выражаются через тригонометрические функции или с помощью сложных геометрических построений, но здесь это ни к чему, на стройплощадке ни один строитель не возьмется за сложные вещи, упуская время.

Поэтому, рассмотрим три самых простых, но тем не менее надежных метода построения прямых углов:

Теорема Пифагора

Это самый часто используемый и очень надежный способ.

Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника и звучит так: сумма квадратов длин катетов равна квадрату длины гипотенузы.

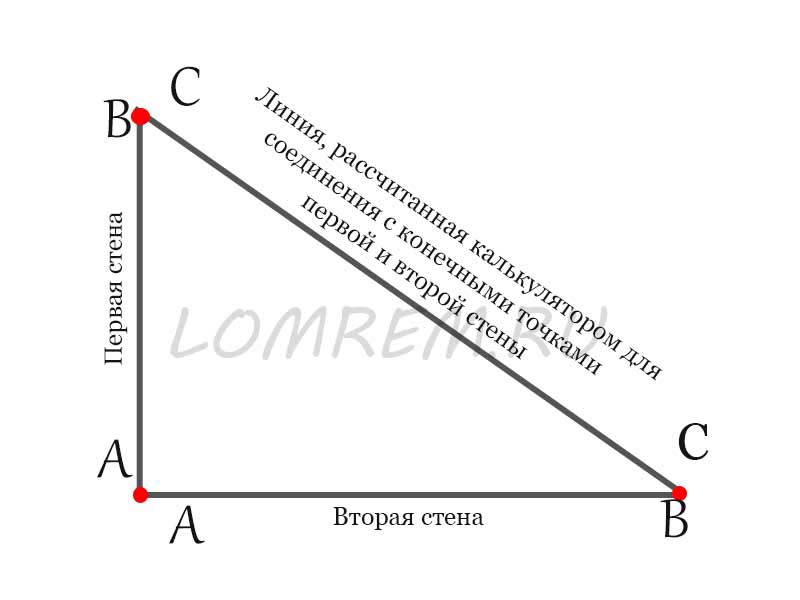
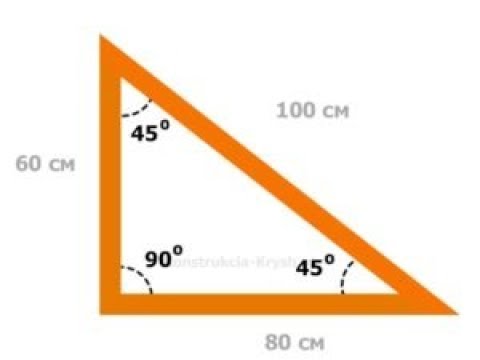
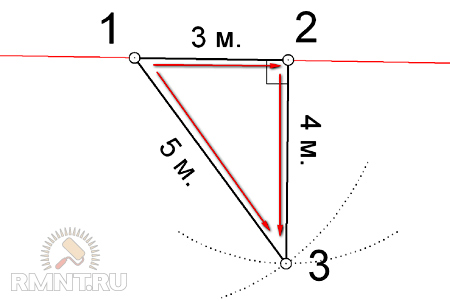
Для построения прямого угла можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома, можно без труда вычислить значение диагонали для своего дома и в дальнейшем работать с полученным значением.

Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Для удобства, существуют производные треугольники от основного, получаемые при умножении сторон треугольника Пифагора на какой-либо коэффициент. К примеру, стороны 3,4,5 умноженные на К=2 (коэффициент 2), дают треугольник со сторонами 6,8,10, при К=3, стороны 9,12,15 и т.д.

Геометрическое построение

Данный способ ни чуть не хуже Пифагорова треугольника, но редко используемый (в силу забывчивости школьных знаний), хотя очень даже эффективный!

Выглядит сложнее, чем на самом деле.

Зная угол здания (точка О), отмечаем две точки О1 и О2 по оси А, равноудаленные от точки О. Одинаковое расстояние откладывается с помощью рулетки.

Точки О1 и О2 являются центрами окружностей одинакового радиуса. Прямая, проведенная через точку пересечения двух окружностей (точка В) и точку О будет давать прямой угол с прямой А.

По факту, этот способ ни чуть не хуже треугольника Пифагора, имея под рукой два колышка и отрезок веревки, построение осей будущего дома производится всего за 20-40 минут в зависимости от размера и сложности здания.

Две рулетки

Вместо построения окружностей из точек О1 и О2, используются две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и прикладываются нулевой отметкой к каждой из точек О1 и О2.

Далее, совмещаем их одинаковыми значениями по мерным шкалам (точка Х) и получаем точку Х, соединив которую с точкой О получим перпендикуляр. В данном случае, построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.

На практике это делается следующим образом: отмечается три контрольные точки по двум рулеткам на пересечении делений (к примеру 1 м. , 3м. и 7м.). Далее, через них протягивается разметочный шнур из точки О. Если все точки пересечения шкал лежат на одной прямой (совпадают со шнуром), то построение выполнено верно.

Это настолько быстро делается, что на первый взгляд может показаться неправдоподобным, но поверьте — геометрия работает со 100% гарантией.

Проверка прямого угла построенного здания

Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется сооружать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.

Все действия аналогичны и главное правило заключается в том, чтобы вынести замеры за пределы строения.

Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками, а после — снимаем замер.

При геометрическом построении, точка пересечения двух окружностей будет лежать не в основании стены, а по «невидимому» продолжению стены в её же плоскости (на рисунке обозначена точкой Х).

При необходимости, все способы свободно комбинируются или взаимозаменяются.

На этом всё, спасибо Вам за уделенное внимание!

Всего доброго!

Поделиться в социальных сетях

Вам может понравиться

Теорема Пифагора — формула, доказательство, задачи

Поможем понять и полюбить математику

Начать учиться

540.8K

Сложно представить, но в научной литературе существует 367 доказательств теоремы Пифагора. В школьной программе мы проходим гораздо меньше — в этом материале познакомимся с главными формулами и их доказательствами.

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

a² + b² = c²,

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c² − b²
• b = √c² − a²
• c = √a² + b²

Запоминаем

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c² < a² + b², значит угол, противолежащий стороне c, является острым.
• если c² = a² + b², значит угол, противолежащий стороне c, является прямым.
• если c² > a² +b², значит угол, противолежащий стороне c, является тупым.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a² + b² = c².

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

∠ACB =∠CHA = 90º,

∠A — общий.

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

∠ACB =∠CHB = 90º,

∠B — общий.

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a² = c * HB, b² = c * AH.
• Сложим полученные равенства:

a² + b² = c * HB + c * AH

a² + b² = c * (HB + AH)

a² + b² = c * AB

a² + b² = c * c

a² + b² = c²

Теорема доказана.

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁² = A₁C₁² + B₁C₁².
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1.

Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

• Пусть катеты a = 6 и b = 8.

• По теореме Пифагора c² = a² + b².

• Подставим значения a и b в формулу:
  c² = 6² + 8² = 36 + 64 = 100
  c = √100 = 10.

Ответ: 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

Как решаем:

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

11² = 8² + 9²

121 ≠ 145

Ответ: треугольник не является прямоугольным.

---

---

 

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

216.3K

Как найти радиус окружности

К следующей статье

249.1K

Как найти периметр треугольника

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Калькулятор прямоугольного треугольника

| День пи

c (гипотенуза)

---

Периметр

Угол 1

Угол 2

Угол 3

Вернуться на страницу калькуляторов

9000 2 Чтобы использовать калькулятор прямого угла, просто введите длины любых двух сторон прямоугольный треугольник в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.

Как найти площадь и стороны прямоугольного треугольника

Сделай сам

Если мы знаем только две стороны прямоугольного треугольника, мы можем использовать эту информацию, чтобы найти третью сторону, площадь и периметр треугольника, и все углы треугольника. Удивительно, правда? Давайте рассмотрим, как мы найдем каждую из этих частей.

Как найти недостающую сторону прямоугольного треугольника

Чтобы найти недостающую сторону прямоугольного треугольника, мы используем знаменитую теорему Пифагора.

Нам нужно быть немного осторожными, чтобы знать, какую сторону мы находим. Прямоугольные треугольники имеют два катета и гипотенузу, которая является самой длинной стороной и всегда находится напротив прямого угла. Когда мы пытаемся найти гипотенузу, мы заменяем две наши известные стороны на и b на . Неважно, какая ножка a , а какая b . Затем мы находим c , складывая квадраты значений a и b и извлечь квадратный корень из обеих частей.

Когда мы пытаемся найти один из катетов, мы вводим известный катет для a и известную гипотенузу для c . Затем мы находим b с помощью простой алгебры (вычитаем значение a в квадрате с обеих сторон, затем извлекаем квадратный корень из обеих сторон).

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника, нам нужно знать только длину двух катетов. Нам вообще не нужна гипотенуза. Это потому, что катеты определяют основание и высоту треугольника в каждом прямоугольном треугольнике. Поэтому мы используем общую формулу площади треугольника (A = основание • высота/2) и подставляем a и b для основание и высота . Итак, наша новая формула для площади прямоугольного треугольника: A = ab/2.

Как найти периметр прямоугольного треугольника

Чтобы найти периметр или расстояние вокруг нашего треугольника, нам просто нужно сложить все три стороны вместе. Если мы знаем только две стороны, нам нужно сначала использовать теорему Пифагора, чтобы найти третью сторону.

Как найти углы прямоугольного треугольника

Чтобы найти углов прямоугольного треугольника, мы используем тригонометрию. Это не так сложно, как кажется. Нам просто нужно найти одну специальную кнопку на наших карманных калькуляторах. Для начала нам нужно знать все длины сторон, поэтому, если мы их еще не знаем, мы сначала воспользуемся теоремой Пифагора, чтобы найти их.

Когда у нас есть все стороны, мы определяем, какой угол мы собираемся найти. Затем мы берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне 9.0016 с . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто помечается как SIN ^-1 . Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой режим, а не на радианный.

Мы можем повторить этот процесс, чтобы найти другой неизвестный угол в треугольнике, еще раз разделив его противоположную сторону на гипотенузу, а затем взяв ARCSIN.

Или мы могли бы продемонстрировать еще больше знаний о треугольниках, используя вычитание, чтобы найти его, поскольку мы знаем, что сумма внутренних углов треугольника должна составлять 180°. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол.

Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача, чтобы попытаться найти стороны, углы, площадь и периметр самостоятельно без него. Затем вы можете использовать его, чтобы проверить наши ответы.

Как рассчитать угол 90 градусов

••• AMLBox/iStock/GettyImages

Обновлено 13 марта 2018 г. угол, является одним из Наиболее распространенные углы, используемые в архитектуре. Угол 90 градусов, образованный двумя перпендикулярными друг другу линиями, является основным геометрическим понятием. Геометрические формы, такие как квадраты и прямоугольники, используют исключительно прямые углы. Существует несколько способов создания 90-градусный угол или определите, равен ли угол 90 градусов, в зависимости от приложения, инструментов и имеющейся информации.

Измерьте угол с помощью транспортира, если это возможно. Если рассматриваемый угол есть на диаграмме или иллюстрации, и вы уверены, что чертеж выполнен в масштабе, то измерение с помощью транспортира является точным и точным способом определения степени угла. Просто совместите нижнюю часть транспортира с прилегающей стороной угла, совместите точку угла с перекрестием транспортира и обратите внимание на отметку измерения, указанную на противоположной стороне.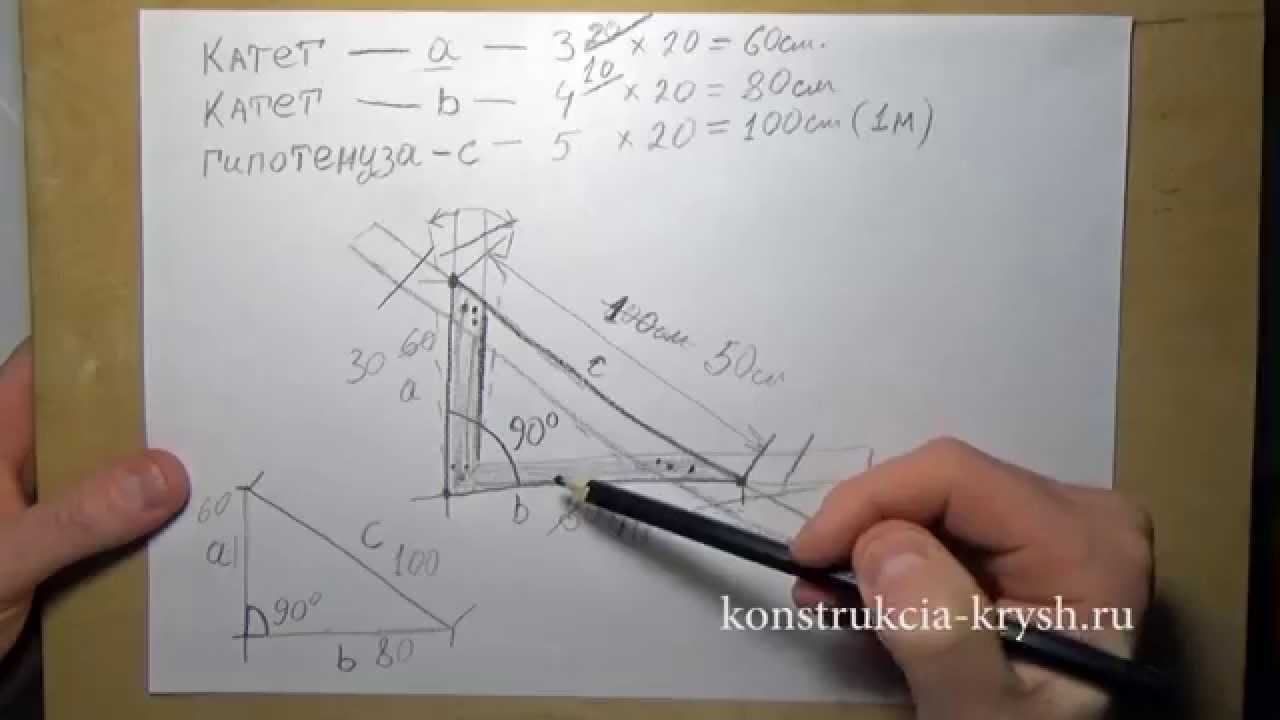

Используйте математический вывод для определения угла. Если анализируемый угол отсутствует на диаграмме, нарисованной в масштабе, или если диаграмма слишком мала для использования транспортира, вы часто можете использовать основные геометрические принципы для определения меры угла. Если угол обозначен маленьким квадратом, а не изогнутой линией, то подразумевается, что угол равен 90 градусам. Если угол является частью фигуры, такой как прямоугольник или квадрат, то угол равен 90 градусов. Если угол является частью треугольника, добавьте меры двух других углов. Три угла треугольника всегда составляют 180 градусов, поэтому, если сумма двух других углов равна 90, то это прямоугольный треугольник с углом 90 градусов. Точно так же четыре угла четырехугольника (формы с четырьмя сторонами) всегда составляют 360. Таким образом, если сложение остальных трех углов дает 270, то рассматриваемый угол является прямым углом. Есть ряд других геометрических теорем и постулатов, которые можно использовать для вывода меры угла.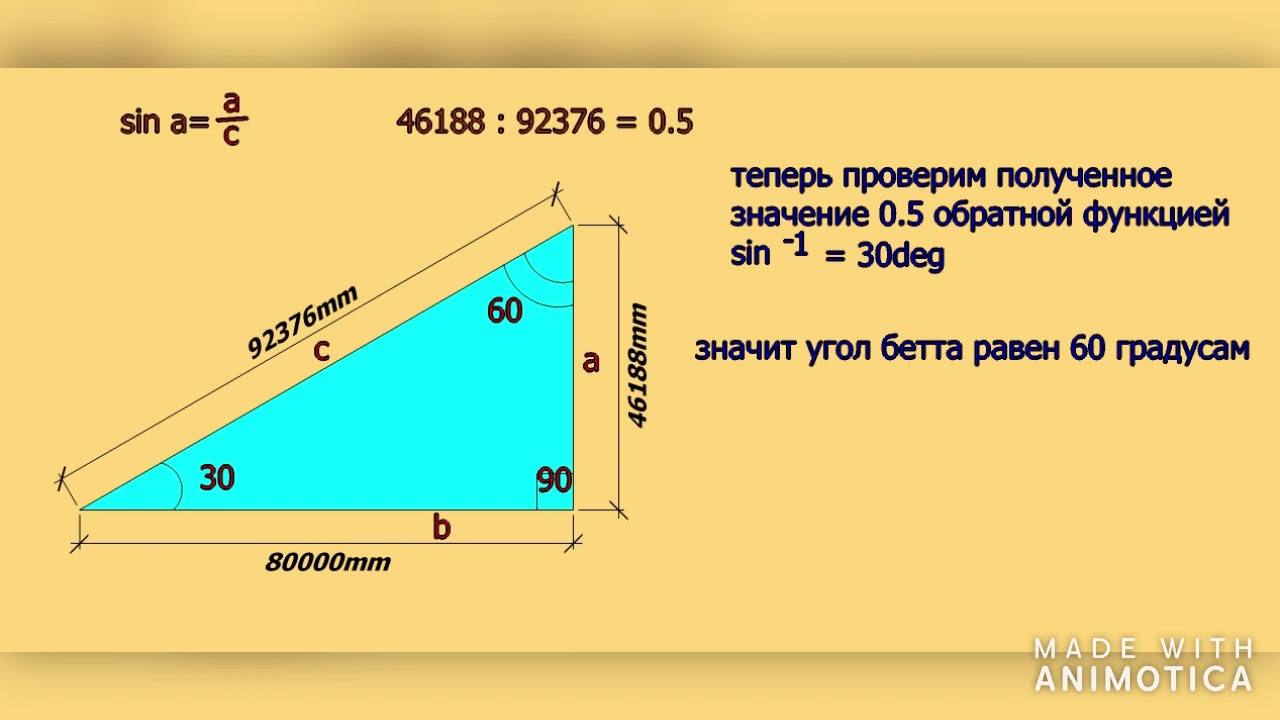

Измерьте угол специальным инструментом. Например, если вы пытаетесь измерить угол среза дерева, вы можете использовать Т-образный угольник или другой измерительный угольник. Если вы пытаетесь измерить угол звезды или какой-либо подобной небесной фигуры, вы можете использовать секстант, угломер или другой подобный измерительный инструмент, основанный на прямой видимости. Кроме того, можно использовать спиртовой уровень, также известный как пузырьковый уровень. Если пузырь находится между двумя параллельными линиями, то уровень находится на отметке 9.Угол 0 градусов от горизонтали. И наоборот, если уровень положить горизонтально или держать сбоку и регулировать до тех пор, пока пузырек не окажется на месте, то уровень будет находиться под углом 90 градусов к вертикали.

Рассчитайте, равен ли угол 90 градусов, используя теорему Пифагора. Эту хорошо известную теорему часто формулируют так: «А в квадрате плюс В в квадрате равно С в квадрате», что указывает на то, что сумма квадратов длин смежных сторон прямоугольного треугольника равна квадрату длины стороны гипотенузы. 2) можно манипулировать и использовать для определения прямого угла. Используя линейку, измерьте стороны угла, а также расстояние между открытыми концами угла. Если эти значения правильно вставляются в формулу, то угол равен 9.Угол 0 градусов.

Вещи, которые вам понадобятся

• Транспортир
• Линейка
• Т-угольник
• Ватерпас

• Базовое понимание геометрических теорем и принципов поможет определить неизвестные углы в технических чертежах и других геометрических фигурах .

Статьи по теме

Ссылки

• Центр подготовки к экзаменам Риджентс: теоремы и постулаты по геометрии
• Риклер: основы инструментов для разметки и измерения

Советы

• Базовое понимание геометрических теорем и принципов поможет вам определять неизвестные углы на технических чертежах и других геометрических фигурах.

Об авторе

Криспин Трубиано работает писателем-фрилансером с 2010 года.