Возводить в квадрат легко и просто
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Шмакова А.Р. 1
1МОУ СОШ №22 п. Беркакит, г. Нерюнгри Республика Саха (Якутия)
Лаптева Т.П. 1
1МОУ СОШ №22 п. Беркакит, г. Нерюнгри Республика Саха (Якутия)
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение.
Математика – очень древняя наука. Многие понятия, правила, законы, формулы уже известны давно, и открыть что-то новое, просто невозможно. Всё равно на уроке математики мы открываем для себя новые знания. Из года в год наши знания увеличиваются. Например, при изучении темы «Степень» узнали, что произведение одинаковых множителей можно записать, как степень данного числа.
Устно возводить в квадрат однозначное число легко, для этого надо знать всего лишь таблицу умножения. А как устно возвести в квадрат двузначное число, меня очень заинтересовало.
Умея это выполнять, мы откажемся от письменного умножения. Конечно, можно посмотреть в таблицу квадратов, но она не всегда под руками.
Цель проекта: Поиск приёмов быстрого возведения чисел в квадрат.
Задачи: 1) Познакомиться с историей возникновения степени числа.
2) Изучить приёмы быстрого возведения чисел в квадрат.
3) Вывести свой способ возведения чисел в квадрат.
4) Выбрать из всех самый оптимальный способ.
Гипотеза: Применение приёмов быстрого возведения чисел в квадрат облегчает вычисления, повышает вычислительную культуру учащихся. Возводить в квадрат легко и просто.
Объект исследования: приёмы быстрого возведения чисел в квадрат.
Методы исследования: Анализ литературы. Поисковый метод. Сравнение.
Актуальность проекта: Во все времена умение производить в уме различные вычисления вызывает восхищение, это отличное упражнение, позволяющее поддержать мозг в состоянии «боевой готовности»[1]. Освоение способов устного возведения чисел в квадрат усиливает интерес к математике, развивает внимание, мышление, память, эрудицию и математические способности.
Основная часть
История возникновения квадрата числа.
Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о
В своей знаменитой «Арифметике» Диофант Александрийский [2] описывает первые натуральные степени чисел так:
«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».
…среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».
П рошло много времени и у Рене Декарта[3] в его «Геометрии» (1637) мы находим современное обозначение степеней а?, а?,… Любопытно, что Декарт считал, что а*а не занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей.
Немецкий ученый Лейбниц[4] считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и
применял знак а2[5].
Приёмы быстрого возведения чисел в квадрат.
У чись считать быстро! Для овладения этим навыком любому человеку нужны:
Способности;
Алгоритмы;
Тренировка;
Опыт.
Давайте познакомимся с некоторыми приёмами возведения в квадрат
Возведение в квадрат числа, оканчивающегося на 5.
352 = 3 · (3 + 1) · 100 + 5 · 5 = 1200 + 25 = 1225.
752 = 5600 + 25 = 5625.
852 = 7225.
Чтобы возвести в квадрат число, оканчивающееся цифрой 5, надо умножить количество его десятков на следующее за ним число и приписать к произведению 25.
Возведение в квадрат числа, первая цифра которого равна 5.
522 = (5 · 5 + 2) · 100 + 2 · 2 = 2700 + 4 = 2704.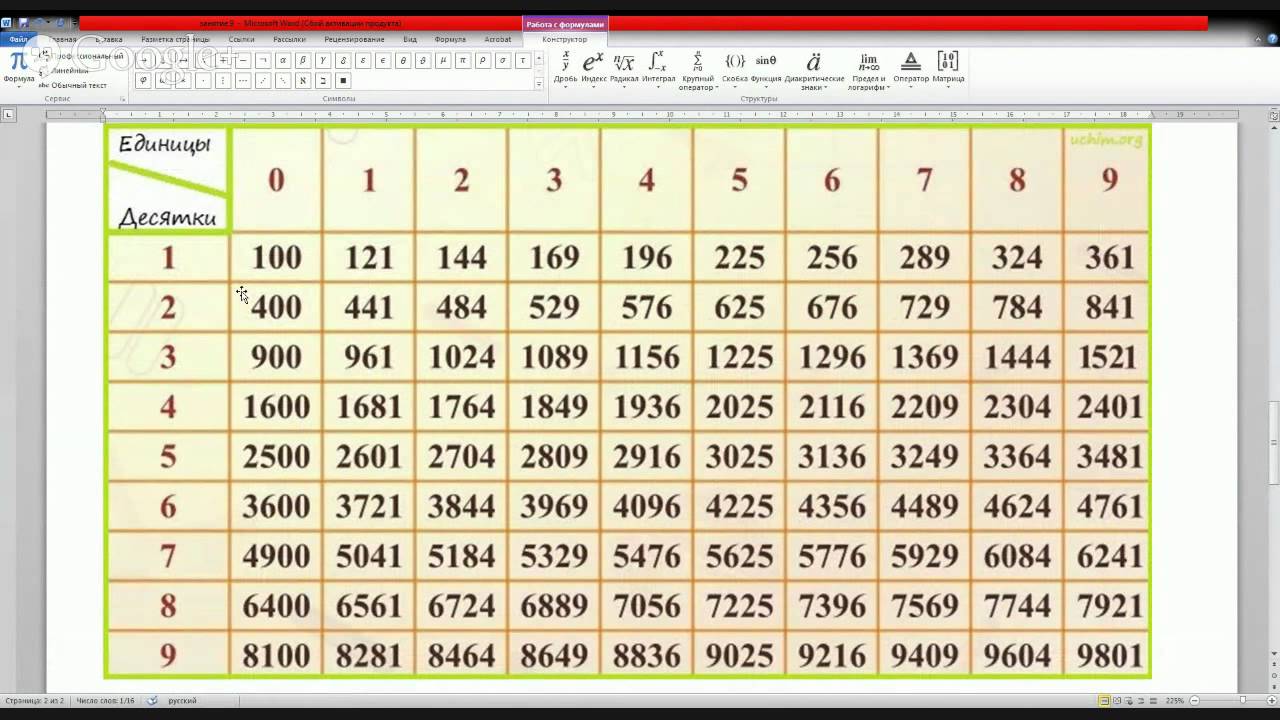
542 = (25 + 4) · 100 + 16 = 2916.
582 = 3300 + 64 = 3364.512 = 2601.
Чтобы возвести в квадрат двузначное число, первая цифра которого равна 5, надо к 25 прибавить число единиц и приписать квадрат числа единиц.
Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.
Возведение в квадрат числа, оканчивающегося на 1.
712; 71→70→702 = 4900; 712 = 4900 + 71 + 70 = 5041.
412 = 1600 + 41 + 40 = 1881.
812 = 6400 + 161 = 6561.
При возведении в квадрат числа, оканчивающегося на 1, нужно округлить число до десятков, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное при округлении.
Возведение в квадрат числа, оканчивающегося на 9.
592; 59 → 60→602 =3600; 592 = 3600 – 60 – 59 = 3600 – 119 = 3481.
292 = 900 – 29 – 30 = 841.
792 = 6400 – 159 = 6241.
При возведении в квадрат числа, оканчивающегося на 9, нужно его округлить до десятков, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное при округлении.
Возведение в квадрат числа, оканчивающегося на 4.
842; 84→85→852 = 7225; 842 = 7225 – 84 – 85 = 7225 – 169 = 7056.
342 = 1225 – 34 – 35 = 1225 – 69 = 1156.
742 = 5625 – 149 = 5476.
При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.
Возведение в квадрат числа, оканчивающегося на 6.
562; 56→55→552 = 3025; 562 = 3025 + 56 + 55 = 3025 + 111 = 3136.
362 = 1225 + 36 + 35 =1296.
762 = 5625 + 151 = 5776.
При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.
Возведение в квадрат числа, близкого к 50.
а) Для чисел от 40 до 50 (числа пятого десятка). Опорное число – 15.
1) 442 = (15 + 4) · 100 + (50 – 44)2 = 1900 + 36 = 1936.
2) 432 = 18 · 100 + 72 = 1800 + 49 = 1849.
3) 482 = 2300 + 4 = 2304.
Чтобы возвести в квадрат числа пятого десятка (41, 42, 43, 44, 45, 46, 47, 48, 49), надо к числу 15 прибавить число единиц числа, затем к полученной сумме приписать квадрат дополнения данного числа до 50.
б) Для чисел от 25 до 40 и до 50. Опорное число – 25.
1) 372 = (37 – 25) · 100 + (50 – 37)2 = 12 · 100 + 132 = 1200 + 169 = 1369.
Для этого приёма надо знать квадраты чисел от 1 до 25.
2) 282 = 3 · 100 + 222 = 300 + 484 = 784.
3) 462 = 2100 + 16 = 2116.
4) 392 = 1400 + 121 = 1521.
Чтобы возвести в квадрат число от 25 до 50, надо из данного числа вычесть 25, результат умножить на 100 и прибавить квадрат дополнения данного числа до 50.
в) Для чисел от 50 до 60 (числа шестого десятка). Опорное число – 25.
1) 572 = (25 +7) · 100 + (57 – 50)2 = 32 · 100 + 72 = 3200 + 49 = 3249.
2) 522 = 2700 + 4 = 2704.
3) 592 = 3481.
Чтобы возвести в квадрат число шестого десятка (51, 52, 53, 54, 55, 56, 57, 58, 59), надо к 25 прибавить число единиц, затем к полученной сумме приписать квадрат разности данного числа и 50.
Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.
г) Для чисел от 50 до 60 и до 75. Опорное слово – 25.
Для этого приёма надо знать квадраты чисел от 1 до 25.
1) 582 = (58 – 25) · 100 + (58 – 50)
2) 712 = 46 · 100 + 212 = 4600 + 441 = 5041.
Чтобы возвести в квадрат числа от 50 до 75, надо из данного числа вычесть 25, результат умножить на 100 и прибавить квадрат разности данного числа и 50.
Возведение в квадрат числа, близкого к 100.
972 = (97 – 3) · 100 + 32 = 9400 + 9 = 9409, где 3 – дополнение 97 до 100.
942 = (94 – 6) · 100 + 62 = 8800 + 36 = 8836.
982 = 9604.
Чтобы возвести в квадрат число, близкое к 100, надо из него вычесть дополнение данного числа до 100, к результату приписать квадрат дополнения.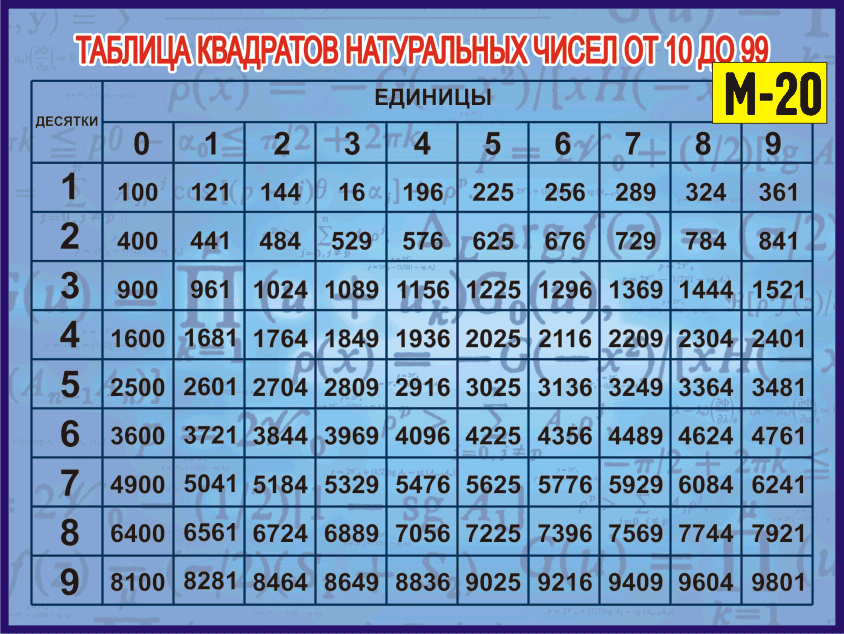
Если квадрат дополнения является однозначным числом, то перед ним записать цифру нуль.
Возведение в квадрат любого двузначного числа.
а) Метод «пирамидка».
382 = (30 + 8)2 = (30 + 8) · (30 + 8) = (30 + 8) · 30 + (30 + 8) · 8 = 30 · 30 + 8 · 30 +
+ 30 · 8 + 8 · 8 = 3 · 3 · 100 + 3 · 8 · 10 + 3 · 8 · 10 + 8 · 8 = 32 · 100 + 3 · 8 · 2 · 10 + + 82 = 9 · 100 + 48 · 10 + 64 = 964 + 480 = 1444.
М ожно оформить решение так: 382 = 964 32 = 3 · 3 = 9 и 82 = 8 · 8 = 64 ⇒ 964
24 3 · 8 · 10 = 240 или 24 десятка
+ 24 3 · 8 · 10 = 240 или 24 десятка, поэтому
1444 можно под числом 964 записать два
раза число 24, сдвинув его на одну
цифру влево, получилась «пирамидка».
272 = 449 + 280 = 729.
842 = 6416 + 640 = 7056.
б) Метод «перекидки».
422 = 42 · 42 = (42 + 2) · 40 + 22 = 44 · 40 + 4 = 1760 + 4 = 1764
782 = (78 + 8) · 70 + 64 = 86 · 70 + 64 = 6020 + 64 = 6084.
в) Метод «округления».
1) Для чисел, у которых цифра единиц больше 5:
472 = 47 · 47 = 50 · (47 – 3) + 32 = 50 · 44 + 9 = 2200 + 9 = 2209.
262 = 30 · 22 + 16 = 660 + 16 = 676.
Для чисел, у которых цифра единиц меньше 5:
732 = 73 · 73 = 70 · (73 + 3) + 32 = 70 · 76 + 9 = 5320 + 9 = 5329.
822 = 80 · 84 + 4 = 6720 + 4 = 6724.
г) Метод замены квадрата числа произведением.
292 = (29 – 9) · (29 + 9) + 92 = 20 · 38 + 81 = 760 + 81 = 841.
862 = (86 – 6) · (86 + 6) + 62 = 80 · 92 + 36 = 7360 + 36 = 7396.
542 = 50 · 58 + 16 = 2900 + 16 = 2916.
д) Метод понижения числа на единицу.
282 = (28 – 1)2 + 28 + (28 – 1) = 272 + 28 + 27 = 729 + 55 = 784.
562 = 552 + 56 + 55 = 3025 + 111 = 3136.
Минус этого приёма в том, что квадрат данного двузначного числа выражаем через квадрат числа на единицу меньше, который надо либо вычислять, либо снова понижать, и так до бесконечности.
Возведение в квадрат любого двузначного числа по методу Алины.
Приёмов возведения двузначных чисел в квадрат много и все они разные. Для каждой группы чисел надо знать своё правило, а удержать все правила в уме иногда невозможно.
Собирая материал для проекта, мне захотелось вывести свой приём быстрого возведения двузначного числа в квадрат.
Очень понравился приём возведения в квадрат чисел, оканчивающихся на 5. Он быстрый и понятный. А можно ли этот приём применить для любого числа? Изучая литературу, я нигде этого способа не увидела. Применяя его для любых двузначных чисел, вот что у меня получилось.
Напомню: 352 = 3 · (3 + 1) · 100 + 52 = 1200 + 25 = 1225.
Возведём по этому способу в квадрат число 36.
Мы знаем, что 362 = 1296.
3 · (3 + 1) · 100 + 62 = 1200 + 36 = 1236, но 1236 1296. Число 1236 < 1296 на 60.
Где же взять число 60? Можно догадаться, что 60 = 30 · 2, то есть удвоенное число десятков. Тогда получаем:
Тогда получаем:
362 = 3 · 4 · 100 + 62 + 30 · 2 = 1236 + 60 = 1296.
Рассмотрим другие примеры.
562 = 5 · 6 · 100 + 62 + 50 · 2 = 3000 + 36 + 100 = 3036 + 100 = 3136.
462 = 2036 + 40 · 2 = 2036 + 80 = 2116.
Я много раз возводила числа в квадрат и увидела такую закономерность:
Выпишем цифры 1, 2, 3, 4, 5, 6, 7, 8, 9.
В этом ряду цифра 5 занимает середину; 4 и 6 отличаются от 5 на 1, они стоят на первом месте от 5; 3 и 7 – на втором; 2 и 8 – на третьем; 1 и 9 на четвёртом.
Пусть, например, надо возвести в квадрат число 39. Цифра 9 стоит на четвёртом месте от цифры 5, число 4 удваиваем, это будет 8, а теперь применяем приём:
392 = 3 · 4 · 100 + 92 + 30 · 8 = 1200 + 81 + 240 = 1281 + 240 = 1521.
240 можно представить так: 30 · 2 · 4, то есть десятки числа удвоить и умножить на номер места цифры единиц от цифры 5.
А как возвести в квадрат число, если цифра единиц меньше 5. Например, 732.
Например, 732.
Число 73 < 75, значит, применяя приём возведения в квадрат для 75, квадрат числа 73 будет меньше.
732 = 5329;
732 = 5609 – применяя приём возведения в квадрат для числа, оканчивающегося на 5. Но 5329 5609.
Решим уравнение: 732 = 5609 – х
5329 = 5609 – x
х = 5609 – 5329
х = 280, где 280 = 70 · 2 · 2, первая двойка удваивает число десятков в числе; вторая двойка обозначает номер места цифры 3 от цифры 5.
Эврика! Способ найден!
732 = 7 · 8 ·100 + 3 · 3 – 70 · 2 · 2 = 5609 – 280 = 5329.
М ожно оформить решение и так: 732 = 5609 7 · 8 = 56; 3 · 3 = 9 ⇒ 5609
— 28 70 · 2 · 2 = 280; это 28
5329 десятков, поэтому второе
число можно подписать
под первым, сдвинув его влево на одну цифру.
Чтобы возвести любое двузначное число в квадрат, надо количество десятков умножить на следующее число и приписать квадрат числа единиц.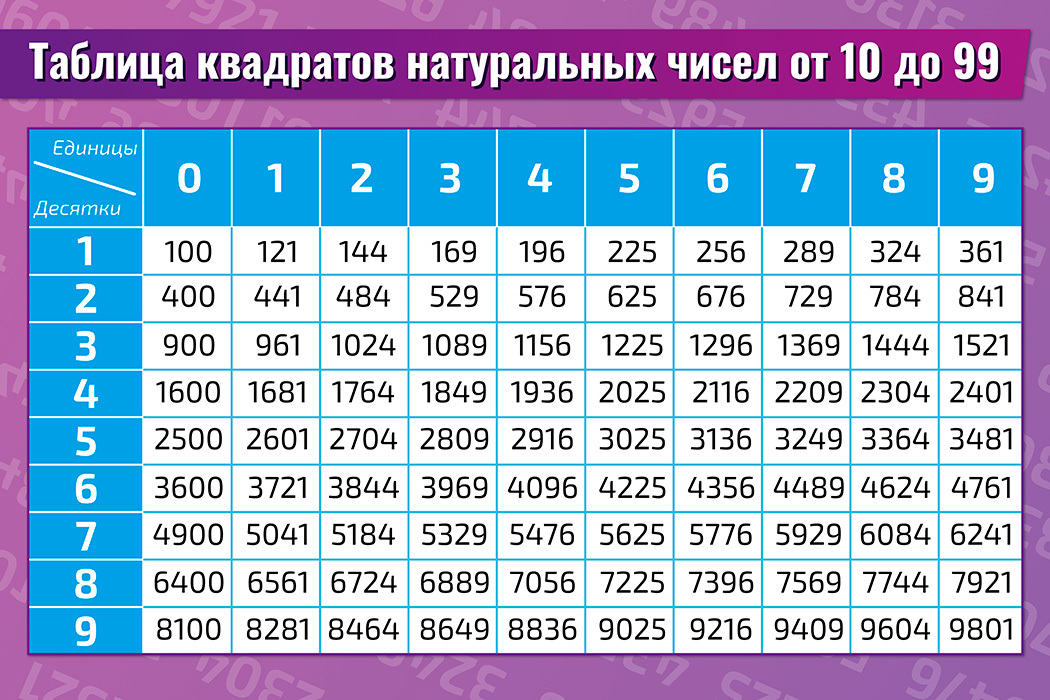 К полученному результату прибавить (или из полученного результата вычесть) удвоенное произведение десятков числа, умноженное на порядковый номер места цифры единиц в числовом ряду 14, 23, 32, 41, 5, 61, 72, 83, 94 от цифры 5.
К полученному результату прибавить (или из полученного результата вычесть) удвоенное произведение десятков числа, умноженное на порядковый номер места цифры единиц в числовом ряду 14, 23, 32, 41, 5, 61, 72, 83, 94 от цифры 5.
Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.
Какой приём возведения двузначного числа в квадрат наиболее простой? Для себя я выбрала два приёма. Мне они оба понятные и несложные.
682 = 62 · 100 + 82 + 60 · 8 + 60 · 8 = 3664 + 480 + 480 = 3664 + 960 = 4624.
682 = 6 · 7 · 100 + 82 + 60 ·2 · 3 = 4264 + 360 = 4624.
Какой приём выберите вы, думайте сами. Вам решать.
Вам решать.
Заключение.
Владение приёмами быстрого возведения двузначного числа в квадрат даёт возможность выбрать в каждом отдельном случае наиболее рациональные и эффективные пути вычислений, что приводит:
к сокращению времени на вычисления;
к защите от массы вычислительных ошибок;
к ведению записи в строчку и отказа от традиционного письменного умножения.
Считаю, что возводить двузначные числа в квадрат легко и просто. Гипотеза доказана.
Умение считать в уме остаётся полезным навыком для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.
Возможность обходиться без калькулятора и в нужный момент оперативно решить поставленную арифметическую задачу – это здорово[5]!
Литература
Умножай с умом. Учебно-методическое пособие для учащихся общеобразовательных учреждений /Лаптева Т. П. – М.: Перо, 2017.
П. – М.: Перо, 2017.
https://ru.wikipedia.org/wiki/Диофант_Александрийский
https://ru.wikipedia.org/wiki/Геометрия_(Декарт)
https://ru.wikipedia.org/wiki/Лейбниц,_Готфрид_Вильгельм
https://mirurokov.ru/открытый-урок/возведение-в-степень/история-возникновения-степени-числа.html
14
Просмотров работы: 15057
Урок 7. Возведение в квадрат в уме
Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.
В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Квадрат суммы и квадрат разности
Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:
Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:
Например:
- 372 = (30+7)2 = 302 + 2*30*7 + 72 = 900+420+49 = 1 369
- 942 = (90+4)2 = 902 + 2*90*4 + 42 = 8100+720+16 = 8 836
Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.
Квадрат близкий к известному квадрату
Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:
На 1 больше:
Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.
- 312 = 302 + 31 + 30 = 961
- 162 = 152 + 15 + 16 = 225 + 31 = 256
На 1 меньше:
Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.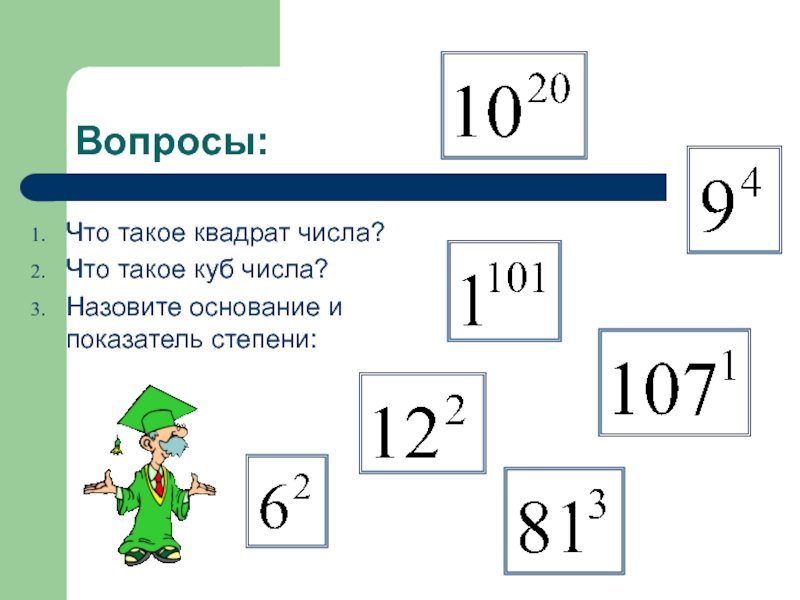
- 192 = 202 – 19 – 20 = 400 – 39 = 361
- 242 = 252 – 24 – 25 = 625 – 25 – 24 = 576
На 2 больше
Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.
- 222 = 202 + 2*(20+22) = 400 + 84 = 484
- 272 = 252 + 2*(25+27) = 625 + 104 = 729
На 2 меньше
Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.
- 482 = 502 – 2*(50+48) = 2500 – 196 = 2 304
- 982 = 1002 – 2*(100+98) = 10 000 – 396 = 9 604
Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).
Квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
- 152 = (1*(1+1)) 25 = 225
- 252 = (2*(2+1)) 25 = 625
- 852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
- 1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Квадрат чисел близких к 50
Посмотрите работу алгоритма на примерах:
- 442 = (25-6)*100 + 62 = 1900 + 36 = 1936
- 532 = (25+3)*100 + 32 = 2800 + 9 = 2809
Квадрат трехзначных чисел
Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:
Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:
4362 = (400+30+6)2= 4002 + 302 + 62 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Cтатистика На весь экран
Евгений Буянов
← 6 Умножение до 100 Экзамен по практике →
| Q1) Подсчитайте количество квадратов на данном рисунке 1) 28 Решение: . как показано. Q2) Сосчитайте количество квадратов на данной фигуре 1) 8 Решение: Рисунок можно пометить, как показано на рисунке. Читать далее: Вопросы по подсчету количества треугольниковСкачать: Практические вопросы по счету геометрических фигурQ3) Сосчитайте количество квадратов на данной фигуре 1) 11 Q4) Подсчитайте количество квадратов на данном рисунке 1) 14 Раствор: . Читать далее: Вопросы по подсчету количества прямоугольниковПодробнее: Ярлыки для геометрических узоровQ5) Подсчитайте количество квадратов на данном рисунке 1) 18 Раствор: . Q6) Подсчитайте количество квадратов на данном рисунке 1) 6 Раствор: 4) 10 : . Рисунок может быть помечен, как показано на рисунке. Читать далее: Вопросы по подсчету количества параллелограммов 1) 13 Решение: . как показано. |
Квадратное число — элементарная математика
Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само себя, полученное произведение называется квадратным числом, или полным квадратом, или просто «квадратом». квадрат.» Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все числа квадратные.
Более формально: квадратное число — это число вида n × n или n 2 , где n — любое целое число.
Объекты, расположенные в виде квадратного массива
Название «квадратное число» происходит от того факта, что эти определенные количества объектов могут быть расположены так, чтобы заполнить идеальный квадрат.
Дети могут поэкспериментировать с монетами (или квадратными плитками), чтобы увидеть, какое их количество можно расположить в идеально квадратном ряду.
Четыре пенни могут:
Девять пенни могут:
И шестнадцать пенни тоже могут:
Но семь пенни или двенадцать пенни не могут быть расположены таким образом. Числа (объектов), которые можно расположить в виде квадратного массива, называются «квадратными числами».
Квадратные массивы должны быть заполнены, если мы хотим подсчитать число как квадратное число. Здесь 12 копеек расположены в виде квадрата, но не полного квадратного массива, поэтому 12 не является квадратным числом.
Число 12 не квадратное.
Детям может понравиться изучение того, сколько монет можно разложить на таком открытом квадрате. Их не называют «квадратными числами», но они следуют интересному шаблону.
Квадраты из квадратных плиток тоже интересно делать. Число квадратных плиток, которые вписываются в квадратный массив, является «квадратным числом».
Вот две платы, 3×3 и 5×5 . Сколько красных плиток в каждой? Черный? Желтый?
Есть ли какие-либо из этих квадратных чисел?
Что, если таким же образом замостить доску 4 × 4 или 6 × 6 ?
Можете ли вы предсказать количество плиток на доске 7 × 7 или 10 × 10 ?
Квадратные числа в таблице умножения
Квадратные числа расположены по диагонали стандартной таблицы умножения.
Соединения с треугольными числами
Если вы посчитаете зеленые треугольники в каждом из этих рисунков, вы увидите последовательность чисел: треугольные числа.
Если посчитать белые треугольники, находящиеся в «промежутках» между зелеными, последовательность чисел начинается с 0 (поскольку в первом дизайне нет пробелов) и продолжается: 1, 3, 6, 10, 15, …, опять треугольные числа!
Удивительно, но если вы посчитаете все крошечные треугольники в каждом дизайне — и зеленые, и белые — цифры будут квадратными!
Связь между квадратными и треугольными числами, вид с другой стороны
Постройте ступенчатое расположение стержней Кюизенера, скажем, W, R, G. Затем постройте следующую ступеньку: W, R, G, P.
Затем постройте следующую ступеньку: W, R, G, P.
Каждый является «треугольным» (если не учитывать ступенчатое ребро). Сложите два последовательных треугольника вместе, и они образуют квадрат: . Этот квадрат такого же размера, как 16 белых палочек, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
Вот еще пример: . Если их сложить вместе, они образуют квадрат, площадь которого равна 64, что опять-таки является квадратом длины (в белых стержнях) самого длинного стержня. (Коричневый стержень имеет длину 8 белых стержней, а 64 — это 8, умноженное на 8, или «8 в квадрате».)
Лестничные ступени из квадратных чисел
Лестничные ступени, которые поднимаются, а затем снова опускаются, как здесь, также содержат квадратное число плиток. Когда плитки расположены в шахматном порядке, как здесь, дополнительное предложение, описывающее количество красных плиток (10), количество черных плиток (6) и общее количество плиток (16), снова показывает связь между треугольные числа и квадратные числа: 10 + 6 = 16.
Предлагая детям 2-го (или даже 1-го) класса построить узоры в виде ступенек и написать числовые предложения, описывающие эти узоры, — хороший способ дать им возможность попрактиковаться с описательными числовыми предложениями. а также подружиться с квадратными числами.
Вот два примера. Цвет используется здесь, чтобы помочь вам увидеть то, что описывается. Детям нравится цвет, но он им не нужен, и они часто видят творческие способы описания узоров ступенек, которые они построили из одноцветных плиток. Или они могут раскрасить 1-дюймовую миллиметровую бумагу, чтобы записать свой рисунок ступенек и показать, как они перевели его в числовое предложение.
Ромбовидная форма из монет также может быть описана числовым предложением 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25.
От одного квадратного числа к следующему: два изображения со стержнями Кюизенера
(1) Начните с W. Добавьте два последовательных стержня, W+R; затем еще два, R+G; затем Г+П; затем….

 е.
9 номер.
е.
9 номер. 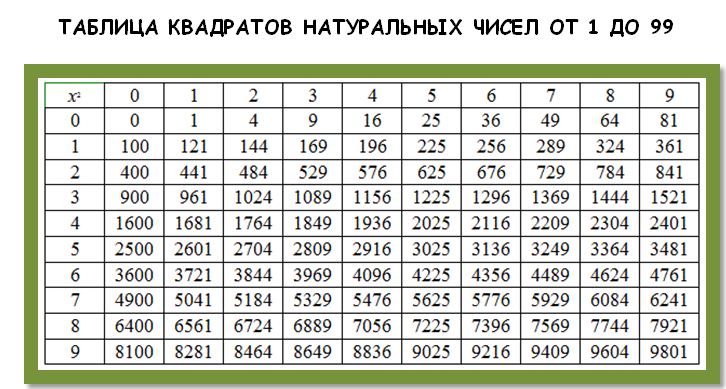
 Рисунок. может быть помечен, как показано.
Рисунок. может быть помечен, как показано.  как показано.
как показано.  0006
0006 е. числом 2.
е. числом 2.