Как сложить число и корень: Квадратный корень — все, что нужно для сдачи ОГЭ и ЕГЭ в 2021 году

Сложение и вычитание квадратных корней примеры. Как складывать квадратные корни

Содержимое:

Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).

Шаги

Часть 1 Постигаем основы

1. 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
   • 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
   • 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
   • 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
2. 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
3. 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
4. 4 У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа! ). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
   • 30√2 — 4√2 + 10√3 =
   • (30 — 4)√2 + 10√3 =
   • 26√2 + 10√3

Часть 2 Практикуемся на примерах

1. 1 Пример 1: √(45) + 4√5.
   • Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
   • Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
   • Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
2. 2 Пример 2: 6√(40) — 3√(10) + √5.
   • Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
   • Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
   • Перемножьте множители перед корнем и получите 12√10.
   • Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
   • Вы получите: (12-3)√10 + √5 = 9√10 + √5.
3. 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
4. 4 Пример 4. √9 + √4 — 3√2.
   • √9 = √(3 х 3) = 3.
   • √4 = √(2 х 2) = 2.
   • Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
   • Окончательный ответ: 5 — 3√2.
5. 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
   • Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
   • Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
   • Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .

• Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.

Предупреждения

• Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
• Никогда не суммируйте и не вычитайте целое число и корень, например, 3 + (2x) 1/2 .
  • Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.

Инструкция

• Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
• Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.
• Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
• Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
  12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
• И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.

Свойства квадратных корней

До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.

В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.

Доказательство. Введем следующие обозначения:https://pandia.

ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.

Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то

Преобразование выражений, содержащих операцию извлечения квадратного корня

До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что

где, напомним, a, b — неотрицательные числа.

Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.

Пример 3. Внести множитель под знак квадратного корня:

Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Действия с корнями.

1. Главная
2. Алгебра
3. Степени и корни
4. Действия с корнями.

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Деление корней с одинаковыми и разными показателями

Чтобы разделить корни с одинаковыми показателями, нужно разделить подкоренные выражения, а показатель корня оставить прежний.

^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Если показатели корней разные, то сначала нужно привести корни к общему показателю, а потом — поделить получившиеся корни с одинаковыми показателями.Можно делить (число на корень или корень на число) — для этого нужно занести под знак корня (в числитель или в знаменатель) это число, возведённое в степень с показателем, как у корня.

^∛‎(729) / _√(25) =
= ^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Возведение корней в степень

Чтобы возвести корень в степень, нужно возвести в эту степень подкоренное выражение, а показатель корня оставить тем же.
(∛‎(125))² = (∛‎(125²))

Извлечение корня из корня

Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить прежним.

Уничтожение иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.

⁷ / _√(5) =
= ^{7 × √(5)} / ₅

Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.

⁷ / _{[ √(7) — √(3) ]} =
= ^{7 × [ √(7) + √(3) ]} / _{[ 7 — 3 ]} =
= ^{7 × [ √(7) + √(3) ]} / ₄

Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.

⁵ / _{[ ∛(7) + ∛(4) ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / _{[ 7 + 4 ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / ₁₁

Квадратный корень

Предварительные навыки

Основные сведения

Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.

Найдём площадь квадрата, длина стороны которого 3 см

S = 3² = 9 см²

Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.

Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.

Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.

Введём для работы с корнями новые обозначения.

Символ кóрня выглядит как . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня .

Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)

Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)

Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.

Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:

Значит квадрат площадью 9 см² имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.

Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9

Получается, что выражение  имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.

Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.

Например, извлечём квадратный корень из числа 4

Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4

Поэтому ответ к выражению вида  записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.

Запишем ответ к выражению  с плюсом и минусом:

---

Определения

Дадим определение квадратному корню.

Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.

То есть число b должно быть таким, чтобы выполнялось равенство b² = a. Число b (оно же корень) обозначается через радикал  так, что . На практике левая и правая часть поменяны местами и мы видим привычное выражение 

Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16

4² = 16

Корень 4 можно обозначить через радикал  так, что .

Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16

(−4)² = 16

Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.

Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b² = a.

В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.

В разговорном языке можно использовать сокращение. К примеру, выражение  полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».

Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.

Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.

Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи можно использовать запись. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.

Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:

Это по причине того, что единица во второй степени равна единице:

1² = 1

и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:

Квадратный корень из нуля равен нулю. То есть справедливо равенство , поскольку 0² = 0.

Выражение вида  смысла не имеет. Например, не имеет смысла выражение , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.

Если выражение вида  возвести во вторую степень, то есть если записать , то это выражение будет равно подкореннóму выражению a

Например, выражение  равно 4

Это потому что выражение  равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.

Еще примеры:

Корень из квадрата числá равен модулю этого числá:

Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5

Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5

Действительно, если не пользуясь правилом , вычислять выражение  обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5

Не следует путать правило  с правилом . Правило  верно при любом a, тогда как правило  верно в том случае, если выражение  имеет смысл.

В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:

Примеры: √4, √9, √16.

Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.

Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.

49 < 64

Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,

√49 < √64

Отсюда:

7 < 8

---

Примеры извлечения квадратных корней

Рассмотрим несколько простых примеров на извлечение квадратных корней.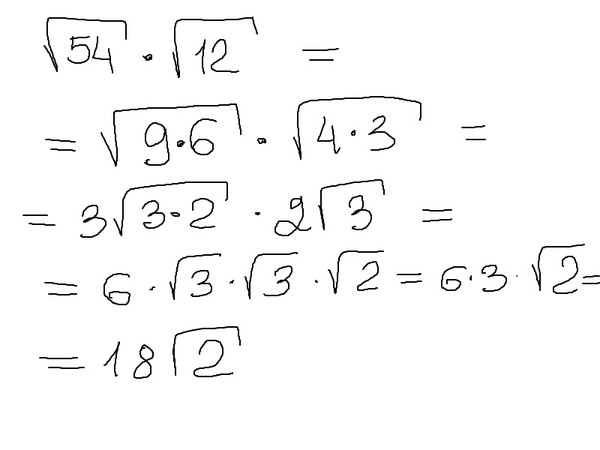

Пример 1. Извлечь квадратный корень √36

Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 6² = 36

√36 = 6

---

Пример 2. Извлечь квадратный корень √49

Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 7² = 49

√49 = 7

В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:

7 × 7 = 49

Но 7 × 7 это 7²

7² = 49

Отсюда, √49 = 7.

---

Пример 3. Извлечь квадратный корень √100

Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 10² = 100

√100 = 10

Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.

---

Пример 3. Извлечь квадратный корень √256

Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.

Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.

Видим, что это число 16. Значит √256 = 16.

---

Пример 4. Найти значение выражения 2√16

В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2

---

Пример 7. Решить уравнение 

В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.

Значение переменной x равно 16, поскольку . Значит корень уравнения равен 16.

Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом .

Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.

Из определения мы знаем, что квадратный корень  равен числу b, при котором выполняется равенство b² = a.

Применим равенство b² = a к нашему примеру . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем , а именно переменная x

В выражении 4² = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.

---

Пример 8. Решить уравнение 

Перенесем −8 в правую часть, изменив знак:

Возведем правую часть во вторую степень и приравняем её к переменной x

Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения  равен 64

---

Пример 9. Решить уравнение 

Воспользуемся определением квадратного корня:

Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x

В выражении 7² = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:

Корень уравнения  равен . Выполним проверку, подставив его в исходное уравнение:

---

Пример 10. Найти значение выражения 

В этом выражении число 2 умножается на квадратный корень из числа 49.

Сначала нужно извлечь квадратный корень и перемножить его с числом 2

---

Приближённое значение квадратного корня

Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.

Например, извлечь квадратный корень  можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 8² = 64. То есть

А извлечь квадратный корень  нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.

Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.

Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.

Найдём значение корня  приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня  будет представлять собой десятичную дробь, у которой после запятой одна цифра.

Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:

√1 = 1

Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2

√4 = 2

√1 меньше, чем √4

√1 < √4

А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:

√1 < √3 < √4

Точные значения корней √1 и √4 известны. Это числа 1 и 2

1 < √3 < 2

Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.

Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1

1,1² = 1,21

Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.

Проверим тогда дробь 1,8

1,8² = 3,24

Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.

Проверим тогда дробь 1,7

1,7² = 2,89

Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈

√3 ≈ 1,7

Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.

В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.

Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8

1,7 < √3 < 1,8

Проверим дробь 1,74

1,74² = 3,0276

Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.

Проверим тогда дробь 1,73

1,73² = 2,9929

Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.

Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:

√3 = 1,732 (вычислено с точностью до тысячных)

√3 = 1,7320 (вычислено с точностью до десятитысячных)

√3 = 1,73205 (вычислено с точностью до ста тысячных).

Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:

√3 ≈ 1

Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.

В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.

---

Приближенное значение квадратного корня с недостатком или избытком

Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.

В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.

С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.

Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:

√3 ≈ 1

Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.

Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2

√3 ≈ 2

Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:

√3 ≈ 2 (с избытком)

Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.

Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.

Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:

√5 ≈ 2,23

---

Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1

√51 ≈ 7

---

Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1

√51 ≈ 7,1

Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01

√51 ≈ 7,14

---

Границы, в пределах которых располагаются корни

Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].

Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 8² = 64. Значит квадратный корень из числа 64 есть 8

---

Пример 2. Извлечь квадратный корень из числа 49

Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 7² = 49

√49 = 7

---

Пример 2. Извлечь квадратный корень из числа 1

Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 1² = 1

√1 = 1

---

Пример 3. Извлечь квадратный корень из числа 100

Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 10² = 100

√100 = 10

Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].

Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:

√37 ≈ 6,08

Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.

Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:

1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100

И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.

Например, 6² = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600

60² = 3600

А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:

600² = 360000

Тогда можно сделать следующий вывод:

Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.

Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3

Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3

---

Пример 2. Извлечём квадратный корень из числа 90000

Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:

---

Пример 3. Извлечем квадратный корень из числа 36000000

Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:

---

Пример 4. Извлечем квадратный корень из числа 2500

Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:

---

Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.

Например, . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:

И наоборот, если в равенстве  уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:

Пример 2. Увеличим в равенстве  подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз

Пример 3. Уменьшим в равенстве  подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз

Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.

Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.

Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:

Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве  подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:

Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.

В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.

Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, .

Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.

Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.

Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:

Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве  подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз

Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.

Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225

Теперь в равенстве уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз

---

Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].

В этом случае применяется таблица квадратов:

Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576

Видим, что это число 24. Значит .

---

Пример 2. Извлечь квадратный корень из числа 432.

Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.

Извлечем квадратный корень из числа 432 с точностью до десятых.

В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.

Проверим, например, число 20,8. Для этого возведём его в квадрат:

20,8² = 432,64

Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7

20,7² = 428,49

Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.

Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.

Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900

3600 < 4225 < 4900

Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:

Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)

Корень 64 не годится. Проверим корень 65

Получается 4225. Значит 65 является корнем числа 4225

---

Тождественные преобразования с квадратными корнями

Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.

Квадратный корень из произведения

Квадратный корень из произведения это выражение вида , где a и b некоторые числа.

Например, выражение  является квадратным корнем из произведения чисел 4 и 9.

Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение  в виде произведения корней . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6

Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36

Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.

Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12

Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.

Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:

В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.

Тогда четыре двойки можно заменить на запись 2² × 2², а две тройки заменить на 3²

В результате будем иметь следующее разложение:

Теперь можно извлекáть квадратный корень из разложения числа 144

Применим правило извлечения квадратного корня из произведения:

Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.

Тогда получится произведение 2 × 2 × 3, которое равно 12

Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.

Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:

затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:

Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:

С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.

Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.

Итак, разложим число 13456 на простые множители:

В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 2². А два числа 29 предстáвим как 29². В результате полýчим следующее разложение числа 13456

Теперь будем извлекать квадратный корень из разложения числа 13456

Итак, если a ≥ 0 и b ≥ 0, то . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

Докажем равенство . Для этого воспользуемся определением квадратного корня.

Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b² = a.

В нашем случае нужно удостовериться, что правая часть равенства  при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.

Итак, выпишем правую часть равенства  и возведём ее во вторую степень:

Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:

Ранее было сказано, что если выражение вида  возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня

Значит равенство  справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.

Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:

, при a ≥ 0 и b ≥ 0, c ≥ 0.

---

Пример 1. Найти значение квадратного корня 

Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

---

Пример 2. Найти значение квадратного корня 

Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:

Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100

Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:

---

Пример 3. Найти значение квадратного корня 

Воспользуемся правилом возведения степени в степень. Степень 11⁴ предстáвим как (11²)².

Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:

В нашем случае квадратный корень из числа (11²)² будет равен 11². Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:

Далее возводим число 11 во вторую степень и получаем окончательный ответ:

Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 11⁴ нужно записать в виде произведения 11² × 11². Затем извлечь квадратный корень из этого произведения:

---

Пример 4. Найти значение квадратного корня

Перепишем степень 3⁴ в виде (3²)², а степень 5⁶ в виде (5³)²

Далее используем правило извлечения квадратного кóрня из произведения:

Далее используем правило извлечения квадратного кóрня из квадрата числа:

Вычислим произведение получившихся степеней и полýчим окончательный ответ:

---

Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения

Запишем корень  в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

---

Пример 6. Найти значение квадратного корня

---

Пример 7. Найти значение квадратного корня

---

Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.

Например, произведение 8 × 4 равно 32

8 × 4 = 32

Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.

(8 × 2) × (4 : 2) = 32

Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.

Например, извлечём квадратный корень из произведения . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.

Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.

Запишем полное решение данного примера:

Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:

---

Пример 9. Найти значение квадратного корня

Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:

---

Если в равенстве поменять местами левую и правую часть, то полýчим равенство . Это преобразовáние позволяет упрощáть вычисление некоторых корней.

Например, узнáем чему равно значение выражения .

Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом , то есть заменим выражение из двух корней  на выражение с одним корнем, под которым будет произведение из чисел 10 и 40

Теперь найдём значение произведения, находящегося под корнем:

А квадратный корень из числа 400 извлекается. Он равен 20

Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.

Например, найдём значение выражения .

Воспользуемся правилом

Сомножитель 32 это 2⁵. Предстáвим этот сомножитель как 2 × 2⁴

Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 2⁴ предстáвим в виде степени с показателем 2

Теперь воспóльзуемся правилом и вычислим окончательный ответ:

---

Пример 12. Найти значение выражения

Воспользуемся правилом

Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7

Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 2² × 2², а две семёрки как 7²

Теперь воспользуемся правилом и вычислим окончательный ответ:

---

Квадратный корень из дроби

Квадратный корень вида равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b

Например, квадратный корень из дроби  равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9

Вычислим квадратные корни в числителе и знаменателе:

Значит, квадратный корень из дроби равен .

Докáжем, что равенство является верным.

Возведём правую часть во вторую степень. Если в результате полýчим дробь , то это будет означать, что равенство верно:

---

Пример 1. Извлечь квадратный корень 

Воспользуемся правилом извлечения квадратного корня из дроби:

---

Пример 2. Извлечь квадратный корень 

Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:

---

Пример 3. Извлечь квадратный корень

Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.

Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:

Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:

---

Пример 4. Найти значение выражения 

Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:

Также можно воспользоваться правилом извлечения квадратного корня из дроби:

В данном примере первый способ оказался проще и удобнее.

---

Пример 5. Найти значение выражения 

Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4

---

Пример 6. Найти значение выражения 

Сначала найдём значение квадратного корня . Он равен 0,6 поскольку 0,6² = 0,36

Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:

---

Вынесение множителя из-под знака корня

В некоторых задачах может быть полезным вынесение множителя из-под знака корня.

Рассмотрим квадратный корень из произведения . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:

В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение  оставим без изменений:

Это и есть вынесение множителя из-под знака корня.

На практике подкореннóе выражение чаще всего требуется разложить на множители.

---

Пример 2. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:

Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:

---

Пример 3. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:

Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:

---

Пример 4. Вынести множитель из-под знака корня в выражении

Воспользуемся правилом извлечения квадратного корня из произведения:

Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:

Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:

---

Пример 5. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 4 и 3

Воспользуемся правилом извлечения квадратного корня из произведения:

Извлечём корень из числа 4, а выражение √3 остáвим без изменений:

---

Пример 6. Упростить выражение 

Предстáвим второе слагаемое в виде . А третье слагаемое предстáвим в виде

Теперь в выражениях и вынесем множитель из-под знака корня:

Во втором слагаемом перемнóжим числа −4 и 4. Остальное перепишем без изменений:

Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:

Вычислим содержимое скобок, полýчим −1

Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3

---

Внесение множителя под знак корня

Рассмотрим следующее выражение:

В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.

Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.

Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15

Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.

Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:

Итак, если данó выражение , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:

Пример 1. Внести множитель под знак корня в выражении

Возведём число 7 во вторую степень и внесём его под знак корня:

---

Пример 2. Внести множитель под знак корня в выражении 

Возведём число 10 во вторую степень и внесем его под знак корня:

---

Пример 3. Внести множитель под знак корня в выражении 

Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида  не имеет смысла.

Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.

Пример 4. Внести множитель по знак корня в выражении 

В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:

---

Пример 5. Выполнить возведéние в степень в следующем выражении:

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)² = a² + 2ab + b²

Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:

Теперь необходимо упростить получившееся выражение.

Для выражений и  применим правило . Ранее мы говорили, что если выражение вида  возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.

А в выражении для множителей и применим правило . То есть заменим произведение корней на один общий корень:

Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом вычислить произведение, которое под кóрнем:

---

 

Задания для самостоятельного решения

Задание 1. Найдите значение квадратного корня:

Решение:

Задание 2. Найдите значение квадратного корня:

Решение:

Задание 3. Найдите значение квадратного корня:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение квадратного корня:

Решение:

Задание 6. Найдите значение квадратного корня:

Решение:

Задание 7. Найдите значение квадратного корня:

Решение:

Задание 8. Найдите значения следующих выражений:

Решение:

Задание 9. Извлеките квадратный корень из числа 4624

Решение:

Задание 10. Извлеките квадратный корень из числа 11025

Решение:

Задание 11. Найдите значение квадратного корня:

Решение:

Задание 12. Найдите значение квадратного корня:

Решение:

Задание 13. Найдите значение квадратного корня:

Решение:

Задание 14. Найдите значение квадратного корня:

Решение:

Задание 15. Найдите значение квадратного корня:

Решение:

Задание 16. Найдите значение выражения:

Решение:

Задание 17. Найдите значение выражения:

Решение:

Задание 18. Найдите значение выражения:

Решение:

Задание 19. Найдите значение выражения:

Решение:

Задание 20. Найдите значение выражения:

Решение:

Задание 21. Найдите значение выражения:

Решение:

Задание 22. Найдите значение выражения:

Решение:

Задание 23. Найдите значение выражения:

Решение:

Задание 24. Найдите значение выражения:

Решение:

Задание 25. Найдите значение выражения:

Решение:

Задание 26. Найдите значение выражения:

Решение:

Задание 27. Найдите значение выражения:

Решение:

Задание 28. Найдите значение выражения:

Решение:

Задание 29. Найдите значение выражения:

Решение:

Задание 30. Найдите значение выражения:

Решение:

Задание 31. Найдите значение выражения:

Решение:

Задание 32. Найдите значение выражения:

Решение:

Задание 33. Найдите значение выражения:

Решение:

Задание 34. Вынести множитель из-под знака корня:

Решение:

Задание 35. Вынести множитель из-под знака корня:

Решение:

Задание 36. Вынести множитель из-под знака корня:

Решение:

Задание 37. Вынести множитель из-под знака корня:

Решение:

Задание 38. Вынести множитель из-под знака корня:

Решение:

Задание 39. Вынести множитель из-под знака корня:

Решение:

Задание 40. Вынести множитель из-под знака корня:

Решение:

Задание 41. Вынести множитель из-под знака корня:

Решение:

Задание 42. Вынести множитель из-под знака корня:

Решение:

Задание 43. Вынести множитель из-под знака корня:

Решение:

Задание 44. Вынести множитель из-под знака корня в следующих выражениях:

Решение:

Задание 45. Внести множитель под знак корня:

Решение:

Задание 46. Внести множитель под знак корня:

Решение:

Задание 47. Внести множитель под знак корня:

Решение:

Задание 48. Внести множитель под знак корня:

Решение:

Задание 49. Внести множитель под знак корня:

Решение:

Задание 50. Внести множитель под знак корня в следующих выражениях:

Решение:

Задание 51. Упростить выражение:

Решение:

Задание 52. Упростить выражение:

Решение:

Задание 53. Упростить выражение:

Решение:

Задание 54. Упростить выражение:

Решение:

Задание 55. Упростить выражение:

Решение:

Задание 56. Упростить выражение:

Решение:

Задание 57. Упростить выражение:

Решение:

Задание 58. Упростить выражение:

Решение:

Задание 59. Упростить выражение:

Решение:

Задание 60. Упростить выражение:

Решение:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Можно ли отнимать корни. Как складывать и вычитать квадратные корни

В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.

Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.

Уравнение, которое нужно упростить:

√2+3√48-4×√27+√128

Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:

Первое число упростить уже нельзя.2×2)

Переписываем выражение с упрощенными слагаемыми:

√2+12×√3-12×√3+8×√2

Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.

Ответ получаем следующий:

√2+12√3-12√3+8√2=9√2

√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.

Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.

Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:

Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:

∛b+∜b=12×√b4 +12×√b3

12√b4 +12×√b3=12×√b4 + b3

Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.

На заметку: показатели степени складываются только при умножении.

Рассмотрим пример, когда в выражении присутствуют дроби.

5√8-4×√(1/4)+√72-4×√2

Будем решать по этапам:

5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.

4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2

Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.

√72-4√2=√(36×2)- 4√2=2√2

10√2+2√2-2=12√2-2

Вот и получился ответ.

Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.

Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.

Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых. Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.

Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.

В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.

Шаги

Часть 1 из 2: Определение корней

Обозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.

• Корень обозначают знаком.
• Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
• Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
• Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
• Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
• Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.

Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.

Нельзя складывать корни с разными подкоренными выражениями, например, (2) + (3) (5). Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).

Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, (64) + (64) (эта сумма не равна (64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 из 2: Упрощение и сложение корней

Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)

• Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
  2 (3) + 2 (50) + (32) + 6 (3) + (81)
• Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
  2 (50) + (32) + 2 (3) + 6 (3) + (81)

Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.

В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)

Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10 (2) + 4 (2) + 2 (3)+ 6 (3) + 3 (3)

Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.

10 (2) + 4 (2) = 14 (2).

2 (3)+ 6 (3) = 8 (3).

Окончательное упрощенное выражение: 14 (2) + 8 (3) + 3 (3)

• Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.

Внимание, только СЕГОДНЯ!

Все интересное

Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…

Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*&ordf-&radic-y нужно внести x под корень. Инструкция 1Определите степень…

Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…

Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…

Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …

Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…

При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…

Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…

Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением.n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…

Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .

Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .

В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .

Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5 .

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89 .

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.

Yandex.RTB R-A-339285-1

Правила сложения и вычитания квадратных корней

Определение 1

Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.

Пример 1

Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.

Действия с корнями: основы

Пример 2

6 50 — 2 8 + 5 12

Алгоритм действия:

1. Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Совет 1

Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.

Пример 3

Давайте попробуем решить данный пример:

6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .

2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .

5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .

Результат упрощения: 30 2 — 4 2 + 10 3

30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .

В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.

Пример 4

• Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
• Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
• Складываем множители у корней: 3 5 + 4 5 = 7 5 .

Пример 5

6 40 — 3 10 + 5:

• Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
• Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
• Перемножаем множители, которые стоят перед корнем: 12 10 ;
• Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
• Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .

Пример 6

Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:

(9 — 4) 5 — 2 3 = 5 5 — 2 3 .

Советы:

• Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
• Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
• Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
• При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Свойства квадратных корней

До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.

В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.

Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.

Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то

Преобразование выражений, содержащих операцию извлечения квадратного корня

До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что

где, напомним, a, b — неотрицательные числа.

Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.

Пример 3. Внести множитель под знак квадратного корня:

Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:

Сложение и вычитание квадратных корней примеры. Как складывать квадратные корни

В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.

Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.

Уравнение, которое нужно упростить:

√2+3√48-4×√27+√128

Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:

Первое число упростить уже нельзя. Переходим ко второму слагаемому.

3√48 раскладываем 48 на множители: 48=2×24 или 48=3×16. из 24 не является целочисленным, т.е. имеет дробный остаток. Так как нам нужно точное значение, то приблизительные корни нам не подходят. Квадратный корень из 16 равен 4, выноси его из-под Получаем: 3×4×√3=12×√3

Следующее выражение у нас является отрицательным, т.е. написано со знаком минус -4×√(27.) Раскладываем 27 на множители. Получаем 27=3×9. Мы не используем дробные множители, потому что из дробей вычислять квадратный корень сложнее. Выносим 9 из-под знака, т.е. вычисляем квадратный корень.2×2)

Переписываем выражение с упрощенными слагаемыми:

√2+12×√3-12×√3+8×√2

Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.

Ответ получаем следующий:

√2+12√3-12√3+8√2=9√2

√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.

Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.

Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:

Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:

∛b+∜b=12×√b4 +12×√b3

12√b4 +12×√b3=12×√b4 + b3

Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.

На заметку: показатели степени складываются только при умножении.

Рассмотрим пример, когда в выражении присутствуют дроби.

5√8-4×√(1/4)+√72-4×√2

Будем решать по этапам:

5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.

4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2

Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.

√72-4√2=√(36×2)- 4√2=2√2

10√2+2√2-2=12√2-2

Вот и получился ответ.

Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.

Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.

Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых.2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.

Инструкция

• Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
• Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.
• Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
• Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
  12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
• И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.

Содержимое:

В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.

Шаги

Часть 1 Определение корней

1. 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
   • Корень обозначают знаком √.
   • Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
   • Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
   • Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
   • Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
   • Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
2. 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
   • Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
   • Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 Упрощение и сложение корней

1. 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
   2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)
   • Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
     2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81)
   • Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
     2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
2. 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
   • В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
   • Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
3. 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
   • 10√(2) + 4√(2) = 14√(2).
   • 2√(3)+ 6√(3) = 8√(3).
   • Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)

• Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.

Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.

Поможет также таблица квадратных корней:

Есть еще способы, которые более сложные, однако очень эффективные:

Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.

Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.

Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.

Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:

Вот видео по теме:

Вычеслить корень квадратный из числа можно несколькими способами.

Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).

Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.

Или при помощи специальной формулы.

Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.

Но если нет калькулятора, то можно это сделать вручную.

Результат получится точным.

Принцип практически такой же как деление столбиком:

Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.

Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.

Для этого нужна таблица квадратов

Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849

Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:

Разложение на простые множители

Разложите подкоренное число на множители, являющиеся квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.

Запишите это как: 400 = (25 х 16).

Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b . Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

В нашем примере извлеките корень из 25 и из 16.

Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.

Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:

Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.

Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.

Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.

Еще один способ разложите подкоренное число на простые множители. Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.

Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.

Рассмотрим другой пример: 88.

= (2 х 4 х 11)

= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.

2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.

Может быть полезным будет еще это обучающее видео:

Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.

Свойства квадратного корня сложение. Как складывать и вычитать квадратные корни

Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.

Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.

Поможет также таблица квадратных корней:

Есть еще способы, которые более сложные, однако очень эффективные:

Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.

Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.

Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.

Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:

Вот видео по теме:

Вычеслить корень квадратный из числа можно несколькими способами.

Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).

Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.

Или при помощи специальной формулы.

Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.

Но если нет калькулятора, то можно это сделать вручную.

Результат получится точным.

Принцип практически такой же как деление столбиком:

Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.

Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.

Для этого нужна таблица квадратов

Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849

Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:

Разложение на простые множители

Разложите подкоренное число на множители, являющиеся квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.

Запишите это как: 400 = (25 х 16).

Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b . Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

В нашем примере извлеките корень из 25 и из 16.

Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.

Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:

Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.

Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.

Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.

Еще один способ разложите подкоренное число на простые множители. Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.

Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.

Рассмотрим другой пример: 88.

= (2 х 4 х 11)

= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.

2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.

Может быть полезным будет еще это обучающее видео:

Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.

Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.

Что такое математический корень?

Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.

Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.

Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.

Какие действия с ними можно выполнять?

По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.

И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.

По каким правилам выполняется их сложение и вычитание?

Сначала нужно запомнить два категорических «нельзя»:

• нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
• нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.

Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .

Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.

Теперь к правилам

1. Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.
2. Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
3. Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
4. Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
5. Вынести из-под знака радикала множитель, который дает целую степень.
6. Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.

В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.

Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.

Первое задание

Вычислить значение выражений:

а) √2 + 3√32 + ½ √128 — 6√18;

б) √75 — √147 + √48 — 1/5 √300;

в) √275 — 10√11 + 2√99 + √396.

а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.

Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:

√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).

Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:

√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.

Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:

√2 + 12√2 + 4 √2 — 12√2.

В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.

б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:

5√5 — 7√3 + 4√3 — 1/5 * 10√3.

После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).

в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:

5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.

Пример с дробными выражениями

√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).

На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:

3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).

Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:

5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.

Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Содержимое:

Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).

Шаги

Часть 1 Постигаем основы

1. 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
   • 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
   • 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
   • 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
2. 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
3. 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
4. 4 У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа! ). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
   • 30√2 — 4√2 + 10√3 =
   • (30 — 4)√2 + 10√3 =
   • 26√2 + 10√3

Часть 2 Практикуемся на примерах

1. 1 Пример 1: √(45) + 4√5.
   • Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
   • Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
   • Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
2. 2 Пример 2: 6√(40) — 3√(10) + √5.
   • Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
   • Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
   • Перемножьте множители перед корнем и получите 12√10.
   • Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
   • Вы получите: (12-3)√10 + √5 = 9√10 + √5.
3. 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
4. 4 Пример 4. √9 + √4 — 3√2.
   • √9 = √(3 х 3) = 3.
   • √4 = √(2 х 2) = 2.
   • Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
   • Окончательный ответ: 5 — 3√2.
5. 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
   • Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
   • Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
   • Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .

• Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.

Предупреждения

• Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
• Никогда не суммируйте и не вычитайте целое число и корень, например, 3 + (2x) 1/2 .
  • Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).

Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.

Yandex.RTB R-A-339285-1

Правила сложения и вычитания квадратных корней

Определение 1

Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.

Пример 1

Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.

Действия с корнями: основы

Пример 2

6 50 — 2 8 + 5 12

Алгоритм действия:

1. Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Совет 1

Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.

Пример 3

Давайте попробуем решить данный пример:

6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .

2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .

5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .

Результат упрощения: 30 2 — 4 2 + 10 3

30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .

В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.

Пример 4

• Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
• Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
• Складываем множители у корней: 3 5 + 4 5 = 7 5 .

Пример 5

6 40 — 3 10 + 5:

• Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
• Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
• Перемножаем множители, которые стоят перед корнем: 12 10 ;
• Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
• Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .

Пример 6

Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:

(9 — 4) 5 — 2 3 = 5 5 — 2 3 .

Советы:

• Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
• Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
• Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .2=400\\ \hline \end{array}\]

  Факт 3.
  Какие действия можно выполнять с квадратными корнями?
  \(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\) , то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\) , а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\) , а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\) . Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл )
  Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\) ; \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\) ; \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\) . \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
  Рассмотрим пример. Найдем \(\sqrt{44100}\) . Так как \(44100:100=441\) , то \(44100=100\cdot 441\) . По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\) , то есть \(441=9\cdot 49\) .
  Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
  \(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\) ). Так как \(5=\sqrt{25}\) , то \ Заметим также, что, например,
  1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
  2) \(5\sqrt3-\sqrt3=4\sqrt3\)
  3) \(\sqrt a+\sqrt a=2\sqrt a\) .2\) , поэтому \(\sqrt{16}=4\) . А вот извлечь корень из числа \(3\) , то есть найти \(\sqrt3\) , нельзя, потому что нет такого числа, которое в квадрате даст \(3\) .
  Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
  Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) и т.д.
  \(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\) .
  Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.

  Факт 5.
  \(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\) , равное расстоянию от точки \(a\) до \(0\) на вещественной прямой.2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
  Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3 \(\bullet\) Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\ &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! \(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.2=168\cdot 168=28224\) .
  Следовательно, \(\sqrt{28224}=168\) . Вуаля!

  Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

  Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

  1. Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
  2. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

  Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

  Деление корней цветов просто необходимо, если вы решили сразу за одно «мероприятие» получить пару сильных и взрослых растений, которые в будущем будут готовы к цветению. Но если рассматривать этот вопрос с иной стороны, то можно сказать, что деление корней может негативно сказаться на состоянии растений, особенно при неправильной работе с корнями.

  Прежде чем разбирать вопрос – как делить корни, необходимо определиться с растениями, которые можно так размножать. Прежде всего, это травянистые экземпляры с хорошей корневой системой. Делить таким образом можно цветы и кустарники.

  Алгоритм деления корней:

  1. Цветок извлеките из грунта и стряхните большой ком земли.

  2. Остатки почвы смойте водой, но не нужно полностью очищать корни, главное, чтобы почва не мешала вам при делении.

  4. Осуществите обрезку побегов на высоту 10 см. Это мероприятие поможет использовать силы цветов для восстановления корней, а не роста побегов.

  5. Если корневые отростки начали твердеть, и видно, что ничего хорошего с них не получиться, то эти корни срезают.

  6. Желтые и сухие побеги, листья сразу уничтожают.

  7. Обратите внимание на то, что центральная часть цветка делиться не должна. Вы отделяете лишь боковые корни.

  8. Срезы обрабатывают древесным углем, а новые растения высаживают в специальные горшки.

  Что вы еще должны знать о делении корней

  Не выполняйте этот процесс во время цветения растения. Лучше проводить его после этого периода. Если соблюсти эту рекомендацию сложно, то за пару дней перед процессом бутоны и цветы уничтожают, иначе цветок прижиться не сможет.

  Кустарник в открытой почве разделяют осенью, а комнатные цветы – весной. Перед извлечением растения из земли, грунт хорошо поливают, чтобы корневая система не повредилась. Ни в коем случае не тяните растение за наземную часть. Корневую систему вынимают вместе с грунтом, стуча по горшку. Если цветок растет на клумбе, то его осторожно подкапывают и достают при помощи садовых инструментов. Для минимального повреждения корневой системы используют острый нож. Корневую систему не ломайте руками! Это негативно скажется на состоянии будущего цветка.

  Обратите внимание! Не делите куст на маленькие части, так как это может негативно сказаться на их росте и развитии. Приживаемость будет минимальной. Не забывайте, что на каждой части должны быть один взрослый побег.

  В открытую почву сразу высаживать растения нельзя, так как им нужен период восстановления, да и лучи солнца на растения повлияют негативно.

  Польза размножения делением куста

  Кроме того, что растений становится больше, они еще и омолаживаются. Ведь спорить бессмысленно с тем, что биологический возраст всех живых существ не вечен, и растение не стало исключением. Так что вы можете при помощи деления корней обновить ваши многолетники без дополнительного выращивания рассады.

  Размножение растений методом деления корня является одним из самых удобных способов, ведь разовая операция позволяет получить сразу несколько взрослых и сильных растений, готовых к цветению или плодоношению. С другой стороны, подходит данный метод не для всех культур, да и при неправильном выполнении может быть губительным для всего растения.

  Делением корня размножают кустарники и травянистые растения, обладающие развитой корневой системой с образованием почек. В эту категорию можно отнести лещину, сирень, являющуюся кустарником , орхидеи, хризантемы, дельфиниумы и пионы, а также многие другие цветы.

  Основные этапы процедуры :

  • Аккуратно извлеките растение из почвы и отряхните жесткой кистью земляной ком.
  • Остатки грунта смойте водой комнатной температуры, погрузив корни в емкость с водой. Всю землю смывать не нужно, главное чтобы грунт не мешал делению.
  • Оцените сколько растений может получиться из данного куста, выбрав основные взрослые побеги и активные почки.
  • Выполните обрезку всех побегов растения на высоту десять сантиметров (необходимо для высоких травянистых растений и кустарников) . Это позволит растению использовать энергию на восстановление корневой системы, не расходуя ее на питание надземной части.
  • Если есть одеревесневшие побеги, например, при размножении розы , их срезают под самый корень.
  • Удаляются все поврежденные и пожелтевшие побеги и листья.
  • Сделайте уверенные разрезы, отделяя боковые части куста. Центральная часть растения не должна разделяться.
  • Обработайте срезы древесным углем, высадите новые растения в подготовленные емкости и выполните полив раствором стимулятора роста.

  Что нужно знать при делении куста

  Размножение данным способом нельзя выполнять во время цветения. Лучше всего разделить после окончания данного периода. Если это затруднительно, за два дня перед делением срезают все цветы и бутоны. Иначе, растение может погибнуть.

  Комнатные цветы лучше разделять в марте по окончанию периода покоя, а кустарники, растущие в открытом грунте, — осенью до начала заморозков.

  Во время деления корневая система должна быть хорошо видна и легко отделяемая от грунта. Чтобы при извлечении не повредить корни, за день до выполнения деления грунт хорошо увлажняют. Нельзя тянуть за надземную часть растения. Корни с земляным комом вынимают, постукивая по цветочному горшку. Если растение находится на клумбе, его аккуратно откапывают используя садовую лопатку и жесткую малярную кисть.

  Для деления корня используют острый нож, чтобы минимально травмировать растения. Садовые ножницы лучше не использовать, поскольку они могут смять срезы корня. Нельзя ломать корни руками!

  Не стоит разделять растение на слишком мелкие части — это может быть губительным для всего куста, поскольку приживаемость будет значительно ниже. На каждой части должен обязательно быть зрелый побег.

  Сразу высаживать в открытый грунт разделенные растения не желательно, поскольку им необходим период восстановления и прямые лучи солнца, а также вредители и болезни будут для них опасны, а потому лучше выдержать пару недель новые саженцы в защищенном грунте. Последний должен быть стерильным и соответствовать условиям роста разделяемого растения.

  Для чего применяется деление куста

  Помимо увеличения количества экземпляров, метод деления корня применяется для комплексного омоложения растений, биологический возраст которых подходит к концу. Таким образом вы сможете обновлять многолетники без выращивания рассады.

  Очень эффективен данный метод, если требуется сохранить декоративные особенности материнского растения, которые при использовании других методов размножения могут быть утрачены.

  Примеры размножения делением корня:

  Видео 1. Размножение орхидеи фаленопсис

  Видео 3. Размножение смородины делением куста

  Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.

  Ниже мы по очереди рассмотрим основные способы извлечения корней.

  Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.

  Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.

  Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.

  Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.

  Приступим.

  Использование таблицы квадратов, таблицы кубов и т.д.

  В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?

  Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .

  
  

  Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.

  Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.

  Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.

  В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .

  
  

  Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.

  Разложение подкоренного числа на простые множители

  Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.

  Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .

  Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.

  Разберемся с этим при решении примеров.

  Пример.

  Извлеките квадратный корень из 144 .

  Решение.

  Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .

  Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.

  Разложим 144 на простые множители:
  

  То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .

  Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .

  Ответ:

  Для закрепления материала рассмотрим решения еще двух примеров.

  Пример.

  Вычислите значение корня .

  Решение.

  Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .

  Ответ:

  Пример.

  Является ли значение корня целым числом?

  Решение.

  Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.

  Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.

  Ответ:

  Нет.

  Извлечение корней из дробных чисел

  Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.

  Разберем пример извлечения корня из дроби.

  Пример.

  Чему равен квадратный корень из обыкновенной дроби 25/169 .

  Решение.

  По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.

  Ответ:

  Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.

  Пример.

  Извлеките кубический корень из десятичной дроби 474,552 .

  Решение.

  Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .

  Ответ:

  .

  Извлечение корня из отрицательного числа

  Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.

  Рассмотрим решение примера.

  Пример.

  Найдите значение корня .

  Решение.

  Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .

  Приведем краткую запись решения: .

  Ответ:

  .

  Порязрядное нахождение значения корня

  В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.

  На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.

  Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.

  Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.

  Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .

  Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.

  Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9 , вычисляя соответственно 0 2 , 1 2 , …, 9 2 до того момента, пока не получим значение, большее подкоренного числа 5 . Все эти вычисления удобно представлять в виде таблицы:
  

  Так значение разряда единиц равно 2 (так как 2 2 5 ). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9 , сравнивая полученные значения с подкоренным числом 5 :
  

  Так как 2,2 2 5 , то значение разряда десятых равно 2 . Можно переходить к нахождению значения разряда сотых:
  

  Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .

  Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.

  Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.

  Определим его значение.
  

  Так как 10 3 2 151,186 , то значение разряда десятков равно 1 . Переходим к единицам.
  

  Таким образом, значение разряда единиц равно 2 . Переходим к десятым.
  

  Так как даже 12,9 3 меньше подкоренного числа 2 151,186 , то значение разряда десятых равно 9 . Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
  

  На этом этапе найдено значение корня с точностью до сотых: .

  В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.

  Список литературы.

  • Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
  • Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
  • Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

  Например, пусть нам надо извлечь квадратный корень из дроби 25/144. 6. Приближенное извлечение квадратных корней. Если D

  Чтобы извлечь квадратный корень из целого числа с точностью до 1, нужно извлекать, как обыкновенно, и отбросить получаемый в конце действия остаток. Для приближеннаго извлечения корня из дроби, нужно предварительно сделать знаменателя полным квадратом.

  В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам.

  Формула столь же проста, как и умножение. У формулы деления корней возможности не так обширны, как у умножения. В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования.

  • Каталог заданий
  • Вопросы и ответы

  Исключительно для того, чтобы формулу деления корней в дело употребить. Рассмотрим формулу деления корней в обратном направлении. В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей!

  Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней!

  Надеюсь, что деление корней проблем не составляет. Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. А почему нет? Умножить корень сам на себя — да все дела! И не только в квадрат можно. В любую степень.

  Это число, которое при возведении в квадрат должно дать двойку. По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится.

  Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут: «где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Итак, откуда в корнях могут появиться отрицательные числа и выражения?

  Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) — всегда число неотрицательное! Это и есть последнее, третье свойство корней.

  • Алгебра
  • 14 баллов

  Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Если х Собственно, это и есть главная трудность в работе с корнями. В отличие от более простых разделов математики, здесь правильный ответ частенько не вытекает автоматически из формул.

  Главный практический совет по работе с квадратными корнями. Если под знаком корня — минус, дальше можно не решать. Если под корнем всё нормально, плюс, а в результате извлечения получается заведомый минус — сделайте из него плюс! Этого требуют правила действий с квадратными корнями.

  24 разделить на корней из 7+1

  Все свойства корней связаны с умножением-делением. На сложение-вычитание корней — не существует специальных формул! Хотя одинаковые корни можно, конечно, складывать-вычитать. Но эти действия к специфическим свойствам корней не имеют никакого отношения.

  Отлично. Корни — не ваша проблема. Нет проблем! Идём в Особый раздел 555. Квадратные корни. Там даны все разъяснения. В этом разделе вы познакомитесь с практической работой с корнями. Дискриминант — это выражение, от которого зависит число корней данного уравнения.

  Понизим степень косинуса по формуле: 1+cos2α=2cos2α. Следовательно, корней нет. При этом трехчлен 4y2-2y+5 при любом значении у будет принимать только положительные значения.

  OFF: Число ПИ разделить на корень из 3, или математика для 1С-ника

  Ведь если разность двух радикалов умножить на их сумму, то получится разность квадратов корней, т.е. получится выражение без знаков радикалов. 1) Представим подкоренное выражение второго множителя в виде квадрата суммы двух выражений, т.е. в виде(a + b)2. Это позволит нам извлечь арифметический квадратный корень.

  ВОЗВЕДЕНИЕ В СТЕПЕНЬ. Напоминаю: здесь а — неотрицательное число (больше или равно нулю), b — положительное (больше нуля)! Иначе формула смысла не имеет… Теперь в нашем арсенале уже две формулы.

  Но именно эти действия вызывают массу проблем… С этим надо разобраться основательно. Не вопрос! Если, конечно, знаете действия со степенями… Пусть у нас есть хорошее число 2. Возведём его в квадрат. Приведём нашу степень к квадрату.

  А если степень нечётная? Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Здесь всё понятно и просто. Не работает эта формула для отрицательных значений.

  Мы же умеем корень из произведения извлекать. Корень в квадрате — штука бесхитростная. Бывает ещё круче, когда корень из смешанного числа надо извлечь! А теперь попрактикуемся в корнях. Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например?

  Сложение и вычитание радикалов (квадратные корни)

  Purplemath

  Так же, как и «обычные» числа, квадратные корни можно складывать. Но возможно, вам не удастся упростить сложение до одного числа. Подобно тому, как «нельзя добавлять яблоки и апельсины», вы не можете комбинировать радикальные термины «непохожие». Чтобы можно было объединить радикальные термины вместе, эти термины должны иметь одну и ту же радикальную часть.

  • Упростить:

  Поскольку радикал в каждом члене один и тот же (является квадратным корнем из трех), то это «одинаковые» термины. Это означает, что я могу комбинировать термины.

  MathHelp.com

  У меня есть две копии радикала, добавлены еще три копии. Всего получается пять копий:

  Этот средний шаг в круглых скобках показывает рассуждение, которое оправдывает окончательный ответ.Возможно, вам никогда не понадобится «показывать» этот шаг, но это то, о чем вы должны подумать.

  ---

  • Упростить:

  Коренная часть одинакова во всех терминах, поэтому я могу добавить это дополнение. Чтобы помочь мне понять, что первый термин означает «одну копию квадратного корня из трех», я вставлю «понял» «1»:

  ---

  Не думайте, что выражения с непохожими радикалами нельзя упростить.Возможно, что после упрощения радикалов выражение действительно может быть упрощено.

  • Упростить:

  Чтобы упростить радикальное сложение, я должен сначала посмотреть, могу ли я упростить каждый радикальный термин. В данном конкретном случае квадратные корни упрощаются «полностью» (то есть до целых чисел):

  ---

  • Упростить:

  У меня есть три копии радикала плюс еще две копии, что дает мне… Погодите! Я могу упростить эти радикалы до целых чисел:

  Не волнуйтесь, если вы не сразу увидите упрощение.Если бы я не заметил до конца, что радикальное упрощение, мои шаги были бы другими, но мой окончательный ответ был бы таким же:

  ---

  • Упростить:

  Могу объединить только радикалы «лайки». Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае я получу два термина в своем ответе.

  Я начну с перестановки терминов, чтобы соединить «похожие» термины вместе, и вставив «понятый» 1 во второй член квадратного корня из трех:

  ---

  Насколько мне известно, нет предпочтительного упорядочивания терминов в такого рода выражениях, поэтому выражение

  также должно быть приемлемым ответом.

  ---

  • Упростить:

  Насколько мне известно, это «непохожие» термины, и я не могу их объединить.Но восьмерка в радикале первого члена множится как 2 × 2 × 2. Это означает, что я могу вытащить 2 из радикала. В этот момент у меня будут термины «нравится», которые я могу комбинировать.

  ---

  • Упростить:

  Я могу упростить большинство радикалов, и это позволит сделать хотя бы небольшое упрощение:

  ---

  • Упростить:

  В этих двух терминах есть «непохожие» радикальные части, и я не могу извлечь ничего из любого из радикалов.Тогда я не могу дальше упрощать выражение

  , и мой ответ должен быть таким:

  (выражение уже полностью упрощено)

  ---

  • Развернуть:

  Чтобы расширить это выражение (то есть умножить его, а затем упростить), мне сначала нужно взять квадратный корень из двух через круглые скобки:

  ---

  Как видите, упрощение включало превращение продукта радикалов в один радикал, содержащий значение продукта (2 × 3 = 6).Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».

  ---

  • Развернуть:

  Как и в предыдущем примере, мне нужно умножить через круглые скобки.

  ---

  • Развернуть:

  Наверное, проще будет это умножение «по вертикали».

  Упрощение дает мне:

  ---

  Выполняя вертикальное умножение, я мог лучше отслеживать свои шаги. Вы должны использовать тот метод умножения, который вам больше подходит. Но знайте, что вертикальное умножение — это не временная уловка для начинающих студентов; Я до сих пор использую эту технику, потому что обнаружил, что при этом я постоянно быстрее и точнее.

  ---

  Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении радикалов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.

  (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

  ---

  ---

  URL: https: // www.purplemath.com/modules/radicals3.htm

  Добавление квадратного корня — математический класс [2021]

  Добавление десятичной формы

  Один из способов сложить квадратные корни — это привести их к десятичной форме. Это особенно просто, если у вас есть калькулятор. Например, квадратный корень из 2 составляет примерно 1,414, что означает, что если вы умножите 1,414 на само, вы почти вернетесь к 2 (примерно 1.999). Если вы хотите прибавить √2 (около 1,414) к √3 (около 1,732), вы получите около 3,146, что приблизительно равно сумме двух квадратных корней.

  Более крупные последовательности квадратных корней можно сложить таким же образом:

  3√40 + 5√10 + 7√3

  = (приблизительно) 3 (6,325) + 5 (3,162) + 7 (1,732)

  = 18.974 + 15.811 + 12.124

  = 46.909

  К сожалению, это не точный ответ, и многие математические задачи требуют точного ответа, даже если вам придется оставить его в радикальной форме.Вот как можно получить точные ответы, в том числе радикалы.

  Упрощение радикалов и «подобных» терминов

  Добавление радикальной формы квадратных корней во многом похоже на добавление переменных выражений. Прежде чем упростить их, вы должны составить форму «Нравится». Квадратные корни являются «подобными» терминами, если они имеют одинаковое значение под корнем. Например, √2 и еще √2 — это «похожие» термины, а √2 и √3 — не «похожие» термины.

  Так можно ли упростить радикалы, чтобы получить лайки? Да, иногда можно.Например, квадратный корень из 8 можно переписать как квадратный корень из 4, умноженного на квадратный корень из 2. √8 = √4 x √2. Поскольку квадратный корень из 4 равен 2 (2 x 2 = 4), это означает, что √8 = 2 √2. Это позволяет нам добавлять некоторые термины с квадратным корнем, которые в противном случае мы не смогли бы сделать.

  А как насчет больших чисел? Например, что бы вы сделали с √200? 200 не имеет простого корня, но его можно разделить на продукты с простыми корнями.

  200 = 2 x 100, поэтому √200 = √2 x √100 = 10√2.

  108 = 3 x 36, поэтому √108 = √3 x √36 = 6√3.

  Добавление выражений квадратного корня в радикальной форме

  Добавление радикальных форм квадратных корней похоже на их сложение. Например, если у меня есть 5 √2, которые нужно добавить к 7 √2, это означает, что у меня их действительно 12. Просто сложите числа перед радикалами (√). Как будто ребята из √2 — это просто пакеты, и вы считаете, сколько их у вас есть. Это легко, если все они похожи на термины.

  5√2 + 3√2 + √2 + 4√2 = (5 + 3 + 1 + 4) √2 = 13√ 2

  Вы можете упростить свои термины, чтобы получить «похожие» термины.Например:

  5√8 + 3√4 + √2 + 4√16

  = 5 (2 (√2)) + 3 (2) + √2 + 4 (4)

  = 10√2 + 6 + √2 + 16

  = 22 + 11√2

  Обратите внимание, что 6 и 16 — это «одинаковые» термины, в то время как 10√2 и √2 также являются подобными терминами. Как только мы собрали «похожие» термины, все готово.

  Попробуем еще. Чтобы упростить отслеживание, мы обозначили «нравится» разными цветами.

  Сначала давайте объединим уже имеющиеся у нас «похожие» термины:

  Теперь давайте упростим термины, которые уже являются полными квадратами (6√9 и 3√4).Мы извлекаем квадратный корень и умножаем его на коэффициент.

  Теперь давайте разделим число 27 на 3 x 9 (это полный квадрат) и объединим два наших члена, у которых нет корня.

  Теперь возьмем 9 из-под корня, взяв из него квадратный корень 3 и коэффициент 5

  У нас снова есть два одинаковых термина, поэтому мы объединим их на последнем этапе.

  И готово! Обратите внимание: какими бы сложными ни были эти проблемы, всего несколько простых операций сведут их к простейшей форме. Хотя это не обязательно для обеспечения точности, рекомендуется переписать эти решения в логическом порядке (например, увеличив размер радикального выражения, как показано ниже).

  Резюме урока

  Квадратный корень из любого интересующего числа — это часть этого числа, которая может быть возведена в квадрат для его получения.3 x 3 = 9, поэтому квадратный корень из 9 равен 3. 1 x 1 = 1, поэтому квадратный корень из 1 равен 1. 2,5 x 2,5 = 6,25, поэтому квадратный корень из 6,25 равен 2,5. Квадратные корни могут быть добавлены путем преобразования их в десятичные значения и последующего сложения, но результат будет неточным. Чтобы точно сложить квадратные корни (радикальные выражения), вы можете только уменьшить их, а затем добавить «похожие» термины (квадратные корни с тем же числом под радикалом или √).

  Сложение и вычитание квадратного корня

  Мы можем складывать или вычитать радикальные выражения только тогда, когда они имеют одно и то же подкоренное выражение и когда они имеют один и тот же радикальный тип, например квадратные корни.Например, сумма [latex] \ sqrt {2} [/ latex] и [latex] 3 \ sqrt {2} [/ latex] равна [latex] 4 \ sqrt {2} [/ latex]. Однако часто можно упростить радикальные выражения, и это может изменить подкоренное выражение. Радикальное выражение [latex] \ sqrt {18} [/ latex] может быть записано с помощью [latex] 2 [/ latex] в подкоренном выражении, как [latex] 3 \ sqrt {2} [/ latex], поэтому [latex ] \ sqrt {2} + \ sqrt {18} = \ sqrt {2} +3 \ sqrt {2} = 4 \ sqrt {2} [/ latex].

  Практическое руководство. Решите радикальное выражение, требующее сложения или вычитания квадратных корней.

  1. Упростите каждое радикальное выражение.
  2. Сложить или вычесть выражения с одинаковыми подкоренными частями.

  Пример 6: Добавление квадратного корня

  Добавьте [латекс] 5 \ sqrt {12} +2 \ sqrt {3} \\ [/ latex].

  Решение

  Мы можем переписать [latex] 5 \ sqrt {12} [/ latex] как [latex] 5 \ sqrt {4 \ cdot 3} [/ latex]. Согласно правилу продукта это становится [латекс] 5 \ sqrt {4} \ sqrt {3} [/ latex]. Квадратный корень из [latex] \ sqrt {4} [/ latex] равен 2, поэтому выражение становится [latex] 5 \ left (2 \ right) \ sqrt {3} [/ latex], то есть [latex] 10. \ sqrt {3} [/ латекс].{2} \ sqrt {2ac} \ text {} [/ latex]

  Попробуй 7

  Вычтите [латекс] 3 \ sqrt {80x} -4 \ sqrt {45x} [/ latex].

  Решение

  Сложение и вычитание квадратного корня — элементарная алгебра

  Цели обучения

  К концу этого раздела вы сможете:

  • Сложить и вычесть как квадратные корни
  • Сложить и вычесть квадратные корни, требующие упрощения

  Перед тем, как начать, пройдите тест на готовность.

  1. Добавь: ⓐ ⓑ.
     Если вы пропустили эту проблему, просмотрите (рисунок).
  2. Упростить:.
     Если вы пропустили эту проблему, просмотрите (рисунок).

  Мы знаем, что для упрощения выражений с квадратными корнями необходимо соблюдать порядок операций. Радикал — это групповой символ, поэтому сначала мы работаем внутри радикала. Упрощаем таким образом:

  Итак, если нам нужно складывать, мы не должны объединять их в один радикал.

  Попытка сложить квадратные корни с разными подкоренными выражениями похожа на попытку сложить непохожие термины.

  Сложение квадратных корней с одним и тем же корневым выражением аналогично сложению одинаковых членов. Мы называем квадратные корни с одним и тем же корневым элементом квадратными корнями, чтобы напомнить нам, что они работают так же, как похожие термины.

  Как квадратные корни

  Квадратные корни с одной и той же подкоренной частью называются квадратными корнями.

  Мы складываем и вычитаем как квадратные корни так же, как складываем и вычитаем как члены. Мы это знаем. Аналогично складываем и получаем

  Сложение и вычитание, как квадратные корни

  Подумайте о добавлении одинаковых терминов с переменными, как в следующих нескольких примерах.Когда у вас есть подкоренные выражения, вы просто добавляете или вычитаете коэффициенты. Когда подкоренные выражения не похожи, вы не можете комбинировать термины.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Когда радикалы содержат более одной переменной, при условии, что все переменные и их показатели идентичны, радикалы подобны.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Сложение и вычитание квадратного корня, требующего упрощения

  Помните, что мы всегда упрощаем извлечение квадратного корня, удаляя наибольший коэффициент полного квадрата.Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Точно так же, как мы используем ассоциативное свойство умножения для упрощения и получения, мы можем упрощать и получать.В следующем примере мы воспользуемся ассоциативным свойством.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  В следующем примере мы удалим постоянные и переменные множители из квадратных корней.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Упростить:.

  Решение

  Упростить:.

  Упростить:.

  Ключевые понятия

  • Чтобы сложить или вычесть квадратные корни, сложите или вычтите коэффициенты и сохраните такой же квадратный корень.
  • Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

  Практика ведет к совершенству

  Сложить и вычесть как квадратные корни

  Упростите следующие упражнения.

  Сложить и вычесть квадратные корни, требующие упрощения

  Упростите следующие упражнения.

  Смешанная практика

  Повседневная математика

  Декоратор решает использовать квадратную плитку в качестве акцентной полосы в дизайне новой душевой кабины, но она хочет повернуть плитки, чтобы они выглядели как ромбы.Она будет использовать 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определите ширину акцентной полосы, упростив выражение. (Округлите до ближайшей десятой доли дюйма.)

  Сюзи хочет использовать квадратные плитки на границе спа, которое она устанавливает на заднем дворе. Она будет использовать большие плитки с площадью 12 квадратных дюймов, средние плитки с площадью 8 квадратных дюймов и маленькие плитки с площадью 4 квадратных дюйма.После того, как участок границы потребует 4 больших плитки, 8 средних плиток и 10 маленьких плиток, чтобы покрыть ширину стены. Упростите выражение, чтобы определить ширину стены.

  Письменные упражнения

  Объясните разницу между одинаковыми радикалами и непохожими радикалами. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

  Объясните процесс определения того, похожи ли два радикала или нет. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

  Самопроверка

  ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

  ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

  Глоссарий

  как квадратные корни

  Квадратные корни с той же подкоренной частью называются квадратными корнями.

  Как рассчитать КВАДРАТНЫЙ КОРЕНЬ в Excel [5 лучших методов] + Добавить символ

  Excel похож на швейцарский армейский нож для вычислений.От математических до финансовых — это все, что вам нужно вычислить. Вы можете рассчитывать от простых до самых сложных в Excel.

  Возьмем, к примеру, КВАДРАТНЫЙ КОРНЬ .

  Квадратный корень — довольно распространенное вычисление, которое мы выполняем в повседневной работе, и в Excel вы можете легко вычислить его.

  Знаете что?

  Я обнаружил, что существует пять различных способов вычисления квадратного корня в Excel. Да, пять разных методов, которые можно использовать в разных ситуациях.

  И сегодня в этом посте я хотел бы поделиться с вами этими пятью простыми методами, чтобы найти квадратный корень из числа в Excel.

  Итак, давайте узнаем вот что…

  Что такое квадратный корень?

  Прежде чем мы научимся его вычислять, важно понять, что это на самом деле означает, как мы его обычно вычисляем.

  Краткое введение: Вычисление квадратного корня является обратным вычислением для возврата к корню из квадрата.

  Итак, когда вы вычисляете квадрат 10, умножая его на себя, получается (10 * 10 = 100).

  Тогда квадратный корень означает возврат от 100 к 10.

  Вы можете узнать больше об этом из Википедии. Но теперь давайте узнаем, как это можно сделать в Excel.

  Лучшие 5 способов вычисления квадратного корня в Excel

  Как я уже сказал, мы можем использовать 5 различных способов вычисления квадратного корня в соответствии с потребностями или личными предпочтениями.

  Не все методы одинаковы, но полезны.

  №1. Используйте функцию КОРЕНЬ, чтобы найти КВАДРАТНЫЙ корень числа

  Если вам нужно использовать только один метод для вычисления квадратного корня, это функция КОРЕНЬ.Это особая функция.

  Вам просто нужно сослаться на ячейку или указать число.

  Синтаксис SQRT:

  Где номер — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень.

  Примеры:

  В приведенном ниже примере у нас есть число 625 в ячейке A1. Итак, чтобы вычислить квадратный корень для этого, мы можем вставить приведенную ниже формулу (панель формул) в B1.

  Возвращенное значение — 25, что является квадратным корнем из 625.

  Как видите, SQRT прост в использовании и удобен в применении.

  Но есть одна особенность.

  Если у вас отрицательное число, как показано ниже, оно вернет # ЧИСЛО !.

  Итак, решение этой проблемы — использовать функцию ABS вместе с SQRT. Вот пример:

  Когда мы используем ABS, он преобразует число в абсолютное число. Это означает, что a преобразует отрицательное число в положительное.

  2. Вычислить КВАДРАТНЫЙ корень числа с помощью функции СТЕПЕНЬ

  Другой способ вычисления квадратного корня — использование функции СТЕПЕНЬ.

  Функция POWER имеет большую мощность, чем SQRT, поскольку она возвращает результат возведения числа N-го в заданную степень.

  Синтаксис POWER:

  Где число — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень, а степень — это показатель степени для увеличения мощности.

  Допустим, нам нужно найти квадратный корень из числа из ячейки A1 (то есть 625), тогда мы можем использовать 1/2 в качестве аргумента мощности в этой функции.

  И формула будет:

  Как вы видите, она возвращает 25 в результате, который является квадратным корнем из 625.

  3. Примените формулу экспоненты, чтобы получить КВАДРАТНЫЙ корень числа

  Если нам нужно чтобы вставить простую формулу (кроме двух вышеуказанных методов) для вычисления квадратного корня, мы можем использовать простую формулу с использованием оператора экспоненты.

  Эта формула похожа на POWER. Единственная разница в том, что вместо функции нам нужно использовать оператор экспоненты.

  В приведенной выше формуле A1 в ячейке, где у нас есть число, для которого нам нужно найти квадратный корень, а затем мы использовали оператор экспоненты, а затем (1/2) для возведения в степень.

  Лучшее преимущество этой формулы — ее применение. Помимо квадратного корня, мы можем использовать его для вычисления кубического корня или любого корня n-й степени. (1/2)

  MsgBox «Квадратный корень» & rng & «is» & sqr, vbOKOnly, «Квадратное значение»

  Else

  MsgBox «Пожалуйста, выберите числовое значение», vbOKOnly, «Error»

  End If

  End Sub

  Как работает этот код

  Когда мы запускаем этот код, он проверяет значение в выбранной ячейке и, если это значение является числом, вычисляет квадратный корень из этого числа и отображает его в окне сообщения.

  Одна вещь, о которой вам нужно позаботиться: если вы выберете более одной ячейки, этот код не будет работать.

  Код-2

  Используя приведенный ниже код, мы можем проверить, чтобы ввести квадратный корень из числа, не имея фактического числа в ячейке.

  Sub getSquareRoot ()

  Dim sq As Long

  Dim sqr As Long

  sq = InputBox («Введите значение для вычисления квадратного корня», «Вычислить квадратный корень»)

  Если IsNumeric (sq) = True, то

  sqr = sq ^ (1/2)

  MsgBox «Квадратный корень» & sq & «is» & sqr, vbOKOnly, «Square Root Value»

  Else

  MsgBox «Пожалуйста, введите число.», vbOKOnly,» Error «

  End If

  End Sub

  Как работает этот код

  Когда мы запускаем этот код, он показывает нам поле ввода с запросом числа, для которого нам нужно получить квадратный корень.

  И когда мы вводим это число, он вычисляет квадратный корень для этих чисел и показывает окно сообщения с квадратным корнем.

  Вы можете использовать любой из приведенных выше кодов, который идеально подходит для вас.

  # 5. Power Query для преобразования чисел в квадратные корни

  Вот еще один способ, который мы можем использовать, если вам нужно преобразовать несколько чисел в их квадратные корни.

  Это Power Query.

  Ниже у нас есть таблица, в которой у нас есть несколько чисел, и здесь мы хотим получить квадратный корень из этих чисел за один раз.

  Примечание: Использование запроса мощности для квадратного корня — это динамический метод, каждый раз, когда вы вводите новое значение в свою таблицу, он будет возвращать квадратный корень из этого числа.

  Теперь выполните следующие простые шаги.

  • Прежде всего, выберите любую ячейку в таблице и перейдите на вкладку «Данные» ➜ «Получить и преобразовать данные» и нажмите «Из таблицы / диапазона».
  • Как только вы щелкнете по нему, Excel откроет редактор мощных запросов и добавит в него эту таблицу.
  • Отсюда нам нужно создать новый столбец со значениями квадратного корня, для этого перейдите на вкладку «Добавить столбец» и нажмите «Пользовательский столбец».
  • На этом этапе у нас открыто окно Custom Column, и в это окно нам нужно добавить следующее:
  1. Прежде всего, введите имя столбца «Square Root» в поле ввода имени столбца.
  2. После этого введите приведенную ниже формулу в поле ввода формулы настраиваемого столбца и нажмите OK.
  • Теперь у нас есть новый столбец с квадратными корнями из числа, которое мы имеем в первом столбце.
  • Отсюда вам нужно удалить первый столбец исходных значений. Итак, щелкните по нему правой кнопкой мыши и выберите удалить.
  • После этого перейдите на вкладку «Домашняя страница» и нажмите «Закрыть и загрузить».
  • Здесь открывается окно для загрузки данных. Прежде всего, выберите существующий рабочий лист и добавьте диапазон B1.Во-вторых, отметьте галочкой «Добавить в модель данных».

  Как я уже сказал, эта таблица динамическая.

  Когда вы вводите новое значение в исходную таблицу данных, оно автоматически вычисляет квадратный корень в вашей новой таблице при ее обновлении.

  И мы здесь не используем никаких формул.

  [Бонусный совет] Как добавить квадратный корень в Excel

  После вычисления квадратного корня из числа следующее, что вы можете сделать, это добавить квадратный корень.

  И для этого у нас есть два разных способа.

  №1. Использование сочетания клавиш

  Простым способом добавления символа квадратного корня является сочетание клавиш Alt + 251.

  При вводе 251 на цифровой клавиатуре необходимо удерживать нажатой клавишу Alt. и как только вы отпустите клавишу Alt, появится символ.

  №2. Добавление квадратного корневого символа путем применения пользовательского форматирования

  Это наиболее эффективный способ добавления символа.

  Все, что вам нужно сделать, это выбрать все ячейки, открыть параметр пользовательского форматирования и добавить форматирование на панель ввода форматирования.

  № 3. VBA для добавления квадратного символа

  Вы также можете использовать приведенный ниже код VBA, чтобы применить настраиваемое форматирование ко всем ячейкам в выделенном фрагменте.

  Sub Radical ()

  Selection.NumberFormat = ChrW (8730) & «General»

  End Sub

  Примечание: Преимущество использования методов # 2 и # 3 в том, что вам не нужно добавлять символ ко всем ячейкам одну за другой, и когда вы добавляете символ в ячейку, значение в ячейке становится текстом и не может использоваться в дальнейшем как число.

  Образец файла

  Загрузите этот образец файла отсюда

  Заключение

  Если вы просто хотите узнать квадратный корень числа, тогда метод VBA является лучшим, выберите ячейку и запустите код.

  В противном случае формулы лучше всего подходят, если вам нужно использовать значение квадратного корня в дальнейших вычислениях, и у нас есть три разные формулы в этом списке.

  Power Query — это динамический метод, и его необходимо попробовать.

  А теперь скажите мне одну вещь.

  Какой ваш любимый метод вычисления квадратного корня в Excel?

  Поделитесь со мной своим мнением в разделе комментариев, я хотел бы услышать от вас. И не забудьте поделиться этим списком со своими друзьями, я уверен, они это оценят.

  Вы должны прочитать это Далее

  1. Рассчитать коэффициент в Excel: Когда дело доходит до Excel, у нас нет какой-либо конкретной единственной функции, которая могла бы помочь нам рассчитать коэффициент. Но вы можете рассчитать его, используя некоторые пользовательские формулы […]
  2. Средневзвешенное значение в Excel: Но я обнаружил, что лучший способ — использовать формулу, комбинируя функции СУММПРОИЗВ и СУММ. Этот метод прост и удобен в применении […]
  3. Сложные проценты в Excel: Сложные проценты — один из наиболее важных финансовых расчетов, который большинство из нас часто выполняет в своей работе. И необходимо научиться вычислять его в Excel […]
  4. Вставить / ввести символ степени в Excel: если вы используете ноутбук, как я, вы обнаружите, что нет клавиши для ввода символа степени.Работая с некоторыми данными, я обнаружил, что в Excel вы можете ввести их пятью разными способами […]
  5. Умножение с помощью специальной вставки: Иногда в Excel вам нужно выполнить несколько быстрых вычислений. И вы можете использовать специальную пасту для этих быстрых вычислений вместо формул […]
  6. Расчет возраста в Excel: В Excel, используя DOB человека, вы можете вычислить его / ее возраст с помощью функции РАЗНДАТ […]
  7. Среднее значение ТОП-5 в Excel: чтобы усреднить 5 лучших результатов из списка, вы можете использовать формулу, основанную на комбинации НАИБОЛЬШИХ и СРЕДНИХ […]

  Пунит использует Excel еще со времен учебы в колледже. Он помог тысячам людей понять возможности электронных таблиц и изучить Microsoft Excel. Вы можете найти его в Интернете, в Твиттере об Excel, на беговой дорожке или иногда в походе в гору.

  Создание математических выражений без прогнозирования в EquatI

  Последнее изменение: пятница, 21 августа 2020 г., 10:17:53 BST

  Только начинаете работать с EquatIO ? Вот несколько быстрых инструкций, которые помогут начать вставку математических формул в документы Google без использования Math Prediction . Обратите внимание: Это не полный список. Обязательно ознакомьтесь с нашими видеоуроками для EquatIO или ознакомьтесь с Вставка геометрических символов !

  В этой статье будет рассказано о вставке показателя степени, создании дробного или смешанного числа, квадратного корня и подстрочного индекса, а также перечисляются некоторые дополнительные команды.), чтобы переместить курсор в слот для экспоненты, где затем можно вставить показатель степени.Когда вы закончите, используйте клавишу со стрелкой вправо (⇨), чтобы выйти из слота экспоненты и продолжить вводить уравнение.

  Итак, допустим, мы хотим показать теорему Пифагора:

  Для подстрочного индекса используйте клавишу подчеркивания (_) для ввода подстрочного индекса. Снова используйте клавишу со стрелкой вправо (⇨), когда закончите вводить нижний индекс, чтобы завершить оставшуюся часть уравнения.

  Так, например, мы можем записать химическую формулу молекулы воды:

  Дроби и смешанные числа

  Чтобы вставить простую дробь, просто введите числитель, нажмите клавишу /, затем введите знаменатель.Используйте клавишу со стрелкой вправо (⇨), чтобы продолжить ввод остальной части уравнения.

  Итак, если бы мы хотели сложить несколько дробей, это выглядело бы так:

  Мы также можем немного усложнить эти дроби, добавив несколько членов к числителю или знаменателю.

  Для этого просто введите числитель, выделите или выберите его, а затем нажмите клавишу /, чтобы вставить дробь.

  Когда вы закончите вводить члены в знаменателе, используйте клавишу со стрелкой вправо (⇨), чтобы перейти к остальной части уравнения.

  Квадратный корень

  Чтобы вставить квадратный корень, просто введите \ sqrt, а затем нажмите клавишу Enter или Tab, чтобы вставить символ квадратного корня. Затем просто введите число или выражение, которое вы хотите включить под квадратный корень. По завершении используйте клавишу Enter, чтобы продолжить ввод остальной части уравнения.

  Так, например, если мы хотим записать квадратный корень из 16, это будет выглядеть так:

  Дополнительные команды

  \ div = знак деления

  \ times = знак умножения

  \ cdot = знак умножения точки

  \ pi = символ пи

  греческих символов

  \ sqrt [3] = кубический корень

  \ sqrt [n] = корень n-й степени

  Как найти квадратный корень иррационального числа

  Обновлено 21 декабря 2020 г.

  Лиза Мэлони

  Иррациональное число не так страшно, как кажется; это просто число, которое не может быть выражено в виде простой дроби или, другими словами, иррациональное число — это бесконечное десятичное число, которое продолжается бесконечное количество разрядов после десятичной точки.Вы можете выполнять большинство операций с иррациональными числами так же, как с рациональными числами, но когда дело доходит до извлечения квадратного корня, вам придется научиться приближать значение.

  Что такое иррациональное число?

  Так что же такое иррациональное число? Возможно, вы уже знакомы с двумя очень известными иррациональными числами: π или «пи», которое почти всегда сокращается до 3,14, но на самом деле продолжается до бесконечности вправо от десятичной точки; и «е», а.к.а. Число Эйлера, которое обычно сокращается до 2,71828, но также продолжается до бесконечности вправо от десятичной точки.

  Но существует гораздо больше иррациональных чисел, и вот простой способ определить некоторые из них: если число под знаком квадратного корня не является точным квадратом, то этот квадратный корень является иррациональным числом.

  Это ужасно громоздко, так что вот пример, чтобы прояснить ситуацию. Также полезно помнить, что полный квадрат — это число, квадратный корень которого является целым числом:

  Является ли √8 иррациональным числом? Если вы запомнили свои идеальные квадраты или потратили время на их поиск, вы узнаете, что

  \ sqrt {4} = 2 \ text {и} \ sqrt {9} = 3

  Так как √8 находится между этими двумя числами, но нет целого числа от 2 до 3, которое было бы его корнем, √8 иррационально.

  Извлечение квадратного корня из иррационального числа

  Когда дело доходит до вычисления квадратного корня из иррационального числа, у вас есть два варианта. Либо введите иррациональное число в калькулятор, либо в онлайн-калькулятор квадратного корня (см. Ресурсы), и в этом случае калькулятор вернет вам приблизительное значение, либо вы можете использовать четырехэтапный процесс, чтобы оценить значение самостоятельно.

  Пример 1: Оцените значение иррационального числа √8.

  Найдите идеальные квадраты по обе стороны от √8 на числовой прямой. В этом случае √4 = 2 и √9 = 3. Выберите тот, который ближе всего к вашему целевому числу. Поскольку 8 намного ближе к 9, чем к 4, выберите

  \ sqrt {9} = 3

  Затем разделите число, корень которого вы хотите — 8, на вашу оценку. Продолжая пример, у вас есть:

  \ frac {8} {3} = 2,67

  Теперь найдите среднее значение результата из шага 2 с делителем из шага 2.Здесь это означает усреднение 3 и 2,67. Сначала сложите два числа, а затем разделите их на два:

  3 + 2,67 = 5,6667

  (На самом деле это повторяющееся десятичное число 5,6666666666, но для краткости оно было округлено до четырех десятичных знаков)

  \ frac {5.6667} {2} = 2.83335

  Результат шага 3 все еще неточный, но приближается. При необходимости повторите шаги 2 и 3, каждый раз используя результат из шага 3 в качестве нового делителя на шаге 2.

  Чтобы продолжить пример, вы должны разделить 8 на результат шага 3 (2,83335), что даст вам:

  \ frac {8} {2,83335} = 2,8235

  (опять же, округление до четырех десятичных знаков ради краткости.)

  Затем вы усредните результат вашего деления с делителем, что даст вам:

  2,83335 + 2,8235 = 5,65685 \\ \, \\ \ frac {5,65685} {2} = 2,828425

  Можно продолжайте этот процесс, повторяя шаги 2 и 3 по мере необходимости, пока ответ не будет настолько точным, насколько вам нужно.

  А как насчет иррациональных квадратных корней?

  Иногда вместо того, чтобы найти квадратный корень из иррационального числа, вам нужно иметь дело с иррациональными числами, которые выражаются в форме квадратного корня — одно из самых известных, о которых вы узнаете, — √2.

  С √2 мало что можно сделать, кроме приближения его значения, как описано выше. Но если вы получаете большее иррациональное число в форме квадратного корня, вы можете иногда использовать тот факт, что

  \ sqrt {cd} = \ sqrt {c} × \ sqrt {d}

  , чтобы переписать ответ в более простой форме.