Как составить пропорции: Как составить и рассчитать пропорцию: онлайн калькулятор

Как составить и рассчитать пропорцию: онлайн калькулятор

Содержание

Онлайн калькулятор пропорций

Формула пропорций

Пропо́рция — это равенство двух отношений, когда a:b=c:d

средние
		╭	члены	╮
1	:	10	=	7	:	70
╰	крайние члены					╯

0,1			=	0,1

1 10 = 7 70

Основные свойства пропорции

Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c

1
10 ✕ 7
70

1 ⋅ 70 = 10 ⋅ 7

Обращение пропорции: если a:b=c:d, то

b:a=d:c

Перестановка средних членов: если a:b=c:d, то a:c=b:d

Перестановка крайних членов: если a:b=c:d, то d:b=c:a

Решение пропорции с одним неизвестным | Уравнение

1 : 10 = x : 70



1
10 = x
70

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение

x = 1 ⋅ 70
10 = 7

Как посчитать пропорцию

Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?

Составим пропорцию:
1 таблетка — 10 кг
 x таблеток — 70 кг

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение:
1 таблетка
x таблеток ✕ 10 кг
70 кг

x = 1 ⋅ 70 : 10 = 7

Ответ: 7 таблеток

Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?

Составим пропорцию:
2 статьи — 5 часов 
x статей — 20 часов

x = 2 ⋅ 20 : 5 = 8

Ответ: 8 статей

Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.

Составить пропорцию

Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:

что тоже самое (это разная форма записи).

Пример:

Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).

Основное правило пропорции:

a:b=c:d

произведение крайних членов равно произведению средних

то есть

a∙d=b∙c

*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.

Если рассматривать форму записи вида:

то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали

a∙d=b∙c

Как видите результат тот же.

Если три элемента пропорции известны, то мы всегда можем найти четвёртый.

Именно в этом суть пользы и необходимость пропорции при решении задач.

Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:

Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.

Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:

1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях «Задачи на проценты. Часть 1!» и «Задачи на проценты. Часть 2!».

2. Многие формулы заданы в виде пропорций:

> теорема синусов

> отношение элементов в треугольнике

> теорема тангенсов

> теорема Фалеса и другие.

3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.

4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:

— часы в минуты (и наоборот).

— единицы объёма, площади.

— длины, например мили в километры (и наоборот).

— градусы в радианы (и наоборот).

здесь без составления пропорции не обойтись.

Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:

Необходимо определить число, которое составляет 35% от 700.

В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:

Можно сказать, что семисот тридцати пяти соответствует 100 процентов.

Иксу соответствует 35 процентов. Значит,

700 – 100%

х – 35 %

Решаем

Ответ: 245

Переведём 50 минут в часы.

Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие — x часов это 50 минут. Значит

1 – 60

х – 50

Решаем:

То есть 50 минут это пять шестых часа.

Ответ: 5/6

Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?

Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:

Одной миле соответствует 1,6 километра.

Икс миль это три километра.

1 – 1,6

х – 3

Ответ: 1,875 миль

Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.

Переведём 65 градусов в радианную меру.

Главное это запомнить, что 180 градусов это Пи радиан.

Обозначим искомую величину как х. Устанавливаем соответствие.

Ста восьмидесяти градусам соответствует Пи радиан.

Шестидесяти пяти градусам соответствует х радиан.

Если записать отношение в общем виде, то получится

То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.

Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!

Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!

Всего доброго!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Определение пропорции, задачи на пропорцию

Пропо́рция – равенство двух отношений, т. е. равенство вида

a : b = c : d, или, в других обозначениях, равенство $\frac{a}{b}=\frac{c}{d}$

Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции.

От « пропорции» никуда не деться, без нее не обойтись во многих задачах. Выход только один – разобраться с этим отношением и пользоваться пропорцией как палочкой-выручалочкой.

Прежде чем приступать к рассмотрению задач на пропорцию, важно вспомнить основное правило пропорции:

В пропорции $\frac{a}{b}=\frac{c}{d}$

произведение крайних членов равно произведению средних

$a\cdot d=b\cdot c$

Если какая-то величина в пропорции неизвестна, ее легко будет найти, опираясь на это правило.

Например,

или

То есть неизвестная величина пропорции – значении дроби, в знаменателе которой – то число, которое стоит напротив неизвестной величины, в числителе – произведение оставшихся членов пропорции (независимо от того, где эта неизвестная величина стоит).

Задача 1.

Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение:+ показать

Мы понимаем, что уменьшение веса семени во сколько-то раз, влечет за собой уменьшение веса получаемого масла во столько же раз. То есть величины связаны прямой зависимостью.

Заполним таблицу:

Неизвестная величина – значение дроби $\frac{7\cdot 5,1}{21}$ , в знаменателе которой – 21 – величина, стоящая напротив неизвестного в таблице, в числителе – произведение оставшихся членов таблицы-пропорции.

Поэтому получаем, что из 7 кг семени выйдет 1,7 кг масла.

Ответ: 1,7
Чтобы правильно заполнять таблицу, важно помнить правило:
Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д

Задача 2.
Перевести $80^{\circ}$ в радианы.
Решение:+ показать
Мы знаем, что $180^{\circ}=\pi$ . Заполним таблицу:
Откуда $80^{\circ}=\frac{80\cdot \pi}{180}=\frac{4\pi}{9}$
Ответ: $\frac{4\pi}{9}$

Задача 3.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27?
Решение: + показать

Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Решение: + показать
Все поле составляет 100%, и поскольку вспахано 82%, то осталось вспахать 100%-82%=18% поля.
Заполняем таблицу:
Откуда получаем, что все поле составляет $\frac{9\cdot100}{18}=50$ (га).
Ответ:

А следующая задача – с засадой.
Задача 5.
Расстояние между двумя городами пассажирский поезд прошел со скоростью 80км/ч за 3 часа. За сколько часов товарный поезд пройдет то же расстояние со скоростью 60 км/ч?
Решение: + показать
Если вы будете решать эту задачу аналогично предыдущей, то получите следующее:
время, которое потребуется товарному поезду, чтобы пройти то же расстояние, что и пассажирским, есть $\frac{3\cdot60}{80}=\frac{9}{4}=2,25$ часа. То есть, получается, что идя с меньшей скоростью, он преодолевает (за одно и тоже время) расстояние быстрее, нежели поезд с большей скоростью.
В чем ошибка рассуждений?
До сих пор мы рассматривали задачи, где величины были прямопропорциональны друг другу, то есть рост одной величины во сколько-то раз, дает рост связанной с ней второй величины во столько же раз (аналогично с уменьшением, конечно). А здесь у нас другая ситуация: скорость пассажирского поезда больше скорости товарного во сколько-то раз, а вот время, требуемое на преодоление одного и того же расстояния, требуется пассажирскому поезду меньшее во столько же раз, нежели товарному поезду. То есть величины друг другу обратно пропорциональны.
Схему, которой мы пользовались до сих пор, надо чуть изменить в данном случае.
Решение:
Рассуждаем так:
Пассажирский поезд со скоростью 80 км/ч ехал 3 ч, следовательно, он проехал $80\cdot3=240$ км. А значит товарный поезд это же расстояние преодолеет за ч.
То есть, если бы мы составляли пропорцию, нам следовало бы поменять местами ячейки правой колонки предварительно. Получили бы: $\frac{3\cdot80}{60}=4$ ч.
Ответ: .

Поэтому, пожалуйста, будьте внимательны при составлении пропорции. Разберитесь сначала, с какой зависимостью имеете дело – с прямой или обратной.
Пропорции | Формулы с примерами
Что такое пропорция?
Определение
Пропорция — это верное равенство двух отношений.

Где a ? 0, b ? 0, c ? 0, d ? 0.
a и d — называют крайними членами пропорции;
b и c — называют средними членами пропорции.
Пример

3 = 18 или 3 : 5 = 18 : 30;

5 30

7 = 21 или 7 : 3 = 21 : 9;

3 9

12 = 48 или 12 : 15 = 48 : 60.

15 60

Основное свойство пропорции
Свойство

Произведение крайних членов пропорции равно произведению ее средних членов.
Пример

12 = 24 , значит 12 • 8 = 4 • 24;

4 8

11 = 33 , значит 11 • 21 = 7 • 33;

7 21

23 = 69 , значит 23 • 42 = 14 • 69.

14 42

Обратное свойство
Свойство Пример

11 • 4 = 2 • 22 значит, 11 = 22 ;

2 4

21 • 6 = 42 • 3 значит, 21 = 42 ;

3 6

33 • 21 = 7 • 99 значит, 33 = 99 .

7 21

Производные пропорции
Правило
Пример

4 = 8 или 7 =
14 или 8 = 17 или 4 = 7 ;

7 14 4 8 4 7 8 14

5 = 10 или 6 = 12 или 10 = 12 или 5 = 6 ;

6 12 5 10 5 6 10 12

9 = 18 или 3 = 6 или 6 = 18 или 9 = 3 .

3 6 9 18 3 9 18 6

Правило
! По трем известным членам пропорции всегда можно найти
ее неизвестный член.
Пример

15 = x , значит x = 15 • 14 = 15 • 2 = 30;

7 14 7

21 = x , значит x = 21 • 9 = 21 • 3 = 63;

3 9 3

33 = 99 , значит x = 4 • 99 = 4 • 3 = 12.

4 x 33

Отношения
Определение
Отношением двух чисел a и b называется их частное a : b.
Показывает во сколько раз a больше b или какую часть число a составляет от b.1
Примеры отношений
Пример 1
Отношение числа 16 к числу 4 равно 16 : 4 = 4, т.е. 16 в 4 раза больше чем,
чем 4.
Пример 2
Отношение числа 4 к числу 12 равно 4 : 12 = 13, т.е. 4 составляет треть
от числа 12.
Пример 3
Масса стакана с жидкостью равна 440г. Стакан весит 40г. Какую часть
всей массы составляет масса стакана? Во сколько раз масса стакана с
жидкостью больше массы жидкости?
Решение:
Масса стакана составляет 40 : 440 = 1 11 часть полной массы.
Масса жидкости равна 440 — 40 = 400г; масса стакана с жидкостью больше массы самой жидкости в 440 : 400 = 1,1 раза.
Как решать пропорции ℹ️ правила нахождения неизвестного члена, основные свойства, методы расчетов, примеры задач с вычислениями, онлайн-калькулятор
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.

Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.

Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:

Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].

Перемножение «крест-накрест»: x * z = y * v.

Перестановка: x / v = y / z и v / x = z / y.

Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.

Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.

Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:

Записать функцию.

Рассмотреть составные части.

Если простой тип, перейти к 5 пункту.

Сложная — разложить на простые элементы, а затем перейти к 5 пункту.

Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.

Определить тип линейности, построив график.

По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.

К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:

Записать соотношение пропорции.

Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.

Применить свойство умножения «крест-накрест».

Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.

Решить уравнение.

Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:

Линейные.

Квадратные.

Кубические.

Биквадратные.

Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap² + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b² — 4ac). Корни зависят от его значения:

Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.

При D равном 0 (один): р = (-b) / 2a.

Если D < 0, то решений нет.

Решение уравнений кубического и биквадратного видов сводятся к разложению на множители. В результате этого происходит понижение степени до двойки. Кроме того, эффективным методом нахождения корней считается введение замены переменной.

Пример решения
Решение уравнений в виде пропорции осуществляется по такому же принципу. При этом рекомендуется использовать любые свойства. Необходимо проходить процесс обучения постепенно. Начинать нужно с простых примеров, а затем практиковаться на сложных заданиях. Первый тип был рассмотрен выше на примере sin (p).
Итак, необходимо решить уравнение [(t — 5) / (t — 2)] = [(t — 5) / (t — 1)]. Для начала следует определить тип функций каждого из элементов. Просмотрев список нелинейных выражений, можно сделать вывод о том, что все члены пропорции являются линейными. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.
Затем следует воспользоваться третьим пунктом алгоритма: (t — 5)(t — 1) = (t — 2)(t — 5). Если раскрыть скобки, то должно получиться такое равенство: t² — t — 5t + 5 =t² -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t² — t — 5t + 5 + 5t — t² — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.

Пропорция
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение  равно отношению
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Предположим, что в классе 10 девочек и 5 мальчиков
Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки
Теперь рассмотрим другой класс в котором две девочки и один мальчик
Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:
Можно сделать вывод, что отношение  пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам
а также отношение 12 девочек к 2 мальчикам
Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение  не пропорционально отношению .
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция  состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями  и  знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции  разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям

Урок 5. пропорции — Математика — 6 класс
Математика
6 класс
Урок № 5
Пропорции
Перечень рассматриваемых вопросов:
Понятие пропорции.
Основное свойство пропорции.
Как правильно составить пропорцию.
Как найти неизвестный член пропорции.
Тезаурус
Равенство двух отношений называют пропорцией.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Основная литература
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.
Рассмотрим 3 способа нахождения неизвестного члена пропорции.
1 способ.
2 способ.
Способ 3.
Задача.
Решение:
Ответ:
1) можно;
2) можно;
3) нельзя;
4) нельзя.
Разбор решения заданий тренировочного модуля
№1. Тип задания: сортировка элементов по категориям.
№2. Тип задания: Подстановка элементов в пропуски в тексте.
Найдите неизвестный член пропорции.
Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Ответ: 3.
пропорций
Пропорция говорит, что два соотношения (или дроби) равны.
Пример:
То есть 1-на-3 равно 2-на-6
Соотношения одинаковы, поэтому они пропорциональны.
Пример: веревка
Длина каната и вес пропорциональны.
Если 20м каната весит 1кг , то:
40м из этой веревки весит 2 кг
200 м из этой веревки весит 10 кг
и т. Д.
Итак:
20 1 знак равно 40 2
Размеры
Когда фигуры «пропорциональны», их относительные размеры одинаковы.
Здесь мы видим, что отношения длины головы к длине тела одинаковы на обоих рисунках.
Итак, они , пропорциональные .
Слишком длинная или короткая голова будет выглядеть плохо!
Пример: международные форматы бумаги (например, A3, A4, A5 и т. Д.) Имеют одинаковые пропорции:
Таким образом, любое произведение искусства или документ может быть изменен для размещения на любом листе.Очень аккуратный.
Работа с пропорциями
СЕЙЧАС, как мы это используем?
Пример: вы хотите нарисовать голову собаки … как долго это должно быть?
Запишем пропорцию с помощью соотношения 10/20 сверху:
? 42 знак равно 10 20
Сейчас мы решаем это с помощью специального метода:
Умножьте через известные углы
, затем разделите на третье число
И мы получаем это:
? = (42 × 10) / 20
= 420/20
= 21
Итак, вы должны нарисовать голову длиной 21 .
Использование пропорций для решения процентов
Процент — это на самом деле соотношение! Сказать «25%» означает «25 на 100»:
25% = 25 100
Мы можем использовать пропорции для решения вопросов с процентами.
Хитрость заключается в том, чтобы поместить то, что мы знаем, в эту форму:
Часть Всего = процентов 100
Пример: что составляет 25% от 160?
Процент 25, целое 160, и мы хотим найти «часть»:
Часть 160 = 25 100
Умножьте через известные углы, затем разделите на третье число:
Часть = (160 × 25) / 100
= 4000/100
= 40
Ответ: 25% из 160 — это 40.
Примечание: мы могли бы также решить эту проблему, выполнив сначала деление, например:
Деталь = 160 × (25/100)
= 160 × 0,25
= 40
Любой метод работает нормально.
Мы также можем найти проценты:
Пример: что такое 12 долларов в процентах от 80 долларов?
Заполните то, что мы знаем:
12 80 = % 100
Умножьте через известные углы, затем разделите на третье число.На этот раз известные углы вверху слева и внизу справа:
процентов = (12 × 100 долларов США) / 80 долларов США
= 1200/80
= 15%
Ответ: 12 $ — 15% из 80
или найти целое:
Пример: цена продажи телефона составляла 150 долларов, что составляло всего 80% от обычной цены. Какая была нормальная цена?
Заполните то, что мы знаем:
150 Всего = 80 100
Умножьте через известные углы, затем разделите на третье число:
Всего = ($ 150 × 100) / 80
= 15000/80
= 187.50
Ответ: нормальная цена телефона была $ 187.50
Использование пропорций для решения треугольников
Мы можем использовать пропорции для решения подобных треугольников.
Пример: какого роста дерево?
Сэм пытался использовать лестницу, рулетку, веревки и другие вещи, но все еще не мог понять, каково было высокое дерево.
Но тогда у Сэма есть умная идея … похожие треугольники!
Сэм измеряет палку и ее тень (в метрах), а также тень дерева, и вот что он получает:
Теперь Сэм делает набросок треугольников и записывает соотношение «Высота к длине» для обоих треугольников:
Высота: Длина тени: ч 2.9 м = 2,4 м 1,3 м
Умножьте через известные углы, затем разделите на третье число:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 м (с точностью до 0,1)
Ответ: дерево 5,4 м высотой.
И ему даже не понадобилась лестница!
«Высота» могла бы быть внизу, если бы она была снизу для ОБА соотношения, например:
Давайте попробуем соотношение «Длина тени к высоте»:
Длина Тени: Высота: 2.9 м ч = 1,3 м 2,4 м
Умножьте через известные углы, затем разделите на третье число:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 м (с точностью до 0,1)
Это тот же расчет, что и раньше.
A «Бетон» Пример
Отношения могут иметь больше, чем два числа !
Например, бетон изготавливается путем смешивания цемента, песка, камней и воды.
Типичная смесь цемента, песка и камней записывается в виде соотношения, например, 1: 2: 6.
Мы можем умножить все значения на одну и ту же сумму и при этом иметь одинаковое соотношение.
10:20:60 соответствует 1: 2: 6
Итак, когда мы используем 10 ведер цемента, мы должны использовать 20 песка и 60 камней.
Пример: вы только что положили 12 ведер камней в смеситель, сколько цемента и сколько песка вы должны добавить для приготовления смеси 1: 2: 6?
Давайте выложим это в стол, чтобы было понятнее:
Цемент Песок Камни
Необходимое соотношение: 1 2 6
у вас есть: 12
У вас есть 12 ведер камней, но соотношение говорит 6.
Это нормально, у вас просто вдвое больше камней, чем в соотношении … поэтому вам нужно вдвое больше, чем всего , чтобы сохранить соотношение.
Вот решение:
Цемент Песок Камни
Необходимое соотношение: 1 2 6
у вас есть: 2 4 12
И соотношение 2: 4: 12 такое же, как 1: 2: 6 (потому что они показывают те же относительно размеров)
Итак, ответ: добавьте 2 ведра цемента и 4 ведра песка. (Вам также понадобится вода и много помешивать ….)
Почему у них одинаковое соотношение? Хорошо, соотношение 1: 2: 6 говорит о том, что :
вдвое больше песка, чем цемента (1: 2: 6)
В 6 раз больше камней, чем цемента (1: 2: 6)
В нашем миксе у нас есть:
вдвое больше песка, чем цемента (2: 4: 12)
В 6 раз больше камней, чем цемента (2: 4: 12)
Так и должно быть!
Это хорошая вещь в отношениях.Вы можете увеличивать или уменьшать суммы, при условии, что относительные размеры одинаковы, а соотношение одинаково.
,
Соотношения и пропорции | Как решить (видео и примеры) // Tutors.com
Соотношения и пропорциональные отношения
Соотношения и пропорции — это похожие фигуры и понятия, которые так же легко спутать, как жабы и лягушки (все жабы — лягушки, но не все лягушки — жабы). Соотношения сравнивают значения, а соотношения сравнивают соотношения.
Какие коэффициенты?
Что такое пропорции?
Как решить пропорции и пропорции
Проблемы со словами
Примеры
Практика
Какие коэффициенты?
Коэффициенты сравнивают значения.Вы можете сравнить количество шатенок с количеством блондинок, или с количеством карандашей в классе, или с количеством шатенок, или … ну, вы поняли. Соотношения сравнивают значения одних и тех же вещей или разных вещей.

Скажем, у вас есть 10 шатенок в классе и 6 блондинок в одном классе. Вы можете установить шесть различных соотношений:
1016: шатенки всем девочкам
610: блондинистые девушки и шатенки
616: блондинки всем девочкам
106: шатенка с блондинкой
1610: все девушки — шатенки
166: все девушки для блондинки
$Ratios & Proportions proper or improper fractions$
Три из этих соотношений являются неправильными дробями; это нормально! Соотношения могут быть записаны как правильные или неправильные дроби.Они также могут быть написаны точкой с запятой, например:
10:16
6:10
6:16
10: 6
16:10
16: 6
Что такое пропорции?
Когда вы сравниваете два отношения, вы используете пропорции . Вы спрашиваете, является ли первое соотношение таким же, меньшим или большим, чем второе. Сравните соотношение коричневых и всех девушек и белокурых девушек:
1016 = 616
10:16 = 6:16

Вы можете видеть, что эти два отношения равны , а не , поэтому они пропорциональны , а не :
1016 16 616
10:16 ≠ 6:16
Как решить пропорции и пропорции
Как бы выглядели пропорциональные дроби? Давайте добавим в класс восемь домашних животных: 5 хомяков и 3 лягушки.Коэффициенты , которые вы можете создать:

5: 3 (хомяки лягушкам)
3: 5 (лягушки хомякам)
5: 8 (хомяки всем домашним животным)
3: 8 (лягушки всем домашним животным)
8: 5 (все питомцы хомякам)
8: 3 (все питомцы лягушки)
Пропорции могут сказать нам, равны ли два отношения или нет. Сравните соотношение хомяков ко всем домашним животным и соотношение шатенок ко всем девочкам:
58 = 1016
5: 8 = 10:16
Вы можете проверить эти дроби несколькими способами, например, путем упрощения 1016 до 58 или путем умножения и деления: 5 × 1610 = 8.
Эти два соотношения пропорциональны друг другу. Соотношение хомяков к питомцам всех классов такое же, как и отношение шатенок ко всем девочкам в классе:
58 = 1016
5: 8 = 10:16
Соотношения и пропорции Задачи на слово
Кулинария, сравнение цен, вождение, инжиниринг, строительство и финансы — это лишь некоторые области, в которых соотношения и пропорции работают каждый день.
Решающие пропорции | Wyzant Resources
Пропорции — это в основном дроби с переменными. Вам нужно будет решить пропорцию для того, чтобы завершить соотношение. Например, вам могут дать дробь или процент чего-то, а затем попросил найти часть целого, или общую сумму этого То же самое, используя уже предоставленную вам дробную часть. Это где переменная приходит в; Вам будет предложено найти переменную с использованием кросс-умножения.После кросс-умножения у вас будет настроено уравнение, которое вы будете в состоянии решить.
Пропорция выглядит так:

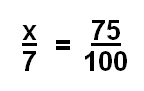
Другой способ сказать, что это будет «Что такое 75% от 7?» Мы знаем, что это означает то же самое вещь, потому что наша вторая дробь — 75/100, которая может быть легко записана в процентах; тогда мы ищем часть (х) целого, 7.Теперь, чтобы решить эту пропорцию, Вы должны пересечь умножить. Чтобы умножить умножение, нужно умножить числитель первой дроби знаменателем второй дроби, а затем вы умножаете знаменатель первой дроби по числителю второй дроби. это будет включать в себя умножение переменных. После того, как вы умножили оба раза, вы установите два числа (одно число, одно переменное число), вы установите эти два равными друг другу.Работа для этих шагов будет выглядеть так:
Шаг первый (умножение числителя на первую дробь и знаменателя второй фракции) в оранжевом.
Шаг второй (умножение знаменателя на первую дробь и числитель второй фракции) находится в воде.
И, третий шаг ниже умножения дроби; это показывает вам, как установить до уравнения, которое вы будете решать дальше.
Теперь после кросс-умножения нужно решить уравнение. В таком случае, уравнение нормальное, и вы можете решить, разделив каждую сторону на 100 (чтобы получить х в одиночестве). Если вам нужна дополнительная помощь в решении уравнений, пожалуйста, прочитайте о решение уравнений с переменными.

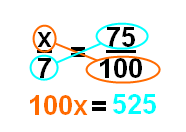
Разделив каждую сторону на 100, вы получите х = 5,25; это говорит вам, что 5.25 это 75% из 7.
Давайте попробуем это снова. На этот раз мы поместим переменную внизу.

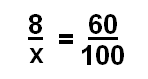
Теперь нам нужно завершить кросс-умножение, что означает, что мы умножаем числитель первой дроби знаменателем второй дроби, а затем умножить знаменатель первой дроби по числителю второй дроби. Хорошо покажите это снова оранжевым цветом и цветом морской волны, как мы это делали в первом примере.

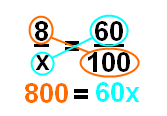
После того, как вы сделаете кросс-умножение, у вас есть простое уравнение для решения с помощью разделение. Вы бы поделили каждую сторону уравнения на 60, чтобы получить х отдельно. С другой стороны, 800, деленное на 60, равно 13,3 (повторяющийся десятичный) или 13 1/3. Решение этого уравнения означает, что 8 составляет 60% от 13,3.
Пока что мы сделали только пропорции, которые были в процентах, а это означает, что второй дробь — это число в качестве числителя, а в качестве знаменателя — 100 (процент).Тем не мение, возможность иметь две фракции вместе, ни одна из них не является процентов, тоже очень реалистично. Мы приведем вам пример этого, и затем дать вам несколько примеров, прежде чем перейти к решению проблем, связанных с пропорции.

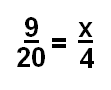
На этот раз переменная находится во второй дроби, но не позволяйте этому сбить вас с толку! Вы собираетесь пересекать умножение, как обычно, чтобы вы могли настроить свое уравнение.Мы покажем перекрестное умножение, еще раз, в оранжевом и голубом, чтобы вы может следовать за

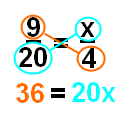
Теперь у вас есть уравнение, которое вы можете снова решить, используя деление. Делить каждая сторона на 20, чтобы получить х один, и увидеть, что х = 1,8.
Вот несколько примеров для вас. Когда вы решите уравнение, введите свой ответ в коробку, чтобы проверить это.Если у вас есть десятичный ответ, округлите его до ближайшего десятый (.1).
Решить для х:

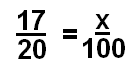
Во-первых, перемножить умножение (показано здесь оранжевым и зеленым цветом), чтобы получить исходное уравнение, что 1700 = 20x

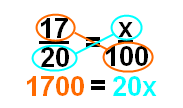
Теперь все, что осталось сделать, это разделить каждую сторону на 20 (чтобы получить х отдельно).однажды вы делите каждую сторону на 20, вы получаете 85. Это означает, что 17 — это 85% от 20.
Окончательный ответ: 85.
85
Решить для х:

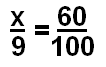
Во-первых, перемножить умножение (показано здесь оранжевым и зеленым цветом), чтобы получить исходное уравнение, что составляет 100x = 540

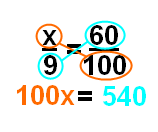
Теперь все, что осталось сделать, это разделить каждую сторону на 100 (чтобы получить х отдельно).однажды Вы делите каждую сторону на 100, вы получаете 5,4, что означает, что 5,4 составляет 60% от 9.
Окончательный ответ: 5,4
{5,4 | 5,40}
Когда использовать пропорции
Мы используем пропорции, чтобы найти проценты и дробные части других чисел, как а также для завершения отношений.Это означает, что иногда вы получите дробь и затем часть или все число, и вас попросят найти соответствующую часть или целое.
Например, вы можете получить следующее как проблему пропорции: один из каждого шесть яблок фермера Джо гнилые. Всего у него 440 яблок. Сколько гнилых?
Мы можем установить это как пропорцию. У нас есть соотношение гнилых яблок: общее количество яблок, что составляет 1: 6 или 1/6.Это будет одна из наших фракций. Теперь нам нужно создать другая фракция, включая переменную. Мы знаем, что у него всего 440 яблок, так что это число будет идти в нижней части дроби (так как это всего). Мы будем использовать переменную x в качестве числителя для этой дроби. Теперь у нас есть оба дроби, поэтому мы устанавливаем нашу пропорцию следующим образом:

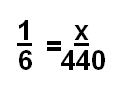
Наш следующий шаг — это умножение.Мы собираемся использовать апельсин и аква, чтобы показать это шаг. Как только мы пересекаем умножение, мы устанавливаем два продукта равными друг другу в порядке установить уравнение, как это:

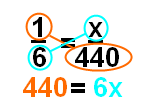
Теперь ваше уравнение имеет вид 440 = 6x, так что вы можете решить его как обычно, разделив каждое сторону 6. Как только вы это сделаете, вы увидите, что х = 73,3 (повторяется), что вы можете округлить до 73,3. Теперь давайте подумаем об этом ответе на секунду.Обычно при общении с целыми элементами мы округляем до ближайшего целого числа. Технически, 73,3 будет округляться до 73. Тем не менее, мы измеряем что-то гнилое. Если 73 целые яблоки, и 1/3 (.3) другого яблока гнилая, мы должны были бы округлить (чтобы 74) и сообщают, что яблоко гнилое. Это потому, что даже частично гнилой яблоко гнилое! Таким образом, наш окончательный ответ будет таким: 74 из 440 яблок гнилые.
Многие пропорции, как и в предыдущем примере, требуют умения настраивать и решать пропорции, но также требуют, чтобы вернуться и посмотреть на ответ, чтобы убедиться, это имеет смысл в связи с заданным вопросом.Особенно при работе на пропорциях иметь дело с людьми — вы не можете иметь дробную или десятичную часть человека! Это всегда хорошая идея, чтобы вернуться и перепроверить свой ответ, чтобы убедиться, что он делает смысл.
Давайте попробуем еще одно слово проблема с пропорциями. В театре FXT есть 35 ряды с 14 стульями в каждом ряду. Если 12 из каждых 14 стульев заполнены, сколько человек сидите в театре FXT?
Это немного сложнее.У нас есть наше соотношение, которое описывает заполненные стулья к Всего стульев — это 12:14 или 12/14. Теперь мы должны выяснить, сколько всего стулья есть. Мы знаем количество рядов и количество стульев в каждом ряду, поэтому мы можем использовать простое умножение, чтобы выяснить, сколько всего стульев. Мы умножаем 35 x 14, чтобы получить 490 — так что мы знаем, что всего 490 стульев. Сейчас, нам нужно выяснить, сколько стульев заполнено, используя это соотношение (12/14) в качестве нашего основа.Мы бы установили пропорцию так:

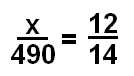
Теперь все отсюда. Вы бы умножить умножение, чтобы получить уравнение, как это:

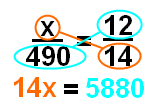
После того, как вы получите свое уравнение, вы можете разделить на число перед х, которое является 14 в этом случае. Итак, разделите каждую сторону уравнения на 14 и получите х = 420. Теперь не забудьте вернуться и убедиться, что этот ответ имеет смысл.Мы искали, чтобы найти количество стульев, которые заполнены в театре, и мы знаем, что соотношение (в дробной форме) — 12/14, поэтому мы ожидаем, что большинство стульев будет заполнено Рассматривая наш ответ, мы видим, что 420 из 490 стульев заполнены, что быть большинством из них. Таким образом, этот ответ имеет смысл.
Теперь вот один для вас, чтобы практиковать самостоятельно.
LaWanda устраивает вечеринку.Она хочет заказать еду, которую большинство ее гостей есть. Она приглашает 80 человек и хочет получить пиццу. 19 из 20 человек, которые едят пиццу Сколько не будете есть пиццу?
Чтобы выяснить, сколько не съест пиццы, сначала нужно выяснить, сколько людей будет съесть пиццу.Во-первых, мы устанавливаем пропорцию с использованием дробного часть людей, которые едят пиццу (19/20), а затем мы устанавливаем ее равной переменной (х) на общее количество человек (80). После этого мы пересекаем умножение, чтобы получить наше уравнение, как это:

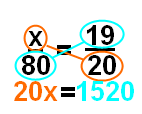
Затем мы должны решить уравнение делением, поэтому мы разделим каждую сторону на 20 чтобы получить х один.Мы получаем х = 76. Мы оглядываемся назад, чтобы убедиться, что это имеет смысл — число меньше 80, но близко к 80; так же, как 19 близко к 20, но меньше чем 20. Таким образом, мы можем сделать вывод, что этот ответ имеет смысл.
Теперь у нас есть последний шаг. Мы пришли к выводу, что 76 человек будут есть пиццу. Но Вопрос спрашивает, сколько будет , а не съесть пиццу.Поэтому мы можем взять общее (80) и вычтите людей, которые будут есть пиццу (76), и получите ответ из 4 человек, которые не будут есть пиццу.
Окончательный ответ: 4 человека.
{4 | 4 человека}
,
Навигация по записям
Previous Post:Роллы на окно – — — , , 420 ., ,
Next Post:Полки с гипсокартона – Ой!