Как умножать целые числа на десятичные: Ошибка 403 — доступ запрещён

Содержание

Как умножить десятичную дробь на натуральное число — Математика для школьников

Оставьте комментарий / От Светлана Михайловна / 11.06.2017 27.01.2018

Рассмотрим, как умножить десятичную дробь на натуральное число.

Правило умножения числа на десятичную дробь

Чтобы умножить десятичную дробь на натуральное число:

1) Умножаем числа, не обращая внимания на запятую.

2) В результате отделяем после запятой столько цифр, сколько их после запятой в десятичной дроби.

Примеры.

Выполнить умножение десятичных дробей на натуральные числа:

1) 12,3∙4;

2) 34,07∙3;

3) 0,54∙25;

4) 52,783∙34;

5) 0,00078∙12.

Решение:

1) 12,3∙4=?

Чтобы умножить десятичную дробь 12,3 на натуральное число 4, сначала умножаем эти числа, не обращая внимания на запятую, то есть умножаем 123 на 4: 123∙4=492.

В полученном произведении отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 12,3, то есть одну цифру: 49,2. Таким образом, 12,3∙4=49,2.

2) 34,07∙3=?

Умножаем числа, не обращая внимания на запятую: 3407∙3=10221.

В результате отделяем после запятой столько цифр, сколько их в десятичной дроби 34,07, то есть две: 102,21.

Таким образом, 34,07∙3=102,21.

3) 0,54∙25=?

Сначала умножим эти числа, не принимая во внимания запятую: 54∙25=1350.

Затем отделяем после запятой столько цифр, сколько их после запятой в десятичной дроби 0,54, то есть две цифры: 13,50. В конце записи после запятой стоит нуль, его следует отбросить:

0,54∙25=13,50=13,5.

4) 52,783∙34=?

Умножаем числа, отбросив запятую: 52783∙34=1794622.

Так как в записи десятичной дроби 52,783 после запятой стоит три цифры, в полученном произведении после запятой также должно стоять три цифры: 1794,622.

Итак, 52,783∙34=1794,622.

5) 0,00078∙12=?

Умножение десятичной дроби на натуральное число заменяем умножением натуральных чисел: 78∙12=936.

Теперь нужно отделить после запятой столько цифр, сколько их после запятой в десятичной дроби 0,00078, то есть пять цифр: 0,00936.

В результате имеем: 0,00078∙12=0,00936.

Поскольку от перемены мест множителей произведение не меняется (переместительное свойство умножения), умножение числа на натуральную дробь проводят точно так же.

Примеры.

Выполнить умножение натуральных чисел на десятичные дроби:

1) 958∙0,007;

2) 31∙0,000046;

Решение:

1) 958∙0,007=?

Умножаем натуральные числа 958 и 7 ( то есть не обращаем внимания на запятую): 958∙7= 6706.

В полученном произведении отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 0,007, то есть три цифры: 6,706.

Таким образом, 958∙0,007=6,706.

2) 31∙0,000046=?

Умножение числа на десятичную дробь заменяем умножением натуральных чисел: 31∙46=1426.

В результате отделяем после запятой столько цифр, сколько их после запятой в записи десятичной дроби 0,000046, то есть шесть цифр: 0,001426 (недостающее количество цифр дополняем двумя нулями и перед запятой также пишем нуль).

Итак, 31∙0,000046=0,001426.

Для умножения десятичных дробей на 10, 100, 1000 и т.д. проще использовать другие правила.

Умножение десятичных дробей: как умножить десятичную дробь на натуральное число

Как умножать десятичные дроби: правило?

Алгоритм и правило умножения десятичных дробей звучит так:

Чтобы умножить одну десятичную дробь на другую, надо, не обращая внимания на запятые, перемножить их как целые числа и в произведении поставить запятую с правой стороны на столько десятичных знаков, сколько их было у двух множителей вместе. Если в произведении меньше десятичных знаков, чем следует выделить, то слева нужно дописать соответствующее количество нулей.

Используем данное правило, решая следующие примеры.

Пример. Найти произведение десятичных дробей 3,051 и 0,05.

Сначала умножим целые числа:

3051 ⋅ 5 = 15255

Теперь определим, где в произведении поставить десятичную запятую. В первом множителе – 3 знака после запятой, во втором – 2, следовательно, вместе будет 5 знаков. В произведении 15255 отсчитываем 5 десятичных знаков справа и ставим запятую, получим десятичную дробь 0,15255

Пример. Найти произведение десятичных дробей 4,125 и 0,008

Умножаем целые числа:

4125 ⋅ 8 = 33000

Поскольку в множителях 3 + 3 = 6 десятичных знаков после запятой, поэтому к числу 33000, имеющему 5 знаков, дописываем слева один ноль (033000) и отделяем запятой: 0,033000, что равно десятичной дроби 0,033

Чтобы найти произведение десятичных дробей, можно их сначала превратить в обыкновенные дроби и выполнить умножение по правилу умножения обыкновенных дробей.

Пример. Умножить десятичные дроби 1,5 и 0,75

Поскольку 1,5 можно превратить в дробь 15/10, а 0,75 = 75/100, выполнить умножение можно следующим образом:

Умножение десятичных дробей в столбик

Умножение десятичных дробей в столбик происходит по принципу умножения натуральных чисел без учета десятичных ком. После завершения умножения нужно поставить десятичную запятую в произведении на столько десятичных знаков, сколько их было у двух множителей вместе, начиная отсчет справа.

Кроме того, для удобства умножения в столбик первым следует записывать число или дробь с большим количеством цифр. Второе число размещают под первым так, чтобы его последняя цифра стояла под последней цифрой первого множителя

Пример. Выполнить умножение десятичных дробей 38,42 и 0,15 в столбик

Начинаем с умножения множителей без учета запятых.

Поставим десятичную запятую в произведении. Поскольку множители имеют 2 + 2 = 4 десятичных знака, отчислим в произведении 4 знака справа и поставим запятую:

Получили произведение дробей 5,7630, что равнозначно 5,763

Пример. Найти произведение десятичных дробей 4,6125 и 0,023, выполнив умножение в столбик

Выполним умножение, игнорируя запятые

Поставим запятую в произведении, разместив ее через 7 знаков справа (ведь 4 + 3 = 7)

Поскольку в произведении 7 цифр, ставим запятую перед первой цифрой 1, и дописываем ноль слева.

Умножение десятичной дроби на 0,1, 0,01, 0,001 и т.д.

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, 0,0001 и т.д., нужно в этой дроби перенести запятую на 1, 2, 3, 4 и т.д. комы влево. Если у дроби не хватает цифр, нужно дописать нули слева.

Пример. Умножить 78,63 на 0,1

Поскольку нужно умножить дробь 78,63 на 0,1, в произведении нужно перенести запятую на 1 знак влево:

78,63 ⋅ 0,1 = 7,863

Проверим, выполнив действие согласно правилу умножения десятичных дробей:

78,63 ⋅ 0,1 = 7863 ⋅1 = 7863. Перенесем запятую на 2 + 1 = 3 знака справа, получим 7,863.

То есть, умножив дроби двумя способами, получили одинаковый результат.

Пример. Умножить 256,32 на 0,001

Поскольку умножение на 0,001 надо перенести запятую влево на 3 знака: 256,32 ⋅ 0,001 = 0,25632

Умножение десятичной дроби на натуральное число

Умножение десятичной дроби на число выполняют по правилу умножения десятичных дробей, то есть перемножают множители, игнорируя запятую. После этого в произведении следует отделить десятичной запятой столько цифр, сколько цифр есть в дроби после запятой.

Пример. Умножить число 8 на десятичную дробь 0,0256

Пример. Умножить число 12 на десятичную дробь 3,45

В результате умножения получили дробь 41,40, ноль слева можно сократить, поэтому 12 ⋅ 3,45 = 41,4

Умножение десятичной дроби на числа 10, 100, 1000, 10000 и т.д.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., нужно в данной дроби перенести запятую справа на столько цифр, сколько нулей записано после 1 в числе, на которое умножаем. Если в десятичной дроби не хватает знаков, то нужно дописать справа необходимое количество нулей.

Пример. Умножить дробь 0,0256 на 10000

Поскольку число 10000 имеет 4 нуля, в дроби 0,0256 при умножении надо перенести запятую вправо на 4 знака:

0,0256 ⋅ 10000 = 256

Пример. Найти произведение дроби 0,4 и числа 1000

Поскольку число 1000 имеет 3 нуля при умножении в дроби 0,4 надо перенести запятую вправо на 3 знака. В дроби 0,4 после запятой 1 знак, поэтому дописываем 2 нуля:

0,400 ⋅ 1000 = 400

Пример. Умножить дробь 0,0039 на 10

0,0039 ⋅ 10 = 0,039

Пример. Умножить дробь 0,0039 на 10000

0,0039 ⋅ 10000 = 0039,0 = 39

Умножение десятичной дроби на обычную дробь или на смешанное число

Чтобы умножить десятичную дробь на обыкновенную дробь или смешанное число, нужно десятичную дробь превратить в обыкновенную и выполнить умножение.

Пример.

Найти произведение 0,4 и 3 5/6

Превратим десятичную дробь в обыкновенную:

0,4 = 4/10 = 2/5

Выполним умножение:

Задача. Максим купил 1 кг мандарин, заплатив 85,5 грн. Сколько стоит 0,5 кг мандарина?

Чтобы найти стоимость 0,5 кг мандарин, нужно 85,5 ⋅0,5 = 42,75 грн.

Ответ: 42,75 грн.

Умножение десятичных дробей

Показать рекламу

Скрыть рекламу
О рекламе

Умножьте без десятичной точки, а затем снова вставьте его в нужное место!

Как умножать десятичные числа

Просто выполните следующие действия:

Умножайте как обычно, игнорируя десятичные точки.
Затем поставьте в ответе запятую — в нем будет столько знаков после запятой, сколько вместе взятых двух исходных чисел.

Другими словами, просто подсчитайте, сколько чисел после запятой в

обоих чисел, которые вы умножаете, тогда в ответе должно быть столько же чисел после и десятичной запятой.

Пример: умножить 0,03 на 1,1

начать с:		0,03 × 1,1
умножить без десятичной точки:		3 × 11 = 33
0. 03 имеет 2 десятичных знака , и 1.1 имеет 1 десятичный знак , поэтому ответ имеет 3 десятичных знака :		0,033

См. анимацию умножения десятичных знаков

Как это работает?

Потому что, когда вы умножаете без десятичной точки, вы действительно сдвигаете десятичную точку вправо до убрать с дороги :

Оригинал:		1 ход:		2 хода:		3 хода:
0,03 × 1,1		0,3 × 1,1		3. × 1,1		3. × 11.

Затем мы выполняем (теперь простое) умножение:

3. × 11. = 33.

Но помните, мы сделали 3 перемещения десятичной точки, поэтому нам нужно отменить это:

3 Ходы:		2 хода:		1 ход:		Правильно
33.		3,3		0,33		0,033

Вот еще несколько примеров:

Пример: умножьте 0,25 на 0,2

начните с:		0,25 × 0,2
умножить без десятичной точки:		25 × 2 = 50
0,25 имеет 2 знаков после запятой, и 0,2 имеет 1 знаков после запятой, , поэтому ответ имеет 3 знаков после запятой:		0,050

Пример: умножьте 102 на 0,22

начните с:		102 × 0,22
умножить без десятичной точки:		102 × 22 = 2244
102 имеет 0 знаков после запятой, и 0,22 имеют 2 знаков после запятой, , поэтому ответ имеет 2 знаков после запятой:		22,44

Здравый смысл

В качестве последней проверки вы можете надеть шляпу здравого смысла и подумать «это правильный размер?» , потому что вы не хотите ни за что платить в десять раз больше, ни получать только одну десятую того, что вам нужно!

И все.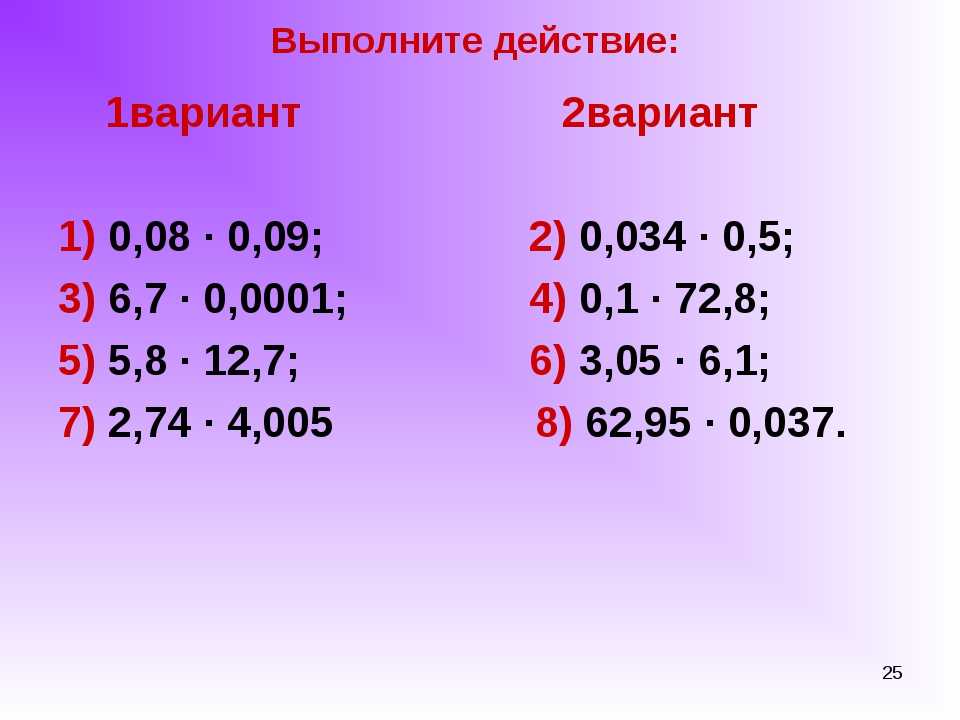

Только помните: в ответе должно быть столько знаков после запятой, сколько в обоих числах, которые вы умножаете.

Десятичные рабочие листы

Умножение десятичных знаков — Примеры | Как умножать десятичные дроби?

Умножение десятичных знаков очень важно, когда мы говорим о группировке предметов. Предположим, вам нужно раздать по 0,25 части плитки шоколада каждому ребенку, а всего детей 12. Сколько плиток шоколада вам понадобится? Чтобы найти необходимое количество плиток шоколада, нужно умножить 12 на 0,25. Умножение десятичных знаков выполняется путем игнорирования десятичной точки и умножения чисел, и тогда количество знаков после запятой в произведении равно общему количеству знаков после запятой в обоих заданных числах.

1.	Как умножать десятичные дроби?
2.	Умножение десятичных дробей на целые числа
3.	Умножение двух десятичных чисел
4.	Часто задаваемые вопросы об умножении десятичных дробей

Как умножать десятичные дроби?

Умножение десятичных дробей имеет ту же процедуру, что и умножение целых чисел, за исключением размещения десятичной точки в произведении. В нашей повседневной жизни мы сталкивались с различными случаями, когда нам приходилось использовать операцию умножения на двух числах, из которых хотя бы одно или оба являются десятичными числами. Представьте, что вы идете с другом на обед. Вы оба заказываете блюдо стоимостью 6,75 долларов каждое. Общий счет составляет $ 15,75, включая налоги. Чтобы рассчитать общую стоимость тарелки в счете, вам нужно умножить 6,75 доллара на 2. Аналогичным образом предположим, что вы планируете подарить своей матери букет цветов на ее день рождения. Каждый цветок стоит 0,75 доллара, всего вы покупаете 6 цветов. Чтобы найти общую стоимость букета, вам нужно умножить 0,75 доллара на 6. В приведенных выше примерах используется умножение десятичных дробей.

Умножение десятичных дробей на целые числа

Умножение десятичных дробей на целые числа аналогично умножению целых чисел, единственное отличие заключается в расположении десятичной точки. Для умножения десятичных дробей на целые числа можно выполнить следующие шаги:

Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа обычным образом.
Шаг 2: После умножения подсчитайте количество знаков после запятой в десятичном числе. Произведение, полученное после умножения, будет иметь такое же количество знаков после запятой.
Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Давайте разберемся в реальной ситуации умножения десятичных чисел на целые числа. Группа из 15 учеников решила внести свой вклад в благотворительный фонд. Каждый студент внес вклад в размере 6,5 долларов США. Какую сумму собрали со всего класса? Здесь вклад одного студента = $6,5. Общий вклад, сделанный 15 студентами = 6,5 × 15 = 9 долларов США.7.5.

Умножение десятичных дробей на 10 100 и 1000

При умножении любой десятичной дроби на 10, 100, 1000 или любую другую степень 10 мы просто сдвигаем десятичную точку вправо на столько знаков, сколько нулей в степень числа 10.

Если мы умножим десятичную дробь на 10, мы сдвинем запятую на одну позицию вправо, так как в числе 10 1 ноль.
Если мы умножаем любое десятичное число на 100, мы сдвигаем десятичную точку на два знака вправо.
Точно так же, если мы умножаем десятичную дробь на 1000, мы сдвигаем десятичную точку на три знака вправо и так далее.

Например, 2,32 × 10 = 23,2, 2,32 × 100 = 232, 2,32 × 1000 = 2320.

Умножение двух десятичных чисел

Этот раздел поможет вам узнать об умножении двух десятичных чисел. Это то же самое, что и у целого числа, но с той лишь разницей, что в этом случае мы должны взять сумму общего количества знаков после запятой в обоих данных числах, и это должно быть равно количеству знаков после запятой в продукт. Чтобы умножить два десятичных знака, выполните шаги, перечисленные ниже:

Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
Шаг 2: После умножения посчитайте общее количество знаков после запятой в обоих числах. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Давайте посмотрим на умножение двух десятичных чисел на изображении ниже:

Примеры умножения десятичных дробей:

1. Умножьте 0,567 на 13,065

Следовательно, 0,567 × 17,040 = 8,567 × 13,040 После запятой 6 цифр.

2. Найдите произведение 16,45 и 8,5

Следовательно, 16,45 × 8,5 = 139,825. Произведение имеет 3 знака после запятой.

Важные примечания:

Это несколько важных примечаний, связанных с концепцией умножения десятичных дробей. Взгляни!

Десятичное умножение следует той же процедуре, что и умножение целых чисел.
Десятичная запятая должна быть поставлена в произведении таким образом, чтобы количество знаков после запятой в произведении равнялось сумме знаков после запятой всех множимых и множителей.
Убедитесь, что в произведении сохранены все нули при размещении десятичной точки.
Если в произведении больше знаков после запятой, чем количество цифр, слева перед размещением запятой в произведении можно вставить нули.
Нули в конце результирующего произведения могут быть опущены.

Попробуйте решить эти сложные вопросы:

Чарли платят 17,45 долларов в час, и на прошлой неделе он отработал 42,5 часа. Сколько денег он заработал на прошлой неделе (округлив до цента)?
Какое общее расстояние проедет автомобиль, если он двигался со скоростью 31,5 км/ч в течение 7 часов 15 минут?

Умножение десятичных знаков Связанные темы

Ознакомьтесь с этими статьями, посвященными умножению десятичных дробей.

Калькулятор деления десятичных дробей
Калькулятор добавления десятичных знаков
Десятичные числа и дроби
Как добавить десятичные дроби?
Деление десятичных дробей
Сложение и вычитание десятичных дробей
Десятичные числа

Умножение десятичных дробей Примеры

Пример 1: Роуз изучает десятичное умножение. Поможешь ей умножить 0,6748 на 14,9?45?
Решение:
Посмотрим, как умножить 0,6748 на 14,945.
Примечание. Нули в конце можно опустить. Следовательно, 0,6748 × 14,945 = 10,084886.
Пример 2: Грейси пошла в продуктовый магазин со своей матерью. Ее мать купила 15 яблок по 1,25 доллара каждое. Помогите Грейси рассчитать сумму, которую должна заплатить ее мать, используя принцип умножения десятичных знаков.
Решение:
Стоимость одного яблока = 1,25 доллара. Таким образом, стоимость 15 яблок = 1,25 × 15 долларов. Следовательно, стоимость 15 яблок составляет 18,75 долларов.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по умножению десятичных дробей

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об умножении десятичных дробей

Как умножить десятичное число на целое?

Чтобы умножить десятичное число на целое, выполните следующие шаги:

Шаг 1: Не обращайте внимания на десятичную точку и умножайте оба числа.
Шаг 2: Подсчитайте количество знаков после запятой в десятичном числе.
Шаг 3: Затем поставьте запятую в произведении так, чтобы количество знаков после запятой в произведении и исходное десятичное число совпадали.

Как умножить десятичные дроби на 1000?

Чтобы умножить десятичные дроби на 1000, сдвиньте запятую на три знака вправо, так как в числе 1000 три нуля.

Как научить умножать десятичные дроби?

Давайте посмотрим, как научить учащихся десятичному умножению следующими способами:

Сначала дайте учащимся понять значение десятичного умножения с помощью демонстрации и визуализации.
Во-вторых, познакомьте учащихся с этапами умножения двух десятичных чисел.
Дайте практические вопросы.

Что такое правило умножения десятичных дробей?

Правила умножения десятичных дробей приведены ниже:

Правила умножения десятичных дробей:

Выполняйте умножение так же, как и с целыми числами.
Если в произведении больше знаков после запятой, чем количество цифр, перед размещением запятой в произведении можно вставить нули, так что слева от запятой будет только один ноль, а знаки после запятой в произведении будут равно общему количеству знаков после запятой в обоих числах.
Десятичная запятая должна быть поставлена в произведении таким образом, чтобы количество знаков после запятой в произведении равнялось сумме знаков после запятой всех множимых и множителей.
Нули в конце дробной части результирующего произведения можно опустить.

Как умножать десятичные дроби меньше 1?

Чтобы умножить два десятичных знака меньше 1, выполните шаги, указанные ниже:

Шаг 1: Сначала игнорируйте десятичную точку и умножайте два числа как обычно.
Шаг 2: После умножения подсчитайте общее количество знаков после запятой в множимом и множитель. Произведение, полученное после умножения, будет иметь это общее количество знаков после запятой.
Шаг 3: Поставьте десятичную точку в полученном произведении после Шаг 2 .

Например: 0,2 × 0,4 = 0,08.

Как умножать положительные и отрицательные десятичные дроби?

Положительные и отрицательные десятичные дроби умножаются так же, как два десятичных дроби.