Как высчитать угол 90 градусов: Как проверить прямой угол без угольника

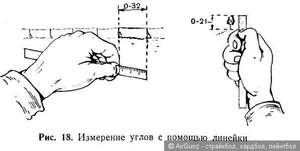Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.

Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.

Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Действительно ли прямой угол?

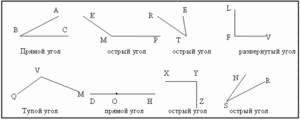Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.

И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство,

Что понадобится для определения прямого угла?

Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.

Для вычисления прямого угла нужно взять:

• Карандаш;
• Строительную рулетку.

И всё. Вот так вот всё просто.

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

1. Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
2. Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
3. В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
4. После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
5. Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
   • Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
   • В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
   • Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

Калькулятор уклонов — посчитать онлайн

Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Посчитать уклон

Посчитать превышение

Посчитать расстояние

Просто введите значения и выберите единицы измерения уклона.

Теория

Как посчитать уклон

Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:

В процентах:

Уклон в % = h / L ⋅ 100

В промилле:

Уклон в ‰ = h / L ⋅ 1000

В градусах:

Уклон в ° = arctg(^h/_L)

Пример

Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:

Уклон дороги = 30/500 ⋅ 100 = 6%

Как посчитать превышение

Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

h = ^{L ⋅ Уклон в %} /₁₀₀

Если уклон в промилле (‰):

h = ^{L ⋅ Уклон в ‰} /₁₀₀₀

Если уклон в градусах (°):

h = L ⋅ tg(α) , где α — уклон в градусах

Пример

Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:

h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м

Как посчитать расстояние

Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

L = ^h / _{Уклон в %} ⋅ 100

Если уклон в промилле (‰):

L = ^h / _{Уклон в ‰} ⋅ 1000

Если уклон в градусах (°):

L = h / tg(α), где α — уклон в градусах

Пример

Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:

L = 6 / 30 ⋅1000 = 200 м

См. также

Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

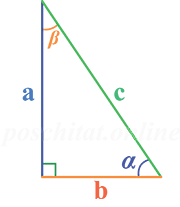
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для угла α:
• угол β
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов
• для угла β:
• угол α
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

tg(β) = ^b/_a

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Как высчитать угол 90 градусов рулеткой

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.

Теорема Пифагора

Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.

А теперь вернемся к нашим замерам и применим теорему на практике.

Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.

Египетский треугольник

Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?

a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.

Как проверить угол с помощью египетского треугольника?

Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.

Как отмерить угол, используя рулетку

Можно самостоятельно смастерить угольник для замера углов:

1. Соединяем две рейки одна перпендикулярно другой.
2. Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
3. Прибиваем третью рейку к одной отметке.
4. Измеряем гипотенузу, прибиваем рейку ко второй метке.
5. Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
6. Обрезаем лишние концы.

Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.

Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.

Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.

У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.

Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.

Один и тот же размер при измерении разными рулетками может не совпадать.

Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.

Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.

Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:

от предмета

Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.

Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.

Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.

Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.

Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.

На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.

Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.

Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.

При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.

Проделав два измерения нужно сложить результаты и получите точный размер.

На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.

Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.

Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.

В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.

Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.

Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.

Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.

А при использовании шурупа легко рисуются окружности нужного диаметра.

Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.

После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.

Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.

Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.

Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.

Писать конечно нужно карандашом, после чего все это легко стирается резинкой.

С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.

Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.

Ровно в месте перегиба и будет требуемый результат — 58см.

Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.

Вытягиваете ленту на 2м 11см и складываете ее пополам.

Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.

Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.

Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.

Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.

Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.

В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.

Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.

Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.

Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.

Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.

Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.

Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.

Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.

Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.

Египетский треугольник. Прямой угол без инструмента. |

15.01.2016 profipol_dp 3 710 просмотра

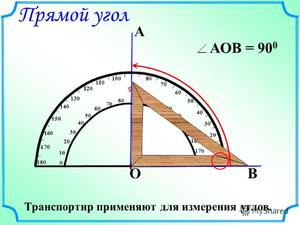
Как выставить угол 90 градусов без специального инструмента (угольника)?

Допустим, у нас есть линия  к которой нам нужно выставить перпендикуляр, т.е. еще одну линию под углом 90 градусов относительно первой. Или у нас есть угол (например, угол комнаты) и нам нужно проверить равен ли он 90 градусам.

Все это можно сделать с помощью одной только рулетки и карандаша.

Есть две отличные штуки, такие как «Египетский треугольник» и теорема Пифагора, которые нам в этом помогут.

Итак, Египетский треугольник — это прямоугольный треугольник с соотношением всех сторон равным 3:4:5 (катет 3: катет 4: гипотенуза 5).

Египетский треугольник напрямую связан с теоремой Пифагора — сумма квадратов катетов равна квадрату гипотенузы (3*3 + 4*4 = 5*5).

Как нам это может помочь? Все очень просто.

Задача №1. Нужно построить перпендикуляр к прямой линии (например, линию под 90 градусов к стене).

Шаг 1. Для этого от точки №1 (где будет наш угол) нужно отмерить на этой линии любое расстояние кратное трем или четырем — это будет наш первый катет (равный трем или четырем частям, соответственно), получаем точку №2.

Для простоты вычислений можно взять расстояние, например 2м (это 4 части по 50см).

Шаг 2. Затем от этой же точки №1 отмеряем 1,5м (3 части по 50см) вверх (выставляем примерный перпендикуляр), чертим линию (зеленая).

Шаг 3. Теперь из точки №2 нужно поставить метку на зеленой линии на расстоянии 2,5м (5 частей по 50см). Пересечение этих меток и будет нашей точкой №3.

Соединив точки №1 и №3 мы получим линию-перпендикуляр нашей первой линии.

Задача №2. Вторая ситуация — есть угол и нужно проверить прямой ли он.

Вот он, наш угол. Крнечно проще проверить большим угольником. А если его нет?

Отмеряем от угла любую длину кратную четырем, в данном случае это 1,6м.

В другую сторону три части, соответственно 1,2м.

И между этими точками должно оказаться пять частей, т.е. 2м.

Как видите, у нас угол оказался прямее всех прямых.

Чего и вам желаем!

---

 

 

Это тоже интересно:

инструмент, разметка укладки кафеля,

Онлайн калькулятор диагоналей для расчета фундамента и крыш

Скачать, сохранить результат

Выберите способ сохранения

Информация

Профессиональное проектирование и формирование фундамента, стен, а также полноценной системы крыши дома требует чёткого выставления геометрических углов и расчёта диагоналей сегментов конструкций. От точности вычислительных манипуляций напрямую зависит безопасность, устойчивость, прочность и долговечность здания. Интерактивный калькулятор диагоналей для расчёта фундамента и крыш поможет безошибочно выполнить все расчётные операции на этапе проектирования дома всего за несколько секунд.

Преимущества калькулятора диагоналей

• Помогает безошибочно рассчитать квадрат конкретной секции фундамента всего в несколько кликов.
• Позволяет самостоятельно выполнить расчёт диагонали прямоугольника или треугольника.
• Помогает быстро рассчитать общую длину и ширину фундамента, а также стен дома.
• Результаты расчётных операций гарантируют чёткое выставление геометрических углов в 90° при монтаже конструкционных элементов фундамента, стен и крыши.
• Экономит уйму времени, сил нервов и средств в процессе проектирования строений всех категорий.
• Расчёт диагоналей основания обеспечивает безупречное обустройство фундамента, что дарит дому безопасность, надёжность и долговечность.
• Возможность бесплатно получить результаты расчётных операций в формате PDF на свой E-mail или мгновенно распечатать их в режиме онлайн.

Безошибочно рассчитайте геометрические параметры фундамента, стен и конструкционных элементов системы крыши уже сегодня. Бесплатно задействуйте онлайн калькулятор диагоналей — сэкономьте силы, время и деньги прямо сейчас!

поделиться и оценить

Смотрите также:

Добавить комментарий

Как построить угол 90 градусов с помощью компаса и линейки или линейки

На этой странице мы покажем, как построить (нарисовать) угол 90 градусов с помощью компаса и линейки или линейки. Есть разные способы сделать это, но в этой конструкции мы используем свойство Теорема Фалеса. Мы создаем круг, где вершина нужного прямого угла — точка на окружности. Теорема Фалеса говорит, что любой диаметр круга стягивает под прямым углом к ​​любой точке круга.

Печатные пошаговые инструкции

Выше анимация доступна как печатная пошаговая инструкция, которую можно использовать для раздаточного материала или когда компьютер недоступен.

Объяснение метода

На самом деле это та же конструкция, что и при построении перпендикуляра в конечной точке луча. Еще один способ сделать это

Доказательство

Эта конструкция работает с использованием теоремы Фалеса. Это создает круг, где вершина желаемого прямого угла является точкой на круге.

	Аргумент	Причина
1	Сегмент AB — это диаметр центра окружности D	AB — прямая линия, проходящая через центр.
2	Угол ACB имеет меру 90 °.	Диаметр круга всегда составляет угол 90 ° к любой точке (С) на круге. См. Теорему Фалеса.

— Q.E.D

Попробуйте сами

Нажмите здесь для печати листа, содержащего две проблемы, чтобы попробовать. Когда вы попадете на страницу, используйте команду печати браузера, чтобы напечатать столько, сколько вы хотите. Печатная продукция не защищена авторским правом.

Страницы других конструкций на этом сайте

Линии

Углы

Треугольники

Прямоугольные треугольники

Треугольных Центров

Круги, дуги и эллипсы

полигонов

неевклидовых конструкций

(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

,

Калькулятор углового преобразования

Использование калькулятора

Преобразование единиц углов путем ввода значения для преобразования, а также единиц измерения от и до.

Как конвертировать единицы углов

Преобразования выполняются с использованием коэффициента пересчета. Зная коэффициент преобразования, преобразование между единицами может стать простой проблемой умножения:

S * C = E

Где S является нашей начальной стоимостью, C является нашим коэффициентом пересчета, и E — это наш конечный результат.

Чтобы просто перевести из любой единицы в градусы, например, из 5 радиан, просто умножьте на значение в правом столбце в таблице ниже.

5 радиан * 57,29578 [градусов / радиан] = 286,4789 градусов

Преобразовать из градусов обратно в единицы в левом столбце разделите на значение в правом столбце или умножьте на обратное значение 1 / x.

286,4789 градусов / 57,29578 [градусов / радиан] = 5 радиан

Чтобы преобразовать любые единицы в левом столбце, скажем, из A в B, вы можете умножить на коэффициент для A, чтобы преобразовать A в градусы, а затем разделить на коэффициент для B, чтобы преобразовать из градусов. Или вы можете найти единственный нужный вам фактор, разделив фактор A на фактор B.

Например, чтобы преобразовать радианы в обороты, вы должны умножить на 57.29578 затем разделите на 360. Или умножьте на 57,29578 / 360 = 0,1591549. Таким образом, для прямого преобразования радиан в обороты вы умножаете на 0,1591549.

Чтобы понять, как конвертировать единицы, следуйте этому примеру. Скажем, вы хотите конвертировать из радианов в градусы. Поскольку вы можете умножить что угодно на 1 и при этом сохранить первоначальное значение, но в разных единицах, установите его так, чтобы радиан отменил, оставив вам градус.

С:
1 градус = 0.01745329 радиан, 1 градус / 0,01745329 радиан = 1

Мы можем записать преобразование как:
1 радиан = 1 радиан * (1 градус / 0,01745329 радиан) = 57,29578 градусов

И теперь у нас есть коэффициент для пересчета в радианы в градусы, поскольку 1 * 57.29578 = 57.29578. Обратите внимание, что в этих значениях есть ошибки округления.

Зная, что 1 радиан = 57.29578 градусов теперь мы можем найти коэффициент преобразования для обратного преобразования. Разделив обе части уравнения на 57,29578, мы получим около 0,01745329 радиан = 1 градус. Таким образом, коэффициент пересчета для пересчета из градусов в радианы составляет около 0,01745329.

Таблица угловых преобразований

Единицы, символы и значения преобразования
используется в угловом переводе в градусы

радиан

рад

градусов

180 / №

57.29578

минуты

‘

градусов

1/60

0,016667

секунд

«

градусов

1/3600

2.777778 E-4

октант

октант

градусов

360/8

45

секстант

секстант

градусов

360/6

60

квадрант

квадрант

градусов

360/4

90

революция

р

градусов

360/1

360

гон

гон

градусов

360/400

0.9

мил

мил

градусов

360/6400

0,05625

Единицы, символы и значения преобразования
используется для углового преобразования в радианы

градусов

°

радиан

π / 180

0.01745329

минуты

‘

радиан

(π / 180) / 60

2.908882 e-04

секунд

«

радиан

(π / 180) / 3600

4.848137 E-06

октант

октант

радиан

2π / 8

0,7853982

секстант

секстант

радиан

2π / 6

1.047196

квадрант

квадрант

радиан

2π / 4

1,570796

революция

р

радиан

2π

6.283185

гон

гон

радиан

2π / 400

0,01570796

мил

мил

радиан

2π / 6400

9.817477 е-4

Ссылки / Дополнительная литература

Национальный институт стандартов и технологий (NIST) — Руководство по использованию международной системы единиц измерения NIST — Приложение B, подразделы B.8 Факторы для единиц, перечисленных в алфавитном порядке и B.9 Факторы для единиц, перечисленных по виду количества или области науки.

Лиде, Дэвид Р.Даниэль (главный редактор). CRC Справочник по химии и физике, 89-е издание Нью-Йорк, Нью-Йорк: CRC Press, p. 1-28, 2008.

Википедия. «Конверсия единиц» Википедия, Свободная энциклопедия. Википедия, «Свободная энциклопедия», последний раз посещалась 26 июня 2011 года.

,

Треугольник Калькулятор

Пожалуйста, предоставьте 3 значения, включая как минимум одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Когда радианы выбраны в качестве единицы измерения угла, они могут принимать значения, такие как pi / 2, pi / 4 и т. Д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединяются тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются исходя из длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковую длину, это называется разносторонним, как показано ниже.

Отметки на краю треугольника представляют собой обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает равную длину.Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различными числами концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет угловые метки, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда вводятся фактические значения, вывод калькулятора будет отражать, как должна выглядеть форма входного треугольника.

Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямые или наклонные. Прямой треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, то есть край, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупом треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.

Факты о треугольнике, теоремы и законы

• Учитывая длины всех трех сторон любого треугольника, каждый угол может быть рассчитан с использованием следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c являются известными значениями.

Площадь Треугольника

Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для расчета площади треугольника включает его основание b и высоту h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка, проведенного от вершины, противоположной основанию, до точки на основании, которая образует перпендикуляр.

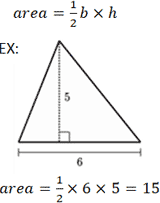
Учитывая длину двух сторон и угол между ними, следующая формула может быть использована для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Дано a = 9, b = 7 и C = 30 °:

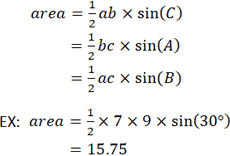
Другой метод расчета площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:

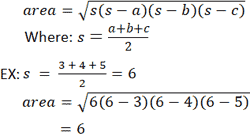
Медиана, инрадиус и оксирадиус

Медиана

Медиана треугольника определяется как длина отрезка, который простирается от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, все из которых будут пересекаться в центроиде (среднее арифметическое положение всех точек в треугольнике) треугольника.Обратитесь к рисунку, приведенному ниже, для пояснения.

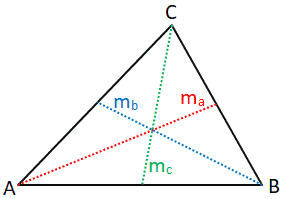
Медианы треугольника представлены отрезками линии m _a , m _b и m _c . Длина каждой медианы может быть рассчитана следующим образом:

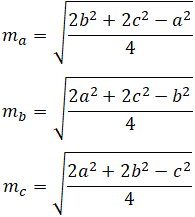
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.

В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m _и может быть рассчитана следующим образом:

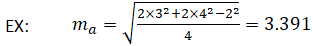
Inradius

Инрадиус — это радиус самого большого круга, который будет помещаться внутри данного многоугольника, в данном случае, треугольника.Inradius перпендикулярен каждой стороне многоугольника. В треугольнике значение радиуса можно определить, построив две угловые биссектрисы для определения стимулятора треугольника. Inradius — это перпендикулярное расстояние между стимулятором и одной из сторон треугольника. Любая сторона треугольника может использоваться до тех пор, пока определяется перпендикулярное расстояние между стороной и стимулятором, поскольку стимулятор, по определению, равноудален от каждой стороны треугольника.

Для целей данного калькулятора, вычисление радиуса рассчитывается с использованием площади (площади) и полупериметра (ов) треугольника, а также следующих формул:

, где a, b и c — стороны треугольника

Circumradius

Циррадиус определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этого круга, где встречаются все перпендикулярные биссектрисы каждой стороны треугольника, является окружным центром треугольника и является точкой, из которой измеряется окружность. Окружный центр треугольника не обязательно должен быть внутри треугольника. Стоит отметить, что все треугольники имеют окружность (круг, проходящий через каждую вершину) и, следовательно, окружность.

Для целей данного калькулятора круговой луч рассчитывается по следующей формуле:

Где a — сторона треугольника, а A — угол, противоположный стороне a

Хотя используются сторона А и угол А, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.

,

Как рассчитать синус особых углов в градусах

2. Образование
3. Математика
4. Исчисление
5. Как рассчитать синус особых углов в градусах

Ян Куанг, Elleyne Kase

Измерять углы в градусах для формул суммы и разности для синуса проще, чем в радианах, потому что сложение и вычитание градусов намного проще, чем сложение и вычитание радиан.Для сложения и вычитания углов в радианах требуется найти общий знаменатель. Кроме того, оценка функций триггера требует, чтобы вы работали в обратном направлении от общего знаменателя, чтобы разделить угол на две дроби с разными знаменателями.

Если вы посмотрите очень внимательно, вы заметите, что 45 градусов — 30 градусов = 15 градусов, а 45 градусов + 30 градусов = 75 градусов. Для углов, которые вы можете переписать в виде суммы или разности специальных углов, вот формулы сумм и разностей для синуса:

В качестве примера выполните следующие шаги, чтобы найти синус 135 градусов:

1. Перепишите угол, используя специальные углы из прямоугольных треугольников.

   Один из способов переписать 135 градусов — это 90 градусов + 45 градусов.

2. Выберите подходящую формулу суммы или разницы.

   В примере из шага 1 используется сложение, поэтому вы хотите использовать формулу суммы, а не формулу разности:

3. Включите информацию, которую вы знаете, в формулу.

   Вы знаете, что

   Следовательно, a = 90 градусов и b = 45 градусов.

   формула дает вам

4. Используйте круг единиц, чтобы найти нужные значения синуса и косинуса.

   Весь круг единицы

   Теперь у вас есть

5. Умножьте и упростите, чтобы найти окончательный ответ.

   Вы в конечном итоге с

Об авторе книги

Мэри Джейн Стерлинг занимается алгеброй, бизнес-исчислением, геометрией и конечной математикой в ​​Университете Брэдли в Пеории, штат Иллинойс, на протяжении более 30 лет.Она является автором нескольких книг «Для чайников», , в том числе «Алгебра» для чайников, «Алгебра II для чайников», и «Алгебра II» для чайников.

,