Калькулятор диагоналей: Калькулятор диагоналей

Вычислить диагональ прямоугольника онлайн, способы и формулы

Одна из основных фигур курса математики – прямоугольник. Впервые о нем заговорили еще в Древнем Египте, а позже и в Древней Греции. Именно свойства его диагоналей помогают решить многие задания учебного курса. Подход, который сейчас используется в геометрии разработал Евклид. Формулы, представленные в данной статье, пригодятся как при решении домашних упражнений, так и на ЕГЭ. Именно такие задачки помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.

• Диагональ прямоугольника через его стороны
• Диагональ прямоугольника через площадь и известную сторону
• Диагональ прямоугольника через периметр и сторону
• Диагональ прямоугольника через диаметр описанной окружности
• Диагональ прямоугольника через радиус описанной окружности
• Диагональ прямоугольника через площадь и острый угол между диагоналями
• Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
• Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
• Что такое диагональ прямоугольника, когда требуется ее вычисление

Диагональ прямоугольника через его стороны

Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:

Где a, b – это стороны, а d – прямая, которую мы ищем.

Сторона (a)

ммсмдмм

Сторона (b)

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через площадь и известную сторону

Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:

Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.

Площадь (S):

мм²см²дм²м²

Сторона (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через периметр и сторону

Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:

Где P – сумма сторон, a и b – любая заданная сторона.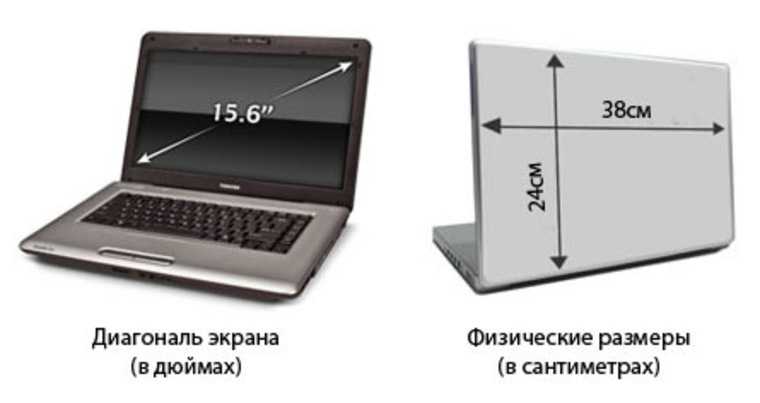

Рассчитать искомый отрезок можно и через соотношение сторон и площадь.

Периметр (P):

ммсмдмм

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через диаметр описанной окружности

Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d

Где d – это обозначенный диаметр.

Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.

Диаметр (d):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через радиус описанной окружности

Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R

Где R – это заданный радиус.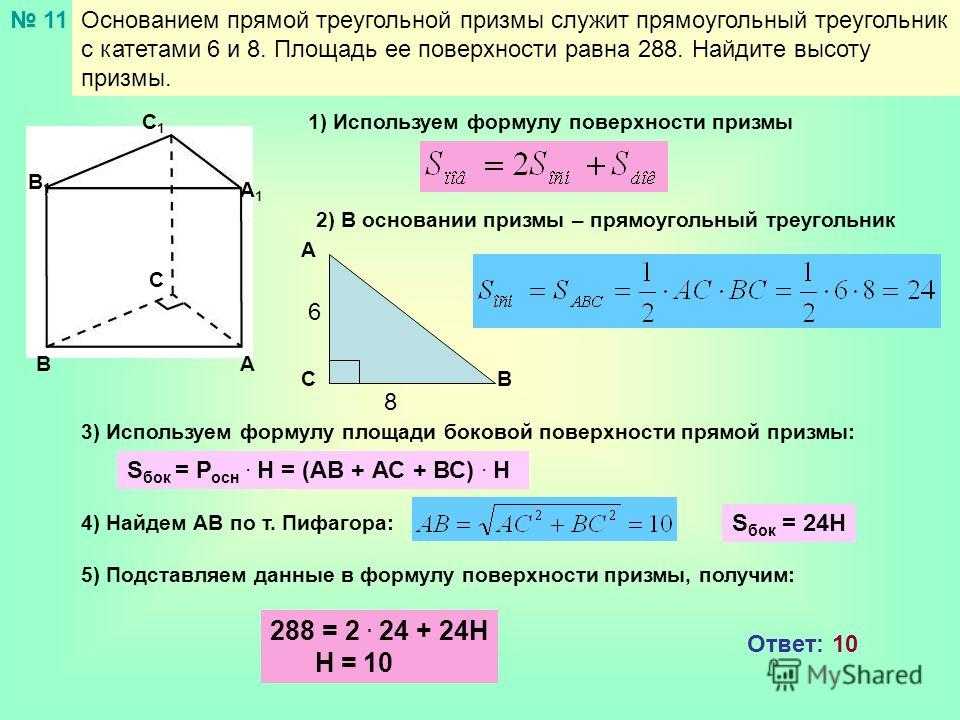

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через площадь и острый угол между диагоналями

Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины). Расчет проводится с равенством:

Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).

Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.

Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.

Площадь (S):

мм²см²дм²м²

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу

Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:

Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.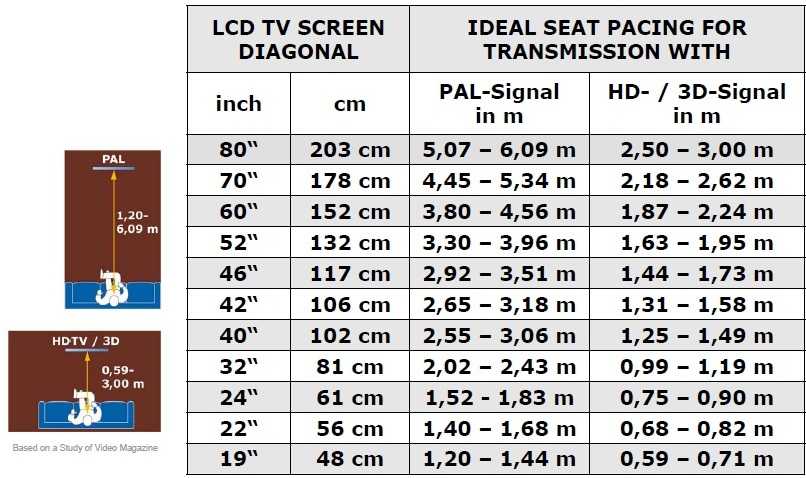

Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу

Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:

Где a – это сторона четырехугольника, а sin a – это прилегающий угол.

Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.

Сторона (a):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Прямоугольник – это частный случай параллелограмма.

Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.

Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.

Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.

Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.

Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника.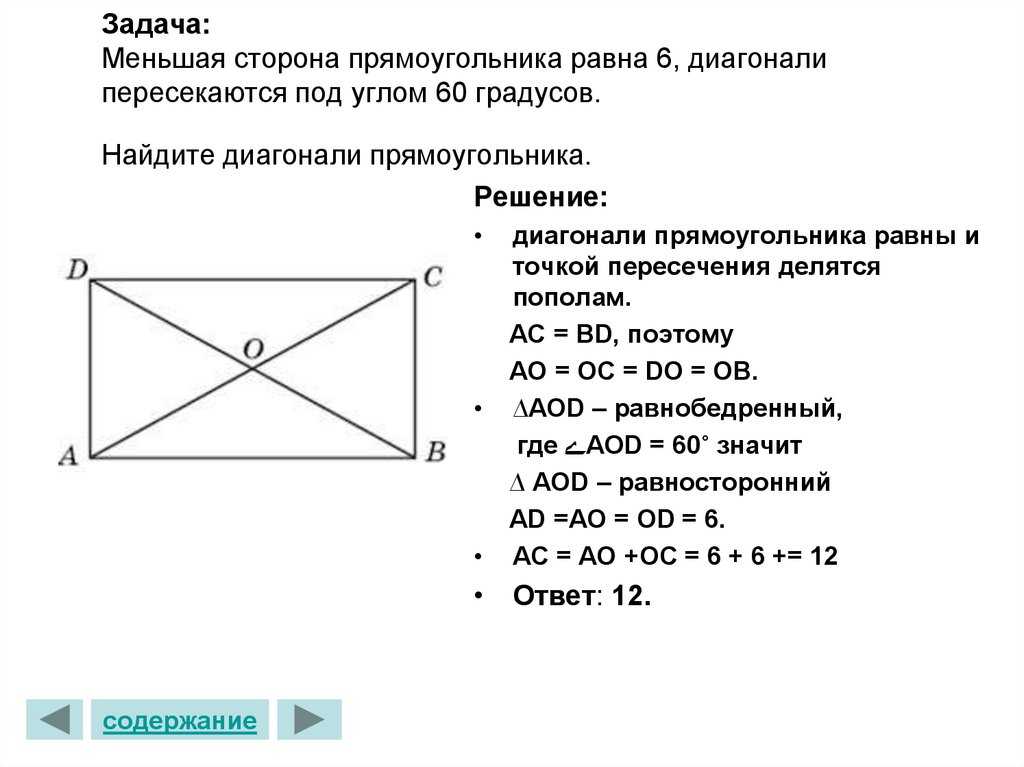

Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.

Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.

Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.

Онлайн-калькулятор расчета площади прямоугольника: через стороны, диагонали

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы для расчета площади прямоугольника по разным исходным данным: через стороны (длину и ширину) или диагонали и угол между ними.

• Расчет площади
  • 1. Через стороны (длину и ширину)
  • 2. Через диагонали и угол между ними

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры указанного размера.

1. Через стороны (длину и ширину)

Формула расчета

S = a ⋅ b

2. Через диагонали и угол между ними

Формула расчета

Примечание: диагонали прямоугольника равны между собой.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор диагонали прямоугольника

Автор Dominik Czernia, PhD

Отзыв от Bogna Szyk

Последнее обновление: 31 января 2023 г.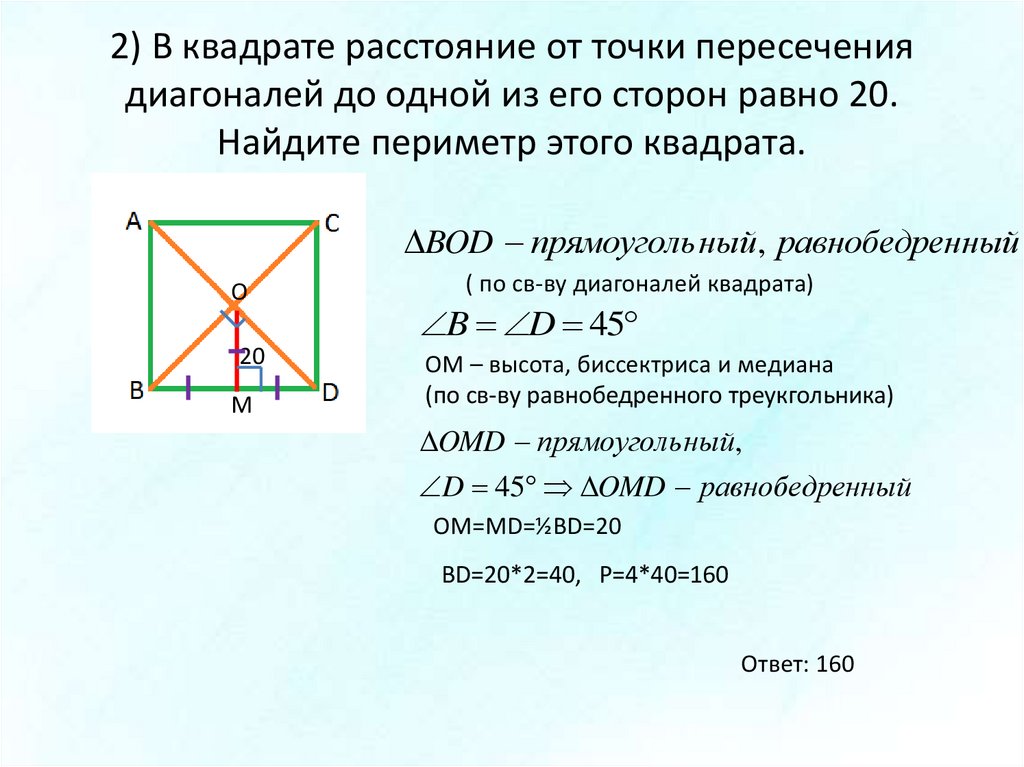

Содержание:

• Важный параметр прямоугольников
• Как найти диагональ прямоугольника данные стороны?
• Какова диагональ прямоугольника?
• Часто задаваемые вопросы

Наш калькулятор диагонали прямоугольника представляет собой обширный инструмент, который быстро находит диагональ и другие параметры прямоугольника. Вы столкнулись с конкретной задачей прямоугольника, и вы не знаете как найти диагональ прямоугольника ? Попробуйте ввести пару параметров в поля рядом с текстом или продолжайте читать, чтобы узнать, каковы возможные диагонали формул прямоугольника .

Важный параметр прямоугольников

Типичный прямоугольник показан на рисунке ниже. Мы отметили пять основных величин, описывающих конкретный прямоугольник. Вы можете использовать их для получения формулы диагонали прямоугольника. Это:

• l – длина ;
• ш – ширина ;
• α – угол между диагоналями ;
• r – радиус описанной окружности ;
• д – диагональ ;

и два других параметра, которые не показаны на рисунке:

• A – площадь ; и
• П – периметр .

Термин прямоугольник происходит от латинского rectangulus , который представляет собой комбинацию двух слов: rectus (справа, правильно) и angulus (угол). Это название происходит от того факта, что прямоугольник представляет собой четырехугольник с четырьмя прямыми углами (4 × 90° = 360°). Его противоположные стороны параллельны и имеют одинаковую длину, а две его диагонали пересекаются посередине и также имеют одинаковую длину.

Квадрат является частным случаем прямоугольника. Его определение состоит в том, что у него все четыре стороны одинаковой длины; в противном случае угол между двумя диагоналями прямой. Попробуйте наши калькуляторы, посвященные квадратам, например, квадратный калькулятор. Они могут быстро оценить периметр, площадь и диагональ любого квадрата, который вам нужен, только по длине его стороны.

Центр прямоугольника равноудален от его вершин; следовательно, вы всегда можете описать окружность на нем .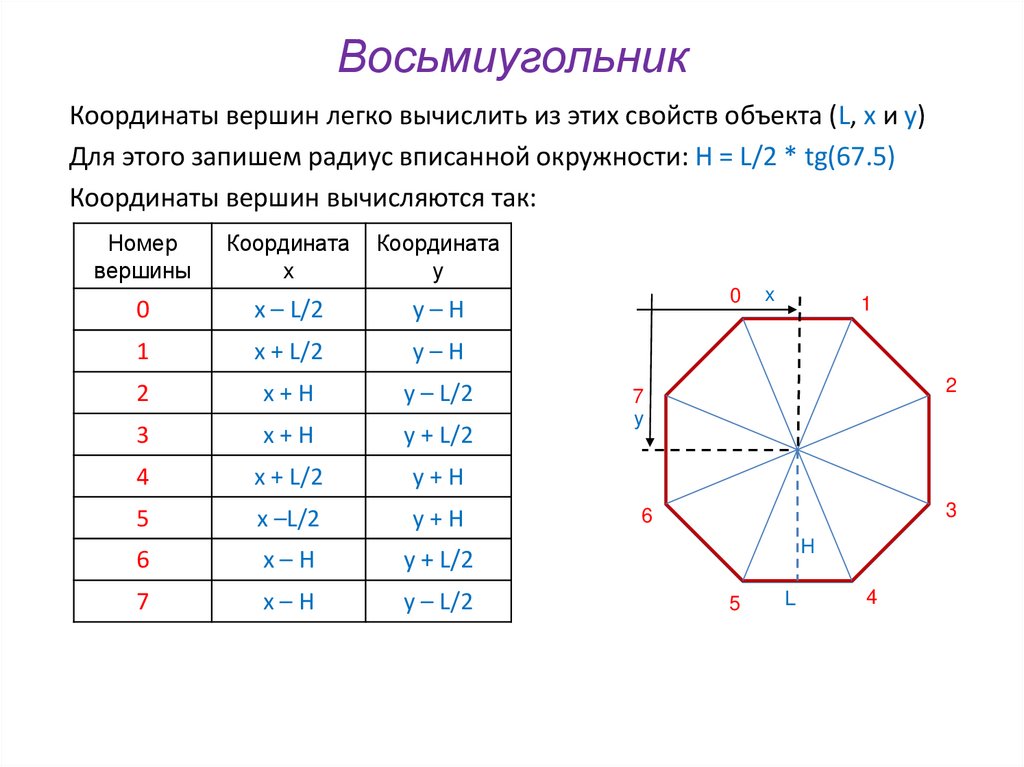 С другой стороны, вы можете вписать круг в прямоугольник, только если это квадрат .

Как найти диагональ прямоугольника по сторонам?

Для определения диагонали прямоугольника необходимо:

1. Записать сторон прямоугольника, которые обозначим через ш и л .
2. Квадрат эти два значения. То есть вычислите l² и w² .
3. Сложите два квадрата значений из шага 2.
4. Извлеките из результата квадратный корень из .
5. Вот оно! Вы только что нашли длину диагонали квадрата.

Почему эта процедура работает?

Чтобы получить диагональ прямоугольника по приведенной выше формуле, разделите прямоугольник на два конгруэнтных прямоугольных треугольника, т. е. треугольники с одним углом 90°. Каждый треугольник будет иметь стороны длины l и w и гипотенузу длины d . Вы можете использовать формулу гипотенузы, например, из калькулятора теоремы Пифагора, чтобы оценить диагональ прямоугольника, которая может быть выражена следующей формулой:

d² = l² + w² ,

и теперь вы должны знать, как чтобы найти диагональ прямоугольника явной формулой — просто извлеките квадратный корень:

d = √(l² + w²) .

Наш калькулятор диагонали прямоугольника позволяет использовать практически любые единицы измерения. Воспользуйтесь нашим конвертером длины или конвертером площади, чтобы узнать, как переключаться между различными единицами измерения (СИ и имперскими).

Какова диагональ прямоугольника?

Иногда вы не можете указать длину двух смежных сторон прямоугольника. Как найти диагональ прямоугольника в этом случае? Ответ дает наш калькулятор диагонали прямоугольника. Во-первых, давайте запишем три основных уравнения для площади, периметра] и радиуса описанной окружности:

1. Площадь прямоугольника: A = w × l ,
2. Периметр прямоугольника P = 2 × w + 2 × l ,
3. Радиус окружности прямоугольника r = d/2 .

С помощью приведенных выше уравнений мы теперь можем вывести различные формулы диагонали прямоугольника , которые используются калькулятором этой диагонали прямоугольника:

1. Дано длина и ширина :
   d = √(l² + w²) ;

2. Даны длина/ширина и площадь :
   d = √(A²/l² + l²) или d = √(A²/w² + w²) ;

3. Даны длина/ширина и периметр :
   d = √(2l² - P × l + P²/4)) или d = √(2w² - P × w + P²/4) ;

4. Даны длина/ширина и угол :
   d = w / sin(α/2) или d = l / cos(α/2) ;

5. Учитывая площадь и периметр :
   d = ½√(P² - 8 × A) ;

6. Учитывая площадь и угол :
   d = √(2 × A / sin(α)) ;

7. Учитывая периметр и угол :
   d = P / (2 × sin(α/2) + 2 × cos(α/2)) ; и

8. Дано радиус описанной окружности :
   д = 2 × г .

Примечание: Угол α между диагоналями лежит перед длиной , как на первом рисунке. Также помните, что калькулятор диагонали прямоугольника предполагает, что длина больше ширины!

Знаете ли вы, что существует особый прямоугольник, называемый золотым прямоугольником? Если нет, воспользуйтесь нашим калькулятором золотых прямоугольников, чтобы узнать, как построить золотые прямоугольники!

Часто задаваемые вопросы

Какова диагональ золотого прямоугольника?

Ответ: 1,176 умножить на длинную сторону. Если вы знаете более короткую сторону золотого прямоугольника, длина диагонали в 1,902 раз больше длины более короткой стороны. Чтобы получить эти ответы, используйте теорему Пифагора.

Как вычислить площадь прямоугольника по диагонали и периметру?

Если известны площадь и периметр прямоугольника, можно найти диагональ по формуле:

диагональ = ½√(P² - 8 × A) ,

, где P — периметр, а A — площадь прямоугольника.

Какова диагональ прямоугольника с периметром 20 и площадью 18?

Ответ: 8 . Чтобы получить этот ответ, примените формулу по диагонали = ½√(P² - 8 × A) . Подставляя данные, мы получаем диагональ = ½√(20² - 8 × 18) = ½√(400 - 144) = ½√256 = ½ × 16 = 8 , как и утверждалось.

Доминик Черня, доктор философии

Длинная сторона (л)

Короткая сторона (w)

Площадь (A)

Периметр (P)

Угол между диагоналями (α)

Радиус окружности (r)

Диагональ

Диагональ 20 3 0 калькуляторы геометрии 📏

ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20

Калькулятор диагонали

Калькулятор диагонали измеряет диагональ, площадь, периметр и диагональный угол прямоугольника. Вам просто нужно ввести всего два значения, чтобы найти диагональ прямоугольника.

Прямоугольник – это четырехугольник, имеющий четыре угла, и все углы равны 90 градусов. Противоположные стороны прямоугольника параллельны и равны по длине. Соседние стороны прямоугольника различны по длине, но диагонали равны по длине и пересекаются в средней точке прямоугольника. Нам нужно ввести длину и ширину в калькулятор диагонали прямоугольника, чтобы найти диагональ прямоугольника.

 

Как найти диагональ прямоугольника?

Мы можем найти диагональ прямоугольника как:

Диагональный = √ (L² + W²)

Где:

I = Длина прямоугольника

W = Width of Prterntled 320303030303030303.

920303030303030302.

W = width of widthangle 32030303030303.

W = width of widthard of uidthard of uidtled of udthant

Площадь прямоугольника:

Площадь прямоугольника можно найти, умножив длину на ширину:

Площадь = l×w

Периметр прямоугольника:

Периметр прямоугольника может измеряется по заданной формуле:

Периметр = 2l + 2w=2(l+w)

Мы можем найти диагональ прямоугольника, площадь и периметр с помощью диагонального калькулятора.

 

Возможности измерения диагонали прямоугольника:

Мы можем столкнуться с различными способами нахождения диагонали прямоугольника.

Из площади и длины:

Сначала нужно найти длину по данной формуле:

l= A /w

Затем

P = 2l + 2w

Длина диагонали прямоугольника = √(l² + w²) 

Из площади и ширины:

Сначала нужно найти ширину:

w= A / l

P = 2l + 2w

2 Диагональ прямоугольника можно измерить следующим образом:

Диагональ = √(l² + w²)

Из периметра и длины:

w = (P – 2l) / 2

Площадь = l× w

Диагональ = √(l² + w²)

Из периметра и ширины:

l= (P – 2w) / 2

Площадь = l× w

Диагональ = √(l² + w²) 

Практический пример:

Измерьте длину диагонали, площадь и периметр прямоугольник, длина которого 4 единицы, а ширина 3 единицы.

Sol:

Длина = 4 единицы

Ширина = 3 единицы

Подставляя значения в приведенное ниже уравнение

.

Диаметр прямоугольника = 5 единиц.

 Длина диагонали прямоугольника = 5 единиц.

Площадь прямоугольника = l×w

Площадь прямоугольника = 4×3 = 12 единиц ²

Периметр прямоугольника = 2l + 2w 

Периметр прямоугольника = 8+ 6

Периметр прямоугольника = 14 единиц

Как пользоваться калькулятором диагонали?

Придерживайтесь следующих шагов для точных расчетов с помощью калькулятора диагональных измерений

Ввод:

Введите любые два из заданных входных данных и нажмите кнопку расчета

Вывод:

• Диагональ прямоугольника
• Площадь прямоугольника
• Периметр прямоугольника
• Окружность, описанная вокруг прямоугольника
• Угол прямоугольника

Ссылки:

Из источника wikipedia.org: Описанные окружности>, Треугольники

Из источника wikihow.