Опубликовано Сложение и вычитание дробей
Сложение и вычитание дробейНавигация по странице:
- Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение обыкновенных дробей
- Сложение смешаных чисел
- Вычитание дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание обыкновенных дробей
- Вычитание смешаных чисел
Сложение дробей
Сложение дробей с одинаковыми знаменателями.
Определение.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | b | = | a + b |
| c | c | c |
Примеры сложения дробей с одинаковыми знаменателями
Пример 1.
Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | 2 | = | 1 + 2 | = | 3 | |
| 5 | 5 | 5 | 5 |
Пример 2.
Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.
Примеры сложения обыкновенных дробей
Пример 3.
Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4.
Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чисел
Примеры сложения смешанных чисел
Пример 5.
Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6.
Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | 5 | |
| 24 | 24 | 24 | 24 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробей
Вычитание дробей с одинаковыми знаменателями.
Определение.
Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | — | b | = | a — b |
| c | c | c |
Примеры вычитания дробей с одинаковыми знаменателями
Пример 7.
Найти разность двух дробей с одинаковыми знаменателями:
| 3 | — | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8.
Найти разность двух дробей с одинаковыми знаменателями:| 8 | — | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.
Примеры вычитания обыкновенных дробей
Пример 9.
Найти разность двух дробей:
| 5 | — | 1 | = | 5 | — | 1·3 | = | 5 | — | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10.
| 3 | — | 1 | = | 3·3 | — | 1·5 | = | 9 | — | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.
Примеры вычитания смешанных чисел
Пример 11.
Найти разность двух смешанных чисел:
| 2 | 1 | — | 1 | 1 | = | 2 | 1·3 | — | 1 | 1·2 | = | (2 — 1) | + | 3 | — | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12.
Найти разность двух смешанных чисел:
| 3 | 1 | — | 1 | 3 | = | 3 | 1·4 | — | 1 | 3·3 | = | 3 | 4 | — | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | — | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13.
Найти разность двух смешанных чисел:
| 1 | 1 | — | 3 | 2 | = | 1 | 1 | — | 3 | 2·2 | = | 1 | 1 | — | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | — | 3 | = | -2 | — | 3 | = | -2 | — | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь
Онлайн калькуляторы дробей
Онлайн упражнения с дробями
Калькулятор Смешанных Чисел — Mathcracker.
ComРешатели Алгебра
Инструкции: Используйте этот калькулятор для вычисления смешанных дробей. Укажите смешанную дробь в поле ниже.
Как использовать этот калькулятор смешанных чисел
Калькулятор смешанных дробей поможет вам вычислить любое алгебраическое выражение со смешанными числами и дробями, которые вы предоставите.
Например, вы можете ввести смешанное число ‘2 3/4’, и калькулятор преобразует его в обычную дробь и уменьшит ее.
После того, как вы ввели смешанное число/ дробное выражение, вам нужно нажать «Вычислить», и все шаги будут показаны для вас.
Что такое смешанная дробь
A смешанная фракция это просто целое число, которое идет вместе с дробью. Формат такой: сначала идет целое число, затем пробел, а затем дробь. Например, следующая дробь является смешанной:
\[2\,\,\frac{2}{3}\]
В данном случае целое число — «2», а дробь — «2/3».
Наличие этих двух элементов вместе в данном случае означает, что мы их складываем. Таким образом, когда мы пишем смешанная дробь, мы имеем в виду следующее:
\[2\,\,\frac{2}{3} = 2 + \frac{2}{3}\]
Как вычислить смешанные числа
Основная идея заключается в простом сокращении смешанного числа до суммы дробей. То есть необходимо разделить целую и дробную части смешанного числа и оперировать ими как обычными дробями.
Каковы этапы вычисления смешанных чисел
- Шаг 1: Четко определите, какое смешанное число мы хотим проанализировать
- Шаг 2: Извлечение целой части и дробной части смешанного числа
- Шаг 3: Преобразуйте целую часть в дробь, а затем просто оперируйте ими как дробями
Зачем иметь дело со смешанными дробями?
Использование смешанных дробей (также известных как смешанные числа) — это своего рода унаследованная нотация.
На самом деле она не имеет заметного значения и не играет никакой важной роли. Но знать, как ими оперировать, полезно, поскольку они время от времени появляются в формулах.
Пример: вычисление смешанного числа
Запишите в виде дроби: \(1\,\,\frac{1}{3}\).
Решение:
Нам нужно упростить следующую заданную смешанную дробь: \(\displaystyle 1 \,\, \frac{ 1}{ 3}\).
Получается следующий расчет:
\( \displaystyle 1 \,\, \frac{ 1}{ 3}\)
This is the given mixed fraction
\( = \,\,\)
\(\displaystyle 1\,\,\frac{ 1}{ 3}\)
By definition, the mixed fraction can be written this way
\( = \,\,\)
\(\displaystyle 1+\frac1{ 3}\)
Using \(3\) as the common denominator
\( = \,\,\)
\(\displaystyle \frac{ 1 \times 3 + 1}{ 3}\)
This is a regular fraction obtained after expanding the denominator
\( = \,\,\)
\(\displaystyle \frac{ 4}{ 3}\)
чем завершается расчет.
Пример: еще одно вычисление смешанных дробей
Вычислите следующее смешанное число \(3 + 2\,\,\frac{2}{3}\).
Решение:
Сначала нужно упростить следующую заданную смешанную дробь: \(\displaystyle 2 \,\, \frac{ 2}{ 3}\).
Получается следующий расчет:
\( \displaystyle 2 \,\, \frac{ 2}{ 3}\)
This is the given mixed fraction
\( = \,\,\)
\(\displaystyle 2\,\,\frac{ 2}{ 3}\)
By definition, the mixed fraction can be written this way
\( = \,\,\)
\(\displaystyle 2+\frac2{ 3}\)
Using \(3\) as the common denominator
\( = \,\,\)
\(\displaystyle \frac{ 2 \times 3 + 2}{ 3}\)
This is a regular fraction obtained after expanding the denominator
\( = \,\,\)
\(\displaystyle \frac{ 8}{ 3}\)
Теперь нам нужно вычислить и упростить следующее выражение: \(\displaystyle 3+\frac{8}{3}\).
Получается следующий расчет:
\( \displaystyle 3+\frac{8}{3}\)
Amplifying in order to get the common denominator 3
\( = \,\,\)
\(\displaystyle 3\cdot\frac{3}{3}+\frac{8}{3}\)
Finding a common denominator: 3
\( = \,\,\)
\(\displaystyle \frac{3\cdot 3+8}{3}\)
Expanding each term: \(3 \times 3+8 = 9+8\)
\( = \,\,\)
\(\displaystyle \frac{9+8}{3}\)
Adding up the terms in the numerator
\( = \,\,\)
\(\displaystyle \frac{17}{3}\)
чем завершается расчет.
Другие дробные вычисления
Смешанные числа реже используются в математических обозначениях, поскольку более практичным является их выражение в виде обычных дробей.
В определенной степени преобразование дробей в смешанные числа почти аналогично
перевод из дробной в десятичную систему
, поскольку вы определяете целую часть и десятичную часть.
Смешанные дроби по сути соответствуют дробному исчислению, в котором «пустое место» между целым числом и дробью можно заменить знаком «+», так что получается простое сложение дробей.
Калькулятор смешанных чисел
Онлайн-калькулятор смешанных чисел — это бесплатный и лучший инструмент, который позволяет складывать, вычитать, умножать и делить дробь смешанных чисел. Проще говоря, этот калькулятор дробей и целых чисел позволяет решать задачи дробей с целыми числами и дробями. Этот калькулятор не только упрощает дроби смешанных чисел, но также показывает пошаговый расчет и результат в десятичной дроби, соответствующей заданным входам.
В этом посте мы поможем вам понять, как складывать (+), вычитать (-), умножать (×) и делить (÷) вручную и с помощью онлайн-калькулятора. Но пришло время изучить некоторые основные термины, знаете что? Читай дальше!
Что такое смешанный номер?Смешанное число можно определить как комбинацию целого числа и правильной дроби, существующих вместе. Из-за такой смеси калькулятор смешанных дробей может складывать, вычитать, умножать и делить каждое смешанное число, чтобы легко решать математические задачи. Кроме того, смешанные числа обычно обозначают цифру, которая существует среди любых двух целых чисел. Его можно создать, объединив 3 части, а именно:
- Целое число
- Числитель
- Знаменатель
На основании этой комбинации смешанное число признается частично целым и частично дробным. Например, если смешанное число равно 2(1/5), то:
- Целое число: 2
- Числитель: 1
- Знаменатель: 5
Онлайн-калькулятор смешанных чисел — это инструмент, который помогает выполнять вычисления с 3 частями смешанных чисел: «целым числом», «знаменателем» и «знаменателем».
Смешанные числа также известны как смешанные дроби. Сложение смешанных дробей удобно выполнять с помощью простой алгебраической формулы, если вы выполняете расчеты вручную. Кроме того, онлайн-калькулятор сложения смешанных чисел позволяет мгновенно складывать смешанные дроби. Формула:
- (A разделить на b) + (c разделить на d) = (a умножить на d) + (b умножить на c)/ (b умножить на d)
Пример:
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Подставьте значения в приведенную выше формулу:
- 1 (4 / 6) + 2 (2 / 4) = 10 / 6 + 10 / 4
- (10*6) + (10*4)/6*4
(60) плюс (40) разделить на (24) = 100 на 24
- При упрощении: 100 / 24 = 25 / 6
- 4 (1/6)= 4,16
Однако для сложения смешанных дробей с помощью калькулятора смешанных дробей можно получить быстрые и безошибочные результаты.
Вычитание смешанных дробей звучит сложно, но вы можете сделать это вручную с помощью формулы. Сложение и вычитание смешанных чисел можно выполнять таким же образом с аналогичным уравнением формулы, но с измененными знаками. Все, что вам нужно сделать, это заменить знак сложения на знак вычитания в приведенной выше формуле:
(A разделить на B) – (C разделить на D)= (A умножить на D) – (B умножить на C) / ( B умножить на D)
Пример:
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Подставьте значения в приведенную выше формулу:
- 1 (4/6) – 2 (2/4) = 10/6 – 10/4
- (10*4) – (10*6)/6*4
- (40)– (60) разделить на 24 = – 20 разделить на 24
- При упрощении: – 5 / 6 = – 0,8333
Однако вы можете легко складывать и вычитать смешанные числа с помощью нашего онлайн-калькулятора смешанных чисел.
Умножение смешанных дробей можно выполнить в три простых шага:
- Преобразовать все неправильные дроби в правильные.
- Примените алгебраическую формулу умножения дробей со смешанными числами: a / b * c / d = a * c / b * d.
- Упростите и уменьшите дробь до возможного значения.
Пример :
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Примените формулу и подставьте в нее значения: a/b*c/d = a*c/b*d.
- 10/ 6 * 10/ 4 = 10 * 10/ 6 * 4
- 100/24
При упрощении уравнения: 100/24 = 26/6 = 4 (1/6)
В десятичных дробях: 4,166.
Тем не менее, умножение смешанных чисел с помощью калькулятора смешанных дробей является наиболее подходящим вариантом для выполнения таких сложных вычислений.
Как делить смешанные дроби? Хватит волноваться! Онлайн-калькулятор деления смешанных дробей позволяет делить смешанные дроби за доли секунд.
Но, если вы хотите показать свою работу в классе (пошагово) по делению смешанных дробей, то мы поможем вам на примере решить такие сложные вычисления вручную.
Пример :
Два смешанных числа:
1 (4 / 6)
2 (2 / 4)
Формула деления смешанных чисел: A / b разделить на c / d = a * d /б*с
Подставив значения в приведенную выше формулу, мы получим: 10 / 6 разделить на 10 / 4 = 10 * 4 / 10 * 6 = 40 / 60
0n упростив, мы получим: 2 / 3 = 0,6667
О Калькулятор смешанных чисел:Этот онлайн-калькулятор смешанных дробей — это интеллектуальный инструмент, который поможет вам складывать, вычитать, умножать и делить дробь смешанных чисел. Этот калькулятор для простых смешанных дробей и позволяет заменить смешанное число на неправильную/правильную дробь или наоборот.
Как использовать этот калькулятор смешанных чисел (сложение, вычитание, умножение и деление): Калькулятор упрощения смешанных дробей — это 100% бесплатный инструмент, который упрощает заданное число смешанных дробей в мгновение ока, просто следуйте инструкциям.
данный шаг для достижения мгновенных результатов:
Входы:
- Все, что вам нужно ввести значения смешанной дроби в соответствующие поля этого калькулятора
- Далее вам просто нужно выбрать знак оператора, с помощью которого вы хотите упростить смешанные числа, это может быть (+, -, ×, ÷)
Помните: Если ваше число смешанных дробей состоит из минуса или знака минус (-), то все, что вам нужно, это поставить минус (-) при добавлении значения в данные поля этого калькулятора.
Выводы:
Итак, после того, как вы заполнили вышеуказанные поля, просто нажмите на кнопку расчета, этот калькулятор покажет:
- Упрощение чисел смешанной дроби
- Пошаговый расчет для заданных смешанных фракций
- Смешанная числовая дробь для данного результата (если возможно)
- Десятичное число предоставленного результата (если возможно)
Кроме того, вы также можете преобразовать смешанное число в неправильную дробь, используя наш бесплатный онлайн-калькулятор смешанных чисел в неправильную дробь.
Все, что вам нужно, это нажать «1» на вашем калькуляторе, а затем знак «плюс» (+). «1» символизирует целое число смешанной дроби и добавляет числитель или верхнее число дроби.
Что такое 8 4 как смешанное число?Наибольший общий делитель 8/4 равен 2, поэтому при делении и числителя, и знаменателя на 2 мы получили ответ 2/1, значит только 2. Значит, 2 дальше не выражаются смешанным числом.
Что такое 7/4 как смешанное число?7/4 выражается смешанным числом или смешанной дробью как 1 3/4, 1 считается целым числом, 3 — числителем, а 4 — знаменателем.
Какие примеры смешанных чисел можно привести?Смешанным числом называется комбинация целого числа и дроби. Например: если у вас есть две целые груши и одна половина груши, вы можете представить это как смешанное число: 2 + 1/2 груши или 2 1/2 груши.
Что такое 9 4 как смешанное число? 9/4 выражается в смешанном числе как 2 1/4, 2 указывается как целое число, 1 как числитель и 4 как знаменатель.
3/2 выражается как смешанная дробь/число как 1 1/2, 1 обозначается как целое число, 1 — числитель, а 2 — знаменатель соответственно.
Что такое 4/3 как смешанное число?4/3 выражается в смешанном числе как 1 1/3.
Что такое 7 3 как смешанное число?7/3 выражается в смешанном числе как 2 1/3.
Что такое 8 на 3 как смешанное число?8 больше 3 или 8/3 выражается в смешанном числе как 2 2/3.
Что такое 11 3 как смешанное число?1 1/3 в виде смешанного числа выражается как 3 2/3.
Еда на вынос: Калькулятор смешанных чисел дает вам пошаговую процедуру сложения, вычитания, умножения и деления для всех заданных смешанных чисел. Более того; он также может мгновенно обрабатывать несколько дробей, а также целые числа. Он может служить решателем дробей и даже калькулятором смешанных дробей.
Вот почему это полная поддержка для студентов и профессионалов, занимающихся вычислениями смешанных чисел, чтобы сэкономить их время и энергию, а также получить точные и точные результаты.
Из источника по математике (wikia): Основное математическое определение смешанного числа вы сможете узнать все о: Упрощении смешанных чисел — Определение с примерами
Из источника greenemath: Операции со смешанными числами Урок — Как складывать, вычитать, умножать и делить смешанные числа
Калькулятор дробей — Вычисление дробей
Вычисление дробей — это специальный калькулятор для умножения, деления, сложения и вычитания двух или более дробей и целых чисел. Он может обрабатывать несколько дробей и целых чисел одновременно. Затем он отображает пошаговые решения любой операции, которую он обработал. Иногда мало кто назовет его решателем дробей, в то время как другие могут сказать, что это калькулятор смешанных чисел или калькулятор смешанных дробей.
Это онлайн-калькулятор с кнопкой дроби. На данный момент он может вычислять до десяти дробей и смешанных чисел. Это полезно для всех учащихся всех классов. Его можно использовать в качестве справочника для всех учителей математики и даже для тех специалистов, которые часто используют дроби на работе или дома.
Упрощение
Backspace
Целые числа
Числители
Знаменатели
Как использовать?
Этот калькулятор был разработан для удобства использования.
- Сложение двух дробей
- Нажмите любую цифру из кнопок числителя.
- Нажмите любую цифру из кнопок знаменателя.
- Нажмите кнопку добавления (+) .
- Нажмите любую цифру из кнопок числителя для второй дроби.
- Нажмите любую цифру из кнопок знаменателя для второй дроби.
- Нажмите кнопку равно (=) , чтобы вычислить ответ. Ответ и решение будут отображаться выше.
- Повторите шаги, описанные выше, за исключением последнего шага.
- Нажмите кнопку добавления (+) .
- Нажмите любую цифру из кнопок числителя для третьей дроби.
- Нажмите любую цифру из кнопок знаменателя для третьей дроби.
- Нажмите кнопку равно (=) , чтобы вычислить ответ, или нажмите кнопку добавления (+) , чтобы добавить другие дроби.
- Тот же процесс будет использован для четвертой, пятой или любого количества фракций. Просто нажмите кнопку равно (=) для вычисления.
- Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку вычитания (-) .
- Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку умножения (x) для умножения и деления (÷) кнопку для разделение.
Важно помнить, что при работе со смешанными числами при использовании этого калькулятора никогда не забывайте вводить целые числа.
Кнопки целых чисел в калькуляторе больше, чем кнопки числителя и знаменателя. Вам нужно только сначала нажать кнопку целого числа, а затем дробь, после чего вы можете перейти к любой операции, которую хотите.
- Нажмите кнопку целого числа, если ваша дробь состоит из целого числа, или вы можете напрямую нажать кнопку числителя, если вам не нужно целое число. Вы не можете нажать кнопку знаменателя, если вы не нажали целое число или кнопку знаменателя. Это означает, что вам нужно сначала нажать кнопку целого числа или числителя. После нажатия кнопки числителя вы больше не можете нажимать кнопку целого числа. Вы можете нажать кнопку целого числа еще раз только в том случае, если вы удалите числитель, нажав кнопку возврата. Нули не должны быть нажаты первыми. Нули будут нажаты после нажатия ненулевых чисел.
- Нажмите кнопку знаменателя для вашего знаменателя. После нажатия вы не можете снова нажать кнопку целого числа или числителя. Вы можете нажать кнопку числителя только в том случае, если вы удалите знаменатель, нажав кнопку возврата.
- Выберите любую операцию.
- Нажмите кнопку Равно , если вы закончили с дробью. Решение будет отображаться выше.
- Нажмите Backspace , если вы хотите удалить по одному номеру за раз.
- Нажмите Кнопка AC для очистки уравнения дроби.
- На данный момент этот калькулятор ограничен только 10 дробями.
Вы можете нажать кнопку числителя только в том случае, если вы удалите знаменатель, нажав кнопку возврата.Калькулятор дробей на мобильных телефонах Android
Выпущен наш калькулятор дробей для мобильных телефонов Android. Он может обрабатывать базовые и сложные операции с дробями и может отображать решение как методом перекрестного умножения, так и методом LCD (наименьший общий знаменатель). Вы можете получить его из магазина Google Play.
Как был выполнен расчет?
Иногда возникают сомнения в том, как выполняются вычисления при использовании нескольких операций. Используя нотацию MDAS, умножение и деление имеют такой же приоритет, но выше, чем сложение и вычитание.
Сложение и вычитание имеют одинаковый приоритет. Сначала обрабатывается более высокий приоритет. Это всегда было правилом, и оно соблюдалось повсеместно. При одинаковом приоритете операция выполняется слева направо.
Калькулятор дроби целого числа
Fraction Calc также является калькулятором дробей целых чисел, потому что он может обрабатывать множество целых чисел. Работа с целыми числами означает, что вам нужно больше учиться и делать дополнительные шаги, преобразовывая целые числа в формат, подходящий для математических операций. Выполнение математических операций с целыми числами означает, что вам нужно выполнить дополнительные действия, чтобы получить правильный ответ. Это означает дополнительную энергию и нагрузку для людей, которые оказались в ситуации, когда им нужно решать целые числа и дроби. Вот почему некоторые люди ищут калькулятор дробей и целых чисел, чтобы не только найти простые решения сложных задач, но и сэкономить время и энергию. Экономия времени и энергии на определенной задаче означает, что вы получаете дополнительные ресурсы для выполнения еще более важной задачи, которая была бы очень полезной.
3 Калькулятор дробей
В большинстве случаев в любой математической арифметике используются только две дроби. Очень редко в какой-либо операции участвуют 3 фракции. Но если это ваш случай, то вам очень повезло, что вы нашли этот инструмент. Вы можете легко использовать этот инструмент в качестве калькулятора 3-х дробей, потому что он может абсолютно решить эту проблему. Это основная цель этого инструмента. Некоторые люди никогда не слышали об этом инструменте, поэтому они специально искали калькулятор с тремя дробями. Но теперь, когда его инструмент создан, я думаю, у них больше нет времени беспокоиться.
Калькулятор кратных дробей
Большинство созданных калькуляторов имеют ограниченные возможности до такой степени, что могут вычислять только две дроби за раз. Но Fraction Calc может даже больше. Он может решить до 10 целых чисел или дробей вместе взятых. Вот почему многие называют его калькулятором кратных дробей. Это очень специализированный калькулятор с целыми числами.
С комбинацией целого числа и дроби трудно иметь дело, но с этим калькулятором кратных дробей вычисления становятся проще. Сложение смешанных чисел, преобразование дробей в целые числа, умножение дробей на целые числа, вычитание смешанных чисел и умножение смешанных дробей — вот некоторые из процессов, которые может выполнять этот калькулятор.
Преимущества и недостатки использования калькулятора дробей.
- Преимущества:
- Прост в использовании.
- Экономит больше времени и энергии.
- Нет необходимости в ручных вычислениях.
- Вычисленный результат точен и точен.
- Это может затруднить вычисление дробей.
- Вы будете очень зависеть от него в будущем.
- Вы можете забыть правила вычисления.
Правила работы с дробями
- Сложение и вычитание дробей
Сложение и вычитание дробей выполняются по одним и тем же правилам.
Они должны иметь одинаковые знаменатели для выполнения выбранной операции. Вы можете сложить или вычесть две дроби, если у них один и тот же знаменатель, если нет; вы должны создать общий знаменатель, прежде чем складывать или вычитать их.
Подобные дроби — это дроби, имеющие одинаковые знаменатели. Чтобы сложить дроби с одинаковым знаменателем, добавьте его числитель. Например, 2/5 + 1/5 = 3/5.
Дроби, имеющие разные знаменатели, не похожи на дроби. Чтобы сложить разные дроби, нужно привести их к общему знаменателю. Самый простой способ сделать это — использовать метод бабочки. Чтобы выполнить метод бабочки, выполните следующие действия.
- Умножьте числитель первой дроби на знаменатель второй дроби. Результатом будет первый числитель дроби.
- Умножить знаменатель первой дроби на знаменатель второй дроби. Результатом будет новый знаменатель первой дроби.
- Умножьте числитель второй дроби на знаменатель первой дроби. Результатом будет новый числитель второй дроби.
- Умножьте знаменатель второй дроби на знаменатель первой дроби. Результат теперь является новым знаменателем второй дроби.
Например: 2/3 + 3/5.
- 2 х 5 = 10.
- 3 х 5 = 15.
- 3 х 3 = 9.
- 5 х 3 = 15.
Новая фракция: 10/15 и 9/15.
15/10 + 15/9 = 15/19.
Новая дробь 19/15.
Чтобы вычесть дроби с одинаковым знаменателем, просто вычтите числитель второй дроби из числителя первой дроби. Пример: 4/6 – 3/6 = 1/6.
Для дробей с разными знаменателями приведите их к одному знаменателю, используя метод бабочки, а затем выполните вычитание после того, как у них будет одинаковый знаменатель.
Правило умножения двух дробей простое. Умножьте числитель первой дроби на числитель второй дроби и умножьте знаменатель первой дроби на знаменатель второй дроби. Пример: 2/3 х 1/5 = 2/15.
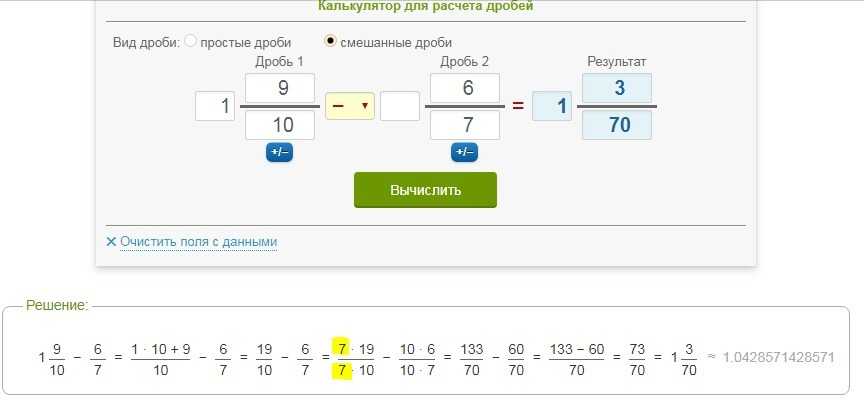
Чтобы разделить две дроби, вы должны сначала инвертировать вторую дробь, а затем начать умножать две дроби.
Пример: 2/3 разделить на 1/5 = 2/3 x 5/1 = 10/3.
Когда вы сокращаете неправильную дробь до наименьшего члена, вам нужно преобразовать ее в смешанное число. Это делается делением числителя на знаменатель. Частное будет целым числом. Остаток будет новым числителем, а знаменатель останется прежним.
При делении или умножении смешанных чисел вам нужно, чтобы оно превратилось в неправильную дробь. Это делается путем умножения целого числа на знаменатель, а затем добавления текущего числителя. Результатом будет новый числитель, а знаменатель останется прежним.
Для дробей с одинаковыми знаменателями дробь с наибольшим числителем является большей, чем дробь с меньшим числителем.
Для дробей с одинаковыми числителями дробь с наибольшим знаменателем меньше дроби с меньшим знаменателем.
Из темы выше мы уже знаем, что есть равнозначные дроби-дроби, одинаковые по значению, даже если у них разные числители и знаменатели.
Упрощение дроби означает использование наименьшего числителя и знаменателя, но одного и того же значения. Дробь имеет простейшую форму, когда нет общего множителя для числителя и знаменателя. Например, вместо использования 7/14 мы можем использовать ½, что является самой простой формой.
Наибольший общий делитель — это наибольшее число, используемое для деления числителя и знаменателя для получения простейшей формы дроби. Например, для дроби 12/30 наибольшее число, на которое можно разделить как числитель, так и знаменатель, равно 6. Разделив его на 6, вы получите его простейшую форму — 2/5.
Факты о дробях
Дроби являются частями целого. Например, один торт на пятерых детей. Итак, торт делится на пять частей. Каждый ребенок получит одну часть торта. Дробь будет 1/5. Каждый ребенок получит 1/5 торта.
Дробь состоит из двух частей. Верхняя половина называется числителем. Нижняя половина называется знаменателем.
Числитель — это часть целого, где она используется или с которой в настоящее время имеют дело.
Существуют три типа дробей: правильная дробь, неправильная дробь и смешанные числа.
Правильная дробь — это дробь, числитель которой всегда меньше знаменателя.
Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.
Смешанное число представляет собой целое число плюс дробь.
Равные дроби — это дроби, которые имеют разные числители и знаменатели, но имеют одинаковое значение, например 1/2, 2/4, 7/14, 8/16, 10/20, 20/40 и 50/100.
Как был создан калькулятор дробей?
Когда я был студентом, у меня был предмет по математике. Одна из тем была о дроби. Хотя эта тема сложна, меня очень удивило, почему трудно определить, правильное решение или нет. Вы должны просмотреть его несколько раз, чтобы убедиться, что ваше решение является правильным. Это произошло не только у меня. Я узнал, что большинство студентов испытывали то же самое.