Опубликовано Решение уравнения x 1. Как решается система уравнений? Методы решения систем уравнения
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0 , где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения .
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
Если a ≠ 0, то х = ‒ b/a .
Пример 1. Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9: 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3 .
Если а = 0 и b = 0 , то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число .
Если а = 0 и b ≠ 0 , то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3. Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
На рисунке 1 изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4. Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме :
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2 ), третьего (Пример. 1, 3 ) и даже с пятого этапа, как в примере 5.
Пример 5. Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4: 2,
х = 1/8 .
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
Ответ: ‒ 0, 125
Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
Ответ: 2,3
Пример 8. Решите уравнение
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
Пример 9. Найдите f(6), если f (x + 2) = 3 7-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 3 7-4 = 3 3 = 27
Ответ: 27.
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ .
Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул.
Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или .
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
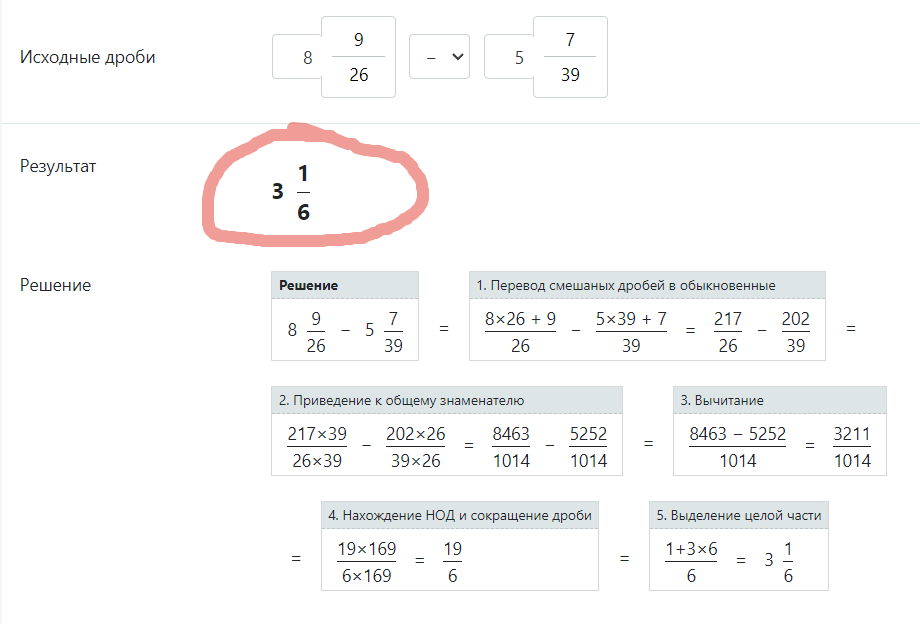
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Выполнить сложение дробей путем сложения их числителей.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Онлайн калькуляторы и конвертеры:
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.
Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
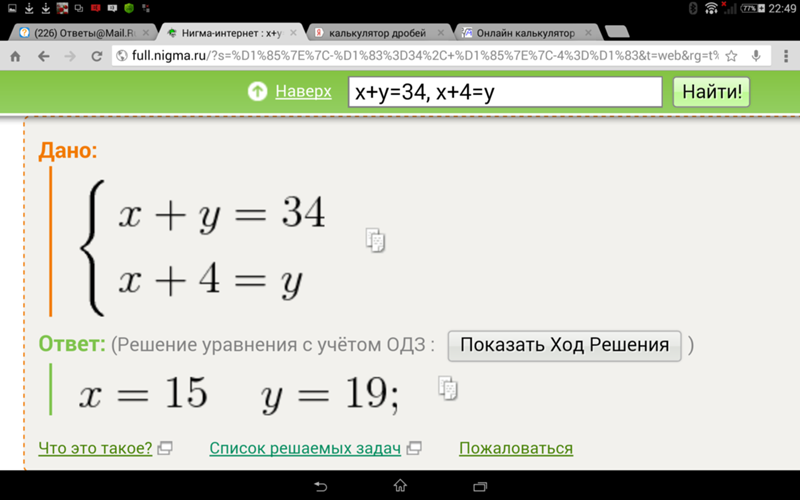
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки
2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)
1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y
2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1
3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.
Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)
Пример №2:
Решим методом почленного сложения (вычитания).
Решение системы уравнений методом сложения
3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)
1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн .
Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Линейные диофантовы уравнения онлайн
Линейным диофантовым уравнением с двумя неизвестными называется уравнение вида:
В основе нашего калькулятора лежит расширенный алгоритм Евклида, записанный в виде цепной дроби.
Однако, в некоторых случаях (например, когда коэффициент
) применяются более простые подходы. Также калькулятор не рассматривает случаи, когда хотя бы один из коэффициентов
или
равен
, так как они приводят к обычному
линейному уравнению.
Если коэффициент не делится нацело на , то линейное диофантово уравнение с двумя неизвестными не имеет решений. Напротив, если делится нацело на , то указанное уравнение имеет бесконечное множество целых решений.
Для решения линейного диофантового уравнения с двумя неизвестными сначала необходимо найти частное решение и , а затем записать общее решение, используя формулы:
Рассмотрим пример решения линейного диофантового уравнения с двумя неизвестными:
Коэффициенты уравнения:
.
Поскольку делится нацело на , то данное уравнение имеет решения в целых числах.
Далее, найдём какое-нибудь конкретное (частное) решение и исходного уравнения. Для этого, сначала необходимо найти частное решение и вспомогательного уравнения с коэффициентом :
а затем умножить найденное частное решение и вспомогательного уравнения на и получить частное решение и исходного уравнения:
Чтобы найти частное решение вспомогательного уравнения используем цепные дроби. Для этого составим дробь
, числителем которой будет коэффициент
, а знаменателем коэффициент
.
Преобразуем данную дробь в цепную дробь:
В полученной цепной дроби отбросим последнюю дробь :
Полученная дробь является отношением частных решений и выбранных с правильным знаком:
Подставляя четыре значения во вспомогательное уравнение, определяем его частное решение:
Теперь, чтобы найти частное решение и исходного уравнения, умножим найденное частное решение и вспомогательного уравнения на :
Используя формулы для общего решения, запишем конечный ответ:
Наш онлайн калькулятор может решить любое линейное диофантово уравнение с двумя неизвестными с описанием подробного хода решения на русском языке.
Чтобы начать работу, необходимо ввести уравнение и задать искомые переменные.
В описании подробного решения встречается функция которая означает — наибольший общий делитель чисел и .
Калькулятор диофантовых уравнений
Переменная-1: xyztupqnms
Переменная-2: xyztupqnms
Дано линейное диофантово уравнение:5x6y19Найти:x- ?y- ?Установить калькулятор на свой сайт
Другие полезные разделы:
Разложение на множители онлайнРешение систем неравенств онлайн
Метод Ньютона онлайн
Оставить свой комментарий:
Алгебраические дроби Калькулятор и Решатель
Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора
Алгебраических дробей .
Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!1
2
3
4
5
6
7
8
900 06 9а
б
в
г
е
g
m
n
u
v
w
x
y
z 9 0007
.
(◻)
+
—
×
◻/◻
/
÷
◻ 90 069 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞
e
π
ln
журнал
журнал ◻
lim
d/dx
D □ x
∫
∫ 9 0069 ◻
|◻|
θ
=
>
<
>=
<=
sin
cos
tan
кроватка
sec
csc
asin
acos
atan
acot
asec
acsc
sinh
cosh
tanh
coth
sech
csch
asinh
acosh
atanh
acoth 9000 7
АШ
АШ
Пример
Решенные проблемы
Сложные задачи
1
Решенный пример алгебраических дробей
$\frac{a}{c\cdot \left(x+\frac{b}{a}\right)\left(x+\frac{d}{c}\right)} $
2
Объединить $x+\frac{b}{a}$ в одну дробь
$\frac{a}{c\frac{b+xa}{a}\left(x+\frac{d}{c} \справа)}$
3
Объединить $x+\frac{d}{c}$ в одну дробь
$\frac{a}{c\frac{b+xa}{a}\frac{d+xc}{c}}$
4
Умножение дроби на $c\frac{d+xc}{c}$
$\frac{a}{\frac{c\left(b+xa\right)\frac{d+xc}{c }}{а}}$
5
Умножение дроби на $c\left(b+xa\right)$
$\frac{a}{\frac{\frac{c\left(d+xc\right)\left(b+xa\ справа)}{c}}{a}}$
6
Упростите дробь $\frac{c\left(d+xc\right)\left(b+xa\right)}{c}$ на $c$
$\frac{a}{\frac{\ влево(d+xc\вправо)\влево(b+xa\вправо)}{a}}$
7
Разделение дробей $\frac{a}{\frac{\left(d+xc\right)\left(b+xa\right)}{a}}$ с помощью Keep, Change, Flip: $a\div \ frac{b}{c}=\frac{a}{1}\div\frac{b}{c}=\frac{a}{1}\times\frac{c}{b}=\frac{a \cdot c}{b}$ 92}{\влево(d+xc\вправо)\влево(b+xa\вправо)}$
Проблемы с математикой?
Доступ к подробным пошаговым решениям тысяч проблем, число которых растет с каждым днем!
Калькулятор пропорций (Решатель) — Найти неизвестное x
РЕЗУЛЬТАТЫ
Как пользоваться этим калькулятором пропорций?
Чтобы решить дроби для неизвестных x с помощью этого решателя пропорций, выполните следующие шаги:
- Введите значения
- Убедитесь, что один вход неизвестен (x).
- Нажмите кнопку « вычислить »
После нажатия кнопки вы получите значение неизвестно x и пошаговое решение методом перекрестного умножения и пропорции.
Неизвестный х 0
Оставьте свой отзыв!
Худший Бедный Средний Хороший Супер
Содержание
| 1 | Что такое пропорция? |
| 2 | Формула пропорции |
| 3 | Перекрестное умножение для решения пропорций |
| 4 | Перекрестное умножение для проверки соотношения между двумя неизвестными переменными |
«Пропорция — это утверждение, которое определяет тот факт, что два отношения имеют равные значения. Например, рассмотрим следующее».
ab=uv\dfrac{a}{b} = \dfrac{u}{v}ba=vu
Приведенное выше математическое утверждение показывает, что значение a/b («a», деленное на «b», ) совпадает со значением u/v («u», деленное на «v»).
Предположим, что если значение (ab)\Big(\dfrac{a}{b}\Big)(ba) равно 10, то (uv)\Big(\dfrac{u}{v}\Big)(vu ) также будет иметь значение 10.
Пропорция между двумя отношениями может быть выражена с помощью 2 форм.
1. Форма дроби
Соотношение между a,b и u,v будет выглядеть следующим образом, если используется формат дроби.
ab=uv\dfrac{a}{b} = \dfrac{u}{v}ba=vu
В форме дроби между каждой парой чисел используется косая черта «/».
2. Форма отношения
Пропорция c,dc,dc,d и e,fe,fe,f будет выглядеть следующим образом, если используется схема отношения.
c:d=e:fc:d = e:fc:d=e:f
В форме соотношения между каждой парой переменных вместо косой черты появляется двоеточие «:».
Формула пропорции
Формула пропорции приведена ниже для пар переменных (a,b)(a,b)(a,b) и (c,d)(c,d)(c,d)
Пропорция =ab=cd\text{Proportion} = \dfrac{a}{b} = \dfrac{c}{d}Proportion=ba=dc
Понятие пропорции используется для определения значения неизвестной переменной X Учтите, что значение X необходимо определить в приведенном ниже уравнении.
366=X10\dfrac{36}{6} = \dfrac{X}{10}636=10X
Решение дается следующим образом:
366=X10\dfrac{36}{6} = \ dfrac{X}{10}636=10X
6=X106 = \dfrac{X}{10}6=10X
X=6×10X = 6 \times10X=6×10
X=60X = 60X=60
Понимание шагов расчета
Вот шаги, которые были выполнены в предыдущем вопросе
Здесь у нас есть два отношения, и одно из них имеет неизвестное значение «x». С помощью концепций пропорций необходимо определить значение X. Здесь нужно знать термины «крайности» и «средства». В приведенном выше примере у нас есть четыре значения (10010)\Big(\dfrac{100}{10}\Big)(10100) и 366=X10\dfrac{36}{6} = \dfrac{X}{10 }636=10X Экстремумы – это значения, формирующие наклон вниз (в данном случае 36 и 10). Однако значения, образующие наклон вверх, равны (6 и X).
Умножьте два крайних значения и два средних значения друг на друга соответственно. Это даст вам следующее уравнение.
366=X10\dfrac{36}{6} = \dfrac{X}{10}636=10X
6=X106 = \dfrac{X}{10}6=10X
X=6 ×10X = 6 \times10X=6×10
X=60X = 60X=60
Перекрестное умножение для решения пропорций
Когда вы решаете пропорцию, применяется понятие перекрестного умножения.
Что такое перекрестное умножение? Когда у вас есть два отношения с ожидаемыми равными значениями, выполняются определенные шаги упрощения. Первым из этих шагов является перекрестное умножение. Например, рассмотрим, что у нас есть следующие два отношения, которые считаются равными.
- cp\dfrac{c}{p}pc
- dq\dfrac{d}{q}qd
Поскольку эти два отношения равны, их можно использовать в форме пропорции. Другими словами, мы можем написать следующее утверждение, чтобы уточнить этот момент.
cp=dq\dfrac{c}{p} = \dfrac{d}{q}pc=qd
Теперь нам нужно выполнить перекрестное умножение, чтобы продолжить процесс вычисления пропорции. В приведенных выше наборах соотношений «c» будет умножаться на «q», а «d» будет умножаться на «p». Эта форма умножения называется перекрестным умножением, потому что значения умножаются в виде двух диагоналей, которые выглядят как крест. Перейдем к шагам импликации.
cp=dq\dfrac{c}{p} = \dfrac{d}{q}pc=qd
c×q=p×dc \times q = p \times dc×q=p×d
Перекрестное умножение для проверки пропорции между двумя неизвестными переменными
Если у вас есть две неизвестные переменные, можно использовать концепцию перекрестного умножения для проверки пропорции между двумя неизвестными переменными.