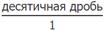Десятичные дроби стали использовать для более удобной записи обыкновенных дробей. Чтобы записать десятичную дробь необходимо целую и дробную части отделить друг от друга запятой. Если дробь не содержит целой части, необходимо поставить ноль перед запятой. Если дробь имеет знаменатель вида 10, 100, 1000 и т.д. и количество цифр в числителе меньше, чем в знаменателе, то для перевода такой дроби в обыкновенную необходимо посчитать число цифр в числителе и число нулей в знаменателе. Например, у дроби
(ноль целых 12 тысячных) 2 цифры в числителе и 3 ноля в знаменателе. 3 – 2 = 1, следовательно, необходимо записать один ноль после запятойПриведем еще пример, дробь
У этой дроби в числителе 1 цифра, 3 ноля в знаменателе. 3 – 1 = 2, следовательно, необходимо записать два ноля после запятой
И последний пример, дробь
У данной дроби в числителе 2 цифры и в знаменателе 2 ноля. 2 – 2 = 0, следовательно, не нужно добавлять ноль после запятой
В случае если знаменатель дроби является числом отличным от чисел типа 10, 100, 1000 и т.д., то тогда необходимо такую дробь привести к знаменателю вида 10, 100, 1000 и т.д. Первым делом необходимо привести дробь к несократимому виду. Затем разложить знаменатель дроби на простые множители. Если в разложении будет хотя бы один множитель отличный от 2 или 5, то такую дробь можно представить только в виде бесконечной десятичной дроби. Если в разложении дроби все множители являются числами 2 или 5, тогда необходимо сделать так, чтобы число двоек и пятерок было одинаковым. Для этого нужно до множить числитель и знаменатель дроби на недостающее количество двоек или пятерок. Например,
| 1∙5∙5 | = | |
| 2∙2∙2∙5∙5∙5 |
Приведем еще один пример
| 6 | 101 | = |
| 2∙2∙2∙5∙5 |
| 6 | 101∙5 | = |
| 2∙2∙2∙5∙5∙5 |
Приведем пример бесконечной десятичной дроби
При переводе данной дроби в десятичную получается бесконечная десятичная дробь
Более подробно о десятичных дробях можно прочитать в данной статье.
Механика
Электричество и магнетизм
Конденсаторы
Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст продробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12).
Как складывать столбиком
Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.
345 + 67 = 412
110
+345
67
412
1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412
Приведем еще один пример: 1567 + 761
1567 + 761 = 2328
1100
+1567
761
2328
1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
4) Под числом 1 нет слагаемого, поэтому просто прибавим 1 + 1 = 2
Как складывать столбиком десятичные дроби
Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02
123.345 + 46.02 = 169.365
+123.345
46.020
169.365
1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365
Приведем следующий пример: 123.99 + 12.99
123.99 + 12.99 = 136.98
001010
+123.99
12.99
136.98
1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Ответ: 136.98
Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.
23 + 0.34 = 23.34
+23.00
0.34
23.34
1) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
4) 3 + 0 = 3. Запишем 3
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34
Как вычитать столбиком
Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.
456 — 89 = 367
..0
—456
89
367
1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.
2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.
3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.
Приведем еще один пример: 307 – 58
307 — 58 = 249
..0
—307
58
249
1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.
2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.
3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.
Как вычитать столбиком десятичные дроби
Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.
Например вычтем столбиком из десятичной дроби 123.478 целое число 56
123.478 — 56 = 67.478
..00000
—123.478
56.000
67.478
Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.
4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
7) Над числом 1 стоит точка, следовательно, 1 – 1 = 0, поэтому на этом решение законченно.
Ответ: 67.478
Еще один пример на вычитание столбиком десятичной дроби из целого числа.
432 — 2.95
432 — 2.95 = 429.05
0..0.0
—432.00
2.95
429.05
1) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Ответ: 429.05
Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:
378.326 — 26.57 = 351.756
00.0.00
—378.326
26.570
351.756
0.07 — 0.009 = 0.061
000.0
—0.070
0.009
0.061
Как умножать столбиком
Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.
На примере будет намного понятнее. Итак, умножим 367 на 12
367 × 12 = 4404
×367
12
734
3670
4404
1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.
2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.
1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367
3. Теперь нам необходимо сложить получившиеся два числа 734 и 367
1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.
Как умножать столбиком десятичные дроби
Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении. На примерах все станет намного понятнее.
Умножим 0.2354 на 12.3997
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×123997
2354
495988
6199850
37199100
247994000
291888938
Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938
×12.3997
0.2354
2.91888938
Умножим 49.265 на 0.0045
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×49265
45
246325
1970600
2216925
Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7. Сдедовательно в ответе после точки будет 7 чисел.
0.2216925
×49.265
0.0045
0.2216925
Как делить столбиком
Как делить столбиком целые числа.
Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.
Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).
На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5
12 : 5 = 2.4
01205
01002.4
0020
0020
0000
При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.
1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4
Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3
7 : 3 = 2.(3)
0703
0602.3
010
009
001
1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 — 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2.333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)
Деление десятичных дробей в столбик примеры
Разделим 3.12 на 3.6
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100
07120360
036001.97
03520
03240
002800
002520
000280
Разделим 9.4 на 45.1
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 10
0940451
00000.2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Перевести обыкновенную дробь в десятичную дробь
Калькулятор онлайн перевод обыкновенных дробей
Рассчитать Очистить Десятичную в обыкновенную\begin{align} \end{align}
Введите обыкновенную дробь, калькулятор переведет ее в десятичную дробь и покажет решение.
Если нельзя перевести в десятичную дробь, калькулятор переведет дробь в бесконечную периодическую десятичную дробь, вычислит период дроби и округлит число до 8 знаков после запятой.
Перевод обыкновенной дроби в десятичную дробь
Несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя b на простые множители не содержит чисел, отличных от 2 и 5.
В результате преобразования получается бесконечная периодическая десятичная дробь .
Простой способ преобразования
Воспользуйтесь калькулятором, разделите числитель дроби на знаменатель в результате получите десятичную дробь.
Пример Преобразовать дробь в десятичную дробь
Разделим с помощью калькулятора числить на знаменатель, получим .
Альтернативный метод преобразования
Привести знаменатель дроби к 10, 100, 1000, 10000 и т.д. Найдите число которое преобразует знаменатель к числу из списка (10, 100, 1000, и т.д.). Умножьте числитель и знаменатель на данное число, затем запишите числитель в виде десятичной дроби, расположив запятую(точку) в зависимости от количества нулей в знаменателе.
В примере показано как переводить дробь в десятичную дробь ручным способом.
Пример Преобразовать дробь в десятичную.
.
.
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Онлайн калькулятор уравнений с дробями |
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: 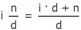
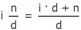
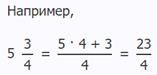
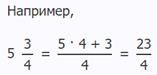
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная


- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.


Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Понравилось? Поделись с друзьями!
| Вам могут также быть полезны следующие сервисы |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
С помощью данного калькулятора онлайн вы можете преобразовать десятичную дробь в обыкновенную или смешанную числовую дробь.
Калькулятор онлайн для перевода десятичной дроби в обыкновенную не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
- Главная
- Математические калькуляторы
- Преобразование десятичной дроби в обыкновенную дробь
Десятичные дроби — это дробные числа, которые представлены в десятичной записи.
Десятичные дроби используются для более компактной записи правильных обыкновенных дробей, знаменателями которых являются числа 10, 100, 1000 и т.д. и смешанные числа, знаменателями дробной части которых являются числа 10, 100, 1000 и т.д.
Например, обыкновенную дробь 810 можно записать в виде десятичной дроби 0,8, а смешанное число 4058100 — в виде десятичной дроби 405,08.
Онлайн калькулятор для преобразование десятичных дробей в обыкновенные дроби позволяет быстро перевести десятичные дроби в обыкновенные дроби.
Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
1. Посчитать, сколько цифр стоит после запятой. Например, у дроби 1,75 таких цифр две, а у 0,0025 — четыре. Обозначим это количество буквой n.
2. Переписать исходное число в виде дроби вида a10n, где a — это все цифры исходной дроби (без «стартовых» нулей слева, если они есть), а n — то самое количество цифр после запятой, которое мы посчитали на первом шаге. Другими словами, необходимо разделить цифры исходной дроби на единицу с n нулями.
3. По возможности сократить полученную дробь.
Например:
0,64 = 64100 = 1625
Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому n = 2. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64.
Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит именно сто.
Затем остаётся лишь сократить числитель и знаменатель на их наибольший общий делитель. НОД (64, 100) = 4.
Поделиться страницей в социальных сетях:Калькулятор десятичной дроби в
Использование калькулятора
Этот калькулятор преобразует десятичное число в дробь или десятичное число в смешанное число. Для повторения десятичных знаков введите, сколько десятичных знаков в вашем десятичном числе повторяется.
Ввод повторяющихся десятичных знаков
- Для повторяющегося десятичного числа, такого как 0,66666 … где 6 повторяется навсегда, введите 0.6, и так как 6 является единственным последним десятичным знаком, который повторяется, введите 1 для десятичных знаков для повторения. Ответ 2/3
- Для повторяющегося десятичного числа, такого как 0,363636 …, где 36 повторяется вечно, введите 0,36, и, поскольку 36 — это только два конечных десятичных знака, которые повторяются, введите 2 для десятичных знаков для повторения. Ответ 4/11
- Для повторяющихся десятичных, таких как 1.8333 … где 3 повторяется вечно, введите 1.83, и так как 3 является единственным последним десятичным знаком, который повторяется, введите 1 для десятичных разрядов для повторения. Ответ 1 5/6
- Для повторяющегося десятичного числа 0,857142857142857142 ….. где 857142 повторяется вечно, введите 0,857142, а поскольку 857142 — это 6 конечных десятичных разрядов, которые повторяются, введите 6 для десятичных знаков для повторения. Ответ 6/7
Как конвертировать отрицательный десятичный дробь в дробь
- Удалить отрицательный знак из десятичного числа
- Выполните преобразование на положительное значение
- Применить отрицательный знак к ответу дроби
Если a = b, то верно, что -a = -b.
Как конвертировать десятичную дробь в
- Шаг 1. Сделайте дробь с десятичным числом в качестве числителя (верхнее число) и 1 в качестве знаменателя (нижнее число).
- Шаг 2: Удалить десятичные разряды умножением. Сначала посчитайте, сколько мест находится справа от десятичной дроби. Далее, учитывая, что у вас есть x десятичных знаков, умножьте числитель и знаменатель на 10 x .
- Шаг 3: Уменьшите дробь.Найдите наибольший общий фактор (GCF) числителя и знаменателя и разделите числитель и знаменатель на GCF.
- Шаг 4. Упростите оставшуюся дробь до смешанной дробной части, если это возможно.
Пример: преобразование 2,625 в дробь
1. Перепишите десятичное число в виде дроби (более 1)
\ (2.625 = \ dfrac {2.625} {1} \)
2.Умножьте числитель и знаменатель на 10 3 = 1000, чтобы исключить 3 десятичных знака
\ (\ dfrac {2.625} {1} \ times \ dfrac {1000} {1000} = \ dfrac {2625} {1000} \)
3. Найдите наибольший общий коэффициент (GCF) 2625 и 1000 и уменьшите дробь, разделив числитель и знаменатель на GCF = 125
\ (\ dfrac {2625 \ div 125} {1000 \ div 125} = \ dfrac {21} {8} \)
4.Упростить неправильную дробь
\ (= 2 \ dfrac {5} {8} \)
Следовательно,
\ (2.625 = 2 \ dfrac {5} {8} \)
Десятичная дробь до
- Для другого примера, преобразуйте 0,625 в дробь.
- Умножьте 0,625 / 1 на 1000/1000, чтобы получить 625/1000. Снижение
- получаем 5/8.
Преобразование повторяющейся десятичной дроби в дробную
- Создайте уравнение, такое что x равно десятичному числу.
- Подсчитайте количество десятичных знаков, у. Создайте второе уравнение, умножив обе стороны первого уравнения на 10 и .
- Вычтите второе уравнение из первого уравнения.
- Решить для х
- Уменьшить дробь.
Пример: преобразование повторяющихся десятичных 2,666 в дробь
1. Создайте уравнение, такое что x равно десятичному числу.
Уравнение 1:
\ (x = 2. \ overline {666} \ tag {1} \)
2. Подсчитайте количество десятичных знаков, у. В повторяющейся десятичной группе 3 цифры, поэтому y = 3. Построить второе уравнение, умножив обе части первого уравнения на 10 3 = 1000
Уравнение 2:
\ (1000 х = 2666.\ overline {666} \ tag {2} \)
3. Вычтите уравнение (1) из уравнения (2)
\ (\ eqalign {1000 x & = & \ hfill2666.666 … \ cr x & = & \ hfill2.666 … \ cr \ hline 999x & = & 2664 \ cr} \)
Получаем
\ (999 x = 2664 \)
4. Решите для х
\ (x = \ dfrac {2664} {999} \)
5. Уменьшите дробь. Найдите наибольший общий коэффициент (GCF) из 2664 и 999 и уменьшите дробь, разделив числитель и знаменатель на GCF = 333
\ (\ dfrac {2664 \ div 333} {999 \ div 333} = \ dfrac {8} {3} \)
Упростить неправильную дробь
\ (= 2 \ dfrac {2} {3} \)
Следовательно,
\ (2.\ overline {666} = 2 \ dfrac {2} {3} \)
Повторение десятичной дроби до
- Для другого примера, преобразовать повторяющиеся десятичные 0,333 в дробь.
- Создайте первое уравнение с x равным повторяющемуся десятичному числу:
х = 0,333 - Есть 3 повторяющихся знака после запятой. Создайте второе уравнение, умножив обе части (1) на 10 3 = 1000:
1000X = 333.333 (2) - Вычтите уравнение (1) из (2), чтобы получить 999x = 333 и решить для х
- x = 333/999
- Уменьшая дробь, получаем х = 1/3
- Ответ: х = 0,333 = 1/3
Связанные калькуляторы
Чтобы преобразовать дробь в десятичную смотри Фракция в десятичный калькулятор.
Список литературы
Википедия. «Повторение десятичной дроби», Википедия, Свободная энциклопедия. Последнее посещение 18 июля 2016 г.
,Калькулятор дробной части— калькулятор дюйма
Преобразуйте десятичное значение в дробь, используя наш калькулятор, введя десятичное значение ниже. Калькулятор найдет уменьшенную дробь и покажет всю работу, чтобы вы могли видеть, как это сделать. Также посмотрите наш калькулятор дроби в десятичную, чтобы узнать, как преобразовать дробь в десятичную.
Решение:
.75 = 34
Преобразуйте десятичную дробь в дробь, поместив десятичную дробь свыше 1 в формате дроби
0.75 = .751
Умножьте числитель и знаменатель на 10, чтобы исключить десятичные разряды
0,75 × 101 × 10 = 7,510
Умножьте числитель и знаменатель на 10, чтобы исключить десятичные разряды
7,5 × 1010 × 10 = 75100
Уменьшите дробь, найдя наибольший общий фактор. Наибольший общий множитель 75 и 100 равен 25
Разделите числитель и знаменатель на наибольший общий множитель (25)
75 ÷ 25100 ÷ 25 = 34
Как преобразовать десятичную дробь в дробную
Десятичные и дробные числа представляют число, которое не является четным целым числом, или число, которое не является целым числом.Каждое десятичное число можно преобразовать в дробь всего за три простых шага.
Обратите внимание, что процесс преобразования повторяющегося десятичного числа отличается.
Шаг первый: создайте начальную фракцию
Первый шаг в преобразовании десятичной дроби в дробь — создать начальную дробь, сделав десятичную часть числителем и поместив ее над 1 в качестве знаменателя.
Например, , чтобы преобразовать 0,75 в дробь, начните с 0,75 дроби с.75 в качестве числителя и 1 в качестве знаменателя.
.75 = .751

Шаг второй: умножьте на десять, чтобы исключить десятичное число
Следующим шагом является умножение числителя и знаменателя на 10, чтобы избавиться от десятичного знака. Продолжайте умножать оба на 10, пока числитель не станет целым числом или целым числом.
Продолжая приведенный выше пример, преобразуем .751 в 75100.
.751 = (.75 × 10) (1 × 10) = 7,510
7.510 = (7,5 × 10) (10 × 10) = 75100
Шаг третий: уменьшите дробь
Последний шаг в преобразовании десятичной дроби в дробь — уменьшить или упростить дробь. Чтобы уменьшить, найдите наибольший общий множитель для числителя и знаменателя. Затем разделите числитель и знаменатель на наибольший общий множитель.
Чтобы завершить приведенный выше пример, мы знаем, что наибольший общий коэффициент 75 и 100 равен 25. Итак, давайте разделим числитель и знаменатель на 25, чтобы решить уменьшенную дробь.
75100 = (75 ÷ 25) (100 ÷ 25)
75100 = 34
Вот совет: используйте наш калькулятор сокращения доли, чтобы легко уменьшить свою долю.
Для отрицательных чисел просто удалите отрицательный символ из начального десятичного числа, затем выполните шаги, описанные выше. После того, как число было преобразовано в форму дроби, добавьте отрицательный знак обратно.
Как конвертировать повторяющиеся десятичные дроби в дроби
Повторение десятичных чисел требует немного другого процесса для преобразования в дроби.Повторяющаяся десятичная дробь — это десятичное число, которое продолжается бесконечно, например 1.1787878. Эти числа обычно выражаются в округлой форме, например, 0,788, или с чертой, подобной этой: 1.178.
Шаг первый: создайте уравнение
Первым шагом в преобразовании повторяющегося десятичного числа является создание алгебраического уравнения для представления десятичного числа.
Например, давайте преобразуем десятичную 1,178 в дробь. Начните с создания уравнения для назначения выражения 1.1787878 до х.
х = 1,1787878
Шаг второй: умножьте на 10, пока повторяющаяся десятичная дробь не окажется слева
Второй шаг — продолжить умножение обеих сторон уравнения на 10, пока повторяющееся число не окажется слева от десятичной точки. Если есть несколько повторяющихся чисел, которые повторяются в шаблоне, то умножьте на 10, пока повторяющийся шаблон не окажется в левой части десятичной точки.
Продолжая приведенный выше пример, давайте умножим обе части уравнения на 10, пока повторяющаяся часть «78» десятичной дроби не окажется в левой части десятичной точки.
x = 1,1787878
10 × x = 10 × 1,1787878
10x = 11,787878
10 × 10x = 10 × 11,787878
100x = 117,87878
10 × 100x = 10 × 117,87878
1000x = 1178,78
Шаг третий: умножьте на 10, пока повторяющаяся десятичная дробь не окажется справа
Третий шаг — создать новое уравнение для x и умножать до тех пор, пока повторяющаяся десятичная часть не окажется справа от десятичной точки.
Основываясь на нашем примере, умножьте обе части уравнения на 10, пока повторяющаяся часть «78» десятичной дроби не окажется справа от десятичной точки.
х = 1,1787878
10 × х = 10 × 1,1787878
10х = 11,78
Шаг четвертый: объединить уравнения
Следующий шаг в этом процессе — объединить уравнения и поместить обе переменные x слева и оба десятичных значения справа.
Давайте сложим уравнения и решим.
1000x — 10x = 1178,78 — 11,788
Шаг пятый: решить
Наконец, решите для x, чтобы преобразовать десятичное значение в дробь.
Давайте сложим уравнения и решим.
1000x — 10x = 1178,78 — 11,78
990x = 1167
990×990 = 1167990
x = 1167990
Десятичные эквиваленты для простых дробей
Альтернативный метод преобразования десятичного значения в дробное — это использование таблицы преобразования, такой как эта. См. Дробные эквиваленты для некоторых общих десятичных значений ниже. Используйте эту таблицу для удобства, чтобы увидеть соответствующую дробь для десятичного числа.
| Десятичное значение | Дробная стоимость |
|---|---|
| 0.0625 | 1/16 |
| 0,08333 | 1/12 |
| 0,1 | 1/10 |
| 0,111 | 1/9 |
| 0,125 | 1/8 |
| 0,1666 | 1/6 |
| 0,2 | 1/5 |
| 0,222 | 2/9 |
| 0,25 | 1/4 |
| 0,333 | 1/3 |
| 0.375 | 3/8 |
| 0,4 | 2/5 |
| 0,444 | 4/9 |
| 0,5 | 1/2 |
| 0,555 | 5/9 |
| 0,6 | 3/5 |
| 0,625 | 5/8 |
| 0,666 | 2/3 |
| 0,75 | 3/4 |
| 0,777 | 7/9 |
| 0.8 | 4/5 |
| 0,8333 | 5/6 |
| 0,875 | 7/8 |
| 0,888 | 8/9 |
Смотрите больше дробных эквивалентов дроби.
,Калькулятор дроби доИспользование калькулятора
Преобразовать дробь в десятичную. Преобразуйте правильные и неправильные дроби в десятичные. Преобразовать соотношение в десятичное. Этот калькулятор показывает шаги и работу по преобразованию дроби в десятичное число.
Как преобразовать дробь в десятичную
В дроби, дробная черта означает «делится на». Таким образом, чтобы найти десятичный эквивалент дроби, такой как 1/4, вам нужно решить математическую задачу: 1, деленное на 4.
1 ÷ 4 = 0,25
Как превратить дробь в задачу деления
Делить числа легко с калькулятором. Если вам нужно сделать длинное деление вручную, поместите верхнее число дроби (числитель) внутри скобки деления и нижнее число (знаменатель) снаружи, слева от скобки деления.
Фракция 1 / 4 становится 1 ÷ 4.Завершите деление, чтобы преобразовать дробь в десятичную.
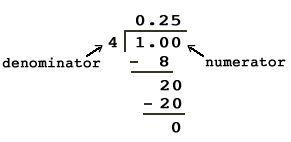
Вы можете сначала уменьшить дробь до наименьших, чтобы сделать математику с длинным делением немного проще. Например, 9/12 = 9 ÷ 12 = 0,75. Использование длинного деления для решения этой проблемы вручную или в вашей голове, уменьшение 9/12 = 3/4, может облегчить проблему. Вы можете даже признать, что 3/4 = 0,75, потому что 3 четверти равняется 75 центам.
Похожие калькуляторы
Вы также можете увидеть наши Калькулятор длинного деления с десятичными знаками для преобразования дроби в десятичную и просмотра работы, связанной с длинным делением.
Если вы хотите помочь уменьшить дроби до минимальных сроков, см. Калькулятор упрощенных фракций.
Чтобы преобразовать десятичную дробь в дробь см. Калькулятор десятичной дроби.
,Фракция вв десятичный калькулятор — дюймовый калькулятор
Преобразуйте дробь в десятичное значение, используя калькулятор дроби в десятичную, введя свою дробь ниже. Вы также можете быть заинтересованы в нашем калькуляторе десятичных дробей или калькуляторе долей в процентах для аналогичных конверсий.
Решение:
52 = 2,5
Найдите десятичную дробь, разделив числитель на знаменатель
52 = 5 ÷ 2 = 2.5
Как конвертировать дроби в десятичные
Число может быть выражено в виде дробной, десятичной или процентной величины, и иногда бывает необходимо преобразовать различные формы для представления числа по-разному. Существует несколько способов преобразования дроби в десятичную, попробуйте один из методов, описанных ниже.
Метод 1: преобразование дроби в десятичные с использованием калькулятора
Самый простой метод преобразования числа дроби в десятичное значение — просто разделить числитель на знаменатель, чтобы получить десятичное значение.Числитель является верхним числом, а знаменатель — нижним.
Например, давайте преобразовать дробь 14 в десятичную с использованием метода деления.
14 = 1 ÷ 4 = 0,25
Таким образом, десятичное значение 14 составляет 0,25
Метод 2: преобразование дроби в десятичные с использованием длинного деления
Длинное деление предлагает другой способ преобразования в десятичную форму. Начните с определения дивиденда и делителя, затем используйте эти значения в длинном делении.Числитель дроби будет делителем, а знаменатель будет делителем.
Затем представьте дивиденд и делитель в форме длинного деления. Вероятно, будет необходимо добавить десятичную дробь и нули, если дивиденд меньше делителя.
Наконец, решите проблему длинного деления, чтобы завершить преобразование из дробной в десятичную.

Метод 3: преобразовать дробь в десятичную с помощью упрощения
Альтернативный метод преобразования дроби в десятичное число состоит в том, чтобы упростить дробь, чтобы числитель был больше 1.Это требует нескольких шагов. Сначала умножьте знаменатель, чтобы получить 100. Для этого попробуйте разделить 100 на знаменатель, чтобы найти кратное число, а затем умножить числитель и знаменатель на кратное.
Последний шаг — переместить десятичную запятую на новом числителе влево на два мест, чтобы изменить дробь до ее десятичного значения.
Например, мы можем преобразовать дробь 14 в десятичное значение, используя этот метод.
Начните с поиска множителя, необходимого для умножения знаменателя, чтобы получить 100.
100 = 4 × 25
Таким образом, кратное число составляет 25 .
Теперь умножьте числитель на кратное (25).
1 × 25 = 25
Таким образом, фракция 14 также может быть представлена как 25100.
14 = 25100
Наконец, переместите десятичное место числителя влево на два места, чтобы получить десятичное значение.
25,0 -> 0,25
Таким образом, десятичное значение 14 составляет 0,25.
Десятичные эквиваленты для простых дробей
Другой способ найти десятичное значение для дроби — это обратиться к таблице преобразования, такой как приведенная ниже, которая показывает десятичные значения нескольких распространенных дробей.
| Фракция | Десятичное число |
|---|---|
| 1/2 | 0,5 |
| 1/3 | 0,333 |
| 2/3 | 0,666 |
| 1/4 | 0,25 |
| 3/4 | 0,75 |
| 1/5 | 0,2 |
| 2/5 | 0.4 |
| 3/5 | 0,6 |
| 4/5 | 0,8 |
| 1/6 | 0,1666 |
| 5/6 | 0,8333 |
| 1/8 | 0,125 |
| 3/8 | 0,375 |
| 5/8 | 0,625 |
| 7/8 | 0,875 |
| 1/9 | 0,111 |
| 2/9 | 0.222 |
| 4/9 | 0,444 |
| 5/9 | 0,555 |
| 7/9 | 0,777 |
| 8/9 | 0,888 |
| 1/10 | 0,1 |
| 1/12 | 0,08333 |
| 1/16 | 0,0625 |
Смотрите больше дробных эквивалентов дроби.
,