Калькулятор экспонента: Посчитать экспоненту — онлайн калькулятор

Экспонента Борна с использованием уравнения Борна-Ланде Калькулятор

✖Энергия решетки кристаллического твердого тела — это мера энергии, высвобождаемой при объединении ионов в соединение.ⓘ Энергия решетки [U]		Джоуль / мольКилоджоуль / моль	+10% -10%
✖Расстояние наибольшего сближения — это расстояние, на которое альфа-частица приближается к ядру.ⓘ Расстояние ближайшего подхода [r0]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Константа Маделунга используется для определения электростатического потенциала одиночного иона в кристалле путем аппроксимации ионов точечными зарядами. ⓘ Постоянная Маделунга [M]			+10% -10%
✖Заряд катиона — это положительный заряд катиона с меньшим количеством электронов, чем у соответствующего атома.ⓘ Заряд катиона [z+]		абкулоновАмпер-часАмпер-минутаАмпер-секундаКулонэлементарному зарядуЭМУ заряженностиESU заряженностиФарадейФранклинкилокулонМегакулонмикрокулонМиллиампер-часМилликулонНанокулонПико кулонстаткулон	+10% -10%
✖Заряд аниона — это отрицательный заряд аниона с большим количеством электронов, чем у соответствующего атома.ⓘ Заряд аниона [z—]		абкулоновАмпер-часАмпер-минутаАмпер-секундаКулонэлементарному зарядуЭМУ заряженностиESU заряженностиФарадейФранклинкилокулонМегакулонмикрокулонМиллиампер-часМилликулонНанокулонПико кулонстаткулон	+10% -10%

✖Показатель Борна — это число от 5 до 12, определенное экспериментально путем измерения сжимаемости твердого тела или полученное теоретически. ⓘ Экспонента Борна с использованием уравнения Борна-Ланде [nborn]

⎘ копия

👎

Формула

сбросить

👍

Экспонента Борна с использованием уравнения Борна-Ланде Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Энергия решетки: 3500 Джоуль / моль —> 3500 Джоуль / моль Конверсия не требуется
Расстояние ближайшего подхода: 60 Ангстрем —> 6E-09 метр (Проверьте преобразование здесь)

Постоянная Маделунга: 1. 2)*Постоянная Маделунга)/(4*pi*[Permitivity-vacuum]*Расстояние ближайшего подхода)

Энергия решетки с использованием исходного уравнения Капустинского

Идти Энергия решетки = ((([Kapustinskii_C]/1.20200)*1.079) *Количество ионов*Заряд катиона*Заряд аниона)/(Радиус катиона+Радиус аниона)

Born Exponent с использованием отталкивающего взаимодействия

Идти Прирожденный экспонент = (log10(Константа отталкивающего взаимодействия/Отталкивающее взаимодействие))/log10(Расстояние ближайшего подхода)

Электростатическая потенциальная энергия между парой ионов

Идти Электростатическая потенциальная энергия между ионной парой = (-(Обвинение^2)*([Charge-e]^2))/(4*pi*[Permitivity-vacuum]*Расстояние ближайшего подхода)

Константа отталкивающего взаимодействия при заданной полной энергии ионов и энергии Маделунга

Идти Константа отталкивающего взаимодействия = (Полная энергия иона-Маделунг Энерджи)*(Расстояние ближайшего подхода^Прирожденный экспонент)

Константа отталкивающего взаимодействия

Идти Константа отталкивающего взаимодействия = Отталкивающее взаимодействие*(Расстояние ближайшего подхода^Прирожденный экспонент)

Отталкивающее взаимодействие

Идти Отталкивающее взаимодействие = Константа отталкивающего взаимодействия/(Расстояние ближайшего подхода^Прирожденный экспонент)

Энергия решетки с использованием энтальпии решетки

Идти Энергия решетки = Энтальпия решетки-(Энергия решетки давления*Энергия решетки молярного объема)

Энтальпия решетки с использованием энергии решетки

Идти Энтальпия решетки = Энергия решетки+(Энергия решетки давления*Энергия решетки молярного объема)

Изменение объема решетки

Идти Энергия решетки молярного объема = (Энтальпия решетки-Энергия решетки)/Энергия решетки давления

Внешнее давление решетки

Идти Энергия решетки давления = (Энтальпия решетки-Энергия решетки)/Энергия решетки молярного объема

Отталкивающее взаимодействие с использованием полной энергии ионов

Идти Отталкивающее взаимодействие = Полная энергия иона-Маделунг Энерджи

Полная энергия иона в решетке

Идти Полная энергия иона = Маделунг Энерджи+Отталкивающее взаимодействие

Число ионов с использованием приближения Капустинского

Идти Количество ионов = Постоянная Маделунга/0. 2)*z⁺*z^—))

Что такое уравнение Борна – Ланде?

Уравнение Борна – Ланде — это средство расчета энергии решетки кристаллического ионного соединения. В 1918 году Макс Борн и Альфред Ланде предложили, что энергия решетки может быть получена из электростатического потенциала ионной решетки и члена потенциальной энергии отталкивания. Ионная решетка моделируется как совокупность твердых упругих сфер, которые сжимаются вместе за счет взаимного притяжения электростатических зарядов к ионам. Они достигают наблюдаемого равновесного расстояния друг от друга из-за уравновешивающего отталкивания на коротком расстоянии.

Share

Copied!

Время разряда аккумулятора в зависимости от тока нагрузки

Я, в общем, дилетант в электротехнике, поэтому прощу прощения за неточности, если они есть, а ниже изложено то, что я могу сказать по поводу времени разряда аккумулятора, потратив на это несколько часов чтения материалов из Интернета. Итак,

Емкость аккумулятора довольно часто указывают в амперчасах, ну или в миллиампер часах.
Казалось бы, все просто — есть, у тебя скажем аккумулятор емкостью (C) 800 миллиамперчасов и устройство с током потребления (I) в 100 миллиампер, значит, по формуле
,
он может обеспечить работу этого устройства на протяжении восьми часов. Так?

Конечно же, не совсем так. Количество электроэнергии, которое можно извлечь из аккумулятора, зависит от тока разряда аккумулятора. То есть при слишком большом токе разряда аккумулятор разряжается очень быстро и отдает меньше электроэнергии. Эффект этот был замечен довольно давно, но первым, кто попробовал учесть его количественно, был Пекерт (Peukert), который модифицировал формулу, внеся показатель, который теперь называют экспонента Пекерта (Peukert’s exponent).

По Пекерту, время разряда аккумулятора равно
,
где n — экспонента Пекерта.
Сp — емкость Пекерта, то есть емкость аккумулятора, измеренная при токе разряда в 1 ампер.
I — ток разряда, для которого делается расчет.

Значение экспоненты Пекерта определяется экспериментально. Оно зависит от типа аккумулятора и даже от его возраста. Обычно значение экспоненты Пекерта лежит в диапазоне от 1.1 до 1.3. Чем она меньше, тем лучше, конечно же.
Для некоторых аккумуляторов производитель его указывает, но это бывает довольно редко. Чаще можно встретить в спецификации данные по емкости аккумулятора для разного времени разряда. Этого в принципе достаточно, чтобы вычислить значение экспоненты Пекерта самому. Калькулятор ниже делает это.

Экспонента Пекерта

Номинальная емкость 1, Ач

Номинальное время 1, ч

Номинальная емкость 2, Ач

Номинальное время 2, ч

Точность вычисления

Знаков после запятой: 2

Экспонента Пекерта

 

Разберемся теперь с емкостью Пекерта; как уже сказано выше, это емкость, или количество электроэнергии, которое может отдать этот аккумулятор при токе разряда в 1 ампер.
Емкость, указанная на аккумуляторе, это, конечно же, не оно. Это емкость, полученная при токе разряда, соответствующем какому-либо значению C-рейтинга (C-Rate).
Емкость с рейтингом 1С, это емкость, получаемая от аккумулятора при разряде его током, соответствующим этой же емкости. То есть 1000 миллиапмерчасов с рейтингом 1С означает, что данный аккумулятор способен обеспечивать ток в 1000 миллиампер в течении 1 часа. Емкость с рейтингом 0.05С это емкость, получаемая от аккумулятора при разряде его током, соответствующим 0.05 емкости. То есть 1000 миллиамперчасов с рейтингом 0.05С означает, что данный аккумулятор способен обеспечивать ток 50 миллиампер в течении 20 часов. Как уже можно догадаться, из-за эффекта Пекерта такой аккумулятор не сможет обеспечить 1000 миллиампер в течении часа. Время будет меньше.
Так вот, некоторые производители указывают C-рейтинг своего аккумулятора. Иногда как C-рейтинг, например, 0.05C или , иногда как «100 Амперчасов за 20 часов». А некоторые производители — не указывают. Наиболее частым значением в этом случае является рейтинг 0.05С () или «за 20 часов». То есть можно смело рассчитывать на 20 часов работы, но при токе в 20 раз меньше тока, соответствующего указанной емкости.

Зная этот рейтинг, можно перейти от емкости, указанной на аккумуляторе, к емкости Пекерта, и использовать ее для расчета.
Емкость Пекерта в этом случае равна
, где
С — емкость аккумулятора
R — рейтинг выраженный в часах, соответсвующий данной емкости, например, 20.
n — экспонента Пекерта
Подробнее можно почитать здесь. Там еще много интересного про формулу Пекерта есть.

Зная емкость, рейтинг в часах, ток нагрузки и экспоненту Пекерта можно рассчитать время разряда. Калькулятор ниже делает это для разного процента разряда.

Зачем нужен процент разряда? Дело в том, что для многих типов аккумуляторов невозможно извлечь всю запасенную энергию, не повредив фатально при этом сам аккумулятор. Это зависит от химии аккумулятора. Поэтому обычно производители указывают допустимую глубину разряда (Depth of Discharge, DOD). Например, если указана глубина разряда 20% (это верно для большинства автомобильных аккумуляторов, кстати), то сильно не рекомендуется использовать более 20% мощности батареи. Иногда даже указывают допустимую дневную норму разряда.

Время разряда батареи в зависимости от тока нагрузки

Ток потребления, А

Емкость батареи, А/ч

Номинальная емкость батареи, Ампер час

Время, ч.

Время работы для номинальной емкости, часы

Экспонента Пекерта

Точность вычисления

Знаков после запятой: 3

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Емкость Пекерта, Ач

 

Номинальный ток разряда, А

 

Из всего вышеизложенного понятно, что при малых токах потребления аккумулятор может обеспечить большее время работы. Это, в принципе так. Но не стоит доводить до крайностей — нельзя взять аккумулятор большой емкости, подключить к нему небольшую нагрузку и рассчитывать, что он сможет работать практически вечно 🙂
Тут в дело вступают уже другие эффекты, например, эффект саморазряда аккумулятора. NiMH аккумуляторы теряют саморазрядом до 30% заряда за месяц.

Поиграться с зависимостью времени работы от тока можно с калькулятором ниже.

Время разряда батареи в зависимости от тока нагрузки

Емкость батареи, А/ч

Номинальная емкость батареи, Ампер час

Время, ч.

Время работы для номинальной емкости, часы

Экспонента Пекерта

Точность вычисления

Знаков после запятой: 3

Номинальный ток разряда, А

 

Емкость Пекерта, Ач

 

Зависимость времени разряда от тока нагрузки

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

 аккумулятор батарея емкость заряд Пекерт разряд ток Физика экспонента электричество

Калькулятор экспоненты

— Примеры, Калькулятор экспоненты онлайн

Калькулятор экспоненты

— это бесплатный онлайн-инструмент, который помогает найти значение выражения, возведенного в степень. Повторное умножение одного и того же числа можно выразить в виде показательного выражения.

Что такое калькулятор экспоненты?

Калькулятор экспоненты помогает вычислить значение экспоненциального выражения. Такое выражение состоит из двух частей — основания и степени (показатель степени). Экспоненты могут быть как отрицательными, так и положительными. Чтобы использовать Калькулятор экспоненты , введите значения в поля ввода.

Калькулятор экспоненты

ПРИМЕЧАНИЕ. Введите положительные базовые значения до 2 цифр и положительные значения экспоненты до 10 цифр.

Как пользоваться калькулятором экспоненты?

Выполните указанные шаги, чтобы найти значение экспоненциального выражения с помощью калькулятора экспоненты.

Шаг 2: Введите значения основания и показателя степени в соответствующие поля ввода.

Шаг 3: Нажмите « Вычислить» , чтобы найти значение экспоненциального выражения.

Шаг 4: Нажмите «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор экспоненты?

Показатель степени используется для представления того, сколько раз число умножается само на себя. Предположим, у нас есть база, обозначенная x, и соответствующая ей мощность, равная n. Это представлено как x ^н . Это означает, что основание x умножается n раз само на себя. Экспоненты очень полезны для представления очень больших или очень маленьких чисел. Если у нас есть отрицательный показатель степени, это означает, что обратное основание умножается многократно. Это дается x ^-n . Это указывает на то, что 1/x умножается n раз. Мы также можем иметь дробные показатели. Степени и корни вместе представлены такими типами показателей. Предположим, у нас есть показатель степени, представленный как x ^1/2 . Это обозначение показывает, что мы должны извлечь квадратный корень из числа x. Кубические корни также могут быть представлены с использованием аналогичных обозначений. Другой тип показателя степени — десятичный показатель степени. Такой показатель выражается в виде десятичных дробей. Чтобы оценить такие показатели степени, десятичную дробь необходимо преобразовать в дробь, прежде чем продолжить.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе экспоненты

Пример 1:

Найдите экспоненциальное значение для 10 ⁴ и проверьте его с помощью калькулятора экспоненты.

Решение:

Основание = 10

Показатель степени = 4

10 ⁴ = 10 × 10 × 10 × 10 = 10 000

90 002 Пример 2:

Найдите экспоненциальное значение для 49 ^0,5 и проверьте это с помощью калькулятора степени.

Решение:

Основание = 49

Показатель степени = 0,5. Это также может быть обозначено как 1/2.

Таким образом, мы должны найти квадратный корень из 49.

49 ^0,5  = 49 ^1/2  = 7.

Теперь попробуйте калькулятор степени, чтобы найти значение следующих показателей степени.

• 14 ⁴
• 29 ^0,5

☛ Статьи по теме:

• Экспоненты
• Экспоненты Правила

☛ Математические калькуляторы:

Рабочие листы по математике и визуальные учебные программы

Калькулятор экспоненты — Калькулятор степени .

Калькулятор степени 

С помощью этого калькулятора степени вы можете найти результат как положительной, так и отрицательной степени. Система ввода проста и понятна. Нажав на «показать еще», вы также сможете увидеть все этапы расчета.

Что такое показатель степени?

Показатель степени может быть определен как

«Показатель степени числа говорит , сколько раз использовать число при умножении».

Например, 3 ехр 4 можно записать так:

3 ⁴ = 3×3×3×3 = 81

Как решить показатели степени?

Есть два типа показателей; положительный и отрицательный.

Положительные показатели

Показатели основания, равные или большие нуля.

Пример:

Решить 5 ³ .

Решение :

Шаг 1: Запишите основание и умножьте его на степень умножения.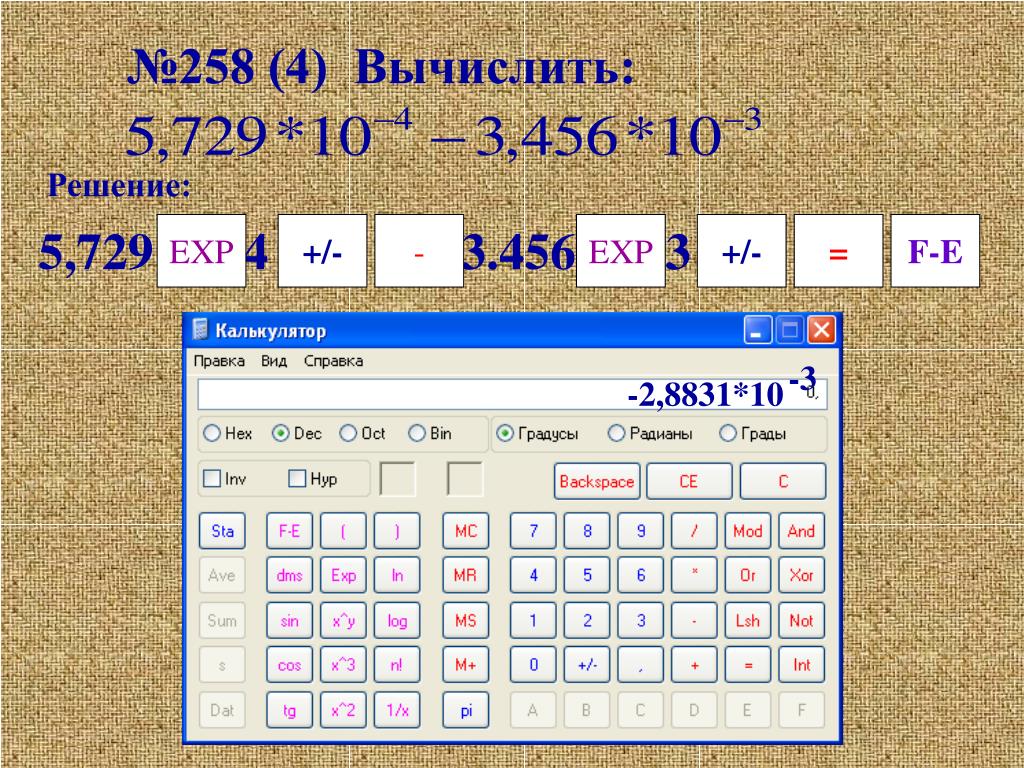

5 ³ = 5 × 5 × 5 (5 в 3-й степени)

Шаг 2: Умножить. Пример 923624 = бесконечность (слишком большое число)

Пример

1,1 увеличено до 10

Решение :

1,1 увеличено до 10 = 2,5937 90 003

Отрицательные показатели степени

Показатели степени меньше нуля.

Пример:

Решить 6 ^-3

Решение :

90 008 Шаг 1: Разделить 6 ^-3 на 1 , чтобы показатель степени был положительным.

6 ^-3 = 1/6 ³  (6 в 3-й степени)

Шаг 2: Запишите основание и умножьте его на степень, умноженную на .

1/6 ³ = 1/(6 × 6 × 6) = 1/216  9000 9

1/6 ³ = 0,00463

Это основы показателей. Копнув немного глубже, вы получите правила или законы показателей. Эти правила помогают свести к минимуму шаги, необходимые для упрощения.

Если вы не используете эти правила и решаете показатели степени на основе ваших базовых знаний о PEMDAS, вы все равно получите тот же результат, но немного позже.

Законы Экспонентов:

Одни говорят, что существует 7 законов, а другие считают, что их 8. Есть также те, кто пишет 10 законов показателей.

В конце концов, это всего лишь количество известных вам сокращений для ускорения вычислений. Количество не имеет особого значения.

Для вашего удобства мы разделили правила экспоненты на категории. т.е. простые и сложные.

Простые правила:

Их тоже можно назвать вводными или законами здравого смысла ????. Вот эти три правила:

• X ¹  = X (что имеет смысл, поскольку существует только одно x ).
• X ⁰  = 1 (Нет x, нет умножения. Допустим, это просто причудливый способ записать единицу).
• X ^-1  = 1/X (это правило уже рассматривалось в отрицательных показателях).

Отказ от ответственности: Эта Категория и название правил не упоминаются ни одним математиком. Они просто разработаны, чтобы сделать правила понятными.

Сложные правила

Под этим заголовком подпадают шесть основных правил. Они могут показаться сложными, но, обратив некоторое внимание, вы сможете их понять.

Правило № 1:

(b ^m )(b ⁿ ) = b ^m+n

Это правило также работает под названием « Закон о продукте ». Когда основания одинаковы, добавляются разные силы.

Это можно объяснить, подумав, сколько раз

b нужно умножить. Возьмем пример.

= (Y ³ )(Y ² )

Сначала Y умножается на три, а затем на два раза.

= (Y x Y x Y)(Y x Y)

Это означает, что окончательный ответ будет одинаковым в обоих случаях. Это потому, что значение Y в конкретной задаче представляет собой конкретную цифру. Невозможно сказать, что Y равно 5, а затем Y также равно 10.

Поскольку они имеют одинаковые значения, степени объединяются.
 Если рассматриваемая проблема не связана с корнями.

Правило № 2:

(b ^m )/(b ⁿ ) = b ^m-n

Очень похоже на предыдущий закон, этот закон называется «Частное право ». Для его объяснения возьмем предыдущий пример со знаком деления.

= (Y ³ )/(Y ² )
= (Y x Y x Y)/(Y x Y)

Два Y в верхнем значении будут компенсированы Y в нижнем ценить. Остается только один Y. Таким же образом, если из 3 вычесть 2, получится один Y. 

Правило № 3:

(axb) ^м  = (a) ^м (b) ^м

“ 900 08 Сила правила продукта ». Когда два значения в произведении имеют одинаковую мощность, их можно разделить.

Независимо от того, умножаете ли вы сначала, а затем решаете степень или решаете степени отдельно, а затем умножаете, результат будет общим.

Правило № 4:

(a/b) ^м  = (a) ^м /(b) ^м

Надеюсь, это имеет смысл после предыдущего закона. Его название — «Сила частного правила».

Правило № 5:

((b) ^m ) ⁿ  = b ^mxn  

« Правило мощности к степени » утверждает, что когда основание (b) возводится в две степени, сначала m, затем n, степени умножаются. Это немного сложно понять, но вы можете увидеть пример проверки ниже.

= (2 ² ) ³  = 2 ^2×3 = 26 = 64

Теперь без применения закона.

= (22) ³ = (4) ³ = 64

Правило № 6:

b ^m/n = 900 49 n √b ^m 

Это « правило дробной мощности ».