Калькулятор логарифмов и антилогарифмов онлайн
Логарифмирование — это операция, обратная возведению в степень. Если вы задаетесь вопросом, в какую степень нужно возвести 2, чтобы получить 10, то вам на помощь придет логарифм.
Обратная операция для возведения в степень
Возведение в степень — это повторяющееся умножение. Для возведения двойки в третью степень нам потребуется вычислить выражение 2 × 2 × 2. Обратная операция для умножения — это деление. Если верно выражение, что a × b = c, то обратное выражение b = a / c так же верно. Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако ab не равно ba, за исключением единственного случая, когда 22 = 42. В выражении ab = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Понятие логарифма
Давайте попробуем решить простое уравнение вида 2x = 16.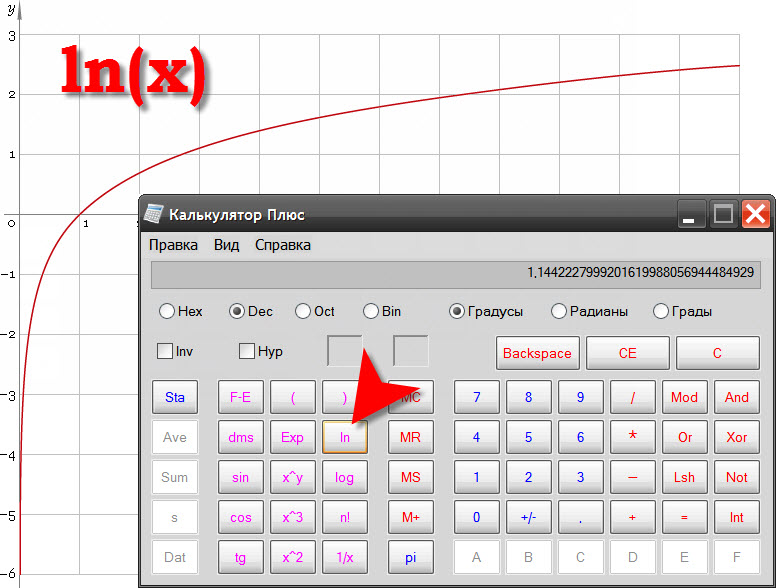 Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Теперь попробуем решить 2x = 20. Сколько раз нужно умножить двойку на саму себя, что бы получить 20? Это сложно, ведь 24 = 16, а 25 = 32. Рассуждая логически, корень этого уравнения располагается между 4 и 5, причем ближе к 4, возможно 4,3? Математики не терпят приблизительных вычислений и хотят знать точный ответ. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.
Выражение log2 20 читается как логарифм 20 по основанию 2. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.
Таким элегантным способом вы можете решить любое простое показательное уравнение. Например, для уравнений:
- 4x = 125, x = log4 125;
- 12x = 432, x = log12 432;
- 5x = 25, x = log5 25.
Последний ответ x = log5 25 математикам не понравится. Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 52 = 25. Поэтому для уравнения вида 5x = 25, x = 2.
Десятичный логарифм
Десятичный логарифм — это функция по основанию 10. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Натуральный логарифм
Натуральный логарифм — это функция по основанию e. В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
В какую степень нужно возвести число e, чтобы получить 10? Ответом был бы loge 10, но математики обозначают натуральный логарифм как ln, поэтому ответ будет записан как ln10. Тоже самое с выражениями loge 35 и loge 40, верная форма записи которых – ln34 и ln40.
Антилогарифм
Антилогарифм — это число, которому соответствует значение выбранного логарифма. Простыми словами, в выражении loga b антилогарифмом считается число ba. Для десятичного логарифма lga, антилогарифм равен 10a, а для натурального lna антилогарифм равняется ea. По сути, это тоже возведение в степень и обратная операция для логарифмирования.
Физический смысл логарифма
Нахождение степеней — чисто математическая задача, но для чего нужны логарифмы в реальной жизни? В начале развития идеи логарифмирования данный математический инструмент использовался для сокращения объемных вычислений.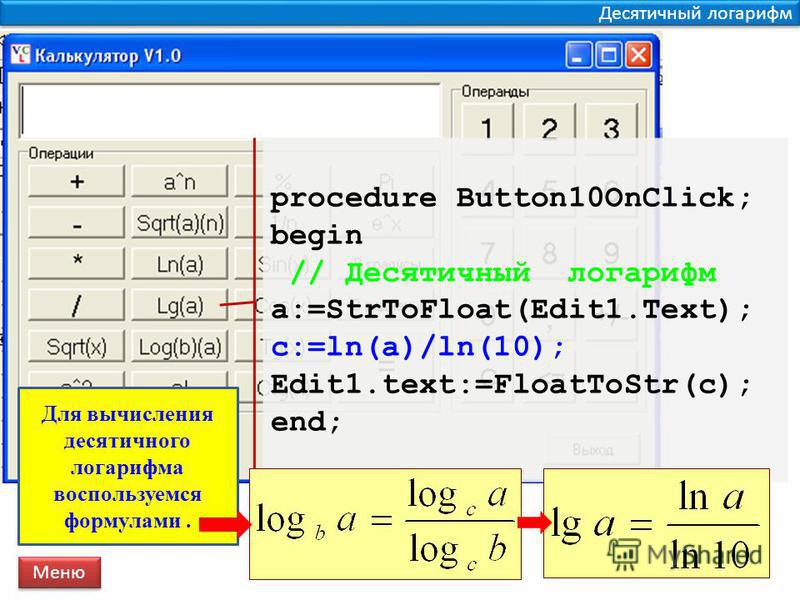 Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Логарифмы нашли применение и в сфере изображения графических процессов. Если требуется нарисовать график функции, которая принимает значения 1, 10, 1 000 и 100 000, то маленькие значения будут невидны и визуально они сольются в точку около нуля. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.
Физический же смысл логарифмирования — это описание временных процессов и изменений. Так, логарифм по основанию 2 позволяет определить, сколько требуется удвоений начального значения для достижения определенного результата. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Наша программа представляет собой сборник из четырех онлайн-калькуляторов, которые позволяют вычислить логарифм по любому основанию, десятичную и натуральную логарифмическую функцию, а также десятичный антилогарифм. Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.
Примеры из реальной жизни
Школьная задача
Как было сказано выше, иррациональные значения по типу log2 345 не требуют дополнительных преобразований, и такой ответ полностью удовлетворит учителя математики. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:
- log7 65 — иррациональное число;
- log3 243 — целое число 5;
- log5 95 — иррациональное;
- log8 512 — целое число 3;
- log2 2046 — иррациональное.

Таким образом, значения log3 243 и log8 512 вам потребуется переписать как 5 и 3 соответственно.
Потенцирование
Потенцирование — это нахождение антилогарифма числа. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:
- для n = 1 antlog = 10;
- для n = 1,5 antlog = 31,623;
- для n = 2,71 antlog = 512,861.
Непрерывный рост
Натуральный логарифм позволяет описывать процессы непрерывного роста. Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.
Поиск количества удесятирений
Допустим, за 30 лет количество персональных компьютеров увеличилось с 250 000 до 1 миллиарда. Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.
Заключение
Несмотря на сложность логарифмов и нелюбовь детей к ним в школьные годы, этот математический инструмент находит широкое применение в науке и статистике. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.
Десятичный логарифм: онлайн калькулятор | BBF.RU
Логарифмирование — операция, которая обратна возведению в степень. Для решения задач на определение количества удесятирений применяются десятичные логарифмы.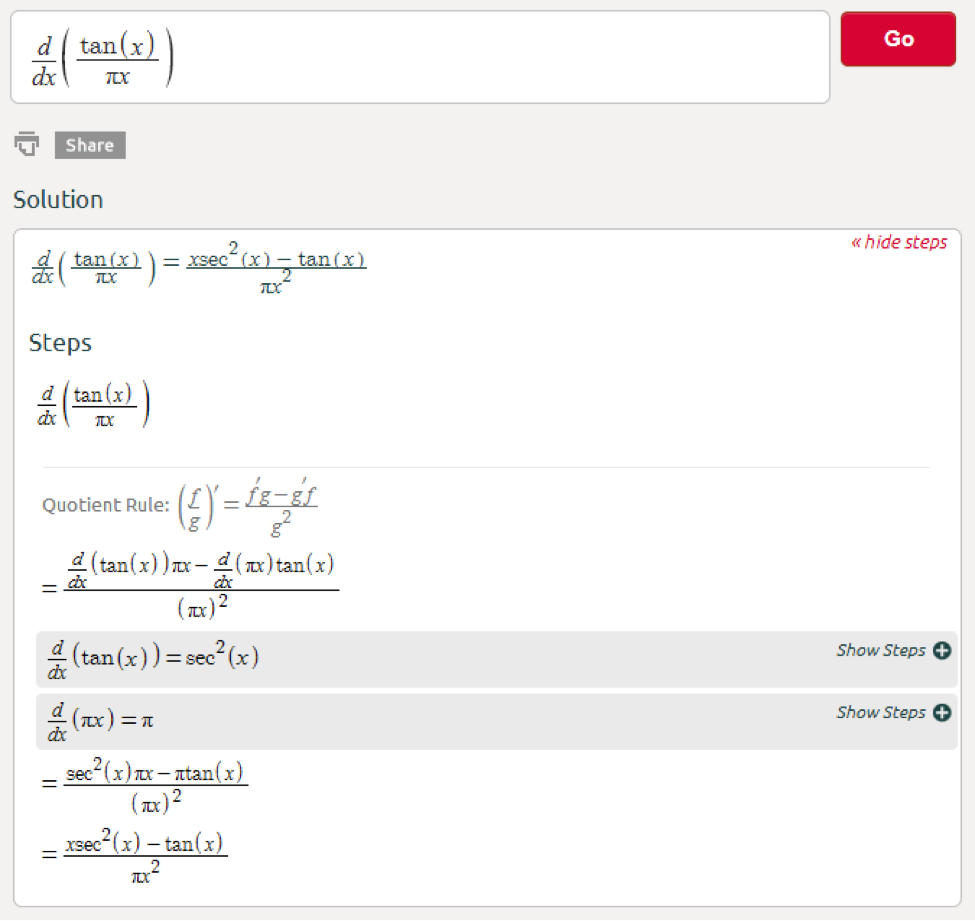
Возведение в степень и логарифм
Мы знаем, что деление и умножение — это обратные математические операции. Если выражение A × B = C правдиво, то справедливо и выражение A = C / B или B = C / A. Для выражения со степенями все не так просто. Выражение AB = BA верно только для двух случаев: когда A и B равны единице или двойке. Во всех остальных случаях такое арифметическое выражение необратимо. Для решения показательных уравнений вида A x = B используются логарифмы.
Пусть у нас есть уравнение 3x = 9. Для решения такого уравнения достаточно задаться вопросом: в какую степень нужно возвести тройку, чтобы получить 9? Элементарно, во вторую. В данном случае x = 2. Изменим немного уравнение и представим, что 3x = 10. Здесь возникает сложный вопрос, как подсчитать икс, если это не целое число? Неизвестное в данном случае будет иррациональным числом, представить которое можно только с заданной степенью точности. Математики нашли элегантный способ для компактной записи таких значений. Решением уравнения 3x = 10 будет x = log 3 10. И все, этого достаточно.
Решением уравнения 3x = 10 будет x = log 3 10. И все, этого достаточно.
Итак, логарифм log A B — это такое число, в которое требуется возвести A, чтобы получить B. A — это основание логарифма, и оно может быть любым положительным числом. Однако существует два особенных числа, для которых были введены собственные логарифмы. Это экспонента (e = 2,71828) и число 10. Логарифмы по основанию е носят название натуральных, а по основанию 10 — десятичных.
Понятие десятичного логарифма
Десятичный логарифм lgA — это такое число, в которое требуется возвести 10, чтобы получить число A. Из программы математики средней школы известно, что любое число можно представить в виде 10 a или простыми словами в виде десятки в некоторой степени. Это достаточно четко иллюстрируется примером, когда число кратно 10:
- 100 = 102;
- 1 000 = 103;
- 10 000 000 = 107.
Но что делать, если через десятку требуется представить число 2077? Здесь на сцену выходят десятичные логарифмы. При помощи логарифма мы можем записать lg2077 и любому математику станет ясно, что это за иррациональное число. Вычислить это значение приблизительно можно следующим образом. Если lg1000 = 3, а lg10000 = 4, то 3 > lg2077 > 4. Так как 2077 значительно ближе к 1 000, чем к 10 000, то и значение логарифма также будет в районе тройки, например, 3,2. Подсчитать более точное значение можно при помощи онлайн-калькулятора, которое будет равно lg2077 = 3,317436… Вычислить точное значение такого логарифма невозможно, так как оно иррационально и бесконечно.
При помощи логарифма мы можем записать lg2077 и любому математику станет ясно, что это за иррациональное число. Вычислить это значение приблизительно можно следующим образом. Если lg1000 = 3, а lg10000 = 4, то 3 > lg2077 > 4. Так как 2077 значительно ближе к 1 000, чем к 10 000, то и значение логарифма также будет в районе тройки, например, 3,2. Подсчитать более точное значение можно при помощи онлайн-калькулятора, которое будет равно lg2077 = 3,317436… Вычислить точное значение такого логарифма невозможно, так как оно иррационально и бесконечно.
История логарифмов
Потребность в логарифмировании возникла в 16-м веке, когда в Европе набирали обороты производство, торговля и мореплавание. Именно тогда бухгалтера и астрономы, математики и мануфактурщики столкнулись с проблемой громоздких вычислений, на решение которых уходило много времени и сил. Ученые постоянно возводили в степень и вычисляли корни, но сложность расчетов замедляла прогресс. Именно тогда математикам пришла идея заменить сложные вычисления степеней и корней на соответствующие операции умножения и деления, а затем — сложения и вычитания. Подобный ход конем позволил ученым производить операции поиска корней и возведения степень над огромными числами, складывая и вычитая при этом соответствующие логарифмы.
Подобный ход конем позволил ученым производить операции поиска корней и возведения степень над огромными числами, складывая и вычитая при этом соответствующие логарифмы.
Первые логарифмические таблицы были созданы в 1614 году шотландским математиком Джоном Непером. Непер был профессиональным математиком, он занимался астрономией и не понаслышке знал о сложностях астрономических расчетов. Позднее знаменитый физик и астроном Пьер-Симон Лаплас говорил, что возникновение логарифмов значительно уменьшило вычислительный труд астронома и удвоило его жизнь. Логарифмические таблицы со временем совершенствовались и в итоге стали универсальным инструментом для громоздких вычислений. Математики старой школы до сих пор используют логарифмические линейки и считают в уме с такой же скоростью, с какой работают современные калькуляторы.
Если вы не застали времена, когда каждый математик имел в своем арсенале логарифмическую линейку и не умеете ими пользоваться, то предлагаем вам наш онлайн-калькулятор.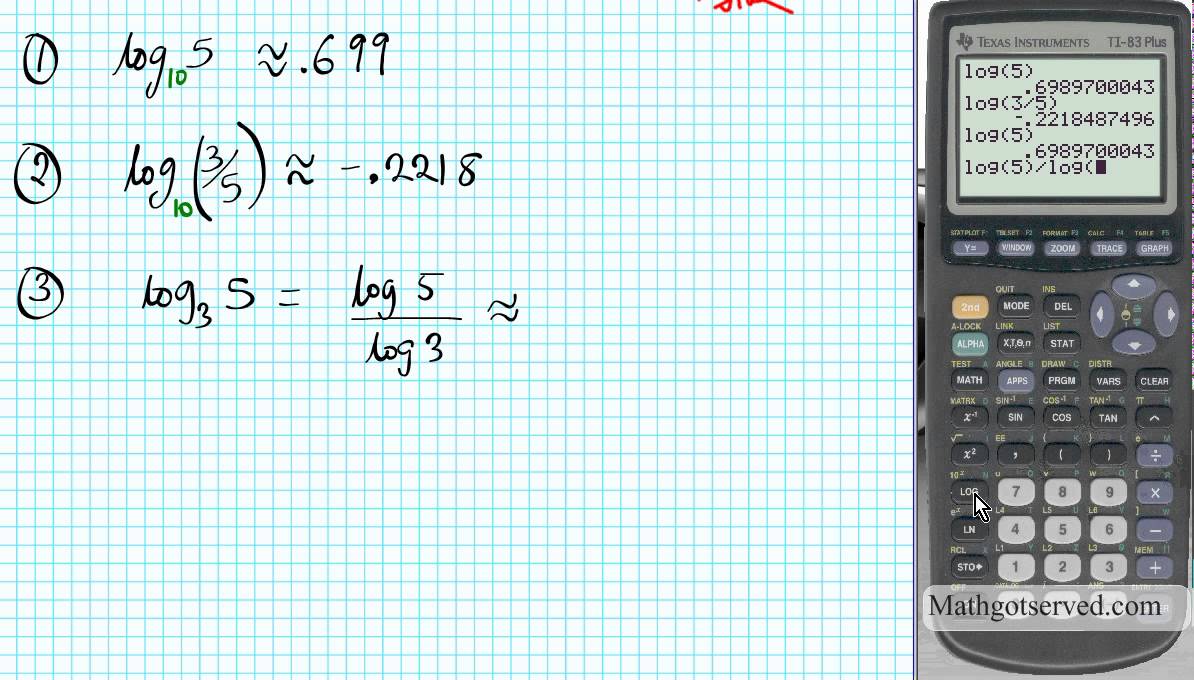 Данная программа предназначена для вычисления любых логарифмов, в том числе и десятичных. Для расчетов вам потребуется выбрать в меню тип «Десятичный» и ввести значения в соответствующие ячейки. Калькулятор может вычислить собственно десятичный логарифм для числа X или вернуть значение числа X, если известен его логарифм.
Данная программа предназначена для вычисления любых логарифмов, в том числе и десятичных. Для расчетов вам потребуется выбрать в меню тип «Десятичный» и ввести значения в соответствующие ячейки. Калькулятор может вычислить собственно десятичный логарифм для числа X или вернуть значение числа X, если известен его логарифм.
Пример работы калькулятора
Расчет логарифмов
Обычно десятичные логарифмы используются для отображения графиков функций, которые имеют как очень малые, так и очень большие значения. Например, функция отображения громкости звука содержит как значения в диапазоне от 1 до 10, так и значения от 100 до 1 000 и от 1 000 до 10 000. Компактно уместить это на одном графике и разглядеть все значения громкости звука можно только при помощи логарифмической шкалы, в которой значения заменены десятичными логарифмами:
- 1 — lg10;
- 2 — lg100;
- 3 — lg1000;
- 4 — lg10000.
Эти значения легко вычислить при помощи калькулятора. Для рассчетов потребуется поочередно ввести в ячейку «Число» значения 10, 100, 1 000 и 10 000. При помощи таких значений на графике можно будет рассмотреть и маленькие значения от 1 до 10 и большие до 10 000.
Для рассчетов потребуется поочередно ввести в ячейку «Число» значения 10, 100, 1 000 и 10 000. При помощи таких значений на графике можно будет рассмотреть и маленькие значения от 1 до 10 и большие до 10 000.
Заключение
Десятичный логарифм — удобный математический инструмент, облегчивший жизнь многим поколениям математиков. Наш онлайн-калькулятор пригодится для вычислений выражений, которые содержат десятичные логарифмы.
Калькулятор онлайн — Решение логарифмических уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x4 = 81
По определению арифметического корня имеем \( x = \sqrt[4]{81} = 3 \)
Задача 2. Решить уравнение 3x = 81
Запишем данное уравнение так: 3x = 34, откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. {-2} = \frac{1}{25}$$
{-2} = \frac{1}{25}$$
Решить уравнение log3(1-x) = 2
По определению логарифма 32 = 1 — x, откуда x = -8
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
1) loga(bc) = logab + logac
3) logabr = r logab
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. {\infty} \frac{1}{n!} $$
$$ e \approx 2,7182818284 $$
{\infty} \frac{1}{n!} $$
$$ e \approx 2,7182818284 $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$
Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, \( a \neq 1 \)
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0
5) Если a > 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0
Если 0 ax принимает положительные значения при 0
отрицательные при х > 1.
Ось Oy является вертикальной асимптотой графика функции y = logax
Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Теорема. Если logax1 = logax2 где a > 0, \( a \neq 1 \), x 1 > 0, x2 > 0, то x1 = x2
Логарифмическая функция y = logax и показательная функция y = ax, где a > 0, \( a \neq 1 \), взаимно обратны.
Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х2 + 4х + 3 = 8, т.е. х2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.
 е. х = -5 не является корнем этого
уравнения.
е. х = -5 не является корнем этого
уравнения.Ответ x = 1
Решить уравнение lg(2x2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x2 — 4x + 12) = lg(x2 + 3x)
откуда
2x2 — 4x + 12 = x2 + 3x
x2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения. 2(x)} $$
2(x)} $$
root(2,x) эквивалентно sqrt(x)
x^(1/2) эквивалентно sqrt(x)
log(x)
log(e,x)
(основание — число e)
При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли.
Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях.
Единственное неудобство — на английском языке, но это не большая цена за качество.
Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли.
Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях.
Единственное неудобство — на английском языке, но это не большая цена за качество.
 .. together using the commom denominator …
.. together using the commom denominator … {-x}} \)
{-x}} \)Если вам что-то осталось не понятно обязательно напишите об этом в Обранной связи и мы дополним эту таблицу.
Онлайн калькулятор логарифмов двоичного, десятичного, по заданному основанию
- Подробности
Калькулятор онлайн рассчитывает: натуральный логарифм ln(b); двоичный логарифм lg2(b); деcятичный логарифм lg(b); логарифм по заданному основанию loga(b).
Помощь на развитие проекта premierdevelopment.ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Для справки:
- натуральный логарифм
- — это логарифм по основанию e, где e — иррациональная константа, приблизительно равная 2,718.
Натуральный логарифм обозначается как ln(b), loge(b) или иногда просто log(b), если основание e подразумевается.
Натуральный логарифм числа b — это показатель степени, в которую нужно возвести число e, чтобы получить b. - двоичный логарифм
- — логарифм по основанию 2. Двоичный логарифм обозначается как lg2(b). Двоичный логарифм числа b есть решение уравнения 2x = b.
- десятичный логарифм
- — логарифм по основанию 10. Десятичный логарифм обозначается как lg(b). Десятичный логарифм числа b есть решение уравнения 10x = b.
- логарифм числа b по основанию a
- — показатель степени, в которую надо возвести основание a, чтобы получить число b. Он обозначается как loga(b).
Логари́фм числа b по основанию a есть решение уравнения ax = b.

II. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолачанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Область определения функции | Онлайн калькулятор
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. 4)
4)
онлайн — ln Calculator
Описание:
Калькулятор ln позволяет вычислить натуральный логарифм числа в режиме онлайн.
ln онлайнОписание:
Функция логарифма Напьера определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, он отмечает ln . Наперовский логарифм также называют натуральным логарифмом .
Калькулятор логарифма позволяет вычислить этого типа логарифма онлайн .
- Вычисление наперовского логарифма
- Производная от наперовского логарифма
- Вычислить цепное правило производных с наперовским логарифмом
- Первообразная наперского логарифма
- Пределы наперовского логарифма
Для вычисления напьера логарифма числа просто введите число и примените
функция ln . Таким образом, для при расчете наперский логарифм числа 1, необходимо ввести
ln (`1`) или
непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.
Производная напьера логарифма равна `1 / x`.
Первообразная напьера логарифма равна `x * ln (x) -x`.
- Пределы наперовского логарифма существуют в точках «0» и «+ oo»:
- Функция логарифма Напьера имеет предел в «0», который равен «-oo».

- Функция напьера логарифма имеет предел в «+ oo», который равен «+ oo».m) = m * ln (а) `
Калькулятор позволяет использовать эти свойства для вычисления логарифмических разложений.
Калькулятор ln позволяет онлайн вычислить натуральный логарифм числа.
Синтаксис:
ln (x), x — это число.Примеры:
ln (`1`), возвращает 0Производный наперовский логарифм:
Чтобы дифференцировать функцию логарифма напьера онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции напьера логарифма
Производная от ln (x) — это производная_вычислителя (`ln (x)`) = `1 / (x)`
Первообразный неаперовский логарифм:
Калькулятор первообразных позволяет вычислить первообразную функции напьера логарифма.
Первообразная от ln (x) — это первообразная_вычислителя (`ln (x)`) = `x * ln (x) -x`
Предел напьера логарифм:
Калькулятор пределов позволяет вычислить пределы функции логарифма напьера.
Предел ln (x) равен limit_calculator (`ln (x)`)
Обратная функция наперовского логарифма:
Функция, обратная к логарифму Напьера — это экспоненциальная функция, обозначенная как exp.
Графический наперовский логарифм:
Графический калькулятор может построить функцию логарифма напьера в интервале ее определения.
Посчитать онлайн через ln (наперский логарифм) Калькулятор
— ln (1) — Solumaths
Описание:
Калькулятор ln позволяет вычислить натуральный логарифм числа в режиме онлайн.
ln онлайнОписание:
Функция логарифма Напьера определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, он отмечает ln . Наперовский логарифм также называют натуральным логарифмом .
Калькулятор логарифма позволяет вычислить этого типа логарифма онлайн .
- Вычисление наперовского логарифма
- Производная от наперовского логарифма
- Вычислить цепное правило производных с наперовским логарифмом
- Первообразная наперского логарифма
- Пределы наперовского логарифма
Для вычисления напьера логарифма числа просто введите число и примените
функция ln . Таким образом, для при расчете наперский логарифм числа 1, необходимо ввести
ln (`1`) или
непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.
Таким образом, для при расчете наперский логарифм числа 1, необходимо ввести
ln (`1`) или
непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.
Производная напьера логарифма равна `1 / x`.
Если u — дифференцируемая функция, цепное правило производных с функцией напьера логарифма и функция u вычисляется по следующей формуле : (ln (u (x)) ‘= `(u’ (x)) / (u (x))`, калькулятор производных может выполнить этот тип расчета, как показано в этом примере вычисление производной ln (4x + 3).
Первообразная напьера логарифма равна `x * ln (x) -x`.
- Пределы наперовского логарифма существуют в точках «0» и «+ oo»:
- Функция логарифма Напьера имеет предел в «0», который равен «-oo».

- Функция напьера логарифма имеет предел в «+ oo», который равен «+ oo».m) = m * ln (а) `
Калькулятор позволяет использовать эти свойства для вычисления логарифмических разложений.
Калькулятор ln позволяет онлайн вычислить натуральный логарифм числа.
Синтаксис:
ln (x), x — это число.Примеры:
ln (`1`), возвращает 0Производный наперовский логарифм:
Чтобы дифференцировать функцию логарифма напьера онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции напьера логарифма
Производная от ln (x) — это производная_вычислителя (`ln (x)`) = `1 / (x)`
Первообразный неаперовский логарифм:
Калькулятор первообразных позволяет вычислить первообразную функции напьера логарифма.
Первообразная от ln (x) — это первообразная_вычислителя (`ln (x)`) = `x * ln (x) -x`
Предел напьера логарифм:
Калькулятор пределов позволяет вычислить пределы функции логарифма напьера.
Предел ln (x) равен limit_calculator (`ln (x)`)
Обратная функция наперовского логарифма:
Функция, обратная к логарифму Напьера — это экспоненциальная функция, обозначенная как exp.
Графический наперовский логарифм:
Графический калькулятор может построить функцию логарифма напьера в интервале ее определения.
Посчитать онлайн через ln (наперский логарифм) Калькулятор
— ln (0) — Solumaths
Описание:
Калькулятор ln позволяет вычислить натуральный логарифм числа в режиме онлайн.
ln онлайнОписание:
Функция логарифма Напьера определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, он отмечает ln . Наперовский логарифм также называют натуральным логарифмом .
Калькулятор логарифма позволяет вычислить этого типа логарифма онлайн .
- Вычисление наперовского логарифма
- Производная от наперовского логарифма
- Вычислить цепное правило производных с наперовским логарифмом
- Первообразная наперского логарифма
- Пределы наперовского логарифма
Для вычисления напьера логарифма числа просто введите число и примените
функция ln . Таким образом, для при расчете наперский логарифм числа 1, необходимо ввести
ln (`1`) или
непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.
Таким образом, для при расчете наперский логарифм числа 1, необходимо ввести
ln (`1`) или
непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.
Производная напьера логарифма равна `1 / x`.
Если u — дифференцируемая функция, цепное правило производных с функцией напьера логарифма и функция u вычисляется по следующей формуле : (ln (u (x)) ‘= `(u’ (x)) / (u (x))`, калькулятор производных может выполнить этот тип расчета, как показано в этом примере вычисление производной ln (4x + 3).
Первообразная напьера логарифма равна `x * ln (x) -x`.
- Пределы наперовского логарифма существуют в точках «0» и «+ oo»:
- Функция логарифма Напьера имеет предел в «0», который равен «-oo».

- Функция напьера логарифма имеет предел в «+ oo», который равен «+ oo».m) = m * ln (а) `
Калькулятор позволяет использовать эти свойства для вычисления логарифмических разложений.
Калькулятор ln позволяет онлайн вычислить натуральный логарифм числа.
Синтаксис:
ln (x), x — это число.Примеры:
ln (`1`), возвращает 0Производный наперовский логарифм:
Чтобы дифференцировать функцию логарифма напьера онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции напьера логарифма
Производная от ln (x) — это производная_вычислителя (`ln (x)`) = `1 / (x)`
Первообразный неаперовский логарифм:
Калькулятор первообразных позволяет вычислить первообразную функции напьера логарифма.
Первообразная от ln (x) — это первообразная_вычислителя (`ln (x)`) = `x * ln (x) -x`
Предел напьера логарифм:
Калькулятор пределов позволяет вычислить пределы функции логарифма напьера.
Предел ln (x) равен limit_calculator (`ln (x)`)
Обратная функция наперовского логарифма:
Функция, обратная к логарифму Напьера — это экспоненциальная функция, обозначенная как exp.
Графический наперовский логарифм:
Графический калькулятор может построить функцию логарифма напьера в интервале ее определения.
Посчитать онлайн через ln (наперский логарифм)
Ln Calculator
Ln Calculator
Калькулятор Ln используется для определения натурального логарифма числа.При выполнении расчетов используются простые формулы. В нем есть одно текстовое поле, в которое вы вводите значение Ln. Чаще всего натуральный логарифм X выражается как; «Ln X» и «logeX». Они обычно используются в некоторых научных контекстах и в нескольких других языках программирования. Логарифм с основанием «е» является натуральным логарифмом и приблизительно эквивалентен числу Эйлера 2,718281828. Калькулятор Ln имеет два элемента управления, которые используются для выполнения различных функций. Кнопка «Рассчитать» используется для преобразования значений, введенных в пустое текстовое поле.Ваши результаты будут отображаться в нижней части калькулятора. Кнопка «Сброс» используется для стирания всех текстовых полей предыдущих расчетов. Это самый быстрый способ сбросить настройки калькулятора, когда вы хотите выполнить новые вычисления.
Это самый быстрый способ сбросить настройки калькулятора, когда вы хотите выполнить новые вычисления.
Например;
Найдите натуральный логарифм 45.Решение;
Введите число 45 в пустое текстовое поле и нажмите знак равенства или кнопку «Рассчитать». Оба они работают одинаково, давая вам точные результаты в зависимости от значения, введенного в текстовое поле.Ответ будет отображаться как; 3.8066624898Калькулятор натурального логарифма также может использоваться для вычисления десятичных значений.
Например;
Найдите натуральный логарифм 0,5Решение;
Введите значение 0,5 в пустое текстовое поле и затем щелкните знак равенства или кнопку «Рассчитать». Ваши результаты будут отображаться как; -0.69314718056Вы также можете использовать «e» для выражения научного обозначения. Важно знать, что калькулятор даст точные результаты в зависимости от значений, введенных в текстовое поле.Существуют различные способы ввода значений Ln. Например. 6e2, 4e-7, 5.78e10
Например;
Определите натуральный логарифм 8e5Решение
Введите 8e5 в пустое текстовое поле и затем щелкните знак равенства или кнопку «Рассчитать».Ваш ответ будет отображаться как; 13.5
Калькулятор журнала
Укажите любые два значения для вычисления третьего в уравнении логарифма log b x = y . Он может принимать «e» в качестве базового ввода.
Связанный научный калькулятор | Калькулятор экспонентыЧто такое журнал?
Логарифм или журнал — это величина, обратная математической операции возведения в степень. Это означает, что логарифм числа — это число, до которого должно быть увеличено фиксированное основание, чтобы получить число. Обычно лог подразумевает, что используется база 10, хотя технически база может быть любой. Когда основание — e, обычно пишется ln, а не log e . log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами.Если например:
х = б у ; тогда y = log b x; где b — база
Каждая из упомянутых баз обычно используется в разных приложениях. База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
Основные правила журнала
Если аргумент логарифма является произведением двух цифр, логарифм можно переписать как сложение логарифма каждой из цифр.
журнал b (x × y) = журнал b x + журнал b y
Пример: журнал (1 × 10) = журнал (1) + журнал (10) = 0 + 1 = 1
Если аргумент логарифма является дробью, логарифм можно переписать как вычитание логарифма числителя минус логарифм знаменателя.
журнал b (x / y) = журнал b x — журнал b y
Пример: журнал (10/2) = журнал (10) — журнал (2) = 1 — 0,301 = 0,699
Если в аргументе логарифма есть показатель степени, показатель степени можно вытянуть из логарифма и умножить.
журнал b x y = y × журнал b x
Пример: журнал (2 6 ) = 6 × журнал (2) = 1,806
Также можно изменить основание логарифма, используя следующее правило.
Для переключения основания и аргумента используйте следующее правило.
Другие десятичные логарифмы, на которые следует обратить внимание, включают:
журнал b (1) = 0
журнал b (b) = 1
log b (0) = undefined
lim x → 0 + журнал b (x) = — ∞
ln (e x ) = x
ln (x) Калькулятор натурального логарифма
ln (x)Калькулятор натурального логарифма ln (x) находит результат функции логарифма по основанию e , что приблизительно равно 2.718 .
Калькулятор натурального журнала пер. Рассчитатьln (x) = y
x: — действительное число, x> 0
Натуральный логарифм: ln
ln (x) = y
ln (x) эквивалентно log e (x)
Примеры натурального логарифма
- ln (2) = log e (2) = 0,6931
- ln (3) = log e (3) = 1,0986
- ln (4) = log e (4) = 1.3862
- ln (5) = log e (5) = 1,609
- ln (6) = log e (6) = 1,7917
- ln (10) = log e (10) = 2.3025
Список таблиц значений функции журнала в экспоненциальных числах с основанием (e).
| log e (x) | Обозначение | Значение | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| log e (1) | ln (1) | 0 | ||||||||||||||||||||||||||||
| log e 904 (2) | 0.693147 | |||||||||||||||||||||||||||||
| лог e (3) | ln (3) | 1.098612 | ||||||||||||||||||||||||||||
| log e (4) | ln (4) | 1.386294 | 1.386294 | 5)ln (5) | 1.609438 | |||||||||||||||||||||||||
| log e (6) | ln (6) | 1.7 | ||||||||||||||||||||||||||||
| log e (7) | e (7) | 1.94591 | ||||||||||||||||||||||||||||
| лог e (8) | ln (8) | 2.079442 | ||||||||||||||||||||||||||||
| log e (9) | ln (9) | 2,197225 | ||||||||||||||||||||||||||||
| log e (10) | ln (10) | 2.302585 | 2.302585 | 11)ln (11) | 2.397895 | |||||||||||||||||||||||||
| log e (12) | ln (12) | 2.484907 | ||||||||||||||||||||||||||||
| log e 4 (13) | 1357 904 2,564949||||||||||||||||||||||||||||||
| лог e (14) | ln (14) | 2.639057 | ||||||||||||||||||||||||||||
| log e (15) | ln (15) | 2,70805 | ||||||||||||||||||||||||||||
| log e (16) | ln (16) | e 772589 | 17)ln (17) | 2.833213 | ||||||||||||||||||||||||||
| log e (18) | ln (18) | 2.8 | ||||||||||||||||||||||||||||
| log e (19) | 19574 e (19) 19574 905 2.944439||||||||||||||||||||||||||||||
| журнал e (20) | ln (20) | 2.995732 | ||||||||||||||||||||||||||||
| log e (21) | ln (21) | 3.044522 | ||||||||||||||||||||||||||||
| log e (22) | ln (22) | e | ln (22) | 3.0 | ln (23) | 3.135494 | ||||||||||||||||||||||||
| log e (24) | ln (24) | 3.178054 | ||||||||||||||||||||||||||||
| log e (25) | e (25) | 3.218876 | ||||||||||||||||||||||||||||
| лог e (26) | ln (26) | 3.258097 | ||||||||||||||||||||||||||||
| log e (27) | ln (27) | 3.295837 | ||||||||||||||||||||||||||||
| log e (28) | ln (28) | 3,332204 | 29)ln (29) | 3.367296 | ||||||||||||||||||||||||||
| log e (30) | ln (30) | 3.401197 | ||||||||||||||||||||||||||||
| log e (31) | 3.433987 | |||||||||||||||||||||||||||||
| лог e (32) | ln (32) | 3.465736 | ||||||||||||||||||||||||||||
| log e (33) | ln (33) | 3.496508 | ||||||||||||||||||||||||||||
| log e (34) | ln (34) | 3.52636161 | 905 35)ln (35) | 3.555348 | ||||||||||||||||||||||||||
| log e (36) | ln (36) | 3.583519 | ||||||||||||||||||||||||||||
| log e (37) | 374e (37) | 3.610918 | ||||||||||||||||||||||||||||
| лог e (38) | ln (38) | 3.637586 | ||||||||||||||||||||||||||||
| log e (39) | ln (39) | 3.663562 | ||||||||||||||||||||||||||||
| log e (40) | ln (40) | e | ln (41) | 3,713572 | log e (42) | ln (42) | 3,73767 | log e (43) | 43574 ln | 43574 ln 3.7612 | лог e (44) | ln (44) | 3.78419 | log e (45) | ln (45) | 3.806662 | log e (46) | ln (46) | 3,8286416 | 3.8286416 | 47) ln (47) | 3.850148 | log e (48) | ln (48) | 3.871201 | log e (494) | 3.89182 | лог e (50) | ln (50) | 3. | |
| log e (51) | ln (51) | 3,931826 | ||||||||||||||||||||||||||||
| log e (52) | ln (52) | e | ln (52) | e 951244 | 53)ln (53) | 3.970292 | ||||||||||||||||||||||||
| log e (54) | ln (54) | 3.988984 | ||||||||||||||||||||||||||||
| log e (554) | 9057 9057 9057 4.007333||||||||||||||||||||||||||||||
| лог e (56) | ln (56) | 4.025352 | ||||||||||||||||||||||||||||
| log e (57) | ln (57) | 4.043051 | ||||||||||||||||||||||||||||
| log e (58) | ln (58) | 4.060444 | 4.060444 | 59)ln (59) | 4.077537 | |||||||||||||||||||||||||
| log e (60) | ln (60) | 4.094345 | ||||||||||||||||||||||||||||
| log e (61) | e (61) | 4.110874 | ||||||||||||||||||||||||||||
| лог e (62) | ln (62) | 4.127134 | ||||||||||||||||||||||||||||
| log e (63) | ln (63) | 4.143135 | ||||||||||||||||||||||||||||
| log e (64) | ln (64) | 4.158883 |
| log e (x) | Обозначение | Значение | ||||
|---|---|---|---|---|---|---|
| log e (65) | ln (65) | 4,174387 | ||||
| 16 ln e (66) | 4.189655 | |||||
| log e (67) | ln (67) | 4.204693 | ||||
| log e (68) | ln (68) | 4.219508 | ||||
| log e (69) | ln (69) | e | ln (69) | 4,234107 | 70)ln (70) | 4.248495 |
| log e (71) | ln (71) | 4.26268 | ||||
| log e (72) | (72)ln 4.276666 | |||||
| лог e (73) | ln (73) | 4.2 | ||||
| log e (74) | ln (74) | 4.304065 | ||||
| log e (75) | ln (75) | 4.317484 | 4.317484 | 76)ln (76) | 4.330733 | |
| log e (77) | ln (77) | 4.343805 | ||||
| log e (78) | e (78) | 4.356709 | ||||
| лог e (79) | ln (79) | 4.369448 | ||||
| журнал e (80) | ln (80) | 4.382027 | ||||
| log e (81) | ln (81) | e (81) | 905 82)ln (82) | 4.406719 | ||
| log e (83) | ln (83) | 4.418841 | ||||
| log e (84) | e (84) | 4.430817 | ||||
| лог e (85) | ln (85) | 4.442651 | ||||
| log e (86) | ln (86) | 4.454347 | ||||
| log e (87) | ln (87) | 4.4659016 | 4.4659016 | 88)ln (88) | 4.477337 | |
| log e (89) | ln (89) | 4.488636 | ||||
| log e (90) | e (90) | 4.49981 | ||||
| журнал e (91) | ln (91) | 4.51086 | ||||
| log e (92) | ln (92) | 4.521789 | ||||
| log e (93) | ln (93) | 4.532599 | 94)ln (94) | 4.543295 | ||
| log e (95) | ln (95) | 4.553877 | ||||
| log e (96) | e (96) | 4.564348 | ||||
| журнал e (97) | ln (97) | 4.574711 | ||||
| log e (98) | ln (98) | 4.584967 | ||||
| log e (99) | ln (99) | 4.59512 | ||||
| ln (100) | 4.60517 | |||||
| log e (101) | ln (101) | 4.615121 | ||||
| log e (102) | 102e (102) | 1024.624973 | ||||
| лог e (103) | ln (103) | 4.634729 | ||||
| лог e (104) | ln (104) | 4.644391 | ||||
| лог e (105) | ln (105) | 4.653916 | 4.653916 | 106)ln (106) | 4.663439 | |
| log e (107) | ln (107) | 4.672829 | ||||
| log e (108) | e (108) | 4.682131 | ||||
| лог e (109) | ln (109) | 4.6 | ||||
| log e (110) | ln (110) | 4.70048 | ||||
| log e (111) | ln (111) | 4.70953 | ||||
| ln (112) | 4.718499 | |||||
| log e (113) | ln (113) | 4.727388 | ||||
| log e (114) | e (114) | 4.736198 | ||||
| лог e (115) | ln (115) | 4.744932 | ||||
| журнал e (116) | ln (116) | 4.75359 | ||||
| log e (117) | ln (117) | e662174 | 4,762174 | 118)ln (118) | 4.770685 | |
| log e (119) | ln (119) | 4.779123 | ||||
| log e (120) | e (120) | 4.787492 | ||||
| лог e (121) | ln (121) | 4.795791 | ||||
| log e (122) | ln (122) | 4.804021 | ||||
| log e (123) | ln (123) | 4.812184 | 4.812184 | 124)ln (124) | 4.820282 | |
| log e (125) | ln (125) | 4.828314 | ||||
| log e (126) 905 (12677 | ) e (126) 905 (12677 | ) 4.836282 | ||||
| лог e (127) | ln (127) | 4.844187 | ||||
| журнал e (128) | ln (128) | 4.85203 |
| log e (x) | Обозначение | Значение | |||||
|---|---|---|---|---|---|---|---|
| log e (129) | ln (129) | 4.859812 | |||||
| 16 log (130) | 4.867534 | ||||||
| log e (131) | ln (131) | 4.875197 | |||||
| log e (132) | ln (132) 4 | 9057 9057 905782802 | |||||
| log e (133) | ln (133) | 4.8 | |||||
| log e (134) | ln (134) | 4.89784 | 905 905 905 135)ln (135) | 4.5 | |||
| log e (136) | ln (136) | 4. | |||||
| log e (137) | 137 4. | 1 | |||||
| лог e (138) | ln (138) | 4.927254 | |||||
| log e (139) | ln (139) | 4.934474 | |||||
| log e (140) | ln (140) | 4.951642 | 4.951642 | 141)ln (141) | 4.94876 | ||
| log e (142) | ln (142) | 4.955827 | |||||
| log e (143) 905 905 4.962845 | |||||||
| лог e (144) | ln (144) | 4.969813 | |||||
| журнал e (145) | ln (145) | 4.976734 | |||||
| log e (146) | ln (146) | 7 | 905 147)ln (147) | 4.9 | |||
| log e (148) | ln (148) | 4.997212 | |||||
| log e (149) | (149) 905 5.003946|||||||
| лог e (150) | ln (150) | 5.010635 | |||||
| журнал e (151) | ln (151) | 5,0 1728 | |||||
| log e (152) | ln (152) | 5,023881 | 5,023881 | 153)ln (153) | 5.030438 | ||
| log e (154) | ln (154) | 5.036953 | |||||
| log e 9057 (155) 905 905 5.043425 | |||||||
| лог e (156) | ln (156) | 5.049856 | |||||
| log e (157) | ln (157) | 5.056246 | |||||
| log e (158) | ln (158) | ln (158) | log 159) | ln (159) | 5.068904 | ||
| log e (160) | ln (160) | 5.075174 | |||||
| log e (161) | 5.081404|||||||
| лог e (162) | ln (162) | 5.087596 | |||||
| log e (163) | ln (163) | 5.09375 | |||||
| log e (164) | ln (164) | 5,0994 905 165) | ln (165) | 5.105945 | |||
| log e (166) | ln (166) | 5.111988 | |||||
| log e (167) | 5.117994|||||||
| лог e (168) | ln (168) | 5.123964 | |||||
| лог e (169) | ln (169) | 5.129899 | |||||
| log e (170) | ln (170) | 5,13541698 | 171) | ln (171) | 5.141664 | ||
| log e (172) | ln (172) | 5.147494 | |||||
| log e 173 | 905 5.153292 | ||||||
| лог e (174) | ln (174) | 5.159055 | |||||
| журнал e (175) | ln (175) | 5.164786 | |||||
| журнал e (176) | ln (176) | e | 5,170484 | 177)ln (177) | 5.17615 | ||
| log e (178) | ln (178) | 5.181784 | |||||
| log e (179 179) 905 905 5.187386 | |||||||
| лог e (180) | ln (180) | 5.192957 | |||||
| log e (181) | ln (181) | 5.198497 | |||||
| log e (182) | ln (182) | (182)ln (182) | 4183) | ln (183) | 5.209486 | ||
| log e (184) | ln (184) | 5.214936 | |||||
| log e 18557 905 905 905 5.220356 | |||||||
| журнал e (186) | ln (186) | 5.225747 | |||||
| log e (187) | ln (187) | 5.231109 | |||||
| log e (188) | ln (188) | ln (189) | 5.241747 | ||||
| log e (190) | ln (190) | 5.247024 | |||||
| log e (194) | 5.252273|||||||
| лог e (192) | ln (192) | 5. |