Калькулятор который делит столбиком. Как делить десятичные дроби
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78.
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27.
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Просто введите делимое и делитель и нажмите кнопку Вычислить.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ.
 Оно должно быть таким, сколько раз делитель помещается в делимом.
Оно должно быть таким, сколько раз делитель помещается в делимом. - Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра.
 Умножение даст 284 и 32.
Умножение даст 284 и 32. - Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.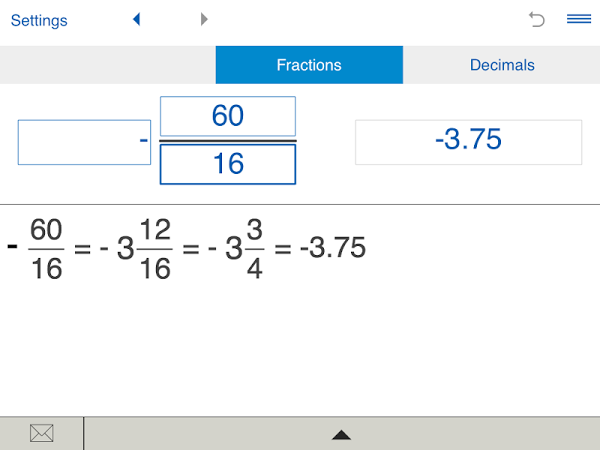
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.
Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить десятичную дробь на число, не обращая внимания на запятую;
2) когда закончится деление целой части, в частном поставить запятую.
Примеры.
Разделить десятичные дроби:
Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84.
2) 19,26: 18
Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.
Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46.
4) 0,1547: 17
Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.
Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.
5) Десятичная дробь может получиться и при делении двух натуральных чисел.
При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.
И еще пара примеров на деление десятичных дробей на натуральные числа:
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т. д.) во время конструирования, игр и наблюдений за природой.
д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
бесконечную десятичную дробь перевести в обыкновенную
Вы искали бесконечную десятичную дробь перевести в обыкновенную? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как бесконечную десятичную дробь перевести в обыкновенную дробь, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «бесконечную десятичную дробь перевести в обыкновенную».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как бесконечную десятичную дробь перевести в обыкновенную,как бесконечную десятичную дробь перевести в обыкновенную дробь,как обыкновенную дробь перевести в десятичную периодическую дробь,как перевести бесконечную десятичную дробь в обыкновенную дробь,как перевести в обыкновенную дробь бесконечную десятичную дробь,как перевести обыкновенную дробь в периодическую десятичную дробь,как перевести смешанную дробь в периодическую дробь,как перевести число в периоде в обыкновенную дробь,как число в периоде перевести в обыкновенную дробь,обыкновенную дробь перевести в десятичную периодическую дробь,онлайн калькулятор перевод периодической дроби в обыкновенную,онлайн перевод периодической дроби в обыкновенную,перевести десятичную периодическую дробь в обыкновенную,перевести обыкновенную дробь в десятичную периодическую,перевести обыкновенную дробь в десятичную периодическую дробь,перевести обыкновенную дробь в периодическую онлайн,перевести периодическую дробь в обыкновенную десятичную дробь,перевести периодическую дробь в обыкновенную онлайн,перевести смешанную периодическую дробь в обыкновенную дробь,перевод бесконечной десятичной дроби в обыкновенную,перевод десятичной бесконечной дроби в обыкновенную,перевод десятичной дроби периодической в обыкновенную,перевод десятичной дроби периодической в обыкновенную дробь,перевод периодической десятичной дроби в обыкновенную,перевод периодической десятичной дроби в обыкновенную дробь,перевод периодической дроби в обыкновенную онлайн,периодическую дробь в обыкновенную онлайн,периодическую дробь перевести обыкновенную дробь в десятичную. (-53) = 6305039478318694 / 9007199254740992
≈ 0.69999999999999995559107901499373838305
(-53) = 6305039478318694 / 9007199254740992
≈ 0.69999999999999995559107901499373838305
Таким образом , правильное представление x как рационального числа было бы 6305039478318694 / 9007199254740992, но это, конечно, не то, что
вы ожидаете. То, что вы ожидаете, — это 7/10 , но есть еще одна проблема:
let x : Double = 69999999999999996/100000000000000000
присваивает точно такое же значение x, оно неотличимо от 0.7 с точностью до Double .
Так должен ли x отображаться как 7/10 или как 69999999999999996/100000000000000000 ?
Как было сказано выше, использование рациональной арифметики было бы идеальным решением.
Если это невозможно, то вы можете преобразовать Double обратно в
рациональное число с заданной точностью .
(Следующее взято из алгоритма для LCM двойников в Swift .)
Непрерывные дроби -это эффективный метод создания (конечной или бесконечной) последовательности дробей h n /k n , которые являются произвольными хорошими приближениями к заданному действительному числу x , и вот возможная реализация в Swift:
typealias Rational = (num : Int, den : Int)
func rationalApproximationOf(x0 : Double, withPrecision eps : Double = 1.0E-6) -> Rational {
var x = x0
var a = floor(x)
var (h2, k1, h, k) = (1, 0, Int(a), 1)
while x - a > eps * Double(k) * Double(k) {
x = 1.0/(x - a)
a = floor(x)
(h2, k1, h, k) = (h, k, h2 + Int(a) * h, k1 + Int(a) * k)
}
return (h, k)
}
Примеры:
rationalApproximationOf(0.333333) // (1, 3)
rationalApproximationOf(0.25) // (1, 4)
rationalApproximationOf(0.1764705882) // (3, 17)
Точность по умолчанию-1.0E-6, но вы можете настроить ее в соответствии со своими потребностями:
rationalApproximationOf(0. 142857) // (1, 7)
rationalApproximationOf(0.142857, withPrecision: 1.0E-10) // (142857, 1000000)
rationalApproximationOf(M_PI) // (355, 113)
rationalApproximationOf(M_PI, withPrecision: 1.0E-7) // (103993, 33102)
rationalApproximationOf(M_PI, withPrecision: 1.0E-10) // (312689, 99532)
142857) // (1, 7)
rationalApproximationOf(0.142857, withPrecision: 1.0E-10) // (142857, 1000000)
rationalApproximationOf(M_PI) // (355, 113)
rationalApproximationOf(M_PI, withPrecision: 1.0E-7) // (103993, 33102)
rationalApproximationOf(M_PI, withPrecision: 1.0E-10) // (312689, 99532)
Swift 3 версия:
typealias Rational = (num : Int, den : Int)
func rationalApproximation(of x0 : Double, withPrecision eps : Double = 1.0E-6) -> Rational {
var x = x0
var a = x.rounded(.down)
var (h2, k1, h, k) = (1, 0, Int(a), 1)
while x - a > eps * Double(k) * Double(k) {
x = 1.0/(x - a)
a = x.rounded(.down)
(h2, k1, h, k) = (h, k, h2 + Int(a) * h, k1 + Int(a) * k)
}
return (h, k)
}
Примеры:
rationalApproximation(of: 0.333333) // (1, 3)
rationalApproximation(of: 0.142857, withPrecision: 1.0E-10) // (142857, 1000000)
Или – как предложил @brandonscript – с struct Rational и инициализатором:
struct Rational {
let numerator : Int
let denominator: Int
init(numerator: Int, denominator: Int) {
self.numerator = numerator
self.denominator = denominator
}
init(approximating x0: Double, withPrecision eps: Double = 1.0E-6) {
var x = x0
var a = x.rounded(.down)
var (h2, k1, h, k) = (1, 0, Int(a), 1)
while x - a > eps * Double(k) * Double(k) {
x = 1.0/(x - a)
a = x.rounded(.down)
(h2, k1, h, k) = (h, k, h2 + Int(a) * h, k1 + Int(a) * k)
}
self.init(numerator: h, denominator: k)
}
}
Пример использования:
print(Rational(approximating: 0.333333))
// Rational(numerator: 1, denominator: 3)
print(Rational(approximating: .pi, withPrecision: 1.0E-7))
// Rational(numerator: 103993, denominator: 33102)
Переводчик простых дробей в десятичные.
 Калькулятор онлайн.Перевод десятичной дроби в обыкновенную
Калькулятор онлайн.Перевод десятичной дроби в обыкновеннуюМы уже говорили, что дроби бывают обыкновенные и десятичные . На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обеими видов дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Содержание урокаВыражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:
Рассмотрим следующий пример. Показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, требуется показать 6 см и 3 мм в сантиметрах, но в дробном виде. 6 целых сантиметров у нас уже есть:
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.
В результате имеем шесть целых сантиметров и три десятых сантиметра:
При этом 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра» .
Эта дробь читается как «шесть целых и три десятых сантиметра» .
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6
Целая часть записана. Сразу же после написания целой части ставим запятую:
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
Любое число, которое представляется в таком виде, называется десятичной дробью .
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
Выглядеть это будет следующим образом:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части стоят числа 10, 100, 1000 или 10000.
Как и смешанное число, десятичная дробь имеет целую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:
Читается как «ноль целых, пять десятых» .
Перевод смешанных чисел в десятичные дробиКогда мы записываем смешанные числа без знаменателя, мы тем самым переводим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того, как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример:
Что это значит? Рассмотрим следующий пример:
Сначала
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать количество нулей в знаменателе дробной части.
Итак, считаем количество нулей в дробной части смешанного числа . В знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2.
Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа находится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем целую часть и ставим запятую:
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно перевести это смешанное число в десятичную дробь. Записываем целую часть и ставим запятую:
И записываем числитель дробной части:
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа находится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смотрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это число 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед число 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала целую часть и ставим запятую:
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа находится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
Теперь смотрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой число 5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и ставим запятую:
Теперь смотрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед числом 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед числом 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и ставим запятую:
Теперь считаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед числом 5 дописать четыре нуля:
Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь. Записываем после запятой числитель дроби
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя. Встречаются неправильные дроби, у которых в знаменателе находятся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные дроби. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять целую часть.
Пример 1.
Дробь является неправильной дробью. Чтобы перевести такую дробь в десятичную дробь, нужно в первую очередь выделить у нее целую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к и изучить его.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10
Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10
Посмотрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Число 11 будет целой частью, число 2 — числителем дробной части, число 10 — знаменателем дробной части.
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
Теперь считаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
В полученной десятичной дроби 11,2 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе находится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим 450 на 100 уголком:
Соберём новое смешанное число — получим . А как переводить смешанные числа в десятичные дроби мы уже знаем.
Записываем целую часть и ставим запятую:
Теперь считаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
В полученной десятичной дроби 4,50 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена верно.
Значит дробь переведена верно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны. Поставим между ними знак равенства:
4,50 = 4,5
Возникает вопрос: а почему так происходит? Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное числоЛюбая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби. Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
и рядом записываем две тысячных:
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Попробуем доказать, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и . Настало время вспомнить основное свойство дроби, которое говорит, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не изменяется.
Настало время вспомнить основное свойство дроби, которое говорит, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не изменяется.
Давайте разделим первую дробь на 10
Получили , а это вторая дробь. Значит и равны между собой и равны одному и тому же значению:
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль по не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?
Пример первый
У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Пример второй
Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.
Пример третий
И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.
Вывод
- Разбиваем дробь на целую и дробную части.
- Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.
- Записываем дробь в обыкновенном виде.
- Сокращаем числитель и знаменатель дроби.
- Записываем полученную дробь.
- Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.
На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.
Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.
1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:
Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:
Примеры:
2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).
Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).
При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:
*Подробнее:
15:13 = 1 остаток 2
4:3 = 1 остаток 1
9:5 = 1 остаток 4
А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:
Например:
*Числитель у нас – это делимое, знаменатель – это делитель.
Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):
3. Десятичную переводим в обыкновенную.
Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015
Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:
*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.
4. Обыкновенную переводим в десятичную.
Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:
Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:
Если имеется целая часть, то тоже ничего сложного:
Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:
А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:
На какие числа умножать числитель и знаменатель?
Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:
Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:
Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
В этой статье мы разберем, как осуществляется перевод обыкновенных дробей в десятичные дроби , а также рассмотрим обратный процесс – перевод десятичных дробей в обыкновенные дроби. Здесь мы озвучим правила обращения дробей и приведем подробные решения характерных примеров.
Навигация по странице.
Перевод обыкновенных дробей в десятичные дроби
Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби .
Сначала мы рассмотрим, как обыкновенные дроби со знаменателями 10, 100, 1 000, … представить в виде десятичных дробей . Это объясняется тем, что десятичные дроби по сути являются компактной формой записи обыкновенных дробей со знаменателями 10, 100, … .
После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.
Теперь обо всем по порядку.
Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби
Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.
«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь после дописывания нулей будет иметь вид .
Например, дробь после дописывания нулей будет иметь вид .
После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.
Дадим правило перевода правильной обыкновенной дроби со знаменателем 10, или 100, или 1 000, … в десятичную дробь . Оно состоит из трех шагов:
- записываем 0 ;
- после него ставим десятичную запятую;
- записываем число из числителя (вместе с дописанными нулями, если мы их дописывали).
Рассмотрим применение этого правила при решении примеров.
Пример.
Переведите правильную обыкновенную дробь 37/100 в десятичную.
Решение.
В знаменателе находится число 100 , в записи которого два нуля. В числителе находится число 37 , в его записи две цифры, следовательно, эта дробь не нуждается в подготовке к переводу в десятичную дробь.
Теперь записываем 0 , ставим десятичную запятую, и записываем число 37 из числителя, при этом получаем десятичную дробь 0,37 .
Ответ:
0,37 .
Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.
Пример.
Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.
Решение.
Количество цифр в числителе равно 3 , а количество нулей в знаменателе равно 7 , поэтому данная обыкновенная дробь нуждается в подготовке к переводу в десятичную. Нам нужно дописать 7-3=4 нуля слева в числителе, чтобы общее количество цифр там стало равно количеству нулей в знаменателе. Получаем .
Осталось составить нужную десятичную дробь. Для этого, во-первых, записываем 0 , во-вторых, ставим запятую, в-третьих, записываем число из числителя вместе с нулями 0000107 , в итоге имеем десятичную дробь 0,0000107 .
Ответ:
0,0000107 .
Неправильные обыкновенные дроби не нуждаются в подготовке при переводе в десятичные дроби. Следует придерживаться следующего правила перевода неправильных обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби :
- записываем число из числителя;
- отделяем десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.

Разберем применение этого правила при решении примера.
Пример.
Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.
Решение.
Во-первых, записываем число из числителя 56888038009, во-вторых, отделяем десятичной запятой 5 цифр справа, так как в знаменателе исходной дроби 5 нулей. В итоге имеем десятичную дробь 568 880,38009 .
Ответ:
568 880,38009 .
Для обращения в десятичную дробь смешанного числа , знаменателем дробной части которого является число 10 , или 100 , или 1 000, … , можно выполнить перевод смешанного числа в неправильную обыкновенную дробь, после чего полученную дробь обратить в десятичную дробь. Но можно пользоваться и следующим правилом перевода смешанных чисел со знаменателем дробной части 10, или 100, или 1 000, … в десятичные дроби :
- при необходимости выполняем «предварительную подготовку» дробной части исходного смешанного числа, дописав необходимое количество нулей слева в числителе;
- записываем целую часть исходного смешанного числа;
- ставим десятичную запятую;
- записываем число из числителя вместе с дописанными нулями.
Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.
Пример.
Переведите смешанное число в десятичную дробь.
Решение.
В знаменателе дробной части 4 нуля, в числителе же находится число 17 , состоящее из 2 цифр, поэтому, нам нужно дописать два нуля слева в числителе, чтобы там число знаков стало равно числу нулей в знаменателе. Выполнив это, в числителе окажется 0017 .
Теперь записываем целую часть исходного числа, то есть, число 23 , ставим десятичную запятую, после которой записываем число из числителя вместе с дописанными нулями, то есть, 0017 , при этом получаем искомую десятичную дробь 23,0017 .
Запишем все решение кратко: .
Несомненно, можно было сначала представить смешанное число в виде неправильной дроби, после чего перевести ее в десятичную дробь. При таком подходе решение выглядит так: .
При таком подходе решение выглядит так: .
Ответ:
23,0017 .
Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби
В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями 10, 100, … , но обыкновенные дроби с другими знаменателями. Сейчас мы разберемся, как это делается.
В некоторых случаях исходная обыкновенная дробь легко приводится к одному из знаменателей 10 , или 100 , или 1 000, … (смотрите приведение обыкновенной дроби к новому знаменателю), после чего не составляет труда полученную дробь представить в виде десятичной дроби. Например, очевидно, что дробь 2/5 можно привести к дроби со знаменателем 10 , для этого нужно числитель и знаменатель умножить на 2 , что даст дробь 4/10 , которая по правилам, разобранным в предыдущем пункте, легко переводится в десятичную дробь 0,4 .
В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.
Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел , а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.
Пример.
Переведите обыкновенную дробь 621/4 в десятичную дробь.
Решение.
Число в числителе 621 представим в виде десятичной дроби, добавив десятичную запятую и несколько нулей после нее. Для начала допишем 2 цифры 0 , позже, при необходимости, мы всегда можем добавить еще нулей. Итак, имеем 621,00 .
Теперь выполним деление столбиком числа 621,000
на 4
. Первые три шага ничем не отличаются от деления столбиком натуральных чисел, после них приходим к следующей картине:
Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:
В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:
На этом деление закончено, а в результате мы получили десятичную дробь 155,25 , которая соответствует исходной обыкновенной дроби.
Ответ:
155,25 .
Для закрепления материала рассмотрим решение еще одного примера.
Пример.
Переведите обыкновенную дробь 21/800 в десятичную дробь.
Решение.
Для перевода данной обыкновенной дроби в десятичную, выполним деление столбиком десятичной дроби 21,000…
на 800
. Нам после первого же шага придется поставить десятичную запятую в частном, после чего продолжить деление:
Наконец-то мы получили остаток 0 , на этом перевод обыкновенной дроби 21/400 в десятичную дробь закончен, и мы пришли к десятичной дроби 0,02625 .
Ответ:
0,02625 .
Может случиться, что при делении числителя на знаменатель обыкновенной дроби мы так и не получим в остатке 0 . В этих случаях деление можно продолжать сколь угодно долго. Однако, начиная с некоторого шага, остатки начитают периодически повторяться, при этом повторяются и цифры в частном. Это означает, что исходная обыкновенная дробь переводится в бесконечную периодическую десятичную дробь . Покажем это на примере.
Пример.
Запишите обыкновенную дробь 19/44 в виде десятичной дроби.
Решение.
Для перевода обыкновенной дроби в десятичную выполним деление столбиком:
Уже сейчас видно, что при делении начали повторяться остатки 8 и 36 , при этом в частном повторяются цифры 1 и 8 . Таким образом, исходная обыкновенная дробь 19/44 переводится в периодическую десятичную дробь 0,43181818…=0,43(18) .
Ответ:
0,43(18) .
В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.
Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.
Понятно, что если обыкновенную дробь можно привести к одному из знаменателей 10, 100, 1 000, … , то полученную дробь легко перевести в конечную десятичную дробь по правилам, разобранным в предыдущем пункте. Но к знаменателям 10, 100, 1 000 и т.д. приводятся далеко не все обыкновенные дроби. К таким знаменателям можно привести лишь дроби, знаменатели которых являются хотя бы одного из чисел 10, 100, … А какие числа могут быть делителями 10, 100, … ? Ответить на этот вопрос нам позволят чисел 10, 100, … , а они таковы: 10=2·5 , 100=2·2·5·5 , 1 000=2·2·2·5·5·5, … . Отсюда следует, что делителями 10, 100, 1 000 и т.д. могут быть лишь числа, разложения которых на простые множители содержат лишь числа 2 и (или) 5 .
Теперь мы можем сделать общий вывод о переводе обыкновенных дробей в десятичные дроби:
- если в разложении знаменателя на простые множители присутствуют лишь числа 2 и (или) 5 , то эту дробь можно перевести в конечную десятичную дробь;
- если кроме двое и пятерок в разложении знаменателя присутствуют другие простые числа, то эта дробь переводится к бесконечную десятичную периодическую дробь.
Пример.
Не выполняя перевод обыкновенных дробей в десятичные, скажите, какие из дробей 47/20 , 7/12 , 21/56 , 31/17 можно перевести в конечную десятичную дробь, а какие — только в периодическую.
Решение.
Разложение на простые множители знаменателя дроби 47/20 имеет вид 20=2·2·5 . В этом разложении присутствуют лишь двойки и пятерки, поэтому эта дробь может быть приведена к одному из знаменателей 10, 100, 1 000, … (в этом примере к знаменателю 100 ), следовательно, может быть переведена в конечную десятичную дробь.
Разложение на простые множители знаменателя дроби 7/12 имеет вид 12=2·2·3 . Так как оно содержит простой множитель 3 , отличный от 2 и 5 , то эта дробь не может быть представлена в виде конечной десятичной дроби, но может быть переведена в периодическую десятичную дробь.
Дробь 21/56
– сократимая, после сокращения она принимает вид 3/8
. Разложение знаменателя на простые множители содержит три множителя, равных 2
, следовательно, обыкновенная дробь 3/8
, а значит и равная ей дробь 21/56
, может быть переведена в конечную десятичную дробь.
Разложение знаменателя на простые множители содержит три множителя, равных 2
, следовательно, обыкновенная дробь 3/8
, а значит и равная ей дробь 21/56
, может быть переведена в конечную десятичную дробь.
Наконец, разложение знаменателя дроби 31/17 представляет собой само 17 , следовательно, эту дробь нельзя обратить в конечную десятичную дробь, но можно обратить в бесконечную периодическую.
Ответ:
47/20 и 21/56 можно перевести в конечную десятичную дробь, а 7/12 и 31/17 — только в периодическую.
Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби
Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?
Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.
Из теоремы о делимости с остатком ясно, что остаток всегда меньше делителя, то есть, если мы выполняем деление некоторого целого числа на целое число q , то остатком может быть лишь одно из чисел 0, 1, 2, …, q−1 . Отсюда следует, что после завершения деления столбиком целой части числителя обыкновенной дроби на знаменатель q , не более чем через q шагов возникнет одна из двух следующих ситуаций:
- либо мы получим остаток 0 , на этом деление закончится, и мы получим конечную десятичную дробь;
- либо мы получим остаток, который уже появлялся ранее, после этого остатки начнут повторяться как в предыдущем примере (так как при делении равных чисел на q получаются равные остатки, что следует из уже упомянутой теоремы о делимости), так будет получена бесконечная периодическая десятичная дробь.
Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.
Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.
Перевод конечных десятичных дробей в обыкновенные дроби
Получить обыкновенную дробь, которая записана в виде конечной десятичной дроби, достаточно просто. Правило перевода конечной десятичной дроби в обыкновенную дробь состоит из трех шагов:
- во-первых, записать данную десятичную дробь в числитель, предварительно отбросив десятичную запятую и все нули слева, если они есть;
- во-вторых, в знаменатель записать единицу и к ней дописать столько нулей, сколько цифр находится после запятой в исходной десятичной дроби;
- в-третьих, при необходимости выполнить сокращение полученной дроби.
Рассмотрим решения примеров.
Пример.
Обратите десятичную дробь 3,025 в обыкновенную дробь.
Решение.
Если в исходной десятичной дроби убрать десятичную запятую, то мы получим число 3 025 . В нем нет нулей слева, которые бы мы отбросили. Итак, в числитель искомой дроби записываем 3 025 .
В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.
Так мы получили обыкновенную дробь 3 025/1 000 . Эту дробь можно сократить на 25 , получаем .
Ответ:
.
Пример.
Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь.
Решение.
Без десятичной запятой исходная десятичная дробь имеет вид 00017 , отбросив нули слева получаем число 17 , которое и является числителем искомой обыкновенной дроби.
В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4
цифры.
В итоге имеем обыкновенную дробь 17/10 000 . Эта дробь несократима, и перевод десятичной дроби в обыкновенную закончен.
Ответ:
.
Когда целая часть исходной конечной десятичной дроби отлична от нуля, то ее можно сразу перевести в смешанное число, минуя обыкновенную дробь. Дадим правило перевода конечной десятичной дроби в смешанное число :
- число до десятичной запятой надо записать как целую часть искомого смешанного числа;
- в числитель дробной части нужно записать число, полученное из дробной части исходной десятичной дроби после отбрасывания в ней всех нулей слева;
- в знаменателе дробной части нужно записать цифру 1 , к которой справа дописать столько нулей, сколько цифр находится в записи исходной десятичной дроби после запятой;
- при необходимости выполнить сокращение дробной части полученного смешанного числа.
Рассмотрим пример перевода десятичной дроби в смешанное число.
Пример.
Представьте десятичную дробь 152,06005 в виде смешанного числа
Дробь может быть преобразована в целое число либо в десятичную дробь. Неправильная дробь, числитель которой больше знаменателя и делится на него без остатка, переводится в целое число, например: 20/5. Делим 20 на 5 и получаем число 4. Если дробь правильная, то есть числитель меньше знаменателя, то тогда преобразовать ее в число (десятичную дробь). Больше информации о дробях вы сможете почерпнуть из нашего раздела — .
Способы преобразования дроби в число
- Первый способ, как перевести дробь в число годится для дроби, которую можно преобразовать в число, являющееся десятичной дробью. Сначала выясним, можно ли перевести заданную дробь в дробь десятичную. Для этого обратим внимание на знаменатель (цифра, которая под чертой или справа от наклонной). Если знаменатель можно разложить на множители (в нашем примере — 2 и 5), которые могут повторяться, то данную дробь реально преобразовать в конечную десятичную дробь.
 Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275 - Второй способ, как перевести дробь в число — более простой: необходимо числитель поделить на знаменатель. Для применения этого способа просто произведем деление, а полученное число и будет той искомой десятичной дробью. Например, надо перевести дробь 2/15 в число. Делим 2 на 15. Получаем 0, 1333… — бесконечная дробь. Записываем так: 0,13(3). Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Самый простой способ по переводу дроби в число — это использование калькулятора или иного вычислительного прибора. Укажем сначала числитель дроби, потом нажмем кнопку со значком «разделить» и набираем знаменатель. После нажатия клавиши «=» мы получаем искомое число.
правила, примеры, решения, как целое число разделить на десятичную дробь
В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.
Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Пример 1Разделите 1,2 на 0,48.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
1,2=1210=65
0,48=48100=1225.
Таким образом, нам надо разделить 65 на 1225. Считаем:
1,2:0,48=62:1225=65·2512=6·255·12=52
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5. О том, как это сделать, мы уже писали ранее.
Ответ: 1,2:0,48=2,5.
Пример 2Посчитайте, сколько будет 0,(504)0,56.
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
0,(504)=0,5041-0,001=0,5040,999=504999=56111
После этого конечную десятичную дробь также переведем в другой вид: 0,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
0,(504):1,11=56111:56100=56111·10056=100111
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Ответ: 0,(504):0,56=0,(900).
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Пример 3Найдите, сколько будет 0,779…/1,5602.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
0,779…≈0,78
1,5602≈1,56
Можем продолжить подсчеты и получить примерный результат: 0,779…:1,5602≈0,78:1,56=78100:156100=78100·100156=78156=12=0,5.
Точность результата будет зависеть от степени округления.
Ответ: 0,779…:1,5602≈0,5.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Пример 4Разделите 2,5 на 45.
Решение
Приведем 2,5 к виду обыкновенной дроби: 25510=512. Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
25,5:45=512:45=512·145=1730
Если перевести результат в десятичную запись, то мы получим 0,5 (6).
Ответ: 25,5:45=0,5(6).
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Определение 1Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Пример 5Вычислите, сколько будет 65,144.
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: 65,14:4=16,285.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Разделите 164,5 на 27.
Решение
Делим сначала дробную часть и получаем:
Отделяем полученную цифру запятой и продолжаем делить:
Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,0(925).
Ответ: 164,5:27=6,0(925).
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10, 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:
Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:
a:b=(a·10):(b·10), a:b=(a·100):(b·100) и так далее.
Сформулируем правило:
Определение 2Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Пример 7Разделите 7,287 на 2,1.
Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72,87 на 21. Запишем полученные числа столбиком и вычислим
Ответ: 7,287:2,1=3,47
Пример 8Вычислите 16,30,021.
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
Видим периодическое повторение остатков 4, 19, 1, 10, 16, 13. В частном повторяются 1, 9, 0, 4, 7 и 5. Тогда наш результат является периодической десятичной дробью 776,(190476).
Ответ: 16,3:0,021=776,(190476)
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Пример 9Подсчитайте, сколько будет 3 5,4.
Решение
Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30,0 на 54. Запишем данные столбиком и вычислим результат:
Повторение остатка дает нам в итоге число 0,(5), которое является периодической десятичной дробью.
Ответ: 3:5,4=0,(5).
Как разделить десятичные дроби на 1000, 100, 10 и др.

Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Пример 10Так, 56,21:10=5,621, а 0,32:100 000=0,0000032.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Пример 11Например, 3,(56):1 000=0,003(56) и 593,374…:100=5,93374….
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000, 100, 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.
Пример 12К примеру, 5,739:0,1=57,39 и 0,21:0,00001=21 000.
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Так, 7,5(716):0,01=757,(167), поскольку после того, как мы перенесли запятую в записи десятичной дроби 7,5716716716… на два знака вправо, у нас получилось 757,167167….
Если же у нас в примере непериодические дроби, то все обстоит проще: 394,38283…:0,001=394382,83….
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
|
Делить столбиком десятичные дроби калькулятор онлайн. Делитель напряжения на резисторах
Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Как работает делитель напряжения на резисторах
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
Резистор, находящийся ближе к плюсу входного напряжения Vвх , обозначен R1 , резистор находящийся ближе к минусу обозначен R2 . Падение напряжения Vвых — это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов.
Расчет делителя напряжения на резисторах основан на законе Ома .
V вых = R2 х V вых / R1 + R2
Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе . Смотрите калькулятор делителя напряжения на резисторах онлайн.
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов .
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V out ? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1 и R2 одинаков пока к выходу V out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2 , расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V out будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V out .
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
В этом случае V out уже не может быть расчитано лишь на основе значений V in , R1 и R2 : сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта V out , получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L . Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
Пропорция сохраняется, V out не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out также будет неравномерным.
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.
Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
Вашему вниманию подборка материалов: Схема традиционного резисторного делителя напряженияДля применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы. Расчет резистивного делителя напряжения[Напряжение на выходе, В ] = [Напряжение питания, В ] * / ( + [Сопротивление резистора R2, Ом ]) Из этой формулы, в частности, видно, что резисторные (резистивные) делители выдают стабильное выходное напряжение, если напряжение питания фиксировано. = [Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ] Эта формула верна для ненагруженного делителя. Если делитель работает на нагрузку, то [Входное сопротивление делителя, Ом ] = [Сопротивление резистора R1, Ом ] + 1 / (1 / [Сопротивление резистора R2, Ом ] + 1 / [Сопротивление нагрузки, Ом ]) [Эквивалентное выходное сопротивление делителя, Ом ] = 1 / (1 / [Сопротивление резистора R1, Ом ] + 1 / [Сопротивление резистора R2, Ом ]) = [Сопротивление резистора R2, Ом ] / ([Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ]) [Действующее / мгновенное / амплитудное напряжение на выходе делителя, В ] = [Коэффициент ослабления сигнала ] * [Действующее / мгновенное / амплитудное напряжение на входе делителя, В ] Эта формула верна, если ток нагрузки делителя равен нулю. Пример — делитель для осциллографаЕсли мы хотим получить осциллограмму высокого напряжения, то сразу приходит в голову делитель напряжения. Изготавливаем делитель, подключаем его вход к источнику высоковольтного сигнала, а выход к входу осциллографа. Должны получить на входе осциллографа уменьшенную копию входного сигнала. Если наш сигнал имеет достаточно большую частоту или просто резкие фронты (например, меандр), то ничего не получится. Осциллограмма не будет похожа на изначальный сигнал. Причина в том, что осциллограф имеет некоторую входную емкость, которая образует с эквивалентным выходным сопротивлением делителя фильтр нижних частот. Все высшие гармоники сигнала подавляются. Кроме того этот фильтр формирует фазовый сдвиг. Это бывает существенным для многолучевых осциллографов, когда мы анализируем соотношения сигналов. Чтобы этого избежать, резистор R1 нужно зашунтировать конденсатором. Качество усилителей звуковой частоты. Обзор, схемы…. Как не спутать плюс и минус? Защита от переполярности. Описание… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис… Соединение светодиодов. Последовательное, параллельное включение оптоэ… Параллельное, последовательное соединение резисторов. Расчет сопротивл… |
Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз. Например, величина входного напряжения 50 В , а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В (рис. 1 ). Для этого используются делители напряжения.
Рис. 1 — Структурная схема делителя напряжения
Они бывают разных типов и выполняются на безе , катушек индуктивности (рис. 2 ). Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Рис. 2 — Элементы, применяемые в качестве делителей напряжения
Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1 и R2 , которые подключены к источнику напряжения U (рис. 3 ). Если сопротивление резисторов одинаковы R1 = R2 , то напряжение источника питания разделится поровну на них U1 = U2 = U/2 .
Рис. 3 — Общая схема делителя напряжения на резисторах
Расчет делителя напряжения на резисторахДавайте разберемся как происходит деление напряжения. Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I , протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U и обратнопропорционален сопротивлению цепи (или ее участка) R , т. е.
откуда
Также следует знать, что в последовательной цепи, т. е. в цепи, в которой все резисторы соединены последовательно, ток I протекает одной и той же величины через все резисторы, а общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений всех резисторов Rобщ = R1+R2 .
Теперь, на основании выше сказанного, давайте определим напряжения на резисторах в зависимости от величины их сопротивлений и напряжения источника питания.
Ток I , протекающий в цепи, равен отношению напряжения U к сумме сопротивлений R1+R2 , т. е.
Падение напряжения на первом резисторе равно
По аналогии находим падение напряжения на втором резисторе
Теперь в выражение (2) и (3) подставим значение тока из выражения (1), в результате получим
Делитель напряжения на резисторах. Различные номиналы резисторовС помощью полученных формул можно определить падение напряжения на резисторе, зная только величину входного напряжения и сопротивления самих резисторов. Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1 и R2 выходное напряжение составляет часто входного (рис. 4 ).
Рис. 4 — Схемы делителей напряжения на резисторах
Следует обратить внимание на то, что величина выходного напряжения зависит от относительного значения сопротивлений резисторов R1 и R2 , а не от абсолютного.
Рис. 5 — Схемы делителей напряжения с одинаковым коэффициентом деления при разных номиналах резисторов
Здесь возникает вопрос: какие же номиналы резисторов R1 и R2 применять, 3 кОм и 1 кОм или 30 кОм и 10 кОм ? Все зависит от конкретного случая. Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1 и R2 , тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Также делитель напряжения можно выполнять из нескольких последовательно соединенных резисторов (рис. 6 ).
Рис. 6 — Схема делителя напряжения с несколькими резисторами
И так, мы рассмотрели резисторный делитель напряжения с фиксированным значением выходного напряжения. Однако часто возникает необходимость в плавном изменении выходного напряжения. Например, при регулировании громкости звука мы плавно изменяем напряжение на усилителе.
Для плавного регулирования величины выходного напряжения применяются переменные и подстроечные резисторы (рис. 7 ).
Рис. 7 — Переменные и подстроечные резисторы
Переменный резистор еще называют потенциометром. Конструктивно он состоит из корпуса, имеющего три вывода, и рукоятки. При вращении ручки осуществляется скользящих контакт подвижной металлической пластины, которая замыкает две токопроводящие графитные дорожки, имеющие разную проводимость в зависимости от длины. Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Схема подключения переменного резистора или же потенциометра приведена ниже (рис. 8 ). Два крайних вывода подключаются к источнику питания, а между средним и одним из крайних выводов снимается выходное напряжение, величину которого можно изменять от нуля до значения входного напряжения Uвых = 0…Uвх .
Рис. 8 — Схема включения переменного резистора для деления напряжения
Если, проворачивая ручку резистора, мы введем все сопротивление (как показано на схеме (рис. 9 )), то выходное напряжение будет равно входному Uвых = Uвх , так как подводимое напряжение будет полностью падать на сопротивлении резистора.
Если же вывести все сопротивление, то выходное напряжение будет равно нулю Uвых = 0 .
Рис. 9 — Схема плавного изменения напряжения
Некоторые виды переменных резисторовВ зависимости от степени относительного изменения сопротивления при вращении рукоятки переменного резистора их разделяют на три типа (рис. 10 ):
1) с линейной зависимостью;
2) с логарифмической зависимостью;
3) с экспоненциальной зависимостью.
Рис. 10 — Зависимости переменных резисторов
Переменные резисторы с логарифмической зависимостью часто используются для регулировки уровня звука, поскольку ухо человека воспринимает звук именно по такой зависимости.
Кроме того переменные резисторы бывают как одинарные, так и сдвоенные. Последние находят широкое применение в звуковой технике.
Делители напряжения на резисторах одинаково работают и рассчитываются как для постоянного, так и для переменного напряжения. Однако, в качестве делителей переменного напряжения также часто используются конденсаторы и реже – катушки индуктивности.
Калькулятор для округления десятичных дробей — Онлайн-калькулятор для округления десятичных дробей
Что такое калькулятор для округления десятичных дробей?
Калькулятор для округления десятичных чисел — это бесплатный онлайн-инструмент для округления десятичных чисел.
Онлайн-калькуляторCuemath поможет вам округлить десятичные числа до ближайшего целого числа, до ближайших десятых, сотых или тысячных долей.
Как пользоваться калькулятором округления десятичных знаков?
Следуйте инструкциям ниже, чтобы использовать калькулятор.
- Шаг 1: Введите десятичное число, которое нужно округлить.
- Шаг 2: Выберите место, до которого нужно округлить число.
- Шаг 3: Щелкните «Рассчитать» , чтобы получить округленное число.
- Шаг 4: Нажмите «Сброс» , чтобы очистить поле и ввести новый номер.
Как округлить десятичное число?
Округление десятичных чисел означает округление десятичных чисел с определенной степенью точности.Это помогает дать приблизительную оценку числа. Десятичные числа можно округлить до ближайшего целого числа, десятых или сотых долей.
- Округление до ближайших десятых означает, что значение должно быть правильно записано с точностью до одного десятичного знака.
Например: когда мы округляем 3,946824 до ближайших десятых, получаем 3,9
- Округление до сотых означает, что значение должно быть правильно записано с точностью до двух десятичных знаков.
Например: когда мы округляем 3.946824 с точностью до сотых, это дает нам 3,95
- Округление до ближайших тысячных долей означает, что значение должно быть правильно записано с точностью до трех десятичных знаков.
Например: когда мы округляем 3,946824 до ближайших сотых, получаем 3,947
Решенный пример:Округлите 456,89 до десятых.
Решение:Значение вместо единицы десятичного числа 456.78 равно 8.
больше 5, поэтому округление этого числа до десятых даст 456,8
Аналогично
- Округление 667,219 до сотых дает 667,22
- Округление 98101,346 до десятых дает 98101,3
Теперь воспользуйтесь калькулятором и округлите следующие десятичные числа:
- 567,239 с точностью до сотых
- 76101,786 с точностью до десятых
- 700.134 с точностью до десятых
Преобразование десятичных часов в часы и минуты за один шаг! • OnTheClock
Вы когда-нибудь задумывались, как преобразовать минуты в десятичные часы? Или десятичные часы в минуты? Ты не один! Нам часто задают этот вопрос!
У нас также есть калькулятор табеля учета рабочего времени , который позволяет вам вводить целую неделю времени входа и выхода.Затем он автоматически рассчитывает часы, включая обед и сверхурочные. Если вы хотите полностью автоматизировать время, обратите внимание на отслеживание рабочего времени сотрудников с помощью OnTheClock.
Вот 3 способа …
Вариант 1. Воспользуйтесь нашим калькулятором десятичных часов / минут
Добавьте этот калькулятор на свой сайт! Нажмите, чтобы узнать как
Вариант 2. Воспользуйтесь нашей таблицей преобразования минут
| Минуты | Десятичные часы | Минуты | Десятичные часы | Минуты | Десятичные часы | ||
| 1 | .02 | 21 | ,35 | 41 | 0,68 | ||
| 2 | 0,03 | 22 | ,37 | 42 | .70 | ||
| 3 | 0,05 | 23 | ,38 | 43 | ,72 | ||
| 4 | 0,07 | 24 | .40 | 44 | ,73 | ||
| 5 | 0,08 | 25 | ,42 | 45 | ,75 | ||
| 6 | .10 | 26 | ,43 | 46 | ,77 | ||
| 7 | 0,12 | 27 | ,45 | 47 | .78 | ||
| 8 | ,13 | 28 | 0,47 | 48 | ,80 | ||
| 9 | ,15 | 29 | .48 | 49 | ,82 | ||
| 10 | ,17 | 30 | ,50 | 50 | ,83 | ||
| 11 | .18 | 31 | ,52 | 51 | ,85 | ||
| 12 | ,20 | 32 | .53 | 52 | .87 | ||
| 13 | ,22 | 33 | ,55 | 53 | 0,88 | ||
| 14 | ,23 | 34 | .57 | 54 | 0,90 | ||
| 15 | ,25 | 35 | ,58 | 55 | 0,92 | ||
| 16 | .27 | 36 | 0,60 | 56 | 0,93 | ||
| 17 | ,28 | 37 | 0,62 | 57 | .95 | ||
| 18 | ,30 | 38 | 0,63 | 58 | 0,97 | ||
| 19 | ,32 | 39 | .65 | 59 | 0,98 | ||
| 20 | ,33 | 40 | 0,67 | 60 | 1,0 |
Вариант 3. Выполните вычисления вручную, например, 8 часов 35 минут
- Разделите 35 минут на 60, e.г, 35 разделить на 60 равно 0,58
- затем добавьте 8 часов назад, 8 часов плюс 0,58 равняется 8,58 часа
Добавить калькулятор продолжительности времени на свой сайт
Теперь вы можете позволить своей команде или своим клиентам использовать этот инструмент. С помощью простого копирования и вставки калькулятор можно добавить на ваш сайт.
нажмите, чтобы скопировать код
Калькулятор времени предоставлен OnTheClock
Минут в десятичное преобразование | Программа учета рабочего времени
Обязанности и ответственность:
- Поддерживать стабильные, надежные и эффективные базы данных
- Оптимизировать и поддерживать устаревшие системы
- Изменять базы данных в соответствии с запросами и проводить тесты
- Решение проблем с использованием базы данных и неисправностей
- Поддерживать связь с разработчиками для улучшения приложений и внедрения передовых методов
- Соберите требования пользователей и определите новые функции
- Разработать технические и учебные пособия
- Обеспечение поддержки управления данными для пользователей
- Убедитесь, что все программы баз данных соответствуют требованиям компании и производительности
- Изучите и предложите новые продукты, услуги и протоколы баз данных
- Использование высокоскоростных методов восстановления транзакций и резервного копирования данных
- Минимизируйте время простоя базы данных и управляйте параметрами, чтобы обеспечить быстрые ответы на запросы
- Обеспечить упреждающую и реактивную поддержку и обучение пользователей в области управления данными
- Определение, обеспечение соблюдения и документирование политик, процедур и стандартов базы данных
- Регулярно проводите тесты и оценки для обеспечения безопасности, конфиденциальности и целостности данных
- Наблюдать за производительностью базы данных, вносить изменения и при необходимости применять новые исправления и версии
Квалификация
Работает или недавно получил степень бакалавра компьютерных наук или смежной области
- Подтвержденный опыт работы администратором базы данных
- Глубокое понимание управления данными (например,грамм. разрешения, восстановление, безопасность и мониторинг)
- Знание разработки программного обеспечения и пользовательского интерфейса веб-приложений
- Практический опыт работы с SQL
- Знакомство с .Net Framework, JavaScript, HTML и SQL Server
- Отличные аналитические и организаторские способности
- Способность понимать требования внешних пользователей и их отношение к решению проблем
- Отличные устные и письменные коммуникативные навыки
- Степень бакалавра компьютерных наук или соответствующей области
| Калькулятор расписания
Об этом калькуляторе тайм-карт
Разработанный специалистами Calculator Soup, этот бесплатный калькулятор рабочего времени отслеживает рабочие часы, перерывы и оплату на ежедневной, еженедельной или ежемесячной основе.Он позволяет несколько перерывов в день и может автоматически вычитать перерывы из общего количества отработанных часов.
Введите время прихода и ухода для каждого рабочего периода. Вы можете поставить двоеточие: между часами и минутами, но это необязательно. Этот калькулятор знает, что такая запись, как 855 означает 8:55 .
Добавьте имя сотрудника, дату или другие примечания и распечатайте отчеты с карточками рабочего времени для своих записей. Ты можешь измените настройки этого настраиваемого калькулятора тайм-карт в соответствии с вашими предпочтениями отображения и требованиями к отчетности по заработной плате.
Доступные настройки:
- Формат времени: 12 или 24 часа военного времени
- Показать или скрыть утра / вечера
- недель за период оплаты: 1, 2, 3 или полный месяц
- Дней в рабочей неделе
- Количество рабочих и перерывов / обедов в день
- Часовая ставка
- Рассчитайте сверхурочную работу с надбавками к оплате, например, за половину или в два раза больше.Варианты включают:
- Сверхурочная работа после отработанных часов в день или неделю
- Сверхурочная работа после 8 часов в день и 40 часов в неделю
- Калифорнийский калькулятор сверхурочной работы для Законы Калифорнии о сверхурочной работе
Наш калькулятор времени сотрудников автоматически переводит время из часов и минут в десятичное.Он также может рассчитать военное время для расчета заработной платы с настройкой 24-часового военного времени. Вы можете указать способ округления десятичных часов в настройках калькулятора.
Администраторы расчета заработной платы могут рассчитывать часы и минуты, отработанные в табеле рабочего времени сотрудников за неделю или за период оплаты. Распечатайте или отправьте по электронной почте отчеты о времени, чтобы сохранить или поделиться.
Как пользоваться калькулятором табелей учета рабочего времени
- Введите числа для раз. Вам не нужны двоеточие: или точка, но вы можете использовать их, если хотите.
- Используйте Tab на вашем компьютере или ∧ ∨ Далее на мобильном устройстве для навигации по полям ввода
- Введите одиночные числа 1–12 для 1:00 — 12:00
- Экономить один день за раз? Введите входные данные и нажмите Рассчитать и сохранить.
Когда вы вернетесь, ваши времена все еще там. Ваш браузер должен разрешить файлы cookie для сохранения данных. - Нажмите «Настройки», чтобы изменить настройки тайм-карты.
- Электронная почта / ссылка Позволяет получить ссылку на вашу табель учета рабочего времени для отправки по электронной почте или публикации.
- Печать / PDF Печать отчета о табеле учета рабочего времени или его сохранение в формате PDF.
- Очистить карту времени Удаляет файлы cookie вашего браузера.Это очистит информацию о часах, ставке, имени и дате. Ваши настройки останутся. Видеть Политика конфиденциальности: файлы cookie для получения дополнительной информации.
Используйте этот бесплатный калькулятор табеля рабочего времени на мобильных устройствах. Он работает как приложение для iPhone или приложение для Android, поскольку автоматически подстраивается под размер экрана вашего мобильного устройства.
Посетите CalculatorSoup.com, чтобы найти другие Калькуляторы времени и даты и наш оригинал Калькулятор тайм-карт.
[1] Десятичные итоги рассчитываются путем преобразования итоговых значений времени (чч: мм). Итоговые десятичные числа не рассчитываются путем добавления десятичных часов дня. Сумма дневных десятичных часов может не равняться расчетному общему десятичному количеству часов за период оплаты из-за разницы в округлении. Люди обычно получают заработную плату в виде еженедельной суммы чч: мм, и это число, которое будет преобразовано в десятичную сумму.
[2] чч: мм — время в часах и минутах.8:15 — это 8 часов 15 минут.
[3] Десятичная дробь — это время в часах только с дробной десятичной частью. 8,25 — это 8,25 часа, а поскольку 0,25 — это четверть часа, 0,25 равно 15 минутам. Таким образом, десятичное представление времени 8,25 часа эквивалентно 8 часам 15 минутам. 8,25 часов = 8:15
Калькулятор стандартной формы — запишите десятичную дробь в стандартной форме
Используйте этот калькулятор, чтобы легко преобразовать число в стандартную форму (также известную как научная нотация, или инженерная нотация).Запишите большое число или десятичную дробь с большим количеством цифр после десятичной точки в стандартной форме.
Какая стандартная форма числа?
Стандартная форма также называется E-notation , научная форма числа или стандартная форма указателя . Это способ выражения чисел, которые считаются слишком большими или слишком маленькими, чтобы их можно было удобно записать в более привычной десятичной форме. Многие калькуляторы поддерживают научный режим работы с такими числами.Несмотря на то, что сейчас это менее необходимо, чем во времена до персональных компьютеров, стандартная форма остается популярной среди инженеров, ученых и математиков, а также студентов, изучающих эти дисциплины.
Форма числа в стандартном обозначении: m x 10 n , что означает « m умножить на 10 в степени n ». Показатель n всегда является целым числом (целым числом), тогда как коэффициент m (мантисса, мантисса) может быть любым действительным числом.Наиболее удобная форма (нормализованное обозначение) — это та, в которой показатель степени выбран таким образом, чтобы коэффициент находился в пределах от 1 до 9. Знак числа записывается обычным образом — с плюсом или минусом перед ним.
Запись чисел в стандартной форме упрощает сравнение порядков. Например, масса протона составляет 0,000 000 000 000 000 000 000 0001 6726 г, а масса электрона — 0,000 000 000 000 000 000 000 000 000 910 938 356 г. Трудно сравнивать эти два способа таким образом, но если мы запишем их как 1.6726 x 10 -24 и 9,109 383 56 x 10 -28 , мы можем просто сравнить показатели степени, и поскольку -24 больше, чем -28, протон примерно на 4 порядка (в 10000 раз) массивнее, чем электрон.
Запись числа в стандартной форме
Следует отметить, что преобразование десятичных чисел в числа стандартной формы не меняет значения числа, а просто меняет его форму, как подсказывает название. Используя наш калькулятор стандартной формы, вы можете быстро и легко выполнить преобразование, однако, если вы хотите сделать это вручную, вот алгоритм для этого.
- Переместите десятичную запятую на столько раз, чтобы число стало меньше 10, но больше 1.
- Если вы переместили десятичную точку влево, добавьте к числу «x 10 n », где n — количество позиций, на которые вы переместили точку. Если вы переместили его вправо, добавьте «x 10 -n », используя ту же логику.
Например, запишем число 12,340,000 в нормализованной стандартной форме. Сначала мы перемещаем десятичную запятую на 7 позиций влево, чтобы число стало 1.2340000. Мы можем отбросить нули в большинстве сценариев (если мы не хотим, чтобы они оставались значащими цифрами для обозначения точности), поэтому после добавления x 10 7 мы можем записать его как 1,234 x 10 7 в экспоненциальной нотации и 1,055 e7 или 1.055e + 7 в обозначении e. Оба типа обозначений предоставляются при использовании нашего онлайн-инструмента.
Десятичный процентный калькулятор преобразования
Чтобы использовать калькулятор преобразования процента в десятичную дробь, введите процент, а затем нажмите табуляцию или щелкните мышью вне.Ответ отобразится автоматически.
Преобразовать проценты в десятичные числа настолько просто, что для этого не нужен калькулятор, хотя здесь он точно сможет. Чтобы выполнить преобразование, просто переместите десятичную запятую на 2 разряда влево и удалите знак процента (%). Нет ничего проще с математикой.
Пример : Чтобы преобразовать 75,6% в десятичную дробь, сдвиньте десятичную дробь на два разряда влево, удалите знак процента, и вы получите ответ 0,756.
Другой метод — взять сумму процентов, разделить ее на 100 и, конечно же, убрать знак процента.
Пример : Снова используя 75,6%, конверсия 0,756 находится путем деления 75,6 на 100 (75,6 / 100).
Таблица преобразований
Для быстрого ознакомления в следующей таблице представлены некоторые распространенные преобразования.
| Процент | Десятичное число |
|---|---|
| 0,1% | 0,001 |
| 0,5% | 0,005 |
| 1% | 0,01 |
| 5% | 0.05 |
| 10% | 0,10 |
| 15% | 0,15 |
| 20% | 0,20 |
| 25% | 0,25 |
| 30% | 0,30 |
| 35% | 0,35 |
| 40% | 0,40 |
| 45% | 0,45 |
| 50% | 0,50 |
| 55% | 0.55 |
| 60% | 0.60 |
| 65% | 0,65 |
| 70% | 0,70 |
| 75% | 0,75 |
| 80% | 0,80 |
| 85% | 0,85 |
| 90% | 0,90 |
| 95% | 0,95 |
| 100% | 1 |
| 200% | 2 |
Учебное пособие по финансовому калькулятору
Финансовый калькулятор Учебники
Учебник по финансовым калькуляторам
Использование финансовых калькуляторов позволяет нам работать с более реалистичными (и, как правило, более сложными) типы проблем временной стоимости денег (TVM).Благодаря использованию большего количества примеров из «реального мира» учащиеся поощряются чтобы проработать проблемы более тщательно, без необходимости выполнять все вычисления вручную. В финансовый калькулятор помогает в понимании финансовых концепций во многом так же, как графический калькулятор для студенты математического анализа.
Однако вы должны понимать, что вы не можете использовать финансовый калькулятор, если не понимаете фундаментальных принципов. концепции временной стоимости денег.На самом деле, очень легко решить проблему с финансовым калькулятором, если вы не знаете, что делаете. Есть распространенные ошибки, которые студенты совершают при первом использовании финансовых калькуляторов. Есть также советы, которые упростят вам знакомство с финансовыми калькуляторами. Прежде чем обсуждать любой из них, мы можем Сначала рассмотрим некоторые из основных функций финансовых калькуляторов.
Рекомендуется использовать Hewlett Packard 10BII или Texas Instruments BA-II Plus.если ты у вас уже есть TI-83 или TI-83-Plus из предыдущего математического класса, этого также достаточно. Есть более дорогие финансовые калькуляторы с еще несколькими прибамбасами (HP12C, HP17BII, HP19BII, даже модели, доступные для использования в КПК, но это не требуется для большинства студентов. Есть также несколько менее дорогих моделей (например, BA-35 Solar), которые будут работать некоторые базовые расчеты TVM; однако эти калькуляторы, как правило, неадекватны, потому что они не обрабатывают неравномерные денежные потоки. не рассчитывать внутренние нормы доходности и доходность к погашению.
Перед первым использованием калькулятора вам необходимо внести некоторые изменения в настройки по умолчанию. Тебе нужно внести эти изменения только один раз.
- Увеличьте количество десятичных знаков. В вашем калькуляторе с завода установлено два (2) знака после запятой. Такой уровень округления может привести к значительным ошибкам во многих проблемах TVM. Чтобы изменить эти настройки с помощью TI BA-II Plus, нажмите 2-ю клавишу , а затем клавишу формата (десятичная клавиша на клавиатура).Вы увидите на экране DEC = 2.00 вместе со словом ENTER и клавишами со стрелками вверх / вниз). Каждый раз, когда вы видите эту стрелку клавиши, это указывает на подменю. Вы можете увидеть другие элементы в подменю, нажав любую из клавиш со стрелками. Чтобы изменить на четыре десятичных разрядов, нажмите клавишу 4 , а затем клавишу ENTER . Чтобы изменить количество десятичных знаков с помощью HP 10BII, нажмите клавишу Shift (клавиша с желтым квадратом на ней), затем клавишу DISP (клавиша =), а затем клавишу 4 .
- Установите в калькуляторе один (1) платеж в год. По умолчанию ваш калькулятор составляет 12 платежей в год (т. Е. Ежемесячно платежи). Хотя ваш калькулятор может обрабатывать множество различных комбинаций платежей и периодов начисления сложных процентов, лучше всего эти расчеты выполняются вручную при первом обучении использованию финансового калькулятора. Чтобы изменить этот параметр на TI BAII Plus, нажмите 2-ю клавишу , а затем клавишу P / Y (клавиша I / Y). Ты увидишь на экране P / Y = 12.0000. Чтобы перейти на годовое начисление сложных процентов, нажмите клавишу 1 , а затем клавишу ENTER . Если сделано правильно, ваш экран должен отображать P / Y = 1.0000. Чтобы изменить этот параметр на HP 10BII, нажмите кнопку 1, клавиша , за которой следует клавиша Shift , за которой следует клавиша P / Y (клавиша PMT). Вы можете проверить, сделано ли это правильно, нажав клавишу Shift и удерживая нажатой клавишу INPUT . Удерживая нажатой кнопку INPUT , экран должен отображать 1 P_Yr , если все сделано правильно.
С другой стороны, есть некоторые вещи, которые вы должны делать каждый раз, когда начинаете новую проблему TVM.
- Убедитесь, что ваш калькулятор настроен на выплаты в конце периода. Оба HP 10BII и TI BAII Plus имеют это значение по умолчанию, но если буквы BGN (BGN обозначают начало периодических платежей) находятся в любом месте экрана, это необходимо изменить. Я рекомендую начинающим пользователям никогда используйте режим «начало», так как вы можете очень легко решить проблемы TVM начала периода, не изменяя эту настройку.
- Установите временные рамки при исследовании сложных проблем TVM. Это поможет вам с вводом данных калькулятора.
- При запуске проблемы TVM всегда очищайте регистры временной стоимости денег. Если вы не будете делать это каждые время, возможно, что число, сохраненное в памяти от ранее решенной проблемы, заставит вас вычислить ошибочный отвечать. На TI BAII Plus нажмите 2nd , затем CLR TVM (клавиша FV), чтобы очистить временная стоимость денег.На HP 10BII нажмите Shift , а затем CLEAR ALL (клавиша INPUT).
- Введите процентные ставки (или темпы роста, или требуемые нормы прибыли и т. Д.) В процентах, а не в десятичном формате. В другом словами, введите 7,5% процентную ставку как 7,5, а не 0,075. Ваш калькулятор узнает, что это процентная ставка, когда вы нажмете клавишу I / Y.
- При вычислении периодических процентных ставок не вводите повторно результат вручную в свой калькулятор. Например, Предположим, вы работаете с проблемой с установленной годовой процентной ставкой 10% и ежемесячным начислением сложных процентов.Периодическая ставка находится разделив 10 на 12 = 0,8333 на калькуляторе. Когда вы закончите этот расчет, просто нажмите кнопку I / Y . Это войдет полное число (до 13 десятичных знаков вместо округленного 0,8333) в регистре TVM и тем самым минимизировать ошибку округления.
- Введите отток денежных средств как отрицательное число. Большинство финансовых калькуляторов требуют, чтобы вы указали информацию о направление денежного потока.


 Оно должно быть таким, сколько раз делитель помещается в делимом.
Оно должно быть таким, сколько раз делитель помещается в делимом. Умножение даст 284 и 32.
Умножение даст 284 и 32. 142857) // (1, 7)
rationalApproximationOf(0.142857, withPrecision: 1.0E-10) // (142857, 1000000)
rationalApproximationOf(M_PI) // (355, 113)
rationalApproximationOf(M_PI, withPrecision: 1.0E-7) // (103993, 33102)
rationalApproximationOf(M_PI, withPrecision: 1.0E-10) // (312689, 99532)
142857) // (1, 7)
rationalApproximationOf(0.142857, withPrecision: 1.0E-10) // (142857, 1000000)
rationalApproximationOf(M_PI) // (355, 113)
rationalApproximationOf(M_PI, withPrecision: 1.0E-7) // (103993, 33102)
rationalApproximationOf(M_PI, withPrecision: 1.0E-10) // (312689, 99532)

 Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275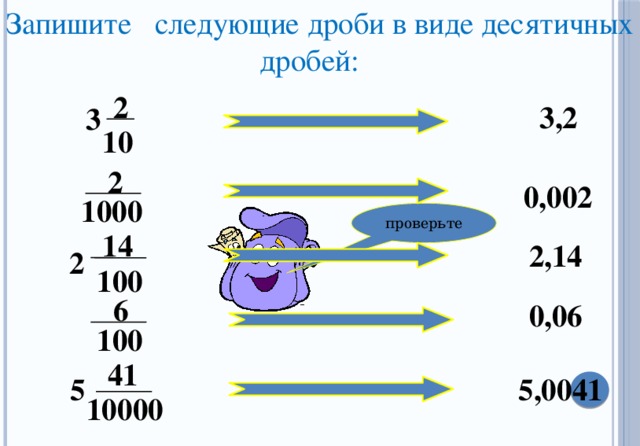 Перевод десятичных чисел в обыкновенную дробь
Перевод десятичных чисел в обыкновенную дробь
 Примеры 45/5, 6.6/76.4, -7/6.7, и т.д.
Примеры 45/5, 6.6/76.4, -7/6.7, и т.д.
 На схеме представлены два аналогичных делителя …
На схеме представлены два аналогичных делителя …