Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
4. Тригонометрический калькулятор онлайн — примеры
Комплекс операций инженерного калькулятораВстроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов
(Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце — знак равенства. x] – Возведение числа Эйлера в степень
x] – Возведение числа Эйлера в степень
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерахКак возвести в степеньЧтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубическийДопустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькулятореЗадача: Найти квадратный корень 36. y», затем указать необходимую степень и так же нажать знак «равно».
y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примерыКак произвести онлайн расчет синусов и косинусов, тангенсовОбратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайнДесятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькулятореСуществующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
4. Тригонометрический калькулятор онлайн — примеры
Комплекс операций инженерного калькулятораВстроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. x] – Возведение числа Эйлера в степень
x] – Возведение числа Эйлера в степень
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерахКак возвести в степеньЧтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубическийДопустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькулятореЗадача: Найти квадратный корень 36. y», затем указать необходимую степень и так же нажать знак «равно».
y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примерыКак произвести онлайн расчет синусов и косинусов, тангенсовОбратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайнДесятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькулятореСуществующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| ← | удаление одного символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» Полностью сбрасывает калькулятор в положение «0» |
| Радианы | радианы | Выражение угла в радианах. Используется только для тригометрических функциях cos, sin, tg, ctg, arcsin, arccos, arctg,arcctg. |
| Градусы | градусы | Выражение угла в градусах. Используется только для тригометрических функциях cos, sin, tg, ctg. |
| sin | sin | Тригонометрическая функция синус. Обозначается как «sin(x)». Угол (x) может быть задан в радианах либо градусах. |
| cos | cos | Тригонометрическая функция косинус. Обозначается как «cos(x)». Угол (x) л может быть задан в радианах либо градусах. |
| tg | tg | Тригонометрическая функция тангенс. Обозначается как «tg(x)». Угол (x) может быть задан в радианах либо градусах. |
| ctg | ctg | Тригонометрическая функция котангенс. Обозначается как «ctg(x)». Угол (x) может быть задан в радианах либо градусах. Обозначается как «ctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| arcsin | arcsin | Обратная тригонометрическая функция арксинус. Обозначается как «arcsin(x)». Угол (x) может быть задан в радианах либо градусах. |
| arccos | arccos | Обратная тригонометрическая функция арккосинус. Обозначается как «arccos(x)». Угол (x) может быть задан в радианах либо градусах. |
| arctg | arctg | Обратная тригонометрическая функция арктангенс. Обозначается как «arctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| arcctg | arcctg | Обратная тригонометрическая функция арккотангенс. Обозначается как «arcctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| ln | ln | Натуральный логарифм. Обозначение ln(x). |
| log | log | Десятичный логарифм.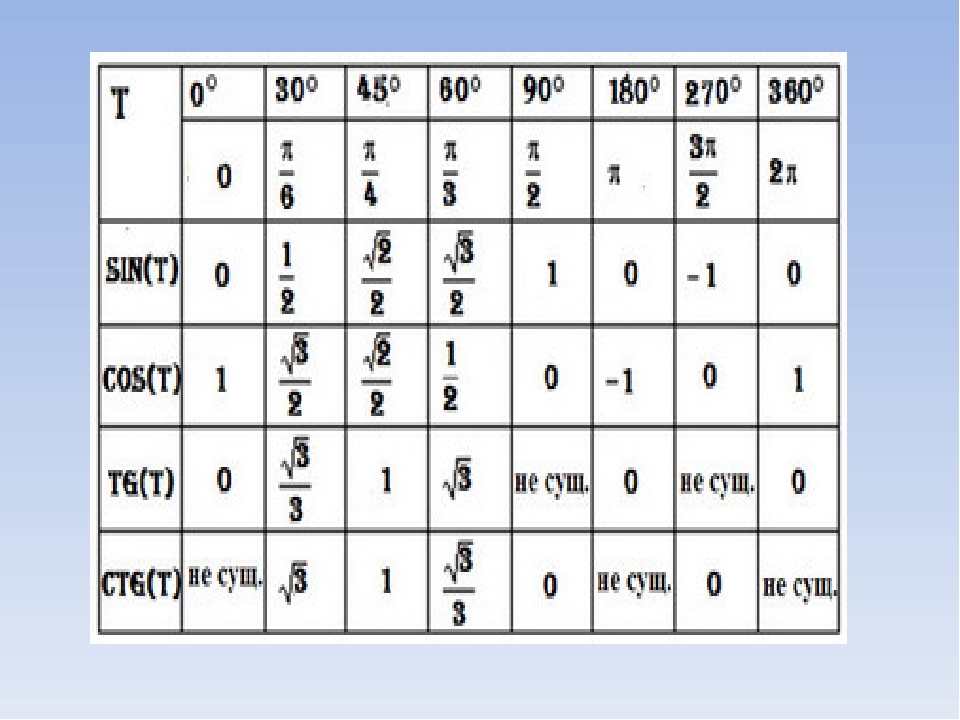 |
| e | e | Число «e» — основание натурального логарифма. Число «e» называют числом Эйлера или числом Непера. Приблизительно равно 2,71828. |
| Pi | число Пи | Число «Пи» — математическая константа. Приблизительно равно 3,14. |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1/x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
Калькулятор онлайн
На этой странице вы найдете отличный интерактивный калькулятор: простой в усвоении и удобный для обширной аудитории пользователей интернета. Онлайн-калькулятор для вычисления математических функций: тригонометрических, матриц, логарифмов, уравнений, и построения графиков. Есть все необходимые функции, быстро загружается, не требует установки на ПК.. Он по праву считается на сегодняшний момент одним из лучших среди сервисов интерактивных математических калькуляторов. Основное преимущество этого онлайн сервиса — это использование инженерного калькулятора с любого компьютера или мобильного устройства в любой удобный для вас момент. Использовать его можно круглосуточно, главное чтобы был выход в интернет. Также ещё одним хорошим подспорьем является то, что сервис предоставляет этот калькулятор абсолютно бесплатно и не требуется никакая регистрация для пользователей.
Онлайн-калькулятор для вычисления математических функций: тригонометрических, матриц, логарифмов, уравнений, и построения графиков. Есть все необходимые функции, быстро загружается, не требует установки на ПК.. Он по праву считается на сегодняшний момент одним из лучших среди сервисов интерактивных математических калькуляторов. Основное преимущество этого онлайн сервиса — это использование инженерного калькулятора с любого компьютера или мобильного устройства в любой удобный для вас момент. Использовать его можно круглосуточно, главное чтобы был выход в интернет. Также ещё одним хорошим подспорьем является то, что сервис предоставляет этот калькулятор абсолютно бесплатно и не требуется никакая регистрация для пользователей.
Интерактивный калькулятор умеет выполнять как простые, так и сложные математические вычисления: извлечения корней, логарифмы, тригонометрические функции, проценты, вычисление матриц, факториалов, интегралов, дробей, векторов и комплексных чисел, решения сложных математических формул, простых уравнений и сложных систем уравнений, так дифференциальных уравнений и их систем, и еще множество других вычислений
Также возможно построение различных графиков, что чрезвычайно удобно для быстрого и наглядного решения сложных математических задач для инженеров, студентов и школьников.
Кнопки и команды онлайн-калькулятора
В списке ниже указаны все клавиши и команды калькулятора и выполняемые ими операции.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(α) | Синус угла |
| cos | cos(β) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin-1 | asin() | Обратный синус |
| cos-1 | acos() | Обратный косинус |
| tan-1 | atan() | Обратный тангенс |
| sinh-1 | asinh() | Обратный гиперболический синус |
| x2 | ^2 | Возведение в квадрат |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp() | Возведение в степень числа Эйлера |
| √x | sqrt(x) | Квадратный корень |
| y√x | sqrt(x,y) | Извлечение корня |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| logyx | log(x,y) | Логарифм |
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица(комплексное число) |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| /x | arg() | Аргумент функции |
| ()3 | () | Вектор с 3 параметрами |
| ()4 | () | Вектор с 4 параметрами |
| Deg | Градусы | |
| Rad | Радианы | Дополнительные функции (набираются только вручную на клавиатуре) |
| ncr() | Биноминальный коэффициент | |
| gcd() | НОД | |
| lcm() | НОК | |
| sum() | Суммарное значение всех решений | |
| factorize() | Разложение на простые множители | |
| diff() | Дифференцирование | |
| Matrix() | Матрицы | |
| Solve() | Уравнения и системы уравнений | |
| Plot() | Построение графиков |
Калькулятор онлайн для расчетов процентов, дробей, степеней
Калькулятор давно и прочно вошел в нашу жизнь. Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.
Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin (α) | Синус угла |
| cos | cos (β) | Косинус |
| tan | tan (y) | Тангенс |
| sinh | sinh () | Гиперболический синус |
| cosh | cosh () | Гиперболический косинус |
| tanh | tanh () | Гиперболический тангенс |
| sin-1 | asin () | Обратный синус |
| cos-1 | acos () | Обратный косинус |
| tan-1 | atan () | Обратный тангенс |
| sinh-1 | asinh () | Обратный гиперболический синус |
| cosh-1 | acosh () | Обратный гиперболический косинус |
| tanh-1 | atanh () | Обратный гиперболический тангенс |
| x2 | ^2 | Возведение в квадрат |
| х3 | ^3 | Возведение в куб |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp () | Возведение в степень числа Эйлера |
| vx | sqrt (x) | Квадратный корень |
| 3vx | sqrt3 (x) | Корень 3-ей степени |
| yvx | sqrt (x,y) | Извлечение корня |
| log2x | log2 (x) | Двоичный логарифм |
| log | log (x) | Десятичный логарифм |
| ln | ln (x) | Натуральный логарифм |
| logyx | log (x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re () | Выделение целой действительной части |
| Im | Im () | Исключение действительной части |
| |x| | abs () | Модуль числа |
| Arg | arg () | Аргумент функции |
| nCr | ncr () | Биноминальный коэффициент |
| gcd | gcd () | НОД |
| lcm | lcm () | НОК |
| sum | sum () | Суммарное значение всех решений |
| fac | factorize () | Разложение на простые множители |
| diff | diff () | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Виды калькуляторов
В зависимости от возможностей и сферы применения калькуляторы бывают простые, бухгалтерские, финансовые, инженерные.
- Бухгалтерскими калькуляторами пользуются бухгалтера и кассиры для арифметических расчетов с денежными суммами.
- Для финансовых расчетов пользуются финансовыми калькуляторами, у которых к стандартному набору математических функций добавлены операции со сложными процентами и функции, характерные для банковской сферы и финансовых приложений.
- Специализированные — это калькуляторы, применяемые для вычислений в конкретной сфере деятельности (строительные, ипотечные, статистические, медицинские).
- Печатающие — калькуляторы, которые с помощью печатающего устройства выводят полученные результаты, расчеты, графики и вычисления на бумажную ленту.
Отдельно выделяются:
- программируемые калькуляторы, используемые для выполнения сложных вычислений по заранее заложенной программе пользователя;
- графические, выполняющие построение и отображение графиков функций.

Простейший калькулятор предназначен выполнять ординарные арифметические расчеты (сложение, вычитание и т.п.), вычислять процент, извлекать квадратный корень, возводить число в степень. Помимо простых расчетов, строителям и архитекторам, инженерно-техническим и научным работникам, математикам и геодезистам, старшеклассникам и студентам технических специальностей очень часто приходится решать важнейшие инженерные задачи, осуществлять сложные математические расчеты.
Представленный на сайте тригонометрический калькулятор выполняет расчет:
- синусов;
- косинусов;
- тангенсов;
- котангенсов.
А также обратных тригонометрических функций:
- арксинусов;
- арккосинусов;
- арктангенсов;
- арккотангенсов.
Все тригонометрические расчеты с углами выполняются в радианах, градах и градусах.
На нашем сайте вы сможете пользоваться инженерным онлайн калькулятором, предназначенным для инженерных и научных расчетов разного уровня сложности.
Инженерный калькулятор позволяет:
- производить сложные расчеты с дробями;
- возводить любое число в степень, извлекать корень из числа;
- рассчитать онлайн проценты, логарифмы, интегралы любой сложности;
- выполнять необходимые математические операции с одной или несколькими матрицами;
- находить производную онлайн как от элементарной, так и от сложной функции;
- решать алгебраические, линейные, логарифмические, тригонометрические и другие уравнения.
Онлайн калькулятор прост и понятен в обращении, применять его не составит труда тем, кто пользуется настольным инженерным калькулятором, принципы работы функций и программ аналогичны. По своему виду инженерный калькулятор онлайн имитирует настоящий калькулятор, поэтому для ознакомления с ним вам не понадобится много времени.
Онлайн калькулятор синуса, косинуса, тангенса и котангенса
Калькулятор онлайн вычисляет тригонометрические функции для любого значения угла α заданного в градусах: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec), версинус (синус-верзус) (versin), коверсинус (косинус-верзус) (vercos), гаверсинус (половина от синус-верзус) (haversin), экссеканс (exsec), экскосеканс (excsc).
Вычислить значения синуса и косинуса для стандартных значений углов можно с помощью тригонометрической окружности (тригонометрического круга). Например по тригонометрическому кругу можно найти значение синуса 45 градусов, косинуса 60 градусов или косинуса 90 градусов.
Вычислить значения для тангенсов и котангенсов можно с помощью таблицы синусов, косинусов, тангенсов и котангенсов. Например по таблице тригонометрических функций можно найти значение тангенса 60 градусов или котангенса 30 градусов.
| Тригонометрические функций на единичной окружности | Тригонометрический круг (тригонометрическая окружность) |
Тригонометрическая таблица основных значений синусов, косинусов, тангенсов и котангенсов.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin(α) | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
| cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
| tg(α) | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 |
| ctg(α) | — | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | — | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | — |
| α | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
I. Для справки:
Для справки:
- тригонометрические функции
- — элементарные функции, которые возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Основные тригонометрические функции:
- синус угла α
- обозначается sin(α) — отношение длины противоположного этому углу катета к гипотенузе;
- косинус угла α
- обозначается cos(α) — отношение прилежащего этому углу катета к гипотенузе.

Остальные тригонометрические функции можно выразить через синус и косинус:
- тангенс
- обозначается tg(α) — отношение длины противоположного углу катета к прилежащему катету;
- котангенс
- обозначается ctg(α) — отношение длины прилежащего к углу катета к противоположному катету;
- секанс
- обозначается sec(α) — отношение длины гипотенузы к прилежащему к углу катету;
- косеканс
- обозначается cosec(α) — отношение длины гипотенузы к противоположному катету.
Редко используемые тригонометрические функции:
- версинус
- обозначается versin(α) — единица минус косинус угла α;
- коверсинус
- обозначается vercos(α) — единица минус синус угла α;
- гаверсинус
- обозначается haversin(α) — половина версинуса угла α;
- экссеканс
- обозначается exsec(α) — секанс угла α минус единица;
- экскосеканс
- обозначается excsc(α) — косеканс угла α минус единица.

II. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Обычный инженерный калькулятор онлайн. ¼ + ½ = ¾.
Обычный калькулятор
Обычный калькулятор позволяет выполнять простые операции на калькуляторе, такие как сложение, вычитание, умножение и деление.
Вы можете воспользоваться быстрым математическим калькулятором
Инженерный калькулятор позволяет выполнять более сложные операции на калькуляторе, такие как синус, косинус, арксинус, арккосинус, тангенс, арктангенс, возведение в степень, экспонента, логарифм, проценты, также есть операции в памяти калькулятора онлайн. Можно набирать прямо с клавиатуры, для этого предварительно кликните на область с калькулятором.
Выполняет простые операции с числами, а также более сложные как
математический калькулятор онлайн.
¼ + ½ = ¾.
Здесь представлены два калькулятора:
- Первый вычисляет как обычный
- Второй вычисляет как инженерный
Правила относятся к калькулятору, который вычисляет на сервере
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Зачем нужен этот он-лайн калькулятор?
Калькулятор онлайн — чем отличается от обычного калькулятора? Во-первых, обычный калькулятор не удобно носить с собой, во-вторых — уже сейчас интернет есть практически везде, по-этому не составить проблем зайти на наш сайт и воспользоваться онлайн калькулятором.
Калькулятор он-лайн — чем он отличается от java-калькулятора, а также от других калькуляторов для операционных систем? — опять же — мобильность. Если Вы находитесь за другим компьютером, то не надо снова устанавливать
Итак, пользуйтесь этим онлайн!
. Простой способ найти sin, cos, tan, cot
Этот калькулятор тригонометрии поможет вам в двух популярных случаях, когда необходима тригонометрия. Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент — тоже беспроигрышный вариант! Введите 2–3 заданных значения во второй части калькулятора, и вы в мгновение ока найдете ответ.Прокрутите вниз, если хотите узнать больше о тригонометрии и о том, где ее можно применить.
Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент — тоже беспроигрышный вариант! Введите 2–3 заданных значения во второй части калькулятора, и вы в мгновение ока найдете ответ.Прокрутите вниз, если хотите узнать больше о тригонометрии и о том, где ее можно применить.
Есть много других инструментов, полезных при решении задач тригонометрии. Ознакомьтесь с двумя популярными тригонометрическими законами: калькуляторами закона синусов и закона косинусов, которые помогают решить любой вид треугольника. Если вы хотите узнать больше о тригонометрических функциях, перейдите к нашим специальным инструментам:
Что такое тригонометрия?
Тригонометрия — это раздел математики. Само это слово происходит от греческого слова trignon (что означает «треугольник») и metron («мера»).Как следует из названия, тригонометрия имеет дело в основном с углами и треугольниками ; в частности, он определяет и использует отношения и соотношения между углами и сторонами в треугольниках. Таким образом, основное приложение — решение треугольников, в частности прямоугольных, а также любого другого типа треугольника, который вам нравится.
Таким образом, основное приложение — решение треугольников, в частности прямоугольных, а также любого другого типа треугольника, который вам нравится.
Тригонометрия имеет множество приложений: от повседневных задач, таких как вычисление высоты или расстояния между объектами, до спутниковой навигационной системы, астрономии и географии.Кроме того, функции синуса и косинуса являются фундаментальными для описания периодических явлений — благодаря им мы можем описывать колебательные движения (как простой маятник) и волны, такие как звук, вибрация или свет.
Тригонометрия и тригонометрические функции используются во многих различных областях науки и техники, если упомянуть лишь некоторые из них: музыка, акустика, электроника, медицина и медицинская визуализация, биология, химия, метеорология, электротехника, машиностроение и гражданское строительство, даже экономика. Тригонометрические функции действительно все вокруг нас!
Калькулятор триггеров нахождение sin, cos, tan, cot, sec, csc
Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах. Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как могут быть интерпретированы функции.
Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как могут быть интерпретированы функции.
Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в калькулятор тригонометрии. Вам нужны только два заданных значения в случае:
- односторонний и односторонний
- с двух сторон
- площадь и одна сторона
Помните, что если вы знаете два угла, этого недостаточно, чтобы найти стороны треугольника.Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут быть разных размеров (не с одинаковой длиной стороны) — такая взаимосвязь называется сходством треугольников . Если стороны имеют одинаковую длину, то треугольники равны и соответствуют .
Если стороны имеют одинаковую длину, то треугольники равны и соответствуют .
Что такое тригонометрия?
Тригонометрия — это исследование отношений внутри треугольника . Для прямоугольных треугольников соотношение между любыми двумя сторонами всегда одинаково и задается в виде тригонометрических соотношений, cos, sin и tan.Тригонометрия также может помочь найти некоторую недостающую информацию о треугольнике , например, правило синуса.
Сложна ли тригонометрия?
Поначалу тригонометрия может быть сложной задачей, но после некоторой практики вы ее освоите! Вот несколько советов по тригонометрии: Обозначьте гипотенузу, смежную и противоположную на вашем треугольнике, чтобы помочь вам понять, какую идентификацию использовать, и запомните мнемонику SOHCAHTOA для тригонометрических отношений!
Для чего используется тригонометрия?
Тригонометрия используется для поиска информации обо всех треугольниках и, в частности, прямоугольных треугольниках. Поскольку треугольников повсюду в природе , тригонометрия используется вне математики, в таких областях, как строительство, физика, химическая инженерия и астрономия.
Поскольку треугольников повсюду в природе , тригонометрия используется вне математики, в таких областях, как строительство, физика, химическая инженерия и астрономия.
Кто изобрел тригонометрию?
Поскольку тригонометрия — это взаимосвязь между углами и сторонами треугольника, никто не придумал ее , она все равно была бы там, даже если бы об этом никто не знал! Первыми, кто открыл часть тригонометрии, были древние египтяне и вавилоняне , но Евклид и Архемид первыми подтвердили идентичность, хотя они сделали это с помощью форм, а не алгебры.
Какой уровень у тригонометрии?
Тригонометрия — это , которые обычно преподают подросткам в возрасте 13-15 лет , что составляет классов 8 и 9 в США и лет 9 и 10 в Великобритании. Точный возраст преподавания тригонометрии зависит от страны, школы и способностей учеников.
Коллекция из 158 тригонометрических калькуляторов, разделенных по типу навыков и уровню
Воспользуйтесь нашим бесплатным калькулятором
Мы стали партнерами Mathway, чтобы предложить бесплатный онлайн-калькулятор тригонометрии. Ниже представлен обширный список других инструментов тригонометрии.
Ниже представлен обширный список других инструментов тригонометрии.
Содержание
Обзор
Как отмечает Академия Хана, тригонометрия — это «изучение свойств треугольников», и она используется во всем: от астрономии до спутниковых систем, архитектуры и многого другого.
В Интернете доступно множество ресурсов, которые помогут вам в изучении тригонометрии.
Ниже представлена коллекция из 158 триггерных калькуляторов, разделенных по типу навыков и уровню.
Введение в тригонометрию
Тригонометрия прямоугольного треугольника
Обучение решению прямоугольных треугольников обеспечивает основу, которую вы будете использовать по мере продвижения в тригонометрии. Следующие ресурсы помогут познакомить вас со свойствами прямоугольных треугольников:
Прямоугольный треугольник EasyCalculation.com — используйте раскрывающиеся меню, чтобы найти угол, противоположную сторону, сторону гипотенузы или смежную сторону, используя известные значения. Включает учебную информацию с мнемоническим устройством для запоминания формулы.
Включает учебную информацию с мнемоническим устройством для запоминания формулы.
VisualTrig.com (включая визуальное отображение) — ознакомьтесь с прямоугольными треугольниками, используя ползунки для настройки свойств предоставленного прямоугольного треугольника. Также доступны варианты Scalene и Circle.
Правый треугольник PageTutor.com — быстрый и простой в использовании, когда вы знаете два значения, их можно использовать для поиска других свойств треугольника.
Правый треугольник CarbideDepot.com — Быстрый и простой в использовании, просто введите значения, которые вы знаете, чтобы найти неизвестные свойства треугольника.
Теоремы о треугольнике
Есть несколько теорем о треугольниках, которые можно использовать, чтобы узнать больше о свойствах треугольников. Следующие инструменты представляют эти теоремы:
Теорема треугольника CalculatorSoup.com — узнайте больше о шести теоремах о треугольнике и о том, как их решить, используя предоставленную учебную информацию.
EasyCalculation.com — Найдите неизвестные свойства треугольников, используя эти шесть простых в использовании ресурсов по теоремам о треугольниках:
1728.Окончательный треугольник org — выберите теорему о треугольнике, которую вы хотите использовать, чтобы узнать свойства своего треугольника. Предоставляются полезные диаграммы и учебная информация, объясняющая теоремы.
Сторона, угол и площадь Had2Know.com — используйте SAS, ASA или SSS, чтобы найти свойства вашего треугольника.
TrianCal — интерактивный инструмент, доступный на испанском и английском языках, который решает переменные и позволяет пользователям делиться ссылками на сгенерированный треугольник.
GradeMathHelp.com’s Triangle — Интересно использовать, просто введите известные значения на треугольной диаграмме. В нем представлена подробная учебная информация, объясняющая, какая теорема будет использоваться для решения вашего треугольника в зависимости от предоставленных значений.
Triangle-Calculator.com’s Triangle — Используйте SSA или SAS для решения неизвестных значений ваших треугольников. Каждый из них имеет полезную маркированную треугольную диаграмму:
Math-Prof.com’s Area of Triangle — Веселая и простая в использовании, введите известные значения прямо на треугольной диаграмме.Затем соответствующая теорема треугольника будет использоваться для определения площади вашего треугольника.
Площадь треугольника CSGNetwork.com — введите известные значения треугольника, чтобы найти площадь. Каждая из них имеет треугольную диаграмму:
SAS Triangle Solver от Algebra.com — Быстрая и простая в использовании треугольная диаграмма с пометкой может использоваться для получения дополнительных сведений о теореме SAS о треугольнике.
Интерактивная область треугольной диаграммы на MathOpenRef.com — перетащите указанную точку, чтобы изменить свойства треугольника на основе метода SAS.Узнайте больше о методе с предоставленной учебной информацией.
Формула Герона
Как объясняет MathIsFun.com, формула Герона названа в честь Героя, греческого инженера и математика. Формула используется для определения площади треугольника, когда известны все три длины сторон. Ниже приведен набор ресурсов, которые используют формулу Герона для определения площади треугольника:
Площадь треугольника формулы Герона на CSGNetwork.com — Простота использования. Введите длины сторон треугольника, чтобы найти его площадь.Также включена некоторая учебная информация о формуле Герона.
Формула Герона на Keisan.Casio.com — Формула Герона и треугольная диаграмма. Введите длину своей стороны, чтобы найти площадь.
Интерактивный треугольник формулы Герона от MathOpenRef.com — удобный способ поэкспериментировать с формулой. Перетащите точку и наблюдайте за изменением значений в правом углу.
OnlineMSchool.com Формула Херона — узнайте больше о формуле Херона из предоставленных объяснений и треугольной диаграммы.
Формула Герона на MathIsFun.com — следуйте простым для понимания инструкциям о том, как использовать формулу Герона, чтобы найти площадь треугольника. Введите длины сторон на треугольной диаграмме, чтобы найти площадь.
Формула Герона на MathWarehouse.com — используйте учебную информацию и пошаговые примеры, чтобы расширить свои знания о формуле Герона. Когда вы вводите длину сторон, площадь вашего треугольника мгновенно корректируется.
Область треугольника KylesConverter.com — Предоставляются простые для понимания учебные пособия и диаграммы в виде классной доски.
Формула Герона на TutorVista.com — быстро и легко использовать, следуйте пошаговым примерам, приведенным, чтобы узнать больше о формуле.
Формула Цапли Nap.st — Проста в использовании, просто введите длину своей стороны, чтобы найти область.
Calculator.Swiftutors.com Формула Херона — взгляните на цветовую версию формулы Херона, чтобы лучше понять каждый из ее элементов.
Решение Heron’s Formula Solver от Algebra.com — учебная информация, объясняющая, когда и почему использовать формулу Heron.Пошаговое объяснение сопровождается результатами.
NCalculators.com’s Triangle Area — Узнайте больше о формуле Heron из предоставленной учебной информации. Также предоставляется треугольная диаграмма, которая поможет вам лучше понять этот метод определения площади треугольника.
Область треугольника Heron на сайтеCalcverter.Blogspot.com — быстро, просто в использовании и содержит образец задачи, чтобы вы могли проверить свои навыки.
Закон синуса
Как объясняет HotMath.com, закон синусов — это – отношения между сторонами и углами непрямых (наклонных) треугольников.Его можно использовать, когда вы знаете «либо два угла и одна сторона треугольника (AAS или ASA), либо две стороны и угол, противоположный одному из них (SSA)». Ниже приведен набор инструментов, которые помогут вам узнать, когда и как использовать закон синуса:
Закон синусов EasyCalculation. com — прочтите разбивку уравнений, которые могут быть сформированы на основе закона синусов. Затем введите известные углы и стороны, чтобы найти неизвестные значения на основе закона синусов.
com — прочтите разбивку уравнений, которые могут быть сформированы на основе закона синусов. Затем введите известные углы и стороны, чтобы найти неизвестные значения на основе закона синусов.
CalculatorSoup.com’s Law of Sines — Используйте предоставленную помеченную треугольную диаграмму и учебную информацию, чтобы лучше понять закон синусов и то, как он используется.Затем используйте раскрывающееся меню, чтобы выбрать известные вам свойства, и найдите неизвестные значения.
Закон синуса и косинуса MathPortal.org — установите флажки, чтобы указать, какие стороны или углы вашего треугольника известны. Нажмите «Показать объяснение», чтобы узнать, как была решена ваша проблема, и узнать, использовался ли для ее решения закон синусов или закон косинусов.
Решающие треугольникиStudyStack.com — Введите известные значения, чтобы найти неизвестные значения и объяснить, почему использовались закон синусов или закон косинусов.
Гиперфизический закон SInes — Представлен факультетом физики и астрономии Университета штата Джорджия, узнайте больше о законе синуса с помощью простой для понимания учебной информации.
Интерактивный закон синусов в треугольнике MathOpenRef.com — перетащите любую точку треугольника и наблюдайте, как значения изменяются в правом углу в соответствии с законом синусов. Также предоставляется пример с пошаговым объяснением и раздел «Что стоит попробовать».
Химико-экология.net’s Law of Cosines and Sines Triangle — Введите ваши известные значения прямо на треугольную диаграмму, а затем закон синусов или закон косинусов будет использоваться для поиска неизвестных значений.
Закон синусов TutorVista.com — используйте учебную информацию и пошаговые примеры, предоставленные, чтобы лучше понять закон синусов.
RapidTables.com’s Sine — Следуйте инструкциям по использованию синуса для решения неизвестных значений вашего треугольника. Также предлагается версия с обратным синусом.
Закон косинусов
Как объясняет TheMathPage.com, когда вы знаете «две стороны треугольника и их угол наклона», закон косинусов можно использовать для определения неизвестной стороны. Используйте приведенные ниже ресурсы, чтобы углубить свое понимание Закона косинусов:
Используйте приведенные ниже ресурсы, чтобы углубить свое понимание Закона косинусов:
Закон косинусов EasyCalculation.com — используйте раскрывающееся меню, чтобы выбрать сторону треугольника, которую вы хотите найти. Затем введите свои известные значения. Закон косинусов используется для решения неизвестной стороны.
Закон косинусов CalculatorSoup.com — узнайте больше о законе косинусов из предоставленной учебной информации и треугольной диаграммы. Выберите сторону или угол, который вы хотите решить, используя раскрывающееся меню.
Закон косинусов TutorVista.com — доступны два варианта. Один использует закон косинусов для решения в случае SAS, а другой решает в случае SSS. Следуйте пошаговым примерам, чтобы лучше понять, когда и как использовать закон косинусов.
Гиперфизический закон косинусов — Представлен факультетом физики и астрономии Университета штата Джорджия, узнайте больше о законе косинусов с помощью простой для понимания учебной информации.
Интерактивный закон косинусов треугольника MathOpenRef.com — перетащите любую точку треугольника и наблюдайте, как значения изменяются в правом углу на основе закона косинусов. Предоставляется пример с пошаговым объяснением и дополнительной учебной информацией.
AJDesigner.Закон косинусов. com — Быстрый и простой в использовании, просто введите известную длину стороны, чтобы найти неизвестный угол.
Закон касательных
Наряду с синусом и косинусом тангенс является другой основной тригонометрической функцией. Как объясняет Wikipedia.org, его можно использовать, «когда известны две стороны и включенный угол или два угла и сторона». Приведенные ниже инструменты работают на основе Закона касательных.
КасательнаяRapidTables.com — Следуйте инструкциям, чтобы найти загар (x). Результаты могут быть представлены в градусах или радианах.
Tangent от Math.com — быстрое и простое в использовании решение для касательного угла путем ввода противоположного и соседнего угла.
Интерактивный касательный треугольник MathOpenRef.com — узнайте больше о функции касательной, перетаскивая точки треугольника и наблюдая, как пересчитываются касательные. Также предоставляется пример с объяснением и подробной обучающей информацией.
TutorVista.com’s Tangent — Подробная учебная информация и пошаговый пример предоставлены, чтобы помочь вам лучше понять функцию касательной.
Котангенс
Как объясняет SparkNotes.com, котангенс — это «величина, обратная касательной». Чтобы узнать больше о котангенсе, воспользуйтесь ресурсами ниже:
КотангенсEndMemo.com — быстро и легко найти котангенс, введя известное значение. Также предоставляется графическое изображение котангенса.
Котангенс AJDesigner.com — Найдите котангенс угла, введя известное значение. Результаты представлены в радианах и градусах.
CalcTool.Котангенс, секанс и косеканс org — введите известный угол, и вы получите котангенс, секанс и косеканс.
Секанс и косеканс
Тригонометрические функции наряду с котангенсом, секансом и косекансом используются нечасто.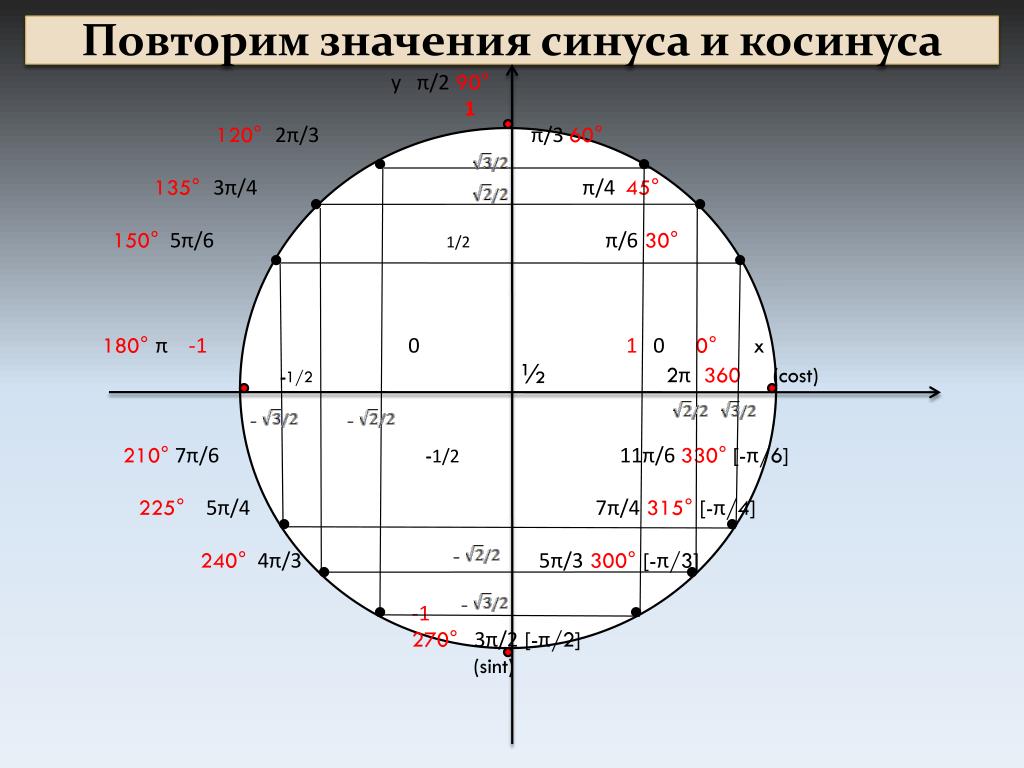 В прямоугольном треугольнике секанс определяется MathOpenRef.com как «длина гипотенузы, деленная на длину прилегающей стороны». Сайт определяет косеканс как «длину гипотенузы, деленную на длину противоположной стороны» в прямоугольном треугольнике.Используйте указанные ниже ресурсы, чтобы найти секанс и косеканс.
В прямоугольном треугольнике секанс определяется MathOpenRef.com как «длина гипотенузы, деленная на длину прилегающей стороны». Сайт определяет косеканс как «длину гипотенузы, деленную на длину противоположной стороны» в прямоугольном треугольнике.Используйте указанные ниже ресурсы, чтобы найти секанс и косеканс.
Секущая AJDesigner.com — проста в использовании и решает секущие угла. Результаты представлены в радианах и градусах.
Косеканс AJDesigner.com — отличный инструмент для поиска косеканса угла. Результаты представлены в радианах и градусах.
Тригонометрические функции
Используйте эти ресурсы, чтобы найти шесть тригонометрических функций: синус, косинус, тангенс, котангенс, секанс и косеканс.
Функции тригонометрииEasyCalculation.com — используйте раскрывающееся меню, чтобы выбрать, какую из шести наиболее распространенных тригонометрических функций вы будете решать. Затем введите свое значение.
Тригонометрические функции CalculatorSoup. com — выберите тригонометрическую функцию, которую необходимо найти, и введите известное значение. Графическая диаграмма предоставляется в качестве визуального представления каждой функции. В этой версии функции вычисляются в радианах.
com — выберите тригонометрическую функцию, которую необходимо найти, и введите известное значение. Графическая диаграмма предоставляется в качестве визуального представления каждой функции. В этой версии функции вычисляются в радианах.
Кейсан.Касио.Тригонометрические функции com — введите известный угол в радианах, а затем используйте раскрывающееся меню, чтобы выбрать функцию, которую вы хотите найти. Помеченная треугольная диаграмма используется в качестве наглядного пособия.
Тригонометрические функции TutorVista.com — Используйте предоставленные пошаговые примеры, чтобы узнать больше о том, как работать с тригонометрическими функциями.
Тригнометрические функцииPlanetCalc.com — Учебная информация предоставлена, чтобы помочь вам лучше понять каждую функцию. Введите известный угол, и будут предоставлены результаты для каждой функции.
Тригнометрические функции RapidTables.com — следуйте предоставленным инструкциям. Также предоставляется информация по каждой функции.
Тригонометрические функции SolveMyMath.com — Выберите, хотите ли вы получать результаты в градусах или радианах. Затем используйте раскрывающееся меню, чтобы выбрать функцию, которую вы будете решать.
Обратные тригонометрические функции
Как объясняет HotMath.com, обратные тригонометрические функции — это –, используемые для нахождения неизвестной меры угла прямоугольного треугольника, когда известны две длины сторон.”Узнайте больше об обратных триггерных функциях, используя ресурсы ниже:
График обратных тригонометрических функций EasyCalculation.com— Узнайте больше о том, как обратные тригонометрические функции представлены на графике, выбрав обратную функцию в раскрывающемся меню. Будут предоставлены координаты и график обратной функции.
Обратные тригонометрические функции CalculatorSoup.com — используйте раскрывающееся меню, чтобы выбрать обратное тригонометрическое значение, которое вы хотите найти. Для получения дополнительной информации см. График обратных тригонометрических функций.
График обратных тригонометрических функций.
Обратные тригонометрические функции Keisan.Casio.com — Быстрый и простой в использовании, выберите обратную тригонометрическую функцию, которую вы хотите найти. Результаты представлены в градусах.
Обратные тригонометрические функцииRapidTables.com — Используйте учебную информацию и таблицу значений, чтобы узнать об обратных функциях синуса, косинуса и тангенса.
Обратные тригонометрические функции GyPlan.com — выберите обратную функцию, которую вы хотите найти, в раскрывающемся меню.Результаты представлены в радианах и градусах.
Интерактивные обратные функции MathOpenRef.com Треугольники — сайт предлагает три интерактивных треугольника, которые помогут вам узнать больше об обратных функциях синуса, косинуса и тангенса. В каждом есть учебная информация, примеры и раздел «Что стоит попробовать».
Обратные тригонометрические функции AJDesigner.com — это быстрые и простые в использовании ресурсы для поиска обратных функций синуса, косинуса и тангенса.
РКМ.Обратные тригонометрические функции com.au — Найдите arcsin, arccos или arctan, если вы знаете синус, косинус и тангенс соответственно. Результаты представлены в градусах и радианах.
Обратные тригонометрические функции EndMemo.com — быстрые и простые в использовании ресурсы для поиска arcsin, arccos и arctan. Прокрутите вниз, чтобы просмотреть пример графика для каждой обратной функции.
Обратные триггерные функции TutorVista.com — Найдите обратные функции в градусах и радианах. Чтобы лучше понять концепцию, следуйте пошаговым примерам задач.
Расширенная тригонометрия
Градусы / Радианы Преобразование
Радианы и градусы — это единицы измерения, наиболее часто используемые для измерения углов. Как объясняет PurpleMath.com, градусы «выражают направленность и размер угла», а радианы служат числовым выражением градусов (например, 360 ° = 2π). Ниже представлена коллекция конвертеров:
Конвертер углов CleaveBooks.co.uk — Введите угол в градусах, чтобы преобразовать его в радианы и другие единицы измерения. Если у вас возникли проблемы, следуйте предоставленным инструкциям.
Если у вас возникли проблемы, следуйте предоставленным инструкциям.
RapidTables.com’s Angle Conversion — Прост в использовании и преобразует градусы в радианы или радианы в градусы, соответственно. Оба инструмента также предоставляют учебную информацию, которая поможет вам лучше понять концепцию:
UnitConversion.org Преобразование градусов в радианы — быстро и легко использовать, введите свой угол в градусах или радианах, и другие единицы будут предоставлены мгновенно.
CalculatorSoup.com’s Angle Conversion — Узнайте больше о том, как работают угловые преобразования, прочитав подробную информацию из учебника.Используйте раскрывающиеся меню, чтобы выбрать тип преобразования, которое вы хотите выполнить.
Угловое преобразование Техасского университета — предоставлено Бюро экономической геологии Техасского университета, быстрое и простое в использовании. Преобразуйте градусы в радианы и наоборот.
ConvertUnits.com преобразовывает градусы в радианы — преобразование градусов в радианы и радиан в градусы выполняется быстро и легко. Дополнительные сведения о преобразовании см. В разделе сведений и определений учебника.
Дополнительные сведения о преобразовании см. В разделе сведений и определений учебника.
Расчет.com Преобразование градусов в радианы. Следуйте приведенной формуле и примеру, чтобы лучше понять, как преобразовать градусы в радианы.
Градусы и радианы Mathinary.com — Быстрый и простой в использовании, узнайте больше о преобразовании радианов и градусов и его практическом применении из предоставленной учебной информации.
Конвертер градусов в радианы на MathPortal.org — конвертирует градусы в радианы и наоборот. К вашим результатам будет предоставлено пошаговое объяснение.
CalculatorPro.com из градусов в радианы — этот конвертер быстр и прост в использовании.
Конвертер градусов и радианов на сайтеUnitJuggler.com — выберите необходимое преобразование и введите свои значения. Результаты ясны и понятны.
Had2Know.com в градусах / радианах — узнайте больше о том, как преобразовать градусы и радианы из подробной информации учебника и круговой диаграммы.
Радианы и градусы MattDoyle.net — с этим конвертером нет наворотов. Пользоваться им быстро и легко.Выберите необходимое преобразование и введите свои значения.
Конвертер единиц TranslatorsCafe.com — Быстрый и простой в использовании, выберите необходимое преобразование и введите свои значения. Ваши результаты будут показаны мгновенно.
Радианы в градусы TutorVista.com — используйте пошаговые примеры, чтобы узнать больше о преобразовании.
PlanetCalc.com: градусы в радианы — быстро и легко использовать, введите свой угол в градусах, и вам будет предоставлено преобразование в радианы.
WolframAlpha.com в градусах и радианах — выберите необходимое преобразование. При преобразовании радианов в градусы будет обеспечено визуальное представление вашего угла внутри круга.
Измерение угла
Углы могут измеряться в градусах или радианах. Ниже приведены инструменты, которые помогут вам научиться измерять углы:
Угловой размер 1728. org — используется для определения угла, расстояния или размера. Углы представлены в градусах, минутах или секундах. Он включает в себя руководство по угловому размеру и примеры использования в реальном мире, например, измерения в астрономии.
org — используется для определения угла, расстояния или размера. Углы представлены в градусах, минутах или секундах. Он включает в себя руководство по угловому размеру и примеры использования в реальном мире, например, измерения в астрономии.
VistualTrig.com’s Angle — Введите либо значение верхнего угла, либо базовую длину, и треугольник изменится соответствующим образом. Или используйте ползунок, чтобы отрегулировать верхний угол треугольника, чтобы увидеть, как изменяются его другие углы.
Единичный круг
Как объясняет MathIsFun.com, единичный круг — это «круг с радиусом 1». В тригонометрии это удобный способ узнать длину и углы. Узнайте больше о единичных кругах с помощью инструментов ниже:
Единичный кругTutorVista.com — Используйте предоставленные пошаговые примеры и помеченную диаграмму, чтобы ознакомиться с работой с единичным кругом.
Интерактивная единичная окружность MathIsFun.com — перетащите курсор по единичной окружности, чтобы увидеть, как изменяются значения синуса, косинуса и тангенса на графике.
AnalyzeMath.com — Выберите функцию: синус, косинус или тангенс. Затем посмотрите, как единичный круг соответствует нарисованному графику.
Тригонометрические идентичности
Как объясняет PurpleMath.com в математике, «идентичность — это уравнение, которое всегда верно». В тригонометрии вы часто будете использовать несколько идентичностей (каждая с разделами ниже).Вот два общих решателя тригонометрических тождеств:
SymboLab.com’s Trigonmetric Identities Solver — Чисто разработанный и простой в использовании ресурс предоставляет пошаговые объяснения того, как проверить тригонометрическую идентичность.
TutorVista.com’s Trigonometric Identities Solver — Следуйте пошаговым инструкциям и примерам, чтобы улучшить свои знания о тригонометрических идентификаторах. Могут быть выполнены тождества «сумма к продукту» и «продукт к сумме».
Пифагорейские тождества
RegentsPrep.org объясняет пифагорейские тождества. Узнайте больше, используя инструмент ниже:
Узнайте больше, используя инструмент ниже:
EasyCalculation.com по пифагорейской идентичности — введите свой угол зрения, а затем следуйте пошаговым результатам, чтобы узнать, как / почему идентичность подтверждается.
Тождества суммы углов и разности
MathWords.com представляет тождества суммы и разности. Узнайте, как с ними работать, используя ресурсы ниже:
Идентификаторы суммы угловEasyCalculation.com — эти ресурсы можно использовать для добавления соответствующих тригонометрических функций.Каждый (кроме косинуса и котангенса) содержит необходимую формулу и диаграмму:
EasyCalculation.com’s Angle-Difference Identities – Узнайте больше о вычитании тригонометрических функций. В каждом (кроме котангенса) есть нужная формула и диаграмма.
Двойные углы идентификации
WolframMathworld.com предлагает взглянуть на формулы двойного угла. Ниже представлена коллекция ресурсов по двойным тождествам:
Программа EasyCalculation. com для определения двойных углов — узнайте, как использовать двойные углы для определения синуса, косинуса и тангенса.Приведены соответствующие формулы функций.
com для определения двойных углов — узнайте, как использовать двойные углы для определения синуса, косинуса и тангенса.Приведены соответствующие формулы функций.
Идентификация двойного угла на MeraCalculator.com — даны объяснение формулы идентичности двойного угла и пример проблемы.
Полуугловые идентичности
MathWords.com предлагает формулы тождеств половинных углов. Ниже представлена коллекция решателей тождеств половинных углов.
EasyCalculation.com Решатель идентичностей полууглов — узнайте, как «найти синус, косинус или тангенс половины заданного угла на основе формулы тригонометрического тождества.”
MeraCalculator.com’s Half-Angle Identity — Предоставляется учебная информация, объясняющая, когда использовать формулу полуугла и формулы для синуса, косинуса и тангенса.
Половина котангенса EasyCalculation.com — Используйте формулу и диаграмму, чтобы узнать больше о том, как найти половину угла котангенса на основе известного значения угла.
Половина угла косинуса EasyCalculation.com — представлены помеченная диаграмма и формула половинного угла косинуса.
Сумма Идентификаторов
MathWords.com представляет формулы «Сумма для идентификации продукта». Ниже приведены ресурсы, которые научат вас их использовать:
EasyCalculation.com «Сумма к идентификаторам продукта» — на сайте представлены эти быстрые и простые в использовании ресурсы для работы с суммой к идентификаторам продукта.
MathCelebrity.com Формулы суммы для продукта и продукта для суммирования — введите сумму для продукта или продукта, чтобы суммировать идентичность, которую вы хотите упростить. Результаты включают пошаговое объяснение того, как это сделать.
Обозначения продукта
Просмотрите продукт для суммирования идентичностей на MathWords.com. Ниже приведены два ресурса, которые помогут вам научиться с ними работать:
Продукт EasyCalculation.com для суммирования идентичностей — быстрый и простой способ «переписать и оценить произведения синусов и / или косинусов в виде сумм». Предоставляются необходимые формулы.
Предоставляются необходимые формулы.
Eguruchela.com для суммирования идентичностей — без наворотов, быстрый ресурс для работы с продуктом для суммирования идентичностей.
Идентификаторы снижения мощности
Chegg.com объясняет формулы снижения мощности. Узнайте больше о работе с ними, используя ресурсы ниже.
EasyCalculation.com’s Power Reduction — Ознакомьтесь с работой с формулами снижения мощности, которые предоставляются в качестве справки.
MeraCalculator.com’s Power Reduction Identity — Узнайте больше о работе с идентификатором снижения мощности, используя предоставленную учебную информацию.
Eguruchela.com’s Power Reduction Identities — простой и легкий в использовании ресурс для работы с идентификаторами снижения мощности.
Тригонометрические уравнения
Как PurpleMath.com объясняет, что решение тригонометрических уравнений требует сочетания того, что вы узнали об углах, с вашими алгебраическими навыками. Ниже представлен набор средств решения тригонометрических уравнений:
Ниже представлен набор средств решения тригонометрических уравнений:
Тригонометрические уравнения EasyCalculation.com — Быстрое и простое в использовании: введите угол и целое число, чтобы найти x. Необходимые формулы представлены в качестве справки.
Тригонометрические уравнения Symbolab.com — аккуратно разработанные и простые в использовании, введите собственное уравнение или воспользуйтесь одним из примеров, чтобы получить пошаговое объяснение того, как решить уравнение.Уравнение также отображается на графике.
Программа для решения тригонометрических уравненийMathPortal.org — Узнайте больше о тригонометрических уравнениях с помощью пошаговых примеров.
WebMath.com’s Simplify a Trigonometric Expression — Введите свое выражение. Этот ресурс будет использовать триггерные идентификаторы, чтобы упростить его. Предоставляется пошаговое объяснение.
Решение уравнений NumberEmpire.com — Используйте «Пример 2», чтобы узнать больше о решении тригонометрических уравнений. Также можно решить множество других уравнений.
Также можно решить множество других уравнений.
Векторные или векторные операции
Как объясняет SparkNotes.com, вектор — это «по сути отрезок линии в определенной позиции, длина и направление которого обозначены стрелкой на конце». Узнайте больше о векторах, используя ресурсы ниже:
MathIsFun.com’s Vector — введите векторы как величину и угол или как координаты x, y и посмотрите, как они взаимодействуют на графике.
Вектор MathPortal.org. Введите координаты вектора в 2D или 3D, а затем выберите операцию, которую хотите выполнить.Установите флажок «Показать объяснение», чтобы шаг за шагом увидеть, как был найден результат.
1728.org’s Vector Addition — быстрый и простой в использовании ресурс для добавления до 10 векторов. Также предоставляются учебная информация и схема.
ВекторOnlineMSchool.com — Найдите длину, величину или норму вектора. Результаты предоставлены пошаговым объяснением.
OnlineMSchool.com: «Сложение и вычитание векторов» — предоставляется краткая учебная информация о том, как складывать и вычитать векторы. Пошаговое объяснение прилагается к результатам.
Пошаговое объяснение прилагается к результатам.
TheCraftyCanvas.com’s Vector & Component Resolver — Выполняет различные функции с использованием векторов, включая «сложение / вычитание векторов, заданные компоненты вектора», «сложение / вычитание векторов, заданные векторы» и «разрешение вектора по его компонентам, заданной величине и направление ».
Величина вектора WolframAlpha.com — Введите конечную точку вектора. Величина вместе с векторным графиком и другой информацией предоставляется вместе с результатами.
ВекторSymbolab.com — введите собственную векторную операцию или функцию или воспользуйтесь одним из примеров, чтобы узнать больше о векторах. Результаты предоставлены пошаговым объяснением.
Векторные операцииEasyCalculation.com — эти быстрые и простые в использовании ресурсы помогут вам складывать и вычитать векторы.
Вектор NCalculators.com — Используйте предоставленную учебную информацию, чтобы узнать больше об этих векторных концепциях.
Операции с векторами TutorVista.com — Используйте примеры задач и пошаговые объяснения, чтобы узнать больше о сложении и вычитании векторов.
Векторные операции CalcTool.org — Быстро и легко использовать, имеется векторная диаграмма. Также включены инструкции по вычитанию векторов с помощью этого инструмента.
Как оценить триггерные функции без калькулятора
Тригонометрия включает вычисление углов и функций углов, таких как синус, косинус и тангенс. Калькуляторы могут быть удобны при поиске этих функций, потому что у них есть кнопки sin, cos и tan. Однако иногда вам не разрешат использовать калькулятор при выполнении домашнего задания или экзамена, или у вас может просто не быть калькулятора.Не паникуйте! Люди вычисляли триггерные функции задолго до появления калькуляторов, и вы тоже можете с помощью нескольких простых приемов.
Триггерные функции графических осей
Оси на стандартном графике находятся под углом 0 градусов, 90 градусов, 180 градусов и 270 градусов.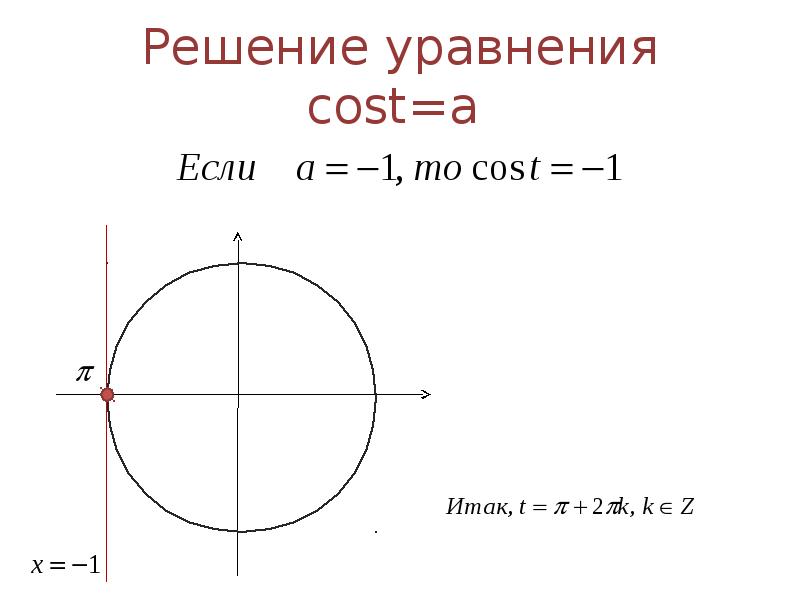 Для этих особых углов проще всего запомнить функции синуса и косинуса, потому что они следуют легко запоминающимся образцам. Косинус 0 градусов равен 1, косинус 90 градусов равен 0, косинус 180 градусов равен -1, а косинус 270 градусов равен 0.Синус следует аналогичному циклу, но он начинается с 0. Таким образом, синус 0 градусов равен 0, синус 90 градусов равен 1, синус 180 градусов равен 0, а синус 270 градусов равен –1.
Для этих особых углов проще всего запомнить функции синуса и косинуса, потому что они следуют легко запоминающимся образцам. Косинус 0 градусов равен 1, косинус 90 градусов равен 0, косинус 180 градусов равен -1, а косинус 270 градусов равен 0.Синус следует аналогичному циклу, но он начинается с 0. Таким образом, синус 0 градусов равен 0, синус 90 градусов равен 1, синус 180 градусов равен 0, а синус 270 градусов равен –1.
Прямоугольные треугольники
Часто, когда вас просят вычислить триггерную функцию угла без калькулятора, вы получите прямоугольный треугольник, а угол, который вас спросят, является одним из углов в треугольнике. Чтобы решить такие проблемы, вам нужно запомнить аббревиатуру SOHCAHTOA. Первые три буквы говорят вам, как найти синус (S) угла: длину противоположной стороны (O), деленную на длину гипотенузы (H).Например, если вам дан треугольник с углами 90 градусов, 12 градусов и 78 градусов, гипотенуза (сторона, противоположная углу 90 градусов) равна 24, а сторона, противоположная углу 12 градусов, равна 5.![]() Вы должны поэтому разделите противоположную сторону на гипотенузу 5/24, чтобы получить 0,21 как синус 12 градусов. Оставшаяся сторона называется смежной стороной, и она используется для вычисления косинуса. Средние три буквы в SOHCAHTOA указывают, что косинус (C) — это смежная сторона (A), деленная на гипотенузу (H).Последние три буквы говорят вам, что касательная (T) угла — это противоположная сторона (O), разделенная гипотенузой (H).
Вы должны поэтому разделите противоположную сторону на гипотенузу 5/24, чтобы получить 0,21 как синус 12 градусов. Оставшаяся сторона называется смежной стороной, и она используется для вычисления косинуса. Средние три буквы в SOHCAHTOA указывают, что косинус (C) — это смежная сторона (A), деленная на гипотенузу (H).Последние три буквы говорят вам, что касательная (T) угла — это противоположная сторона (O), разделенная гипотенузой (H).
Специальные треугольники
Треугольники 30-60-90 и 45-45-90 используются для запоминания триггерных функций некоторых часто используемых углов. Для треугольника 30-60-90 нарисуйте прямоугольный треугольник, два других угла которого составляют примерно 30 градусов и 60 градусов. Стороны равны 1, 2 и квадратный корень из 3. Наименьшая сторона (1) противоположна наименьшему углу (30 градусов).Самая большая сторона (2) — это гипотенуза, противоположная наибольшему углу (90 градусов). Квадратный корень из 3 противоположен оставшемуся углу в 60 градусов. В треугольнике 45-45-90 нарисуйте прямоугольный треугольник, два других угла которого равны. Гипотенуза — это квадратный корень из 2, а две другие стороны равны 1. Итак, если вас попросят найти косинус 60 градусов, вы должны нарисовать треугольник 30-60-90 и заметить, что смежная сторона равна 1, а гипотенуза равна 2. Следовательно, косинус 60 градусов равен 1/2.
В треугольнике 45-45-90 нарисуйте прямоугольный треугольник, два других угла которого равны. Гипотенуза — это квадратный корень из 2, а две другие стороны равны 1. Итак, если вас попросят найти косинус 60 градусов, вы должны нарисовать треугольник 30-60-90 и заметить, что смежная сторона равна 1, а гипотенуза равна 2. Следовательно, косинус 60 градусов равен 1/2.
Таблицы триггеров
Если вам не задан треугольник или специальный угол, вы можете прибегнуть к использованию таблицы триггеров, в которой определенные триггерные функции были вычислены и занесены в таблицу для каждого градуса от 0 до 90. Пример триггерной таблицы: предоставлено в разделе «Ресурсы» этой статьи.
Обратный синус, косинус и тангенс. Как SOHCAHTOA может рассчитывать углы. Как использовать эти функции …
Обратный путь SOHCAHTOA против суммы внутренних углов
Сравните этот метод с проверенной теоремой о том, что сумма внутренних углов треугольника равна 180 °.
Что такое степень измерения LNM?
Внутренний угол Sum Way Поскольку общая величина внутренних углов треугольника составляет 180 градусов, мы можем проверить меру LNM.
180 ° -16 ° — 90 ° = 74 °
В качестве альтернативы, вы можете использовать инверсию одной из функций SOHCAHTOA, в данном случае инверсию синуса (sin -1 )! Чтобы найти угол прямоугольного треугольника, все, что нам нужно знать, — это длина двух сторон! Затем используйте те же соотношения SOHCAHTOA — только по-другому См. Пример ниже.
Обратный путь SOHCAHTOAsin -1 (73,24 / 76,19) = 74 °
YouTube Vid: как рассчитать обратный SOHCAHTOA
Хорошее видео о том, как использовать калькулятор TI-Graphing для вычисления обратного синуса, косинуса или тангенса.
Сравните синус с обратным синусом.
Общая разница: синус — это отношение двух фактических сторон прямоугольного треугольника (противоположная гипотенуза и ) грех (B) = AC / ABОбратный или sin -1 — это операция, которая использует те же две стороны прямоугольного треугольника , что и синус (противоположный гипотенузе), чтобы найти меру угла (в данном случае b) sin -1 (AC / AB) = Измерьте угла B
Ключевое различие : Хотя и синус, и обратный синус включают противоположную сторону и гипотенузу прямоугольного треугольника, результаты этих двух операций очень, очень разные.Одна операция (синус) находит соотношение этих двух сторон; другая операция, обратная синусу, фактически вычисляет величину угла (B в приведенном выше примере) с использованием противоположной стороны и гипотенузы.
Задача 1
Используйте обратный синус, косинус или тангенс, чтобы вычислить меру затененного угла слева.
Измерение угла
Задача 2
Используйте обратный синус, косинус или тангенс, чтобы вычислить меру затененного угла слева.
Измерение углаЗадача 3
Какова мера заштрихованного угла слева?
Измерение углаЗадача 4
Поскольку вы знаете все 3 стороны, вы можете использовать любое из следующего:
= грех -1 (7/25) = 16.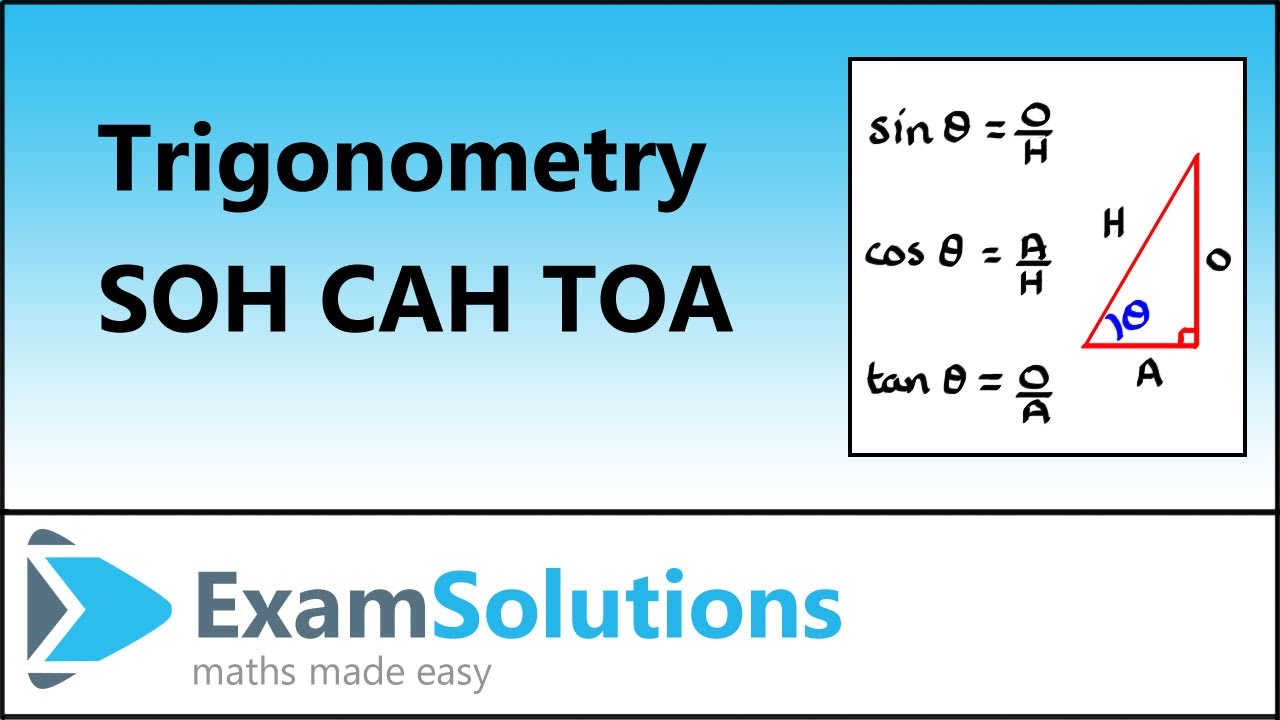 3 °
3 ° = cos -1 (6/15) = 16,3 °
= tan -1 (7/24) = 16,3 °
Проблема 5
Поскольку вы знаете все 3 стороны, вы можете использовать любое из следующего:
= грех -1 (8/10) = 53.13 °= cos -1 (6/10) = 53,13 °
= tan -1 (8/6) = 53,13 °
Как калькуляторы выполняют тригонометрию?
Конфиденциальность и файлы cookie: этот сайт использует файлы cookie. Продолжая использовать этот сайт, вы соглашаетесь на их использование.
Продолжая использовать этот сайт, вы соглашаетесь на их использование. Чтобы узнать больше, в том числе о том, как управлять файлами cookie, см. Здесь: Политика использования файлов cookie
Как ваш калькулятор НЕ РАБОТАЕТ
Самый простой и наименее точный способ вычислить синус и косинус угла — это измерить физический объект.\ circ $ не совпадает по фазе с другой катушкой — но если ваш калькулятор не был извлечен из навигационного компьютера бомбардировщика Boeing 50-х годов, ваш калькулятор делает это иначе. Ваш калькулятор также не обращается к таблицам значений, тщательно составленным вручную путем сложения углов и тригонометрических тождеств полууглов, что было нормой для математиков, ученых и инженеров до середины века.
Если вы похожи на меня, вы предположили, что современные калькуляторы аппроксимируют синус и косинус полиномиальными функциями, используя методы исчисления и анализа.(Если вы очень похожи на меня, вы сказали об этом старшекласснику на первом году обучения, изо всех сил пытаясь сделать ключевые идеи рядов Тейлора доступными без ссылок на исчисление. ) Однако эти алгебраические приближения медленно сходятся. Сложный компьютер может сократить путь, сохранив старые огромные таблицы в памяти и , а затем Чебышевская аппроксимация, чтобы получить последние несколько цифр точности. Но как насчет вашего карманного или научного калькулятора, или, если уж на то пошло, графического калькулятора TI — где добавление этой архитектуры было бы дорогостоящим хлопотом?
) Однако эти алгебраические приближения медленно сходятся. Сложный компьютер может сократить путь, сохранив старые огромные таблицы в памяти и , а затем Чебышевская аппроксимация, чтобы получить последние несколько цифр точности. Но как насчет вашего карманного или научного калькулятора, или, если уж на то пошло, графического калькулятора TI — где добавление этой архитектуры было бы дорогостоящим хлопотом?
Аббревиатура со странной заглавной буквы
Введите CORDIC, цифровой компьютер с вращением координат — алгоритм, разработанный Джеком Волдером из Convair, чтобы в полной мере использовать сильные стороны появившихся в то время цифровых компьютеров.\ circ) \ примерно 0,97 \ ldots / 1 $.
Само по себе это устраняет необходимость хранить огромную таблицу — грубо говоря, каждое новое меньшее вращение уточняет результат до дополнительной двоичной цифры точности, и все, что необходимо сохранить, — это инструкции для поворота на этот угол. Действительно, аналогичные методы использовались для тех таблиц, созданных вручную: метод, описанный до сих пор, представляет собой геометрическую перспективу использования тригонометрических тождеств суммы углов. Однако алгоритм Волдера не останавливается на достигнутом.\ circ $ — угол.
Однако алгоритм Волдера не останавливается на достигнутом.\ circ $ — угол.
Оба эти уточнения схемы, казалось бы, усложняют нашу жизнь; в конце концов, мы теряем и красивые рациональные углы, и гипотенузу, которая остается неизменной на длине 1. Однако мы увидим, что фактические вычисления более просты и даже проще в двоичной арифметике. Если вам особенно нравятся матрицы преобразований, вы можете приостановить чтение прямо сейчас, чтобы понять, почему это происходит самостоятельно (или прочтите это в превосходных «Элементарных функциях и калькуляторах» Ричарда Пэрриса) — но если вы хотите увидеть более чисто геометрическое объяснение, читайте дальше!
CORDIC: геометрическое обоснование
Давайте посмотрим на простой пример этих правил в действии.Скажем, у нас есть прямоугольный треугольник со сторонами длиной $ a $, $ b $ и $ c $ в соответствии с известным условием. Пусть $ c $ — гипотенуза, а сторона $ a $ примыкает к углу $ \ theta $:
Прямоугольный треугольник.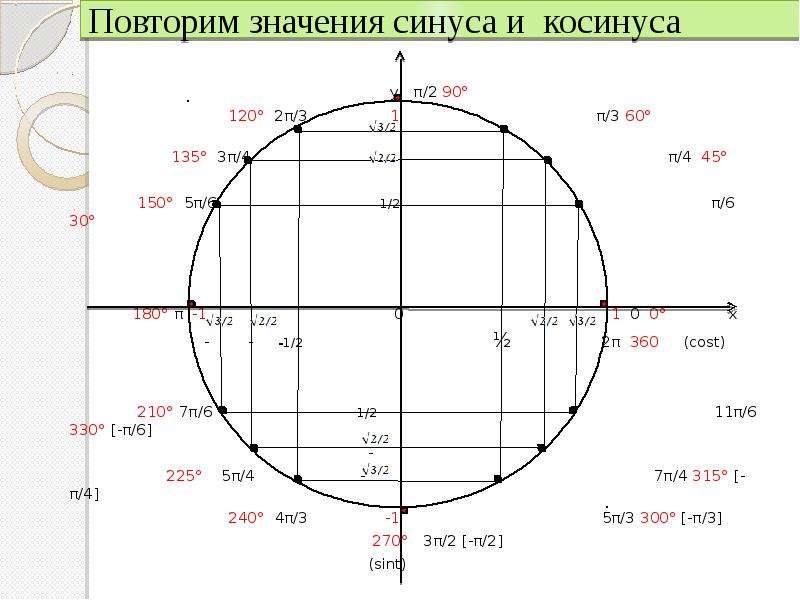 \ circ $! Таким образом, размеры прямоугольного треугольника с углом $ \ theta + \ varphi $ могут составлять $ a- \ frac {b} {2} $ на соседней стороне и $ b + \ frac {a} {2} $ на противоположной стороне. сторона:
\ circ $! Таким образом, размеры прямоугольного треугольника с углом $ \ theta + \ varphi $ могут составлять $ a- \ frac {b} {2} $ на соседней стороне и $ b + \ frac {a} {2} $ на противоположной стороне. сторона:
Длины сторон треугольника с углом $ \ theta + \ varphi $.n} $, если бы мы искали $ \ varphi $ с касательной, уменьшенной вдвое n раз. Изменение длин сторон всегда будет определяться этим маленьким треугольником, который — поскольку его стороны построены параллельно сторонам исходного треугольника — всегда будет похож на исходный треугольник, а его масштаб будет определяться отношением касательных к новому треугольнику. треугольник в веере.
Что может делать ваш калькулятор
Чтобы построить веер и отслеживать координаты точки, нам нужно только повторить этот небольшой процесс разделения и сложения, пока мы не подойдем достаточно близко к желаемому углу.n $, перемещая десятичную точку на $ n $ разрядов. Многие более простые калькуляторы используют двоичную кодировку десятичной дроби вместо чистой двоичной, сохраняя каждую цифру десятичного числа отдельно в двоичном представлении, что добавляет некоторые морщинки, но в основном следует тому же принципу.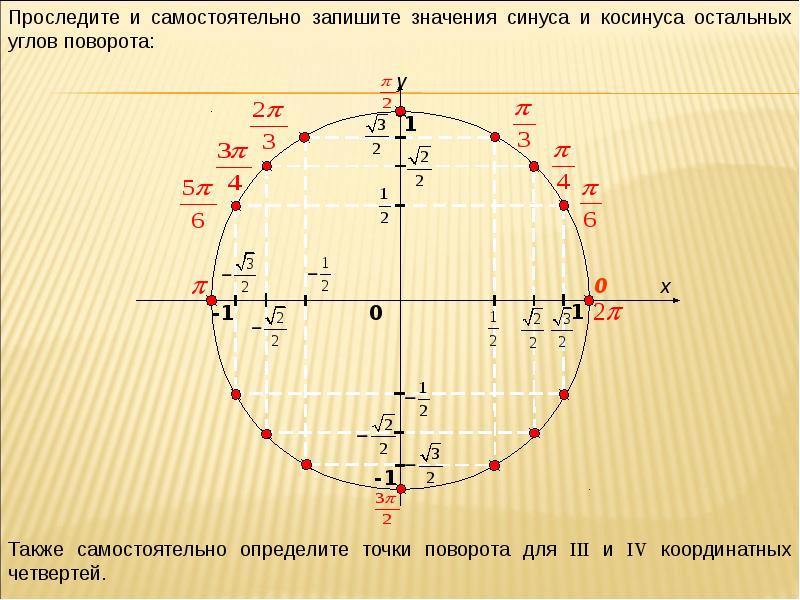 Остается только сложение.
Остается только сложение.
Для вычисления отношений синуса и косинуса нам нужна только одна дополнительная информация: длина гипотенузы. Здесь «веер» полезен, особенно если мы сделаем еще одну оговорку — мы никогда не оставляем за собой угол или треугольник.\ circ $ — один из наиболее удобных углов для достижения этой цели. Более обычная реализация CORDIC была бы настроена на уменьшение касательной вдвое в двадцать или тридцать раз, чтобы гарантировать точность до пяти десятичных знаков.
Итак, мы можем вычислить поскольку и косинус с помощью только одной вычислительно затратной задачи: деления на заданное число в конце. Однако эти вычислительные затраты уменьшаются, и умная алгоритмическая бережливость CORDIC начала терять популярность. Процессоры Intel не использовали CORDIC со времен 486 года, и даже некоторые современные графические калькуляторы отказались от этого метода в пользу полиномиального подхода.Но даже несмотря на то, что когда-нибудь CORDIC может перестать быть инструментом, который люди используют сами, его невероятная простота, дешевая реализация и проверенная точность позволят использовать его в специализированных процессорах и специализированных машинах до тех пор, пока специализированная электроника должна знать, как проводить измерения. треугольники.
Упражнение для читателя
Поскольку гиперболические тригонометрические функции имеют много общих свойств со своими тригонометрическими аналогами по окружности, неудивительно, что CORDIC также может вычислять $ \ sinh $, $ \ cosh $, $ \ tanh $ и остальные гиперболические отношения. — хотя значения на гиперболе могут сдвигаться достаточно быстро, чтобы оставлять «промежутки», которых нельзя достичь одним только гиперболическим тангенсом.x $ означает, что базовый метод CORDIC можно даже адаптировать для оценки показателей и логарифмов. Если вы можете описать геометрическое обоснование для гиперболического, экспоненциального или логарифмического вариантов, как в приведенном выше круговом случае, дайте мне знать — я устал смотреть на матрицы.
W.L. Фельдхузен — преподаватель математики в южном Вермонте. Они проявляют особый интерес к истории преподавания математики, истории вычислений и к сложным геометрическим интерпретациям простых элементов алгебры.
blog.willfeldhusen.com + Другие статьи W.L.
Единичный круг: функции синуса и косинуса
Результаты обучения
- Найдите значения функции для синуса и косинуса специальных углов.
- Укажите область и диапазон функций синуса и косинуса.
- Используйте исходные углы для оценки тригонометрических функций.
- Оцените значения синуса и косинуса с помощью калькулятора.
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичного круга, круга с центром в начале координат и радиусом 1, как показано на рисунке 2.Угол (в радианах), который пересекает [latex] t [/ latex], образует дугу длиной [latex] s [/ latex]. Используя формулу [latex] s = rt [/ latex] и зная, что [latex] r = 1 [/ latex], мы видим, что для единичного круга , [latex] s = t [/ latex].
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление, в котором будет разворачиваться положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс] t [/ латекс] мы можем обозначить пересечение конечной стороны и единичного круга его координатами, [латекс] \ left (x, y \ right) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f \ left (t \ right) = \ cos t [/ latex] и [latex] f \ left (t \ right) = \ sin t [/ latex] соответственно. Это означает [латекс] x = \ cos t [/ latex] и [латекс] y = \ sin t [/ latex].
Рис. 2. Единичная окружность с центральным углом [латекс] t [/ латекс] радиан
A Общее примечание: Unit Circle
Единичная окружность имеет центр [латекс] \ влево (0,0 \ вправо) [/ латекс] и радиус [латекс] 1 [/ латекс].В единичном круге длина перехваченной дуги равна радианам центрального угла [латекс] 1 [/ латекс].
Пусть [latex] \ left (x, y \ right) [/ latex] будет конечной точкой единичной окружности дуги длиной [латекс] s [/ latex]. Координаты [latex] \ left (x, y \ right) [/ latex] этой точки могут быть описаны как функции угла.
Определение функций синуса и косинуса
Теперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как координаты [latex] \ left (x, y \ right) [/ latex] соотносятся с длиной дуги и углом .Синусоидальная функция связывает действительное число [латекс] t [/ латекс] с координатой y точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [латекс] t [/ латекс] равен значению y конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 2 синус равен [latex] y [/ latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — это координата y соответствующей точки на единичной окружности.
Функция косинуса угла [латекс] t [/ latex] равна значению x конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 3 косинус равен [латекс] х [/ латекс].
Рисунок 3
Поскольку понятно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: [latex] \ sin t [/ latex] то же самое, что [latex] \ sin \ left (t \ right) [ / latex] и [latex] \ cos t [/ latex] то же самое, что и [latex] \ cos \ left (t \ right) [/ latex].{2} [/ латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Общее примечание: функции синуса и косинуса
Если [латекс] t [/ latex] является действительным числом и точка [латекс] \ left (x, y \ right) [/ latex] на единичном круге соответствует углу [латекса] t [/ latex] , затем
[латекс] \ cos t = x [/ латекс]
[латекс] \ sin t = y [/ латекс]
Как сделать: по точке
P [латекс] \ left (x, y \ right) [/ latex] на единичной окружности, соответствующей углу [латекс] t [/ latex], найдите синус и косинус.- Синус [latex] t [/ latex] равен y -координате точки [latex] P: \ sin t = y [/ latex].
- Косинус [latex] t [/ latex] равен x -координате точки [latex] P: \ text {cos} t = x [/ latex].
Пример 1: Поиск значений функции для синуса и косинуса
Точка [латекс] P [/ латекс] — это точка на единичной окружности, соответствующая углу [латекс] t [/ латекс], как показано на рисунке 4. Найдите [латекс] \ cos \ left (t \ right) [/ latex] и [latex] \ text {sin} \ left (t \ right) [/ latex].
Рисунок 4
Показать решениеМы знаем, что [latex] \ cos t [/ latex] — это координата x соответствующей точки на единичном круге, а [latex] \ sin t [/ latex] — это координата y соответствующей точки. точка на единичной окружности. Итак:
[латекс] \ begin {align} x & = \ cos t = \ frac {1} {2} \\ y & = \ sin t = \ frac {\ sqrt {3}} {2} \ end {align} [/ латекс]
Попробуйте
Определенный угол [латекс] t [/ латекс] соответствует точке на единичной окружности в [латекс] \ left (- \ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) [/ latex], как показано на рисунке 5.Найдите [латекс] \ cos t [/ latex] и [латекс] \ sin t [/ latex].
Рисунок 5
Показать решение[латекс] \ cos \ left (t \ right) = — \ frac {\ sqrt {2}} {2}, \ sin \ left (t \ right) = \ frac {\ sqrt {2}} {2} [/ латекс]
Нахождение синусов и косинусов углов на оси
Для квадрантных углов соответствующая точка единичной окружности попадает на ось x- или y . В этом случае мы можем легко вычислить косинус и синус из значений [latex] x [/ latex] и [latex] y [/ latex].\ circ \ right) = 1 \ end {align} [/ latex]
Косинус 90 ° равен 0; синус 90 ° равен 1.
Попробуйте
Найдите косинус и синус угла [латекс] \ пи [/ латекс].
Показать решение[латекс] \ cos \ left (\ pi \ right) = — 1 [/ латекс], [латекс] \ sin \ left (\ pi \ right) = 0 [/ latex]
Пифагорейская идентичность
Рисунок 7
Теперь, когда мы можем определить синус и косинус, мы узнаем, как они соотносятся друг с другом и с единичной окружностью. {2} t = 1 [/ латекс]
Как сделать: учитывая синус некоторого угла [латекс] t [/ латекс] и его положение в квадранте, найдите косинус [латекс] t [/ латекс].
- Подставьте известное значение [латекс] \ sin \ left (t \ right) [/ latex] в пифагорейскую идентичность.
- Решите относительно [латекс] \ cos \ left (t \ right) [/ latex].
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [latex] t [/ latex].
Пример 3: Нахождение косинуса из синуса или синуса из косинуса
Если [латекс] \ sin \ left (t \ right) = \ frac {3} {7} [/ latex] и [latex] t [/ latex] находится во втором квадранте, найдите [latex] \ cos \ left (т \ справа) [/ латекс].{2} \ left (t \ right) = \ frac {40} {49} \\ \ text {cos} \ left (t \ right) = \ pm \ sqrt {\ frac {40} {49}} = \ pm \ frac {\ sqrt {40}} {7} = \ pm \ frac {2 \ sqrt {10}} {7} \ end {gather} [/ latex]
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицательный. \ circ [/ latex] или [latex] \ frac {\ pi} {4} [/ latex], как показано на рисунке 9.Треугольник \ circ [/ latex] — это равнобедренный треугольник, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
Рисунок 9
При [latex] t = \ frac {\ pi} {4} [/ latex], что составляет 45 градусов, радиус единичной окружности делит пополам первый квадрантный угол . Это означает, что радиус лежит вдоль линии [латекс] y = x [/ latex].{2} = \ frac {1} {2} \\ x = \ pm \ frac {1} {\ sqrt {2}} \ end {gather} [/ latex]
В квадранте I [латекс] x = \ frac {1} {\ sqrt {2}} [/ latex].
При [латексе] t = \ frac {\ pi} {4} [/ latex] или 45 градусах,
[латекс] \ begin {собранный} \ left (x, y \ right) = \ left (x, x \ right) = \ left (\ frac {1} {\ sqrt {2}}, \ frac {1} {\ sqrt {2}} \ right) \\ x = \ frac {1} {\ sqrt {2}}, y = \ frac {1} {\ sqrt {2}} \\ \ cos t = \ frac { 1} {\ sqrt {2}}, \ sin t = \ frac {1} {\ sqrt {2}} \ end {gather} [/ latex]
Если мы затем рационализируем знаменатели, мы получим
[латекс] \ begin {align} \ cos t & = \ frac {1} {\ sqrt {2}} \ frac {\ sqrt {2}} {\ sqrt {2}} = \ frac {\ sqrt {2} } {2} \\ \ sin t & = \ frac {1} {\ sqrt {2}} \ frac {\ sqrt {2}} {\ sqrt {2}} = \ frac {\ sqrt {2}} {2 } \ end {align} [/ latex]
Следовательно, [латекс] \ left (x, y \ right) [/ latex] координаты точки на окружности радиусом [латекс] 1 [/ latex] под углом [латекс] 45 ^ \ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) [/ latex].\ circ [/ latex], как показано на рисунке 12.
Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [латекс] 2y [/ latex], и поскольку все стороны равны, мы также можем сделать вывод, что [latex] r = 2y [/ latex] или [latex] y = \ frac {1} {2 } г [/ латекс]. Поскольку [латекс] \ sin t = y [/ latex],
[латекс] \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} r [/ latex]
А поскольку [latex] r = 1 [/ latex] в нашем единичном круге ,
[латекс] \ begin {align} \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} \ left (1 \ right) = \ frac {1} {2 } \ end {align} [/ latex]
Используя тождество Пифагора, мы можем найти значение косинуса.\ circ [/ латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс] ABC [/ латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13
Угол наклона [латекс] ABD [/ латекс] составляет 30 °. Так, если двойной, угол [латекс] ABC [/ латекс] равен 60 °. [latex] BD [/ latex] — это серединный перпендикуляр к [latex] AC [/ latex], поэтому он разрезает [latex] AC [/ latex] пополам. Это означает, что [latex] AD [/ latex] — это [latex] \ frac {1} {2} [/ latex] радиус или [latex] \ frac {1} {2} [/ latex].\ circ [/ latex] — это [латекс] \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \ [/ latex], поэтому мы можем найти синус и косинус.
[латекс] \ begin {собранный} \ left (x, y \ right) = \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ x = \ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \\ \ cos t = \ frac {1} {2}, \ sin t = \ frac {\ sqrt {3} } {2} \ end {gather} [/ latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
| Угол | 0 | [латекс] \ frac {\ pi} {6} [/ latex], или 30 ° | [латекс] \ frac {\ pi} {4} [/ latex], или 45 ° | [латекс] \ frac {\ pi} {3} [/ latex], или 60 ° | [латекс] \ frac {\ pi} {2} [/ latex], или 90 ° |
| Косинус | 1 | [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] \ frac {1} {2} [/ латекс] | 0 |
| Синус | 0 | [латекс] \ frac {1} {2} [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] | 1 |
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.
Рисунок 14
Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы вычисляем [латекс] \ cos \ left (30 \ right) [/ latex] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в радианном режиме.
Как: заданный угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример 4: Использование графического калькулятора для поиска синуса и косинуса
Вычислить [латекс] \ cos \ left (\ frac {5 \ pi} {3} \ right) [/ latex] с помощью графического калькулятора или компьютера.\ circ [/ latex], например, включив коэффициент преобразования в радианы как часть входных данных:
SIN (20 × π ÷ 180) ВВОД
Попробуйте
Вычислить [латекс] \ sin \ left (\ frac {\ pi} {3} \ right) [/ latex].
Показать решениеприблизительно 0,866025403
Определение области и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны.Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут входить в функции? Поскольку углы меньше 0 и углы больше [латекс] 2 \ pi [/ latex] все еще могут быть нанесены на единичный круг и имеют реальные значения [latex] x, y [/ latex] и [latex] r [/ latex], не существует нижнего или верхнего предела углов, которые могут входить в функции синуса и косинуса. Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичный круг , как показано на рисунке 15. Границы координаты x следующие: [latex] \ left [-1,1 \ right] [/ latex]. Границы координаты y также являются [latex] \ left [-1,1 \ right] [/ latex]. Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].
Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса.Поскольку значение синуса — это координата y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x . Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь то же значение x , но будет иметь противоположное значение y .Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на рисунке 16, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ begin {array} {ccc} \ sin \ left (t \ right) = \ sin \ left (\ alpha \ right) \ hfill & \ text {и} \ hfill & \ cos \ left (t \ right) = — \ cos \ left (\ alpha \ right) \ hfill \\ \ sin \ left (t \ right) = — \ sin \ left (\ beta \ right) \ hfill & \ text {и} \ hfill & \ cos \ left (t \ right) = \ cos \ left (\ beta \ right) \ hfill \ end {array} [/ latex]
Рисунок 16
Напомним, что опорный угол угла — это острый угол [латекс] t [/ латекс], образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. \ circ \ mathrm {-t} | [/ latex].\ circ [/ latex]
Попробуйте
Найдите опорный угол [латекса] \ frac {5 \ pi} {3} [/ latex].
Показать решение[латекс] \ frac {\ pi} {3} [/ латекс]
Использование опорных углов
А теперь давайте вернемся к колесу обозрения, представленному в начале этого раздела. Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Какая у всадника новая высота? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов, или при отрицательном угле .Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат [latex] \ left (x, y \ right) [/ latex] для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для оценки тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если мы знаем косинус или синус его опорного угла.Абсолютные значения косинуса и синуса угла такие же, как и у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений y в этом квадранте.
Общее примечание: Использование опорных углов для определения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы.Знак (положительный или отрицательный) можно определить по квадранту угла.
Как: для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значения x в квадранте исходного угла.\ circ \ right) = \ frac {1} {2} [/ latex]
- [латекс] \ frac {5 \ pi} {4} [/ latex] находится в третьем квадранте. Его опорный угол составляет [латекс] \ frac {5 \ pi} {4} — \ pi = \ frac {\ pi} {4} [/ latex]. Косинус и синус [latex] \ frac {\ pi} {4} [/ latex] оба равны [latex] \ frac {\ sqrt {2}} {2} [/ latex]. В третьем квадранте значения [latex] x [/ latex] и [latex] y [/ latex] отрицательны, поэтому:
[латекс] \ cos \ frac {5 \ pi} {4} = — \ frac {\ sqrt {2}} {2} \ text {и} \ sin \ frac {5 \ pi} {4} = — \ гидроразрыв {\ sqrt {2}} {2} [/ latex]
Попробуйте
а.\ circ \ right) = \ frac {- \ sqrt {2}} {2} [/ latex]
б. [латекс] \ cos \ left (- \ frac {\ pi} {6} \ right) = \ frac {\ sqrt {3}} {2}, \ sin \ left (- \ frac {\ pi} {6} \ right) = — \ frac {1} {2} [/ latex]
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности. Они показаны на рисунке 19.Найдите время, чтобы узнать координаты [latex] \ left (x, y \ right) [/ latex] всех основных углов в первом квадранте.
В дополнение к изучению значений специальных углов, мы можем использовать опорные углы, чтобы найти координаты [latex] \ left (x, y \ right) [/ latex] любой точки на единичной окружности, используя то, что мы знаем об опорных углах. вместе с удостоверениями личности
[латекс] \ begin {собрано} x = \ cos t \\ y = \ sin t \ end {собрано} [/ latex]
Сначала мы находим опорный угол, соответствующий данному углу.Затем мы берем значения синуса и косинуса опорного угла и даем им знаки, соответствующие значениям квадранта y и x .
Как сделать: учитывая угол точки на окружности и радиус окружности, найдите координаты [latex] \ left (x, y \ right) [/ latex] точки.
- Найдите опорный угол, измерив наименьший угол к оси x .
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для [латекс] x [/ латекс] и [латекс] y [/ латекс]
в данном квадранте.
Пример 7: Использование единичной окружности для поиска координат
Найдите координаты точки на единичной окружности под углом [latex] \ frac {7 \ pi} {6} [/ latex].
Показать решениеМы знаем, что угол [латекс] \ frac {7 \ pi} {6} [/ латекс] находится в третьем квадранте.
Во-первых, давайте найдем опорный угол, измерив угол к оси x .Чтобы найти опорный угол угла, конечная сторона которого находится в квадранте III, мы находим разность угла и [латекс] \ pi [/ латекс].
[латекс] \ frac {7 \ pi} {6} — \ pi = \ frac {\ pi} {6} [/ latex]
Затем находим косинус и синус опорного угла:
[латекс] \ begin {gather} \ cos \ left (\ frac {\ pi} {6} \ right) = \ frac {\ sqrt {3}} {2} \\ \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} \ end {gather} [/ latex]
Мы должны определить соответствующие знаки для x и y в данном квадранте.Поскольку наш исходный угол находится в третьем квадранте, где оба [latex] x [/ latex] и [latex] y [/ latex] отрицательны, косинус и синус отрицательны.
[латекс] \ begin {gather} \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \\ \ sin \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {1} {2} \ end {gather} [/ latex]
Теперь мы можем вычислить координаты [latex] \ left (x, y \ right) [/ latex], используя тождества [latex] x = \ cos \ theta [/ latex] и [latex] y = \ sin \ theta [ /латекс].
Координаты точки: [latex] \ left (- \ frac {\ sqrt {3}} {2}, — \ frac {1} {2} \ right) [/ latex] на единичной окружности.{2} t = 1 [/ латекс]
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла [латекс] t [/ латекс] равен значению y конечной точки единичной окружности дуги длиной [латекс] t [/ латекс], тогда как косинус угол [latex] t [/ latex] равен x -значению конечной точки.
- Значения синуса и косинуса наиболее точно определяются, когда соответствующая точка единичной окружности попадает на ось.
- Когда синус или косинус известны, мы можем использовать пифагорову тождество, чтобы найти другое. Пифагорейская идентичность также полезна для определения синусов и косинусов особых углов.
- Калькуляторы и программное обеспечение для построения графиков полезны для поиска синусов и косинусов, если известна правильная процедура ввода информации.
- Все функции синуса и косинуса являются действительными числами.
- Диапазон функций синуса и косинуса: [latex] \ left [-1,1 \ right] [/ latex].
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус его опорного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это размерный угол [латекс] t [/ латекс],
, образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. - Опорные углы можно использовать для определения синуса и косинуса исходного угла.
- Опорные углы также можно использовать для определения координат точки на окружности.
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- y -значение точки на единичной окружности, соответствующей заданному углу
- единичный круг
- круг с центром в [латекс] \ влево (0,0 \ вправо) [/ латекс]
и радиусом
— Найдите стороны и углы по правилу cos
Воспользуйтесь бесплатным онлайн-калькулятором закона косинусов, который поможет найти неизвестные длины сторон или углов треугольника.Вы можете вычислить все остальные оставшиеся стороны и измерить углы в треугольнике, используя различные формы закона косинуса.
А теперь начните читать, чтобы узнать больше о правилах косинуса.
Что такое закон косинусов?Закон косинусов — это набор формул, которые связывают длину сторон треугольника с одним из его углов косинуса. Обычно предпочтение отдается закону косинуса, когда заданы три стороны треугольника для нахождения любого угла A, B или C треугольника или двух смежных сторон и задан один угол.0 $$
Однако онлайн-калькулятор закона синусов поможет вам найти неизвестные углы и длины сторон треугольника.
Как работает калькулятор закона косинусов?Калькулятор закона косинуса поможет вам найти все неизвестные пропущенные значения треугольника, выполнив следующие шаги:
Ввод:- Сначала вам нужно выбрать сторону или угол треугольника, который требуется из выпадающего меню, затем калькулятор отобразит соответствующую форму формулы закона косинусов.
- Теперь поместите все значения в соответствующее поле.
- Затем выберите коррелированные единицы.
- После ввода всех значений нажмите кнопку «Рассчитать».
Калькулятор закона косинусов отображает следующие результаты, используя формулу закона косинуса:
- Размеры всех углов и длин сторон.
- А также, значения различных характеристик треугольника.
- В конце концов, он рисует диаграмму для заданных значений.
Характеристики Triangle:
Периметр P = \ (a + b + c \)
Полупериметр s = \ (0,5 * (a + b + c) \)
Площадь A = \ (\ sqrt {s * (s — a) * (s — b) * (s — c)} \)
Радиус круга в треугольнике r = \ (\ sqrt {(s — a) * (s — b) * (s — c) / s} \)
Радиус окружности вокруг треугольника R = \ (\ frac {(abc)} {(4AS)} \)
Где:
a = сторона треугольника a, b = сторона треугольника b, c = сторона треугольника c
A = угол A, B = угол B, C = угол C
R = радиус окружности по окружности
r = радиус внутреннего круга
P = периметр
с = полупериметр
A = Площадь
Какова роль теоремы Пифагора в законе косинусов?Закон косинуса — это модифицированная версия теоремы Пифагора, которая используется для нахождения неизвестных значений сторон и углов непрямых треугольников.
Как мы можем доказать закон косинусов?Мы можем доказать закон косинусного уравнения, используя четыре различных следующих метода:
- Формула расстояния
- Тригонометрия
- Теорема Птолемея
- Теорема Пифагора
Калькулятор закона косинусов абсолютно бесплатен для вычисления сторон и углов треугольника. Вычисление всех тригонометрических измерений вручную — действительно сложная задача, которая увеличивает вероятность ошибок.Таким образом, с помощью этого удобного калькулятора вы можете предотвратить риск получения точных значений, а также этот онлайн-калькулятор помогает как студентам, так и преподавателям решать задачи, связанные с законом косинусов.
Артикул:
Из источника в Википедии: теорема Птолемея, тупой случай, теорема Пифагора, формула расстояния.
Из источника Versity Tutors: Применение закона косинусов, теоремы Пифагора, двух сторон и включенного угла-SAS.

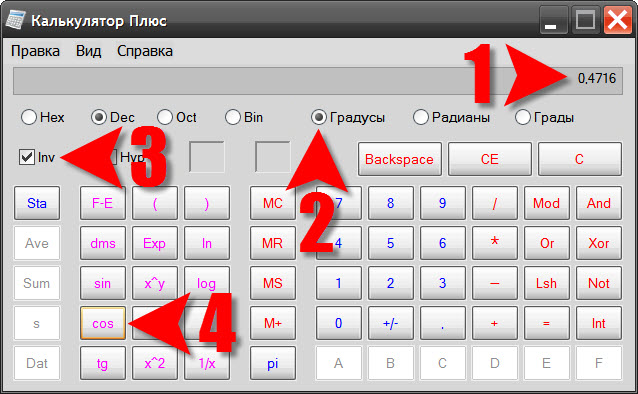
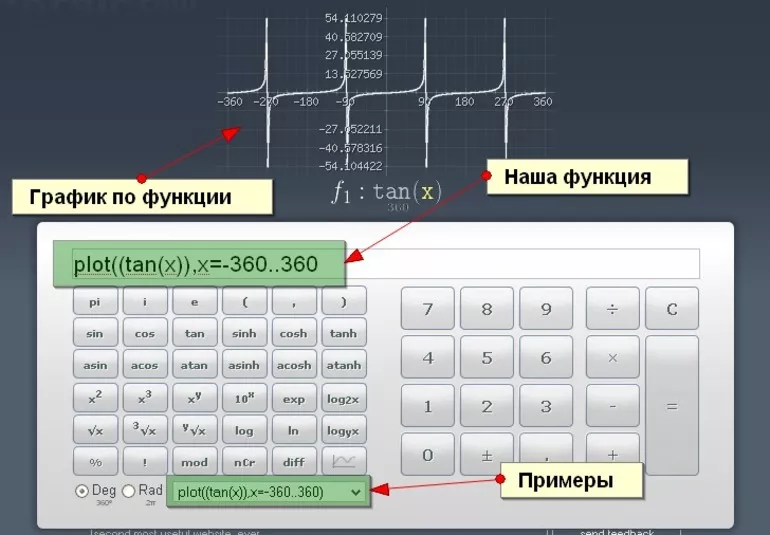

 3
3 14159..
14159..