Определения синуса, косинуса, тангенса и котангенса
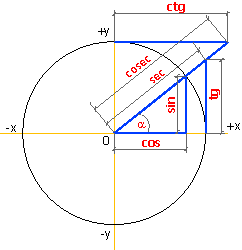
 Синус угла
Синус угла 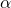 (обозначается
(обозначается 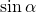 ) – ордината точки
) – ордината точки 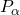 , полученной поворотом точки
, полученной поворотом точки 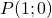 вокруг начала координат на угол
вокруг начала координат на угол 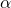 .
.
Косинус угла 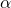
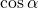 ) – абсцисса точки
) – абсцисса точки 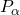 , полученной поворотом точки
, полученной поворотом точки 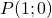 вокруг начала координат на угол
вокруг начала координат на угол 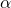 .
.Тангенс угла 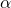 (обозначается
(обозначается 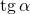 ) – отношение синуса угла
) – отношение синуса угла 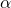
![\[\operatorname{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f3cba66971d7fd1d95998220eb211676_l3.png)
Котангенс угла  (обозначается
(обозначается  ) – отношение косинуса угла
) – отношение косинуса угла  к его синусу, т.е.
к его синусу, т.е.
![\[\operatorname{ctg}\alpha = \frac{\cos\alpha}{\sin\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f6efc9004c51766c5c3efc271d310896_l3.png)
Таблица значений синуса, косинуса, тангенса и котангенса
Калькулятор синусов, косинусов, тангенсов и котангенсов
Данный калькулятор поможет легко вычислить значения этих тригонометрических функций от углов, заданных в градусах, радианах или градах.
Онлайн калькулятор: Тригонометрические функции
 Простейшие тригонометрические функции
Простейшие тригонометрические функцииТригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.

Тригонометрические функции
Единицы измерения Точность вычисленияЗнаков после запятой: 10
save Сохранить extension Виджет
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Косеканс: (отношение длины гипотенузы к противоположному катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
4. Тригонометрический калькулятор онлайн — примеры
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце — знак равенства.

- [Inv] – обратная функция для sin, cos, tan, переключает интерфейс на другие функции
- [ ( ] и [ ) ] — вводит скобки
- [Int] – отображает целую часть десятичного числа
- [Sinh] — гиперболический синус
- [Sin] – синус заданного угла
- [X2] – возведение в квадрат (формула x^2)
- [n!] — вычисляет факториал введенного значения — произведение n последовательных чисел, начиная с единицы до самого введенного числа, например 4!=1*2*3*4, то есть 24
- [Dms] – переводит из десятичного вида в формат в градусы, минуты, секунды.
- [Cosh] — гиперболический косинус
- [Cos] – косинус угла
- [xy] – возведение икса в степ. игрик (формула x^y)
- [y√x] – извлечение корня в степени y из икс
- [Pi] – число Пи, выдает значение Pi для расчетов
- [tanh] — гиперболический тангенс
- [tan] – тангенс угла онлайн, tg
- [X3] — помогает возвести в степень 3, в куб (формула x^3)
- [3√x] — извлечь корень кубический
- [F – E] — переключает ввод чисел в экспоненциальном представлении и обратно
- [Exp] — позволяет вводить данные в экспоненциальном представлении.
- [Mod] — позволяет нам вычислить остаток от деления одного числа на другое
- [Log] – рассчитывает десятичный логарифм
- [10^x] – возведение десяти в произвольную степень
- [1/X] — подсчитывает обратную величину
- [e^x] – Возведение числа Эйлера в степень
- [Frac] – отсекает целую часть, оставляет дробную
- [sinh-1] – обратный гиперболический синус
- [sin-1] – арксинус или обратный синус, arcsin или 1/sin
- [deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее
- [cosh-1] — обратный гиперболический косинус
- [cos-1] – аркосинус или обрат. косинус arccos или 1/cos
- [2*Pi] – рассчитывает число Пи, помноженное на два
- [tanh-1] – обрат. гиперболический тангенс
- [tan-1] – арктангенс или обратный тангенс, arctg
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерах
Как возвести в степень
Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[xy] «икс в степени игрик», [X2] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Инженерный калькулятор онлайн
Современный уклад жизни требует постоянной динамики. Производя расчеты на калькуляторе, мы заметно экономим свое время, не рискуем в чем-то ошибиться и получаем точный результат. Благодаря изобретению данного устройства, многие люди забыли что такое недостачи и погрешности в расчетах. Однако калькулятор калькулятору рознь, и если примитивные вычислительные функции можно сделать на математической модели, то сложнейшие расчеты возможно совершить только при помощи инженерной. Отныне приобретать данное чудо современной техники не нужно – достаточно обратиться за помощью к нашему инженерному калькулятору онлайн! Программа работает без дополнительной установки – достаточно зайти на электронную страницу и начать действовать.
Функции инженерного калькулятора онлайн
Калькулятор математического типа поможет вам совершить только примитивные расчеты. С его помощью можно сделать то, чему нас учили в начальных классах средней школы:
- сложение;
- вычитание;
- деление;
- умножение;
- вычитание процентов;
- возведение числа в степень;
- нахождение корня квадратного.
Инженерный калькулятор онлайн включает в себя все эти и дополнительные функции, которые необходимы для проведения сложных расчетов. Теперь вам не придется тратить дополнительные деньги на покупку этого устройства, ведь сделать вычисления можно на нашем сайте.
Помимо вышеперечисленных, наш универсальный калькулятор поможет вам выполнить такие расчеты:
Нахождение:
- синуса угла;
- тангенса;
- косинуса;
- котангенса;
- арксинуса;
- арктангенса;
- арккосинуса;
- арккотангенса.
Интерфейс инженерного калькулятора онлайн
Выполнить все вышеперечисленные расчеты достаточно просто. Наш инженерный калькулятор онлайн обладает понятным интерфейсом, а потому работать с ним весьма удобно. По своему виду он полностью имитирует настоящий калькулятор, поэтому долгого изучения функций вам не потребуется. Несмотря на это мы прилагаем подробную инструкцию и описание каждой клавиши.
Пользоваться нашей программой выгодно еще и потому, что расчеты производятся моментально – вам не нужно обновлять страницу сайта, ведь калькулятор работает во флеш-режиме. Ежедневно нашей программой пользуется огромное количество людей. Среди них ученики высших заведений, преподаватели, архитекторы-проектировщики, ученые и другие люди, заинтересованные в точности расчетов. Инженерный калькулятор онлайн не требует скачивания и установки дополнительных плагинов, а потому вы можете начать пользоваться им прямо сейчас!
Инженерный калькулятор: инструкция.
На данной странице находится лучший инженерный калькулятор онлайн. Он предназначен для решения инженерных, научных и других математических задач. Вы можете пользоваться им бесплатно и без регистрации. Этот калькулятор будет полезен инженерам, строителям, ученым, математикам, школьникам, студентам, аспирантам и экономистам. Он поможет вычислить синус и косинус, тангенс и котангенс, возвести число в квадрат, в степень или решить логарифм.
Управление: мышь / клавиатура (в т.ч. «Backspace», «Del» и «Enter»).
Расшифровка стандартных кнопок:
«M+» — добавить число в память (либо прибавить к тому, которое уже в памяти).
«M-» — вычесть число, которое на экране из числа, которое в памяти.
«MR» — вывести число из памяти на экран.
«MC» — очистить память.
«+/-» — преобразовать положительное число в отрицательное и наоборот.
«AC» — общий сброс (вместе с памятью).
«C» — простой сброс (без памяти).
«Xy» — возвести в степень (например, 10 ^ 4 = 10000).
Расшифровка кнопок левого блока (слева направо):
«sin» — синус угла.
«asin» — арксинус угла.
«π» — число Пи.
«cos» — косинус угла.
«acos» — арккосинус угла.
«e» — число Эйлера (основание натурального логарифма).
«tg» — тангенс угла.
«atg» — арктангенс угла.
«ctg» — котангенс угла.
«actg» — арккотангенс угла.
«x2» — возвести число в квадрат.
«log2x» — двоичный логарифм.
«10x» — возвести число 10 в степень, находящуюся на экране.
«logyx» — логарифм по основанию «y».
«1/x» — разделить число 1 на текущее число.
Зачем нужен инженерный калькулятор?
Многофункциональный инженерный онлайн калькулятор, предназначенный для выполнения сложных инженерных и научно-технических расчетов. Очень удобный и точный. Доступна функция памяти. Калькулятор управляется с помощью мыши или клавиатуры. При желании можно изменять размер кальулятора («+» и «-» в углу).
Калькулятор выполняет все базовые инженерные и математические действия. Помимо стандартной арифметики и алгебры, вычисляются следующие функции: синус угла, косинус угла, арксинус угла, арккосинус угла, тангенс, котангенс, арктангенс, арккотангенс угла, число «пи», основание Эйлера, двоичные логарифм, логарифм по основанию, возведение в кадрат, возведение в степень и многое другое.
| Вид: | инженерный/научный |
| Запуск: | онлайн |
| Тип: | бесплатный |
| Функций | 25 |
| Память | есть |
| Размеры | маленький, средний, большой |
Решение тригонометрических уравнений онлайн
В общем виде, тригонометрическое уравнение можно записать следующим образом:
f(trig(x)) = 0
где f — некоторая произвольная функция, trig(x) — некоторая тригонометрическая функция.
Как правило, метод решения тригонометрических уравнений заключается в преобразовании исходного уравнения к более простому, решение которого известно. Преобразования осуществляются при помощи различных тригонометрических формул.
Например, рассмотрим решение тригонометрического уравнения:
Используя формулу косинуса двойного угла, преобразуем данное уравнение:
Полученное уравнение является простейшим и легко решается. Наш онлайн калькулятор, построенный на системе Wolfram Alpha способен решить более сложные тригонометрические уравнения с описанием подробного хода решения.
Таблица синусов и косинусов. Онлайн-калькулятор
В даннной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Чтобы рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″ или -1775° 15′ 22″ )
можно воспользоваться калькулятором синусов и косинусов.
Примечание: в калькуляторе этот знак означает,
что можно поставить отрицательное значение угла. При нажатии на этот знак минус появится, при повторном нажатии исчезнет.
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | -0.51503807 | |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Калькулятор синусов и косинусов
Рассчитать
Исходный угол: 180° 20′ 54″Расчетный угол в градусах: 180.34833333333°
Синус (sin) = -0.006079526
Косинус (cos) = -0.999981520
Тангенс (tg) = 0.006079638
Котангенс (ctg) = 164.483467955
Другие таблицы
Таблица тангенсов и котангенсов
Sine, Cosine, Tangent
Три функции, но та же идея.
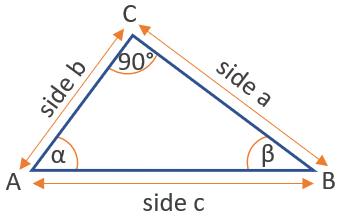
Правый Треугольник
Sine, Cosine и Tangent являются основными функциями, используемыми в тригонометрии, и основаны на прямоугольном треугольнике.
Перед тем, как застрять в функциях, полезно присвоить name каждой стороне прямоугольного треугольника:
- «Противоположно» противоположно углу θ
- «Смежный» прилегает (рядом) к углу θ
- «Гипотенуза» длинная
Adjacent всегда рядом с углом
и противоположный противоположен углу
Sine, Cosine и Tangent
Sine, Cosine и Tangent (часто сокращенно до sin, cos и tan) — это отношение сторон прямоугольного треугольника:
Для данного угла θ каждое отношение остается тем же
, независимо от того, насколько велик или мал треугольник
Чтобы рассчитать их:
Разделите длину одной стороны другой стороной
Пример: что такое синус 35 °?
Используя этот треугольник (длины даны только до одного десятичного знака):
| sin (35 °) | = ПротивоположныйГипотенуза |
| = 2.+84,9 | |
| = 0,57 … | |
| cos (35 °) | = AdjacentHypotenuse |
| = 4.04.9 | |
| = 0,82 … | |
| tan (35 °) | = ПротивоположноПрилегающие |
| = 2.+84,0 | |
| = 0,70 … |
Размер не имеет значения
Треугольник может быть большим или маленьким, а соотношение сторон остается неизменным.
Только угол меняет соотношение.
Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:
Ухороших калькуляторов есть грех, cos и tan, чтобы вам было легче. Просто установите угол и нажмите кнопку.
Но вам все равно нужно помнить , что они значат!
в форме изображения:
Практика здесь:
Sohcahtoa
Как запомнить? Подумайте «Sohcahtoa» !
Это работает так:
Soh … | Sine = O напротив / Hypotenuse | ||||||||||||||||||||||||||||||||||||||||
… ХАГ … | Cosine = Adjacent / Hypotenuse | ||||||||||||||||||||||||||||||||||||||||
.
ExamplesПример: каковы синус, косинус и тангенс 30 °? Классический 30 ° треугольник имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону
√3: Теперь мы знаем длины, мы можем вычислить функции:
(достаньте свой калькулятор и проверьте его!) Пример: каковы синус, косинус и тангенс 45 °? Классический 45 ° треугольник имеет две стороны 1 и гипотенузу √2:
Why?Почему важны эти функции?
Пример: Используйте функцию sine, чтобы найти «d»Мы знаем:
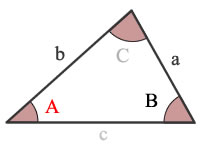
И мы хотим знать «д» (расстояние вниз) . Начать с: грех 39 ° = противоположность / гипотенуза грех 39 ° = д / 30 Spap Sides: d / 30 = sin 39 ° Используйте калькулятор, чтобы найти грех 39 °: d / 30 = 0,6293 … Умножьте обе стороны на 30: d = 0,6293… x 30 d = 18,88 до 2 знаков после запятой. Глубина «d» составляет 18,88 м ExerciseПопробуйте это бумажное упражнение, в котором вы можете вычислить функцию синуса. для всех углов от 0 ° до 360 °, а затем график результата.Калькулятор — вычисляет cos (x) для градусов или радианов. Используйте этот калькулятор, чтобы легко вычислить косинус угла в градусах или радианах. Функция косинуса (cos (x))Синус — это тригонометрическая функция угла, обычно определяемая для острых углов в прямоугольном треугольнике как отношение длины соседней стороны к гипотенузе. Это дополнение к синусу. На иллюстрации ниже cos (α) = b / c и cos (β) = a / c.
В приведенном выше графике cos (α) = b / c.Из этого определения следует, что косинус любого угла всегда меньше или равен единице, и он может принимать отрицательные значения. Косинус угла в 90 градусов равен нулю, поскольку для его вычисления нам понадобится треугольник с двумя углами в 90 градусов, который является определением прямой линии. Поскольку третья сторона треугольника не существует (длина равна 0), косинус равен нулю (0, деленное на длину гипотенузы, равно 0). Вы можете использовать этот косинус калькулятор, чтобы проверить это. A Обычно используемый закон тригонометрии, который тривиально выводится из определения косинуса, представляет собой закон косинусов: c2 = a2 + b2 — 2ab · cosγ Связанные тригонометрические функцииВзаимное выражение от косинуса — это секущий: sec (x), иногда записываемый как secant (x), который дает отношение длины гипотенузы к длине стороны, противоположной углу. Задействованием от косинуса является функция арккозина: acos (x) или arccos (x), которая принимает значения от 0 до 180 градусов. Как вычислить косинус угла?Наш косинусный калькулятор поддерживает ввод в градусах и радианах, поэтому, после того как вы измерили угол или посмотрели план или схему, вы просто вводите измерение и нажимаете «вычислить». Вот как это легко. Применения функции косинусаФункция косинуса может использоваться для моделирования периодических явлений в физике, биологии, общественных науках и т. Д.{-1} \ left [\ dfrac {a \ sin B} {b} \ right] \) * Единицы длины предназначены только для справки, поскольку значение результирующих длин всегда будет одинаковым, независимо от того, какие единицы измерения. Использование калькулятораИспользует закон синусов для вычисления неизвестных углов или сторон треугольника. Для расчета неизвестных значений необходимо ввести 3 известных значения. Некоторые варианты расчета избыточны, но в любом случае включены для точных буквенных обозначений. Методы расчетаЧтобы вычислить любой угол, A, B или C, скажем B, введите противоположную сторону b, затем другую пару угловых сторон, такую как A и a или C и c.Выполненные расчеты соответствуют метод бокового угла (SSA) и использовать закон синусов только для выполнения расчетов для других неизвестных. Чтобы вычислить любую сторону, a, b или c, скажем, b, введите противоположный угол B, а затем другую пару угловых сторон, такую как A и a или C и c. Выполненные расчеты соответствуют метод угол-угол (AAS) и использовать закон синусов только для выполнения расчетов для других неизвестных. 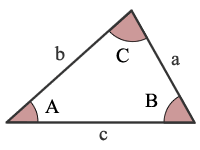 За СинусовЕсли a, b и c — длины ножек треугольника, противоположных углам A, B и C соответственно; тогда закон синусов гласит: \ (\ dfrac {a} {\ sin A} = \ dfrac {b} {\ sin B} = \ dfrac {c} {\ sin C} \) Уравнения из решения закона синусов для углов A, B и C\ (A = \ sin ^ {- 1} \ left [\ dfrac {a \ sin B} {b} \ right] \) \ (A = \ sin ^ {- 1} \ left [\ dfrac {a \ sin C} {c} \ right] \) \ (B = \ sin ^ {- 1} \ left [\ dfrac {b \ sin A} {a} \ right] \) \ (B = \ sin ^ {- 1} \ left [\ dfrac {b \ sin C} {c} \ right] \) \ (C = \ sin ^ {- 1} \ left [\ dfrac {c \ sin A} {a} \ right] \) \ (C = \ sin ^ {- 1} \ left [\ dfrac {c \ sin B} {b} \ right] \) Уравнения из решения закона синусов для сторон a, b и c\ (a = \ dfrac {b \ sin A} {\ sin B} \) \ (a = \ dfrac {c \ sin A} {\ sin C} \) \ (b = \ dfrac {a \ sin B} {\ sin A} \) \ (b = \ dfrac {c \ sin B} {\ sin C} \) \ (c = \ dfrac {a \ sin C} {\ sin A} \) \ (c = \ dfrac {b \ sin C} {\ sin B} \) Треугольные характеристикиТреугольный периметр, P = a + b + c Треугольный полупериметр, с = 0.5 * (a + b + c) Треугольник, K = √ [s * (s-a) * (s-b) * (s-c)] Радиус вписанного круга в треугольник, r = √ [(s-a) * (s-b) * (s-c) / s] Радиус описанной окружности вокруг треугольника, R = (abc) / (4K) Ссылки / Дальнейшее чтениеВайштайн, Эрик У. «Закон синусов» MathWorld— веб-ресурс Wolfram. Закон Синусов. Sine, Cosine, Tangent, объяснено и с примерами и практикой выявления противоположных, смежных сторон и гипотенузы На этой странице объясняется соотношение синуса, косинуса и тангенса, дается обзор их диапазона значений и приводятся практические проблемы по определению сторон, которые противоположны и смежны с данным углом. Функции синуса, косинуса и тангенса выражают соотношения сторон прямоугольного треугольника. В каких треугольниках ниже SOHCAHTOA применяется?Покажи ответ
Интерактивные углы SOHCAHTOAПопробуйте активировать $$ \ angle A $$ или $$ \ angle B $$, чтобы изучить, как соседние и противоположные стороны меняются в зависимости от угла. Status: Угол активирован: $$ \ red {none} \ text {, в ожидании выбора угла.} $$Ответ: sine угла всегда является отношением $$ \ frac {противоположная сторона} {гипотенуза} $$. $ синус (угол) = \ frac {\ text {противоположная сторона}} {\ text {hypotenuse}} $ Пример 1$$ sin (\ angle \ red L) = \ frac {противоположный} {гипотенуза} \\ sin (\ angle \ red L) = \ frac {9} {15} $$ Пример 2$$ sin (\ angle \ red K) = \ frac {противоположный} {гипотенуза} \\ sin (\ angle \ red K) = \ frac {12} {15} $$ Помните: Когда мы используем слова «противоположный» и «смежный», мы всегда должны иметь в виду определенный угол. $ косинус (угол) = \ frac {\ text {смежная сторона}} {\ text {hypotenuse}} $ Пример 1$$ cos (\ angle \ red L) = \ frac {смежный} {гипотенуза} \\ cos (\ angle \ red L) = \ frac {12} {15} $$ Пример 2$$ cos (\ angle \ red K) = \ frac {смежный} {гипотенуза} \\ cos (\ angle \ red K) = \ frac {9} {15} $$ Диапазон значений CosineДля тех, кто чувствует себя комфортно в «Math Speak», область и диапазон косинусов следующие.
Косинус угла имеет диапазон значений от -1 до 1 включительно. Ниже приведена таблица значений, иллюстрирующая некоторые ключевые значения косинуса, которые охватывают весь диапазон значений.
tangent угла всегда является отношением (противоположная сторона / смежная сторона). Калькулятор синуса онлайн — Расчет греха — производная — antiderivative Summary:Синхронная тригонометрическая функция для вычисления синуса угла в радианах, градусы или градианы. Грех онлайнОписание:Калькулятор позволяет использовать большинство тригонометрических функций, есть возможность рассчитать sine, косинус и касательная угла через функции с тем же именем., Тригонометрическая функция . Синус Синхронный калькулятор позволяет через функцию sin вычислить online sine синус угла в радианах, вы должны сначала
выберите желаемую единицу измерения, нажав на кнопку параметров модуля расчета.После этого вы можете начать свои расчеты.
Для рассчитать синус онлайн из ‘pi / 6`, введите
sin (`pi / 6`), после расчета результат
`1 / 2` возвращается.
Обратите внимание, что функция синуса может распознать некоторые специальные углы и сделать
расчеты со специальными связанными значениями в точной форме.
Для рассчитать синус угла в градусах, сначала нужно выбрать нужную единицу
нажав на кнопку опций модуля расчета модуля.После этого вы можете начать свое исчисление.
Чтобы вычислить синус 90, введите sin (90), после вычисления
restults 1 возвращается.
Чтобы рассчитать синус угла в градусах, сначала необходимо выбрать нужную единицу измерения.
нажав на кнопку опций модуля расчета модуля. После этого вы можете начать свое исчисление. Чтобы вычислить синус 50, введите sin (50) после вычисления:
результат `sqrt (2) / 2` возвращается.
Обратите внимание, что функция синуса может распознавать некоторые специальные углы и выполнять
исчисление со специальными связанными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах.Вот таблица
общих значений Производная синуса равна cos (x).
Антипроизводное синуса равно -cos (x).
Функция sine является нечетной функцией, для каждого действительного x, `sin (-x) = — sin (x)`.
Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало контрольной точки как точки симметрии. Калькулятор имеет решатель, который позволяет решить
уравнение с синусом
в форме cos (х) = а.
Расчеты для получения результата являются подробными, поэтому можно будет решать уравнения, такие как
`Sin (х) = 1 / 2`
или
`2 * Sin (х) = SQRT (2)`
с этапами расчета.
, чтобы дифференцировать функцию синуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции синуса Производное от sin (x) является производным (`sin (x)`) = `cos (x)` Антипроизводный калькулятор позволяет рассчитать антипроизводное функции синуса. An — производное от sin (x) — antiririvative (`sin (x)`) = `-cos (x)` Калькулятор пределов позволяет вычислять пределы функции синуса. Предел грех (х) является пределом (`грех (х)`) Функция , обратная функции sine, — это арксинус, отмеченный arcsin. Вот вопрос, который я однажды получил от читателя: Точно, что произойдет, когда я введу синус (или cos или tan и т.д. в этом отношении) угла в свой калькулятор? Я набираю его, и он волшебным образом дает мне ответ, число, которое по существу не связано с углом, который я ввел. Калькулятор просто считывает список, созданный людьми, которые использовали линейки для физического измерения расстояния на графике, или существует математическая функция, которая его определяет? A или компьютерная программа не считывают список, но используют алгоритм, который дает приблизительное значение для синуса заданного угла.Существует несколько таких алгоритмов, которые используют только четыре основные операции (+, -, ×, /), чтобы найти синус, косинус или тангенс заданного угла. Один из способов — взять определенное количество терминов (чем больше терминов вы берете, тем точнее приближение) из ряда Тейлора для синуса: sin x = x — x3 / 3! + x5 / 5! — x7 / 7! + …, где х в радианах. Например, чтобы узнать синус 23, сначала преобразуйте 23 в радианы, разделив его на 180, а затем умножив на π.Мы получаем 23/180 π = 0,401425727958696 ≈ 0,4014257, Затем используйте приведенную выше формулу для получения значения sin 0,4014257: Calculator даст SIN 23 = 0.390731128489274 поэтому формула получила это право в течение первых семи знаков после запятой (и существует даже оценку погрешности, которая сообщает вам об ошибке максимальной вы делаете, когда вы используете определенное количество терминов из серии Тейлор). Посмотрите, насколько близко многочлен, образованный из первых четырех членов ряда Тейлора, приближается к синусоиде около начала координат. На самом деле они выглядят одинаково на изображении, но мы знаем, что они не совсем одинаковые, просто очень-очень близко — даже приведенный выше расчет показывает, что Калькуляторы на самом деле не используют ряды Тейлора, а алгоритм CORDIC для поиска значений тригонометрических функций. Алгоритм Cordic основан на представлении об угле как о фазе комплексного числа в комплексной плоскости, а затем о вращении комплексного числа путем его умножения на последовательность постоянных значений. Для прямоугольного треугольника: Функция sine sin принимает угол θ и дает отношение противоположное гипотенуза Функция обратная синус sin-1 принимает соотношение напротив гипотенузы и дает угол θ И косинус и касательная следуют аналогичной идее. sin (35 °) = противоположно / гипотенуза = 2.8 / 4,9 = 0,57 … sin-1 (напротив / гипотенуза) = sin-1 (0,57 …) = 35 ° Синус, косинус и тангенс основаны на прямоугольном треугольнике Это очень похожие функции …
поэтому мы посмотрим на Sine Function, а затем на Inverse Sine, чтобы узнать, что это такое. The синус угла θ составляет: или проще: sin (θ) = противоположность / гипотенуза Используя этот треугольник (длины даны только до одного десятичного знака): sin (35 °) = противоположность / гипотенуза Функция синуса может помочь нам решить такие вещи: Мы знаем И мы хотим знать «д» (расстояние вниз) . Начать с: грех 39 ° = противоположность / гипотенуза грех 39 ° = д / 30 Spap Sides: d / 30 = sin 39 ° Используйте калькулятор, чтобы найти грех 39 °: d / 30 = 0.6293 … Умножьте обе стороны на 30: d = 0,6293… x 30 d = 18,88 до 2 десятичных знаков Глубина «d» составляет 18,88 м Но иногда нам нужно найти angle. Вот тут и появляется «Обратный синус». Отвечает на вопрос «какой из angle имеет синус, равный противоположному / гипотенузе?» Символ для обратного синуса — sin-1, а иногда arcsin. Мы знаем И мы хотим знать угол «а» Начните с: sin a = противоположность / hypotenuse грех = 18,88 / 30 Расчет 18,88 / 30: sin a 0,6293 … Что из angle имеет синус, равный 0,6293 …? Обратный синус: a = sin−1 (0.6293 …) Используйте калькулятор, чтобы найти sin−1 (0,6293 …): a ° = 39,0 ° (с 1 десятичным знаком) Угол «а» составляет 39,0 ° Синусоидальная функция: sin (30 °, ) = 0.5 Обратный синус: sin−1 (0.5) = 30 ° На своем калькуляторе попробуйте использовать sin, а затем sin-1, чтобы увидеть, что происходит Обратный синус показывает только один угол … но есть и другие углы, которые могут работать. На самом деле бесконечно много углов, потому что вы можете продолжать добавлять (или вычитать) 360 °: Помните это, потому что бывают моменты, когда вам действительно нужен другой угол! Синус угла θ: sin (θ) = противоположность / гипотенуза и обратный синус: sin-1 (напротив / гипотенуза) = θ Точно такая же идея, но с разными соотношениями сторон. Косинус угла θ: cos (θ) = Соседний / Гипотенуза и обратный косинус: cos-1 (соседний / гипотенуза) = θ cos a ° = Смежный / Гипотенуза cos a = 6750/8100 = 0,8333 … a ° = cos-1 (0.8333 …) = 33,6 ° (до 1 десятичного знака) Тангенс угла θ: tan (θ) = противоположный / соседний Так что обратный тангенс равен: tan-1 (напротив / рядом) = θ tan x ° = Противоположно / Смежно tan x ° = 300/400 = 0,75 x ° = tan-1 (0.75) = 36,9 ° (с точностью до 1 знака после запятой) Иногда sin-1 называется asin или arcsin И, наконец, вот графики синуса, обратного синуса, косинуса и обратного косинуса: Вы заметили что-нибудь о графиках? Здесь Cosine и Обратный косинус нанесены на тот же график: Это зеркальные изображения (примерно по диагонали) Но почему обратный косинус обрезается сверху и снизу (точки на самом деле не являются частью функции)…? , потому что быть функцией, он может дать только один ответ Но мы видели ранее, что бесконечно много ответов, и пунктирная линия на графике показывает это. Так да там are бесконечно много ответов … … но представьте, что вы вводите 0,5 в свой калькулятор, нажимаете cos-1, и это дает вам бесконечный список возможных ответов. |