Калькулятор смешанных чисел: Калькулятор рациональных выражений

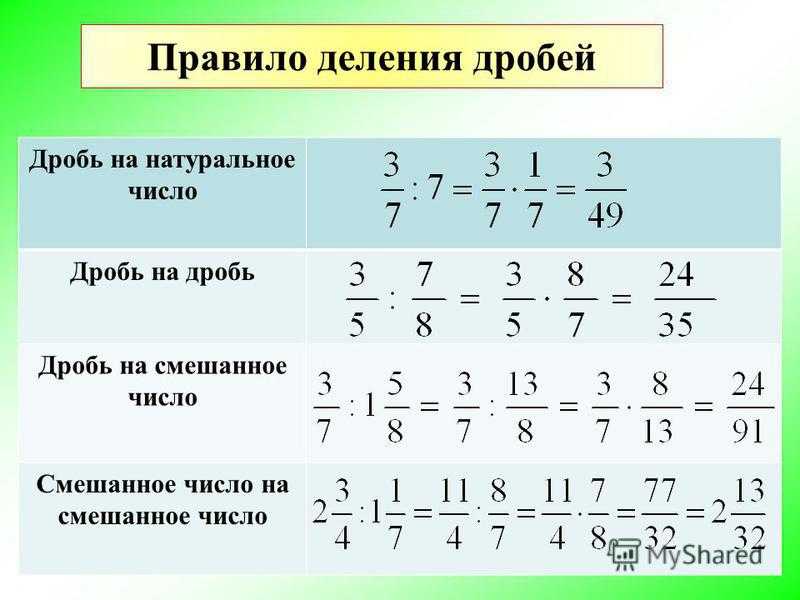
Инструменты и калькуляторы – Math

Miniwebtool

• — Трехсторонний процентный калькулятор.
• — Дробное сложение, вычитание, умножение и деление.
• — Вычисляет квадратный корень числа. Максимальная точность 1000 цифр.
• — Преобразование двоичных чисел в десятичные, шестнадцатеричные и т. д.
• — Вычисляет стандартное отклонение набора чисел.
• — Используйте квадратные уравнения для решения квадратных уравнений.
• — Вычисляет множители числа.
• — Преобразование шестнадцатеричных чисел в десятичные, двоичные и т. д.
• — Преобразование десятичной дроби в дробную.
• — Сгенерируйте список указанного количества простых чисел.
• — Рассчитайте необходимый размер выборки.
• — Выполнять вычисления сложения, вычитания, умножения и деления в экспоненциальной записи.
• — Двоичное сложение, вычитание, умножение и деление.
• — Рассчитать доверительные интервалы.
• — Вычисляет логарифм по основанию b числа x.
• — Вычисляет простую факторизацию числа.
• — Вычисляет наклон линии через две точки.
• — Рассчитать комбинацию.
• — Вычисляет кубический корень числа.
• — Упростите дроби до минимальных дробей.
• — Вычисляет наибольший общий делитель.
• — Сложение, вычитание, умножение и деление шестнадцатеричных чисел.
• — Найдите пропущенные значения пропорционально.
• — Вычисляет факториал неотрицательного целого числа.
• — Вычислите наименьшее общее кратное.
• — Вычислите процентное увеличение от одного числа к другому.
• — Вычислить перестановки.
• — Вычислите площадь круга.
• — Вычислить среднее значение любого набора чисел.
• — Вычисляет показатель степени (возведенный в степень n).
• — Преобразование из десятичного числа в десятичное.
• — Вычислите процентное изменение от старого значения к новому значению.
• — Преобразование римских цифр в стандартные цифры и наоборот.
• — Вычислите дисперсию любого набора чисел.
• — Преобразование десятичного числа в двоичное.
• — Преобразование десятичного числа в шестнадцатеричное
• — Рассчитайте соответствующие числа по золотому сечению.
• — Преобразование шестнадцатеричного числа в десятичное
• — Найдите пропущенные значения пропорционально.
• — Найдите форму пересечения наклона уравнения прямой.
• — Вычислите объем цилиндра.
• — Преобразование двоичного числа в десятичное.
• — Вычисляет длину гипотенузы прямоугольного треугольника.
• — Вычисляет медиану набора чисел.
• — Найдите середину между двумя точками.
• — Вычисляет антилог.
• — Преобразует целое число из одного основания в другое.
• — Выяснить, равны ли две дроби.
• — Вычисляет среднее значение набора чисел.
• — Вычисляет диапазон набора чисел.
• — преобразовать двоичное число в шестнадцатеричное
• — Вычислите площадь, периметр, диаметр или радиус круга.
• — Рассчитывает период полураспада экспоненциального распада.
• — Вычисляет логарифм по основанию 2 числа.
• — Вычислить среднее значение, медиану, моду и диапазон.
• — Создайте список квадратных чисел.
• — Вычисляет стандартную ошибку среднего.
• — Вычисляет межквартильный диапазон набора чисел.
• — Вычисляет натуральный логарифм числа.
• — Вычисляет коэффициент вариации для набора чисел.
• — Решите задачу об экспоненциальном росте.
• — преобразовать шестнадцатеричное число в двоичное
• — Выполняет арифметику по модулю над числами.
• — Вычисляет выборочное стандартное отклонение набора чисел.
• — Вычисляет выборочную дисперсию набора чисел.
• — Вычислите площадь трапеции.
• — Вычисляет сумму n-го члена и первых n членов арифметической прогрессии.
• — Выполнять сложение, вычитание, умножение и деление двух комплексных чисел.
• — Найдите середину между двумя точками.
• — Вычисляет процент уменьшения от одного числа до другого.
• — Вычисляет простой делитель числа.
• — Вычисляет первую квартиль, вторую квартиль и третью квартиль набора чисел.
• — Вычислите площадь, периметр и диагональ квадрата.
• — Вычислите площадь поверхности цилиндра.
• — Вычисляет общий делитель двух чисел.
• — Преобразование десятичного числа в восьмеричное.
• — Преобразовать градусы в радианы.
• — Вычисляет сумму n-го члена и первых n членов геометрической прогрессии.
• — Вычислите объем конуса.
• — Вычислите объем шара.
• — Преобразование двоичного числа в восьмеричное.
• — Вычислите биномиальные коэффициенты.
• — Вычисляет гамма-функцию.
• — Вычислить среднее геометрическое любого набора чисел.
• — Вычисляет золотой прямоугольник по длине одной грани.
• — Преобразование восьмеричных чисел в десятичные, двоичные и т. д.
• — Перевести радианы в градусы.
• — Вычислите площадь параллелограмма.
• — Вычисляет среднее абсолютное отклонение набора чисел.
• — Вычислить шаблон набора чисел.
• — Преобразование восьмеричного числа в десятичное число.
• — Вычисляет выборочное среднее для набора чисел.
• — Решите задачу о сложном росте.
• — преобразовать дробь в проценты
• — Вычисляет логарифм по основанию 10 числа.
• — Упростите любую дробь до такой степени, что ее нельзя будет уменьшить дальше.
• — Вычисляет сумму набора чисел.
• — Вычисляет сумму последовательных квадратов.
• — Вычисляет произведение набора чисел.
• — Вычислите объем куба.
• — Вычислите объем пирамиды.
• — Создайте список чисел куба.
• — Вычисляет функцию ошибки.
• — Решите задачу об экспоненциальном распаде.
• — Недостающие значения рассчитываются для завершения золотого сечения.
• — Создайте список чисел Фибоначчи.
• — Вычислите площадь поверхности конуса.
• — Выполнять побитовые и побитовые операции.
• — Сравните две дроби, чтобы определить, какая из них больше или меньше.
• — Восьмеричное сложение, вычитание, умножение и деление.
• — Преобразование восьмеричного числа в двоичное.
• — Вычисляет выбросы для набора чисел.
• — Вычисляет дисперсию совокупности набора чисел.
• — Вычисляет относительное стандартное отклонение набора чисел.
• — Вычисляет медианный диапазон набора чисел.
• — Вычисляет процентную ошибку.
• — Преобразование процентов в десятичные дроби.
• — Вычисляет стандартное отклонение генеральной совокупности набора чисел.
• — Вычислите площадь поверхности куба.
• — Вычислите площадь поверхности прямоугольной призмы.
• — Вычисляет среднее отклонение набора чисел.
• — Преобразование десятичных дробей в проценты.
• — Вычислите площадь, периметр и диагональ прямоугольника.
• — Преобразование экспоненциальной записи в обычную десятичную запись.
• — Преобразование шестнадцатеричного числа в восьмеричное.
• — Вычислите частное и остаток.
• — Сортировка чисел в порядке возрастания или убывания.
• — Вычисляет объем прямоугольной призмы.
• — Вычислите площадь эллипса.
• — Вычислите площадь равностороннего треугольника.
• — Вычисляет среднее арифметическое набора чисел.
• — Преобразование целого числа из одного основания в другое.
• — Найдите количество цифр в числе.
• — Вычисляет среднеквадратичное значение набора чисел.
• — Вычислите площадь сектора.
• — Вычислите периметр эллипса.
• — Преобразование восьмеричного числа в шестнадцатеричное.
• — Вычислите площадь поверхности шара.
• — Преобразование десятичной системы в экспоненциальное представление.
• — Вычисляет среднее гармоническое набора чисел.
• — Проверяет, является ли число простым.
• — Коэффициенты конверсии указаны в процентах.
• — Вычисляет сумму последовательных кубов.
• — Вычисляет бета-функцию.
• — Превратите дроби в смешанные числа.
• — Вычислите экспоненциальный интеграл.
• — Вычисляет дополнительную функцию ошибки.
• — Определить, делится ли число на другое число.
• — Разделите число на две части.
• — Сгенерируйте первые n простых чисел.
• — Вычисляет среднее абсолютное отклонение набора чисел.
• — Преобразование смешанных чисел в дроби.
• — Вычисляет межквартильное отклонение для набора чисел.
• — Вычисление куба и кубического корня числа.
• — Найдите минимальное и максимальное значения в наборе чисел.
• — Сгенерируйте первые n цифр числа e.
• — Сгенерируйте первые n цифр числа Пи.
• — Рассчитайте годовой процентный прирост.
• — Вычисляет сумму последовательных целых чисел.
• — Вычисляет объем эллипсоида.

Перевод дробных чисел из одной системы счисления в другую

РаботаИнженерныеКонвертеры

Перевод дробных чисел из одной системы счисления в другую

После того, как я сделал несколько калькуляторов для перевода между разными системами счисления — вот список от первой до последней версии, от самого простого к сложному: Перевод числа в другие системы счисления, Перевод из десятичной системы счисления, Перевод из одной системы счисления в другую — в комментариях стали периодически спрашивать — а что же, мол, дробные числа, как же их переводить? И когда спросили больше трех раз, я таки решил изучить этот вопрос.

Результатом стал калькулятор, который вы видите ниже, он умеет переводить и дробные числа в том числе. Как водится, для любознательных под калькулятором немного теории.

Перевод дробных чисел из одной системы счисления в другую

Исходное число

Исходное основание

Основание системы счисления исходного числа

Основание результата

Основание системы счисления переведенного числа

Точность вычисления

Знаков после запятой: 8

Переведенное число

 

Исходное число в десятичной системе счисления

 

Переведенное число в десятичной системе счисления

 

Погрешность перевода (в десятичном выражении)

 

Максимальная погрешность перевода (в десятичном выражении)

 

Теперь теория. Я, честно говоря, думал, что вопрос довольно сложный, но при ближайшем рассмотрении все оказалось проще простого. Надо было только держать в голове тот факт, что речь идет о позиционных системах счисления.
В чем тут суть? Рассмотрим на примере десятичного числа 6.125. Это дробное число в десятичной системе счисления представляется так:

Все просто, не так ли? Та же самая простота сохраняется и при записи дробного числа в любой другой системе счисления. Возьмем, например, горячо любимую каждым программистом двоичную систему и число, например, 110.001. Эта запись есть не что иное как

Да-да, число для примера было выбрано не просто так. То есть, 110.001 в двоичной системе есть 6.125 в десятичной. Принцип, я думаю, ясен.

Есть только одно но — все-таки из-за того, что здесь участвую дроби с разными знаменателями, не всегда одно и тоже число можно одинаково точно выразить в разных системах счисления. Что я имею в виду?

Возьмем, например, число . Отлично смотрится в десятичной системе счисления. Но вот если попробовать получить запись этого числа в двоичной системе счисления — будут проблемы. Попробуем, пока не устанем

Продолжать можно еще довольно долго, но уже сейчас видно, что 0.8 в десятичной системе это 0.11001100…(дальше очень много цифр) в двоичной. Если честно, то это периодическое число с перидом 1100, так что мы никогда не сможем выразить его точно в двоичной системе счисления. 110011001100… будет продолжаться до бесконечности.

Поэтому перевод дробного числа из одной системы счисления в другую чаще всего дает погрешность. Погрешность эта зависит от того, сколько разрядов мы используем для записи дробной части переведенного числа. Возьмем пример с числом 0.8 и используем для записи его двоичного представления шесть разрядов после запятой — 0.110011. Полученное число вовсе не 0.8, а 0.796875, разница при этом составляет 0.003125. Это и есть наша погрешность перевода десятичного числа 0.8 в двоичный вид при использовании шести разрядов после запятой.

Вес крайнего правого разряда (самого младшего разряда) называется разрешением (resolution) или точностью (precision), и определяет наименьшее неравное нулю число, которое может быть представлено данным числом разрядов. Для нашего примера это . При этом максимально возможная погрешность представления числа, как нетрудно сообразить, не превышает половины этого веса, или 0.0078125. Так что для 0.8 мы имеем еще и не самую плохую погрешность.

Вот, собственно, и все.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Перевод из одной системы счисления в другую
• • Перевод из десятичной системы счисления
• • Калькулятор с поддержкой разных систем счисления
• • Перевод числа в другие системы счисления
• • Дополнение числа
• • Раздел: Конвертеры ( 55 калькуляторов )

 #информатика #системасчисления дробные числа Информатика Конвертеры перевод из системы счисления системы счисления

 PLANETCALC, Перевод дробных чисел из одной системы счисления в другую

Timur2020-11-03 14:19:28

Калькулятор смешанных чисел

Ресурсы Живой конкурс Практика Проблемы Математические задачи Пошаговая работа Мгновенный математический решатель Создатель задач в классе Школы рядом с вами

Академики КГ 1 класс 2 класс 3 класс 4 класс 5-й класс 6 класс CCSS для математики

• Академики
• Ресурсы
• Безопасность
• Цены
• регистр
• Авторизоваться

1-й КЛАСС2-й КЛАСС3-й КЛАСС4-й КЛАСС5-й КЛАСС6-й КЛАСС

Сложение дробейВычитание дробейУмножение дробейДробное делениеОбратное числоДней между двумя датамиПродолжительность времениУпрощение отношенияЭквивалентные отношенияНайти отсутствующие в таблице пропорцийПроверить формы в пропорцияхСоотношенияРазмерыЗаполнить соотношение ПериметрLCMGCFLCDНайти LCM из GCFНайти GCF из LCMDecimal Преобразование в дробиПреобразование в десятичные числаУмножение целых чиселРазложение десятичных чиселРазложение десятичных чисел в словахВычитание нескольких десятичных знаковПриведение значения к десятичному Десятичное в месте значенийОкругление десятичного числаУпрощение числового выраженияАрифметика дробейАрифметика смешанных чиселПроверка високосного годаПреобразование дробей и смешанных чиселПреобразование обычных единиц измеренияDraw Bar Graph

Вход 1

Операторы

+-x÷

Вход 2

35/3 +48/5 = 154/15

показать тренировку

Вопрос:
3 5/3 + 4 8/5 = ?
Ответ:

Перевести смешанную дробь в дробь

3

53

=

(3 x 3) + 53

=

9 + 53

3 02 143

4

85

=

(4 x 5) + 85

=

20 + 85

=

285

143

2 +

0 0 5

8002 34 Найдите lcm для обоих знаменателей
LCM(3, 5) = 15
Приравнять все знаменатели

143

=

14 х 153 х 15

=

14 х 515

90 010203

0002 285

=

28 х 155 х 15

=

28 х 315

=

8415

7015

+

8415

=

70 + 8415

= 3

2 104003

002 3

53

+

4

85

=

154/ 15

Вышеуказанная дробь является нижней дробью. Итак, преобразуем дробь в смешанную дробь

15415

=

15015

+

415

= 10

03

035 9002

53

+

4

85

=

10

415

Калькулятор смешанных чисел, который показывает работу для нахождения суммы, сложения, разности, деления, произведения и частного с помощью таких операций два смешанных числа. Пошаговое вычисление помогает родителям помочь своим детям, учащимся 4, 5 или 6 класса, проверить работу и ответы на домашние задания по сложению, вычитанию, умножению и делению неправильных дробей, а также задачи по предварительной алгебре или числам и операциям — дроби (NF) единых базовых государственных стандартов (ОКГОС) по математике.

Калькулятор неправильных дробей для смешанных чисел

Создано Ханной Памула, доктором философии

Отзыв написан Домиником Черниа, доктором философии, и Джеком Боуотером

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Что такое неправильная дробь? Определение неправильной дроби
• Как из неправильной дроби сделать смешанное число?
• Калькулятор неправильных дробей для смешанных чисел — пример

Добро пожаловать в калькулятор неправильных дробей для смешанных чисел — инструмент, который позволяет вам мгновенно преобразовать неправильную дробь в смешанное число . В короткой статье ниже вы узнаете основы, например, что такое неправильная дробь, и пошаговые инструкции о том, как превратить неправильную дробь в смешанное число. Чтобы выполнить обратную задачу, посетите наш калькулятор смешанных чисел и неправильных дробей.

Поскольку вы уже здесь и смотрите 👀 на этот калькулятор неправильных дробей для смешанных чисел, мы подозреваем, что вас могут заинтересовать другие темы дробей. По этой причине мы создали всеобъемлющий калькулятор дробей, который может выполнять семь основных операций с дробями. Если вы просто хотите выполнить задачу, противоположную этому инструменту

Что такое неправильная дробь? Определение неправильной дроби

Говоря об определении неправильной дроби, нам нужно начать с небольшого уточнения — что такое дробь вообще?

💡 Дробь говорит нам, сколько равных частей целого у нас есть . Мы записываем его как отношение целых чисел, разделенных чертой или косой чертой.

Мы называем верхнее число числителем , а нижнее число знаменателем .

Итак, в приведенном выше примере у нас есть 1 часть из 6 — 1/6 читается как одна шестая.

Теперь мы можем вернуться к нашему центральному вопросу: что такое неправильная дробь? Согласно определению:

💡 Дробь неправильная, если числитель больше (или равен) знаменателю.

Поскольку числитель больше или равен нижнему числу, мы иногда называем неправильную дробь тяжелой дробью сверху . Примеры неправильных дробей:

• 🍰 10 кусочков торта, когда каждый торт разрезали на 6 кусочков;

• 🍫 8 рядов шоколадки, когда вся шоколадка 5 рядов;

• 🍊 21 часть апельсина, если разрезать каждый апельсин на 8 равных частей.

Как из неправильной дроби сделать смешанное число?

Итак, что означает преобразование неправильных дробей в смешанные числа? Всего смешанная дробь — это просто еще один способ выражения неправильной дроби . Но как это работает?

Посмотрите еще раз на предыдущее изображение. В каждом из этих примеров у нас есть более одного целого, верно? Так, например, вместо того, чтобы говорить, что у нас есть 8 рядов шоколада (и в каждой плитке по 5 рядов), мы могли бы сказать: «Эй, у меня есть одна целая плитка шоколада и еще 3 части из 5». неправильные дроби в смешанные числа работает!

Давайте шаг за шагом рассмотрим наш пример, чтобы увидеть, как превратить неправильную дробь в смешанное число:

1. Разделите числитель на знаменатель (верхнее число на нижнее).

   Если вы разделите 8 на 5, вы получите частное (целое число) и остаток:

   ⁸⁄₅ = 1 остаток 3 = 1 R 3

   (узнайте, как это сделать с помощью калькулятора остатка)

2. Найти целую часть смешанного числа — взять целое число из деления:

   1

3. Найдите дробную часть смешанного числа — остаток от деления будет новым числителем, а знаменатель останется прежним:

   ⅗

4. Чтобы получить смешанное число, сложите числа :

   1 ⅗

Вот и все, ⁸⁄₅ = 1 ⅗

Иногда нужно также упростить смешанную дробь, но здесь это не так.