1 упростите выражение
Вы искали 1 упростите выражение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 упростите выражение, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 упростите выражение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 упростите выражение,2 упростите выражение,2 упростить выражение 1 2,3 4x 2 5 упростить,3 упростить выражение,4 упростите выражение,4 упростить выражение,7 класс алгебра упростить выражение онлайн калькулятор,x y x упростить,алгебра как упростить выражение,алгебра упрощение выражений,алгебраическое выражение упростить,вы упростите,выражение онлайн,выражение решить онлайн,выражения решение онлайн,выразить из формулы онлайн,выразить онлайн,выразить онлайн переменную,выразить формулу онлайн,дроби упростить выражение,дробное выражение как упростить,как правильно упрощать выражения,как решать упростите выражение,как решать упростить выражение,как упростить,как упростить выражение,как упростить выражение алгебра,как упростить выражение дробное,как упростить выражения,как упростить дробное выражение,как упростить пример,как упростить уравнение,как упрощать,как упрощать выражение,как упрощать выражения,как упрощать уравнения,калькулятор алгебраических выражений,калькулятор алгебраических выражений онлайн калькулятор,калькулятор алгебраических выражений с буквами,калькулятор буквенных выражений,калькулятор буквенных выражений онлайн,калькулятор выражений,калькулятор выражений с буквами,калькулятор для упрощения выражений,калькулятор для упрощения выражений с дробями,калькулятор дробей упрощение выражений,калькулятор онлайн буквенных выражений,калькулятор онлайн подобные слагаемые,калькулятор онлайн упростить выражение,калькулятор онлайн упрощение выражений,калькулятор онлайн упрощение дробных выражений,калькулятор онлайн упрощения выражений,калькулятор подобных слагаемых,калькулятор преобразования выражений,калькулятор раскрытие скобок,калькулятор раскрытие скобок онлайн,калькулятор раскрытия скобок онлайн,калькулятор рациональных выражений с решением онлайн,калькулятор тождественных выражений,калькулятор упростите выражение,калькулятор упростите выражение с дробями,калькулятор упростите выражение с корнями,калькулятор упростить,калькулятор упростить выражение,калькулятор упростить выражение онлайн с дробями,калькулятор упростить выражение онлайн с дробями с буквами,калькулятор упрощение выражений,калькулятор упрощение выражений дробей,калькулятор упрощение выражений онлайн,калькулятор упрощение выражений с дробями,калькулятор упрощение выражений со степенями онлайн,калькулятор упрощение многочлена онлайн,калькулятор упрощения,калькулятор упрощения выражений,калькулятор упрощения выражений онлайн,калькулятор упрощения выражений онлайн калькулятор,калькулятор упрощения выражений с буквами,калькулятор упрощения выражений с буквами и степенями и дробями,калькулятор упрощения выражений с дробями,калькулятор упрощения выражений с дробями и степенями и буквами,калькулятор упрощения выражений с дробями и степенями и с буквами,калькулятор упрощения выражения,калькулятор упрощения дробей с буквами и степенями,математика выражение упростить,онлайн выражение,онлайн выражение формул,онлайн выразить,онлайн калькулятор буквенных выражений,онлайн калькулятор преобразование рациональных выражений,онлайн калькулятор раскрытие скобок,онлайн калькулятор раскрытия скобок,онлайн калькулятор спростить вираз,онлайн калькулятор упростите выражение,онлайн калькулятор упростить выражение,онлайн калькулятор упрощение выражений,онлайн калькулятор упрощение выражений с дробями,онлайн калькулятор упрощение выражений со степенями,онлайн калькулятор упрощение дробных выражений,онлайн калькулятор упрощение многочлена,онлайн калькулятор упрощения выражений,онлайн преобразование выражений,онлайн преобразование тригонометрических выражений,онлайн преобразователь в многочлен,онлайн преобразователь формул,онлайн раскройте скобки,онлайн раскрытие скобок,онлайн решение алгебраических выражений,онлайн решение выражений,онлайн решение выражения,онлайн решение рациональных выражений,онлайн решения выражений,онлайн сокращение выражений,онлайн сокращение многочленов,онлайн упроститель выражений,онлайн упростить,онлайн упростить выражение со степенями,онлайн упростить дробное выражение,онлайн упрощение выражений с дробями,онлайн упрощение выражений с корнями,онлайн упрощение выражений со степенями,онлайн упрощение дробных выражений,онлайн упрощение многочленов,онлайн упрощения выражений,подобные слагаемые калькулятор онлайн,подобные слагаемые онлайн калькулятор,преобразование выражений онлайн,преобразование иррациональных выражений онлайн калькулятор,преобразование рациональных выражений калькулятор онлайн,преобразование рациональных выражений онлайн калькулятор,преобразование формул онлайн,преобразования выражений калькулятор,преобразовать в многочлен выражение онлайн,преобразовать выражение в многочлен онлайн,преобразовать выражение онлайн,преобразовать многочлен в выражение онлайн,преобразуйте в дробь выражение онлайн,преобразуйте в многочлен выражение онлайн калькулятор,преобразуйте дробь в выражение онлайн,приведи подобные слагаемые онлайн калькулятор,пример упростить,пример упростить выражение,примеры упростите выражение,примеры упрощение выражений,примеры упрощения,раскрытие скобок калькулятор,раскрытие скобок калькулятор онлайн,раскрытие скобок онлайн,раскрытие скобок онлайн калькулятор,раскрытия скобок онлайн калькулятор,раскрыть скобки онлайн,раскрыть скобки онлайн калькулятор,рациональных выражений онлайн калькулятор с решением,решение алгебраических выражений онлайн,решение выражений,решение выражений онлайн,решение выражения,решение выражения онлайн,решение онлайн алгебраических выражений,решение онлайн выражения,решение примеров на упрощение выражений,решение упростите выражение,решения выражений онлайн,решите выражение,решить выражение,решить выражение онлайн,решить выражение онлайн со степенями,решить онлайн выражение,сократить выражение,сократить выражение онлайн,сократить выражение онлайн с подробным решением,сократить многочлен онлайн,сократить онлайн выражение,сократить уравнение онлайн,сокращение выражений,сокращение выражений онлайн,сокращение многочленов онлайн,сокращение уравнений онлайн,способы упрощения выражений,спростити вираз,спростити вираз онлайн,спростити вираз онлайн калькулятор,спростити вираз приклади,спростить вираз,спростить вираз онлайн калькулятор,спростіть вираз,спрощення виразів,упрости,упрости выражение,упрости выражения,упростите,упростите 3 4х 2 5,упростите алгебраическое выражение,упростите вы,упростите выражение,упростите выражение 1,упростите выражение 2,упростите выражение 2 3x 2,упростите выражение 3,упростите выражение a,упростите выражение x,упростите выражение x 2 x 8 x,упростите выражение x 3 x 4,упростите выражение а,упростите выражение дроби,упростите выражение дробное,упростите выражение дробь,упростите выражение и,упростите выражение калькулятор,упростите выражение калькулятор онлайн,упростите выражение калькулятор онлайн с решением,упростите выражение калькулятор с дробями,упростите выражение калькулятор с дробями и степенями,упростите выражение калькулятор с степенями,упростите выражение калькулятор с степенями и дробями,упростите выражение онлайн,упростите выражение онлайн калькулятор,упростите выражение онлайн калькулятор с решением,упростите выражение онлайн с дробями,упростите выражение онлайн с дробями и степенями,упростите выражение онлайн с дробями и степенями с решением,упростите выражение онлайн с корнями,упростите выражение примеры,упростите выражение решение,упростите выражение с дробями,упростите выражение с дробями онлайн,упростите выражение с корнями калькулятор,упростите выражение с корнями онлайн,упростите выражения,упростите выражения а,упростите выражения калькулятор,упростите выражения калькулятор онлайн,упростите выражения онлайн,упростите дробное выражение,упростите уравнение,упростите уравнение онлайн,упроститель выражений,упроститель выражений онлайн,упростить 2x 4 6x 6,упростить x 2 x,упростить алгебраическое выражение,упростить векторное выражение онлайн,упростить выражение,упростить выражение 3,упростить выражение алгебра как,упростить выражение алгебраическое,упростить выражение дроби,упростить выражение дробное,упростить выражение дробное онлайн,упростить выражение дробное онлайн калькулятор с решением,упростить выражение как решать,упростить выражение калькулятор,упростить выражение калькулятор онлайн,упростить выражение онлайн,упростить выражение онлайн калькулятор,упростить выражение онлайн калькулятор с дробями,упростить выражение онлайн калькулятор с дробями и буквами,упростить выражение онлайн калькулятор с корнями,упростить выражение онлайн калькулятор с решением,упростить выражение онлайн калькулятор с решением с дробями,упростить выражение онлайн калькулятор с решением с дробями и буквами,упростить выражение онлайн калькулятор с решением с дробями и корнями,упростить выражение онлайн калькулятор с решением с корнями,упростить выражение онлайн калькулятор с решением со степенями,упростить выражение онлайн калькулятор со степенями,упростить выражение онлайн калькулятор со степенями с решением,упростить выражение онлайн с дробями,упростить выражение онлайн с дробями буквами и степенями онлайн,упростить выражение онлайн с дробями и буквами,упростить выражение онлайн с дробями и буквами 8 класс,упростить выражение онлайн с дробями и буквами калькулятор,упростить выражение онлайн с дробями и степенями,упростить выражение онлайн с дробями калькулятор,упростить выражение онлайн с корнями,упростить выражение онлайн с корнями и степенями,упростить выражение онлайн с корнями калькулятор,упростить выражение онлайн с решением,упростить выражение онлайн со степенями,упростить выражение примеры,упростить выражение с дробями,упростить выражение с дробями и буквами,упростить выражение с дробями и буквами 8 класс онлайн,упростить выражение с дробями и буквами онлайн калькулятор,упростить выражение с дробями и с степенями онлайн,упростить выражение с дробями и степенями онлайн,упростить выражение с дробями онлайн,упростить выражение с дробями онлайн калькулятор,упростить выражение с дробями онлайн калькулятор с решением,упростить выражение с корнями онлайн,упростить выражение с корнями онлайн калькулятор,упростить выражение с корнями онлайн калькулятор с решением,упростить выражение с корнями онлайн калькулятор с решением с дробями,упростить выражение со степенями онлайн,упростить выражение со степенями онлайн калькулятор,упростить выражение со степенями онлайн калькулятор с решением,упростить выражение что такое,упростить выражения,упростить выражения онлайн,упростить дробное выражение,упростить дробное выражение онлайн,упростить дробное выражение онлайн калькулятор с решением,упростить дробь онлайн с буквами,упростить дробь онлайн с буквами и степенями,упростить дробь с буквами онлайн,упростить как,упростить калькулятор,упростить многочлен онлайн,упростить онлайн,упростить онлайн выражение с корнями,упростить онлайн выражение со степенями,упростить тригонометрическое выражение онлайн,упростить тригонометрическое выражение онлайн калькулятор с решением,упростить уравнение,упростить уравнение онлайн,упростить уравнение онлайн с решением,упрощать как,упрощение алгебраические выражения,упрощение алгебраических выражений,упрощение выражений,упрощение выражений алгебра,упрощение выражений дробей,упрощение выражений дробей калькулятор,упрощение выражений дробных,упрощение выражений дробных онлайн,упрощение выражений калькулятор,упрощение выражений калькулятор онлайн,упрощение выражений калькулятор онлайн с корнями,упрощение выражений онлайн,упрощение выражений онлайн калькулятор,упрощение выражений онлайн калькулятор с дробями,упрощение выражений онлайн калькулятор с решением,упрощение выражений онлайн калькулятор со степенями,упрощение выражений онлайн с дробями,упрощение выражений онлайн с корнями,упрощение выражений онлайн с решением,упрощение выражений примеры,упрощение выражений с дробями,упрощение выражений с дробями калькулятор,упрощение выражений с дробями онлайн,упрощение выражений с дробями онлайн калькулятор,упрощение выражений с корнями онлайн,упрощение выражений с решением онлайн,упрощение выражений со степенями калькулятор онлайн,упрощение выражений со степенями онлайн калькулятор,упрощение дробей онлайн с буквами,упрощение дробей онлайн со степенями и буквами,упрощение дробей с буквами онлайн,упрощение дробных выражений,упрощение дробных выражений калькулятор онлайн,упрощение дробных выражений онлайн,упрощение дробных выражений онлайн калькулятор,упрощение корней онлайн,упрощение многочленов онлайн,упрощение онлайн,упрощение тригонометрических выражений онлайн,упрощение уравнений,упрощение уравнений онлайн,упрощение уравнения,упрощения,упрощения выражений,упрощения выражений онлайн калькулятор,упрощения выражений примеры,упрощения выражения калькулятор,формула упрощения выражения,формулы для упрощения выражений,формулы упрощения,формулы упрощения выражений,формулы упрощения выражения,что такое упростить выражение.
Где можно решить любую задачу по математике, а так же 1 упростите выражение Онлайн?
Решить задачу 1 упростите выражение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Сокращение обыкновенных дробей. Онлайн калькулятор
Сокращение дроби — это замена данной дроби, на равную ей дробь, у которой числитель и знаменатель меньше, чем у данной дроби.
Сокращение дроби выполняется путём деления числителя и знаменателя на одно и то же число.
Сократить можно только такую дробь, у которой члены имеют какой-нибудь общий делитель, помимо единицы.
Например, дробь можно сократить, а дробь нельзя, так как у первой дроби числитель и знаменатель имеют общие делители помимо единицы (это 2 и 4), а числитель и знаменатель второй дроби не имеют никакого общего делителя, кроме единицы.
Дробь, которую нельзя сократить, называется несократимой дробью.
Сокращение можно произвести или постепенно или сразу, выполнив деление членов дроби на НОД.
При постепенном сокращении дробь сокращают более одного раза. Сначала подбирают наименьший общий делитель (кроме единицы) для обоих членов дроби и сокращают дробь на него. Полученную после сокращения дробь, если можно, сокращают таким же путём снова и такое постепенное сокращение продолжают до тех пор, пока не получится несократимая дробь. 3
3
Формулы возведения выражения больше трех можно при помощи треугольника Паскаля.
Источники:
- формула раскрытия скобок
Заключенные в скобки математические действия могут содержать переменные и выражения разной степени сложности. Для перемножения таких выражений придется искать решение в общем виде, раскрывая скобки и упрощая полученный результат. Если же в скобках содержатся операции без переменных, только с численными значениями, то раскрывать скобки не обязательно, так как при наличии компьютера его пользователю доступны весьма значительные вычислительные ресурсы – проще воспользоваться ими, чем упрощать выражение.
Инструкция
Перемножайте последовательно каждое (или уменьшаемое с ), содержащееся в одной скобке, на содержимое всех остальных скобок, если требуется получить результат в общем виде. Например, пусть исходное выражение записано так: (5+x)∗(6-х)∗(x+2). Тогда последовательное перемножение (то есть раскрытие скобок) даст следующий результат: (5+x)∗(6-х)∗(x+2) = (5∗6-5∗х)∗(5∗x+5∗2) + (6∗x-х∗x)∗(x∗x+2∗x) = (5∗6∗5∗x+5∗6∗5∗2) — (5∗х∗5∗x+5∗х∗5∗2) + (6∗x∗x∗x+6∗x∗2∗x) — (х∗x∗x∗x+х∗x∗2∗x) = 5∗6∗5∗x + 5∗6∗5∗2 — 5∗х∗5∗x — 5∗х∗5∗2 + 6∗x∗x∗x + 6∗x∗2∗x — х∗x∗x∗x — х∗x∗2∗x = 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³.
Упрощайте после результат, сокращая выражения. Например, полученное на предыдущем шаге выражение можно упростить таким образом: 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³ = 100∗x + 300 — 13∗x² — 8∗x³ — x∗x³.
Воспользуйтесь калькулятором, если требуется перемножить икс равен 4.75, то есть (5+4.75)∗(6-4.75)∗(4.75+2). Для вычисления этого значения перейдите на сайт поисковика Google или Nigma и введите выражение в поле запроса в его исходном виде (5+4.75)*(6-4.75)*(4.75+2). Google покажет 82.265625 сразу, без нажатия кнопки, а Nigma нуждается в отправке данных на сервер нажатием кнопки.
П
родолжаю цикл методических статей на тему преподавания. Пришло время рассмотреть особенности индивидуальной работы репетитора по математике с учащимися 7-х классов . С великим удовольствием поделюсь своими соображениями о формах подачи одной из важнейших тем курса алгебры в 7 классе — «раскрытие скобок». Дабы не пытаться объять необъятное, остановимся на ее начальной ступени и разберем методику работы репетитора с умножением многочлена на многочлен. Как репетитор по математике действует в сложных ситуациях, когда слабый ученик не воспринимает классическую форму объяснения? Какие задания нужно готовить для сильного семиклассника? Рассмотрим эти и другие вопросы.
С великим удовольствием поделюсь своими соображениями о формах подачи одной из важнейших тем курса алгебры в 7 классе — «раскрытие скобок». Дабы не пытаться объять необъятное, остановимся на ее начальной ступени и разберем методику работы репетитора с умножением многочлена на многочлен. Как репетитор по математике действует в сложных ситуациях, когда слабый ученик не воспринимает классическую форму объяснения? Какие задания нужно готовить для сильного семиклассника? Рассмотрим эти и другие вопросы.
Казалось бы, ну что здесь сложного? «Скобки — это проще простого», — скажет любой отличник. «Есть распределительный закон и свойства степеней для работы с одночленами, общий алгоритм для любого количества слагаемых. Умножай каждое на каждое и приводи подобные». Однако, не все так просто в работе с отстающими. Вопреки стараниям репетитора по математике, учащиеся умудряются допускать ошибки самого разного калибра даже в простейших преобразованиях. Характер ошибок поражает своей разноплановостью: от мелких пропусков букв и знаков, до серьезных тупиковых «стоп-ошибок».
Что мешает школьнику правильно выполнить преобразования? Почему возможно непонимание?
Индивидуальных проблем существует огромное множество и одним из главных препятствий на пути усвоения и закрепления материала является затруднения в своевременном и быстром переключении внимания, сложность в обработке большого объема информации. Возможно, кому-то покажется странным, что я говорю о большом объеме, но слабому ученику 7 класса может не хватить ресурсов памяти и внимания даже для четырех слагаемых. Мешают коэффициенты, переменные, степени (показатели). Ученик путает очередность операций, забывает какие одночлены уже перемножены, а какие остались не тронутыми, не может вспомнить как их умножают и т. д.
Числовой подход репетитора по математике
Конечно же, нужно начинать с объяснений логики построения самого алгоритма. Как это сделать? Нужно поставить задачу: как изменить порядок действий в выражении , чтобы не поменялся результат? Я довольно часто привожу примеры, объясняющие работу тех или иных правил, на конкретных числах. А уже затем заменяю их буквами. Техника использования числового подхода будет описана ниже.
А уже затем заменяю их буквами. Техника использования числового подхода будет описана ниже.
Проблемы мотивации .
В начале урока репетитору по математике трудно собрать ученика, если он не понимает актуальности изучаемого. В рамках программы за 6 — 7 класс сложно найти примеры использования правила умножения многочленов. Я бы сделал упор на необходимость учиться менять порядок действий в выражениях То, что это помогает решать задачи, ученик должен знать по опыту сложения подобных слагаемых. Ему же приходилось их складывать в при решении уравнений. Например, в 2х+5х+13=34 он использует, что 2х+5х=7х. Репетитор по математике просто должен акцентировать на этом внимание школьника.
Учителя математики часто называют прием раскрытия скобок правилом «фонтанчика» .
Этот образ хорошо запоминается и его обязательно нужно использовать. Но как это правило доказывается? Напомним классическую форму, использующую очевидные тождественные преобразования:
(a+b)(c+d)=(a+b) c+(a+b) d=ac+bc+ad+bd
Репетитору по математике трудно что-либо здесь комментировать. Буквы говорят сами за себя. Да и не нужны сильному ученику 7 класса подробные объяснения. Однако, что делать со слабым, который в упор не видит в этой «буквенной мешанине» какого-либо содержания?
Основной проблемой, мешающей восприятию классического математического обоснования «фонтанчика», является непривычная форма записи первого множителя. Ни в 5 классе, ни 6 классе школьнику не приходилось перетаскивать первую скобку к каждому слагаемому второй. Дети имели дело только с числами (коэффициентами), расположенными, чаще всего, слева от скобок, например:
К окончанию 6 класса у школьника формируется визуальный образ объекта – определенное сочетание знаков (действий), связанных со скобками. И любое отклонение от привычного вида в сторону чего-то нового может дезориентировать семиклассника. Именно визуальный образ пары «число+скобка» репетитор по математике берет в оборот при объяснениях.
Можно предложить следующее объяснение. Репетитор рассуждает: «Если бы перед скобкой стояло какое-нибудь число, например 5, то смогли бы мы изменить порядок действий в этом выражении? Конечно. Тогда сделаем это . Подумай, изменится ли его результат, если вместо числа 5 мы вписать сумму 2+3, заключенную в скобки? Любой ученик скажет репетитору: «Какая разница, как писать: 5 или 2+3». Прекрасно. Получится запись . Репетитор по математике берет небольшую паузу, чтобы ученик зрительно запомнил картинку-образ объекта. Затем обращает его внимание на то, что скобка, как и число, «распределилась» или «прыгнула» к каждому слагаемому. Что это означает? Это означает, что данную операцию можно выполнять не только с числом, но и со скобкой. Получились две пары множителей и . С ними большая часть учеников легко справляется самостоятельно и выписывает репетитору результат . Важно сопоставить получившиеся пары с содержанием скобок 2+3 и 6+4 и станет понятно как они открываются.
Если необходимо, то после примера с числами репетитор по математике проводит буквенное доказательство. Оно оказывается легкой прогулкой по тем же самым частям предыдущего алгоритма.
Формирование навыка раскрытия скобок
Формирование навыка умножения скобок — один из важнейших этапов работы репетитора по математике с темой. И даже более важный чем этап объяснения логики правила «фонтанчика». Почему? Обоснования преобразований забудутся уже на следующий день, а навык, если он вовремя сформирован и закреплен, останется. Ученики выполняют операцию механически, как будто извлекают из памяти таблицу умножения. Этого и нужно добиваться. Почему? Если каждый раз при раскрытии скобок школьник будет вспоминать о том, почему раскрывается так, а не иначе, он забудет о задаче, которую решает. Именно поэтому оставшееся время урока репетитор по математике бросает на то, чтобы трансформировать понимание в механическое запоминание. Эта стратегия часто используется и в других темах.
Как репетитору сформировать у школьника навык раскрытия скобок? Для этого ученик 7 класса должен выполнить ряд упражнений в достаточном для закрепления количестве. При этом возникает другая проблема. Слабый семиклассник не справляется с возросшим количеством преобразований. Пусть даже мелких. И ошибки сыплются одна за другой. Что должен предпринять репетитор по математике? Во-первых, нужно рекомендовать подрисовывать стрелки от каждого слагаемого к каждому. Если ученик очень слабый и не способен быстро переключаться с одного вида работы на другой, теряет концентрацию при выполнении несложных команд преподавателя, то репетитор по математике сам рисует эти стрелки. Причем не все сразу. Сначала репетитор соединяет первое слагаемое левой скобки с каждым слагаемым правой скобки и просит выполнить соответствующее умножение. Только после этого стрелки направляются от второго слагаемого в ту же правую скобку. Иными словами репетитор разделяет процесс на два этапа. Лучше выдерживать небольшую временную паузу (5-7 секунд) между первой и второй операцией.
При этом возникает другая проблема. Слабый семиклассник не справляется с возросшим количеством преобразований. Пусть даже мелких. И ошибки сыплются одна за другой. Что должен предпринять репетитор по математике? Во-первых, нужно рекомендовать подрисовывать стрелки от каждого слагаемого к каждому. Если ученик очень слабый и не способен быстро переключаться с одного вида работы на другой, теряет концентрацию при выполнении несложных команд преподавателя, то репетитор по математике сам рисует эти стрелки. Причем не все сразу. Сначала репетитор соединяет первое слагаемое левой скобки с каждым слагаемым правой скобки и просит выполнить соответствующее умножение. Только после этого стрелки направляются от второго слагаемого в ту же правую скобку. Иными словами репетитор разделяет процесс на два этапа. Лучше выдерживать небольшую временную паузу (5-7 секунд) между первой и второй операцией.
1) Один набор стрелок нужно рисовать над выражениями, а другой под ними.
2) Важно пропускать между строчками хотя бы пару клеток . Иначе запись будет очень плотной, а стрелки залезут не только на предыдущую строку, но и смешаются со стрелками от следующего упражнения.
3) В случае умножения скобок в формате 3 на 2 стрелки проводятся от короткой скобки к длинной. Иначе этих «фонтанчиков» будет не два, а три. Реализация третьего заметно усложняется в виду отсутствия для стрелок свободного пространства.
4) стрелки всегда направляются из одной точки. Один мой ученик все время порывался их поставить рядом и вот, что у него получалось:
Такое расположение не позволяет выделять и фиксировать текущее слагаемое, с которым ученик работает на каждом из этапов.
Работа пальцев репетитора
4) Для удержания внимания на отдельной паре умножаемых слагаемых, репетитор по математике прикладывает к ним два пальца. Это надо делать так, чтобы не закрывать ученику обзор. Для наиболее невнимательных школьников можно использовать метод «пульсации». Репетитор по математике подводит первый палец к началу стрелки (к одному из слагаемых) и фиксирует его, а вторым «стучит» по ее концу (по второму слагаемому). Пульсация помогает собрать внимание на том слагаемом, на которое ученик умножает. После того, как выполнено первое умножение на правую скобку, репетитор по математике говорит: «Теперь работаем с другим слагаемым». Репетитор передвигает к нему «неподвижный палец», а «пульсирующим» пробегает по слагаемым из другой скобки. Пульсация работает словно «поворотник» в автомобиле и позволяет собирать внимание рассеянного ученика на проводимой им операции. Если ребенок пишет мелко, то вместо пальцев используются два карандаша.
Пульсация помогает собрать внимание на том слагаемом, на которое ученик умножает. После того, как выполнено первое умножение на правую скобку, репетитор по математике говорит: «Теперь работаем с другим слагаемым». Репетитор передвигает к нему «неподвижный палец», а «пульсирующим» пробегает по слагаемым из другой скобки. Пульсация работает словно «поворотник» в автомобиле и позволяет собирать внимание рассеянного ученика на проводимой им операции. Если ребенок пишет мелко, то вместо пальцев используются два карандаша.
Оптимизация повторения
Как и при изучении любой другой темы курса алгебры умножение многочленов можно и нужно интегрировать с ранее пройденным материалом. Для этого репетитор по математике использует специальные задания-мостики, позволяющие найти применение изучаемого в различных математических объектах. Они не только соединяют темы в единое целое, но и весьма эффективно организуют повторение всего курса математики. И чем больше мостиков построит репетитор, тем лучше.
Традиционно в учебниках алгебры для 7 класса расскрытие скобок интегрируется с решением линейных уравнений. В конце cписка номеров всегда имеются задания такого порядка: решить уравнение . При раскрытии скобок квадраты сокращаются и уравнение легко решается средствами 7 класса. Однако, почему-то про построение графика линейной функции авторы учебников благополучно забывают. Дабы исправить этот недостаток я бы посоветовал репетиторам по математике включать скобоки в аналитические выражения линейных функций, например . На таких упражнениях ученик не только тренирует навыки проведения тождественных преобразований, но еще и повторяет графики. Можно попросить найти точку пересечения двух «монстров», определить взаимное расположение прямых, найти точки их пересечения с осями и т.д.
Колпаков А.Н. Репетитор по математике в Строгино. Москва
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
Раскрыть скобки означает избавить выражение от этих скобок.
Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.
И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).
Правило раскрытия скобок при сложении
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.
2 + (7 + 3) = 2 + 7 + 3
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.
Пример. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.
2 − (7 + 3) = 2 − (+ 7 + 3)
При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.
2 − (+ 7 + 3) = 2 − 7 − 3
Раскрытие скобок при умножении
Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.
Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.
(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5
На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Раскрываем скобки при делении
Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.
Пример. (9 + 6) : 3=9: 3 + 6: 3
Как раскрыть вложенные скобки
Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.
При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть.
Пример. 12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Калькулятор полей
Кнопка Калькулятор полей в таблице атрибутов позволяет осуществлять расчёты на основе существующих значений атрибутов или заданных функций, например для расчёта длины или площади геометрических объектов. Результаты могут быть записаны в новую колонку атрибутов или использоваться для обновления значений существующей колонки.
Прежде чем нажать иконку «Калькулятора полей» (см. figure_attributes_3), необходимо перевести слой в режим редактирования. В появившемся диалоговом окне сначала необходимо выбрать одну из опций: «Обновить существующее поле», «Обновить только выбранные объекты» или создать «Новое поле» таблицы атрибутов, куда будут добавлены результаты вычислений.
Figure Attributes 3:
Калькулятор полей
Чтобы добавить новое поле, необходимо указать его имя, тип (целое число (integer), десятичное (real) или текст (string)), размер, и точность (только для десятичного числа), см. figure_attributes_3. Например, если задать размер поля, равный 10, а точность 3, то это будет означать, что в поле может быть записано шестизначное число, десятичная запятая и 3 знака после запятой, определяющие точность.
Секция Функции содержит все доступные операторы, а также поля и значения. Описание функции отображается в поле Описание функции. В поле Выражение отображается выражение, составленое из элементов группы Функции. Наиболее часто используемые операторы вынесены на отдельную панель Операторы.
Описание функции отображается в поле Описание функции. В поле Выражение отображается выражение, составленое из элементов группы Функции. Наиболее часто используемые операторы вынесены на отдельную панель Операторы.
Выберите раздел Поля и значения в списке Функции чтобы увидеть список имеющихся атрибутов. Для добавления атрибута в поле “Выражение дважды щелкните по его имени в списке Поля и значения. В общем случае вы можете использовать разные поля, функции и величины при составлении выражения. Чтобы просмотреть значения поля, выделите поле в списке, затем вызовите конекстное меню и воспользуйтесь одним из вариантов Загрузить все уникальные значения или Загрузить 10 уникальных значений. Справа появится поле Значения полей, заполненное значениями. Чтобы добавить значение в поле Выражения, сделайте двойной щелчок по нему в списке Значения полей.
Группы Операторы, Функции, Преобразования, Строковые, Геометрические и Записи предоставляют различные функции. В группе Операторы находятся арифметические и логические операторы. В Функции — математические функции. Группа Преобразования содержит функции преобразования типов данных друг в друга. Раздел Строковые предоставляет функции обработки строк, а группа Геометрические — функции для работы с геометрией объекта. И, наконец, группа Записи содержит функции для нумерации записей таблицы. Чтобы добавить функцию в поле Выражение дважды щелкните по её имени в списке.
Приведём небольшой пример использования калькулятора поле». Рассмотрим процесс расчёта длины объектов слоя railroads из демонстрационного набора данных QGIS:
Добавьте shape-файл railroads.shp в QGIS и нажмите кнопку Открыть таблицу атрибутов.
 3=8
a = b a and b are equal
a > b a is larger than b
a < b a is smaller than b
a <> b a and b are not equal
a != b a and b are not equal
a <= b a is less than or equal to b
a >= b a is larger than or equal to b
a ~ b a matches the regular expression b
+ a positive sign
— a negative value of a
|| joins two values together into a string ‘Hello’ || ‘ world’
LIKE returns 1 if the string matches the supplied pattern
ILIKE returns 1 if the string matches case-insensitive the supplied
pattern. ILIKE can be used instead of LIKE to make the match case-insensitive
IS returns 1 if a is the same as b
OR returns 1 when condition a or b is true
AND returns 1 when condition a and b are true
NOT returns 1 if a is not the same as b
column name «column name» value of the field column name
‘string’ a string value
NULL null value
a IS NULL a has no value
a IS NOT NULL a has a value
a IN (value[,value]) a is below the values listed
a NOT IN (value[,value]) a is not below the values listed
3=8
a = b a and b are equal
a > b a is larger than b
a < b a is smaller than b
a <> b a and b are not equal
a != b a and b are not equal
a <= b a is less than or equal to b
a >= b a is larger than or equal to b
a ~ b a matches the regular expression b
+ a positive sign
— a negative value of a
|| joins two values together into a string ‘Hello’ || ‘ world’
LIKE returns 1 if the string matches the supplied pattern
ILIKE returns 1 if the string matches case-insensitive the supplied
pattern. ILIKE can be used instead of LIKE to make the match case-insensitive
IS returns 1 if a is the same as b
OR returns 1 when condition a or b is true
AND returns 1 when condition a and b are true
NOT returns 1 if a is not the same as b
column name «column name» value of the field column name
‘string’ a string value
NULL null value
a IS NULL a has no value
a IS NOT NULL a has a value
a IN (value[,value]) a is below the values listed
a NOT IN (value[,value]) a is not below the values listedУсловия
Условные операторы и функции
CASE evaluates multiple expressions and return a result CASE ELSE evaluates multiple expressions and return a result coalesce returns the first non-NULL value from the expression list regexp_match returns true if any part of a string matches the supplied regular expressionФункции
Математические функции, такие как квадратный корень, синус, косинус и др.
sqrt(a) square root of a abs returns the absolute value of a number. sin(a) sinus of a cos(a) cosinus of a tan(a) tangens of a asin(a) arcussinus of a acos(a) arcuscosinus of a atan(a) arcustangens of a atan2(y,x) arcustangens of y/x using the signs of the two arguments to determine the quadrant of the result exp exponential of an value ln value of the natural logarithm of the passed expression log10 value of the base 10 logarithm of the passed expression log value of the logarithm of the passed value and base round number to number of decimal places rand random integer within the range specified by the minimum and maximum argument (inclusive) randf random float within the range specified by the minimum and maximum argument (inclusive) max largest value in a set of values min smallest value in a set of values clamp restricts an input value to a specified range scale_linear transforms a given value from an input domain to an output range using linear interpolation scale_exp transforms a given value from an input domain to an output range using an exponential curve floor rounds a number downwards ceil rounds a number upwards $pi pi as value for calculationsПреобразования
Функции преобразования типов данных, например строки в целое число, целого в строку.

toint converts a string to integer number toreal converts a string to real number tostring convert number to string todatetime convert a string into Qt data time type todate convert a string into Qt data type totime convert a string into Qt time type tointerval converts a string to a interval type. Can be used to take days, hours, month, etc off a dateДата и время
Функции для работы с датой и временем.
$now current date and time age difference between two dates year extract the year part from a date, or the number of years from a Interval month extract the month part from a date, or the number of months from a Interval week extract the week number from a date, or the number of weeks from a Interval day extract the day from a date, or the number of days from a Interval hour extract the hour from a datetime or time, or the number of hours from a Interval minute extract the minute from a datetime or time, or the number of minutes from a Interval second extract the second from a datetime or time, or the number of minutes from a IntervalСтроки
Функции для работы со строками, такие как поиск, замена, изменение регистра.
lower convert string a to lower case upper convert string a to upper case title converts all words of a string to title case (all words lower case with leading capital letter) trim removes all leading and trailing whitespace (spaces, tabs, etc) from a string length length of string a replace returns a string with the the supplied string replaced regexp_replace(a,this,that) returns a string with the supplied regular expression replaced regexp_substr returns the portion of a string which matches a supplied regular expression substr(*a*,from,len) returns a part of a string concat concatenates several strings to one strpos returns the index of a regular expression in a string left returns a substring that contains the n leftmost characters of the string right returns a substring that contains the n rightmost characters of the string rpad returns a string with supplied width padded using the fill character lpad returns a string with supplied width padded using the fill character format formats a string using supplied arguments format_number returns a number formatted with the locale separator for thousands. Also truncates the number to the number of supplied places
format_date formats a date type or string into a custom string format
Also truncates the number to the number of supplied places
format_date formats a date type or string into a custom string formatЦвет
Функции для работы с различными формами представления цвета.
color_rgb returns a string representation of a color based on its red, green, and blue components color_rgba returns a string representation of a color based on its red, green, blue, and alpha (transparency) components ramp_color returns a string representing a color from a color ramp color_hsl returns a string representation of a color based on its hue, saturation, and lightness attributes color_hsla returns a string representation of a color based on its hue, saturation, lightness and alpha (transparency) attributes color_hsv returns a string representation of a color based on its hue, saturation, and value attributes color_hsva returns a string representation of a color based on its hue, saturation, value and alpha (transparency) attributes color_cmyk returns a string representation of a color based on its cyan, magenta, yellow and black components color_cmyka returns a string representation of a color based on its cyan, magenta, yellow, black and alpha (transparency) componentsГеометрия
Функции, работающие с геометрией (длина, площадь и т.п.).
xat retrieves a x coordinate of the current feature yat retrieves a y coordinate of the current feature $area returns the area size of the current feature $length returns the area size of the current feature $perimeter returns the perimeter length of the current feature $x returns the x coordinate of the current feature $y returns the y coordinate of the current feature $geometry returns the geometry of the current feature.
 Can be used
for processing with other functions.
geomFromWKT returns a geometry created from a Well-Known Text (WKT) representation.
geomFromGML returns a geometry from a GML representation of geometry
bbox
disjoint returns 1 if the Geometries do not share any space together
intersects returns 1 if the geometries spatially intersect
(share any portion of space) and 0 if they don't
touches returns 1 if the geometries have at least one point in common,
but their interiors do not intersect
crosses returns 1 if the supplied geometries have some, but not all,
interior points in common.
contains returns true if and only if no points of b lie in the exterior of a,
and at least one point of the interior of b lies in the interior of a
overlaps returns 1 if the Geometries share space, are of the same dimension,
but are not completely contained by each other.
within returns 1 if the geometry a is completely inside geometry b
buffer returns a geometry that represents all points whose distance
from this geometry is less than or equal to distance
centroid returns the geometric center of a geometry
convexHull returns the convex hull of a geometry. It represents the
minimum convex geometry that encloses all geometries within the set
difference returns a geometry that represents that part of geometry a that
does not intersect with geometry a
distance returns the minimum distance (based on spatial ref) between
two geometries in projected units
intersection returns a geometry that represents the shared portion
of geometry a and geometry b
symDifference returns a geometry that represents the portions of a and b
that do not intersect
combine returns the combination of geometry a and geometry b
union returns a geometry that represents the point set union of the geometries
geomToWKT returns the Well-Known Text (WKT) representation of the
geometry without SRID metadata
Can be used
for processing with other functions.
geomFromWKT returns a geometry created from a Well-Known Text (WKT) representation.
geomFromGML returns a geometry from a GML representation of geometry
bbox
disjoint returns 1 if the Geometries do not share any space together
intersects returns 1 if the geometries spatially intersect
(share any portion of space) and 0 if they don't
touches returns 1 if the geometries have at least one point in common,
but their interiors do not intersect
crosses returns 1 if the supplied geometries have some, but not all,
interior points in common.
contains returns true if and only if no points of b lie in the exterior of a,
and at least one point of the interior of b lies in the interior of a
overlaps returns 1 if the Geometries share space, are of the same dimension,
but are not completely contained by each other.
within returns 1 if the geometry a is completely inside geometry b
buffer returns a geometry that represents all points whose distance
from this geometry is less than or equal to distance
centroid returns the geometric center of a geometry
convexHull returns the convex hull of a geometry. It represents the
minimum convex geometry that encloses all geometries within the set
difference returns a geometry that represents that part of geometry a that
does not intersect with geometry a
distance returns the minimum distance (based on spatial ref) between
two geometries in projected units
intersection returns a geometry that represents the shared portion
of geometry a and geometry b
symDifference returns a geometry that represents the portions of a and b
that do not intersect
combine returns the combination of geometry a and geometry b
union returns a geometry that represents the point set union of the geometries
geomToWKT returns the Well-Known Text (WKT) representation of the
geometry without SRID metadataЗаписи
Функции для работы с идентификаторами записей.

$rownum returns the number of the current row $id returns the feature id of the current row $scale returns the current scale of the map canvas
Поля и значения
Содержит спсиок полей слоя. Отсюда также можно получить список значений поля.
Выберите имя слоя, затем вызовите констексное меню, из которого и выполняется загрузка значений поля.
Сокращение уравнения онлайн. Как упростить математическое выражение
Буквенное выражение (или выражение с переменными) — это математическое выражение, которое состоит из чисел, букв и знаков математических операций. Например, следующее выражение является буквенным:
a + b + 4
С помощью буквенных выражений можно записывать законы, формулы, уравнения и функции. Умение манипулировать буквенными выражениями — залог хорошего знания алгебры и высшей математики.
Любая серьезная задача в математике сводится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с буквенными выражениями.
Чтобы работать с буквенными выражениями, нужно хорошо изучить базовую арифметику: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто изучить, а понять досконально.
Содержание урокаПеременные
Буквы, которые содержатся в буквенных выражениях называются переменными . Например, в выражении a+b+4 переменными являются буквы a и b . Если вместо этих переменных подставить любые числа, то буквенное выражение a+b+4 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных . Например, изменим значения переменных a и b . Для изменения значений используется знак равенства
a = 2, b = 3
Мы изменили значения переменных a и b .
 Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти:
Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти:2 + 3 + 4 = 9
Когда происходит умножение переменных, то они записываются вместе. Например, запись ab означает то же самое, что и запись a×b . Если подставить вместо переменных a и b числа 2 и 3 , то мы получим 6
2 × 3 = 6
Слитно также можно записать умножение числа на выражение в скобках. Например, вместо a×(b + c) можно записать a(b + c) . Применив распределительный закон умножения, получим a(b + c)=ab+ac .
Коэффициенты
В буквенных выражениях часто можно встретить запись, в которой число и переменная записаны вместе, например 3a . На самом деле это короткая запись умножения числа 3 на переменную a и эта запись выглядит как 3 × a .
Другими словами, выражение 3a является произведением числа 3 и переменной a . Число 3 в этом произведении называют коэффициентом . Этот коэффициент показывает во сколько раз будет увеличена переменная a . Данное выражение можно прочитать как «a три раза» или «трижды а «, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три a «
К примеру, если переменная a равна 5 , то значение выражения 3a будет равно 15.
3 × 5 = 15
Говоря простым языком, коэффициент это число, которое стоит перед буквой (перед переменной).
Букв может быть несколько, например 5abc . Здесь коэффициентом является число 5 . Данный коэффициент показывает, что произведение переменных abc увеличивается в пять раз. Это выражение можно прочитать как «abc пять раз» либо «увеличить значение выражения abc в пять раз», либо «пять abc «.

Если вместо вместо переменных abc подставить числа 2, 3 и 4, то значение выражения 5abc будет равно 120
5 × 2 × 3 × 4 = 120
Можно мысленно представить, как сначала перемножились числа 2, 3 и 4, и полученное значение увеличилось в пять раз:
Знак коэффициента относится только к коэффициенту, и не относится к переменным.
Рассмотрим выражение −6b . Минус, стоящий перед коэффициентом 6 , относится только к коэффициенту 6 , и не относится к переменной b . Понимание этого факта позволит не ошибаться в будущем со знаками.
Найдем значение выражения −6b при b = 3 .
−6b −6×b . Для наглядности запишем выражение −6b в развёрнутом виде и подставим значение переменной b
−6b = −6 × b = −6 × 3 = −18
Пример 2. Найти значение выражения −6b при b = −5
Запишем выражение −6b в развёрнутом виде
−6b = −6 × b = −6 × (−5) = 30
Пример 3. Найти значение выражения −5a + b при a = 3 и b = 2
−5a + b это короткая форма записи от −5 × a + b , поэтому для наглядности запишем выражение −5×a+b в развёрнутом виде и подставим значения переменных a и b
−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда буквы записаны без коэффициента, например a или ab . В этом случае коэффициентом является единица:
но единицу по традиции не записывают, поэтому просто пишут a или ab
Если перед буквой стоит минус, то коэффициентом является число −1 . Например, выражение −a на самом деле выглядит как −1a . Это произведение минус единицы и переменной a. Оно получилось следующим образом:
−1 × a = −1a
Здесь кроется небольшой подвох. В выражении −a минус, стоящий перед переменной a на самом деле относится к «невидимой единице», а не к переменной a .
 Поэтому при решении задач следует быть внимательным.
Поэтому при решении задач следует быть внимательным.К примеру, если дано выражение −a и нас просят найти его значение при a = 2 , то в школе мы подставляли двойку вместо переменной a и получали ответ −2 , не особо зацикливаясь на том, как это получалось. На самом деле происходило умножение минус единицы на положительное число 2
−a = −1 × a
−1 × a = −1 × 2 = −2
Если дано выражение −a и требуется найти его значение при a = −2 , то мы подставляем −2 вместо переменной a
−a = −1 × a
−1 × a = −1 × (−2) = 2
Чтобы не допускать ошибок, первое время невидимые единицы можно записывать явно.
Пример 4. Найти значение выражения abc при a=2 , b=3 и c=4
Выражение abc 1×a×b×c. Для наглядности запишем выражение abc a , b и c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Найти значение выражения abc при a=−2 , b=−3 и c=−4
Запишем выражение abc в развёрнутом виде и подставим значения переменных a , b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Найти значение выражения − abc при a=3 , b=5 и c=7
Выражение − abc это короткая форма записи от −1×a×b×c. Для наглядности запишем выражение − abc в развёрнутом виде и подставим значения переменных a , b и c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Найти значение выражения − abc при a=−2 , b=−4 и c=−3
Запишем выражение − abc в развёрнутом виде:
−abc = −1 × a × b × c
Подставим значение переменных a , b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Как определить коэффициент
Иногда требуется решить задачу, в которой требуется определить коэффициент выражения.
 В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа.
В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа.Чтобы определить коэффициент в выражении, нужно отдельно перемножить числа, входящие в это выражение, и отдельно перемножить буквы. Получившийся числовой сомножитель и будет коэффициентом.
Пример 1. 7m×5a×(−3)×n
Выражение состоит из нескольких сомножителей. Это можно отчетливо увидеть, если записать выражение в развёрнутом виде. То есть, произведения 7m и 5a записать в виде 7×m и 5×a
7 × m × 5 × a × (−3) × n
Применим сочетательный закон умножения, который позволяет перемножать сомножители в любом порядке. А именно, отдельно перемножим числа и отдельно перемножим буквы (переменные):
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен −105 . После завершения буквенную часть желательно расположить в алфавитном порядке:
−105amn
Пример 2. Определить коэффициент в выражении: −a×(−3)×2
−a × (−3) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6.
Пример 3. Определить коэффициент в выражении:
Перемножим отдельно числа и буквы:
Коэффициент равен −1. Обратите внимание, что единица не записана, поскольку коэффициент 1 принято не записывать.
Эти казалось бы простейшие задачи могут сыграть с нами очень злую шутку. Часто выясняется, что знак коэффициента поставлен неверно: либо пропущен минус либо наоборот он поставлен зря. Чтобы избежать этих досадных ошибок, должна быть изучена на хорошем уровне.
Слагаемые в буквенных выражениях
При сложении нескольких чисел получается сумма этих чисел. Числа, которые складывают называют слагаемыми. Слагаемых может быть несколько, например:
1 + 2 + 3 + 4 + 5
Когда выражение состоит из слагаемых, вычислять его намного проще, поскольку складывать легче, чем вычитать. Но в выражении может присутствовать не только сложение, но и вычитание, например:
1 + 2 − 3 + 4 − 5
В этом выражении числа 3 и 5 являются вычитаемыми, а не слагаемыми.
 Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:1 + 2 + (−3) + 4 + (−5)
Не суть, что числа −3 и −5 теперь со знаком минуса. Главное, что все числа в данном выражении соединены знаком сложения, то есть выражение является суммой.
Оба выражения 1 + 2 − 3 + 4 − 5 и 1 + 2 + (−3) + 4 + (−5) равны одному и тому значению — минус единице
1 + 2 − 3 + 4 − 5 = −1
1 + 2 + (−3) + 4 + (−5) = −1
Таким образом, значение выражения не пострадает от того, что мы где-то заменим вычитание сложением.
Заменять вычитание сложением можно и в буквенных выражениях. Например, рассмотрим следующее выражение:
7a + 6b − 3c + 2d − 4s
7a + 6b + (−3c) + 2d + (−4s)
При любых значениях переменных a, b, c, d и s выражения 7a + 6b − 3c + 2d − 4s и 7a + 6b + (−3c) + 2d + (−4s) будут равны одному и тому же значению.
Вы должны быть готовы к тому, что учитель в школе или преподаватель в институте может называть слагаемыми даже те числа (или переменные), которые ими не являются.
Например, если на доске будет записана разность a − b , то учитель не будет говорить, что a — это уменьшаемое, а b — вычитаемое. Обе переменные он назовет одним общим словом — слагаемые . А всё потому, что выражение вида a − b математик видит, как сумму a + (−b) . В таком случае выражение становится суммой, а переменные a и (−b) становятся слагаемыми.
Подобные слагаемые
Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть. Например, рассмотрим выражение 7a + 6b + 2a . Слагаемые 7a и 2a имеют одинаковую буквенную часть — переменную a . Значит слагаемые 7a и 2a являются подобными.
Обычно подобные слагаемые складывают, чтобы упростить выражение или решить какое-нибудь уравнение.
 Эту операцию называют приведением подобных слагаемых .
Эту операцию называют приведением подобных слагаемых .Чтобы привести подобные слагаемые, нужно сложить коэффициенты этих слагаемых, и полученный результат умножить на общую буквенную часть.
Например приведём подобные слагаемые в выражении 3a + 4a + 5a . В данном случае, подобными являются все слагаемые. Сложим их коэффициенты и результат умножим на общую буквенную часть — на переменную a
3a + 4a + 5a = (3 + 4 + 5)×a = 12a
Подобные слагаемые обычно приводят в уме и результат записывают сразу:
3a + 4a + 5a = 12a
Также, можно рассуждать следующим образом:
Было 3 переменные a , к ним прибавили еще 4 переменные a и ещё 5 переменных a. В итоге получили 12 переменных a
Рассмотрим несколько примеров на приведение подобных слагаемых. Учитывая, что данная тема очень важна, на первых порах будем записывать подробно каждую мелочь. Несмотря на то, что здесь всё очень просто, большинство людей допускают множество ошибок. В основном по невнимательности, а не по незнанию.
Пример 1. 3a + 2a + 6a + 8 a
Сложим коэффициенты в данном выражении и полученный результат умножим на общую буквенную часть:
3a + 2a + 6a + 8a = (3 + 2 + 6 + 8) × a = 19a
Конструкцию (3 + 2 + 6 + 8)×a можно не записывать, поэтому сразу запишем ответ
3a + 2a + 6a + 8a = 19a
Пример 2. Привести подобные слагаемые в выражении 2a + a
Второе слагаемое a записано без коэффициента, но на самом деле перед ним стоит коэффициент 1 , который мы не видим по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
2a + 1a
Теперь приведем подобные слагаемые. То есть, сложим коэффициенты и результат умножим на общую буквенную часть:
2a + 1a = (2 + 1) × a = 3a
Запишем решение покороче:
2a + a = 3a
2a+a , можно рассуждать и по-другому:
Пример 3.
 Привести подобные слагаемые в выражении 2a − a
Привести подобные слагаемые в выражении 2a − a Заменим вычитание сложением:
2a + (−a)
Второе слагаемое (−a) записано без коэффициента, но на самом оно выглядит как (−1a). Коэффициент −1 опять же невидимый по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
2a + (−1a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть:
2a + (−1a) = (2 + (−1)) × a = 1a = a
Обычно записывают короче:
2a − a = a
Приводя подобные слагаемые в выражении 2a−a можно рассуждать и по-другому:
Было 2 переменные a , вычли одну переменную a , в итоге осталась одна единственная переменная a
Пример 4. Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
6a − 3a + 4a − 8a = 6a + (−3a) + 4a + (−8a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение покороче:
6a − 3a + 4a − 8a = −a
Встречаются выражения, которые содержат несколько различных групп подобных слагаемых. Например, 3a + 3b + 7a + 2b . Для таких выражений справедливы те же правила, что и для остальных, а именно складывание коэффициентов и умножение полученного результата на общую буквенную часть. Но чтобы не допустить ошибок, удобно разные группы слагаемых подчеркнуть разными линиями.
Например, в выражении 3a + 3b + 7a + 2b те слагаемые, которые содержат переменную a , можно подчеркнуть одной линией, а те слагаемые которые содержат переменную b , можно подчеркнуть двумя линиями:
Теперь можно привести подобные слагаемые. То есть, сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b .

3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же повторимся, выражение несложное, и подобные слагаемые можно приводить в уме:
3a + 3b + 7a + 2b = 10a + 5b
Пример 5. Привести подобные слагаемые в выражении 5a − 6a −7b + b
Заменим вычитание сложение там, где это можно:
5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнём подобные слагаемые разными линиями. Слагаемые, содержащие переменные a подчеркнем одной линией, а слагаемые содержание переменные b , подчеркнем двумя линиями:
Теперь можно привести подобные слагаемые. То есть, сложить коэффициенты и полученный результат умножить на общую буквенную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1)×b = −a + (−6b)
Если в выражении содержатся обычные числа без буквенных сомножителей, то они складываются отдельно.
Пример 6. Привести подобные слагаемые в выражении 4a + 3a − 5 + 2b + 7
Заменим вычитание сложением там, где это можно:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Приведем подобные слагаемые. Числа −5 и 7 не имеют буквенных сомножителей, но они являются подобными слагаемыми — их необходимо просто сложить. А слагаемое 2b останется без изменений, поскольку оно единственное в данном выражении, имеющее буквенный сомножитель b, и его не с чем складывать:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение покороче:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Слагаемые можно упорядочивать, чтобы те слагаемые, которые имеют одинаковую буквенную часть, располагались в одной части выражения.
Пример 7. Привести подобные слагаемые в выражении 5t+2x+3x+5t+x
Поскольку выражение является суммой из нескольких слагаемых, это позволяет нам вычислять его в любом порядке. Поэтому слагаемые, содержащие переменную t , можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
5t + 5t + 2x + 3x + x
Теперь можно привести подобные слагаемые:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение покороче:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю.
 Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.Пример 8. Привести подобные слагаемые в выражении 3t − 4t − 3t + 2t
Заменим вычитание сложением там, где это можно:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t
Слагаемые 3t и (−3t) являются противоположными. Сумма противоположных слагаемых равна нулю. Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
В итоге у нас останется выражение (−4t) + 2t . В данном выражении можно привести подобные слагаемые и получить окончательный ответ:
(−4t) + 2t = ((−4) + 2)×t = −2t
Запишем решение покороче:
Упрощение выражений
«упростите выражение» и далее приводится выражение, которое требуется упростить. Упростить выражение значит сделать его проще и короче.
На самом деле мы уже занимались упрощением выражений, когда сокращали дроби. После сокращения дробь становилась короче и проще для восприятия.
Рассмотрим следующий пример. Упростить выражение .
Это задание буквально можно понять так: «Примените к данному выражению любые допустимые действия, но сделайте его проще» .
В данном случае можно осуществить сокращение дроби, а именно разделить числитель и знаменатель дроби на 2:
Что ещё можно сделать? Можно вычислить полученную дробь . Тогда мы получим десятичную дробь 0,5
В итоге дробь упростилась до 0,5.
Первый вопрос, который нужно себе задавать при решении подобных задач, должен быть «а что можно сделать?» . Потому что есть действия, которые можно делать, и есть действия, которые делать нельзя.

Ещё один важный момент, о котором нужно помнить, заключается в том, что значение выражение не должно измениться после упрощения выражения. Вернемся к выражению . Данное выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получаем значение данного выражения, которое равно 0,5
Но мы упростили выражение и получили новое упрощенное выражение . Значение нового упрощенного выражения по-прежнему равно 0,5
Но выражение мы тоже попытались упростить, вычислив его. В итоге получили окончательный ответ 0,5.
Таким образом, как бы мы не упрощали выражение, значение получаемых выражений по-прежнему равно 0,5. Значит упрощение выполнялось верно на каждом этапе. Именно к этому нужно стремиться при упрощении выражений — значение выражения не должно пострадать от наших действий.
Часто требуется упрощать буквенные выражения. Для них справедливы те же правила упрощения, что и для числовых выражений. Можно выполнять любые допустимые действия, лишь бы не изменилось значение выражения.
Рассмотрим несколько примеров.
Пример 1. Упростить выражение 5,21s × t × 2,5
Чтобы упростить данное выражение, можно отдельно перемножить числа и отдельно перемножить буквы. Это задание очень похоже на то, которое мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21s × t × 2,5 упростилось до 13,025st .
Пример 2. Упростить выражение −0,4 × (−6,3b) × 2
Второе произведение (−6,3b) можно перевести в понятный для нас вид, а именно записать в виде (−6,3)×b , затем отдельно перемножить числа и отдельно перемножить буквы:
− 0,4 × (−6,3b) × 2 = − 0,4 × (−6,3) × b × 2 = 5,04b
Таким образом, выражение −0,4 × (−6,3b) × 2 упростилось до 5,04b
Пример 3. Упростить выражение
Распишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно перемножим буквы:
Таким образом, выражение упростилось до −abc.
 Данное решение можно записать покороче:
Данное решение можно записать покороче:При упрощении выражений, дроби можно сокращать в процессе решения, а не в самом конце, как мы это делали с обычными дробями. Например, если в ходе решения мы наткнёмся на выражение вида , то вовсе необязательно вычислять числитель и знаменатель и делать что-то вроде этого:
Дробь можно сократить, выбирая по множителю в числителе и в знаменателе и сокращать эти множители на их наибольший общий делитель. Другими словами, использовать , в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Например, в числителе множитель 12 и в знаменателе множитель 4 можно сократить на 4. Четвёрку храним в уме, а разделив 12 и 4 на эту четвёрку, ответы записываем рядом с этими числами, предварительно зачеркнув их
Теперь можно перемножить получившиеся маленькие множители. В данном случае их немного и можно перемножить в уме:
Со временем можно обнаружить, что решая ту или иную задачу, выражения начинают «толстеть», поэтому желательно приучиться к быстрым вычислениям. То, что можно вычислить в уме, нужно вычислять в уме. То, что можно быстро сократить, нужно быстро сокращать.
Пример 4. Упростить выражение
Таким образом, выражение упростилось до
Пример 5. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение упростилось до mn .
Пример 6. Упростить выражение
Запишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно буквы. Для удобства вычислений десятичную дробь −6,4 и смешанное число можно перевести в обыкновенные дроби:
Таким образом, выражение упростилось до
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Пример 7. Упростить выражение
Перемножим отдельно числа и отдельно буквы.
 Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби:
Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби:Таким образом, выражение упростилось до abcd . Если пропустить подробности, то данное решение можно записать значительно короче:
Обратите внимание на то, как сократилась дробь. Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Теперь поговорим о том, чего делать нельзя. При упрощении выражений категорически нельзя перемножать числа и буквы, если выражение является суммой, а не произведением.
Например, если требуется упростить выражение 5a + 4b , то нельзя записывать следующим образом:
Это равносильно тому, что если бы нас попросили сложить два числа, а мы бы их перемножали вместо того, чтобы складывать.
При подстановке любых значений переменных a и b выражение 5a +4b обращается в обыкновенное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
a = 2 , b = 3
Тогда значение выражения будет равно 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем полученные результаты складывают. А если бы мы попытались упростить данное выражение, перемножив числа и буквы, то получилось бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае получилось 22 , во втором случае 120 . Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
После упрощения выражения, его значение не должно изменяться при одних и тех же значениях переменных. Если при подстановке в изначальное выражение любых значений переменных получается одно значение, то после упрощения выражения должно получаться то же самое значение, что и до упрощения.
С выражением 5a + 4b на самом деле ничего делать нельзя.
 Оно не упрощается.
Оно не упрощается.Если в выражении содержатся подобные слагаемые, то их можно сложить, если нашей целью является упрощение выражения.
Пример 8. Упростить выражение 0,3a−0,4a+a
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или покороче: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a−0,4a+a упростилось до 0,9a
Пример 9. Упростить выражение −7,5a − 2,5b + 4a
Чтобы упростить данное выражение можно привести подобные слагаемые:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или покороче −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (−2,5b) осталось без изменений, поскольку его не с чем было складывать.
Пример 10. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Коэффициент был для удобства вычисления.
Таким образом, выражение упростилось до
Пример 11. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до .
В данном примере целесообразнее было бы сложить первый и последний коэффициент в первую очередь. В этом случае мы получили бы короткое решение. Выглядело оно будет следующим образом:
Пример 12. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до.
Слагаемое осталось без изменения, поскольку его не с чем было складывать.
Данное решение можно записать значительно короче. Выглядеть оно будет следующим образом:
В коротком решении пропущены этапы замены вычитания сложением и подробная запись, как дроби приводились к общему знаменателю.
Ещё одно различие заключается в том, что в подробном решении ответ выглядит как , а в коротком как .
 На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа.
На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа.Тождества. Тождественно равные выражения
После того, как мы упростили любое выражение, оно становится проще и короче. Чтобы проверить, верно ли упрощено выражение, достаточно подставить любые значения переменных сначала в предыдущее выражение, которое требовалось упростить, а затем в новое, которое упростили. Если значение в обоих выражениях будет одинаковым, то выражение упрощено верно.
Рассмотрим простейший пример. Пусть требуется упростить выражение 2a × 7b . Чтобы упростить данное выражение, можно по отдельности перемножить числа и буквы:
2a × 7b = 2 × 7 × a × b = 14ab
Проверим верно ли мы упростили выражение. Для этого подставим любые значения переменных a и b сначала в первое выражение, которое требовалось упростить, а затем во второе, которое упростили.
Пусть значения переменных a , b будут следующими:
a = 4 , b = 5
Подставим их в первое выражение 2a × 7b
Теперь подставим те же значения переменных в выражение, которое получилось в результате упрощения 2a×7b , а именно в выражение 14ab
14ab = 14 × 4 × 5 = 280
Видим, что при a=4 и b=5 значение первого выражения 2a×7b и значение второго выражения 14ab равны
2a × 7b = 2 × 4 × 7 × 5 = 280
14ab = 14 × 4 × 5 = 280
То же самое произойдет и для любых других значений. Например, пусть a=1 и b=2
2a × 7b = 2 × 1 × 7 × 2 =28
14ab = 14 × 1 × 2 =28
Таким образом, при любых значениях переменных выражения 2a×7b и 14ab равны одному и тому же значению.
 Такие выражения называют тождественно равными .
Такие выражения называют тождественно равными .Делаем вывод, что между выражениями 2a×7b и 14ab можно поставить знак равенства, поскольку они равны одному и тому же значению.
2a × 7b = 14ab
Равенством называют любое выражение, которые соединено знаком равенства (=).
А равенство вида 2a×7b = 14ab называют тождеством .
Тождеством называют равенство, которое верно при любых значениях переменных.
Другие примеры тождеств:
a + b = b + a
a(b+c) = ab + ac
a(bc) = (ab)c
Да, законы математики, которые мы изучали, являются тождествами.
Верные числовые равенства также являются тождествами. Например:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
Решая сложную задачу, чтобы облегчить себе вычисление, сложное выражение заменяют на более простое выражение, тождественно равное предыдущему. Такую замену называют тождественным преобразованием выражения или просто преобразованием выражения .
Например, мы упростили выражение 2a × 7b , и получили более простое выражение 14ab . Это упрощение можно называть тождественным преобразованием.
Часто можно встретить задание, в котором сказано «докажите, что равенство является тождеством» и далее приводится равенство, которое требуется доказать. Обычно это равенство состоит из двух частей: левой и правой части равенства. Наша задача состоит в том, чтобы выполнить тождественные преобразования с одной из частей равенства и получить другую часть. Либо выполнить тождественные преобразования с обеими частями равенства и сделать так, чтобы в обеих частях равенства оказались одинаковые выражения.
Например, докажем, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножим числа и буквы по отдельности:
0,5 × 5 × a × b = 2,5ab
2,5ab = 2,5ab
В результате небольшого тождественного преобразования, левая часть равенства стала равна правой части равенства.
 Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, приводить подобные слагаемые, а также упрощать некоторые выражения.
Но это далеко не все тождественные преобразования, которые существуют в математике. Тождественных преобразований намного больше. В будущем мы ещё не раз в этом убедимся.
Задания для самостоятельного решения:Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых урокахАлгебраическое выражение в записи которого наряду с действиями сложения, вычитания и умножения используют также деление на буквенные выражения, называется дробным алгебраическим выражением. Таковы, например, выражения
Алгебраической дробью мы называем алгебраическое выражение, имеющее вид частного от деления двух целых алгебраических выражений (например, одночленов или многочленов). Таковы, например, выражения
Третье из выражений ).
Тождественные преобразования дробных алгебраических выражений имеют по большей части своей целью представить их в виде алгебраической дроби. Для отыскания общего знаменателя используется разложение на множители знаменателей дробей — слагаемых с целью отыскания их наименьшего общего кратного. При сокращении алгебраических дробей может нарушаться строгая тождественность выражений: необходимо исключать значения величин, при которых множитель, на который производится сокращение, обращается в нуль.
Приведем примеры тождественных преобразований дробных алгебраических выражений.
Пример 1. Упростить выражение
Все слагаемые можно привести к общему знаменателю (удобно при этом изменить знак в знаменателе последнего слагаемого и знак перед ним):
Наше выражение равно единице при всех значениях кроме этих значениях оно не определено и сокращение дроби незаконно).
Пример 2. Представить в виде алгебраической дроби выражение
Решение.
 За общий знаменатель можно принять выражение . Находим последовательно:
За общий знаменатель можно принять выражение . Находим последовательно:Упражнения
1. Найти значения алгебраических выражений при указанных значениях параметров:
2. Разложить на множители.
Приложение
Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
= Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады.
Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых.
В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта.
Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида.
За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера.
Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной.
По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности.
Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины.
Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.Замечание 1
Логическую функцию можно записать с помощью логического выражения, а затем можно перейти к логической схеме. Упрощать логические выражения надо для того, чтобы получить как можно более простую (а значит, и более дешёвую) логическую схему.
 По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.Для упрощения логических выражений используют законы алгебры логики .
Какие-то преобразования похожи на преобразования формул в классической алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), а другие преобразования основаны на свойствах, которыми операции классической алгебры не обладают (использование распределительного закона для конъюнкции, законов поглощения, склеивания, правил де Моргана и др.).
Законы алгебры логики формулируются для базовых логических операций — “НЕ” – инверсия (отрицание), “И” – конъюнкция (логическое умножение) и “ИЛИ” – дизъюнкция (логическое сложение).
Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее дважды, то в итоге логическое значение не изменится.
Закон исключенного третьего гласит, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если $A=1$, то $\bar{A}=0$ (и наоборот), а, значит, конъюнкция этих величин всегда равно нулю, а дизъюнкция равна единице.
$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$
Упростим эту формулу:
Рисунок 3.
Отсюда следует, что $A = 0$, $B = 1$, $C = 1$, $D = 1$.
Ответ: в шахматы играют ученики $B$, $C$ и $D$, а ученик $A$ не играет.
При упрощении логических выражений можно выполнять такую последовательность действий :
- Заменить все “небазовые” операции (эквивалентность, импликацию, исключающее ИЛИ и др.) на их выражения через базовые операции инверсию, конъюнкцию и дизъюнкцию.
- Раскрыть инверсии сложных выражений по правилам де Моргана таким образом, чтобы операции отрицания остались только у отдельных переменных.
- Затем упростить выражение, используя раскрытие скобок, вынесение общих множителей за скобки и другие законы алгебры логики.
Пример 2
Здесь последовательно использованы правило де Моргана, распределительный закон, закон исключенного третьего, переместительный закон, закон повторения, вновь переместительный закон и закон поглощения.

Зачастую в задачах требуется привести упрощенный ответ. Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.
Шаги
Правильный порядок выполнения математических операций
Запомните правильный порядок выполнения математических операций. При упрощении математического выражения необходимо соблюдать определенный порядок действий, так как некоторые математические операции имеют приоритет над другими и должны быть сделаны в первую очередь (на самом деле несоблюдение правильного порядка выполнения операций приведет вас к неправильному результату). Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.
- Обратите внимание, что знание правильного порядка выполнения операций позволит вам упростить большинство простейших выражений, но для упрощения многочлена (выражения с переменной) необходимо знать специальные приемы (смотрите следующий раздел).
Начните с решения выражения в скобках. В математике скобки указывают на то, что заключенное в них выражение должно быть выполнено в первую очередь. Поэтому при упрощении любого математического выражения начинайте с решения выражения, заключенного в скобки (при этом неважно, какие операции нужно выполнить внутри скобок). Но помните, что работая с выражением, заключенным в скобки, следует соблюдать порядок проведения операций, то есть члены в скобках сначала перемножаются, делятся, складываются, вычитаются и так далее.
- Например, упростим выражение 2x + 4(5 + 2) + 3 2 — (3 + 4/2) . Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
- Выражение во второй паре скобок упрощается до 5, потому что сначала нужно разделить 4/2 (согласно правильному порядку выполнения операций).
 Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
- Выражение во второй паре скобок упрощается до 5, потому что сначала нужно разделить 4/2 (согласно правильному порядку выполнения операций).
- Если в скобках есть еще одна пара скобок, начните упрощение с решения выражения во внутренних скобках, а затем переходите к решению выражения во внешних скобках.
- Например, упростим выражение 2x + 4(5 + 2) + 3 2 — (3 + 4/2) . Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
Возведите в степень. Решив выражения в скобках, перейдите к возведению в степень (помните, что у степени есть показатель степени и основание степени). Возведите соответствующее выражение (или число) в степень и подставьте результат в данное вам выражение.
- В нашем примере единственным выражением (числом) в степени является 3 2: 3 2 = 9. В данном вам выражении вместо 3 2 подставьте 9 и вы получите: 2x + 4(7) + 9 — 5.
Умножьте. Помните, что операция умножения может обозначаться следующими символами: «х», «∙» или «*». Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.
- В нашем примере присутствуют две операции умножения: 2x (два умножить на переменную «х») и 4(7) (четыре умножить на семь). Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
Разделите. Помните, что операция деления может обозначаться следующими символами: «/», «÷» или «–» (последний символ вы можете встретить в дробях). Например 3/4 – это три, деленное на четыре.
- В нашем примере операции деления больше нет, так как вы уже разделили 4 на 2 (4/2) при решении выражения в скобках. Поэтому вы можете перейти к следующему шагу. Помните, что в большинстве выражений нет сразу всех математических операций (только некоторые из них).
Сложите. При сложении членов выражения вы можете начать с самого крайнего (слева) члена, или можете сначала сложить те члены выражения, которые легко складываются.
 Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.- В нашем примере 2x + 28 + 9 + 5 присутствуют две операции сложения. Начнем с самого крайнего (слева) члена: 2x + 28; вы не можете сложить 2х и 28, потому что не знаете значения переменной «х». Поэтому сложите 28 + 9 = 37. Теперь выражение можно переписать так: 2х + 37 — 5.
Вычтите. Это последняя операция в правильном порядке выполнения математических операций. На этом этапе вы также можете прибавлять отрицательные числа или же делать это на этапе сложения членов – это никак не отразится на конечном результате.
- В нашем примере 2х + 37 — 5 присутствует только одна операция вычитания: 37 — 5 = 32.
На этом этапе, проделав все математические операции, вы должны получить упрощенное выражение. Но если данное вам выражение содержит одну или несколько переменных, то помните, что член с переменной останется таким, как есть. Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
- В нашем примере окончательный ответ: 2х + 32. Вы не сможете сложить два члена, пока не узнаете значение переменной «х». Узнав значение переменной, вы с легкостью упростите этот двучлен.
Упрощение сложных выражений
Сложение подобных членов. Помните, что вычитать и складывать можно исключительно подобные члены, то есть члены с одинаковой переменной и одинаковым показателем степени. Например, можно сложить 7x и 5x, но нельзя складывать 7x и 5x 2 (так как здесь показатели степени разные).
- Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy 2 и -3xy 2 , но нельзя складывать 2xy 2 и -3x 2 y или 2xy 2 и -3y 2 .

- Рассмотрим пример: x 2 + 3x + 6 — 8x. Здесь подобными членами являются 3x и 8x, поэтому их можно сложить. Упрощенное выражение выглядит так: x 2 — 5x + 6.
- Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy 2 и -3xy 2 , но нельзя складывать 2xy 2 и -3x 2 y или 2xy 2 и -3y 2 .
Упростите числовую дробь. В такой дроби и в числителе, и в знаменателе находятся числа (без переменной). Числовая дробь упрощается несколькими способами. Во-первых, просто разделите знаменатель на числитель. Во-вторых, разложите числитель и знаменатель на множители и сократите одинаковые множители (так как при делении числа на само себя вы получите 1). Другими словами, если и у числителя, и у знаменателя есть один и тот же множитель, его можно отбросить и получить упрощенную дробь.
- Например, рассмотрим дробь 36/60. При помощи калькулятора разделите 36 на 60 и получите 0,6. Но вы можете упростить эту дробь и по-другому, разложив числитель и знаменатель на множители: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так как 6/6 = 1, то упрощенная дробь: 1 х 6/10 = 6/10. Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
Если дробь содержит переменную, можно сократить одинаковые множители с переменной. Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).
- Рассмотрим пример: (3x 2 + 3x)/(-3x 2 + 15x). Это выражение можно переписать (разложить на множители) в виде: (x + 1)(3x)/(3x)(5 — x). Так как член 3x находится и в числителе, и в знаменателе, его можно сократить, и вы получите упрощенное выражение: (х + 1)/(5 — х). Рассмотрим другой пример: (2x 2 + 4x + 6)/2 = (2(x 2 + 2x + 3))/2 = x 2 + 2x + 3.
- Обратите внимание, что вы не можете сокращать любые члены – сокращаются только одинаковые множители, которые присутствуют как в числителе, так и в знаменателе. Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).
Раскройте скобки. Для этого умножьте член, стоящий за скобкой, на каждый член в скобках. Иногда это помогает упростить сложное выражение. Это относится как к членам, которые являются простыми числами, так и к членам, которые содержат переменную.
- Например, 3(x 2 + 8) = 3x 2 + 24, а 3x(x 2 + 8) = 3x 3 + 24x.
- Обратите внимание, что в дробных выражениях скобки раскрывать не нужно, если и в числителе, и в знаменателе присутствует одинаковый множитель. Например, в выражении (3(x 2 + 8))/3x скобки раскрывать не нужно, так как здесь можно сократить множитель 3 и получить упрощенное выражение (x 2 + 8)/x. С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x 3 + 24x)/3x.
Разложите на множители многочлены. При помощи этого метода можно упростить некоторые выражения и многочлены. Разложение на множители – это операция, противоположная раскрытию скобок, то есть выражение записывается в виде произведения двух выражений, каждое из которых заключено в скобки. В некоторых случаях разложение на множители позволяет сократить одинаковое выражение. В особых случаях (как правило, с квадратными уравнениями) разложение на множители позволит вам решить уравнение.
- Рассмотрим выражение x 2 — 5x + 6. Оно раскладывается на множители: (x — 3)(x — 2). Таким образом, если, например, дано выражение (x 2 — 5x + 6)/(2(x — 2)), то вы можете переписать его в виде (x — 3)(x — 2)/(2(x — 2)), сократить выражение (х — 2) и получить упрощенное выражение (х — 3)/2.
- Разложение многочленов на множители применяется для решения (нахождения корней) уравнений (уравнение – это многочлен, приравненный к 0). Например, рассмотрим уравнение x 2 — 5x + 6 = 0. Разложив его на множители, вы получите (х — 3)(х — 2) = 0. Так как любое выражение, умноженное на 0, равно 0, то мы можем записать так: х — 3 = 0 и х — 2 = 0. Таким образом, х = 3 и х = 2, то есть вы нашли два корня данного вам уравнения.
Как освободиться от иррациональности в знаменателе: способы, примеры, решения
При изучении преобразований иррационального выражения очень важным является вопрос о том, как освободиться от иррациональности в знаменателе дроби. Целью этой статьи является объяснение этого действия на конкретных примерах задач. В первом пункте мы рассмотрим основные правила данного преобразования, а во втором – характерные примеры с подробными пояснениями.
Понятие освобождения от иррациональности в знаменателе
Начнем с пояснения, в чем вообще заключается смысл такого преобразования. Для этого вспомним следующие положения.
Об иррациональности в знаменателе дроби можно говорить в том случае, если там присутствует радикал, он же знак корня. Числа, которые записаны при помощи такого знака, часто относятся к числу иррациональных. Примерами могут быть 12, -2x+3, x+yx-2·x·y+1, 117-5 . К дробям с иррациональными знаменателями также относятся те, что имеют там знаки корней различной степени (квадратный, кубический и т.д.), например, 343, 1x+x·y4+y. Избавляться от иррациональности следует для упрощения выражения и облегчения дальнейших вычислений. Сформулируем основное определение:
Определение 1Освободиться от иррациональности в знаменателе дроби – значит преобразовать ее, заменив на тождественно равную дробь, в знаменателе которой не содержится корней и степеней.
Такое действие может называться освобождением или избавлением от иррациональности, смысл при этом остается тем же. Так, переход от 12 к 22 , т.е. к дроби с равным значением без знака корня в знаменателе и будет нужным нам действием. Приведем еще один пример: у нас есть дробь xx-y . Проведем необходимые преобразования и получим тождественно равную ей дробь x·x+yx-y, освободившись от иррациональности в знаменателе.
После формулировки определения мы можем переходить непосредственно к изучению последовательности действий, которые нужно выполнить для такого преобразования.
Основные действия для избавления от иррациональности в знаменателе дроби
Для освобождения от корней нужно провести два последовательных преобразования дроби: умножить обе части дроби на число, отличное от нуля, а затем преобразовать выражение, получившееся в знаменателе. Рассмотрим основные случаи.
В наиболее простом случае можно обойтись преобразованием знаменателя. Например, мы можем взять дробь со знаменателем, равным корню из 9. Вычислив 9, мы запишем в знаменателе 3 и избавимся таким образом от иррациональности.
Однако гораздо чаще приходится предварительно умножать числитель и знаменатель на такое число, которое потом позволит привести знаменатель к нужному виду (без корней). Так, если мы выполним умножение 1x+1 на x+1, мы получим дробь x+1x+1·x+1 и сможем заменить выражение в ее знаменателе на x+1. Так мы преобразовали 1x+1 в x+1x+1 , избавившись от иррациональности.
Иногда преобразования, которые нужно выполнить, бывают довольно специфическими. Разберем несколько наглядных примеров.
Как преобразовать выражение в знаменателе дроби
Как мы уже говорили, проще всего выполнить преобразование знаменателя.
Пример 1Условие: освободите дробь 12·18+50 от иррациональности в знаменателе.
Решение
Для начала раскроем скобки и получим выражение 12·18+2·50. Используя основные свойства корней, перейдем к выражению 12·18+2·50. Вычисляем значения обоих выражений под корнями и получаем 136+100. Здесь уже можно извлечь корни. В итоге у нас получилась дробь 16+10, равная 116. На этом преобразования можно закончить.
Запишем ход всего решения без комментариев:
12·18+50=12·18+2·50==12·18+2·50=136+100=16+10=116
Ответ: 12·18+50=116.
Пример 2Условие: дана дробь 7-x(x+1)2. Избавьтесь от иррациональности в знаменателе.
Решение
Ранее в статье, посвященной преобразованиям иррациональных выражений с применением свойств корней, мы упоминали, что при любом A и четных n мы можем заменить выражение Ann на |A| на всей области допустимых значений переменных. Следовательно, в нашем случае мы можем записать так: 7-xx+12=7-xx+1 . Таким способом мы освободились от иррациональности в знаменателе.
Ответ: 7-xx+12=7-xx+1.
Избавление от иррациональности методом умножения на корень
Если в знаменателе дроби находится выражение вида A и само выражение A не имеет знаков корней, то мы можем освободиться от иррациональности, просто умножив обе части исходной дроби на A. Возможность этого действия определяется тем, что A на области допустимых значений не будет обращаться в 0. После умножения в знаменателе окажется выражение вида A·A, которое легко избавить от корней: A·A=A2=A. Посмотрим, как правильно применять этот метод на практике.
Пример 3Условие: даны дроби x3 и -1×2+y-4. Избавьтесь от иррациональности в их знаменателях.
Решение
Выполним умножение первой дроби на корень второй степени из 3. Получим следующее:
x3=x·33·3=x·332=x·33
Во втором случае нам надо выполнить умножение на x2+y-4 и преобразовать получившееся выражение в знаменателе:
-1×2+y-4=-1·x2+y-4×2+y-4·x2+y-4==-x2+y-4×2+y-42=-x2+y-4×2+y-4
Ответ: x3=x·33 и -1×2+y-4=-x2+y-4×2+y-4 .
Если же в знаменателе исходной дроби имеются выражения вида Anm или Amn (при условии натуральных m и n), нам нужно выбрать такой множитель, чтобы получившееся выражение можно было преобразовать в Ann·k или An·kn (при натуральном k). После этого избавиться от иррациональности будет несложно. Разберем такой пример.
Пример 4Условие: даны дроби 7635 и xx2+1415. Избавьтесь от иррациональности в знаменателях.
Решение
Нам нужно взять натуральное число, которое можно разделить на пять, при этом оно должно быть больше трех. Чтобы показатель 6 стал равен 5, нам надо выполнить умножение на 625. Следовательно, обе части исходной дроби нам придется умножить на 625:
7635=7·625635·625=7·625635·62=7·625655==7·6256=7·3656
Во втором случае нам потребуется число, большее 15, которое можно разделить на 4 без остатка. Берем 16. Чтобы получить такой показатель степени в знаменателе, нам надо взять в качестве множителя x2+14. Уточним, что значение этого выражения не будет 0 ни в каком случае. Вычисляем:
xx2+1415=x·x2+14×2+1415·x2+14==x·x2+14×2+1416=x·x2+14×2+1444=x·x2+14×2+14
Ответ: 7635=7·3656 и xx2+1415=x·x2+14×2+14.
Избавление от иррациональности методом умножения на сопряженное выражение
Следующий метод подойдет для тех случаев, когда в знаменателе исходной дроби стоят выражения a+b, a-b, a+b, a-b, a+b, a-b. В таких случаях нам надо взять в качестве множителя сопряженное выражение. Поясним смысл этого понятия.
Для первого выражения a+b сопряженным будет a-b, для второго a-b – a+b . Для a+b – a-b, для a-b – a+b, для a+b – a-b, а для a-b – a+b. Иначе говоря, сопряженное выражение – это такое выражение, в котором перед вторым слагаемым стоит противоположный знак.
Давайте рассмотрим, в чем именно заключается данный метод. Допустим, у нас есть произведение вида a-b·a+b . Оно может быть заменено разностью квадратов a-b·a+b=a2-b2, после чего мы переходим к выражению a−b, лишенному радикалов. Таким образом, мы освободились от иррациональности в знаменателе дроби с помощью умножения на сопряженное выражение. Возьмем пару наглядных примеров.
Пример 5Условие: избавьтесь от иррациональности в выражениях 37-3 и x-5-2.
Решение
В первом случае берем сопряженное выражение, равное 7+3. Теперь производим умножение обеих частей исходной дроби на него:
37-3=3·7+37-3·7+3=3·7+372-32==3·7+37-9=3·7+3-2=-3·7+32
Во втором случае нам понадобится выражение -5+2, которое является сопряженным выражению -5-2. Умножим на него числитель и знаменатель и получим:
x-5-2=x·-5+2-5-2·-5+2==x·-5+2-52-22=x·-5+25-2=x·2-53
Возможно также перед умножением выполнить преобразование: если мы вынесем из знаменателя сначала минус, считать будет удобнее:
x-5-2=-x5+2=-x·5-25+2·5-2==-x·5-252-22=-x·5-25-2=-x·5-23==x·2-53
Ответ: 37-3=-3·7+32 и x-5-2=x·2-53.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеВажно обратить внимание на то, чтобы выражение, полученное в итоге умножения, не обращалось в 0 ни при каких переменных из области допустимых значений для данного выражения.
Пример 6Условие: дана дробь xx+4. Преобразуйте ее так, чтобы в знаменателе не было иррациональных выражений.
Решение
Начнем с нахождения области допустимых значений переменной x. Она определена условиями x≥0 и x+4≠0. Из них можно сделать вывод, что нужная область представляет собой множество x≥0.
Сопряженное знаменателю выражение представляет собой x-4. Когда мы можем выполнить умножение на него? Только в том случае, если x-4≠0 . На области допустимых значений это будет равносильно условию x≠16. В итоге мы получим следующее:
xx+4=x·x-4x+4·x-4==x·x-4×2-42=x·x-4x-16
Если x будет равен 16, то мы получим:
xx+4=1616+4=164+4=2
Следовательно, xx+4=x·x-4x-16 при всех значениях x, принадлежащих области допустимых значений, за исключением 16. При x=16 получим xx+4=2.
Ответ: xx+4=x·x-4x-16, x∈[0, 16)∪(16, +∞)2, x=16.
Преобразование дробей с иррациональностью в знаменателе с использованием формул суммы и разности кубов
В предыдущем пункте мы выполняли умножение на сопряженные выражения с тем, чтобы потом использовать формулу разности квадратов. Иногда для избавления от иррациональности в знаменателе полезно воспользоваться и другими формулами сокращенного умножения, например, разностью кубов a3−b3=(a−b)·(a2+a·b+b2). Этой формулой удобно пользоваться, если в знаменателе исходной дроби стоят выражения с корнями третьей степени вида A3-B3, A32+A3·B3+B32. и т.д. Чтобы применить ее, нам нужно умножить знаменатель дроби на неполный квадрат суммы A32+A3·B3+B32 или разность A3-B3. Точно также можно применить и формулу суммы a3+b3=(а)·(a2−a·b+b2).
Пример 7Условие: преобразуйте дроби 173-23 и 34-2·x3+x23 так, чтобы избавиться от иррациональности в знаменателе.
Решение
Для первой дроби нам нужно воспользоваться методом умножения обеих частей на неполный квадрат суммы 73 и 23, поскольку потом мы сможем выполнить преобразование с помощью формулы разности кубов:
173-23=1·732+73·23+23273-23·732+73·23+232==732+73·23+232733-233=723+7·23+2237-2==493+143+435
Во второй дроби представим знаменатель как 22-2·x3+x32. В этом выражении виден неполный квадрат разности 2 и x3 , значит, мы можем умножить обе части дроби на сумму 2+x3 и воспользоваться формулой суммы кубов. Для этого должно быть соблюдено условие 2+x3≠0, равносильное x3≠-2 и x≠−8:
34-2·x3+x23=322-2·x3+x32==3·2+x322-2·x3+x32·2+x3=6+3·x323+x33==6+3·x38+x
Подставим в дробь -8 и найдем значение:
34-2·83+823=34-2·2+4=34
Подведем итоги. При всех x, входящих в область значений исходной дроби (множество R), за исключением -8, мы получим 34-2·x3+x23=6+3·x38+x. Если x=8, то 34-2·x3+x23=34.
Ответ: 34-2·x3+x23=6+3·x38+x, x≠834, x=-8.
Последовательное применение различных способов преобразования
Часто на практике встречаются более сложные примеры, когда мы не можем освободиться от иррациональности в знаменателе с помощью всего одного метода. Для них нужно последовательно выполнять несколько преобразований или подбирать нестандартные решения. Возьмем одну такую задачу.
Пример NУсловие: преобразуйте 574-24, чтобы избавиться от знаков корней в знаменателе.
Решение
Выполним умножение обеих частей исходной дроби на сопряженное выражение 74+24 с ненулевым значением. Получим следующее:
574-24=5·74+2474-24·74+24==5·74+24742-242=5·74+247-2
А теперь применим тот же способ еще раз:
5·74+247-2=5·74+24·7+27-2·7+2==5·74+24·7+272-22=5·74+74·7+27-2==5·74+24·7+25=74+24·7+2
Ответ: 574-24=74+24·7+2.
Обратная польская запись онлайн
Символ Операция Стек Выходная строка s добавить к выходной строке sqrt ( поместить в стек ( sqrt x добавить к выходной строке ( sqrt, x ) 1) присоединить содержимое стека до скобки в обратном порядке к выходной строке; 2) удалить скобку из стека. sqrt, x — поместить в стек — sqrt, x 1 добавить к выходной строке — sqrt, x, 1 / поместить в стек -, / sqrt, x, 1 2 добавить к выходной строке -, / sqrt, x, 1, 2 * 1) присоединить стек в обратном порядке к выходной строке; 2) поместить новую операцию в стек. -, * sqrt, x, 1, 2, / s добавить к выходной строке -, * sqrt, x, 1, 2, /, sin ( поместить в стек -, *, ( sqrt, x, 1, 2, /, sin x добавить к выходной строке -, *, ( sqrt, x, 1, 2, /, sin, x ^ поместить в стек -, *, (, ^ sqrt, x, 1, 2, /, sin, x 2 добавить к выходной строке -, *, (, ^ sqrt, x, 1, 2, /, sin, x, 2 — 1) присоединить стек в обратном порядке к выходной строке; 2) поместить новую операцию в стек., 2, — Упростите радикальные рациональные выражения с помощью программы «Пошаговое решение математических задач»
В разделе 3 главы 1 есть несколько очень важных определений, которые мы использовали много раз. Поскольку эти определения приобретают новое значение в этой главе, мы повторим их.
Когда алгебраическое выражение состоит из частей, соединенных знаками + или -, эти части вместе с их знаками называются членами выражения.
a + b состоит из двух членов.
2x + 5y — 3 состоит из трех членов.В a + b термины a и b. В 2x + 5y — 3 термины 2x, 5y и -3. Когда алгебраическое выражение состоит из частей, которые нужно умножить, эти части называются коэффициентами выражения.
ab имеет множители a и b.
Очень важно уметь различать термины и факторы. Правила, применяемые к условиям, в целом не применяются к факторам. Называя термины или факторы, необходимо учитывать все выражение.
С этого момента во всей алгебре вы будете использовать слова , термин и коэффициент , . Убедитесь, что вы понимаете определения. Показатель степени — это число, используемое для обозначения того, сколько раз коэффициент должен использоваться в продукте. Показатель степени обычно записывается как меньшее (по размеру) число немного выше и правее множителя, на который влияет показатель степени.
Показатель степени иногда называют «степенью».«Например, 5 3 можно обозначить как« пять в третьей степени ». Обратите внимание на разницу между 2x 3 и (2x) 3 . Используя круглые скобки в качестве символов группировки, мы видим, что
2x 3 означает 2 (x) (x) (x), тогда как (2x) 3 означает (2x) (2x) (2x) или 8x 3 .
Если не используются скобки, показатель степени влияет только на коэффициент, непосредственно предшествующий ему. В таком выражении, как 5x 4
5 — коэффициент ,
x — основание ,
4 — показатель степени .
5x 4 означает 5 (x) (x) (x) (x).Обратите внимание, что экспонента влияет только на основание.
Многие студенты допускают ошибку, умножая основание на показатель степени. Например, они скажут 3 4 = 12 вместо правильного ответа,
3 4 = (3) (3) (3) ( 3) = 81.Когда мы пишем буквальное число, такое как x, будет понятно, что коэффициент равен единице, а показатель степени равен единице. Это может быть очень важно во многих операциях.
x означает 1x 1 .
ЗАДАЧИ
По завершении этого раздела вы сможете правильно применить первый закон экспонент.
Теперь, когда мы рассмотрели эти определения, мы хотим установить очень важные законы экспонент.Эти законы вытекают непосредственно из определений.
Первый закон экспонент Если a и b — натуральные числа, а x — действительное число, то
Чтобы умножить множители с одинаковым основанием, сложите экспоненты. Применительно к любому правилу, закону или формуле мы всегда должны быть очень осторожны, чтобы выполнить требуемые условия, прежде чем пытаться применить их. Обратите внимание, что в приведенном выше законе база одинакова для обоих факторов.Этот закон применяется только при соблюдении этого условия.
Эти факторы не имеют одинакового основания. Показатель степени 1 обычно не записывается. Когда мы пишем x, предполагается показатель степени: x = x1. Это необходимо для применения законов экспонент.
Если выражение содержит результат различных оснований, мы применяем закон к одинаковым основаниям.
УМНОЖЕНИЕ МОНОМОВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Распознать моном.
- Найдите произведение нескольких одночленов.
Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.
не является мономом, поскольку задействована операция сложения. предполагает операцию разделения. Чтобы найти произведение двух одночленов , умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.
Вы помните первый закон экспонентов? Умножьте 5 на 3 и сложите показатели x.
Помните, что если показатель не записан, подразумевается показатель, равный единице.МОНОМИЛЫ, УМНОЖЕННЫЕ НА ПОЛИНОМЫ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Распознавать многочлены.
- Определите биномы и трехчлены.
- Найдите произведение одночлена на двучлен.
Многочлен — это сумма или разность одного или нескольких одночленов.
Обычно, если существует более одной переменной, многочлен записывается в алфавитном порядке. Для некоторых многочленов используются специальные имена. Если полином состоит из двух членов, он называется биномом .
Если многочлен состоит из трех членов, он называется трехчленом .
В процессе удаления скобок мы уже отметили, что на все термины в скобках влияет знак или число, стоящее перед скобками. Теперь мы расширим эту идею, чтобы умножить одночлен на многочлен.
Размещение 2x непосредственно перед скобками означает умножение выражения в скобках на 2x. Обратите внимание, что каждый член умножается в 2 раза. Опять же, каждый член в скобках умножается на 3y 2 Опять же, каждый член в круглых скобках умножается на 3y 2 .
В каждом из этих примеров мы используем свойство распределения .ПОЛИНОМИЧЕСКИЕ ТОВАРЫ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите произведение двух биномов.
- Используйте свойство распределения, чтобы умножить любые два полинома.
В предыдущем разделе вы узнали, что произведение A (2x + y) расширяется до A (2x) + A (y).
Теперь рассмотрим произведение (3x + z) (2x + y).
Поскольку (3x + z) находится в круглых скобках, мы можем рассматривать его как единственный множитель и расширять (3x + z) (2x + y) так же, как A (2x + y). Это дает нам
Если мы теперь расширим каждый из этих терминов, у нас будет
Обратите внимание, что в окончательном ответе каждый член одной круглой скобки умножается на каждый член другой круглой скобки.
Обратите внимание, что это приложение свойства распределения. Обратите внимание, что это приложение свойства распределения. Так как — 8x и 15x — аналогичные термины, мы можем объединить их, чтобы получить 7x.
В этом примере мы смогли объединить два термина, чтобы упростить окончательный ответ.
Здесь мы снова объединили некоторые термины, чтобы упростить окончательный ответ. Обратите внимание, что порядок терминов в окончательном ответе не влияет на правильность решения.
Свойство коммутативности позволяет изменять порядок. Попытайтесь создать систему для умножения каждого члена одной круглой скобки на каждый член другой.В этих примерах мы взяли первый член в первом наборе круглых скобок и умножили его на каждый член во втором наборе круглых скобок. Затем мы взяли второй член первого набора и умножили его на каждый член второго набора, и так далее. ПОЛНОМОЧИЯ И КВАДРАТНЫЕ КОРНИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Правильно применяйте второй закон экспонент.
- Найдите квадратные корни и главные квадратные корни чисел, являющихся точными квадратами.
Теперь мы хотим установить второй закон экспонент. Обратите внимание на следующие примеры, как этот закон выводится с использованием определения показателя степени и первого закона экспоненты.
по значению показателя 3.
Теперь по первому закону экспонент имеем
В целом отметим, что
Это означает, что ответ будет
.Помните, чтобы умножить общее основание, добавьте экспоненты. Если мы просуммируем член a b раз, мы получим произведение a и b. Отсюда мы видим, что
Второй закон экспонент Если a и b — натуральные числа, а x — действительное число, то
.Другими словами, «чтобы возвести степень основания x в степень, умножьте степень».
.
Обратите внимание, что каждый показатель должен быть умножен на 4. Обратите внимание, что когда факторы сгруппированы в круглых скобках, на каждый фактор влияет показатель степени.
.
Опять же, каждый множитель должен быть возведен в третью степень.
Используя определение показателей, (5) 2 = 25. Мы говорим, что 25 — это квадрат 5. Теперь мы вводим новый термин в наш алгебраический язык. Если 25 равно квадрату 5, то говорят, что 5 является квадратным корнем из 25.
Если x 2 = y, то x представляет собой квадратный корень из y.
Обратите внимание, мы говорим, что 5 — это , это квадратный корень из , а не , как квадратный корень из .Вы скоро поймете, почему. .
Из последних двух примеров вы заметите, что 49 имеет два квадратных корня, 7 и — 7. Это правда, что на самом деле каждое положительное число имеет два квадратных корня.
Фактически, один квадратный корень положительный, а другой отрицательный. .
Каковы квадратные корни из 36? Главный квадратный корень положительного числа — это положительный квадратный корень.
Символ «» называется знаком корня и обозначает основную часть
обозначает главный квадратный корень или положительный квадратный корень из 9. Обратите внимание на разницу в этих двух задачах.
а. Найдите квадратные корни из 25.
b. Находить .Очень важно понимать разницу между этими двумя утверждениями. Для а. ответ будет +5 и -5, поскольку (+ 5) 2 = 25 и (- 5) 2 = 25.
Для б. ответ — +5, поскольку знак корня представляет собой главный или положительный квадратный корень.
Целые числа, такие как 16, 25, 36 и т. Д., Квадратные корни которых являются целыми числами, называются полными квадратными числами . В настоящее время нас интересуют только квадратные корни из полных квадратных чисел. В следующей главе мы будем иметь дело с оценкой и упрощением указанного квадратного корня из чисел, которые не являются точными квадратными числами.Иногда можно увидеть символ +/-.Это означает, что требуются оба квадратных корня из числа. Например,
+/- 5 — это краткий способ написания + 5 и -5.ЗАКОНОДАТЕЛЬСТВО О ПОДРАЗДЕЛЕНИИ ДЕЯТЕЛЬНОСТИ
ЗАДАЧИ
По завершении этого раздела вы должны уметь правильно применять третий закон экспонент.
Прежде чем приступить к установлению третьего закона экспонент, мы сначала рассмотрим некоторые факты о действии деления.
- Разделение двух чисел можно обозначить знаком деления или написанием одного числа поверх другого с полосой между ними.Шесть, разделенная на два, записывается как
- Деление связано с умножением по правилу, если тогда а = быть. Это проверка для всех проблем с разделением. Например, мы знаем это, потому что 18 = (6) (3).
- Деление на ноль невозможно. Для оценки нам необходимо найти число, которое при умножении на ноль даст 5. Такого числа не существует.
- Ненулевое число, разделенное на себя, равно 1.
. Умножьте значения в кружках, чтобы получить.
Это очень важно! Если a — любое ненулевое число, то не имеет значения.Из (3) мы видим, что выражение типа as не имеет смысла, если мы не знаем, что y 0. В этом и будущих разделах всякий раз, когда мы будем писать дробь, будет предполагаться, что знаменатель не равен нулю. Теперь, чтобы установить закон деления показателей, воспользуемся определением показателей.
Важно! Прочтите этот абзац еще раз! Мы знаем, что = 1.Мы также предполагаем, что x представляет собой ненулевое число. В таком примере нам не нужно разделять количества, если мы помним, что количество, разделенное само на себя, равно единице. В приведенном выше примере мы могли бы написать
Три x в знаменателе разделят три x в числителе. Помните, что 1 должна быть записана, если это единственный член в числителе. Из предыдущих примеров мы можем обобщить и прийти к следующему закону:
Третий закон экспонент Если a и b — натуральные числа, а x — ненулевое действительное число, то
Если мы попытаемся использовать только ту часть закона, которая указывает на такое выражение, как, например, мы получим
На данный момент отрицательные показатели не определены.Мы обсудим их позже.РАЗДЕЛЕНИЕ МОНОМИАЛА НА МОНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете упростить выражение, уменьшив дробь, включающую коэффициенты, а также используя третий закон экспонент.
Мы должны помнить, что коэффициенты и показатели управляются разными законами, потому что они имеют разные определения. При делении одночленов коэффициенты делятся, а показатели вычитаются согласно закону деления показателей.
Если деление невозможно или если с помощью коэффициентов возможно только уменьшение дроби, это не влияет на использование закона экспонент для деления.
Уменьшите этот тип дроби в два этапа:
1. Уменьшите коэффициенты.
2. Используйте третий закон экспонент.РАЗДЕЛЕНИЕ ПОЛИНОМА НА МОНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете разделить многочлен на одночлен.
Разделение многочлена на одночлен требует еще одного очень важного факта в дополнение к тому, что мы уже использовали. Дело в том, что если в числителе дроби несколько членов, то каждый член нужно разделить на знаменатель.
Таким образом, мы фактически используем в этом процессе свойство распределения. РАЗДЕЛЕНИЕ ПОЛИНОМА НА БИНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете правильно применить алгоритм деления в столбик для деления полинома на бином.
Процесс деления многочлена на другой многочлен будет ценным инструментом в последующих разделах. Здесь мы разработаем методику и обсудим причины, по которым она работает в будущем.
Этот метод называется алгоритмом длинного деления . Алгоритм — это просто метод, которому необходимо точно следовать. Поэтому представим его в пошаговом формате и на примере.
Вспомните три выражения в разделе деления:
Если нас попросят расположить выражение в порядке убывания, мы напишем.Нулевой коэффициент дает 0x 3 = 0. По этой причине член x 3 отсутствовал или не был записан в исходном выражении.Решение
Шаг 1: Расположите как делитель, так и делимое в порядке убывания переменной (это означает, что сначала наивысший показатель степени, затем следующий наивысший второй и т. Д.) И укажите нулевой коэффициент для любых пропущенных членов. (В этом примере нет необходимости менять расположение и отсутствуют пропущенные термины.) Затем расположите делитель и делимое следующим образом:
Шаг 2: Чтобы получить первый член частного, в этом случае разделите первый член дивиденда на первый член делителя. Мы записываем это следующим образом:
Шаг 3: Умножьте весь делитель на член, полученный на шаге 2. Вычтите результат из делимого следующим образом:
Убедитесь, что вы указываете частное непосредственно над количеством, на которое делите.В этом случае x делится на x 2 x раз. Шаг 4: Разделите первый член остатка на первый член делителя, чтобы получить следующий член частного. Затем умножьте весь делитель на полученный член и снова вычтите следующим образом:
Первый член остатка (-2x — 14) равен -2x.
Умножьте (x + 7) на -2.Этот процесс повторяется до тех пор, пока остаток не станет равен нулю (как в этом примере) или степень первого члена остатка не станет меньше степени первого члена делителя.
Как и в арифметике, деление проверяется умножением. Мы должны помнить, что (частное) X (делитель) + (остаток) = (делимое).
Чтобы проверить этот пример, мы умножаем (x + 7) и (x — 2), чтобы получить x 2 + 5x — 14.
Поскольку это дивиденд, ответ правильный.
Опять же, (частное) X (делитель) + (остаток) = (делимое) Ответ: x — 3. Проверяя, находим (x + 3) (x — 3)
Распространенная ошибка — забыть написать пропущенный член с нулевым коэффициентом. РЕЗЮМЕ
Ключевые слова
- Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.
- Многочлен — это сумма или разность одного или нескольких одночленов.
- Бином — это многочлен, состоящий из двух членов.
- Трехчлен — это многочлен, состоящий из трех членов.
- Если x 2 = y, то x представляет собой квадратный корень из y.
- Главный квадратный корень положительного числа — это положительный квадратный корень.
- Символ называется корнем и указывает на главный квадратный корень числа.
- Квадратный корень совершенного квадратного числа имеет целые числа.
Процедуры
- Первый закон экспонент: x a x b = x a + b .
- Чтобы найти произведение двух одночленов, умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.
- Чтобы умножить многочлен на другой многочлен, умножьте каждый член одного многочлена на каждый член другого и объедините одинаковые члены.
- Второй закон экспонент: (x a ) b = x ab .
- Третий закон экспонент
- Чтобы разделить одночлен на одночлен, разделите числовые коэффициенты и используйте третий закон экспонент для буквальных чисел.
- Чтобы разделить многочлен на одночлен, разделите каждый член многочлена на одночлен.
- Чтобы разделить многочлен на бином, используйте алгоритм деления в столбик.
Упростить калькулятор — Solumaths
Краткое описание:
Калькулятор, который может упростить алгебраическое выражение онлайн.
упростить онлайнОписание:
Упростить выражение или отменить выражение означает уменьшить его путем группировки терминов. Калькулятор позволяет с помощью этой функции компьютерной алгебры сокращать алгебраическое выражение.Используемая с функцией expand, функция simpleify может разворачивать и сворачивать литеральное выражение.
Упростить алгебраическое выражение
Калькулятор может выполнять расчет с буквами (буквальный расчет), эта функция позволяет группировать, собирать члены выражения, чтобы получить сокращенную форму этого выражения.
Чтобы упростить выражение , введите выражение , чтобы отменить и примените функцию упрощения.Таким образом, для упрощения выражения после a + 2a, введите команду simpleify (`a + 2a`) или непосредственно a + 2a, после вычисления возвращается сокращенная форма выражения 3a.
Возможности упрощения калькулятора применимы к буквенно-цифровым выражениям и, следовательно, также к чисто числовым выражениям.
Упростить числовое выражение
Упрощенный калькулятор также применяется к числовым выражениям, он позволяет выполнять точные вычисления с числами:
- Например, калькулятор может упростить следующее выражение 1 + 2-5, чтобы получить результат этого расчета, введите упрощать (`1 + 2-5`), калькулятор возвращает -2
- Другой пример выражения, в котором калькулятор может упростить `1 + 2-5 / 3`, чтобы уменьшить это выражение, введите упрощать (`1 + 2-5 / 3`), после вычисления результата возвращается «4/3».
Упростить дроби
Этот калькулятор дает возможность упростить дробь , чтобы сделать Вычисление выражения , состоящее из дробей и дать результат в виде неприводимой дроби в виде специализированной калькулятор дробей делает. В калькулятор дробей однако особенность состоит в том, чтобы предоставить этапы расчетов, позволяющих получить уменьшенная фракция .к`). Следует отметить, что в этой дроби показатель степени числителя и показатель степени знаменателя содержат буквы. Благодаря своим буквальным вычислительным возможностям калькулятор может легко упростить эту дробь.
Упростить комплексные числа
Калькулятор позволяет управлять комплексными числами в их алгебраической форме, он может упростить выражение, состоящее из комплексных чисел , как и калькулятор комплексных чисел .
Упростите функции благодаря их свойствам
Калькулятор использует разные методы для упрощения математических выражений: он использует четность функций для упрощения определенных результатов.
Например, чтобы упростить следующее выражение simpleify (`cos (x) + cos (-x)`), калькулятор использует четность функции косинуса. Для некоторых расчетов калькулятор указывает свойства, используемые для упрощения результатов, как показано в предыдущем примере.
Упростить тригонометрические выражения
Калькулятор также позволяет манипулировать тригонометрическими выражениями, он может упростить этот тип выражения, используя обычные тригонометрические формулы .
Таким образом, можно использовать этот калькулятор в качестве калькулятора тригонометрии для упрощает тригонометрические выражения , такие как следующие Упростить (`cos (x + pi / 2) + cos (-x) + sin (x + pi)`).Для некоторых вычислений калькулятор указывает свойства, используемые для уменьшения результатов, как показано в предыдущем примере.
Упростите Surds
Калькулятор также позволяет упрощать сурды, он может упростить извлечение квадратного корня, используя свойства функции извлечения квадратного корня. 2` Рассчитывайте онлайн с упрощением (Упростить калькулятор)
Логическая алгебра — Курс цифровой электроники
Булева алгебра, логическая алгебра, позволяет применять к логике правила, используемые в алгебре чисел.Он формализует правила логики. Булева алгебра используется для упрощения логических выражений которые представляют собой комбинационные логические схемы. Он сокращает исходное выражение до эквивалентного выражения с меньшим количеством терминов, что означает, что для реализации требуется меньше логических вентилей. комбинационная логическая схема.
Калькулятор логических выражений
Используйте калькулятор, чтобы найти сокращенное логическое выражение или проверить свои собственные ответы.
Ваш ответ
- Примечания:
- Используйте ~ * + для обозначения НЕ И ИЛИ соответственно.Не пропускайте оператор * для операции И.
- (~ AB) + (B ~ C) + (AB) вернет ошибку
- (~ A * B) + (B * ~ C) + (A * B) в порядке
- Логические операции следуют порядку приоритета НЕ И ИЛИ. Выражения внутри скобок () всегда оцениваются первыми, имея приоритет над порядком приоритета.
- Пожалуйста, вводите только переменные, константы вроде 0,1 не допускаются.
- Переменные E, I, N, O, Q, S не допускаются
Упрощение логических выражений
Ниже показан пример использования алгебраических методов для упрощения логического выражения
~ (A * B) * (~ A + B) * (~ B + B) ~ (A * B) * (~ A + B) * 1 6 — Закон дополнения ~ (A * B) * (~ A + B) 5 — Закон идентичности (~ A + ~ B) * (~ A + B) 8 — Закон ДеМоргана ~ A + ~ B * B 4 — Закон распределения ~ A + 0 6 — Закон дополнения ~ A 5 — Закон идентичности Каждая строка дает новое выражение и правило или правила, использованные для его вывода из предыдущего.Обычно есть несколько способов достичь результата.
Законы булевой алгебры
Законы логической алгебры используются для упрощения логических выражений.
- Идемпотентный закон
- Ассоциативный закон
- (A * B) * C = A * (B * C)
- (A + B) + C = A + (B + C)
- Коммутативный закон
- А * В = В * А
- А + В = В + А
- Распределительное право
- А * (В + С) = А * В + А * С
- A + (B * C) = (A + B) * (A + C)
- Закон о личности
- А * 0 = 0 А * 1 = А
- А + 1 = 1 А + 0 = А
- Закон о дополнении
- Закон об инволюции
- Закон ДеМоргана
- ~ (A * B) = ~ A + ~ B
- ~ (A + B) = ~ A * ~ B
Законы о резервировании
- Поглощение
- А + (А * В) = А
- А * (А + В) = А
- (А * В) + (А * ~ В) = А
- (А + В) * (А + ~ В) = А
- А + (~ А * В) = А + В
- А * (~ А + В) = А * В
Основные логические законы
Каждый закон описывается двумя частями, которые являются двойными друг другу.Принцип двойственности
- Перестановка операций + (ИЛИ) и * (И) в выражении.
- Замена элементов 0 и 1 в выражении местами.
- Не меняет форму переменных.
Применение булевой алгебры
Проектирование комбинационной логической схемывключает следующие этапы.
- Из проектной спецификации найдите таблицу истинности
- Из таблицы истинности выведите логическое выражение «Сумма произведений».
- Используйте логическую алгебру, чтобы упростить логическое выражение. Чем проще логическое выражение, тем меньше логических элементов будет использоваться.
- Используйте логические элементы для реализации упрощенного логического выражения.
Присоединяйтесь к обсуждению
Поскольку доходы от рекламы падают, несмотря на увеличение числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда. Благодаря щедрости наших посетителей, которые давали ранее, вы можете использовать этот сайт бесплатно.
Если вы получили пользу от этого сайта и можете, пожалуйста, отдать 10 долларов через Paypal . Это позволит нам продолжаем в будущее. Это займет всего минуту. Спасибо!
Я хочу дать!
© 2021 Emant Pte Ltd Co., рег. № 200210155R | Условия использования | Конфиденциальность | О нас
Калькулятор бесплатного срока
Этот калькулятор упрощает термины, которые могут содержать дроби, скобки или степени.Термины «>
Что такое термин?
Термин — это слово для обозначения всего, что состоит из чисел, переменных и арифметических знаков. Это означает, что это так же, как и термины.Термин, содержащий знак квадратного корня, называется корневым термином. Член, содержащий дробь, называется дробным членом.
Особый набор терминов — это многочлены, состоящие только из чисел и степеней x.
Термин — это вычисление, состоящее из чисел и переменных.Переменные представляют собой буквы, обозначающие числа. Обычно неизвестно, за какими числами стоят переменные. Поэтому нельзя сильно упрощать термины.
Для чего нужны термины?
Чтобы иметь возможность производить расчеты с вещами, которых вы не знаете. Например, вы можете продавать вафли за доллары и торт за доллары. Сколько денег ты зарабатываешь? Ну, это зависит от того, сколько вы продаете. За w проданных вафель вы зарабатываете доллары. За k проданных тортов вы зарабатываете доллары. Итак, вы зарабатываете доллары, и вот вам срок.Если вы сейчас продаете, например, колебания и кусочки торта, вам просто нужно вставить вместо w и k и обнаружить, что вы заработали доллары, то есть доллары.Как упростить термины?
Вы можете, например, сложите все появляющиеся числа вместе.
Пример:
Вы также можете объединить элементы, принадлежащие одной и той же переменной, например или же .
Если появляются разные переменные, упрощение не всегда возможно. Например, невозможно упростить, не зная чего-то о a, b и c.Что расширяется?
Если член находится в скобках и это число на что-то умножается, вы можете умножить каждое слагаемое этого члена (это означает: умножаемые части разделяются знаками + или -.Пример:
Как я могу понять, что запрещено условиями?
Простое правило: все, что подходит для каждого числа, подходит и для условий.Можно еще примеры?
Конечно. Это Mathepower. Просто введите свое упражнение, и Mathepower упростит ваш термин.Что делает эта программа?
Он шаг за шагом упрощает условия. В Mathepower есть расчетные сценарии почти для каждой части школьной математики, которые помогут вам решать ваши упражнения или проверять решения.{\ frac {3} {2}} \], и вы получите нежелательный результат, а не тот, который планировали. Поэтому разумно используйте круглые скобки для группировки терминов, которые вы собираетесь сгруппировать.
Как вы решаете алгебраические выражения шаг за шагом?
Необходимо учитывать несколько правил. Главный из них — это соблюдение правильного порядка операций с использованием правила PEMDAS. Сначала вам нужно удалить круглые скобки, соблюдая порядок операций. Затем вам нужно будет сократить дробные части и радикалы по мере их появления в выражении.{1/2})) \)
Помимо этого калькулятора алгебраических выражений, вы можете изучить наш раздел решателей алгебры и калькуляторов, чтобы увидеть, какие другие калькуляторы могут быть вам полезны.
Если у вас есть какие-либо предложения или вы хотите сообщить о неисправном решателе / калькуляторе, пожалуйста, не стесняйтесь обращаться к , свяжитесь с нами .
Калькулятор упрощенных выражений
Автор Сообщение JogjoBap Зарегистрировано: 01.10.2002
Откуда: Арканзас, США.Размещено: 28 декабря, четверг, 11:59 Привет, ребята и девчонки! Недавно я нанял репетитора по математике, который помогал мне разобраться в некоторых темах алгебры.Мои проблемные области включали такие темы, как упрощение калькулятора выражений и сокращение дробей. Теперь этот учитель оказался таким тупым, что вместо того, чтобы помочь мне сейчас, я запутался еще больше, чем был раньше. Я до сих пор не могу решить проблемы по этим темам. Приближается время экзамена. Мне нужен кто-нибудь, чтобы мне помочь. Есть ли что-то конкретное, что можно сделать, чтобы получить какую-то помощь? У меня есть довольно большой набор вопросов, которые помогут мне изучить эти темы, но проблема в том, что я просто не могу их разгадать, сколько бы усилий я ни приложил.Пожалуйста помоги! Наверх IlbendF Зарегистрировано: 11.03.2004
Откуда: НидерландыРазмещено: 28 декабря, четверг, 17:24 Алгебратор — последний фаворит тех, кто изучает калькуляторы упрощенных выражений.Я знаю пару профессоров, которые на самом деле просят своих студентов иметь копию этого программного обеспечения у себя дома. Наверх Момепи Зарегистрировано: 22.07.2004
Откуда: ИрландияРазмещено: 29 декабря, пятница, 09:53 Алгебратор действительно поможет вам упростить калькулятор выражений.Я исследовал все программное обеспечение по алгебре в сети. Это очень логично. Вы просто даете свою проблему, и она создаст полный пошаговый отчет о решении. Это очень помогло мне с разницей кубов, квадратных уравнений и корней. Это поможет вам лучше понять алгебру. Я был огорчен тем, что отдал целое состояние репетиторам по математике, которые не могли уделить мне достаточно времени и внимания. Это недорогой инструмент, который может полностью изменить ваше отношение к математике. Было бы приятно использовать Алгебратор.Возьми это. Наверх Момепи Зарегистрировано: 22.07.2004
Откуда: ИрландияРазмещено: 30 декабря, суббота, 20:43 Алгебратор — это программа, которую я использовал на нескольких курсах алгебры — алгебре колледжа, промежуточной алгебре и алгебре 1.Это действительно отличная математическая программа. Я помню, как приходил к решению проблем с одночленами, трехчленом в виде полного квадрата и непохожими знаменателями. Я просто набирал задачу из учебного пособия, нажимал «Решить» и получал пошаговое решение моей домашней работы по алгебре. Очень рекомендую программу. Наверх _Xabna Зарегистрировано: 10.07.2002
Вылет: ШвецияРазмещено: 1 января, понедельник, 08:33 Сейчас однозначно хотелось бы самому попробовать эту штуку.Где я могу получить свою копию? Может ли кто-нибудь помочь мне в покупке этого программного обеспечения? Наверх ЧС` Зарегистрирован: 04.07.2001
Откуда: Виктория, остров Гонконг, Гонконг.Размещено: 3 января, среда, 12:06 Вы можете заказать это программное обеспечение онлайн: https: // polymathlove.ru / умножение-и-деление-фракции-2.html. Вы не пожалеете, что потратили на это деньги, к тому же это не так дорого, учитывая глубину знаний, которые вы получаете от его использования. Они даже предлагают безусловную гарантию возврата денег. Всего наилучшего для вашего задания. Наверх Калькулятор упрощающих радикалов
Пример: использование калькулятора упрощающих радикалов
Скажите, что вы только что узнали о корнях и о том, как упростить радикалы .Это не мешает вашему учителю дать всему классу задание, которое попытается выполнить самостоятельно , пока они сидят за своим столом с телефоном в руке. Похоже, они думают, что упрощение радикальных выражений займет у вас достаточно времени, чтобы просмотреть ленту новостей. Почему бы нам не доказать, что они неправы?
Задача: найти сумму, произведение и частное от
2√6и⁴√64. Другими словами, нам нужно вычислить2√6 + ⁴√64,2√6 * ⁴√64и2√6 / ⁴√64.Что ж, , как повезло, что у нас под рукой есть упрощающий калькулятор радикалов от Omni!
Начнем с сумма . В калькуляторе мы видим возможность выбрать радикальное выражение, которое мы хотим найти . Нас интересует сложение двух значений, поэтому мы выбираем « сумма » в « Выражение ». Это вызовет появление символического представления операции.
Далее нам нужно ввести числа .Калькулятор упрощенных радикальных выражений показывает сумму как
a * ⁿ√b + c * ᵐ√d, поэтому для нашего случая мы вводимa = 2,b = 6,n = 2,c = 1,d = 64,m = 4.(обратите внимание, что
n = 2является значением по умолчанию, поскольку обычно мы имеем дело с квадратными корнями. Кроме того, нам действительно не нужно было вводитьc = 1— калькулятор понимает пустые поля дляaиcкак1с.)После того, как мы дадим все числа, мы сможем считать результат под полями переменных. Обратите внимание, как калькулятор дает пошаговое решение вашей проблемы.
Для , продукта и частного , мы повторяем вышеуказанные шаги (
a,bи т. Д. Не меняются), но выбираем правильный вариант в разделе « Expression » —* product *и* частное *соответственно.Тем не менее, в ужасные времена, когда вы не можете пользоваться Интернетом, давайте посмотрим, , как упростить радикалы самостоятельно, , без помощи нашего инструмента.
Начнем с суммы :
2√6 + ⁴√64. Прежде всего, нам нужно найти разложение на простые множители двух чисел под радикалами:6 = 2 * 3,64 = 2 * 2 * 2 * 2 * 2 * 2 = 2⁶.Первый корень имеет порядок
2, поэтому нам нужно найти пары одного и того же числа в факторизации. Мы видим, что не существует , так что слагаемое уже находится в простейшей форме.Для второго, нам понадобится четверка .Действительно, есть одно такое решение (четыре
2с), которое оставляет только две2с. Вытаскиваем из корня числа, представляющие группы по четыре, а остальные оставляем внутри.2√6 + ⁴√64 = 2√6 + ⁴√ (2⁶) = 2√6 + 2 * ⁴√ (2²)К сожалению, это еще не конец . Во втором слагаемом мы видим, что порядок корня и степени всех (т. Е. Единственного) чисел под ним имеют общий множитель —
2.Таким образом, мы уменьшаем два числа на этот коэффициент.2√6 + ⁴√64 = 2√6 + 2 * ⁴√ (2²) = 2√6 + 2√2Обратите внимание, как мы не записали
²со вторым корнем, потому что, по соглашению, мы пишем квадратные корни без этого числа .Два слагаемых имеют разные номера под корнями (но одинаковый порядок корней), поэтому мы не можем их сложить — это простейшая форма выражения .
Теперь для упрощения радикального выражения с произведением :
2√6 * ⁴√64.Два корня имеют порядки2и4соответственно, иlcm (2,4) = 4. Следуя инструкциям, приведенным в разделе выше, получаем:2√6 * ⁴√64 = 2 * ⁴√ (6² * 64) = 2 * ⁴√2304.Далее, находим разложение на простые множители числа под корнем:
2304 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 = 2⁸ * 3².Мы ищем четверок одного и того же простого числа в факторизации и находим два: пару четверок из
2с.Вытаскиваем их из корня и получаем2√6 * ⁴√64 = 2 * ⁴√2304 = 2 * ⁴√ (2⁸ * 3²) = 2 * 2 * 2 * ⁴√3² = 8 * ⁴√3².У нас есть ситуация, аналогичная той, что была у нас с суммой: порядок корня и степени простых чисел под ним имеют общий множитель . Сокращаем их и получаем окончательный ответ:
2√6 * ⁴√64 = 8 * ⁴√3² = 8√3.Наконец, давайте посмотрим, как упростить радикальное выражение с частным:
2√6 / ⁴√64.Напомним, чтоlcm (2,4) = 4и инструкции из предыдущего раздела для получения:2√6 / ⁴√64 = (2/64) * ⁴√ (6² * 64³) = 0,03125 * ⁴√9,437,184.Находим разложение на простые множители числа под корнем:
9 437 184 = 2²⁰ * 3²,и найдите четверок одинаковых простых чисел . В данном случае мы имеем пять четверок из
2. Вытаскиваем их из корня и получаем:2√6 / ⁴√64 = 0.03125 * ⁴√9 437 184 = 0,03125 * ⁴√ (2²⁰ * 3²) = 0,03125 * 2⁵ * ⁴√ (3²) = ⁴√ (3²).Опять же, мы можем уменьшить порядок корня и степени простых чисел под ним. Это дает нам окончательный ответ:
2√6 / ⁴√64 = ⁴√ (3²) = √3.Возможно, на то, чтобы написать все подробности, потребовалось некоторое время, но сами операции не были такими уж ужасными.


 3=8
a = b a and b are equal
a > b a is larger than b
a < b a is smaller than b
a <> b a and b are not equal
a != b a and b are not equal
a <= b a is less than or equal to b
a >= b a is larger than or equal to b
a ~ b a matches the regular expression b
+ a positive sign
— a negative value of a
|| joins two values together into a string ‘Hello’ || ‘ world’
LIKE returns 1 if the string matches the supplied pattern
ILIKE returns 1 if the string matches case-insensitive the supplied
pattern. ILIKE can be used instead of LIKE to make the match case-insensitive
IS returns 1 if a is the same as b
OR returns 1 when condition a or b is true
AND returns 1 when condition a and b are true
NOT returns 1 if a is not the same as b
column name «column name» value of the field column name
‘string’ a string value
NULL null value
a IS NULL a has no value
a IS NOT NULL a has a value
a IN (value[,value]) a is below the values listed
a NOT IN (value[,value]) a is not below the values listed
3=8
a = b a and b are equal
a > b a is larger than b
a < b a is smaller than b
a <> b a and b are not equal
a != b a and b are not equal
a <= b a is less than or equal to b
a >= b a is larger than or equal to b
a ~ b a matches the regular expression b
+ a positive sign
— a negative value of a
|| joins two values together into a string ‘Hello’ || ‘ world’
LIKE returns 1 if the string matches the supplied pattern
ILIKE returns 1 if the string matches case-insensitive the supplied
pattern. ILIKE can be used instead of LIKE to make the match case-insensitive
IS returns 1 if a is the same as b
OR returns 1 when condition a or b is true
AND returns 1 when condition a and b are true
NOT returns 1 if a is not the same as b
column name «column name» value of the field column name
‘string’ a string value
NULL null value
a IS NULL a has no value
a IS NOT NULL a has a value
a IN (value[,value]) a is below the values listed
a NOT IN (value[,value]) a is not below the values listed
 Also truncates the number to the number of supplied places
format_date formats a date type or string into a custom string format
Also truncates the number to the number of supplied places
format_date formats a date type or string into a custom string format Can be used
for processing with other functions.
geomFromWKT returns a geometry created from a Well-Known Text (WKT) representation.
geomFromGML returns a geometry from a GML representation of geometry
bbox
disjoint returns 1 if the Geometries do not share any space together
intersects returns 1 if the geometries spatially intersect
(share any portion of space) and 0 if they don't
touches returns 1 if the geometries have at least one point in common,
but their interiors do not intersect
crosses returns 1 if the supplied geometries have some, but not all,
interior points in common.
contains returns true if and only if no points of b lie in the exterior of a,
and at least one point of the interior of b lies in the interior of a
overlaps returns 1 if the Geometries share space, are of the same dimension,
but are not completely contained by each other.
within returns 1 if the geometry a is completely inside geometry b
buffer returns a geometry that represents all points whose distance
from this geometry is less than or equal to distance
centroid returns the geometric center of a geometry
convexHull returns the convex hull of a geometry. It represents the
minimum convex geometry that encloses all geometries within the set
difference returns a geometry that represents that part of geometry a that
does not intersect with geometry a
distance returns the minimum distance (based on spatial ref) between
two geometries in projected units
intersection returns a geometry that represents the shared portion
of geometry a and geometry b
symDifference returns a geometry that represents the portions of a and b
that do not intersect
combine returns the combination of geometry a and geometry b
union returns a geometry that represents the point set union of the geometries
geomToWKT returns the Well-Known Text (WKT) representation of the
geometry without SRID metadata
Can be used
for processing with other functions.
geomFromWKT returns a geometry created from a Well-Known Text (WKT) representation.
geomFromGML returns a geometry from a GML representation of geometry
bbox
disjoint returns 1 if the Geometries do not share any space together
intersects returns 1 if the geometries spatially intersect
(share any portion of space) and 0 if they don't
touches returns 1 if the geometries have at least one point in common,
but their interiors do not intersect
crosses returns 1 if the supplied geometries have some, but not all,
interior points in common.
contains returns true if and only if no points of b lie in the exterior of a,
and at least one point of the interior of b lies in the interior of a
overlaps returns 1 if the Geometries share space, are of the same dimension,
but are not completely contained by each other.
within returns 1 if the geometry a is completely inside geometry b
buffer returns a geometry that represents all points whose distance
from this geometry is less than or equal to distance
centroid returns the geometric center of a geometry
convexHull returns the convex hull of a geometry. It represents the
minimum convex geometry that encloses all geometries within the set
difference returns a geometry that represents that part of geometry a that
does not intersect with geometry a
distance returns the minimum distance (based on spatial ref) between
two geometries in projected units
intersection returns a geometry that represents the shared portion
of geometry a and geometry b
symDifference returns a geometry that represents the portions of a and b
that do not intersect
combine returns the combination of geometry a and geometry b
union returns a geometry that represents the point set union of the geometries
geomToWKT returns the Well-Known Text (WKT) representation of the
geometry without SRID metadata
 Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти:
Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти:
 Поэтому при решении задач следует быть внимательным.
Поэтому при решении задач следует быть внимательным. В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа.
В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа. Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых: Эту операцию называют приведением подобных слагаемых .
Эту операцию называют приведением подобных слагаемых . Привести подобные слагаемые в выражении 2a − a
Привести подобные слагаемые в выражении 2a − a 
 Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
 Данное решение можно записать покороче:
Данное решение можно записать покороче: Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби:
Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби: Оно не упрощается.
Оно не упрощается. На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа.
На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа. Такие выражения называют тождественно равными .
Такие выражения называют тождественно равными . Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством. За общий знаменатель можно принять выражение . Находим последовательно:
За общий знаменатель можно принять выражение . Находим последовательно: Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады.
Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых.
В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых.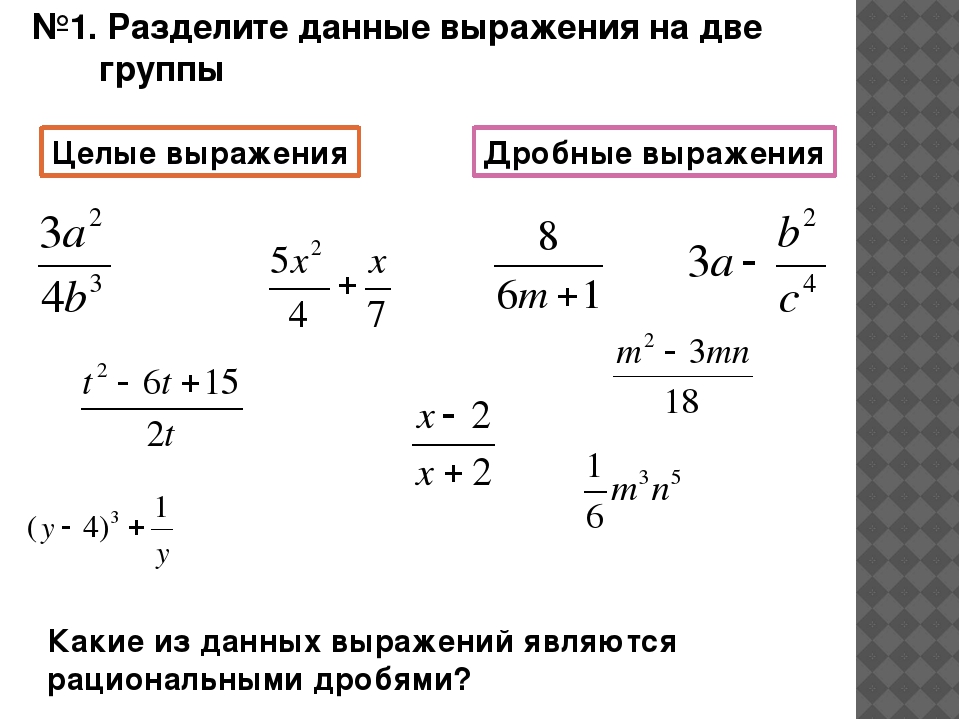 Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта.
Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида.
За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера.
Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной.
По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности.
Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины.
Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время. По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
 Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2. Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.