Сравнение натуральных чисел, знаки сравнения. Онлайн калькулятор
Сравнить два числа — это значит определить, равны они или нет, если нет, то определить, какое из них больше, а какое — меньше.
Равные и неравные натуральные числа
Если записи двух натуральных чисел одинаковы, то говорят, что эти числа равны между собой. Числа, которые равны, называются равными. Если записи двух натуральных чисел отличаются, то говорят, что эти числа не равны. Числа, которые не равны, называются неравными.
Пример. Натуральное число 34 равно числу 34 (их записи одинаковы), а натуральные числа 63 и 67 не равны (их записи различны). Следовательно числа 34 и 34 — равные, а 63 и 67 — неравные.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
=, > и <.
При записи сравнения эти знаки располагают между числами.
Первый знак =
называется знаком равенства и заменяет собой слово равно
или равняется
. Например, если числа a и b равны, то пишут a = b и говорят: a равно b
.
Запись, которая состоит из математических выражений, между которыми ставится знак =
называется равенством.
Пример.
4 = 4 — равенство.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Два других знака >
и <
называются знаками неравенства и означают: знак >
— больше
, а знак <
— меньше
. Например, если число a больше числа b, то пишут a > b и говорят:
Например, если число a больше числа b, то пишут a > b и говорят: a больше b
или пишут b < a и говорят: b меньше a
.
Знаки >
и <
должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак >
или <
называется неравенством.
Пример.
5 > 4 — неравенство.
2 < 7 — неравенство.
2 + 3 < 7 — неравенство (подобные записи представляют собой неравенство двух числовых выражений, и означают неравенство значений этих выражений).
Неравенства могут быть как верными (например, 2 < 9 — верное неравенство), так и неверными (например, 5 > 8 — неверное неравенство).
Кроме неравенств со знаками >
и <
, которые называются строгими, используются нестрогие неравенства, для которых введены знаки ⩾
и ⩽
. Знак
Знак ⩾
читается больше или равно
, знак ⩽
— меньше или равно
. Нестрогое неравенство допускает случай равенства левой и правой его частей. Так, например, 7 ⩽ 7 — верное неравенство.
Также для записи неравенства двух натуральных чисел может применяться знак ≠
. Знак ≠
читается не равно
. Например, запись a ≠ b — означает a не равно b.
Обычно, если не оговорено иное, понятие неравенства относится только к записям со знаками >
, <
, ⩾
и ⩽
.
Правила чтения равенств и неравенств
Равенства и неравенства читаются слева направо. Левая часть равенства читается в именительном падеже, а правая — в дательном.
Пример. 7 = 7 — семь равно семи.
Левая часть неравенства читается в именительном падеже, а правая — в родительном.
Пример. 11 > 9 — одиннадцать больше девяти, 3 < 5 — три меньше пяти.
Правила сравнения чисел
Правило сравнения с помощью натурального ряда:
Из двух натуральных чисел меньше то, которое в натуральном ряду встречается раньше (т. е. находится левее), и больше то, которое в натуральном ряду встречается позже (т. е. находится правее).
Следовательно, в натуральном ряде каждое число, кроме 1, больше предыдущего.
Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Число 1 меньше числа 3 (1 < 3), так как в натуральном ряду число 1 находится левее числа 3. Число 7 больше числа 4 (7 > 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
4026
4019
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда.
Если количество цифр в записи, сравниваемых чисел, разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
Для удобства сравнения можно записать их одно под другим:
38 526 734
38 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
Пример. Известно, что 4 < 7, а 7 < 16. Эти два неравенства удобнее представить в виде двойного неравенства:
4 < 7 < 16.
Двойные неравенства принято читать с середины. Например, неравенство 2 < 4 < 5 читается так:
.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 < 34, 8 < 11 и 34 > 8, которые можно записать как двойное неравенство:
Сравнивая данные числа между собой, получим три неравенства 11 < 34, 8 < 11 и 34 > 8, которые можно записать как двойное неравенство:
8 < 11 < 34.
Аналогичным образом строятся тройные, четверные и т. д. неравенства.
Пример. Известно, что 12 < 15, 47 > 15, 47 < 112, тогда можно записать
12 < 15 < 47 < 112.
Калькулятор сравнения чисел
Данный калькулятор поможет вам сравнить натуральные числа. Просто введите два числа и нажмите кнопку Сравнить
.
больше меньше или равно калькулятор
Вы искали больше меньше или равно калькулятор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и больше меньше или равно онлайн калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «больше меньше или равно калькулятор».
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «больше меньше или равно калькулятор».Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как больше меньше или равно калькулятор,больше меньше или равно онлайн калькулятор,больше меньше калькулятор,больше меньше онлайн калькулятор,какое число больше онлайн,калькулятор больше меньше,калькулятор больше меньше или равно,калькулятор больше меньше или равно онлайн,калькулятор больше меньше онлайн,калькулятор для сравнения чисел,калькулятор дробей с разными знаменателями сравнения,калькулятор дробей сравнение,калькулятор дробей сравнение дробей,калькулятор меньше больше,калькулятор онлайн больше меньше,калькулятор онлайн больше меньше или равно,калькулятор онлайн сравнение дробей,калькулятор онлайн сравнение чисел,калькулятор сравнение дробей десятичных,калькулятор сравнение дробей с разными знаменателями,калькулятор сравнение дробей с решением онлайн,калькулятор сравнение чисел,калькулятор сравнение чисел онлайн,калькулятор сравнение чисел онлайн калькулятор,калькулятор сравнений,калькулятор сравнения,калькулятор сравнения десятичных дробей,калькулятор сравнения дробей,калькулятор сравнения дробей онлайн калькулятор,калькулятор сравнения дробей с разными знаменателями,калькулятор сравнения чисел,калькулятор сравните числа,онлайн калькулятор больше меньше,онлайн калькулятор сравнение десятичных дробей,онлайн калькулятор сравнение дробей,онлайн калькулятор сравнение чисел,онлайн калькулятор сравнить числа,онлайн сравнение,онлайн сравнение корней,онлайн сравнение чисел,онлайн сравните числа,онлайн сравнитель дробей,сравнение десятичных дробей калькулятор онлайн,сравнение десятичных дробей онлайн калькулятор,сравнение дробей калькулятор онлайн с решением,сравнение дробей онлайн калькулятор,сравнение дробей с разными знаменателями онлайн калькулятор,сравнение онлайн,сравнение чисел десятичных онлайн,сравнение чисел калькулятор,сравнение чисел калькулятор онлайн,сравнение чисел онлайн,сравнение чисел онлайн калькулятор,сравнение чисел онлайн калькулятор больше меньше,сравнения калькулятор,сравните числа калькулятор,сравните числа онлайн,сравнить два числа онлайн,сравнить десятичные числа онлайн,сравнить дроби онлайн калькулятор,сравнить дроби онлайн калькулятор с решением,сравнить онлайн числа,сравнить числа калькулятор онлайн,сравнить числа онлайн,сравнить числа онлайн десятичные,сравнить числа онлайн калькулятор,что больше онлайн калькулятор.
Где можно решить любую задачу по математике, а так же больше меньше или равно калькулятор Онлайн?
Решить задачу больше меньше или равно калькулятор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор сравнения чисел онлайн. Сравнение дробей: правила, примеры, решения
Сравнение дробей. В этой статье разберём различные способы используя которые можно сравнить две дроби. Рекомендую посмотреть весь по дробям и изучать последовательно.
В этой статье разберём различные способы используя которые можно сравнить две дроби. Рекомендую посмотреть весь по дробям и изучать последовательно.
Прежде чем показать стандартный алгоритм сравнения дробей давайте разберём некоторые случаи, в которых сразу глядя на пример можно сказать которая из дробей будет больше. Здесь нет особой сложности, немного аналитики и всё готово. Посмотрите на следующие дроби:
В строке (1) сразу можно определить какая дробь больше, в строке (2) это сделать затруднительно и тут применим «стандартный» (или его можно назвать наиболее часто применяемым) подход для сравнения.
Способ первый – аналитический.
1. Перед нами две дроби:
Числители равны, знаменатели неравны. Какая из них больше? Ответ очевиден! Больше та, у которой меньше знаменатель, то есть три семнадцатых. Почему? Простой вопрос: Что больше – одна десятая часть от чего либо или одна тысячная? Конечно же, одна десятая.
Получается, что при равных числителях больше та дробь, у которой меньше знаменатель. Не имеет значения стоят ли в числителях единицы или другие равные числа, суть не меняется.
Не имеет значения стоят ли в числителях единицы или другие равные числа, суть не меняется.
Дополнительно к этому можно добавить следующий пример:
Какая из данных дробей больше (х положительное число)?
На основании уже представленной информации не трудно сделать вывод.
*Знаменатель первой дроби меньше, значит она больше.
2. Теперь рассмотрим вариант когда в одной из дробей числитель больше знаменателя. Пример:
Понятно, что первая дробь больше единицы, так как числитель больше знаменателя. А вторая дробь меньше единицы, поэтому без вычислений и преобразований можем записать:
3. При сравнении некоторых обыкновенных неправильных дробей явно видно, что у одной из них целая часть больше. Например:
В первой дроби целая часть равна трём, а во второй единице, поэтому:
4. В некоторых примерах также явно видно какая дробь больше, например:
Видно, что первая дробь меньше 0,5. Почему? Если выразить подробно, то:
а вторая больше 0,5:
Поэтому можно ставить знак сравнения:
Способ второй. «Стандартный» алгоритм сравнения.
«Стандартный» алгоритм сравнения.
Правило! Чтобы сравнить две дроби, необходимо чтобы знаменатели были равны. Тогда сравнение осуществляется по числителям. Больше будет та дробь, у которой больше числитель.
*Это и есть основное ВАЖНОЕ ПРАВИЛО, которым пользуются для сравнения дробей.
Если даны две дроби с неравными знаменателями, то необходимо их привести к такому виду, чтобы они были равны. Для этого используется дроби.
Сравним следующие дроби (знаменатели неравны):
Приведём их:
Как привести дроби к равным знаменателям? Очень просто! Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой.
Ещё примеры:
Обратите внимание, что знаменатель вычислять не обязательно (видно что они равны), для сравнения достаточно вычислить только числители.
*Все дроби, которые мы рассмотрели выше (первый способ) можно сравнить также используя этот подход.
На этом можно было бы закончить … Но есть ещё один «беспроигрышный» способ сравнения.
Способ третий. Деление столбиком.
Посмотрите пример:
Согласитесь, что для того чтобы привести к общему знаменателю и затем сравнить числители необходимо выполнить относительно объёмные вычисления. Используем следующий подход — выполним деление столбиком:
Как только мы обнаруживаем разницу в результате, то процесс деления можно остановить.
Вывод: так как 0,12 больше чем 0,11, то вторая дробь будет больше. Таким образом, можно поступать со всеми дробями.
На этом всё.
С уважением, Александр.
Существуют определённые правила сравнения чисел. Рассмотрим следующий пример.
Вчера термометр показывал 15˚ C, а сегодня показывает 20˚ C. Сегодня теплее, чем вчера. Число 15 меньше числа 20, можем записать так: 15
А сейчас рассмотрим отрицательные температуры. Вчера на улице было -12˚ C, а сегодня -8˚ C. Сегодня теплее, чем вчера. Поэтому считают, что число -12 меньше числа -8. На горизонтальной координатной прямой точка со значением -12 расположена левее точки со значением -8. Можем записать так: -12
Поэтому считают, что число -12 меньше числа -8. На горизонтальной координатной прямой точка со значением -12 расположена левее точки со значением -8. Можем записать так: -12
Итак, если сравнивать числа с помощью горизонтальной координатной прямой, из двух чисел меньшим считается то, изображение которого на координатной прямой расположено левее, а большим то, изображение которого расположено правее. Например, у нас на рисунке А > B и C, но B > C.
На координатной прямой положительные числа располагаются справа от нуля, а отрицательные – слева от нуля, всякое положительное число больше нуля, а всякое отрицательное меньше нуля, и поэтому всякое отрицательное число меньше всякого положительного числа.
Значит, первое на что необходимо обратить внимание при сравнении чисел, – это знаки сравниваемых чисел. Число с минусом (отрицательное) всегда меньше положительного.
Если же мы сравниваем два отрицательных числа, то нужно сравнить их модули: большим будет то число, модуль которого меньше, а меньшим то число, модуль которого меньше. Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7
Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7
Сравнение обыкновенных дробей
Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
Можно сравнивать дроби только с одинаковыми знаменателями.
Алгоритм сравнения обыкновенных дробей
1) Если у дроби есть целая часть, сравнение начинаем именно с неё. Большей будет та дробь, у которой целая часть больше. Если целой части у дробей нет или они равны, переходим к следующему пункту.
2) Если дроби с разными знаменателями необходимо привести их к общему знаменателю.
3) Сравниваем числители дробей. Большей будет та дробь, у которой числитель больше.
Обратите внимание, дробь с целой частью всегда будет больше дроби без целой части.
Сравнение десятичных дробей
Десятичные дроби можно сравнивать только с одинаковым количеством цифр (знаков) справа от запятой.
Алгоритм сравнения десятичных дробей
1) Обращаем внимание на количество знаков справа от запятой. Если количество цифр одинаковое, можем приступать к сравнению. Если – нет, дописываем нужное количество нулей в одной из десятичных дробей.
2) Сравниваем десятичные дроби слева направо: целые с целыми, десятые с десятыми, сотые с сотыми и т.д.
3) Большей будет та дробь, в которой одна из частей окажется больше, чем в другой дроби (сравнение начинаем с целых чисел: если целая часть одной дроби больше, значит, и вся дробь больше).
Например, сравним десятичные дроби:
1) Допишем в первой дроби необходимое количество нулей, чтобы уравнять количество знаков после запятой
57,300 и 57,321
2) Сравнивать начинаем слева направо:
целые с целыми: 57 = 57;
десятые с десятыми: 3 = 3;
сотые с сотыми: 0
Так как сотые первой десятичной дроби оказались меньше, вся дробь и будет меньше:
57,300
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.
Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.
Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.
В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы
Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:
Из двух положительных чисел больше то число, модуль которого больше.
Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.
Например, сравним те же числа 4 и 1, применяя вышеприведенное правило
Находим модули чисел:
|4| = 4
|1| = 1
Сравниваем найденные модули:
4 > 1
Отвечаем на вопрос:
4 > 1
Для отрицательных чисел существует другое правило, выглядит оно следующим образом:
Из двух отрицательных чисел больше то число, модуль которого меньше.
Например, сравним числа −3 и −1
Находим модули чисел
|−3| = 3
|−1| = 1
Сравниваем найденные модули:
3 > 1
Отвечаем на вопрос:
−3
Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.
Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой
Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.
Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2
Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».
Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса
Напомним, что это знак плюса
Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.
Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия.
Пример 1. Сравнить рациональные числа
Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем
Пример 2.
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули:
Пример 3. Сравнить числа 2,34 и
Сравнить числа 2,34 и
Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем
Пример 4. Сравнить рациональные числа и
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Пример 5.
Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем
Пример 6. Сравнить рациональные числа 0 и
Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем
Пример 7 . Сравнить рациональные числа 4,53 и 4,403
Сравнить рациональные числа 4,53 и 4,403
Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.
Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль
Находим модули чисел
Сравниваем найденные модули:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403
Пример 8. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.
Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.
Пример 9. Сравнить рациональные числа 15,4 и 2,1256
Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256
поэтому и дробь 15,4 больше, чем дробь 2,1256
15,4 > 2,1256
Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа
154000 > 21256
Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.
Пример 10. Сравнить рациональные числа −15,2 и −0,152
Сравнить рациональные числа −15,2 и −0,152
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.
А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2
−0,152 > −15,2
Пример 11. Сравнить рациональные числа −3,4 и −3,7
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:
В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули
Сравниваем найденные модули:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7
−3,4 > −3,7
Пример 12. Сравнить рациональные числа 0,(3) и
Сравнить рациональные числа 0,(3) и
Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.
Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Содержание урока Сравнение дробей с одинаковыми знаменателямиДроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителямиСледующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:
Каждый согласиться с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Например, сравнить дроби и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10−8=2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите .
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю.
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше . На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.
Получается, что делили каждый целый круг на одно и то же число 5 , а брали разное количество частей: больше взяли — большая дробь и получилась.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?
Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.
Примеры. Сравнить обыкновенные дроби:
Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12: 4=3 ). Для 2-й дроби дополнительный множитель 2 (12: 6=2 ). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9, то и сама первая дробь меньше второй дроби.
Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9, то и сама первая дробь меньше второй дроби.
| Вам могут также быть полезны следующие сервисы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дроби | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор интервальных повторений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Учим дроби наглядно | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сокращения дробей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор преобразования неправильной дроби в смешанную | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор преобразования смешанной дроби в неправильную | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сложения, вычитания, умножения и деления дробей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор возведения дроби в степень | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор перевода десятичной дроби в обыкновенную | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор перевода обыкновенной дроби в десятичную | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сравнения дробей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор приведения дробей к общему знаменателю | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы (тригонометрия) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор синуса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор косинуса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор тангенса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор котангенса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор секанса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор косеканса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арксинуса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арккосинуса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арктангенса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арккотангенса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арксеканса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор арккосеканса угла | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы систем счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор перевода чисел из арабских в римские и из римских в арабские | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор перевода чисел в различные системы счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Системы счисления теория | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N2 | Двоичная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N3 | Троичная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N4 | Четырехичная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N5 | Пятеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N6 | Шестеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N7 | Семеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N8 | Восьмеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N9 | Девятеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N11 | Одиннадцатиричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N12 | Двенадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N13 | Тринадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N14 | Четырнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N15 | Пятнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N16 | Шестнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N17 | Семнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N18 | Восемнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N19 | Девятнадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N20 | Двадцатеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N21 | Двадцатиодноричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N22 | Двадцатидвухричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N23 | Двадцатитрехричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N24 | Двадцатичетырехричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N25 | Двадцатипятеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N26 | Двадцатишестеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N27 | Двадцатисемеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N28 | Двадцативосьмеричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N29 | Двадцатидевятиричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N30 | Тридцатиричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N31 | Тридцатиодноричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N32 | Тридцатидвухричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N33 | Тридцатитрехричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N34 | Тридцатичетырехричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N35 | Тридцатипятиричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N36 | Тридцатишестиричная система счисления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы (Теория чисел) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор выражений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор со скобками | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор разложения числа на простые множители | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор НОД и НОК | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор НОД и НОК по алгоритму Евклида | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор НОД и НОК для любого количества чисел | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Представление многозначных чисел в виде суммы разрядных слагаемых | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор деления числа в данном отношении | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор процентов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор перевода числа с Е в десятичное | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения факториала числа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения логарифма числа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор квадратных уравнений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор остатка от деления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор корней с решением | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения периода десятичной дроби | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы площади геометрических фигур | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Площадь квадрата | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Площадь прямоугольника | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы (Комбинаторика) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения числа перестановок из n элементов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения числа сочетаний из n элементов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения числа размещений из n элементов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Генератор Pdf с примерами | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёры решения примеров | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажер сложения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр вычитания | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр умножения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр деления | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр таблицы умножения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажер счета для дошкольников | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажер счета на внимательность для дошкольников | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажер решения примеров с разными действиями | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёры решения столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр сложения столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр вычитания столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр умножения столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тренажёр деления столбиком с остатком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы решения столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сложения, вычитания, умножения и деления столбиком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор деления столбиком с остатком | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы линейная алгебра и аналитическая геометрия | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сложения и вычитания матриц | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор умножения матриц | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор транспонирование матрицы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения определителя (детерминанта) матрицы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения обратной матрицы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длина отрезка. Онлайн калькулятор расстояния между точками | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Онлайн калькулятор нахождения координат вектора по двум точкам | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения модуля (длины) вектора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор сложения и вычитания векторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор скалярного произведения векторов через координаты | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор векторного произведения векторов через координаты | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор смешанного произведения векторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор умножения вектора на число | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения угла между векторами | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор проверки коллинеарности векторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор проверки компланарности векторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конвекторы величин | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конвертер единиц длины | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конвектор единиц скорости | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конвектор единиц ускорения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькуляторы (физика) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Механика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления скорости, времени и расстояния | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления ускорения, скорости и перемещения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления времени движения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор времени | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Импульс тела. Калькулятор вычисления импульса, массы и скорости | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Оптика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор отражения и преломления света | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Электричество и магнетизм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор Закона Ома | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор Закона Кулона | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор напряженности E электрического поля | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения точечного электрического заряда Q | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор нахождения силы F действующей на заряд q | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления расстояния r от заряда q | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления потенциальной энергии W заряда q | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления потенциала φ электростатического поля | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления электроемкости C проводника и сферы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Конденсаторы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Калькулятор вычисления энергии W заряженного конденсатора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор вычисления энергии W заряженного конденсатора. b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом: \( \displaystyle \begin{array}{l}a>b>1\ \ \Leftrightarrow \ \ {{\log }_{a}}x<{{\log }_{b}}x\\1>a>b>0\ \ \Leftrightarrow \ \ {{\log }_{a}}x>{{\log }_{b}}x\end{array}\) Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же \( x\). Если же основание меньше \( 1\), то все наоборот, так как соответствующая функция монотонно убывающая. Пример. Сравните числа: \( {{\log }_{3}}5\) и \( {{\log }_{8}}26\). Решение: Согласно вышеописанным правилам: \( \displaystyle \left. \begin{array}{l}{{\log }_{8}}26>{{\log }_{8}}25\\{{\log }_{8}}25>{{\log }_{9}}25={{\log }_{3}}5\text{ }\end{array} \right|\Rightarrow \text{ }{{\log }_{8}}26>{{\log }_{3}}5\) А теперь формула для продвинутых. Сравнить дроби-калькулятор сравнение дробей-какая дробь больше-какая дробь меньше. Калькулятор сравнения дробей с разными знаменателямиПродолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их. Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше. Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится. В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом: Из двух положительных чисел больше то число, модуль которого больше. Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос. Например, сравним те же числа 4 и 1, применяя вышеприведенное правило Находим модули чисел: |4| = 4 |1| = 1 Сравниваем найденные модули: 4 > 1 Отвечаем на вопрос: 4 > 1 Для отрицательных чисел существует другое правило, выглядит оно следующим образом: Из двух отрицательных чисел больше то число, модуль которого меньше. Например, сравним числа −3 и −1 Находим модули чисел |−3| = 3 |−1| = 1 Сравниваем найденные модули: 3 > 1 Отвечаем на вопрос: −3 Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1. Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше. Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше». Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда. Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия. Пример 1. Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем Пример 2. Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше. Находим модули чисел: Сравниваем найденные модули: Пример 3. Сравнить числа 2,34 и Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем Пример 4. Сравнить рациональные числа и Находим модули чисел: Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Пример 5. Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем Пример 6. Сравнить рациональные числа 0 и Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем Пример 7 . Сравнить рациональные числа 4,53 и 4,403 Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше. Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль Находим модули чисел Сравниваем найденные модули: Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403 Пример 8. Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Находим модули чисел: Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю: Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше. Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные. Пример 9. Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256 поэтому и дробь 15,4 больше, чем дробь 2,1256 15,4 > 2,1256 Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа 154000 > 21256 Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа. Пример 10. Сравнить рациональные числа −15,2 и −0,152 Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152. А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2 −0,152 > −15,2 Пример 11. Сравнить рациональные числа −3,4 и −3,7 Требуется сравнить два отрицательных числа. В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули Сравниваем найденные модули: Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7 −3,4 > −3,7 Пример 12. Сравнить рациональные числа 0,(3) и Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью. Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь Находим модули чисел: Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю: Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Понравился урок? Сравнение дробей. В этой статье разберём различные способы используя которые можно сравнить две дроби. Рекомендую посмотреть весь по дробям и изучать последовательно. Прежде чем показать стандартный алгоритм сравнения дробей давайте разберём некоторые случаи, в которых сразу глядя на пример можно сказать которая из дробей будет больше. Здесь нет особой сложности, немного аналитики и всё готово. Посмотрите на следующие дроби: В строке (1) сразу можно определить какая дробь больше, в строке (2) это сделать затруднительно и тут применим «стандартный» (или его можно назвать наиболее часто применяемым) подход для сравнения. Способ первый – аналитический. 1. Перед нами две дроби: Числители равны, знаменатели неравны. Какая из них больше? Ответ очевиден! Больше та, у которой меньше знаменатель, то есть три семнадцатых. Получается, что при равных числителях больше та дробь, у которой меньше знаменатель. Не имеет значения стоят ли в числителях единицы или другие равные числа, суть не меняется. Дополнительно к этому можно добавить следующий пример: Какая из данных дробей больше (х положительное число)? На основании уже представленной информации не трудно сделать вывод. *Знаменатель первой дроби меньше, значит она больше. 2. Теперь рассмотрим вариант когда в одной из дробей числитель больше знаменателя. Пример: Понятно, что первая дробь больше единицы, так как числитель больше знаменателя. А вторая дробь меньше единицы, поэтому без вычислений и преобразований можем записать: 3. При сравнении некоторых обыкновенных неправильных дробей явно видно, что у одной из них целая часть больше. Например: В первой дроби целая часть равна трём, а во второй единице, поэтому: 4. Видно, что первая дробь меньше 0,5. Почему? Если выразить подробно, то: а вторая больше 0,5: Поэтому можно ставить знак сравнения: Способ второй. «Стандартный» алгоритм сравнения.
*Это и есть основное ВАЖНОЕ ПРАВИЛО, которым пользуются для сравнения дробей. Если даны две дроби с неравными знаменателями, то необходимо их привести к такому виду, чтобы они были равны. Для этого используется дроби. Сравним следующие дроби (знаменатели неравны): Приведём их: Как привести дроби к равным знаменателям? Очень просто! Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой. Ещё примеры: Обратите внимание, что знаменатель вычислять не обязательно (видно что они равны), для сравнения достаточно вычислить только числители. *Все дроби, которые мы рассмотрели выше (первый способ) можно сравнить также используя этот подход. На этом можно было бы закончить … Но есть ещё один «беспроигрышный» способ сравнения. Способ третий. Деление столбиком. Посмотрите пример: Согласитесь, что для того чтобы привести к общему знаменателю и затем сравнить числители необходимо выполнить относительно объёмные вычисления. Используем следующий подход — выполним деление столбиком: Как только мы обнаруживаем разницу в результате, то процесс деления можно остановить. Вывод: так как 0,12 больше чем 0,11, то вторая дробь будет больше. Таким образом, можно поступать со всеми дробями. На этом всё. С уважением, Александр. Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом. Yandex.RTB R-A-339285-1 Сравнение дробей с одинаковыми знаменателямиКогда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 . Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот. Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример. Пример 1 Произвести сравнение заданных дробей 65 126 и 87 126 . Решение Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 . Ответ: 87 126 > 65 126 . Сравнение дробей с разными знаменателямиСравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю. Если имеются дроби с разными знаменателями, для их сравнения необходимо:
Рассмотрим данные действия на примере. Пример 2 Произвести сравнение дробей 5 12 и 9 16 . Решение В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 . После сравнения дробей получаем, что 20 48 Ответ: 5 12 Имеется еще один способ сравнения дробей с разными знаменателями. Пример 3 Произвести сравнение дробей 5 18 и 23 86 . Решение Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 . Ответ: 5 18 > 23 86 . Сравнение дробей с одинаковыми числителямиЕсли дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот. Рассмотрим на примере. Пример 4 Произвести сравнение дробей 54 19 и 54 31 . Решение Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила. Ответ: 54 19 > 54 31 . Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей. Сравнение дроби с натуральным числомСравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Пример 4 Необходимо выполнить сравнение 63 8 и 9 . Решение Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 Ответ: 63 8 Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter В повседневной жизни нам часто приходится сравнивать дробные величины. Чаще всего это не вызывает каких-либо трудностей. Действительно, всем понятно, что половина яблока больше, чем четверть. Но когда необходимо записать это в виде математического выражения, это может вызвать затруднения. Применяя следующие математические правила, вы легко можете справиться с этой задачей. Как сравнивать дроби с одинаковыми знаменателямиТакие дроби сравнивать удобнее всего. Из двух дробей с одинаковыми знаменателями, но разными числителя, большей будет та, числитель которой больше, а меньшей – та, числитель которой меньше. Например, сравнить дроби 3/8 и 5/8. Знаменатели в этом примере равны, следовательно, применяем это правило. 3 И действительно, если разрезать две пиццы на 8 долей, то 3/8 доли всегда меньше, чем 5/8. Сравнение дробей с одинаковыми числителями и разными знаменателямиВ этом случае сравнивают размеры долей-знаменателей. Следует применять правило: Если у двух дробей числители равны, то больше та дробь, знаменатель которой меньше. Например, сравнить дроби 3/4 и 3/8. В этом примере числители равны, значит, используем второе правило. У дроби 3/4 знаменатель меньше, чем у дроби 3/8. Следовательно 3/4>3/8 И действительно, если вы съедите 3 куска пиццы, разделенной на 4 части, то будете более сыты, чем если бы съели 3 куска пиццы, разделенной на 8 частей. Сравнение дробей с разными числителями и знаменателямиПрименяем третье правило: Сравнение дробей с разными знаменателями нужно привести к сравнению дробей с одинаковыми знаменателями. Для этого необходимо привести дроби к общему знаменателю и использовать первое правило. Например, необходимо сравнить дроби и . Для определения большей дроби приведем эти две дроби к общему знаменателю:
Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом. Навигация по странице. Сравнение дробей с одинаковыми знаменателямиСравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3 доли 1/7 , а дробь 8/7 соответствует 8 долям 1/7 , поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8 , то есть, к сравнению числителей. Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями : из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше. Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями. Пример. Какая дробь больше: 65/126 или 87/126 ? Решение. Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87
дроби 87/126
больше числителя 65
дроби 65/126
(при необходимости смотрите сравнение натуральных чисел). Ответ: Сравнение дробей с разными знаменателямиСравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю . Итак, чтобы сравнить две дроби с разными знаменателями, нужно
Разберем решение примера. Пример. Сравните дробь 5/12 с дробью 9/16 . Решение. Сначала приведем данные дроби с разными знаменателями к общему знаменателю (смотрите правило и примеры приведения дробей к общему знаменателю). В качестве общего знаменателя возьмем наименьший общий знаменатель, равный НОК(12, 16)=48
. Тогда дополнительным множителем дроби 5/12
будет число 48:12=4
, а дополнительным множителем дроби 9/16
будет число 48:16=3
. Сравнив полученные дроби, имеем . Следовательно, дробь 5/12 меньше, чем дробь 9/16 . На этом сравнение дробей с разными знаменателями завершено. Ответ: Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом. Для сравнения дробей a/b и c/d , их можно привести к общему знаменателю b·d , равному произведению знаменателей сравниваемых дробей. В этом случае дополнительными множителями дробей a/b и c/d являются числа d и b соответственно, а исходные дроби приводятся к дробям и с общим знаменателем b·d . Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b и c/d свелось к сравнению произведений a·d и c·b . Отсюда вытекает следующее правило сравнения дробей с разными знаменателями : если a·d>b·c , то , а если a·d Рассмотрим сравнение дробей с разными знаменателями этим способом. Пример. Сравните обыкновенные дроби 5/18 и 23/86 . Решение. В этом примере a=5 , b=18 , c=23 и d=86 . Вычислим произведения a·d и b·c . Имеем a·d=5·86=430 и b·c=18·23=414 . Так как 430>414 , то дробь 5/18 больше, чем дробь 23/86 . Ответ: Сравнение дробей с одинаковыми числителямиДроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей. Существует такое правило сравнения дробей с одинаковыми числителями : из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше. Рассмотрим решение примера. Пример. Сравните дроби 54/19 и 54/31 . Решение. Так как числители сравниваемых дробей равны, а знаменатель 19
дроби 54/19
меньше знаменателя 31
дроби 54/31
, то 54/19
больше 54/31
. Сортировка дробей: онлайн калькулятор | BBF.RUДробь – это соотношение двух чисел, при помощи которого можно представить любой элемент рационального множества. По способу записи дробные числа делятся на обыкновенные вида m/n и десятичные. Обыкновенные дроби с разными числителями и знаменателями сложно отсортировать по возрастанию/убыванию на интуитивном уровне, как это происходит с десятичными. Для этого и нужен наш калькулятор. Представление рациональных чисел в виде дробиКогда люди столкнулись с проблемой отделения части от целого, они придумали дроби. Если разделить круглый торт на 4 куска, то каждый кусочек лакомства будет представлять собой 1/4 от целого торта. С введением десятичной системы исчисления 1/4 превратилась в 0,25 и для современных людей такое обозначение четвертой части чего-либо гораздо понятнее. Однако 0,25 можно выразить бесконечным количеством дробей: 1/4, 2/8, 25/100 или 752/3008. Последняя дробь так и вовсе неочевидна и интуитивно непонятно, какое число она собой представляет. Такая проблема возникает и в случаях, когда перед глазами множество самых разных дробей. Узнать какое дробное число больше или меньше на первый взгляд очень сложно: приходится подсчитывать в уме соотношение чисел или приводить их к общему знаменателю. В зависимости от представленного набора дробей, их сортировка происходит по-разному. Дроби с одинаковыми знаменателямиСортировка таких дробей не представляет ничего сложного. Если у рациональных чисел одинаковый знаменатель, то их упорядочивание осуществляется по числителям. Например, для набора 1/5, 10/5, 4/5 и 3/5 очевидно, что элементы сортируются:
Главное правило: смотрим на числители и выполняем сортировку по ним. Дроби с одинаковыми числителямиНабор рациональных чисел может выглядеть иначе: знаменатели все разные, но числитель один и тот же. К примеру, у нас есть набор: 3/5, 3/20, 3/10, 3/7. Как их отсортировать? Во всех случаях мы делим тройку на разные числа, и чем больше знаменатель, тем меньше значение дроби.
Чем больше знаменатель – тем меньше значение дроби. Главное правило: смотрим на знаменатели и сортируем числа в обратном порядке. Абсолютно разные дробиПредыдущие примеры были слишком простыми. В большинстве случаев наборы рациональных чисел содержат совершенно разные дроби, с различными числителями и знаменателями. В этой ситуации единственным верным способом сортировки становится метод привидения всех элементов к общему знаменателю. Существует три метода определения общего знаменателя: использование максимального знаменателя, последовательный перебор кратных или разложение на простые множители. Первый метод подразумевает проверку наибольшего знаменателя на делимость остальными. Если максимальный знаменатель делится с остатком, то он умножается на 2, 3, 4 и так далее до тех пор, пока не станет кратным всем остальным знаменателям. Второй метод сложнее, так как нам требуется последовательно выписывать кратные числа для каждого знаменателя до тех пор, пока не найдутся общие, что тоже неудобно. Самый удобный, а потому и наиболее распространенный метод поиска НОК состоит в разложении на простые множители. Каждое целое число можно разложить на простые множители единственным способом с точностью до порядка расположения сомножителей. К примеру, число 30 можно разложить на 2 × 3 × 5, а число 20 на 2 × 2 × 5. Наименьшее общее кратное для этих чисел представляет собой число, которое состоит из общих для этих чисел неделимых множителей. Для данной пары это 2 × 2 × 3 × 5 = 60. Проводить данные операции вручную дело долгое и утомительное. Наша программа автоматически сортирует обыкновенные и десятичные дроби по возрастанию или убыванию. Для этого вам достаточно ввести значения через пробел в форму калькулятора и сделать один клик мышкой. Особенность программы состоит в том, что в случае разнородного набора рациональных чисел (десятичные и обыкновенные дроби), калькулятор вначале сортирует десятичные, а затем обыкновенные дроби. Таким образом, калькулятор разделяет смешанные наборы на две совокупности обыкновенных и десятичных дробей и сортирует их по отдельности. Рассмотрим примерПример сортировкиПусть у нас есть совокупность разнородных чисел: 1/5, 2/9, 0,75, 5/7, 0,2, 6/13, 0,35, 8/15. На первый взгляд не угадаешь, какое из этих чисел наибольшее, а какое – наименьшее. Вручную нам пришлось бы раскладывать на множители или подбирать кратные, но при помощи компьютера мы можем на выбор:
Давайте попробуем и то, и другое. Представим нашу совокупность в виде десятичных дробей: 0,2 0,22 0,75 0,71 0,2 0,46 0,35 0,53 Мы просто подсчитали значение заданных дробей и расположили соответственно исходному ряду. Отсортировать такие числа проще простого, но опять же, это лишние усилия на промежуточные операции. Давайте просто введем наш ряд в форму калькулятора и получим ответ:
ЗаключениеСортировка дробных значений необходима при обработке любых данных, поэтому на практике вы можете столкнуться с необходимостью упорядочивания различных значений. Ученикам же наш калькулятор пригодится для проверки решений по арифметике. Калькулятор сравнения дробейИспользование калькулятора Сравните дроби, чтобы определить, какая дробь больше, а какая меньше. Как сравнивать дробиЧтобы сравнить дроби с разными знаменателями, преобразуйте их в эквивалентные дроби с одинаковым знаменателем.
Пример: Сравните 5/6 и 3/8. Найдите ЖК-дисплей: кратные 6 равны 6, 12, 18, 24, 30 и т. Д. Кратные 8 равны 8, 16, 24, 32 и т. Преобразуйте каждую дробь в ее эквивалентную дробь с помощью ЖК-дисплея. \ (\ dfrac {5} {6} \ times \ dfrac {4} {4} = \ dfrac {20} {24} \) Для 3/8 умножьте числитель и знаменатель на 3, чтобы получить LCD = 24 в знаменателе. \ (\ dfrac {3} {8} \ times \ dfrac {3} {3} = \ dfrac {9} {24} \) Сравните дроби. Поскольку знаменатели похожи, вы можете сравнивать числители. 20 больше 9, поэтому: с \ (\ dfrac {20} {24}> \ dfrac {9} {24} \) заключаем \ (\ dfrac {5} {6}> \ dfrac {3} {8} \) Для получения дополнительной информации о дробях см. Ссылки: Справка по дробям Нахождение наименьшего общего знаменателя. Калькулятор сравнения дробей — Дюймовый калькуляторСравните дроби, десятичные дроби и проценты, чтобы найти, какие из них больше, меньше или равны. Решение:123 меньше 1.75 Этапы сравнения дробей и чиселШаг первый: преобразовать все числа в десятичные 123 = 1,6666666666667 1,75 = 1,75 Шаг второй: сравнить десятичные значения 1,6666666666667Шаг третий: перепишите числа с использованием исходных значений Как сравнивать дроби Сравнение дробей может показаться сложной задачей; это немного похоже на сравнение яблок и апельсинов. Метод первый: сравнение дробей путем преобразования в десятичные сначалаПервый способ сравнить дроби — преобразовать их в десятичное значение. Разделите числитель каждой дроби на знаменатель, затем сравните десятичные значения. Вот совет: используйте наш калькулятор дробей в десятичные, чтобы получить десятичное значение для вашей дроби. Вы также можете ознакомиться с нашей таблицей десятичных эквивалентов, чтобы увидеть десятичные эквиваленты общих дробей. Метод второй: сравнение дробей по общему знаменателюДругой способ сравнения дробей — это переписать все дроби в эквивалентные дроби с тем же знаменателем. Для этого найдите наибольший общий знаменатель, а затем приравняйте знаменатели каждой дроби. Начните с поиска наименьшего общего знаменателя, который мы иногда называем наименьшим общим знаменателем. Это наименьшее число, на которое поровну делится каждый знаменатель. Например, найдем наименьший общий знаменатель 6 и 9. 6 × 3 = 18 Затем разделите наименьший общий знаменатель на знаменатель дроби, чтобы найти кратное. Затем умножьте числитель на кратное, чтобы получить новый числитель. Поставьте новый числитель над наименьшим общим знаменателем, чтобы получить новую дробь. Например, преобразует 16 в дробь со знаминателем 18. 18 ÷ 6 = 3 Вы захотите повторить этот шаг для каждой дроби, пока все они не будут иметь одинаковый знаменатель. Вы также можете использовать калькулятор эквивалентных дробей или нашу эквивалентную диаграмму дробей, чтобы увидеть эквиваленты для обычных дробей, что может помочь ускорить преобразование. Наконец, сравните числители, чтобы определить, какая дробь является наибольшей или наименьшей. Например, сравните 318 с 218, чтобы увидеть, какое из них наибольшее. числитель # 1 = 3 Таким образом, 318 больше 218 Метод третий: сравнение дробей с одинаковым числителемЕсли у дробей одинаковый числитель, сравните их, сравнивая знаменатели. Когда числители совпадают, дробь с меньшим знаменателем больше.Другими словами, чем больше знаменатель, тем меньше число. Как сравнивать дроби с десятичными знаками и процентыШаги по сравнению дробей с десятичными знаками и процентными значениями немного отличаются. Сначала преобразуйте каждое число в десятичную форму. Разделите числители дробей на знаменатель и разделите проценты на 100. Во-вторых, сравните десятичные значения друг с другом, чтобы определить, какое из них меньше или больше. Наконец, перепишите оператор сравнения, используя исходные числа, и добавьте правильный оператор, найденный на предыдущем шаге. Возможно, вас заинтересует наш калькулятор дробей. Сравните два числа с помощью числовой строкиБыстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение сложных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь Электричество, Стоимость разложения, Целые числа, Наибольшие общие факторы, Наименьшие общие фракции, AddingFractions, Сравнение фракций, Преобразование фракций, Преобразование в десятичные дроби, Преобразование в десятичные дроби, Преобразование дробей в десятичные дроби, Преобразование в десятичные дроби ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, Equation from slopeLines Theotation, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок Калькулятор сравнения ссуд
Переключить навигацию
 Кредит 1Сумма займа$ Процентная ставка% СрокГод Заем 2Сумма займа$ Процентная ставка% СрокГод Добавить ссуду Дата начала Поделиться Результатами: Поделиться результатами
График погашения
Последние калькуляторы
Популярные калькуляторы
ресурсов
 com. Все права защищены. Контакт / Заявление об ограничении ответственности / Политика конфиденциальности / Политика в отношении файлов cookie / Условия использования / Не продавать мою личную информацию Калькулятор сравнения соотношения com. Все права защищены. Контакт / Заявление об ограничении ответственности / Политика конфиденциальности / Политика в отношении файлов cookie / Условия использования / Не продавать мою личную информацию Калькулятор сравнения соотношения| Калькуляторы соотношений от iCalculator ™ Калькулятор сравнения соотношений, который позволяет сравнивать два или более соотношений, чтобы увидеть, совпадают ли они (вы можете сравнить до 10 соотношений, используя этот калькулятор соотношений). Этот калькулятор соотношений также позволяет рассчитывать и сравнивать эквивалентные соотношения, чтобы убедиться, что одно соотношение равно другому соотношению, вы можете выбрать метод расчета, который вы предпочитаете, сравнение рационов может быть рассчитано с использованием любого отношения к доле, отношения к проценту или соотношению в десятичную.Параметры одинаково точны, но каждый позволяет увидеть, как сравниваются два отношения, используя разные математические подходы. После того, как калькулятор сравнения коэффициентов сравнит введенные коэффициенты, он выделит (зеленым фоном) коэффициенты, которые совпадают с сравниваемым коэффициентом, и создаст таблицу эквивалентных коэффициентов.
Внимание! Когда фон красный, соотношения не равны. Когда фон зеленый, соотношения равны, и вычисления будут отображаться. Если вы нашли калькулятор сравнения соотношений полезным, пожалуйста, уделите секунду, чтобы поделиться и / или оставить нам оценку. ★ ★ ★ ★ ★ [49 голосов] Зачем нам нужно сравнивать коэффициенты? Может показаться странным, зачем мы сравниваем коэффициенты? Ответ приходит во многих формах: вы можете смешивать бетон в правильном соотношении, чтобы построить бетонный фундамент на строительной площадке, где нужно учитывать три отдельных размера целых, или вы можете учитывать размер порции калорий в пицце, где У вас есть несколько пицц и приходят друзья, некоторые могут есть меньше пиццы, другие больше, и вы хотите подумать о том, как вы нарезаете пиццу, чтобы убедиться, что пиццы достаточно для еды и / или правильный размер калорий / порции.Это всего лишь два простых примера соотношений в повседневной жизни, где у вас может быть несколько соотношений, и вам, возможно, придется подумать, одинаковы ли эти отношения. Поистине удивительно, сколько ситуаций требует от вас расчета соотношения. Простое соотношение, такое как 1: 2, 2: 4, 3: 9, 4:16, 5:15 и т. Д., Очень легко визуализировать, и сравнение соотношений, когда они маленькие числа, может быть довольно простой задачей с использованием мысленной арифметики Фактически, мозг, вероятно, вычисляет и сравнивает эти простые соотношения и формирует вывод еще до того, как вы даже начнете записывать формулу вручную и начали сравнивать соотношения ручкой и бумагой. Не все отношения настолько просты, и сложные отношения, такие как 1234: 98375, 194: 2918, 177: 199, 1982: 1028763, могут быть очень сложными для сравнения. При сравнении этих соотношений обычно быстрее использовать калькулятор сравнения соотношений, подобный этому, предоставляемый iCalculator, поскольку он позволяет сравнивать несколько соотношений одновременно и видеть, одинаковы ли соотношения, независимо от того, насколько сложным является соотношение. Вы также можете использовать Калькулятор сравнения соотношений, чтобы проверить свои ответы, где вы вручную сравниваете два или более соотношений, это особенно полезно для проверки того, что вы используете правильную математическую формулу и вычисления при изучении математики. Как сравнивать коэффициентыВы можете сравнивать коэффициенты, сравнивая их визуально и используя мысленную арифметику, чтобы увидеть, совпадают ли два отношения, или вы можете использовать математическую формулу для сравнения соотношений. Мысленная арифметика идеально подходит для простого сравнения соотношений, но более сложные отношения лучше сравнивать с математикой, особенно если вы работаете над сложной формулой для физики, химии или математики или, возможно, разрабатываете подробные допуски в рамках инженерного проекта. Существует три различных способа сравнения двух соотношений с использованием математической формулы:
Вы, конечно, можете использовать их методы для сравнения более двух соотношений, но вы обычно будете сравнивать одно соотношение с другим несколько раз, поэтому мы склонны ссылаться на сравнение соотношений и сравнение двух соотношений, даже если вам может потребоваться сравнить несколько соотношений. Как вы, наверное, заметили, сравнение двух или более соотношений изначально требует преобразования соотношений из их стандартного выражения в выражение, которое делает сравнение более практичным. Процесс преобразования отношения довольно прост, хотя важно убедиться, что коэффициенты выражаются одинаково.В частности, это отношение части к части или части к целому. Большинство соотношений выражаются как части к целому, это означает, что начальное число является частью второго числа. например 1: 2 предполагают, что целое равно 2, а часть целого равна одному. Частичное соотношение — это когда как первое, так и второе числа составляют часть единого целого. Итак, если мы снова воспользуемся соотношением 1: 2, 1 будет частью, а два также частью, так что на самом деле целое будет 1 + 2. Преобразование отношения в дробьПреобразование отношения в дробь — очень простой процесс, хотя может быть сложнее с более сложными отношениями. Проще говоря, первое число в соотношении становится числителем дроби, а второе число становится знаменателем дроби, давайте посмотрим на это на примере формулы: A: B = A / B Здесь мы предлагаем более подробное руководство и онлайн-калькулятор для преобразования отношения в дробь. Преобразование отношения в десятичное числоПреобразование отношения в десятичное число рассчитывается путем деления первого числа отношения на второе число в пределах отношения, давайте посмотрим на это на примере формулы: A : B = A ÷ B Преобразование отношения в проценты Преобразование отношения в проценты — еще одно простое вычисление. A: B = (A ÷ B) × 100 Как использовать калькулятор сравнения соотношений
СводкаМы надеемся, что вы нашли это руководство и калькулятор для сравнения двух или более соотношений полезными.Теперь вы должны хорошо понимать, как сравнивать коэффициенты, методы сравнения соотношений и, конечно же, теперь у вас есть доступ к отличному калькулятору коэффициентов, когда вам нужно сравнить коэффициенты. Вы также можете использовать наш Калькулятор эквивалентных соотношений, который позволяет вам генерировать несколько соотношений, которые равны исходному соотношению, это удобно, когда вам нужно выразить соотношение в другой числовой форме. Математические калькуляторыВам также могут пригодиться следующие математические калькуляторы. Изменение в процентах — увеличение и уменьшение в процентах Для объяснения и повседневных примеров использования процентов, как правило, см. Нашу страницу Проценты: Введение . Для более общих расчетов процентов см. Нашу страницу Калькуляторы процентов . Для расчета увеличения в процентах:Первый: вычислите разницу (увеличение) между двумя числами, которые вы сравниваете. Увеличение = новый номер — исходный номер Затем: разделите увеличение на исходное число и умножьте ответ на 100. % увеличение = Увеличение ÷ Исходное число × 100 . Если ваш ответ отрицательный, то это процентное уменьшение. Для расчета уменьшения в процентах:Первый: вычислите разницу (уменьшение) между двумя числами, которые вы сравниваете. Уменьшение = исходный номер — новый номер Затем: разделите уменьшение на исходное число и умножьте ответ на 100. % Уменьшение = Уменьшение ÷ Исходное число × 100 Если ваш ответ отрицательный, то это процентное увеличение. Если вы хотите рассчитать процентное увеличение или уменьшение нескольких чисел, мы рекомендуем использовать первую формулу. Положительные значения указывают на процентное увеличение, тогда как отрицательные значения указывают на процентное уменьшение. Калькулятор процентного измененияИспользуйте этот калькулятор для вычисления процентного изменения двух чисел. Подробнее: Калькуляторы процентов Примеры — увеличение и уменьшение в процентахВ январе Дилан проработал 35 часов, в феврале — 45.5 часов — на сколько процентов увеличилось рабочее время Дилана в феврале? Чтобы решить эту проблему, сначала мы вычисляем разницу в часах между новым и старым числами. 45,5 — 35 часов = 10,5 часов. Мы видим, что в феврале Дилан проработал на 10,5 часов больше, чем в январе — это его увеличение на . Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январское) число: 10,5 ÷ 35 = 0. Наконец, чтобы получить процентное значение, мы умножаем ответ на 100. Это просто означает перемещение десятичной точки на два столбца вправо. 0,3 × 100 = 30 Таким образом, в феврале Дилан отработал на 30% больше часов, чем в январе. В марте Дилан снова проработал 35 часов — столько же, сколько он работал в январе (или 100% его январских часов). Какова процентная разница между февральскими часами Дилана (45.5) и его мартовские часы (35)? Сначала рассчитайте уменьшение количества часов, то есть: 45,5 — 35 = 10,5 Затем разделите уменьшение на исходное число (февральские часы) так: 10,5 ÷ 45,5 = 0,23 (с точностью до двух знаков после запятой). Наконец, умножьте 0,23 на 100, чтобы получить 23%. Часы Дилана в марте были на 23% меньше, чем в феврале. Вы могли подумать, что, поскольку между часами работы Дилана в январе (35) и февралем (45.5) часов, что между его часами февраля и мартом также будет 30% сокращение. Как видите, это предположение неверно. Причина в том, что наше исходное число в каждом случае разное (35 в первом примере и 45,5 во втором). Это подчеркивает, насколько важно рассчитывать процентное соотношение от правильной начальной точки. Иногда проще показать процентное уменьшение как отрицательное число — для этого следуйте приведенной выше формуле для расчета процентного увеличения — ваш ответ будет отрицательным числом, если было уменьшение.В случае Дилана увеличение на часов в период с февраля по март составляет -10,5 (отрицательно, потому что это уменьшение). Следовательно, -10,5 ÷ 45,5 = -0,23. -0,23 × 100 = -23%. Часы Дилана могут быть отображены в таблице данных как:
Расчет значений на основе процентного изменения Иногда бывает полезно рассчитать фактические значения на основе процентного увеличения или уменьшения. Вы можете увидеть заголовки вроде:
Эти заголовки дают представление о тенденции — когда что-то увеличивается или уменьшается, но часто нет реальных данных. Без данных цифры процентного изменения могут вводить в заблуждение. Кередигион, графство в Западном Уэльсе, имеет очень низкий уровень насильственных преступлений. Полицейские отчеты Кередигиона за 2011 год показали 100% рост насильственных преступлений. Это поразительное число, особенно для тех, кто живет или думает о переезде в Кередигион. Однако, когда исследуются основные данные, выясняется, что в 2010 году в Кередигионе было зарегистрировано одно насильственное преступление. Когда мы встречаемся с реальными цифрами, восприятие количества насильственных преступлений в Ceredigion значительно меняется. Чтобы определить, насколько что-то увеличилось или уменьшилось в реальном выражении, нам нужны реальные данные. Возьмем для примера « осадков в Великобритании этим летом было на 23% выше среднего » — мы можем сразу сказать, что в Великобритании за лето выпало почти на четверть (25%) осадков больше, чем в среднем. Однако, не зная, каков средний уровень осадков или сколько осадков выпало за рассматриваемый период, мы не можем определить, сколько осадков выпало на самом деле. Расчет фактического количества осадков за период, если известно среднее количество осадков. Если мы знаем, что среднее количество осадков составляет 250 мм, мы можем рассчитать количество осадков за период, вычислив 250 + 23%. Первая тренировка 1% от 250, 250 ÷ 100 = 2,5. Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%. 2,5 × 23 = 57,5. Таким образом, общее количество осадков за рассматриваемый период составило 250 + 57,5 = 307,5 мм. Расчет среднего количества осадков, если известно фактическое количество осадков. Если в новостном сообщении говорится о новом измерении и процентном увеличении, « в Великобритании количество осадков было на 23% выше среднего… Выпало 320мм дождя… ». В этом примере мы знаем, что общее количество осадков составило 320 мм. Мы также знаем, что это на 23% выше среднего. Другими словами, 320 мм соответствует 123% (или 1,23 раза) от среднего количества осадков. Чтобы вычислить среднее значение, мы разделим общую сумму (320) на 1,23. 320 ÷ 1,23 = 260,1626. Округленное до одного десятичного знака, среднее количество осадков составляет 260,2 мм . Теперь можно рассчитать разницу между средним и фактическим количеством осадков: Мы можем сделать вывод, что 59,8 мм составляет 23% от среднего количества осадков (260,2 мм), и что в реальном выражении выпало на 59,8 мм больше осадков, чем в среднем. Мы надеемся, что вы нашли эту страницу полезной — почему бы не заглянуть на другие наши страницы, посвященные навыкам счета? Или дайте нам знать о предмете, который вы хотели бы обсудить на SkillsYouNeed — Свяжитесь с нами .
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 {2}14<2,25}}\end{array}\)
{2}14<2,25}}\end{array}\)
 Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2
Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2 Сравнить рациональные числа
Сравнить рациональные числа  Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа Сравнить рациональные числа и
Сравнить рациональные числа и Сравнить рациональные числа 15,4 и 2,1256
Сравнить рациональные числа 15,4 и 2,1256 Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:
Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны: Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)
Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3) Почему? Простой вопрос: Что больше – одна десятая часть от чего либо или одна тысячная? Конечно же, одна десятая.
Почему? Простой вопрос: Что больше – одна десятая часть от чего либо или одна тысячная? Конечно же, одна десятая. В некоторых примерах также явно видно какая дробь больше, например:
В некоторых примерах также явно видно какая дробь больше, например:


 Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d
Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d Результат сравнения возможет при сравнении их знаменателей.
Результат сравнения возможет при сравнении их знаменателей. Для детального рассмотрения ниже приведем пример.
Для детального рассмотрения ниже приведем пример. В этом случае используйте правило:
В этом случае используйте правило:

 Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126
больше дроби 65/126
.
Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126
больше дроби 65/126
. Получаем и .
Получаем и .


 Очевидно, что число 3 деленное на 20 в любом случае меньше 3 деленного на 5. Если подсчитать эти значения мы получим десятичные дроби 0,06 и 0,6, и такие значения нетрудно сопоставить. Сортировка таких дробей выполняется по знаменателям, но в обратном порядке. Для нашего примера сортировка будет выглядеть так:
Очевидно, что число 3 деленное на 20 в любом случае меньше 3 деленного на 5. Если подсчитать эти значения мы получим десятичные дроби 0,06 и 0,6, и такие значения нетрудно сопоставить. Сортировка таких дробей выполняется по знаменателям, но в обратном порядке. Для нашего примера сортировка будет выглядеть так: В общем случае поиск общего знаменателя сводится к задаче определения наименьшего общего кратного (НОК).
В общем случае поиск общего знаменателя сводится к задаче определения наименьшего общего кратного (НОК).
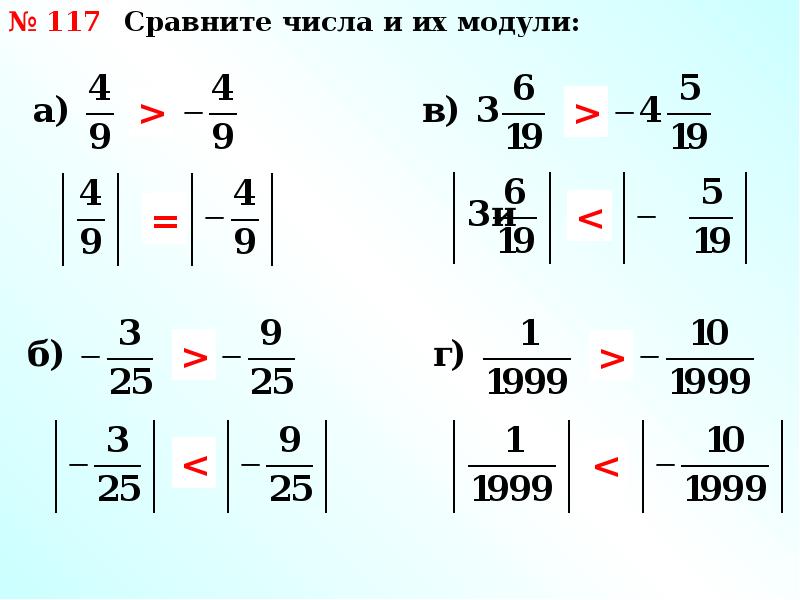
 Вы также можете использовать этот калькулятор для сравнения смешанных чисел, сравнения десятичных чисел, сравнения целых чисел и сравнения неправильных дробей.
Вы также можете использовать этот калькулятор для сравнения смешанных чисел, сравнения десятичных чисел, сравнения целых чисел и сравнения неправильных дробей. Д. Наименьшее общее кратное — 24, поэтому мы используем это как наименьшее общий знаменатель.
Д. Наименьшее общее кратное — 24, поэтому мы используем это как наименьшее общий знаменатель. Наш
Калькулятор дробей,
Упростите калькулятор дробей и
Калькулятор смешанных чисел.
Наш
Калькулятор дробей,
Упростите калькулятор дробей и
Калькулятор смешанных чисел. К счастью, есть несколько методов сравнения одной дроби с другой.
К счастью, есть несколько методов сравнения одной дроби с другой. Если вы не знаете, как это сделать, наш калькулятор наименьшего общего знаменателя поможет вам его найти.
Если вы не знаете, как это сделать, наш калькулятор наименьшего общего знаменателя поможет вам его найти. Дробь с большим числителем — это большее число.
Дробь с большим числителем — это большее число.
 Ваша поддержка помогает нам бесплатно предоставлять калькулятор и подобные инструменты.
Ваша поддержка помогает нам бесплатно предоставлять калькулятор и подобные инструменты.

 Важным моментом является то, что независимо от того, сравниваете ли вы два отношения или двадцать отношений, метод вычисления и сравнения отношений остается неизменным. Давайте подробно рассмотрим каждый метод сравнения отношений.
Важным моментом является то, что независимо от того, сравниваете ли вы два отношения или двадцать отношений, метод вычисления и сравнения отношений остается неизменным. Давайте подробно рассмотрим каждый метод сравнения отношений. Это означает, что в соотношении частей к части у нас фактически есть два отношения, в нашем примере 1: 2 часть-часть совпадает с отношениями 1: 3 и 2: 3 частей к целому.В большинстве ситуаций вы обычно сталкиваетесь с отношениями части к целому, и мы продолжим примеры в этом руководстве по соотношению, используя отношения части к целому.
Это означает, что в соотношении частей к части у нас фактически есть два отношения, в нашем примере 1: 2 часть-часть совпадает с отношениями 1: 3 и 2: 3 частей к целому.В большинстве ситуаций вы обычно сталкиваетесь с отношениями части к целому, и мы продолжим примеры в этом руководстве по соотношению, используя отношения части к целому. Сначала вы повторяете шаги, необходимые для преобразования отношения в дробь, а именно: возьмите первое число отношения и разделите его на второе число в пределах отношения.Затем мы умножаем полученное десятичное число на 100, чтобы получить процентное значение, давайте посмотрим на это на примере формулы:
Сначала вы повторяете шаги, необходимые для преобразования отношения в дробь, а именно: возьмите первое число отношения и разделите его на второе число в пределах отношения.Затем мы умножаем полученное десятичное число на 100, чтобы получить процентное значение, давайте посмотрим на это на примере формулы:


 3 (См. Наши инструкции и примеры деления на странице , раздел .)
3 (См. Наши инструкции и примеры деления на странице , раздел .)
 В средствах массовой информации часто можно увидеть примеры того, когда это может быть полезно.
В средствах массовой информации часто можно увидеть примеры того, когда это может быть полезно. Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
