Как умножать дроби с разными и одинаковыми знаменателями
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.
Дроби могут быть двух видов:
- Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя:
Неправильной — ту, у которой числитель больше знаменателя или равен ему:
Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.
Основные правила дробей
|
Умножение дробных чисел
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Как умножить дробь на дробь
Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:
Важно проверить возможность сокращения — так решать будет легче:
Как умножить смешанные дроби
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как умножить дробь на натуральное число
Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.
Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.
Решение задач
Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как решаем: перемножим делимое и натуральное число.
Ответ:
Задание 2. Выполнить умножение 4/15 и 55/6.
Как решаем:
- перемножим числители между собой и знаменатели соответственно
- сократим полученное
- выделим целую часть
Ответ:
Задание 3.
 Выполнить умножение одной целой трех седьмых на шесть.
Выполнить умножение одной целой трех седьмых на шесть.Как решаем:
- переводим смешанное число в неправильную дробь,
- умножаем делимое на натуральное число,
- сократим полученное,
- преобразуем в смешанное число.
Ответ:
Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
ДРОБИ!!! ПОЛНЫЙ РАЗБОР ПРИМЕР С ДРОБЯМИ
Действия с дробями проходят через всю школьную математику. В жизни мы не очень много с ними сталкиваемся, хотя постоянно слышим и говорим — половина, четверть, треть.
В жизни мы не очень много с ними сталкиваемся, хотя постоянно слышим и говорим — половина, четверть, треть.
Но на всех экзаменах будут примеры на дроби и действия с ними. Очень редкие калькуляторы помогут вам в этом. Да ещё вам сначала придётся научиться использовать такой хитрый калькулятор. Довольно часто вычисления с дробями встречаются в физике,
химии и изредка в биологии.
Дроби были придуманы людьми для того, чтобы справиться с проблемой деления с остатком.
8: 2 = 4 (ровно, без остатка), а 9: 2 = 4 и остаток 1.
Действия с Дробями
Дробить — значит разбивать на более мелкие части. И в математике дробь — это что-то меньше, чем целая единица. Мне нравится использовать для примера тортики. Почему-то ученики с удовольствием придумывают способы для того, чтобы разделить тортики на несколько равных частей. Собственно, это и есть применение математики в жизни.
Если мы разделим тортик на две части, то их называют половинки, или если в виде
дроби — «одна вторая».
1 число над дробью называется ЧИСЛИТЕЛЬ, он показывает какое количество (ЧИСЛО) частей мы взят.
2 число под дробью называется ЗНАМЕНАТЕЛЬ, он показывает на сколько равных частей мы разбили целое (тортик, например)
Если ученик сам не смог вспомнить — как называются числитель и знаменатель, то надо ему на них показать, назвать и попросить самому дать определения этим словам, а потом потренировать, показывая ему на примеры дробей. Эти слова часто используют
в математике, физике и даже просто в жизни: вы слышали когда-нибудь — «надо их к одному знаменателю привести»? «Привести», кстати, в математике означает не «переместить к нужному пункту что-то или кого-то». Как «привести машину к подъезду».
В математике «привести» — значит сделать действия в соответствии с правилами, чтобы получилось что-то одно или одинаковое с чем-то. То есть надо сделать так, чтобы у дробей были одинаковые знаменатели.
Попросите ученика разделить «тортики» (круги) на 4 равные части, на 8 частей,
на 3 части. Пусть поищут способы, чтобы части были равными.
Пусть поищут способы, чтобы части были равными.
Скажите, что когда делим на 4 части, то одна из частей называется одна ЧЕТВЁРТАЯ,
две таких части — две четвёртых, три — три четвертых. Пусть он попрактикуется в названии разных дробей пока не поймёт это очень хорошо.
Потом спросите — как нам сложить одинаковые части? Одна четвёртая и одна четвёртая будет сколько? Правильно — две четвёртых. То есть, если мы складываем дроби с одинаковым знаменателем — мы не трогаем знаменатели, они остаются теми же,
нарисовать на тортике — что у него получается, какие части торта и пусть он сравнит наглядно с тем, что должно получиться при правильном сложении.
Далее нам надо сложить дроби с разными знаменателями. Если у него трудности, то мы объясняем, как это делается на таком примере:
Эти части тортика — разные по величине.
 Их можно сдвинуть вместе, и мы получим какую-то реальную часть тортика:
Их можно сдвинуть вместе, и мы получим какую-то реальную часть тортика:Но в числовом примере нам надо их ещё как-то записать, а для устного ответа — назвать правильными словами. Для этого нам надо разбить эти части на более мелкие, которые будут
одинаковы. Например так:
Вот в этих более мелких частях мы и запишем ответ. Если мы разделим каждую одну четвёртую на три части, а одну третью на четыре, то это будут более мелкие и одинаковые —
двенадцатые части. Одна четвёртая будет состоять из трёх двенадцатых, а одна третья из четырёх двенадцатых. И вместе это будет — семь двенадцатых.
Надо потренировать ученика складывать разные дроби до уверенности. Потом те же принципы применяются при сложении дробей в алгебре в 6 классе и старше — где вместо
чисел будут разные буквы и целые выражения. Но правила сложения и умножения дробей
ТЕ ЖЕ самые.
Умножение Дробей
Если ученик легко складывает дроби, то я перехожу к умножению дробей. Тут надо просто
запомнить правило:
При умножении дробей числитель умножается на числитель,
а знаменатель — на знаменатель.
Конечно, надо до уверенности попрактиковаться в этом действии!
Деление Дробей
При делении дробей можно, конечно, разделить числитель на числитель, а знаменатель
на знаменатель. Но это не всегда получается — если мы в предыдущем примере попробуем
разделить 2 на 3 и 5 на 7, то вряд ли получится что-то удобное. Потому делают так:
Вторую
дробь переворачивают, и первую дробь умножают на ПЕРЕВЁРНУТУЮ вторую дробь.
Это правило надо понять и усвоить. И, конечно, надо до уверенности попрактиковаться
в этом действии!
Использование дробей в Python — CodeRoad
Я использую здесь классы для ввода дроби (когда заданы числитель и знаменатель), а также для сложения и умножения двух дробей вместе. По какой-то причине импортированный модуль фракций корректно работает только для части программы; метод gcd работает, но метод фракции (где при задании двух чисел помещается в формат фракции) не работает, вместо этого выбрасывая NameError (в частности, «глобальное имя ‘Fractions’ не определено»).
Что я делаю не так? Я относительно новичок в Python, и любые предложения о том, как сделать этот код более жестким с большим количеством исключений, будут очень признательны.
Вот мой код:
import fractions
class FractionClass:
# Initialize starting numerator and denominator.
n = 0
d = 0
def __init__(self, numerator, denominator):
self.n = numerator
self.d = denominator
# Function that adds fractions, whichs throws NameError if gcd() doesn't work!
def add_fractions(self, other):
try:
sum_numerator = self.n + other.n
sum_denominator = fractions.gcd(self.d, other.d)
return(sum_numerator, sum_denominator)
except NameError:
print("Methods aren't defined.")
# Function that multiplies fractions, whichs throws NameError if gcd() doesn't work!
def multiply_fractions(self, other):
try:
product_numerator = self.n * other.
n
product_denominator = self.d * other.d
return(product_numerator, product_denominator)
except NameError:
print("Methods aren't defined.")
# Enter input function.
def user_input():
try:
print("Enter a numerator and denominator:")
n, d = [int(x) for x in input().split()]
print("Enter a numerator and denominator:")
n2, d2 = [int(x) for x in input().split()]
# Check used to debug for denominators that aren't the minimum of 1 (0 can't be divided!)
check = 1 / d
check = 1 / d2
# print(check)
# Exception for d = 0.
except ZeroDivisionError:
print("\n You didn't enter the minimum denominator.")
print("Set denominator to minimum default.")
d = 1
# Exception for not entering a space in between numbers.
except UnboundLocalError:
print("You didn't enter your numbers in properly! Try again.")
# Exception for not entering all required. except NameError:
print("\n You didn't enter two numbers.")
# Exception for user input both or one of them, not being integers.
except TypeError:
print("\n You didn't enter all valid numbers.")
# General exception case.
except:
print("Something went wrong!")
fract = FractionClass(n,d)
another_fraction = FractionClass(n2, d2)
total_sum = fract.add_fractions(another_fraction)
# Unpacks total sum tuple.
# Puts in fraction format.
sum_numerator, sum_denominator = total_sum
add_output = fractions.Fraction(sum_numerator, sum_denominator)
total_product = fract.multiply_fractions(another_fraction)
# Unpacks product sum tuple.
# Puts in fraction format.
product_numerator, product_denominator = total_product
multiply_output = fractions.Fraction(product_numerator, product_denominator)
print(add_output, multiply_output)
except NameError:
print("\n You didn't enter two numbers.")
# Exception for user input both or one of them, not being integers.
except TypeError:
print("\n You didn't enter all valid numbers.")
# General exception case.
except:
print("Something went wrong!")
fract = FractionClass(n,d)
another_fraction = FractionClass(n2, d2)
total_sum = fract.add_fractions(another_fraction)
# Unpacks total sum tuple.
# Puts in fraction format.
sum_numerator, sum_denominator = total_sum
add_output = fractions.Fraction(sum_numerator, sum_denominator)
total_product = fract.multiply_fractions(another_fraction)
# Unpacks product sum tuple.
# Puts in fraction format.
product_numerator, product_denominator = total_product
multiply_output = fractions.Fraction(product_numerator, product_denominator)
print(add_output, multiply_output)
Поделиться Источник user1739537 10 декабря 2012 в 21:34
2 ответа
- Добавление Дробей
Я создаю метод сложения двух дробей любого типа, то есть целых, радикальных и т.
 д. Это то, что у меня есть до сих пор. Если числитель и знаменатель обеих дробей являются целыми числами, то это легко сделать. Но если это радикальные или любые другие комплексные числа, я должен изменить свой код….
д. Это то, что у меня есть до сих пор. Если числитель и знаменатель обеих дробей являются целыми числами, то это легко сделать. Но если это радикальные или любые другие комплексные числа, я должен изменить свой код…. - Java Калькулятор Дробей: Синтаксический Анализ
Я делаю калькулятор дробей Java для школы, и одна из самых больших проблем, с которыми я сталкиваюсь, — это синтаксический анализ. Я могу использовать его, когда использую только числа, но поскольку это калькулятор дробей, мы включаем подчеркивания(для смешанных чисел) и обратные косые черты для…
6
Вам не нужен свой собственный класс, чтобы умножить две дроби:
>>> from fractions import Fraction as F
>>> F("1/2")
Fraction(1, 2)
>>> F("3/4")
Fraction(3, 4)
>>> F("1/2") * F("3/4")
Fraction(3, 8)
>>> F("1/2") + F("3/4")
Fraction(5, 4)
>>> F(5, 8) + F(4, 7)
Fraction(67, 56)
Что касается ошибки, о которой Вы упомянули, то это маловероятно, так как у вас нигде в коде нет имени «Fractions», и вы не отправили обратную трассировку. Скорее всего, вы используете какую-то старую версию своего кода.
Скорее всего, вы используете какую-то старую версию своего кода.
Поделиться lqc 10 декабря 2012 в 22:52
0
Есть еще одно место на линии 26:
except NameError:
Так и должно быть
except NameError:
Вы также должны проверить и исправить отступ. Иначе нет тела — ничто не называется.
Поделиться pepr 10 декабря 2012 в 22:35
Похожие вопросы:
PHP: можно ли использовать range() для дробей?
Можно ли использовать функцию range() в PHP для создания списка дробей или десятичных дробей?
CLR Regex для дробей
Мне нужен CLR Regex для дробей или целых чисел и дробей, где 1/2 правильно 12 2/3 тоже правильно и знак минус может всплывать непосредственно перед любым числом. Сначала я придумал -?([0-9]*…
Сначала я придумал -?([0-9]*…
Python/BeautifulSoup Разбор HTML Дробей
Вопросы Почему вывод в последних двух случаях BOTH unicode, но в одном случае он показывает дробь, а в другом — какой-то другой код, представляющий дробь? Какой самый чистый способ для меня перейти…
Добавление Дробей
Я создаю метод сложения двух дробей любого типа, то есть целых, радикальных и т. д. Это то, что у меня есть до сих пор. Если числитель и знаменатель обеих дробей являются целыми числами, то это…
Java Калькулятор Дробей: Синтаксический Анализ
Я делаю калькулятор дробей Java для школы, и одна из самых больших проблем, с которыми я сталкиваюсь, — это синтаксический анализ. Я могу использовать его, когда использую только числа, но поскольку…
сложение двух дробей в python
Я пытаюсь сложить две дроби в python если вход 1/4 + 1/4,, я ожидаю результата 1/2 Я построил класс дробей с методом __add__ для сложения from fractions import gcd class fraction: def __init__(self,. ..
..
Нахождение числа приведенных дробей
Я работаю над этой проблемой последние два дня. Я чувствую, что нахожусь в опасной близости, но что-то не совсем щелкает. Хотелось бы, чтобы свежая пара глаз пробежала через это — открытая для любых…
Преобразование дробей в серии Dataframe в плавающие
В Python 3.x, как я могу преобразовать столбец Dataframe, содержащий строки дробей и значения NaN в поплавки? Я попробовал несколько вещей, но не нашел адекватного решения. Так что если у меня есть…
Ошибка памяти в Python при использовании дробей
Я использую последовательность Штерна-Броко для генерации дробей. Эти дроби были добавлены к списку. Теперь мне нужно изменить этот список дробей, так как задача требует, чтобы я удовлетворял 2…
Python-правильное сложение дробей
Я хотел бы сделать некоторые вычисления с дробями, сохраняя все числа в виде дробей и никогда не преобразуя их в десятичные. Например, 1/2+1/4=3/4. мы можем сделать это в Python, например, используя…
Например, 1/2+1/4=3/4. мы можем сделать это в Python, например, используя…
Сложение дробей | Онлайн калькулятор
Сложение дробей с одинаковыми знаменателями:
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.Формула
Сложим две дроби с одинаковым с одинаковыми знаменателями
По формуле складываем числители, а знаменатель оставляем исходный
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: При сокращении дроби у нас получится число 1/2
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК — наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение:
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример:
Решение:
Вычисляем целую часть, и получаем ответ
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
Пример:
Подставляем цифры в формулу:
Получаем:
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей с помощью онлайн калькулятора:
Вам помог этот калькулятор?Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
Деление в столбик с запятыми калькулятор. Калькулятор дробей: решение уравнений с дробями
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры.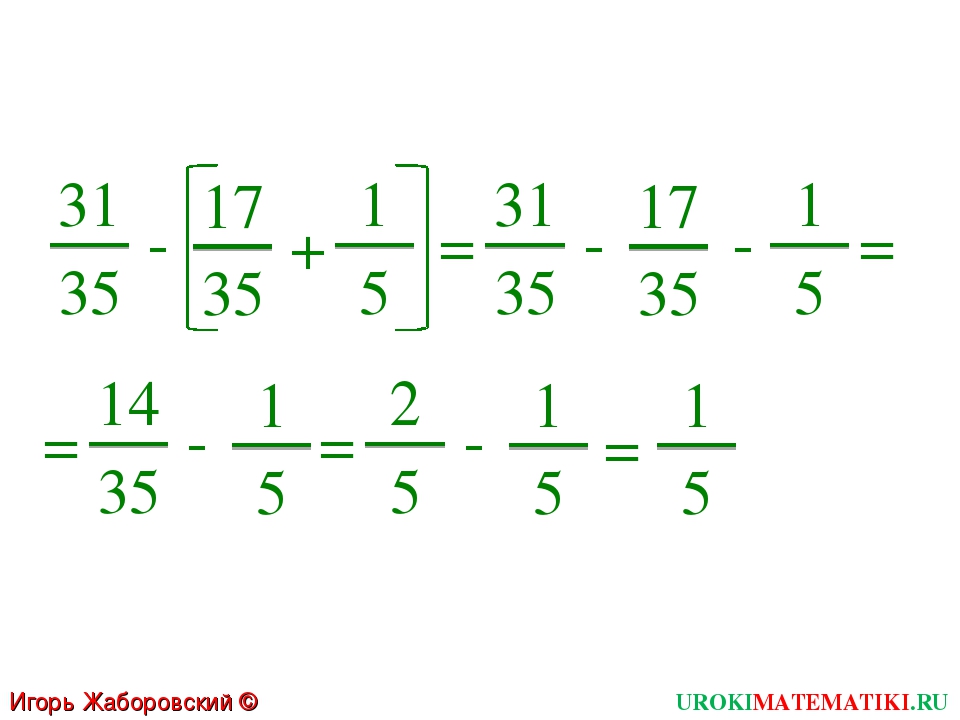 Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат.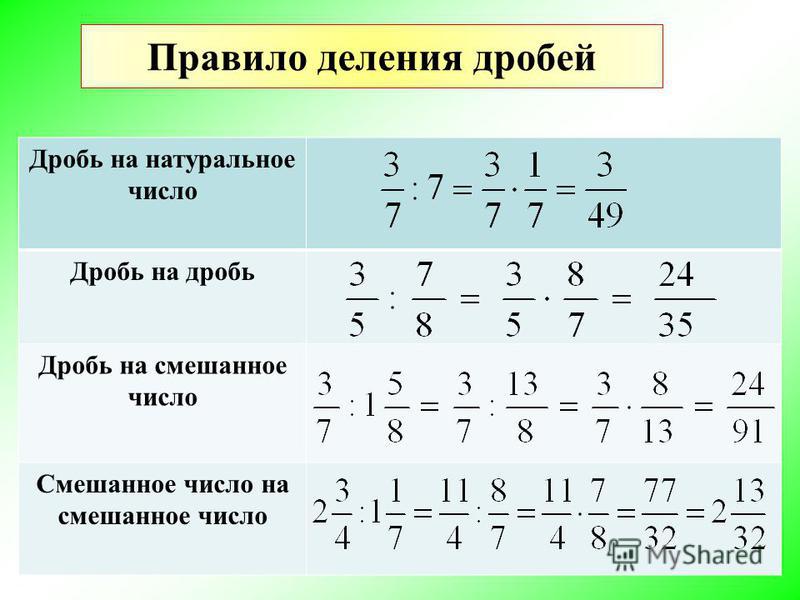 При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Простые арифметические действия — это основа дальнейшего обучения детей точным наукам. Математика сопровождает людей повсюду на протяжении всей жизни, а потому важно понимать её с самых азов.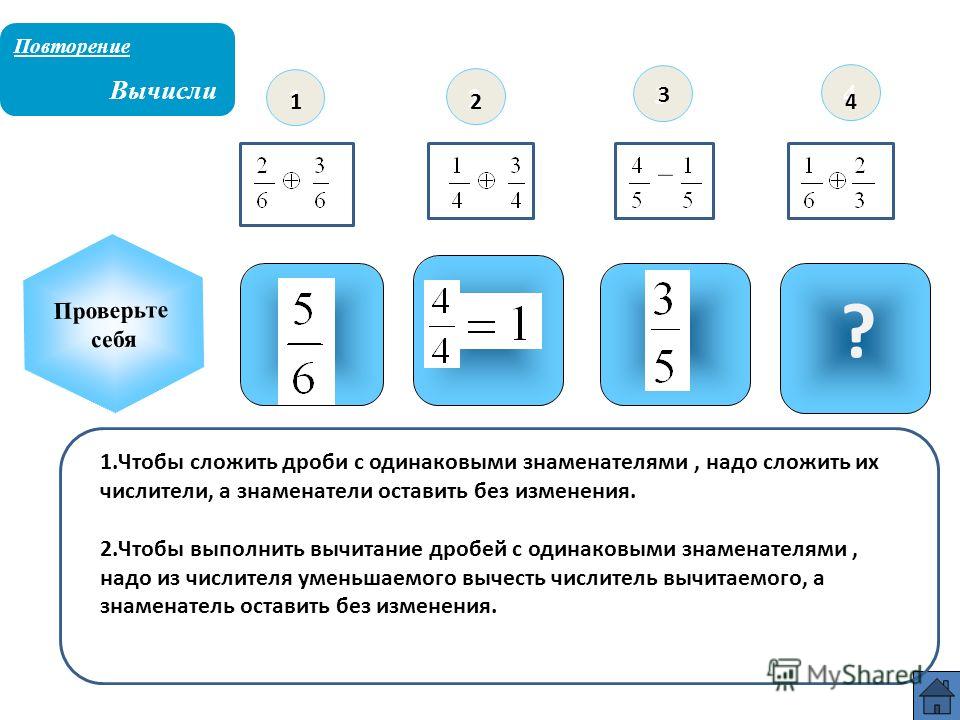 Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.
Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.
Как вычитать десятичные дроби в столбик
При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными
Действия с десятичными дробями производятся так же, как и с натуральными. Основные правила, которые важно знать при решении примеров на вычитание в столбик:
- Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей.
 Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50. - Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего. Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
- Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
- Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.
Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее
Вычитание всегда можно проверить сложением.
Карточки для уроков
Чтобы было проще изучить алгоритм действий, можно распечатать для детей специальные карточки-памятки, которые помогут быстрее освоить новый материал.
Фотогалерея: варианты карточек для занятий
Видео: как вычитать десятичные дроби столбиком
Освоив это простое действие, дети смогут в дальнейшем лучше учиться, ведь примеры с десятичными дробями решают не только на математике, но и на физике, химии, астрономии. Главное — понять алгоритм.
Фарафонова Наталия Игоревна
После прохождения темы «Действия с десятичными дробями» для отработки навыка счета и проверки усвоения материала можно провести индивидуальную работу с учащимися по карточкам. Каждый учащийся должен без ошибок выполнить задания по всем действиям. По каждому действию представлено много вариантов, это дает возможность каждому учащемуся несколько раз решить задание по каждому действию с десятичными дробями и добиться безошибочного результата или выполнить задание с минимальным количеством ошибок. Так как каждый учащийся выполняет индивидуальное задание, учитель имеет возможность, по мере представления ему выполненных заданий, с каждым учеником обсудить их персонально. Если ученик допустил ошибки, то учитель исправляет их, и предлагает сделать задание из другого варианта. Так, до тех пор, пока учащийся не выполнит все задание или его большую часть без ошибок. Карточки лучше делать на цветной бумаге.
На последнем этапе работы, можно предложить решить пример, содержащий несколько действий.
За каждый безошибочно выполненный вариант, независимо от того, с какой попытки было верно выполнено задание, учащимся можно поставить отличную отметку, можно выставить среднюю оценку, после выполнения всей работы, на усмотрение учителя.
Сложение десятичных дробей.
1 вариант
7,468 + 2,85
9,6 + 0,837
38,64 + 8,4
3,9 + 26,117
2 вариант
19,45 + 34,8
4,9 + 0,716
75,86 + 4,2
5,6 + 44,408
3 вариант
24,38 + 7,9
6,5 + 0,952
48,59 + 1,8
35,906 + 2,8
4 вариант
7,6 + 319,75
888,99 + 4,5
64,15 + 18,9
4,5 + 0,738
5 вариант
7,62 + 8,9
25,38 + 0,09
12,842 + 8,6
412 + 78,83
6 вариант
70,7 + 3,8645
3,65 + 0,89
61,22 + 31.719
12,842 + 8,6
Ответы: 1 вариант: 10,318; 10,437; 47,04; 30,017;
2 вариант: 54,25; 5,616; 80,06; 50,008;
3 вариант: 32,28; 7,452; 50,19; 38,706;
4 вариант: 327,35; 893,49; 83,05; 5,238;
5 вариант: 16,52; 25,47; 21,442; 490,83;
6 вариант: 74,5645; 4,54; 92,939; 21,442;
Вычитание десятичных дробей.
1 вариант
26,38 — 9,69
41,12 — 8,6
5,2 — 3,445
7 — 0,346
2 вариант
47,62 — 8,78
54,06 — 9,1
7,1 — 6,346
3 — 1,551
3 вариант
50,41 — 9,62
72,03 — 6,3
9,2 — 5,453
4 — 2,662
4 вариант
60,01 — 8,364
123,61 — 69,8
8,7 — 4,915
10 — 3,817
5 вариант
6,52 — 3,8
7,41 — 0,758
67,351 — 9,7
22 — 0,618
6 вариант
4,5 — 0,496
61,3 — 20,3268
24,7 — 15,276
50 — 2,38
Ответы: 1 вариант: 16,69; 32,52; 1,755; 6,654;
2 вариант: 38,84; 44,96; 0,754; 1,449;
3 вариант: 40,79; 65,73; 3,747; 1,338;
4 вариант: 51,646; 53,81; 3,785; 6,183;
5 вариант: 2,72; 6,652; 57,651; 21,382;
6 вариант: 4,004; 40,9732; 9,424; 47,62;
Умножение десятичных дробей.
1 вариант
7,4 · 3,5
20,2 · 3,04
0,68 · 0,65
2,5 · 840
2 вариант
2,8 · 9,7
6,05 · 7,08
0,024 · 0,35
560 · 3,4
3 вариант
6,8 · 5,9
6,06 · 8,05
0,65 · 0,014
720 · 4,6
4 вариант
34,7 · 8,4
9,06 · 7,08
0,038 · 0,29
3,6 · 540
5 вариант
62,4 · 2,5
0,038 · 9
1,8 · 0,009
4,125 · 0,16
6 вариант
0,28 · 45
20,6 · 30,5
2,3 · 0,0024
0,0012 · 0,73
7 вариант
68 · 0,15
0,08 · 0,012
1,4 · 1,04
0,32 · 2,125
8 вариант
4,125 · 0,16
0,0012 · 0,73
1,4 · 1,04
720 · 4,6
Ответы: 1 вариант: 25,9; 61,408; 0,442; 2100;
2 вариант: 27,16; 42,834; 0,0084; 1904;
3 вариант: 40,12; 48,783; 0,0091; 3312;
4 вариант: 291,48; 64,1448; 0,01102; 1944;
5 вариант: 156; 0,342; 0,0162; 0,66;
6 вариант: 12,6; 628,3; 0,00552; 0,000876;
7 вариант: 10,2; 0,00096; 1,456; 0,68;
8 вариант: 0,66; 0,000876; 1,456; 3312;
Деление десятичной дроби на натуральное число.
1 вариант
62,5: 25
0,5: 25
9,6: 12
1,08: 8
2 вариант
0,28: 7
0,2: 4
16,9: 13
22,5: 15
3 вариант
0,75: 15
0,7: 35
1,6: 8
0,72: 6
4 вариант
2,4: 6
1,5: 75
0,12: 4
1,69: 13
5 вариант
3,5: 175
1,8: 24
10,125: 9
0,48: 16
6 вариант
0,35: 7
1,2: 3
0,2: 5
7,2: 144
7 вариант
151,2: 63
4,8: 32
0,7: 25
2,3: 40
8 вариант
397,8: 78
5,2: 65
0,9: 750
3,4: 80
9 вариант
478,8: 84
7,3: 4
0,6: 750
5,7: 80
10 вариант
699,2: 92
1,8: 144
0,7: 875
6,3: 24
Ответы: 1 вариант: 2,5; 0,02; 0,8; 0,135;
2 вариант: 0,04; 0,05; 1,3; 1,5;
3 вариант: 0,05; 0,02; 0,2; 0,12;
4 вариант: 0,4; 0,02; 0,03; 0,13;
5 вариант: 0,02; 0,075; 1,125; 0,03;
6 вариант: 0,05; 0,4; 0,04; 0,05;
7 вариант: 2,4; 0,15; 0,28; 0,0575;
8 вариант: 5,1; 0,08; 0,0012; 0,0425;
9 вариант: 5,7; 1,825; 0,0008; 0,07125;
10 вариант: 7,6; 0,0125; 0,0008; 0,2625;
Деление на десятичную дробь.
1 вариант
32: 1,25
54: 12,5
6: 125
2 вариант
50,02: 6,1
34,2: 9,5
67,6: 6,5
3 вариант
2,8036: 0,4
3,1: 0,025
0,0008: 0,16
4 вариант
4: 32
303: 75
687,4: 10
1,59: 100
5 вариант
5: 16
336: 35
412,5: 10
24,3: 100
6 вариант
41,82: 6,8
73,44: 3,6
7,2: 0,045
32,89: 4,6
Ответы: 1 вариант: 25,6; 4,32; 0,048;
2 вариант: 8,2; 3,6; 10,4;
3 вариант: 7,009; 124; 0,005;
4 вариант: 0,125; 4,04; 68,74; 0,0159;
5 вариант: 0,3125; 9,6; 41,25; 0,243;
6 вариант: 6,15; 20,4; 160; 7,15;
Совместные действия с десятичными дробями.
824,72 — 475: (0,071 + 0,929) + 13,8
(7,351 + 12,649) ·105 — 95,48 — 4,52
(3,82 — 1,084 + 12,264)·(4,27 + 1,083 — 3,353) + 83
278 — 16,7 — (15,75 + 24,328 + 39,2)
57,18 ·42 — 74,1: 13 + 21,35: 7
(18,8: 16 + 9,86 ·3) ·40 — 12,73
(2 — 0,25 ·0,8) : (0,16: 0,5 — 0,02)
(3,625 + 0,25 + 2,75) : (28,75 + 92,25 — 15) : 0,0625
Ответы: 1) 363,52; 2) 2000; 3) 113; 4) 182,022; 5) 2398,91; 6) 1217,47; 7) 6; 8) 1.
Инструкция
Научитесь переводить десятичные дроби в обыкновенные. Посчитайте, сколько знаков отделено запятой. Одна цифра справа от запятой означает, что знаменатель — 10, две — 100, три — 1000 и так далее. Например, десятичная дробь 6,8 как «шесть целых, восемь ». При преобразовании ее напишите сначала количество целых единиц — 6. В знаменателе напишите 10. В числителе будет стоять число 8. Получится, что 6,8 = 6 8/10. Вспомните правила сокращения. Если числитель и знаменатель делятся на одно и то же число, то дробь можно сократить на общий делитель. В данном случае это число 2. 6 8/10 = 6 2/5.
Попробуйте сложить десятичные дроби. Если вы делаете это в столбик, то будьте внимательны. Разряды всех чисел должны находиться строго друг под другом, — под запятой. Правила сложения точно такие же, как и при действии с . Прибавьте к тому же числу 6,8 другую десятичную дробь — например, 7,3. Запишите тройку под восьмеркой, запятую — под запятой, а семерку — под шестеркой. Складывать начните с последнего разряда. 3+8=11, то есть 1 запишите, 1 запомните. Далее сложите 6+7, получите 13. Прибавьте то, что оставалось в уме и запишите результат — 14,1.
Вычитание выполняется по тому же принципу. Разряды запишите друг под другом, запятую — под запятой. Ориентируйтесь всегда по ней, особенно если количество цифр после нее в уменьшаемом меньше, чем в вычитаемом. Отнимите от заданного числа, например, 2,139. Двойку запишите под шестеркой, единицу — под восьмеркой, остальные две цифры — под следующими разрядами, которые можно обозначить нулями. Получится, что уменьшаемое не 6,8, а 6,800. Выполнив данное действие, вы получите в итоге 4,661.
Действия с отрицательными десятичными дробями выполняются точно так же, как и с целыми числами. При сложении минус выносится за скобку, а в скобках пишутся заданные числа, и между ними ставится плюс. В итоге получается отрицательное число. То есть при сложении -6,8 и -7,3 вы получите тот же самый результат 14,1, но со знаком «-» перед ним. Если вычитаемое больше уменьшаемого, то минус тоже выносится за скобку, из большего числа вычитается меньшее. Вычтите из 6,8 число -7,3. Преобразуйте выражение следующим образом. 6,8 — 7,3= -(7,3 — 6,8) = -0,5.
Для того чтобы умножить десятичные дроби, на время забудьте о запятой. Перемножьте их так, как будто перед вами целые числа. После этого сосчитайте количество знаков, стоящих справа после запятой в обоих сомножителях. Отделите столько же знаков и в произведении. Перемножив 6,8 и 7,3, в итоге вы получите 49,64. То есть справа от запятой у вас окажутся 2 знака, в то время как в множимом и множителе их было по одному.
Разделите заданную дробь на какое-нибудь целое число. Это действие выполняется точно так же, как и с целыми числами. Главное — не забыть про запятую и в начале поставить 0, если количество целых единиц не делится на делитель. Например, попробуйте разделить те же самые 6,8 на 26. В начале поставьте 0, поскольку 6 меньше, чем 26. Отделите его запятой, дальше уже пойдут десятые и сотые. В итоге получится приблизительно 0,26. На самом деле в данном случае получается бесконечная непериодическая дробь, которую можно округлить до нужной степени точности.
При делении двух десятичных дробей воспользуйтесь свойством, что при умножении делимого и делителя на одно и то же число частное не меняется. То есть преобразуйте обе дроби в целые числа, в зависимости от того, сколько знаков стоит после запятой. Если вы хотите разделить 6,8 на 7,3, достаточно умножить оба числа на 10. Получится, что делить нужно 68 на 73. Если же в одном из чисел разрядов после запятой больше, преобразуйте в целое число сначала его, а затем уже и второе число. Умножьте его на то же число. То есть при делении 6,8 на 4,136 увеличьте делимое и делитель не в 10, а в 1000 раз. Разделив 6800 на 1436, получите в результате 4,735.
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей.
Допустим, дано уравнение следующего вида:
Данное уравнение можно решить двумя разными способами.
Способ № 1:
Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит число, то умножаем это число на каждый член в скобках:
Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону, целый числе в другую:
\[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\]
Делим 2 части на число перед \
\[ — 2x = — 17\]
Ответ: \
Способ № 2:
В этом способе умножим левую и правую части на 10:
Это линейное уравнение, которое решается по аналогии с 1 способом:
\[ — 72x + 52x = 17 — 144 — 43\]
\[ — 20x = — 170\]
Ответ: \
Где можно решить десятичные уравнения онлайн?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Подписаться на еженедельную рассылку izhneftyanic.ru
3 клас калькулятор — motyloptom.ru
Скачать 3 клас калькулятор txt
Математический калькулятор с расширенными возможностями. Удобный и простой инженерный калькулятор с богатым арсеналом возможностей для математических расчетов и между тем с приятным и понятным интерфейсом, способен выполнять практически любые арифметические действия и сложные математические вычисления. Этот калькулятор умеет делить столбиком, выдавая подробное объяснение как учили в школе.
Поддержка чисел с запятыми и результата с остатком. Деление столбиком онлайн калькулятор может разделить столбиком два числа выдавая полностью расписанный процесс деления. Калькулятор деления в столбик поддерживает целые числа, десятичные дроби,отрицательные числа и результат с остатком. Калькулятор.
Простой математический онлайн калькулятор. Умеет складывать, делить, умножать и вычитать числа в десятичной системе счисления. Также производит расчет выражений в скобках. Как посчитать пропорцию — простой и понятный онлайн калькулятор, плюс немного теории. Как посчитать пропорцию.
Пропорция – это очень удобный математический инструмент, который нашёл широкое применение в различных сферах нашей жизни. Чтобы посчитать пропорцию воспользуйтесь нашим простым онлайн калькулятором: Онлайн калькулятор. = X. 0. Цель и ожидаемый результат: научиться выполнять вычисления с помощью калькулятора. Задачи урока:узнать, какие приспособления для вычислений использовались с древних времён; познакомиться с п. Цель и ожидаемый результат: научиться выполнять вычисления с помощью калькулятора.
Задачи урока: узнать, какие приспособления для вычислений использовались с древних времён; познакомиться с программой Калькулятор.
Удобный онлайн-калькулятор для осуществления математических расчетов. А также осуществляет расчеты сложных выражений, пример: ()/(*4)*(8+3*1)= Select rating 1 2 3 4 5. Рейтинг: (Голосов ). Сообщить об ошибке. Простой математический онлайн калькулятор. Умеет складывать, делить, умножать и вычитать числа в десятичной системе счисления. Также производит расчет выражений в скобках. Калькулятор онлайн. Вычисление выражения с числовыми дробями. Умножение, вычитание, деление, сложение и сокращение дробей с разными знаменателями.
С помощью данного калькулятора онлайн вы можете умножить, вычесть, поделить, сложить и сократить числовые дроби с разными знаменателями. Программа работает с правильными, неправильными и смешанными числовыми дробями.
djvu, EPUB, doc, fb2Похожее:
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения окончательной неправильной дроби. |
| Умножить | Показывает последний шаг умножения. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД для уменьшения дроби. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Калькулятор умножения дробей
Наш калькулятор умножения дробей поможет вам умножить любые две дроби или смешанные числа.
В этом калькуляторе замечательно то, что он также покажет вам все тренировки на этом пути!
Если вы хотите умножить две дроби вместе, пожалуйста используйте калькулятор выше.
Чтобы ввести дробь, вы должны ввести числитель с последующим знаком «/». за которым следует знаменатель. Например. 4/5 или 23/7
Чтобы ввести смешанную дробь, сначала введите целое число, а затем пробел. за которым следует числитель, за которым следует ‘/’, за которым следует знаменатель.Например. 3 1/5 (3 и одна пятая).
Вы также можете использовать калькулятор для умножения дроби на целое число.
Взгляните на еще несколько наших ресурсов, похожих на эти.
У нас есть ряд калькуляторов дробей, которые помогут вам решить все ваши проблемы с дробями.
Если вы хотите сложить или вычесть, умножить или разделить, упростить или преобразовать дроби, у нас есть калькулятор для вас.
Здесь вы найдете подборку рабочих листов дроби, предназначенных для помощи Ваш ребенок понимает, как умножить две смешанные дроби вместе.
Как только ваш ребенок научится умножать дроби, он будет готов научиться делить дроби или умножать дробь на смешанную дробь или умножьте две смешанные дроби вместе.
Использование этих листов поможет вашему ребенку:
- умножить дробь на смешанное число;
- перемножает две смешанные фракции вместе;
Здесь вы найдете бесплатную онлайн-справку по математике Math Salamanders о дробях.
Существует широкий спектр справочных страниц, в том числе справка по следующим вопросам:
- определений фракций;
- эквивалентных фракций;
- преобразование неправильных дробей;
- как складывать и вычитать дроби;
- как переводить дроби в десятичные дроби и проценты;
- как упростить дроби.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Калькулятор умножения дробей на целые числа
Что такое умножение дробей на целое число?
Калькулятор умножения дроби с целым числом — это бесплатный онлайн-инструмент, который дает произведение дробного числа и целого числа. Этот калькулятор поможет вам работать быстрее и даст результат в течение нескольких секунд.
Как пользоваться калькулятором умножения дроби на целое число?
Чтобы использовать калькулятор, выполните следующие действия:
- Шаг 1: Введите дробное число и целое число в соответствующие поля ввода.
- Шаг 2: Нажмите «Рассчитать» , чтобы найти продукт.
- Шаг 3: Нажмите «Сброс» , чтобы очистить поле и ввести новый набор чисел.
Как умножить дробь на целое число?
Чтобы умножить дробь на целое число, нам просто нужно выполнить несколько простых шагов:
- Первый шаг — проверить, является ли данная дробь правильной или неправильной.
- Соответственно преобразовать смешанную дробь и целое число в неправильную дробь.
- В качестве числителя укажите целое число, а в знаменателе — 1.
- Затем умножьте числители обеих дробей.
- После этого умножьте знаменатели обеих дробей и затем упростите результат.
Умножение: 6/10 × 4
Решение:Здесь у нас есть одна правильная дробь и целое число, поэтому нам просто нужно преобразовать целое число в неправильную дробь, добавив 1 в качестве знаменателя.
6/10 × 4 = 6/10 × 4/1
= 24/10 = 12/5 = \ (2 \ frac {2} {5} \)
Следовательно, произведение 6/10 и 4 равно \ (2 \ frac {2} {5} \)
Аналог,
- 20.11 × 5 = \ (2 \ frac {3} {5} \)
- 23/25 × 2 = \ (1 \ frac {21} {25} \)
Теперь вы можете использовать калькулятор, чтобы найти следующее произведение:
- 3/7 × 14
- 34/56 × 8
- 11/17 × 5
Статьи по теме
Как считать дроби
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь состоит из двух чисел, расположенных одно над другим. Первое число, которое находится над линией, — это числитель . Второе число, расположенное под чертой, — это знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-то делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из».Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Как можно представить дроби?
Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби.
- Правильная дробь — это дробь, в которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
- У неправильной дроби числитель больше, чем знаменатель. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
- Смешанное число объединяет целое число и дробь. Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).
Упрощение дробей
Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.
Есть два способа упростить дробь.
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54
- Снова разделите на 2, чтобы получить 6/27
- Разделите на 3, чтобы получить 2/9
Сложение дробей
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить дробь ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½).
Дополнение: Пример 2
Допустим, вы хотите сложить дроби ⅓ и ⅙.
Чтобы знаменатели совпадали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей
Вычитание дробей работает аналогично:
- Шаг 1. Убедитесь, что знаменатели совпадают
- Шаг 2. Вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: Пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей
Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
На дроби
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и вы получите 3/2.
Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции.
Распространенные ошибки и на что следует обратить внимание
При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам нужно умножить дробь.
Возьмем для примера сложение ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Прочие распространенные ошибки включают:
- При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы у них был общий знаменатель.
- Изменение знаменателя дроби без внесения необходимых изменений в числитель.
- Непонимание вопроса полностью; например, деление вместо вычитания или умножение вместо сложения.
- Не менять знаменатель при ответах на вопросы, относящиеся к умножению или сложению.
Понимание взаимосвязи между смешанными числами и неправильными дробями и того, как переводить одно в другое, имеет решающее значение для работы с дробями.
Калькулятор дробей — онлайн-инструмент для упрощения дробей
Поиск инструмента
Калькулятор с дробями
Инструмент / Калькулятор с дробями и упрощением.Вычисление с использованием дробей включает определенные шаги вычисления числителя и знаменателя, прежде чем упрощать.
Результаты
Калькулятор с дробями — dCode
Тег (и): символическое вычисление
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Инструмент / Калькулятор с дробями и упрощением.Вычисление с использованием дробей включает определенные шаги вычисления числителя и знаменателя, прежде чем упрощать.
Ответы на вопросы
Как упростить дроби до неразложимой формы?
dCode сначала выполняет вычисления (сложение, вычитание, умножение или любое другое вычисление исходного математического выражения) и превращает их в несводимые дроби, сводя их к одному знаменателю. В результате дано упрощение в виде дроби в несократимой форме.
Пример: $$ \ frac12 + \ frac14 = \ frac34 $$
dCode позволяет проверять результаты школьных упражнений и скоро покажет пошаговые расчеты, а пока используйте инструменты LCM и GCD.
Как привести к тому же знаменателю?
dCode может вычислять наименьшее общее кратное знаменателей для реализации сложения и вычитания.
Пример: Если знаменатели добавляемых дробей равны 8 и 3, то НОК (8,3) = 24 и дробь должна иметь знаменатель 24: 15 / 8-2 / 3 = 29/24.
Умножение числителя подразумевает умножение знаменателя, чтобы сохранить равенство дроби.
Как складывать дроби?
Сложение дробей требует уменьшения дробей до одного знаменателя (попытка упростить дроби заранее, если возможно), затем добавления числителей (попытка упростить полученную дробь, если возможно).
Пример: $$ \ frac {1} {2} + \ frac {1} {3} = \ frac {1 \ times 3} {2 \ times 3} + \ frac {1 \ times 2} { 3 \ times 2} = \ frac {3} {6} + \ frac {2} {6} = \ frac {3 + 2} {6} = \ frac {5} {6} $$
Как вычесть дроби?
Вычитание дробей такое же, как и сложение, за исключением того, что вам нужно вычитать числители, а не складывать их.
Пример: $$ \ frac {1} {2} — \ frac {1} {3} = \ frac {1 \ times 3} {2 \ times 3} — \ frac {1 \ times 2} { 3 \ times 2} = \ frac {3} {6} — \ frac {2} {6} = \ frac {3-2} {6} = \ frac {1} {6} $$
Как умножать дроби?
Умножение на дробей состоит в умножении числителя между ними, а затем знаменателей между ними (постарайтесь упростить дроби до и / или после, если это возможно).
Пример: $$ \ frac {1} {2} \ times \ frac {2} {3} = \ frac {1 \ times 2} {2 \ times 3} = \ frac {2} {6} = \ frac {1} {3} $$
Как разделить дроби?
деление дробей можно записать как умножение первой дроби на обратную величину второй дроби (обращение числителя и знаменателя).Затем примените технику умножения.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Калькулятор с дробями». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) никакие данные, скрипт, копипаст или доступ к API не будут бесплатными, то же самое для калькулятора с загрузкой дробей для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Ключевые слова
дробь, числитель, знаменатель, частное, то же самое, сложение, вычитание, умножение, деление, упрощение, упрощение, шаг, выражение, математика, переменная, уменьшение, калькулятор
Ссылки
Источник: https: // www.dcode.fr/fractions-calculator
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Как разделить дроби с разными знаменателями
Обновлено 12 ноября 2018 г.
Лиза Мэлони
Когда вы складываете или вычитаете две дроби, обе дроби должны иметь одинаковые знаменатели. Но для умножения или деления дробей знаменатели не имеют значения. При умножении вы просто перебираете дробь, умножая все числители вместе, а затем все знаменатели вместе.Деление на дроби работает точно так же, с добавлением еще одного шага в начале.
TL; DR (слишком долго; не читал)
Чтобы разделить дроби, независимо от знаменателей, переверните вторую дробь (делитель) вверх ногами, а затем умножьте результат на первую дробь (делимое).
Так a / b ÷ c / d = a / b × d / c = ad / bc
Обзор: умножение дробей с разными знаменателями
Перед тем, как перейти к делению дробей, уделите время рассмотрению процесса умножения дробей.Вам также понадобится этот навык для решения задач разделения.
Если вы столкнулись с проблемой умножения вида
\ frac {a} {b} × \ frac {c} {d}
, то знаменатели не имеют значения. Все, что вам нужно сделать, это перемножить числители и записать их как числитель вашего ответа; затем умножьте знаменатели и умножьте их на знаменатель вашего ответа.
Пример 1: Вычислить
\ frac {2} {5} × \ frac {1} {3}
Помните, что для умножения не имеет значения, имеют ли ваши дроби одинаковые знаменатели.Все, что вам нужно сделать, это умножить прямо поперек, что дает:
\ frac {2 × 1} {5 × 3}
, что при упрощении дает:
\ frac {2} {15}
Если вы Вы можете упростить свой ответ, исключив множители как в числителе, так и в знаменателе. Но в данном случае дальнейшее упрощение невозможно, поэтому ваш полный ответ:
\ frac {2} {5} × \ frac {1} {3} = \ frac {2} {15}
Теперь о делении дробей.
Теперь, когда вы рассмотрели, как умножать дроби, деление дробей работает почти так же — вам просто нужно добавить один дополнительный шаг.Переверните вторую дробь (также известную как делитель) вверх ногами, а затем измените операцию на умножение вместо деления.
Итак, если ваша исходная задача деления выглядит так:
\ frac {a} {b} ÷ \ frac {c} {d}
Первое, что вы делаете, это переворачиваете вторую дробь вверх ногами, в результате чего получается d / c ; затем измените знак деления на знак умножения, что даст вам:
\ frac {a} {b} × \ frac {d} {c}
И поскольку вы практиковали умножение дробей, вы знаете, как решить эту проблему.Просто умножьте числители и знаменатели, и вы получите результат:
\ frac {a} {b} ÷ \ frac {c} {d} = \ frac {ad} {bc}
Два примера деления Дроби
Теперь, когда вы знаете процесс деления дробей, пора попрактиковаться на нескольких примерах.
Пример 2: Вычислить
\ frac {1} {3} ÷ \ frac {8} {9}
Помните, ваш первый шаг — перевернуть вторую дробь вверх ногами и изменить операцию на умножение.Это дает вам:
\ frac {1} {3} × \ frac {9} {8}
Теперь просто умножьте и упростите:
\ frac {1 × 9} {3 × 8} = \ frac {9} {24} = \ frac {3} {8}
\ frac {1} {3} ÷ \ frac {8} {9} = \ frac {3} {8}
Пример 3: Вычислить
\ frac {11} {10} ÷ \ frac {5} {7}
Обратите внимание, что одна из этих дробей неверна (ее числитель больше знаменателя). Но это не меняет процесса деления дробей, поэтому переверните эту вторую дробь вверх дном и измените операцию на умножение:
\ frac {11} {10} × \ frac {7} {5}
Как и раньше, умножьте и упростите, если можете:
\ frac {11 × 7} {10 × 5} = \ frac {77} {50}
77 и 50 не имеют общих факторов, поэтому вы не можете упростить дальше.Итак, ваш окончательный ответ:
\ frac {11} {10} ÷ \ frac {5} {7} = \ frac {77} {50}
Уловка для запоминания
Если вам трудно это запомнить, это может помочь вспомнить, что умножение и деление — взаимные операции; то есть одно отменяет другое. Когда вы переворачиваете дробь вверх дном, это тоже называется обратным. Таким образом, d / c является обратной величиной c / d , и наоборот.
Это означает, что когда вы делите дробь, вы фактически выполняете обратную операцию над обратной дробью .Чтобы проблема разрешилась, должны быть обе эти противоположности. Если у вас есть только одна из них — скажем, если вы выполнили обратную операцию (умножение), не взяв сначала обратную величину этой второй дроби, — ваш ответ будет неправильным.
Как насчет деления смешанных чисел?
Если вас просят разделить смешанные числа, будьте осторожны — это ловушка! Прежде чем продолжить, вы должны преобразовать это смешанное число в неправильную дробь. Как только это будет сделано, вы будете следовать тому же процессу, который вы использовали бы для правильных дробей.См. Пример 3 выше, чтобы проиллюстрировать, как это работает. Он включает неправильную дробь 11/10, которую также можно записать как смешанное число 1 1/10.
Дробные суммы | Как найти сумму дробей
В этом посте мы узнаем, как найти сумму дробей .
Прежде чем вы начнете складывать дроби, рекомендуется знать, как вычислить наименьшее общее кратное ( НОК) двух или более чисел.
Чтобы вычислить сумму дробей , важно, чтобы дроби имели одинаковый знаменатель .
Сумма дробей с одинаковым знаменателем
Чтобы сложить дроби с одинаковым знаменателем, вам нужно сложить числители и оставить тот же знаменатель.
Например:
Поскольку две дроби имеют одинаковый знаменатель, нам нужно сохранить тот же знаменатель , который равен 4, и сложить числители .
3 + 2 = 5
И результат суммы дробей:
Сумма дробей с разными знаменателями
К сложите дроби с разными знаменателями. , первое, что вам нужно сделать, это найти общий знаменатель : это наименьшее общее кратное имеющихся у вас знаменателей.Затем мы умножаем каждый числитель на число, на которое мы умножили знаменатель. Наконец, мы складываем полученные числители и сохраняем тот же знаменатель.
Например,
Первое, что нужно сделать, это найти общий знаменатель между 3 и 5. Для этого мы вычисляем наименьшее общее кратное между обоими числами.
НОК (3,5) = 15
Итак, 15 — общий знаменатель двух дробей.
Теперь нам нужно умножить каждый числитель на число, на которое мы умножили знаменатель.Для этого мы делим НОК на начальный знаменатель и умножаем результат на числитель этой дроби.
Для первой дроби:
15/3 = 5
5 х 2 = 10
Итак, 10 — числитель первой дроби.
Для второй фракции:
15/5 = 3
3 х 4 = 12
Итак, 12 — числитель второй дроби.
Теперь все, что нам осталось сделать, это добавить числители:
10 + 12 = 22
И результат суммы дробей:
Я надеюсь, что благодаря этой публикации вы узнали, как находить сумму дробей.
Не стесняйтесь оставлять свои комментарии!
А если вы хотите узнать больше о математике, войдите в Smartick и получите бесплатную пробную версию!
Подробнее:
Команда по созданию контента.



 except NameError:
print("\n You didn't enter two numbers.")
# Exception for user input both or one of them, not being integers.
except TypeError:
print("\n You didn't enter all valid numbers.")
# General exception case.
except:
print("Something went wrong!")
fract = FractionClass(n,d)
another_fraction = FractionClass(n2, d2)
total_sum = fract.add_fractions(another_fraction)
# Unpacks total sum tuple.
# Puts in fraction format.
sum_numerator, sum_denominator = total_sum
add_output = fractions.Fraction(sum_numerator, sum_denominator)
total_product = fract.multiply_fractions(another_fraction)
# Unpacks product sum tuple.
# Puts in fraction format.
product_numerator, product_denominator = total_product
multiply_output = fractions.Fraction(product_numerator, product_denominator)
print(add_output, multiply_output)
except NameError:
print("\n You didn't enter two numbers.")
# Exception for user input both or one of them, not being integers.
except TypeError:
print("\n You didn't enter all valid numbers.")
# General exception case.
except:
print("Something went wrong!")
fract = FractionClass(n,d)
another_fraction = FractionClass(n2, d2)
total_sum = fract.add_fractions(another_fraction)
# Unpacks total sum tuple.
# Puts in fraction format.
sum_numerator, sum_denominator = total_sum
add_output = fractions.Fraction(sum_numerator, sum_denominator)
total_product = fract.multiply_fractions(another_fraction)
# Unpacks product sum tuple.
# Puts in fraction format.
product_numerator, product_denominator = total_product
multiply_output = fractions.Fraction(product_numerator, product_denominator)
print(add_output, multiply_output)
 д. Это то, что у меня есть до сих пор. Если числитель и знаменатель обеих дробей являются целыми числами, то это легко сделать. Но если это радикальные или любые другие комплексные числа, я должен изменить свой код….
д. Это то, что у меня есть до сих пор. Если числитель и знаменатель обеих дробей являются целыми числами, то это легко сделать. Но если это радикальные или любые другие комплексные числа, я должен изменить свой код…. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.