Калькулятор уравнений с фигурными скобками: решение уравнений со скобками

Содержание

Уравнения с фигурной скобкой

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и « x », и « y ».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки

или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».

Чтобы выразить неизвестное, нужно выполнить два условия:

перенести неизвестное, которое хотим выразить, в левую часть уравнения;
разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.

При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.

x = 7 − 5y

3x − 2y = 4

Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.

x = 7 − 5y

3(7 − 5y) − 2y = 4

Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение « 3(7 − 5y) − 2y = 4 » отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*) .

x = 7 − 5y

3(7 − 5y) − 2y = 4 (*)

Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.

x + 5y = 7	(x + 5y) + (3x − 2y) = 7 + 4
+ =>	x + 5y + 3x − 2y = 11
3x − 2y = 4	4x + 3y = 11

При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».

Для этого умножим первое уравнение на « −3 ».

При умножении уравнения на число, на это число умножается каждый член уравнения.

x + 5y = 7 | ·(−3)

3x − 2y = 4

x · (−3) + 5y · (−3) = 7 · (−3)

3x − 2y = 4

−3x −15y = −21

3x − 2y = 4

Теперь сложим уравнения.

−3x −15y = −21	(−3x −15y ) + (3x − 2y) = −21 + 4
+ =>	− 3x − 15y + 3x − 2y = −21 + 4
3x − 2y = 4	−17y = −17 \|:(−17)
y = 1

Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».

Ответ: x = 2; y = 1

Пример решения системы уравнения способом подстановки

x − 3y = 17

x − 2y = −13

Выразим из первого уравнения « x ».

x = 17 + 3y

x − 2y = −13

Подставим вместо « x » во второе уравнение полученное выражение.

x = 17 + 3y

(17 + 3y) − 2y = −13 (*)

Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».

x = 17 + 3 · (−30)

y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения способом сложения

Рассмотрим систему уравнений.

3(x − y) + 5x = 2(3x − 2)

4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

3x − 3y + 5x = 6x − 4

4x − 2x − 2y = 4 − 3y

8x − 3y = 6x − 4

2x −2y = 4 − 3y

8x − 3y − 6x = −4

2x −2y + 3y = 4

2x − 3y = −4

2x + y = 4

Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».

Для этого достаточно умножить первое уравнение на « −1 ».

2x − 3y = −4 | ·(−1)

2x + y = 4

2x · (−1) − 3y · (−1) = −4 · (−1)

2x + y = 4

−2x + 3y = 4

2x + y = 4

Теперь при сложении уравнений у нас останется только « y » в уравнении.

−2x + 3y = 4	(−2x + 3y ) + (2x + y) = 4 + 4
+ =>	− 2x + 3y + 2x + y = 4 + 4
2x + y = 4	4y = 8 \| :4
y = 2

Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».

В данной статье рассказывается о скобках в математике и рассматриваются виды и применения, термины и методы использования при решении или для описания материала. В заключение будут решены подобные примеры с подробными комментариями.

Основные виды скобок, обозначения, терминология

Для решения заданий в математике используются три вида скобок: ( ) , [ ] , < >. Реже встречаются скобки такого вида ] и [ , называемые обратными, или и > , то есть в виде уголка. Их применение всегда парное, то есть имеется открывающаяся и закрывающаяся скобка в любом выражении, тогда оно имеет смысл . скобки позволяют разграничить и определить последовательность действий.

Скобки для указания порядка выполнения действий

Основное предназначение скобок – указание порядка выполняемых действий. Тогда выражение может иметь одну или несколько пар круглых скобок. По правилу всегда выполняется первым действие в скобках, после чего умножение и деление, а позже сложение и вычитание.

Рассмотрим на примере заданное выражение. Если дан пример вида 5 + 3 – 2 , тогда очевидно, что действия выполняются последовательно. Когда это же выражение записывается со скобками, тогда их последовательность меняется. То есть при ( 5 + 3 ) – 2 первое действие выполняется в скобках. В данном случае изменений не будет. Если выражение будет записано в виде 5 + ( 3 – 2 ) , тогда в начале производятся вычисления в скобках, после чего сложение с числом 5 . На исходное значение в этом случае оно не повлияет.

Рассмотрим пример, который покажет, как при изменении положения скобок может измениться результат. Если дано выражение 5 + 2 · 4 , видно, что вначале выполняется умножение, после чего сложение.

Когда выражение будет иметь вид ( 5 + 2 ) · 4 , то вначале выполнится действие в скобках, после чего произведется умножение. Результаты выражений будут отличаться.

Выражения могут содержать несколько пар скобок, тогда выполнения действий начинаются с первой. В выражении вида ( 4 + 5 · 2 ) − 0 , 5 : ( 7 − 2 ) : ( 2 + 1 + 12 ) видно, что первым делом выполняются действия в скобках, после чего деления, а в конце вычитание.

Существуют примеры, где имеются вложенные сложные скобки вида 4 · 6 – 3 + 8 : 2 и 5 · ( 1 + ( 8 – 2 · 3 + 5 ) – 2 ) ) – 4 . Тогда начинается выполнение действий с внутренних скобок. Далее производится продвижение к внешним.

Если имеется выражение 4 · 6 – 3 + 8 : 2 , тогда очевидно, что в первую очередь выполняются действия в скобках. Значит, следует отнять 3 от 6 , умножить на 4 и прибавить 8 . В конце следует разделить на 2 . Только так можно получить верный ответ.

На письме могут быть использованы скобки разных размеров. Это делается для удобства и возможности отличия одной пары от другой. Внешние скобки всегда большего размера, чем внутренние. То есть получаем выражение вида 5 – 1 : 2 + 1 2 + 3 – 1 3 · 2 · 3 – 4 . Редко встречается применение выделенных скобок ( 2 + 2 · ( 2 + ( 5 · 4 − 4 ) ) ) · ( 6 : 2 − 3 · 7 ) · ( 5 − 3 ) или применяют квадратные, например, [ 3 + 5 · ( 3 − 1 ) ] · 7 или фигурные < 5 + [ 7 − 12 : ( 8 − 5 ) : 3 ] + 7 − 2 >: [ 3 + 5 + 6 : ( 5 − 2 − 1 ) ] .

Перед тем, как приступить к решению, важно правильно определить порядок действий и разобрать все необходимые пары скобок. Для этого следует добавлять разные виды скобок или менять их цвет. Пометка скобки другим цветом удобна для решения, но занимает много времени, поэтому на практике чаще всего применяют круглые, фигурные и квадратные скобки.

Отрицательные числа в скобках

Если необходимо изобразить отрицательные числа, тогда применяют круглые скобки в выражении. Такая запись, как 5 + ( − 3 ) + ( − 2 ) · ( − 1 ) , 5 + – 2 3 , 2 5 7 – 5 + – 6 7 3 · ( – 2 ) · – 3 , 5 предназначена для того, чтобы упорядочить отрицательные числа в выражении.

Скобки не ставятся для отрицательного числа того, когда оно располагается в начале любого выражения или дроби. Если имеем пример вида − 5 · 4 + ( − 4 ) : 2 , то очевидно, что знак минуса перед 5 можно не заключать в скобки, а при 3 – 0 , 4 – 2 , 2 · 3 + 7 + 3 – 1 : 2 число 2 , 2 записано вначале, значит скобки также не нужны. Со скобками можно записать выражение ( − 5 ) · 4 + ( − 4 ) : 2 или 3 – 0 , 4 – 2 , 2 · 3 + 7 + 3 – 1 : 2 . Запись, где имеются скобки, считается более строгой.

Знак минуса может находиться не только перед числом, но и перед переменными, степенями, корнями, дробями, функциями, тогда их следует заключить в скобки. Это такие записи, как 5 · ( − x ) , 12 : ( − 22 ) , 5 · – 3 + 7 – 1 + 7 : – x 2 + 1 3 , 4 3 4 – – x + 2 x – 1 , 2 · ( – ( 3 + 2 · 4 ) , 5 · ( – log 3 2 ) – ( – 2 x 2 + 4 ) , sin x · ( – cos 2 x ) + 1

Скобки для выражений, с которыми выполняются действия

Использование круглых скобок связано с указанием в выражении действий, где имеется возведение в степень, взятие производной, функции.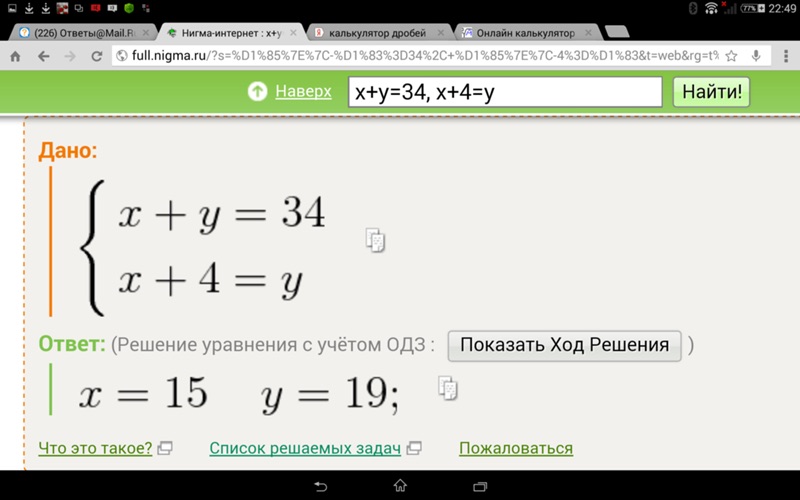 x + 3 на выходе получим 2 x + 3 .

Основание степени не нуждается в скобках. Поэтому запись принимает вид 0 3 , 5 x 2 + 5 , y 0 , 5 . Если в основании имеется дробное число, тогда можно использовать круглые скобки. Получаем выражения вида ( 0 , 75 ) 2 , 2 2 3 32 + 1 , ( 3 · x + 2 · y ) – 3 , log 2 x – 2 – 1 2 x – 1 .

Если выражение основания степени не взять в скобки, тогда показатель может относиться ко всему выражению, что повлечет за собой неправильное решение. Когда имеется выражение вида x 2 + y , а – 2 – это его степень, то запись примет вид ( x 2 + y ) – 2 . При отсутствии скобок выражение приняло бы вид x 2 + y – 2 , что является совершенно другим выражением.

Если основанием степени является логарифм или тригонометрическая функция с целым показателем, тогда запись приобретает вид sin , cos , t g , c t g , a r c sin , a r c cos , a r c t g , a r c c t g , log , ln или l g . При записи выражения вида sin 2 x , a r c cos 3 y , ln 5 e и log 5 2 x видим, что скобки перед функциями не меняют значения всего выражения, то есть они равноценны. Получаем записи вида ( sin x ) 2 , ( a r c cos y ) 3 , ( ln e ) 5 и log 5 x 2 . Допустимо опущение скобок.

Скобки в выражениях с корнями

Использование скобок в подкоренном выражении бессмысленно, так как выражение вида x + 1 и x + 1 являются равнозначными. Скобки не дадут изменений при решении.

Скобки в выражениях с тригонометрическими функциями

Если имеются отрицательные выражения у функций типа синус, косинус, тангенс, котангенс, арксинус, арккосинус, арктангенс, арккотангенс, тогда необходимо использовать круглые скобки. Это позволит правильно определить принадлежность выражения к имеющейся функции. То есть получим записи вида sin ( − 5 ) , cos ( x + 2 ) , a r c t g 1 x – 2 2 3 .

При записи sin , cos , t g , c t g , a r c sin , a r c cos , a r c t g и a r c c t g при имеющемся числе скобки не используют. Когда в записи присутствует выражение, тогда имеет смысл их поставить. То есть sin π 3 , t g x + π 2 , a r c sin x 2 , a r c t g 3 3 с корнями и степенями, cos x 2 – 1 , a r c t g 3 2 , c t g x + 1 – 3 и подобные выражения.

Если в выражении содержатся кратные углы типа х , 2 х , 3 х и так далее, скобки опускаются. Разрешено записывать в виде sin 2 x , c t g 7 x , cos 3 α . Во избежание двусмысленности скобки можно добавить в выражение. Тогда получаем запись вида sin ( 2 · x ) : 2 вместо sin 2 · x : 2 .

Скобки в выражениях с логарифмами

Чаще всего все выражения логарифмической функции заключаются в скобки для дальнейшего правильного решения. То есть получаем ln ( e − 1 + e 1 ) , log 3 ( x 2 + 3 · x + 7 ) , l g ( ( x + 1 ) · ( x − 2 ) ) . Опущение скобок разрешено в том случае, когда однозначно понятно, к какому выражению относится сам логарифм. Если есть дробь, корень или функция можно записывать выражения в виде log 2 x 5 , l g x – 5 , ln 5 · x – 5 3 – 5 .

Скобки в пределах

При имеющихся пределах используют скобки для представления выражения самого предела. То есть при суммах, произведениях, частных или разностях принято записывать выражения в скобках. Получаем, что lim n → 5 1 n + n – 2 и lim x → 0 x + 5 · x – 3 x – 1 x + x + 1 : x + 2 x 2 + 3 . Опущение скобок предполагается, когда имеется простая дробь или очевидно, к какому выражению относится знак. Например, lim x → ∞ 1 x или lim x → 0 ( 1 + x ) 1 x .

Скобки и производная

При нахождении производной часто можно встретить применение круглых скобок. Если имеется сложное выражение, тогда вся запись берется в скобки . Например, ( x + 1 ) ‘ или sin x x – x + 1 .

Подынтегральные выражения в скобках

Если необходимо проинтегрировать выражение, то следует записать его в круглых скобках. Тогда пример примет вид ∫ ( x 2 + 3 x ) d x , ∫ – 1 1 ( sin 2 x – 3 ) d x , ∭ V ( 3 x y + z ) d x d y d z .

Скобки, отделяющие аргумент функции

При наличии функции чаще всего применяются круглые скобки для их обозначения. Когда дана функция f с переменной х , тогда запись принимает вид f ( x ) . Если имеются несколько аргументов функций, то такая функция получит вид F ( x , y , z , t ) .

Скобки в периодических десятичных дробях

Использование периода обусловлено применением скобок при записи. Сам период десятичной дроби заключается в скобки. Если дана десятинная дробь вида 0 , 232323 … тогда очевидно, что 2 и 3 мы заключаем в круглые скобки. Запись приобретает вид 0 , ( 23 ) . Это характерно для любой записи периодической дроби.

Скобки для обозначения числовых промежутков

Для того, чтобы изобразить числовые промежутки применяют скобки четырех видов: ( ) , ( ] , [ ) и [ ] . В скобках прописываются промежутки, в каких функция существует, то есть имеет решение. Круглая скобка означает, что число не входит в область определения, квадратная – входит. При наличии бесконечности принято изображать круглую скобку.

То есть при изображении промежутков получим, что ( 0 , 5 ) , [ − 0 , 5 , 12 ) , – 10 1 2 , – 5 2 3 , [ 5 , 700 ] , ( − ∞ , − 4 ] , ( − 3 , + ∞ ) , ( − ∞ , + ∞ ) . Не вся литература одинаково использует скобки. Есть случаи, когда можно увидеть запись такого вида ] 0 , 1 [ , что означает ( 0 , 1 ) или [ 0 , 1 [ , что значит [ 0 , 1 ) , причем смысл выражения не меняется.

Обозначения систем и совокупностей уравнений и неравенств

Системы уравнений, неравенств принято записывать при помощи фигурной скобки вида < . Это означает, что все неравенства или уравнения объединены этой скобкой. Рассмотрим на примере использования скобки. Система уравнений вида x 2 – 1 = 0 x 2 + x – 2 = 0 или неравенства с двумя переменными x 2 – y >0 3 x + 2 y ≤ 3 , cos x 1 2 x + π 3 = 0 2 x 2 – 4 ≥ 5 -система, состоящая из двух уравнений и одного неравенства.

Использование фигурных скобок относится к изображению пересечения множеств. При решении системы с фигурной скобкой фактически приходим к пересечению заданных уравнений. Квадратная скобка служит для объединения.

Уравнения и неравенства обозначаются [ скобкой в том случае, если необходимо изобразить совокупность. Тогда получаем примеры вида ( x – 1 ) ( x + 7 ) = 0 x – 2 = 12 + x 2 – x + 3 и x > 2 x – 5 y = 7 2 x + 3 y ≥ 1

Можно встретить выражения, где имеются и система и совокупность:

x ≥ 5 x 3 x > 4 , 5

Фигурная скобка для обозначения кусочной функции

Кусочная функция изображается при помощи одиночной фигурной скобки, где имеются формулы, определяющие функцию, содержащие необходимые промежутки. Посмотрим на примере формулы с содержанием промежутков типа x = x , x ≥ 0 – x , x 0 , где имеется кусочная функция.

Скобки для указания координат точки

Для того, чтобы изобразить координатные точки в виде промежутков, используют круглые скобки. Они могут быть расположены как на координатной прямой, так и в прямоугольной системе координат или n-мерном пространстве.

Когда координата записывается как А ( 1 ) , то означает, что точка А имеет координату со значением 1 , тогда Q ( x , y , z ) говорит о том, что точка Q содержит координаты x , y , z .

Скобки для перечисления элементов множества

Множества задаются при помощи перечисления элементов, входящих в его область. Это выполняется при помощи фигурных скобок, где сами элементы прописываются через запятую. Запись выглядит таким образом А = < 1 , 2 , 3 , 4 >. Видно, что множество состоит из значений, перечисленных в скобках.

Скобки и координаты векторов

При рассмотрении векторов в системе координат используется понятие координат вектора. То есть при обозначении используют координаты, которые записаны в виде перечисления в скобках.

Учебники предлагают два вида обозначения: a → 0 ; – 3 или a → 0 ; – 3 . Обе записи равнозначны и имеют значение координат 0 , – 3 . При изображении в трехмерном пространстве добавляется еще одна координата. Тогда запись выглядит так: A B → 0 , – 3 , 2 3 или A B → 0 , – 3 , 2 3 .

Обозначение координат может быть как со значком вектора на самом векторе, так и без. Но запись координат производится через запятую в виде перечисления. Запись принимает вид a = ( 2 , 4 , − 2 , 6 , 1 2 ) , где вектор обозначается в пятимерном пространстве. Реже можно увидеть обозначение двумерного пространства в виде a = 3 – 7

Скобки для указания элементов матриц

Частое применение скобок предусмотрено в матрицах. Все элементы фиксируются при помощи круглых скобок вида A = 4 2 3 – 3 0 0 12 .

Реже можно увидеть использование квадратных скобок.
Тогда матрица приобретает вид A = 4 2 3 – 3 0 0 12 .

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Для чего нужно уметь решать системы уравнений? Где они они могут пригодиться?

Все, что нужно знать о решении системы уравнений – в этой статье.

Помни, твоя цель – хорошо сдать ОГЭ или ЕГЭ и поступить в институт твоей мечты.

Let’s go. (Поехали!)

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.

Объединяем уравнения в систему с помощью фигурной скобки:

СИСТЕМА УРАВНЕНИЙ И МЕТОДЫ ЕЕ РЕШЕНИЯ

Метод подстановки

Это самый простой метод, но зачастую – самый трудоемкий. Идея проста – нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной.

Затем точно так же выражаем и подставляем другую переменную и т.д., пока не получим уравнение с одной переменной. После его решения и нахождения одной из переменных – последовательно возвращаемся к ранее выраженным, подставляя найденные значения.

Непонятно? Давай рассмотрим на примере

Пример 1.

Из второго уравнения очень просто выразить :

Теперь подставим то, что получилось вместо в первое уравнение:

Мы получили уравнение с одной неизвестной, которое очень просто решить:

А теперь вернемся к выраженному и подставим в него полученное значение :

Ответ:

Ответ, кстати, принято записывать как координаты, то есть в таком виде: . В случае трех неизвестных: , и так далее.

То есть ответ в нашем примере запишется так:

Ответ:

Попробуй сам решить несколько примеров методом подстановки:

Ответы:

1) Здесь проще всего выразить из второго уравнения неравенства –

, а затем подставить в первое.

Ответ:

2) Выражаем из второго уравнения и подставляем в первое.

Ответ:

3) Здесь лучше выразить из первого уравнения:

, а затем уже подставлять во второе.

Ответ:

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки. Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера. Для этого сперва выразим в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно ):

Видно, что графики пересекаются в точке с координатами .

Графический метод – самый неточный. Практически его можно применять только для систем линейных уравнений (вида ), графиками которых являются прямые. Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (лучше использовать его только для иллюстраций).

Метод сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений. То есть:

(но ни в коем случае не наоборот: )

Действительно, мы ведь имеем право прибавить к обеим частям уравнения одно и то же число, например, прибавим к первому уравнению число :

Но раз , в правой части можем заменить на :

Пример 2

Сложим эти уравнения (левые части друг с другом, и правые – тоже друг с другом):

Вот как! просто уничтожился в результате сложения. Скажу сразу, это и была цель всего действия: складываем уравнения только тогда, когда при этом получим более простое уравнение.

Остается теперь только подставить в любое уравнение вместо число :

Ответ:

Пример 3.

Очевидно, здесь сложение ничего не даст. Придется решать другим методом? Нет! Иначе метод сложения был бы полезен слишком редко. Мы ведь можем умножать любое уравнение на любое ненулевое число? Так давай умножим первое уравнение на такое число, чтобы потом при сложении какая-то переменная исчезла. Лучше всего умножить на :

Теперь можно складывать:

Теперь подставим в первое уравнение системы:

Ответ:

Теперь порешай сам (методом сложения):

Ответы:

1. На что здесь надо умножить, чтобы коэффициенты при x или y были противоположными? Хм. Как из получить или из получить ? Умножать на дробное число? Слишком громоздко получится. Но ведь можно умножить оба уравнения! Например, первое на , второе на :

Теперь, сложив уравнения, мы можем легко найти .

Подставляем в любое из уравнений и находим .

Ответ: .

2. Решать нужно аналогично первому примеру – сначала нужно умножить первое уравнение на , а второе на , и сложить.

Ответ: .

3. Первое умножаем на , а второе на и складываем.

Ответ: .

4. Умножать можно и на дроби, то есть делить. Умножим первое уравнение на , а второе на :

Теперь сложим уравнения:

Подставив в первое уравнение, найдем :

Ответ:

Тренировка без подсказок

Теперь попробуй сам определить наиболее рациональный способ решения, а затем проверь ответы. Подсказок уже не будет!

Ответы:

Как видишь, система уравнений – базовая, но не самая сложная тема, используй методы, описанные в этой статье, и ты без труда справишься с решением систем.

КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ

Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных:

Методы решения систем уравнений:

1. Решение методом подстановки

Нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной, повторять подобную процедуру пока не будут найдены все переменные.

2. Решение графическим методом

Если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Графический метод – самый неточный. Практически его можно применять только для систем линейных уравнений (вида ), графиками которых являются прямые. Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (только для иллюстраций).

3. Решение методом сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений.

Но ни в коем случае не наоборот:

ТЕПЕРЬ ТЕБЕ СЛОВО.

Мы постарались объяснить что такое системы уравнений и как их решать.

Теперь хотелось бы послушать тебя.

Как тебе статья?

Получается ли у тебя решать системы уравнений?

У тебя есть вопросы? Предложения?

Напиши в комментариях.

И удачи на экзаменах!

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

Стать учеником YouClever,

Подготовиться к ОГЭ или ЕГЭ по математике,

А также получить доступ к учебнику YouClever без ограничений.

можно кликнув по этой ссылке.

Помогите. Произошел сбой в системе мозга( Вы все хорошо разьясняете, но надо решить систему, где в уравнениях есть степени..и тут пошло(( первое уравнение системы: 5 в степени х минус 5 в степени у равно 100 второе уравнение системы: 5 в степени х-1 плюс 5 в степени у-1 равно 30 Если есть возможность, помогите подробно разобрать его. 3 x=3 Ответ готов! Получилась пара чисел (3;2)

Как репетитор по математике оформляет объединение систем

Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена. Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?

К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований. Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.

Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:

Когда репетитор по математике вводит квадратную скобку?

К пониманию разницы между скобками лучше всего подводить ученика постепенно, начиная с 8 класса, когда изучается тема «неравенства». В решении самих неравенств восьмиклассники используют понятие «пересечение ответов» . Почему бы репетитору по математике не показать что такое «объединение ответов»? Задачи на объединение присутствуют в учебнике Макарычева, но они ограничиваются операцияями с уже сформированными промежутками. Это не совсем то, что нужно. Вот пример, на котором репетитор по математике мог бы объяснить назначение квадратной скобки:

Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).

Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия:

К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.

Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко. Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.

Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного. Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.

Может ли репетитор по математике обойтись без квадратной скобки

Да, вполне. Для этого применяются стрелочный эквивалент. Например:

Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение. Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.

Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.

Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.

Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации. При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.

Репетитор по математике, Колпаков А.Н. Москва.

Если «Калькулятор» поддерживает «{» (фигурные скобки) и «[‘(боковые фигурные скобки)

Вы действительно задали здесь два вопроса, но тем не менее:

Должен ли «Калькулятор» поддерживать «{» (фигурные скобки) и «[‘(боковые скобки)?

Да, доступность — это ключевое слово здесь. Не так, как в «физически ослабленных», но как в «обученном поведении». Некоторые люди просто хотят использовать фигурные или прямоугольные фигурные скобки, потому что именно так они катятся на бумаге, и вы хотите, чтобы барьер между реальным применением и виртуальным приложением был как можно ниже.

Пользователи должны иметь возможность использовать шаблоны взаимодействия, которые они уже знают (что-то еще будет разочаровывать), поэтому поддержка этих брекетов дает им больше удобства и не повредит никому, кто хочет использовать только круглые скобки.

Должен ли я оптимизировать свою программу для подхода программиста или подхода математика?

Почему бы не обоим? Вероятно, вы знаете, что для многих IDE и редакторов выделяется подсветка скобок, где выделены две соответствующие фигурные скобки, если ваш курсор находится на одном из них. Другой подход — это цветовое кодирование, используемое в Excel, как указано стереоактивностью.

Оба эти подхода применимы и легко читаются как для программистов, так и для написания стилей математиков. Это то, где ваше виртуальное приложение может соответствовать одному в реальной жизни, что всегда приятно.

Кроме того, что вы действительно подразумеваете под оптимизацией? Каковы были ваши идеи по оптимизации одного из двух?

[несколько фигурных скобок] может затруднить обработку (обнаружение ошибок синтаксиса, несогласованных фигурных скобок).

Это, конечно, правильно, но вам больше всего нравится пользователь, а не программист. (И давайте будем честными, несогласованные фигурные скобки — это не то, что нужно реализовать. Если мы говорим о физическом калькуляторе, вам следует, конечно, учитывать стоимость строительства, но я предполагаю, что ваш вопрос должен был рассматривать только приложения.)

Кроме того, именно эти дополнительные фигурные скобки используются в первую очередь: обнаружение ошибок мыслей. Если вы пишете несогласованные брекеты, у вас наверняка есть что-то извращенное в вашем уме. Предоставление пользователю намека на это, безусловно, позволит улучшить их опыт.

В общем, позволяя пользователям адаптировать известные шаблоны, нужно что-то желаемое в каждом приложении и, как известно, является ключевым фактором интуитивности. Таким образом, поддержка обоих стилей письма, включая проверку соответствия фигурных скобок, представляется лучшим решением.

Метод интервалов, решение неравенств

Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Что нельзя делать в неравенстве, даже под пытками:

1) Домножать на знаменатель.

2) Умножать/делить на отрицательное число, не меняя знак.

3) Убирать бездумно логарифм или основание.

Начнем с простого:

Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:

А само значение −4 нам подходит?

Нет, поэтому ставим круглые скобочки ()

Ответ: x ∈ ( −4; +oo).

Разберемся со скобками:

Когда мы включаем точку (корень числителя), или стоят знаки нестрогие (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».

Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:

Ответ: x ∈ ( 0; +oo).

Следующий пример уже с дробью:

Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:

к.ч. (корни числителя)

к.з. (корни знаменателя)

Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:

Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:

Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:

Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».

Ответ: x ∈ (2; 7].

Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:

Отметим на прямой решение каждого неравенства.

Решением системы «{» является тот участок, который подходит обоим неравенствам.

Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.

Мой любимый пример:

Покажу мастер-класс, как делать не надо. Дома не повторять!

А теперь через метод интервалов разберемся, как сделать правильно:

Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:

В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».

Ответ: x ∈ (−3; 3).

Перейдем к квадратному уравнению:

Разложим на множители и подставим x = 10, чтобы определить знак:

Нам требуются положительные значения:

Второй способ разложить на множители:

Ответ: x ∈ (−oo; −1) ∪ (5; +oo).

А теперь простой, но крайне показательный пример:

Убирать квадрат ни в коем случае нельзя. Простенький контрпример:

Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).

Проверим это:

В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

Только точка «0» не подходит, 0 > 0 — неверно!

Ответ: x ∈ R \ {0} или x ∈ (−oo; 0) ∪ (0; +oo).

Переходим на новый уровень:

Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)

По методу координат найдем корни числителя и знаменателя:

Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).

Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.

Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.

Ответ: (−oo; − 6) ∪ {0} ∪ [ 3; +oo).

Дальше интереснее:

По той же схеме корни числителя и знаменателя:

Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:

Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.

Ответ: {−3} ∪ (−2; +oo).

Закрепляем последовательность:

Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?

Подставим x = 10 и расставим знаки:

Ответ: [ −oo; −5) ∪ [ 3; 5).

Все скользкие моменты разобрали, стало понятнее?

Резюме:

Если знак строгий (>, <), все точки выколотые (в круглые скобки).
Если знак нестрогий (≥, ≤), корни числителя закрашенные, точки знаменателя выколотые [в квадратные скобки].
Если корень является решением уравнения четное кол-во раз (2, 4, 6, 8), то в этой точке знак меняться не будет.
Отдельная точка записывается {в фигурных скобках}.

Нашел ошибку/опечатку — напиши.

Группа с полезной информацией и легким математическим юмором.

Скобки (скобки)

Скобки — это символы, которые используются попарно для группировки предметов.

Типы кронштейнов включают:

круглые скобки или «круглые скобки» ()
«квадратные скобки» или «квадратные скобки» []
скобки или «фигурные скобки» {}
«Кронштейны угловые» <>

(Примечание.

Угловые скобки могут сбивать с толку, поскольку они
выглядят как знаки «меньше» и «больше»)

Когда мы видим что-то внутри скобок, мы делаем это в первую очередь (как описано в разделе «Порядок операций»).

Пример: (3 + 2) × (6-4)

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, поэтому они выполняются первыми:

(3 + 2) × (6-4)

= (5) × (2)

= 5 × 2

= 10

Без скобок сначала производится умножение:

3 + 2 × 6 — 4
= 3 + 12 — 4
= 11 (не 10)

При более сложной группировке хорошо использовать разных типов скоб :

Пример: [(3 + 2) × (6–4) + 2] × 4

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, а квадратные скобки говорят нам выполнить все вычисления внутри них перед умножением на 4:

[(3 + 2) × (6–4) + 2] × 4

= [(5) × (2) + 2] × 4

= [10 + 2] × 4

= 12 × 4

= 48

Фигурные скобки

Фигурные скобки {} используются в наборах:

Пример: {2, 4, 6, 8}

Набор четных чисел от 2 до 8

Как писать о неравенствах и манипулировать ими | Колледж алгебры

Результаты обучения

Используйте обозначение интервалов для выражения неравенства.
Используйте свойства неравенств.

Указание решения неравенства, такого как [латекс] x \ ge 4 [/ латекс], может быть достигнуто несколькими способами.

Мы можем использовать числовую линию, как показано ниже. Синий луч начинается с [latex] x = 4 [/ latex] и, как указано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает в себя все действительные числа, большие или равные 4.

Мы можем использовать нотацию конструктора наборов : [latex] \ {x | x \ ge 4 \} [/ latex], что переводится как «все действительные числа x , такие, что x больше или равно 4.Обратите внимание, что фигурные скобки используются для обозначения набора.

Третий метод — это обозначение интервала , где наборы решений указываются круглыми или квадратными скобками. Решения для [latex] x \ ge 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex]. Это, пожалуй, самый полезный метод, поскольку он применим к концепциям, изучаемым позже в этом курсе, и к другим курсам математики более высокого уровня.

Основная концепция, которую следует помнить, заключается в том, что круглые скобки представляют решения больше или меньше числа, а скобки представляют решения, которые больше или равны или меньше или равны числу.Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «равны». Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, чем [latex] 1 [/ latex] включительно.В таблице ниже представлены возможные варианты.

The entries in the tenth row are: all real numbers less than a and greater than b; {x| x < a and x > b}; (negative infinity, a) union (b, infinity). The entries in the eleventh row are: All real numbers; {x| x is all real numbers}; (negative infinity, infinity).»>

Указанный набор	Обозначение конструктора множеств	Интервальное обозначение
Все действительные числа от a до b , за исключением a или b	[латекс] \ {x \| a	[латекс] \ влево (а, б \ вправо) [/ латекс]
Все действительные числа больше a , но не включая a	[латекс] \ {x \| x> a \} [/ латекс]	[латекс] \ слева (a, \ infty \ right) [/ латекс]
Все действительные числа меньше b , но не включая b	[латекс] \ {x \| x	[латекс] \ влево (- \ infty, b \ right) [/ латекс]
Все действительные числа больше a , включая a	[латекс] \ {x \| x \ ge a \} [/ латекс]	[латекс] \ влево [a, \ infty \ right) [/ латекс]
Все действительные числа меньше b , включая b	[латекс] \ {x \| x \ le b \} [/ латекс]	[латекс] \ влево (- \ infty, b \ right] [/ латекс]
Все действительные числа от a до b , включая a	[латекс] \ {x \| a \ le x	[латекс] \ влево [а, б \ вправо) [/ латекс]
Все действительные числа от a до b , включая b	[латекс] \ {x \| a	[латекс] \ слева (a, b \ справа] [/ латекс]
Все действительные числа от a до b , включая a и b	[латекс] \ {x \| a \ le x \ le b \} [/ латекс]	[латекс] \ левый [a, b \ right] [/ латекс]
Все действительные числа меньше a или больше b	[латекс] \ {x \| x b \} [/ латекс]	[латекс] \ left (- \ infty, a \ right) \ чашка \ left (b, \ infty \ right) [/ latex]
Все вещественные числа	[латекс] \ {x \| x \ text {все вещественные числа} \} [/ latex]	[латекс] \ влево (- \ infty, \ infty \ right) [/ латекс]

Пример: использование интервальной записи для выражения всех действительных чисел, больше или равных

Используйте обозначение интервала, чтобы указать все действительные числа, большие или равные [latex] -2 [/ latex].

Показать решение

Используйте скобку слева от [latex] -2 [/ latex] и круглые скобки после бесконечности: [latex] \ left [-2, \ infty \ right) [/ latex]. Скобка указывает, что [latex] -2 [/ latex] включен в набор со всеми действительными числами, большими, чем [latex] -2 [/ latex], до бесконечности.

Попробуй

Используйте обозначение интервала для обозначения всех действительных чисел между [latex] -3 [/ latex] и [latex] 5 [/ latex] включительно.

Показать решение

[латекс] \ влево [-3,5 \ вправо] [/ латекс]

Пример: использование интервальной записи для выражения всех действительных чисел, меньших или равных

a или больше или равных b

Запишите интервал, выражающий все действительные числа, меньшие или равные [latex] -1 [/ latex] или больше или равные [latex] 1 [/ latex].

Показать решение

Для этого примера нам нужно написать два интервала. Первый интервал должен указывать все действительные числа, меньшие или равные 1. Итак, этот интервал начинается с [latex] — \ infty [/ latex] и заканчивается на [latex] -1 [/ latex], что записывается как [latex] ] \ left (- \ infty, -1 \ right] [/ latex].

Второй интервал должен показывать все действительные числа, большие или равные [latex] 1 [/ latex], что записывается как [latex] \ left [1, \ infty \ right) [/ latex]. Однако мы хотим объединить эти два набора.Мы достигаем этого, вставляя символ объединения, [latex] \ cup [/ latex], между двумя интервалами.

[латекс] \ left (- \ infty, -1 \ right] \ чашка \ left [1, \ infty \ right) [/ latex]

Попробуй

Выразите все действительные числа меньше [латекс] -2 [/ latex] или больше или равные 3 в интервальной нотации.

Показать решение

[латекс] \ left (- \ infty, -2 \ right) \ чашка \ left [3, \ infty \ right) [/ latex]

Использование свойств неравенств

Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как с уравнениями, но не точно так же. Мы можем использовать свойство сложения и свойство умножения , чтобы помочь нам решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число, мы должны перевернуть символ неравенства.

Общее примечание: свойства неравенств

[латекс] \ begin {array} {ll} \ text {Свойство добавления} \ hfill & \ text {If} a 0, \ text {then} ac bc. \ hfill \ end {array} [/ latex]

Эти свойства также применимы к [latex] a \ le b [/ latex], [latex] a> b [/ latex] и [latex] a \ ge b [/ latex].

Пример: демонстрация свойства сложения

Проиллюстрируйте свойство сложения для неравенств, решив каждое из следующих решений:

[латекс] x — 15 <4 [/ латекс]
[латекс] 6 \ ge x — 1 [/ латекс]
[латекс] x + 7> 9 [/ латекс]

Показать решение

Свойство сложения для неравенств гласит, что если неравенство существует, сложение или вычитание одного и того же числа с обеих сторон не меняет неравенства.

[латекс] \ begin {array} {ll} x — 15 <4 \ hfill & \ hfill \\ x - 15 + 15 <4 + 15 \ hfill & \ text {Добавьте 15 с обеих сторон.} \ Hfill \\ x <19 \ hfill & \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {ll} 6 \ ge x — 1 \ hfill & \ hfill \\ 6 + 1 \ ge x — 1 + 1 \ hfill & \ text {Добавить 1 с обеих сторон}. \ Hfill \\ 7 \ ge x \ hfill & \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {ll} x + 7> 9 \ hfill & \ hfill \\ x + 7-7> 9-7 \ hfill & \ text {Вычтите 7 с обеих сторон}.\ hfill \\ x> 2 \ hfill & \ hfill \ end {array} [/ latex]

Попробуй

Решить [латекс] 3x — 2 <1 [/ латекс].

Пример: демонстрация свойства умножения

Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих решений:

[латекс] 3x <6 [/ латекс]
[латекс] -2x — 1 \ ge 5 [/ латекс]
[латекс] 5-x> 10 [/ латекс]

Показать решение

[латекс] \ begin {array} {l} 3x <6 \ hfill \\ \ frac {1} {3} \ left (3x \ right) <\ left (6 \ right) \ frac {1} {3} \ hfill \\ x <2 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {ll} -2x — 1 \ ge 5 \ hfill & \ hfill \\ -2x \ ge 6 \ hfill & \ hfill \\ \ left (- \ frac {1} {2} \ right) \ left (-2x \ right) \ ge \ left (6 \ right) \ left (- \ frac {1} {2} \ right) \ hfill & \ text {Умножить на} — \ frac {1} {2}. \ Hfill \\ x \ le -3 \ hfill & \ text {Обратное неравенство}. \ Hfill \ end {array} [/ latex]

[латекс] \ begin {array} {ll} 5-x> 10 \ hfill & \ hfill \\ -x> 5 \ hfill & \ hfill \\ \ left (-1 \ right) \ left (-x \ right )> \ left (5 \ right) \ left (-1 \ right) \ hfill & \ text {Умножить на} -1.\ hfill \\ x <-5 \ hfill & \ text {Обратное неравенство}. \ hfill \ end {array} [/ latex]

Попробуй

Решите [латекс] 4x + 7 \ ge 2x — 3 [/ латекс].

Алгебраическое решение неравенств с одной переменной

Как показали примеры, мы можем выполнять те же операции с обеими сторонами неравенства, как и с уравнениями; совмещаем похожие сроки и выполняем операции. Чтобы решить, мы изолируем переменную.

Пример: алгебраическое решение неравенства

Решите неравенство: [латекс] 13 — 7x \ ge 10x — 4 [/ латекс].

Показать решение

Решение этого неравенства аналогично решению уравнения до последнего шага.

[латекс] \ begin {array} {ll} 13 — 7x \ ge 10x — 4 \ hfill & \ hfill \\ 13 — 17x \ ge -4 \ hfill & \ text {Переместите переменные члены в одну сторону неравенства} . \ hfill \\ -17x \ ge -17 \ hfill & \ text {Изолировать термин переменной}. \ hfill \\ x \ le 1 \ hfill & \ text {Разделение обеих сторон на} -17 \ text {отменяет неравенство }. \ hfill \ end {array} [/ latex]

Множество решений задается интервалом [latex] \ left (- \ infty, 1 \ right] [/ latex] или всеми действительными числами, меньшими чем 1 включительно.

Попробуй

Решите неравенство и запишите ответ, используя интервальную запись: [latex] -x + 4 <\ frac {1} {2} x + 1 [/ latex].

Показать решение

[латекс] \ слева (2, \ infty \ right) [/ латекс]

Пример: решение неравенства с дробями

Решите следующее неравенство и запишите ответ в интервальной записи: [latex] — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x [/ latex ].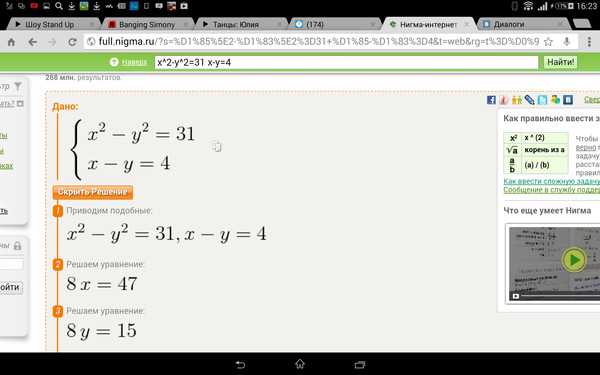

Показать решение Мы начинаем решать так же, как при решении уравнения.

[латекс] \ begin {array} {ll} — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x \ hfill & \ hfill \\ — \ frac {3} {4} x- \ frac {2} {3} x \ ge — \ frac {5} {8} \ hfill & \ text {Поместите переменные члены на одну сторону}. \ hfill \\ — \ frac {9} {12} x- \ frac {8} {12} x \ ge — \ frac {5} {8} \ hfill & \ text {Записать дроби с общим знаменателем}. \ hfill \\ — \ frac {17} {12} x \ ge — \ frac {5} {8} \ hfill & \ hfill \\ x \ le — \ frac {5} {8} \ left (- \ frac {12} {17} \ right) \ hfill & \ text {Умножение на отрицательное число отменяет неравенство}. \ hfill \\ x \ le \ frac {15} {34} \ hfill & \ hfill \ end {array} [/ latex]

Набор решений — это интервал [latex] \ left (- \ infty, \ frac {15} {34} \ right] [/ latex].

Попробуй

Решите неравенство и запишите ответ в интервальной записи: [latex] — \ frac {5} {6} x \ le \ frac {3} {4} + \ frac {8} {3} x [/ latex].

Показать решение

[латекс] \ left [- \ frac {3} {14}, \ infty \ right) [/ latex]

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Удаление условных обозначений группировки: круглые, квадратные, фигурные

Правила снятия скобок

Кронштейны и скобы

2 уровень

Отношение a — b к b — a

Правила снятия скобок

Перед круглыми скобками будет стоять знак плюс +

a + ( b — c + d )

или знак минус —

a — ( b — c + d ).

Если перед круглыми скобками стоит знак плюс +
, просто удалите их. Ничего не меняется.

a + ( b — c + d ) = a + b — c + d .

Когда скобкам предшествует знак минус —
меняет знак каждого члена в скобках.
Измените + на — и — на +.

a — ( b — c + d ) = a — b + c — d .

Знак b в скобках понимается как +. Таким образом, после удаления скобок этот термин становится — b .

— c в скобках становится + c . И + d становится — d .

Другими словами: Чтобы вычесть сумму, вычтите каждый член суммы .

a — ( b — c + d ) = a — b + c — d .

Вычтем b . Вычтите — c — то есть сложите. И вычтите d .

Мы можем обосновать эти две возможности примерами из арифметики, потому что алгебра абстрагирована — взята из — арифметики.

Например, вот как мы можем вычислить 256 + 98:

	256 + 98	=	256 + 100 — 2

		=	356 — 2

		=	354.
То есть

	256 + (100 — 2)	=	256 + 100 — 2.

Когда мы убираем эти скобки, ничего не меняется.

А вот как рассчитать 256 — 98:

	256 — 98	=	256–100 + 2

		=	156 + 2

		=	158.

То есть

	256 — (100 — 2)	=	256 — 100 + 2.

Когда мы убираем эти скобки, знак каждого члена в скобках меняется.

Проблема 1.Убрать круглые скобки.

a) p + ( q — r + s ) = p + q — r + s

b) p — ( q — r + s ) = p — q + r — s

В каждой из следующих задач снимите скобки, а затем упростите
, добавив числа.

Например,

( x — 3) — ( y — 4)	=	x -3 — y + 4

	=	x — y + 1.

Знак перед ( x — 3) понимается как +. Поэтому знаки в этих скобках не меняются.

Но предшествующий знак ( y -4) стоит минус. Следовательно, y меняется на −y, а −4 меняется на +4.

Наконец, в алгебре принято писать буквальные термины, x — y , слева от числового члена.

Проблема 2. ( x + 2) + ( y + 8)	=	х + 2 + у + 8

	=	x + y + 10.

Проблема 3. ( x + 2) — ( y + 8)	=	x + 2 — y — 8

	=	x — y — 6.

Проблема 4. ( x — 2) + ( y + 8)	=	x — 2 + y + 8

	=	х + у + 6.

Задача 5. ( x — 2) — ( y + 8)	=	x — 2 — y — 8

	=	x — y — 10.

Задача 6. ( x — 2) — ( y — 8)	=	x -2 — y + 8

	=	x — y + 6.

Задача 7. ( x — 2) + ( y — 8)	=	x — 2 + y — 8

	=	x + y — 10.

Задача 8. ( a — 2) + ( b + 3) — ( c — 7)	=	а — 2 + б + 3 — в + 7

	=	a + b — c + 8.

Задача 9. ( a — 5) — ( b + 6) — ( c — 9)	=	a — 5 — b — 6 — c + 9

	=	а — б — в — 2.

Задача 10.( a + 2) — ( b — 3) + ( c — 8) — ( d + 1)

	=	a + 2 — b + 3 + c — 8 — d — 1

	=	a — b + c — d — 4.

Опять же, когда перед круглыми скобками стоит знак минус, каждый знак внутри них меняется. Мы видели это раньше в правиле Урока 3:

a — (- b ) = a + b .

Задача 11. — (- x + y )

x — y .

Задача 12.- ( x — y )

— x + y .

Задача 13.

— ( x + y -2)

— x — y + 2.

Задача 14. Запишите отрицание

a — b + c — d .

— a + b — c + d .

Пример 1. Размещение скобок. Правила алгебры действуют в обоих направлениях. Следовательно, поскольку мы можем убрать скобки, мы также можем их разместить. Мы можем написать

a — b + c — d

следующими способами:

a — ( b — c + d )

( a — b ) — (- c + d )

a — ( b — c ) — d

И так далее.

Задача 15. Перепишите каждое из следующего, заключив скобки.

a) — x + y = — ( x — y ).

б) — х — у = — ( x + y )

c) — a + b — c + d = — ( a — b + c — d ).

d) Заключите в скобки b и c :

a — b + c — d = a — ( b — c ) — d .

Кронштейны и скобы

Скобки [] и фигурные скобки {} выполняют ту же функцию, что и круглые скобки. Все они группирующие символы. После скобок мы используем скобки для наглядности.После скобок, подтяжки.

Удаление скобок или фигурных скобок происходит по тем же правилам, что и скобки.

Пример 2. a — [ b — ( c — d + e )]

Удалим все символы группировки. Сделаем это, удалив скобки в первую очередь. Затем мы сделаем это снова, удалив сначала круглые скобки. Студент должен уметь делать это в любом случае.

Итак, после снятия скобок:

a — [ b — ( c — d + e )]

a — b + ( c — d + e ).

В квадратных скобках содержится два термина. Первый член — b . Второй член — ( c — d + e ).(См. Проблему 1c выше.) Поскольку перед скобками стоит -, знак каждого из двух членов изменяется. Знаки в пределах срока ( c — d + e ) не меняются.

Наконец, мы убираем круглые скобки, которым предшествует +:

a — b + c — d + e .

Теперь давайте решим ту же проблему, сначала убрав круглые скобки:

a — [ b — ( c — d + e )]	=	a — [ b — c + d — e ]

	=	a — b + c — d + e .

Поскольку перед круглыми скобками стоит -, каждый знак внутри них меняется. А поскольку скобкам также предшествует -, каждый знак внутри них меняется.

Проблема 16.

a) Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y + z )]	=	w + x — ( y + z )

	=	w + x — y — z

Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y + z )]	=	w + [ x — y — z )]

	=	w + x — y — z

б) Сначала снимите скобки, затем снимите скобки.

w — [ x + ( y — z )]	=	w — x — ( y — z )

	=	w — x — y + z

Сначала снимите скобки, затем снимите скобки.

w — [ x + ( y — z )]	=	w — [ x + y — z ]

	=	w — x — y + z

c) Сначала снимите скобки, затем снимите скобки.

w — [ x — ( y + z )]	=	w — x + ( y + z )

	=	w — x + y + z

Сначала снимите скобки, затем снимите скобки.

w — [ x — ( y + z )]	=	w — [ x — y — z )]

	=	w — x + y + z

d) Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y — z )]	=	w + x — ( y — z )

	=	w + x — y + z

Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y — z )]	=	w + [ x — y + z ) [

	=	w + x — y + z

Проблема 17. Удалите все символы группировки. Упрощайте по мере продвижения, оценивая числа. Сначала снимите скобы.

a) 5 — [3 — ( x — 2)]	=	5 — 3 + ( x — 2)

	=	2 + x — 2

	=	х .

b) 5 — [3 — ( x + 2)]	=	5–3 + ( х + 2)

	=	2 + х + 2

	=	х + 4.

c) −5 + [3 — ( x — 2)]	=	−5 + 3 — ( х -2)

	=	−2 — х + 2

	=	— х .

d) 5 — [−3 — ( x + 2)]	=	5 + 3 + ( х + 2)

	=	8 + х + 2

	=	х + 10.

Проблема 18.

a) Сначала снимите скобки, затем скобки, затем скобки.
а) Упростите, добавив числа.

10 — {2 + [3 — ( x — 5)]}	=	10 — 2 — [3 — ( x — 5)]

	=	8 — 3 + ( x — 5)

	=	5 + x — 5

	=	х .

Сначала удалите скобки, затем скобки, затем скобки.

10 — {2 + [3 — ( x — 5)]}	=	10 — {2 + [3 — x + 5]}

	=	10 — {2 + 3 — x + 5}

	=	10–10 + х

	=	х .

б) Сначала снимите скобки, затем скобки, затем скобки.

8 + {2 — [12 + ( x — 2)]}	=	8 + 2 — [12 + ( x — 2)]

	=	10 — 12 — ( x — 2)

	=	−2 — х + 2

	=	— х .

Сначала удалите скобки, затем скобки, затем скобки.

8 + {2 — [12 + ( x — 2)]}	=	8 + {2 — [12 + x — 2]}

	=	8 + {2 — 12 — x + 2}

	=	8 + 2 — 12 — х + 2

	=	— х .

2-й уровень

Следующий урок: Добавление похожих терминов

Содержание | Дом

Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.

Вопросы или комментарии?

Эл. Почта: themathpage@yandex. com

Как вставить фигурные скобки в Microsoft Word и Excel

Для удовлетворения определенных требований вам может потребоваться вставить фигурные скобки в документ Word или электронную таблицу Excel.Но помимо обычных фигурных скобок иногда также нужны фигурные скобки индивидуального размера, которые могут содержать несколько строк текста. В этом посте я расскажу о 4 наиболее часто используемых методах вставки как обычных, так и индивидуальных фигурных скобок. Скриншоты основаны на Word, но шаги почти такие же в Excel.

1. Ввод с клавиатуры

Для обычных фигурных скобок вы можете найти соответствующие клавиши на клавиатуре. Просто нажмите правую клавишу, удерживая нажатой [Shift] , и фигурные скобки будут введены немедленно.

2. Вставить уравнение

Перейдите на Вставьте вкладку , щелкните Уравнение в разделе Символы .

Затем вы перейдете на вкладку Design (Инструменты для уравнений) . Щелкните Bracket , чтобы развернуть раскрывающееся меню. Здесь вы можете найти все виды скобок, просто выберите фигурные скобки (или одиночные фигурные скобки), чтобы вставить их.

3.Вставить фигуры

Переключитесь на Вставьте вкладку и выберите Фигуры . Вы можете найти фигурные скобки в разделе Основные формы . Ничего страшного, если вам нужна только левая или правая скобка, просто выберите соответствующую скобку.

Вставленные таким образом кронштейны можно настроить по своему усмотрению. Перетащите границу, чтобы настроить ее размер, направление и расположение, пока не будете довольны результатом. Более того, вы даже можете изменить его цвет и эффект.

4. Microsoft Equation 3.0

Перейдите на Вставьте вкладку и выберите Объект > Объект…

Выберите Microsoft Equation 3. 0 в списке типа Объект на вкладке Создать новый . Щелкните OK , чтобы реализовать его.

Затем появится инструмент Microsoft Equation.Щелкните значок скобки в нижнем левом углу, чтобы развернуть меню, и выберите фигурные скобки в списке. Он будет немедленно вставлен в ваш документ.

Вам также может понравиться

Что такое скобки [] {} и круглые скобки ()?

Хотя эти символы — (), [], {} и? ? — регулярно появляются в наших книгах и экранах, все они имеют странное, неожиданное происхождение. Давайте изучим их поближе и узнаем их настоящие имена!

Что такое скобки ?

Если вы когда-нибудь видели эти ключи на своем компьютере: {}, [] или <>, тогда вы знаете, где находятся все типы скобок , молодец!

Слово скобка связано с французским braguette от названия гульфикной брони, которая буквально представляет собой часть вокруг… эээ, мужскую треску, которая, среди прочего, имеет сходство с архитектурными особенностями скобки. Согласно Etymonline, «типографская скобка (« знаки, используемые для примечания, ссылки, объяснения и т. Д. », Ранее называвшаяся пряжками ) впервые записана в 1750 году, так называемая, из-за ее сходства с двойными опорами в плотницких работах (смысл подтвержден с 1610-х годов) ». Примерно в 1880 году скобок также стали обозначать «группу, заключенную в скобки как имеющие равное положение в некоторой системе оценок». Итак, это (брекетинг с другими), вероятно, откуда тогда пришли спортивные брекеты. Ага!

Что такое квадратные скобки []?

Квадратные скобки ([]) используются внутри круглых скобок для обозначения чего-либо, подчиненного подчиненному предложению.Вот пример из 13-го издания Чикагского руководства по стилю : «Во время длительного визита в Австралию Глейк и его помощник (Джеймс Грин, который позже должен был провести собственное исследование нелетающей птицы [киви] в Нью-Йорке). Зеландия) провела несколько трудных месяцев, наблюдая за выживанием казуаров и эму ».

Что такое фигурные скобки {}?
У них {} множество имен; они называются скобками , фигурными скобками или волнистыми скобками .Обычно такие скобки используются для списков, но в Интернете они также означают объятие при электронном общении.
Что такое угловые скобки <> или ? ? ?
Последний запутанный символ? ? называется угловым кронштейном или шевроном . Первоначально это слово означало rafter на старофранцузском и, вероятно, произошло от латинского термина caper , что означает «коза». Этот символ чем-то напоминает задние лапы этих животных, верно? Сегодня его чаще всего используют в сложных математических задачах.Скобки, скобки и шевроны также используются в информатике и программировании.
Что такое круглые скобки ()?
Самый известный из этих символов — это, вероятно, (), называемый скобками . Интересный факт: одна из них называется круглой скобкой , а в паре множественное число скобок . Круглая скобка буквально означает «положить рядом», от греческих корней par- , -en, и тезис. За пределами США их можно назвать круглыми скобками .
Использование круглых скобок в печатном английском датируется по крайней мере 1572 годом.
Пишите умнее с нашим тезаурусом Grammar Coach ™! Получите помощь по орфографии, предложения синонимов, проверку грамматики и многое другое! Войти Сейчас!
Скобки и скобки письменные
Как использовать круглые скобки в письме?
Грамматически они действуют как запятые и служат для выделения части предложения или обсуждения.Скобки также можно использовать в качестве прерывания в предложениях, чтобы создать более неформальный и непринужденный стиль письма.
Круглые скобки смещают текст, который не важен для смысла предложения. Такие вещи, как дополнительная информация, пояснения, отступления или цитаты. Информация в круглых скобках может состоять из числа или слова или состоять из нескольких предложений. Круглые скобки всегда появляются парами. Они часто используются там, где уместны запятые.
Предложение должно стоять само по себе без информации в скобках.Например: «Маленькая девочка ( и ее кукла ) перескочила через парк к своей матери».
В письменной форме круглые скобки также могут использоваться для обозначения единственного слова во множественном числе. Например: «Девушка (и) упала в яму».
Формат
MLA также использует круглые скобки для цитирования в тексте.
Чтобы узнать больше о скобках в письменной форме и о том, как использовать знаки препинания с ними, прочтите нашу статью, в которой подробно рассматриваются скобки.
Как писать в квадратных скобках?
Квадратные скобки [] используются для заключения раздела написания или печати, чтобы отделить его от основного текста. Их можно использовать как круглые скобки, но в письменной форме они используются реже.
Одно из основных употреблений квадратных скобок в письменной форме — соединение со словом sic . Чтобы узнать больше о точном цитировании с помощью sic , прочтите наше более подробное описание этого термина.
Другой способ использования квадратных скобок в письменной форме — вставка слова или имени для пояснения (которых нет в исходном тексте). Как и sic выше, он помогает прояснить написанное.Например: «Она [Малия] сказала мне, что это неправильно».
Как использовать фигурные скобки в письме?
Фигурные скобки {} нечасто используются в письменной форме, они чаще встречаются в математике и программировании (прокрутите немного вниз, чтобы узнать, как это сделать).
Но, когда вы действительно видите их в письменном виде здесь и там, основные способы их использования — это хранить списки пунктов или содержать термин или термины, которые равны написанному.
Вот несколько примеров:
Списки: Это все мои друзья {Сэм, Илья, Малик, Бри}.
Равные условия: используйте предпочитаемую вами платформу социальных сетей {Twitter, Instagram, Facebook, Tiktok}.
Как использовать угловые скобки в письменной форме?
В письменной форме угловые скобки встречаются редко… то есть в английском языке. В других языках угловые скобки используются в двойных << >> и заменяют кавычки.
Когда они используются в английском письме, они могут иногда сигнализировать о точке данных, например: «Доставка произошла в <> <>.
Вы также можете использовать двойные угловые скобки, чтобы отметить действие или установить статус, например << Out to Lunch >>.
Круглые и квадратные скобки в математике
Когда дело доходит до скобок в математических уравнениях, они используются для обозначения порядка, вы знаете, как в порядке операций .
Правильный порядок обращения к уравнениям в круглых скобках следующий: сначала решите уравнения в круглых скобках (), затем в квадратных скобках [], а затем в фигурных скобках {}.
Фигурные скобки {} также могут использоваться в математических наборах. Наборы — это просто группа чисел. Пример: {1, 3, 5, 7, 9}.
Как использовать угловые скобки в математике?
Угловые скобки обычно используются в математике как знаки «меньше» и «больше». Примеры включают: 8 <16 или 20> 1.
Есть несколько специализированных применений угловых скобок в сложных математических областях, таких как квантовая механика… но мы позволим экспертам объяснить эти применения.
Скобки и скобки в программировании
Каждый тип скобок и круглых скобок также выполняет определенную функцию в программировании. Прокрутите, чтобы посмотреть, что это такое.
Как использовать круглые скобки в программировании?
В программировании, особенно в Javascript, скобки используются, чтобы показать, что слово является функцией.
Пример: showMyWordList («Список элементарных слов»).
Как использовать квадратные скобки в программировании?
Квадратные скобки используются для массивов, особенно в Javascript.
Пример: var color = [«синий», «бирюзовый», «бирюзовый»].
Как использовать фигурные скобки в программировании?
Фигурные скобки используются, чтобы показать, где функция начинается и заканчивается. Просто.
Как использовать угловые скобки в программировании?
Угловые скобки используются в программировании иначе: как знаки «меньше» и «больше». Это означает, что они вообще не содержат никакой информации, когда дело доходит до программирования таким образом; вместо этого они представляют, если значение меньше или больше другого значения в коде.
Если вы думаете, что эти грамматические символы сбивают с толку, подождите, пока вы не встретите интерробанг и другие необычные и недостаточно используемые знаки.
Вычисления формул многокамерного массива Excel
Выполнение вычислений в нескольких ячейках с помощью одной формулы массива Excel
В Excel формула массива выполняет вычисления для одного или нескольких элементов массива.
Формулы массива заключены в фигурные скобки « {} ».Они добавляются в формулу путем одновременного нажатия клавиш Ctrl, Shift и . Введите после ввода формулы в ячейку или ячейки.
Типы формул массива
Есть два типа формул массива:
Формулы массива с одной ячейкой — формулы, выполняющие несколько вычислений в одной ячейке листа;
Формула массива с несколькими ячейками — формулы, выполняющие одни и те же вычисления в нескольких ячейках рабочего листа.
Как работает формула многоячеечного массива
На изображении выше формула массива с несколькими ячейками расположена в ячейках от C2 до C6 и выполняет ту же математическую операцию умножения данных в диапазонах от A1 до A6 и от B1 до B6.
Поскольку это формула массива, каждый экземпляр или копия формулы абсолютно одинаковы, но каждый экземпляр использует разные данные в своих вычислениях и дает разные результаты.
Например:
Экземпляр формулы массива в ячейке C1 умножает данные ячейки A1 на данные в ячейке B1 и возвращает результат 8;
Экземпляр формулы массива в ячейке C2 умножает данные ячейки A2 на данные в ячейке B2 и возвращает результат 18;
Экземпляр формулы массива в C3 умножает данные в ячейке A3 на данные в ячейке B3 и возвращает результат 72.
Создание базовой формулы
Пример формулы многоячеечной матрицы
Формула на изображении выше умножает данные из столбца A на данные из столбца B.Для этого вводятся диапазоны, а не отдельные ссылки на ячейки, как в обычных формулах:
{= A2: A6 * B2: B6}
data-type = «code»>
Создание базовой формулы
Первым шагом в создании формулы массива с несколькими ячейками является добавление одной и той же базовой формулы ко всем ячейкам, в которых будет находиться формула массива с несколькими ячейками.
Это делается путем выделения или выбора ячеек перед началом формулы.
Приведенные ниже шаги охватывают создание формулы массива с несколькими ячейками, показанной на изображении выше, в ячейках с C2 по C6:
Выделите ячейки с C2 по C6 — это ячейки, в которых будет располагаться формула массива с несколькими ячейками;
Введите на клавиатуре знак равенства ( = ), чтобы начать формулу основания.
Выделите ячейки от A2 до A6, чтобы ввести этот диапазон в базовую формулу;
Введите символ звездочки ( * ) — оператор умножения — следуя диапазону A2: A6;
Выделите ячейки с B2 по B6, чтобы ввести этот диапазон в базовую формулу;
На этом этапе оставьте рабочий лист как есть — формула будет завершена на последнем шаге учебного пособия, когда будет создана формула массива.
Создание формулы массива
Последний шаг — это преобразование базовой формулы, расположенной в диапазоне C2: C6, в формулу массива.
Создание формулы массива в Excel выполняется нажатием клавиш Ctrl , Shift и Enter на клавиатуре.
При этом формула будет заключена в фигурные скобки: {}, что означает, что теперь это формула массива.
Удерживайте нажатыми клавиши Ctrl и Shift на клавиатуре, затем нажмите и отпустите клавишу Enter , чтобы создать формулу массива.
Отпустите клавиши Ctrl и Shift .
Если все сделано правильно, формулы в ячейках с C2 по C6 будут заключены в фигурные скобки, и каждая ячейка будет содержать другой результат, как показано на первом изображении выше.
Результат ячейки C2: 8 - формула умножает данные в ячейках A2 * B2 C3: 18 - формула умножает данные в ячейках A3 * B3 C4: 72 - формула умножает данные в ячейках A4 * B4 C5: 162 - формула умножает данные в ячейках A5 * B5 C6: 288 - формула умножает данные в ячейках A6 * B6
Когда вы щелкаете по любой из пяти ячеек в диапазоне C2: C6, завершается формула массива:
{= A2: A6 * B2: B6}
data-type = «code»>
отображается в строке формул над листом.
Спасибо, что сообщили нам!
Расскажите, почему!
Другой Недостаточно деталей Трудно понять
Основные учебные пособия — MathType — Документация
Шрифты и стили
Это руководство представляет собой введение в систему стилей MathType. Мы продемонстрируем, как изменить шрифты в ваших уравнениях, изменив определения стилей. Использование стилей позволит вам быстро и легко добиться желаемого форматирования и позволит создавать уравнения с единообразным внешним видом.См. Раздел «Меню стилей» для получения дополнительной информации о стилях, шрифтах и размерах.
На следующих этапах мы создадим уравнение
и поэкспериментируйте с изменением внешнего вида уравнения, используя различные определения стилей. Эта анимация показывает краткое изложение того, что вы будете делать в этом руководстве:
Убедитесь, что вы используете стиль
Math
Убедитесь, что на панели стиля строки состояния отображается «Math». Если это не так, выберите «Математика» в меню «Стиль».Если текущий стиль MathType не является Math , его автоматическое назначение стиля не будет действовать, и остальная часть этого учебника не будет иметь особого смысла.
Создайте уравнение
Создайте уравнение, используя шаблон дроби уменьшенного размера для дроби и вставив ϕ и σ , выбрав их из палитры строчных греческих букв или используя Ctrl + G / ⌘ + G ярлык. (Если вы используете ярлык, помните, что после нажатия начального ярлыка — Ctrl + G / ⌘ + G — вы должны затем нажать букву, связанную с желаемым греческим символом.В данном случае это либо f, либо s соответственно.) Оператор • находится на палитре. Уравнение теперь должно выглядеть так:
Определите стили
В меню «Стиль» выберите «Определить». При необходимости нажмите кнопку Simple, чтобы отобразить это диалоговое окно:
Измените «Основной шрифт» на Евклид, замените «Греческий и математический шрифты» на Евклид символ и Евклид Экстра, как показано в диалоговом окне выше, а затем нажмите Применить. Теперь ваше уравнение на экране будет выглядеть так:
Шрифты Euclid, поставляемые с MathType, основаны на шрифтах Computer Modern, которые обычно используются с TeX, поэтому они придают вашим документам TeX-подобный вид, который вы могли бы предпочесть для некоторых типов работы.Еще одним преимуществом шрифтов Евклида является то, что их обычные и греческие символы имеют одинаковый размер, тогда как время и символ несколько не совпадают. Конечно, если вы используете шрифты Евклида в своих уравнениях, вы, вероятно, захотите также использовать Евклид в качестве основного основного шрифта в вашем текстовом документе.
Внешний вид TeX
Мы включили файл настроек MathType с именем TeXLook.eqp, который содержит настройки шрифта и интервала, которые делают уравнения MathType похожими на TeX. Он находится в папке Preferences внутри папки MathType.См. «Меню настроек» для получения более подробной информации об использовании файлов настроек.
Возврат к настройкам по умолчанию
Если диалоговое окно «Определение стилей» еще не открыто, откройте его. Щелкните Параметры по умолчанию (некоторые версии: «По умолчанию»; другие — «Заводские настройки»), чтобы вернуться к использованию шрифтов Times New Roman и Symbol.
Расширенные настройки
Нажмите кнопку «Дополнительно», чтобы отобразить более развернутую форму диалогового окна «Определение стилей»:
СОВЕТ
Изменения, внесенные в этом диалоговом окне, применяются к текущему уравнению.Отметьте «Использовать для новых уравнений», чтобы также использовать настройки для новых уравнений.
Имена одиннадцати стилей перечислены в диалоговом окне вместе со шрифтом и стилем символов, присвоенным каждому из них. В только что созданном уравнении используются функции, переменные, L.C. Греческий, Числовой и Символьный стили. Буквы «exp» распознаются как аббревиатура экспоненциальной функции и им присваивается стиль функции; u , x и y обрабатываются как переменные и им присваивается стиль «Переменная»; φ и σ , являющиеся строчными буквами греческого алфавита, имеют букву L. C. (нижний регистр) греческий стиль, а числа в дроби используют числовой стиль. Символы =, •, (,) и + используют стиль символа. (Полоса дробей является внутренней для MathType и не использует стиль.) Эти стили применяются автоматически при создании уравнения, поскольку вы используете стиль Math. Это автоматическое назначение стиля является преимуществом, которое вы получаете, используя стиль Math при создании уравнений.
Подробнее о стилях
Тема стилей MathType более подробно рассматривается в меню «Стиль».
Мы собираемся изменить некоторые стили, чтобы вы понимали, как они влияют на внешний вид уравнения. Обычно вы бы так не работали; вы можете изменить шрифты с помощью простой версии этого диалогового окна.
Установить шрифт для стиля функции
Стиль функции в настоящее время определен для использования шрифта Times New Roman. Щелкните стрелку справа от названия шрифта в строке «Функция» и выберите другой шрифт. Вам нужно будет выбрать шрифт, который будет заметно отличаться от Times New Roman, чтобы эффект от изменения был очевиден. Хорошим выбором будет шрифт без засечек, например Arial.
Посмотреть эффект от изменения стиля
Нажмите кнопку ОК. Ваше уравнение будет повторно отображено с использованием нового определения стиля функции. Ваше уравнение должно выглядеть следующим образом, если вы выбрали шрифт Arial для стиля Function:
Аббревиатура функции exp отображается с использованием нового шрифта. Конечно, вы, вероятно, не захотите, чтобы ваше уравнение выглядело так — мы просто демонстрируем эффект изменения определения стиля функции.
Определение стиля Variable используется для всех обычных буквенных символов, кроме символов в сокращениях функций. В текущем уравнении это включает x , x и y . Очень часто, согласно соглашению, единственное различие между стилями «Переменная» и «Функция» заключается в том, чтобы стиль переменной был определен курсивом. Давайте переопределим стиль Variable, чтобы он соответствовал новому определению стиля Function.
Выбор шрифта
Быстрый способ выбрать шрифт — щелкнуть список и затем ввести первую букву имени.Вы также можете использовать полосу прокрутки в списке для быстрого перемещения.
Установить другие стили
Еще раз выберите «Определить» в меню «Стиль». В диалоговом окне «Определение стилей» щелкните стрелку рядом с именем шрифта для стиля Variable и выберите тот же шрифт, который назначен стилю Function. Убедитесь, что стиль курсивного символа отмечен для переменной, но не для функции.
Давайте также изменим стиль Number, чтобы он использовал тот же шрифт, что и Function и Variable.Вы обнаружите, что это улучшает вид уравнения. Наконец, отключите курсивный шрифт для L.C. Греческий стиль, сняв флажок в столбце Стиль символа. Строчные греческие буквы обычно выделяются курсивом, но давайте поэкспериментируем с этим. Обратите внимание, что для стиля символа вы можете назначать шрифты только с той же кодировкой (расположением символов), что и шрифт символа. Обычно это ограничивает ваш выбор шрифтом Symbol, шрифтом Euclid Symbol или другим подобным шрифтом.
Посмотреть эффект от изменения стиля
Нажмите ОК .Ваше уравнение будет повторно отображено с использованием новых определений стиля. Если вы используете рекомендованные нами шрифты, уравнение должно выглядеть следующим образом:
«Переменные» u , x и y , а также числа в дроби ½ теперь используют новые определения шрифта, а строчные греческие буквы φ и σ больше не выделяются курсивом. Вы можете использовать определения стилей, подобные этим, для уравнений в документе, текст которого написан в Arial.
Чтобы сбросить определения стилей, откройте диалоговое окно «Определить стили» и нажмите «Настройки по умолчанию» (в некоторых версиях: «Заводские настройки»).
СОВЕТ
Можно также дважды щелкнуть или щелкнуть правой кнопкой мыши панель «Стиль» в строке состояния, чтобы отобразить меню «Стиль».
Работая с этим руководством, вы, вероятно, заметили, что каждый из стилей также указан как команда в меню «Стиль». Это позволяет вам явно назначить определенный стиль выбранным или набираемым впоследствии символам. Команду «Другое» в меню «Стиль» можно использовать для назначения любого шрифта, доступного на вашем компьютере, выбранным или вводимым впоследствии символам.Подробнее см. В меню «Стиль».
Включение текста в уравнение
В нашем следующем руководстве мы покажем вам, как вводить слова и фразы в уравнение, а также как обрабатывать сокращения имен функций, которые MathType не распознает. Мы собираемся создать следующее уравнение:
Начать уравнение
Сначала откройте новое окно MathType, используя один из уже изученных вами методов. Затем введите Prob (A | B) . Результат будет
Используя свою встроенную таблицу имен функций, MathType распознал Pr как сокращение от «вероятности» и установил его в стиле Function, в то время как o и b рассматриваются как переменные. В этом руководстве мы хотим использовать Prob, а не просто Pr, в качестве нашего сокращения для «вероятности». Вы можете подумать, что можете решить проблему, просто выделив o и b не курсивом, но мы не рекомендуем этого делать. Если вы просто удалите курсив, MathType по-прежнему будет рассматривать o и b как переменные, чего мы не предполагали. Правильный подход — выбрать Prob и выбрать Function в меню Style. Это удалит курсив, но также сообщит MathType, что Prob — это имя функции, что повлияет на интервалы и перевод на такие языки, как LaTeX и MathML.
Управление курсивом
Чтобы назначить обычный (не курсив) стиль именам функций, используйте функцию в меню «Стиль», а не просто удаляйте курсив.
Создать дробь
Создайте дробь в среднем члене уравнения. Вы можете скопировать и вставить Prob ( A | B ) и изменить его для повторного использования в числителе и знаменателе. Вы можете найти ∩, установленный символ пересечения, на палитре. Теперь ваше уравнение должно выглядеть так
Копирование и перетаскивание
Чтобы повторно использовать часть существующего уравнения, выберите часть и затем используйте «Копировать и вставить» или перетащите.Если вы нажмете и удерживаете Ctrl (Mac: ⌥ ) при перетаскивании, будет создана копия выделенной области.
Создать другую дробь
Постройте дробь в правой части уравнения, снова используя шаблон. Точка вставки будет помещена в числитель, и вы сможете ввести текст.
Ввод текста
Перед вводом обычных слов и фраз выберите «Текст» в меню «Стиль».
Выбрать
Стиль текста Если вы просто начнете вводить символы в слот числителя, MathType будет считать, что это переменные, поэтому они будут выделены курсивом, а любые вводимые вами пробелы будут проигнорированы.Чтобы ввести обычные слова и фразы, вы должны сначала выбрать «Текст» в меню «Стиль». Затем введите Вероятность того, что встретятся и A, и B, . Числитель нашей дроби будет выглядеть так:
Это то, что мы хотим, за исключением того, что слово «оба» должно быть жирным, а буквы A и B должны быть выделены курсивом.
Изменить
и на полужирный
Выделите слово «оба» и выберите «Другой» в меню «Стиль». Появится диалоговое окно «Другой стиль», в котором можно напрямую изменить шрифт и стиль (полужирный и курсив) выбранных символов.Щелкните Полужирный, а затем ОК.
Марка
A и B курсив
Далее мы хотим выделить переменные A и B курсивом. Мы могли бы сделать это напрямую, снова используя «Другой» в меню «Стиль», но на самом деле это не передало бы правильного значения. Лучше выбрать переменную A и выбрать Math из меню Style, а затем повторить для переменной B. Это делает A и B курсивом, но также указывает MathType рассматривать их как математические переменные.
Введите знаменатель
Введите знаменатель дроби, используя тот же метод, который мы использовали для числителя.
Это завершает уравнение, но мы можем использовать его, чтобы проиллюстрировать еще несколько возможностей MathType.
Новые имена функций
Вы можете настроить список функций, которые MathType автоматически распознает.
Если вы регулярно используете аббревиатуру «Prob» для обозначения вероятности, вам надоест постоянно вручную менять ее на стиль Function, и вам нужно, чтобы MathType делал это за вас автоматически. В меню «Настройки» выберите «Распознанные функции».Введите Prob в качестве имени новой функции и нажмите кнопку «Добавить». Кроме того, если вы не хотите, чтобы MathType распознавал Pr как сокращение от «вероятности», вы можете выбрать Pr в списке распознаваемых функций и нажать кнопку «Удалить».
Теперь попробуйте воссоздать то же уравнение, чтобы увидеть, насколько оно проще.
Использование панели инструментов MathType
В предыдущих уроках мы видели две формулы, которые были очень похожи в том смысле, что у них было много общих терминов.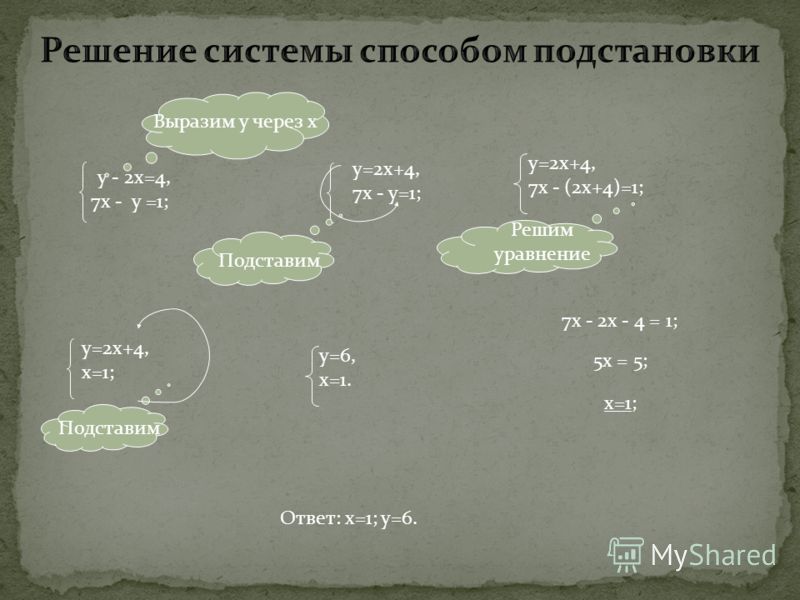 Это типично для многих разделов математики. Например, рассмотрим эти формулы из элементарной статистики:
Многие статистические формулы используют символы μ и σ, и они часто включают различные комбинации таких терминов, как, и. Имея дело с повторяющимися формулами, подобными этой, вы можете сэкономить много времени, настроив MathType. Чтобы сэкономить время на создание статистических формул, мы собираемся поместить σ в маленькую полосу. Мы также создадим выражения для и и поместим их на панели с вкладками.Затем мы будем использовать их для создания второго из приведенных выше уравнений.
Размеры значков панели инструментов
Используя команду «Настройки рабочего пространства» в меню «Настройки», вы можете изменить размер значков панели инструментов.
Вот как добавить эти символы и выражения на настраиваемую панель инструментов:
Панели инструментов должны быть видны
Прежде чем мы начнем, убедитесь, что панель инструментов MathType видна и что видны маленькая полоса, а также маленькая и большая полоски с вкладками. При необходимости используйте команды в меню «Просмотр», чтобы сделать их видимыми.
Откройте палитру
греческих символов (строчные)
Щелкните палитру символов и отпустите кнопку мыши. Палитра появится.
Добавьте σ к маленькому стержню
Теперь, удерживая нажатой Alt ( ⌘ на Mac), щелкните σ и, удерживая левую кнопку мыши нажатой, перетащите ее на маленькую полосу. Вы увидите, как указатель мыши меняет форму, когда он проходит по различным областям панели инструментов.Когда указатель выглядит так, перетаскиваемый элемент не может быть оставлен в этом месте, и отпускание кнопки мыши не будет иметь никакого эффекта. Когда указатель выглядит так в Windows или так на Mac, он находится над допустимой целевой областью, и при отпускании кнопки мыши объект вставляется в это место. Теперь отпустите кнопку мыши над маленькой полосой, как показано здесь:
Символ будет добавлен в конец полосы. Теперь, чтобы вставить этот символ в уравнение, вам нужно всего лишь щелкнуть по нему на маленькой панели, а не искать его на палитрах. Маленькая полоса — хорошее место для часто используемых символов, поскольку она всегда доступна и может содержать много элементов.
Добавление новых символов
Вы можете добавить любой символ из любого шрифта на вашем компьютере на панель инструментов. Введите его в область уравнения, выберите его и перетащите на панель инструментов. Используйте диалоговое окно «Вставить символ» (в меню «Правка» — подробности см. В разделе «Вставка символов, отсутствующих в палитре»), чтобы найти символ, удерживайте нажатой клавишу Alt и перетащите символ на панель инструментов.В результате MathType имеет доступ к практически неограниченному количеству символов.
Добавить выражение в большую панель с вкладками
Далее мы собираемся добавить большую панель с вкладками. Полосы с вкладками похожи на маленькую полосу по принципу работы, однако они разделены на категории, что позволяет размещать гораздо большее количество элементов. Щелкните вкладку Статистика, чтобы отобразить элементы MathType по умолчанию для статистических уравнений. В большой панели с вкладками должно быть место для еще одного элемента (на панели есть место для 8 элементов).Если его нет, выберите другую вкладку, на которой есть место.
Создайте выражение
Удалите текущее содержимое окна MathType и создайте обычным способом. Для этого вам нужно будет использовать шаблон (а не шаблон или символ).
Редактирование выражений панели инструментов
Вы можете редактировать выражение панели инструментов двойным щелчком, если вы работаете в Windows. Кроме того, в Windows или Mac вы можете редактировать выражение панели инструментов, щелкнув правой кнопкой мыши и выбрав «Редактировать» (Windows) или «Редактировать выражение» (Mac).Откроется новое окно MathType, содержащее выражение. Внесите изменения, закройте окно, сохраните изменения, и панель инструментов обновится.
Выберите и перетащите выражение на большую панель с вкладками
Чтобы добавить это выражение на панель инструментов, выберите его и перетащите на большую панель с вкладками. Когда вы отпустите кнопку мыши, вы увидите, что выражение появляется на панели.
Добавить дробь к маленькой полосе с вкладками
Создайте и перетащите это выражение на маленькую панель с вкладками.Вы можете сделать дробь в полном размере, используя шаблон, или вы можете сделать дробную часть, используя шаблон. Когда вы закончите, мы готовы создать формулу
Советы и напоминания
Создание этой формулы не требует каких-либо новых методов, поэтому мы не собираемся давать вам обычные пошаговые инструкции. Вот несколько полезных советов и напоминаний:
Вы можете вставить σ , щелкнув его на маленькой панели, что намного быстрее, чем использование палитры.
Вы можете вставить, щелкнув по нему на большой панели с вкладками.
Быстрый способ создания — вставить, перетащить X , чтобы выбрать его, и ввести Y , чтобы заменить.
Обратите внимание, что два члена в фигурных скобках в нижней строке формулы идентичны, за исключением того, что один включает X, а другой — Y. Чтобы создать второй член, просто продублируйте первый и замените X на Y.
Вы можете продублировать термин, выделив его, удерживая Ctrl ( ⌥ на Mac) и перетащив его в желаемое место (без Ctrl / ⌥ термин перемещается).
Изменение порядка панели инструментов
Панель инструментов MathType изначально заполнена выражениями, полезными для многих различных областей математики. Однако вы можете переименовать или удалить существующие вкладки, а также изменить порядок или удалить любые символы или выражения, которые есть на панели инструментов по умолчанию. Вы также можете изменить любое из выражений, если они не совсем подходят для вашего конкретного использования.
Чтобы переместить символ или выражение на панели инструментов, удерживайте Alt (Mac: ⌘ ) и перетащите элемент на новое место.Вы можете вставить элемент между двумя другими, поместив его между ними.
Попробовать
Попробуйте это, перетащив σ с маленькой полоски (шаг 3 выше) на маленькую полоску с вкладками. Выбор места для размещения предмета полностью зависит от вас; символ или выражение можно разместить на любой из полос.
Теперь удалим σ из Small Tabbed Bar.
Удаление символов и выражений с панели инструментов
Щелкните правой кнопкой мыши σ и выберите «Удалить» в появившемся контекстном меню.Вы также можете удалить другие выражения, которые вы добавили на панели с вкладками.
Удаление элементов панели инструментов (только Windows)
Другой способ удалить элемент в MathType для Windows — это Alt + Перетащите его с панели и отпустите указатель мыши над недопустимой целью, например, за пределами окна MathType.
Изменить названия вкладок
Вы также можете изменить названия вкладок в соответствии с вашей конкретной ситуацией. Дважды щелкните вкладку «Статистика», чтобы открыть диалоговое окно «Свойства вкладки», где вы можете изменить имя вкладки и изменить ее сочетание клавиш.
Если вы предпочитаете вводить текст с помощью мыши, вы можете использовать интерфейс клавиатуры панели инструментов. Вы можете передать фокус клавиатуры компоненту панели инструментов, используя следующие команды клавиатуры:
Палитра или панель Windows Mac
Палитра символов F5 ⌘ + F5
Палитра шаблонов F6 ⌘ + F6
Малый стержень F7 ⌘ + F7
Бар с большими выступами F8 ⌘ + F8
Стержень с малыми выступами F9 ⌘ + F6
После того, как полоса окажется в фокусе, вы можете использовать ← и → для перемещения выделения и Введите , чтобы вставить выбранный элемент (или открыть соответствующее меню). Esc закрывает меню или возвращает фокус в область уравнения. Вы можете переключать вкладки, набрав Ctrl + F10 ( ⌘ + F10 на Mac), n, где n — номер вкладки для активации. Например, ввод Ctrl + F10 , 2 активирует вторую вкладку.
Выбор места на панели инструментов
Некоторые символы и шаблоны используются настолько часто, что вам может не понадобиться размещать их на панели инструментов.Вероятно, вы запомнили сочетания клавиш для их вставки, поэтому от того, чтобы они занимали ценное место на панели инструментов, мало что можно получить. В эту категорию особенно попадают греческие символы; как только вы узнаете, что вы можете вставить β , нажав Ctrl + G или ⌘ + G , за которым следует B (называемый Ctrl + G, B в Windows или Command + G , B на Mac), вероятно, вам не нужно будет добавлять эти символы на панель инструментов.
Однако может иметь смысл добавить на панель инструментов символы из любых специальных шрифтов. Самый простой способ — использовать диалоговое окно «Вставить символ» (выберите команду «Вставить символ» в меню «Правка»), которое является чрезвычайно мощным инструментом для просмотра символов в шрифте. Вы также можете Alt + Перетащить или ⌘ + Перетащить символа из этого диалогового окна на панель инструментов. Вы можете добавить на панель инструментов столько символов из ваших шрифтов, сколько вам понадобится.Затем вы можете ввести эти символы в любое время в свои уравнения, независимо от ваших текущих определений стиля.
Это подходит для использования панели инструментов MathType, поэтому выберите «Выбрать все» ( Ctrl + A / ⌘ + A) в меню «Правка» и нажмите Backspace или Удалить , чтобы очистить окно для следующего урока.
Расстояние и выравнивание
В следующем примере мы представляем некоторые возможности MathType для управления интервалом и выравниванием в уравнениях и других выражениях. Мы собираемся создать следующую пару неравенств:
Обратите внимание, что эти выражения расположены так, что их знаки «меньше или равно» выровнены по вертикали, и оба они содержат конструкцию «lim sup» типа, который мы раньше не использовали.
Расширяющиеся интегралы
Знаки интеграла обычно имеют постоянный размер. Вы можете создать расширяющийся интеграл, удерживая нажатой Shift при выборе интегрального шаблона из палитры интегралов.
Вы можете создать эти выражения следующим образом:
Вставить определенный интеграл
Вставьте определенный интегральный шаблон, щелкнув или используя ярлык Ctrl + I / ⌘ + I .Введите подынтегральное выражение (большая ячейка) и введите 0 и 1 в качестве пределов интегрирования (две маленькие ячейки). Вероятно, вы не захотите, чтобы круглые скобки в подынтегральном выражении были «расширяющимися», поэтому вы можете просто вводить их с клавиатуры, а не использовать шаблон. Ваше выражение теперь должно выглядеть так:
Добавьте тонкое пространство
Чтобы улучшить внешний вид нашего выражения, мы должны вставить тонкий промежуток (одна шестая em) между a ( x ) и dx в подынтегральном выражении.MathType не может делать это автоматически, поэтому мы предоставляем вам удобный способ вручную ввести пространство правильного размера.
Шаблон в круглых скобках
Вы можете использовать шаблон вместо ввода (и). Использование шаблона может придать вашему документу более единообразный вид. Шаблон также включает больше места вокруг себя, поэтому вам может не понадобиться добавлять тонкое пространство, как показано здесь. Мы пытаемся научить вас различным способам создания выражений; очевидно, что окончательный выбор остается за вами!
Палитра содержит набор из пяти значков, представляющих часто используемые пространства.Поместите точку вставки между «)» и «d», щелкнув там, и вставьте тонкий промежуток, выбрав (он находится в левом столбце во второй строке палитры пробелов и многоточий) или нажав Ctrl + Пробел (ярлык тот же Win / Mac).
Выход из подынтегрального выражения
Переместите точку вставки из прорези интеграла в положение, показанное ниже. Вы должны сделать это, чтобы команды выравнивания работали правильно. Не создавайте остальную часть выражения в слоте подынтегральной функции.
Показать размещение
Команда «Показать размещение» в меню «Вид» показывает различные слоты и помогает избежать ошибок.
Символ неравенства
Щелкните ≤ на маленькой панели.
Включить нижний индекс
Теперь мы хотим построить структуру «lim sup». Начнем с того, что щелкнем значок в палитре. Этот значок представляет собой шаблон подчеркивания: любые символы, введенные в верхний слот, будут полноразмерными, а символы в нижнем слоте будут уменьшены до размера «нижнего индекса».
Тип
lim sup
Точка вставки расположена в верхнем слоте, поэтому вы можете ввести limsup . MathType будет использовать ваш стиль «Функция» (возможно, простой стиль) для этих символов и вставит тонкий пробел между «lim» и «sup».
Примечание. lim sup не является определенной функцией в MathType, но lim и sup по отдельности являются определенными функциями, поэтому внешний вид все равно будет правильным.
Введите нижний индекс
Переместите точку вставки вниз в нижнюю прорезь, щелкнув внутри нее или нажав клавишу Tab, и введите n → ∞. Символы → и ∞ очень распространены в математике, поэтому они были добавлены в стандартную маленькую полосу MathType. Разумеется, они также доступны в палитрах символов. Следуя соглашениям о наборе (как всегда), MathType не будет создавать интервалы вокруг символа →, поскольку он находится в нижнем индексе, но вы можете вставить пробелы, если хотите.
Выйти из нижнего индекса
Нажмите Tab, чтобы переместить точку вставки из нижнего слота, и введите оставшуюся часть этого первого выражения. Самый быстрый способ сделать это — просто набрать Ctrl + G f Ctrl + L n Tab (a) . Если вам нравится сочетание клавиш Ctrl + G , вам может быть интересно узнать, что есть несколько других, которые работают аналогичным образом. Например, если вы нажмете Ctrl + U , следующему набираемому символу будет присвоен стиль Пользовательский 1, который вы определили с помощью команды «Определить» в меню «Стиль».Таким образом, вы можете получить доступ к любому символу в любом шрифте всего двумя нажатиями клавиш, даже если он отсутствует в палитрах символов.
Создание сваи

Нажмите Введите . Это создаст новую строку непосредственно под первым выражением, так что теперь у вас есть «стопка», состоящая из двух строк. Должно получиться так:
Выбор слота
Вы можете дважды щелкнуть по слоту, чтобы выбрать его содержимое, или введите Ctrl + Shift + S.
Копирование и вставка в MathType
Чтобы сэкономить время, мы собираемся создать второе выражение, изменив копию первого. Выделите все первое выражение, дважды щелкнув где-нибудь рядом со знаком ≤, скопируйте его в буфер обмена и затем вставьте в новый пустой слот. Теперь у вас должны быть две идентичные копии первого выражения, одна непосредственно под другой. Теперь просто отредактируйте нижнюю копию, чтобы получить второе выражение. Чтобы изменить & Straightphi; От до ψ , выберите & Straightphi; и нажмите Ctrl + G / ⌘ + G , а затем y .
Различное выравнивание
Наконец, мы собираемся поэкспериментировать с разными способами согласования двух выражений. Их можно центрировать или выравнивать по правому краю с помощью команд «Выровнять по центру» и «Выровнять по правому краю» в меню «Формат». Попробуйте, просто чтобы посмотреть, как это выглядит.
Выровнять по =
Фактически, вы, вероятно, захотите выровнять эти два выражения так, чтобы их знаки ≤ находились прямо друг над другом. Для этого мы выбираем команду «Выровнять по =» в меню «Формат».Это будет работать, даже если у нас есть знаки ≤, а не знаки =. Вы можете выровнять выражения другими способами, используя символы выравнивания. Вы просто вставляете символ выравнивания в каждое выражение в двух точках, которые вы хотите выровнять. (Однако символы выравнивания примечаний, вставленные в слоты шаблона, не будут работать.) Размещение символа выравнивания справа от каждого из двух знаков ≤ даст те же результаты, что и использование, например, команды Align at =. Символ выравнивания представлен значком на палитре символов — он находится на палитре.
Что делать, если неравенства по-прежнему не совпадают? Если это произойдет, есть большая вероятность, что вы не выполнили описанные выше шаги, в частности шаг 3. В меню MathType View выберите Show Nesting . Мы упоминали об этом на шаге 3, но здесь есть реальное преимущество; это позволяет вам видеть структуру выражений. Обратите внимание, что в этом случае первое неравенство имеет символ ≤ внутри подынтегральной функции, а второе неравенство нет (немного увеличено для ясности): переместите части выражения за пределы подынтегрального выражения, которые ему не принадлежат, и неравенства должны быть выровнены.
Отрегулируйте межстрочный интервал
Вы также можете настроить межстрочный интервал или интерлиньяж (т. Е. Величину вертикального промежутка между двумя выражениями). Вы можете сделать это, поместив точку вставки где-нибудь во внешнем слоте второго выражения (не внутри шаблона), или выбрав второе выражение и выбрав команду Межстрочный интервал в меню «Формат». Когда вы расположите их по своему вкусу, выражения будут завершены.
Теперь мы закончили с этими выражениями, поэтому пора выбрать «Выделить все» в меню «Правка» и нажать Backspace, чтобы очистить окно для следующего урока.
Простая матрица
В следующем уроке мы проиллюстрируем мощные возможности MathType для компоновки матриц. Построим следующее матричное уравнение:
Матрица довольно проста, и мы сможем очень легко ее создать, используя шаблон матрицы. Если вам нужны более гибкие возможности форматирования для матриц и табличных макетов, вы должны использовать вкладки, как показано в разделе «Форматирование с вкладками».
Начать уравнение
Введите несколько первых членов уравнения до второго знака равенства.MathType распознает, что «det» является сокращением для детерминантной функции, и автоматически установит для нее простой римский шрифт, поэтому вам не придется возиться с ней. Быстрый способ получить λ — нажать Ctrl + G / ⌘ + G , за которым следует буква l (строчная L). Также обратите внимание, что I и A представляют матрицы в нашем уравнении, поэтому мы присвоили им стиль Vector-Matrix. Это заставляет их выделяться жирным шрифтом. Ярлык Ctrl + B назначит стиль Vector-Matrix следующему символу, поэтому вы можете нажать Ctrl + B , затем I , чтобы получить I, и Ctrl + B за ним следует A для A. Кроме того, вы можете просто сначала ввести все символы, а затем выбрать их и изменить их стили с помощью команд в меню «Стиль». В любом случае ваше уравнение должно выглядеть так:
Вертикальные полосы
Введите второй знак = и вставьте шаблон вертикальной полосы, щелкнув значок. Он находится в палитре.
Вставка матрицы 2 × 2
Вставьте матричный шаблон 2 × 2 внутри вертикальных полос, выбрав значок на палитре.Теперь ваше уравнение должно выглядеть так:
Начать ввод содержимого матрицы
Точка вставки будет в верхнем левом слоте матрицы 2 × 2, поэтому введите здесь выражение λ — a ₁₁.
Копирование и вставка матричных элементов
Нам лень, поэтому мы собираемся создать другие записи в матрице путем вырезания и вставки. Выберите λ — a ₁₁, дважды щелкнув по нему, скопируйте его в буфер обмена и вставьте в другие три слота в матрице. Результат должен быть таким, как показано ниже; это, конечно, неправильно, но мы исправим это через несколько минут.
Перетаскивание
Вы также можете перетащить термин в другие слоты. Не забудьте удерживать нажатой клавишу Ctrl / ⌘ при перетаскивании, чтобы скопировать термин.
Добавить отступы
Далее мы собираемся добавить немного дополнительного пространства между вертикальными полосами и элементами матрицы. Это чисто дело вкуса, поэтому вы можете пропустить эту часть, если хотите, чтобы ваша матрица выглядела так, как она есть сейчас.Прежде чем вводить пробелы, нам нужно расположить точку вставки так, чтобы она находилась внутри вертикальных полос, но слева от матрицы и за ее пределами. Вы можете сделать это, щелкнув где-нибудь рядом с позицией, указанной стрелкой на предыдущем рисунке. Затем просто введите один или два тонких промежутка, нажав Ctrl + Пробел / ⌘ + Пробел . Проделайте то же самое с правой частью матрицы. Если вы выберете команду «Показать все» в меню «Просмотр», вы сможете увидеть свои пространства.Они должны выглядеть так:
Исправьте вставленные записи
После краткого отступления от шага 6 пора исправить записи в нашей матрице. Сначала удалите λ из верхнего правого слота. Самый быстрый способ сделать это — поместить точку вставки справа от нее и нажать Backspace . Сделайте то же самое с λ в нижнем левом гнезде. Обратите внимание, что MathType регулирует интервал после знаков минус, чтобы отразить тот факт, что теперь они являются унарными операторами, а не бинарными операторами (отрицание, а не вычитание).
Продолжить исправление записей
Измените все индексы в матрице на желаемые значения. «11» в верхнем левом слоте уже правильная, но у нас должно быть «12» в верхнем правом слоте, «21» в нижнем левом и «22» в нижнем правом. Вы можете дважды щелкнуть существующие индексы, чтобы выбрать их, а затем ввести над ними правильные значения, как в текстовом редакторе.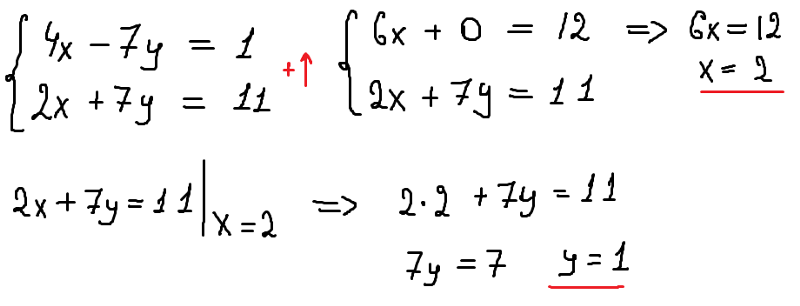 Теперь ваше уравнение должно выглядеть так:
Изменение матрицы
Подменю «Матрица» в меню «Формат» содержит команды для добавления и удаления строк и столбцов.
Почти закончено…
Уравнение теперь практически завершено, хотя есть еще несколько вариантов форматирования, которые вы, возможно, захотите попробовать. Во-первых, вы можете сдвинуть всю матрицу вниз, чтобы ее верхняя строка была выровнена с остальной частью уравнения. Для этого поместите точку вставки в любое место матрицы и выберите «Выровнять по верхнему краю» в меню «Формат». Кроме того, было бы неплохо выровнять записи в каждом столбце по правому краю. Для этого поместите точку вставки где-нибудь в матрице, выберите команду «Изменить матрицу» в подменю «Матрица» в меню «Формат» и нажмите кнопку «Вправо» в диалоговом окне.
Наконец, если вы возражаете против того, что MathType увеличил интервалы после унарных знаков минус, вы можете снова вставить пробелы, хотя это будет означать отклонение от стандартных правил набора текста. Они должны быть толстыми (одна треть em). Толстое пространство является средним во втором ряду палитры пространств и эллипсов. Если вы предпочитаете использовать клавиатуру, вы можете вставить толстый пробел, нажав Ctrl + Shift + Пробел / ⌘ + Shift + Пробел .В качестве альтернативы, поскольку толстое пространство имеет ту же ширину, что и два тонких промежутка, вы можете получить те же результаты, дважды нажав Ctrl + Пробел / ⌘ + Пробел .
Если вы решили внести все изменения, предложенные на этом этапе, ваше уравнение должно выглядеть примерно так:
Если вы переходите к следующему руководству, нажмите Ctrl + Alt / ⌘ + Alt , чтобы выбрать все, затем нажмите Backspace или Delete , чтобы очистить экран.
Нумерация уравнений в Microsoft Word:
• Нумерация и ссылки в основных уравнениях
В этом руководстве описывается, как использовать команды MathType для нумерации уравнений в документах Microsoft Word. Хотя в Word есть собственный метод нумерации уравнений (подписей), Word размещает подписи над или под элементом, а не сбоку, как обычно нумеруются уравнения. Используя команды MathType, добавленные в Word, вы можете вводить встроенные, отображаемые и нумерованные уравнения отображения одним щелчком мыши.
Те же Windows и Mac
Обратите внимание, что описанный здесь процесс одинаков для платформ Windows и Mac. Найдите на вкладке MathType на ленте Word команды, которые мы описываем ниже , если вы не используете Word 2011 для Mac. В этой версии вы можете найти значки на плавающей панели инструментов MathType и команды в меню MathType в строке меню Word. Также, если вы используете Word 2011, обратите внимание на наше предупреждение о MathType и Office 2011.
Мы собираемся создать следующую часть документа, чтобы проиллюстрировать команды нумерации уравнений.
Однако мы собираемся создать его в несколько нереалистичной последовательности, чтобы продемонстрировать мощь и гибкость команд нумерации.
Начать новый документ
Запустите Microsoft Word и создайте новый документ. Введите следующий текст: Теперь у нас есть два основных уравнения:
Вставьте уравнение для отображения с правым номером
Нажмите кнопку на вкладке Word MathType.
Начало главы / раздела
Появится диалоговое окно с вопросом, хотите ли вы создать новый разрыв главы / раздела в начале этого документа.Мы объясним значение этого позже в руководстве. А пока просто нажмите ОК.
Используемые стили Word
Строка, содержащая уравнение, отформатирована с использованием стиля Word MTDisplayEquation, который можно изменить, чтобы повлиять на все уравнения отображения в документе.
Создайте первое уравнение
В открывшемся окне MathType введите следующее уравнение:
Закройте окно MathType. Обратите внимание, что в документе Word уравнение центрировано, а номер уравнения выровнен по правому полю.
Создайте еще одно пронумерованное уравнение
Повторите шаг 3 и вставьте в документ Word следующее уравнение:
Добавить текст
Введите следующий текст в начале следующей строки: Вычитание
Вставьте ссылку на уравнение
Теперь давайте вставим ссылку на второе уравнение отображения. Нажмите кнопку Вставить ссылку на вкладке MathType:
Появится диалоговое окно «Вставить ссылку на уравнение» с краткими инструкциями по вставке ссылки на номер уравнения.Когда вы ознакомитесь с процессом, вы можете щелкнуть поле Больше не показывать . На данный момент щелкните OK, затем дважды щелкните номер уравнения (1.2). Вы увидите, что в ваше предложение вставлено число (1.2).
Ссылки на уравнения
Вы можете быстро перейти к уравнению в документе, дважды щелкнув любую из его ссылок. Затем нажмите Shift + F5, чтобы вернуться к ссылке.
В больших документах попробуйте разделить окно на две части (ищите split в справке Word).Вставьте ссылки в одну панель и прокрутите и дважды щелкните номера формул в другой.
Вы можете разместить ссылки на номера формул в сносках и концевых сносках.
Продолжить ссылку
Введите из , а затем введите ссылку на уравнение (1.1), используя метод, описанный на предыдущем шаге. Вы можете ввести пробел до и после ссылки.
Продолжите с другим пронумерованным уравнением
Тип дает и вставляет следующее нумерованное уравнение дисплея:
Еще текст и еще одна ссылка
В начале следующей строки введите Используя и вставьте ссылку на уравнение (1.3). Завершите строку, набрав , мы можем показать, что
Встроенное уравнение
Нажмите кнопку на вкладке Word MathType и вставьте следующее уравнение:
Обратите внимание, как это уравнение вставлено в строку текста (отсюда и название встроенное уравнение). Word также выравнивает уравнение по базовой линии текста. Ваш документ должен теперь выглядеть так:
Теперь мы вставим другое уравнение в середину этого примера, чтобы продемонстрировать автоматическую перенумерацию.
Подробнее
Поместите точку вставки перед словом Вычитание и введите следующий текст (нажимать введите необязательно): Сложив эти два вместе, мы получим
Другое пронумерованное уравнение
Вставьте это нумерованное уравнение отображения:
Вы увидите, что новое уравнение пронумеровано (1.3), а следующий номер уравнения и его ссылка были изменены на (1.4). Ваш документ должен теперь выглядеть как пример в начале этого руководства.
Номера уравнений
Если вы уже вставили уравнение отображения без номера, вы можете вставить только номер с помощью команды «Вставить номер уравнения».
Если обновление происходит медленно
Если обновление занимает слишком много времени, снимите флажок «Обновлять номера уравнений автоматически» в диалоговом окне «Форматировать номера уравнений». Затем используйте команду «Обновить числа в уравнении», чтобы вручную обновить числа.
Когда вы вставляете номер уравнения или ссылку на уравнение, все числа в документе обновляются.Однако при перемещении или удалении номера уравнения необходимо использовать команду «Обновить номера уравнения» на вкладке MathType для восстановления числовой последовательности. Он находится здесь:
Также имейте в виду, что удаление номера уравнения не приводит к автоматическому удалению каких-либо ссылок на него; вам придется сделать это самому. Их можно найти с помощью команды «Обновить номера формул», в результате чего Word будет отображать сообщение об ошибке вместо каждой ссылки. Затем вы можете удалить их.
Форматы чисел в уравнениях
Вы также можете управлять форматом чисел в уравнениях.Обратите внимание на команду «Форматировать» на предыдущем снимке экрана.
Весь документ
Чтобы изменить формат существующих номеров формул, вы должны установить флажок Целый документ. В противном случае вы устанавливаете формат только для следующего числа, которое вы вставляете.
Форматирование чисел в уравнениях
Выберите команду «Форматировать числа в уравнении» (показано выше). Установите флажок «Весь документ» (чтобы изменить существующие номера) и измените параметр «Встраивание» на <> (угловые скобки).Предварительный просмотр показывает результат ваших настроек. Нажмите OK, и вы увидите, что номера формул и ссылки меняются на новый формат. Вы можете поэкспериментировать с некоторыми настройками — существует множество возможных комбинаций.
Обрыв главы / раздела
Номера разделов . Если вы не хотите, чтобы номера секций включались, вы можете отключить их в диалоговом окне «Формат номеров уравнений».
Формат номера уравнения по умолчанию включает номер раздела и номер уравнения, e.г., (1.1). При необходимости вы также можете указать номер главы. Номера глав и разделов определяются ближайшим предыдущим разрывом главы / раздела в документе. Эти разрывы вставляются и изменяются с помощью команд на вкладке MathType в Word. Мы уже вставили один в начале этого документа как часть вставки первого номера уравнения. Теперь изменим его значение.
Показать разрывы глав / разделов
Вы можете отображать и скрывать разрывы глав / разделов, нажимая кнопку на вкладке Word Home.Это показывает и скрывает стиль MTEquationSection.
Изменить номер раздела на 2
Выберите команду Modify Break на вкладке MathType. Он находится здесь:
Место разрыва раздела будет выделено, и откроется диалоговое окно «Изменить разрыв раздела / раздела». Предположим, мы работаем над Разделом 2 книги, поэтому мы хотим, чтобы номер раздела был 2, а номер уравнения — 1. Нажмите кнопку «Номер раздела:» и введите 2. Опция «Далее» может быть полезной. если ваш документ содержит несколько разделов и вы хотите, чтобы они были пронумерованы последовательно.(Помните, что нет связи между разделами Word и разрывами глав / разделов MathType. Вы можете связать их, разместив разрывы в соответствующих местах в документе). Теперь нажмите ОК. Разрыв главы / раздела будет скрыт, а номера формул в документе будут начинаться с 2.
Если вы выполнили эти шаги, ваш документ должен выглядеть примерно так:
Команды нумерации формул MathType могут также поддерживать три уровня нумерации, например.g., номера главы, раздела и уравнения. Вы также можете контролировать формат чисел и создавать свои собственные форматы. В следующем руководстве показано, как это сделать; мы будем использовать документ, созданный в этом руководстве, поэтому не удаляйте его!
• Расширенная нумерация уравнений
Простой пример нумерации уравнений, показанный в предыдущем руководстве, достаточен для многих документов, но иногда вам может потребоваться создать третий уровень чисел. Например, ваш документ может требовать номеров глав, разделов и формул.Или вы можете обнаружить, что встроенные числовые форматы не соответствуют вашим потребностям, и вы хотите создать собственный числовой формат. В этом руководстве показано, как выполнить обе задачи.
Открыть предыдущий документ
Откройте документ, созданный в предыдущем уроке. Если вы не сохранили его, скачайте наш и используйте его в этом руководстве.
Открыть окно
Форматировать числа уравнения
Откройте диалоговое окно «Формат чисел в уравнениях». Это находится на вкладке MathType в Word в группе Equation Numbers.Щелкните направленный вниз треугольник справа от «Вставить число» и выберите «Формат». (Если вы используете Word 2011 для Mac, команда «Форматировать числа уравнения» находится в меню MathType в Word. Будьте осторожны, чтобы не выбирать команду с таким же названием Форматировать уравнения .)
Откроется диалог:
Включить
Номер главы
Настройки должны выглядеть так, как показано выше. Верхняя группа элементов управляет форматом чисел. Мы хотим добавить номер главы, поэтому установите флажок «Номер главы».Обратите внимание, как превью изменилось на <1.1.1>.
Включить
Весь документ
Убедитесь, что выбран «Весь документ», чтобы внесенные нами изменения применялись к существующим номерам уравнений. Затем нажмите ОК .
Вы заметите, что документ был изменен, и номера формул теперь читаются как <1.2.1>, <1.2.2> и т. Д. Это потому, что разрыв главы / раздела в начале документа устанавливает номер главы равным 1. Это был добавлен в документ, когда мы вставили первый номер уравнения.Представим, что мы хотим сделать это Главой 2.
Открыть диалоговое окно «Изменить разрыв».
Выберите команду Modify Break на вкладке MathType. Он находится здесь:
Вы увидите, что сам разрыв также стал видимым в документе Word. Вот диалог:
Изменить номер главы
Измените значение номера главы на 2 и нажмите OK. Теперь цифры в документе должны выглядеть так: <2.2.1>, <2.2.2> и т. Д.
А теперь попробуем более кардинально изменить формат чисел.Мы установим формат так, чтобы числа читались как Уравнение 2.2.1, Уравнение 2.2.2 и т. Д.
Расширенное форматирование
Выберите команду «Форматировать числа в уравнении», как описано в шаге 2 выше. Установите переключатель «Расширенный формат» и введите Equation # C1. # S1. # E1 в поле Format :. Вы увидите, как изменится предварительный просмотр.
Убедитесь, что выбран «Весь документ», и нажмите ОК. Номера формул в документе следует обновить.
Таким образом вы можете экспериментировать с различными пользовательскими форматами.Синтаксис, используемый для форматов, очень прост: все символы используются буквально, за исключением конструкций #Cx, #Sx и #Ex, где x указывает числовое представление и может быть одним из 1, a, A, i, I.
Быстрый способ научиться управлять форматированием — это нажать кнопку «Простой формат» и затем изменить различные параметры. Текст в расширенном формате по-прежнему отображается и обновляется каждый раз, когда вы вносите изменения во встроенные форматы. Полная информация находится в справке по этому диалогу.
• Нумерация уравнений в длинных документах
В двух предыдущих руководствах содержалась информация, которую вам необходимо знать, чтобы сделать это руководство максимально полезным. Если вы еще не работали с этими руководствами, мы рекомендуем сделать это сейчас, если вы не часто используете нумерованные уравнения и уже знакомы с концепциями.
Сценарий, который мы рассмотрим в этом руководстве, предполагает, что вы работаете над рукописью, состоящей из нескольких глав, каждая из которых содержится в отдельном документе.Ваши уравнения пронумерованы с указанием номера главы и номера уравнения, без номеров разделов или заключительных символов, таких как круглые скобки, например, в этом примере уравнения:
Открыть образцы документов
Для этого урока мы создали 3 документа Word, которые будут главами 1-3 нашей рукописи. Откройте этот файл и распакуйте его в удобное место на вашем компьютере.
Глава 1. Форматирование чисел в уравнениях
Откройте наш образец документа Глава 1.docx и на вкладке Word MathType откройте диалоговое окно Format Equation Numbers . (Напомним, что это вложено в команду Insert Number на вкладке MathType.) Настройте номера формул, как в приведенном выше примере — укажите номер главы, не включайте номер раздела или корпус и используйте одно тире (дефис) как разделитель. Убедитесь, что Изменить формат номера уравнения для параметров применяется к Новые номера уравнений и Весь документ .
Примечание 1: Если вы создаете эти документы самостоятельно, вы, вероятно, захотите также установить для параметра внизу диалогового окна значение Использовать формат по умолчанию для новых документов . В противном случае вам придется проходить этот процесс для каждой главы вашей рукописи.
Примечание 2: Для трех примеров глав, которые вы скачали для этого руководства, мы уже установили формат уравнения для главы 2 и главы 3. Вам не нужно будет делать это снова в этом руководстве.
Глава 1. Вставьте нумерованные уравнения
В Chapter 1.docx ,
вставьте уравнение с правым номером (по вашему выбору) сразу после 2-го абзаца. Помните, что вам не нужно сначала вставлять перевод строки; MathType сделает это за вас.
В диалоговом окне «Вставить номер уравнения » убедитесь, что настройки должны начинаться с главы 1 и раздела 1 (хотя номер раздела не имеет значения).
Теперь вставьте еще одно уравнение с правым номером сразу после первого.Ваш документ должен выглядеть примерно так, конечно, с вашими уравнениями вместо наших:
Для пронумерованных уравнений, которые не отцентрованы между полями:
Возможно, в вашем руководстве по стилю указано положение уравнения, отличное от центра. Возможно, вы не работаете с руководством по стилю, но предпочитаете форму уравнения с отступом 2 см от левого поля. Какой бы ни была причина, по которой вы не хотите, чтобы ваши уравнения центрировались на линии, пожалуйста, не размещайте их вручную.Есть гораздо более простой и элегантный способ сделать это. Правильный способ сделать это — изменить стиль Word MTDisplayEquation. У нас есть статья, описывающая этот стиль и показывающая, как его изменить. Пожалуйста, прочтите эту статью для получения дополнительной информации.
Форматирование уравнения
Когда вы вставляете MathType формула чисел , форматирование чисел будет соответствовать форматированию стиля Word Normal для вашего документа. Если вы изменили текст — шрифт, размер, цвет и т. Д.- при использовании кнопок на вкладке «Главная» в Word вместо использования стилей результаты будут непредсказуемыми, а стиль номеров формул может не соответствовать стилю текста документа. Мы рекомендуем всегда использовать стили для форматирования.
Напротив, когда вы вставляете MathType , уравнения , они будут стилизованы в соответствии с вашими настройками в меню Style и Size MathType (с помощью команды Define в обоих меню). Вы должны явно установить стиль своих уравнений, какой вы хотите.
Глава 2 — Вставить разрыв главы в уравнение
Теперь откройте Chapter 2.docx . Давайте вставим уравнение с правым номером после первого абзаца. Когда вы щелкаете, он не сразу вставляет число и не открывает MathType, как обычно. Первое, что вы увидите, это этот диалог:
Установите номер Начальной главы на 2 . Поскольку мы не используем номера разделов, эта запись не будет иметь значения, поэтому оставим его равным 1. Как только вы нажмете OK, MathType вставит число в документ, и MathType откроется для вас, чтобы создать уравнение.Ваш документ должен выглядеть примерно так:
Если это начинает казаться рутиной, продолжайте читать; у нас есть несколько важных моментов.
Глава 3 — Вставить нумерованное уравнение
Откройте Chapter 3.docx и, ничего больше не делая, вставьте нумерованное уравнение после первого абзаца. Чем вы заметили отличие от включения уравнения во 2-ю главу? Вы не видели диалоговое окно «Вставить номер уравнения»? Это потому, что мы уже вставили в документ разрыв главы.Вы, вероятно, не будете вставлять разрыв главы отдельно, но вы можете , и иногда вам нужно. Так будет, если у вас уже есть уравнения в документе, и вы решили разбить его на несколько глав и / или разделов и хотели бы, чтобы уравнения были пронумерованы соответствующим образом. В этом случае нет необходимости удалять и повторно вставлять номера уравнений. Просто вставьте перерывы там, где они вам нужны.
Вот как мы вставили разрыв в Главу 3 …
Щелкните, чтобы поместить точку вставки (курсор) в начало заголовка главы.Необязательно, чтобы он находился именно в этом месте. Все, что необходимо, это чтобы оно появилось перед первым нумерованным уравнением в главе или разделе. Мы рекомендуем взять за правило ставить разрыв в начале названия. Таким образом вы устраняете проблемы, возникающие, когда вы вставляете разрыв в произвольное место, а затем вставляете другое нумерованное уравнение перед разрывом. Если поставить разрыв в начале названия, этого никогда не произойдет.
На вкладке MathType в Word щелкните Chapters & Sections в группе Equation Numbers .
Щелкните Вставить разрыв .
Установите флажок рядом с Новая глава , щелкните переключатель рядом с номером главы и введите 3 в поле.
Нажмите ОК.
Когда вы это сделаете, вы увидите, что некоторые вещи происходят довольно быстро, но если вы внимательно посмотрите, вы, вероятно, увидите красный текст, вставленный перед названием главы, а затем он исчезнет.Посмотрим, из чего состоит этот скрытый текст. На вкладке «Главная страница» Word нажмите кнопку Показать / скрыть :. Когда вы это сделаете, вы увидите это:
Объединение глав в единый документ
Пришло время объединить несколько документов нашей рукописи в один документ. Мы можем сделать это с помощью копирования и вставки, но это еще не все.
Мы не будем работать с оригиналом, поэтому создадим новый документ Word.Если в вашей рукописи используется специальный шаблон, естественно, вы захотите использовать тот же шаблон для объединения документов. В случае с нашими примерами документов все они основаны на шаблоне Normal, поэтому достаточно просто щелкнуть File> New (или использовать ярлык).
Если вы щелкнули «Показать / скрыть» в предыдущем разделе, вероятно, он все еще активен, и вы должны увидеть знак абзаца (черта) в документе. Если вы этого не видите, щелкните Показать / Скрыть.
Откройте главу 1, если она еще не открыта.Если вы не видите скрытых меток и текста, щелкните Показать / Скрыть. Это должно выглядеть примерно так:
Выделите все содержимое документа. Самый простой и лучший способ сделать это — использовать сочетание клавиш Ctrl + A (Windows) или Command + A (Mac).
Скопируйте выделенный текст.
Переключитесь на новый документ, созданный на шаге 1, и вставьте скопированный текст в этот документ. Не перемещайте точку вставки (курсор). Он должен продолжать мигать как раз перед последней чертой в конце документа.
Повторите шаги с 3 по 6 для главы 2 и главы 3.
Если вы предпочитаете отключать метки форматирования, вы можете нажать «Показать / Скрыть», чтобы скрыть их. Теперь ваш объединенный документ должен включать главы с 1 по 3, а уравнения должны быть последовательно пронумерованы.
Настройка документа Microsoft Word
При создании документа Microsoft Word, содержащего уравнения, следует учитывать несколько моментов.Вы, вероятно, захотите, чтобы основной текст соответствовал уравнениям с точки зрения шрифтов и размеров, и вы, как правило, хотите, чтобы все уравнения в документе использовали согласованное форматирование, то есть одинаковые настройки шрифта и размера, а также любые другие специальные настройки. вы, возможно, сделали в MathType.
Стили Word
Если вы не знакомы со стилями Word, мы настоятельно рекомендуем вам потратить несколько минут, чтобы узнать, как их использовать. В справке Word найдите стили.
Хотя Word и MathType позволяют напрямую выделять текст и изменять его шрифты и размеры, мы настоятельно рекомендуем вместо этого использовать стили.Обе программы используют этот подход, потому что он позволяет очень легко изменить внешний вид документа или уравнения. Вы просто меняете определение стиля (например, с Times New Roman на Arial или с обычного шрифта с 12 пт на курсив 10 пт), и ваш документ или формула немедленно переформатируются с новыми настройками.
Предположим, вам необходимо создать документ, в котором основной шрифт — Times New Roman 10 пунктов. Первым шагом является определение настроек MathType для соответствия документу Word.
Открыть диалоговое окно «Определить стили
» MathType
В MathType откройте диалоговое окно «Определение стилей» и установите в качестве основного шрифта Times New Roman, используя простую или расширенную панель.Убедитесь, что установлен флажок «Использовать для новых уравнений», и нажмите «ОК».
Заводские настройки
Нажмите «Заводские настройки», чтобы сбросить значения на шрифт Times New Roman, 12 пунктов.
Открыть диалоговое окно «Определить размеры
» в MathType
Откройте диалоговое окно «Определение размеров» и установите для параметра «Полный размер» значение 10 пунктов. Поскольку другие измерения по умолчанию выражаются в процентах, MathType рассчитает их за вас. Снова отметьте опцию «Использовать для новых уравнений» и нажмите OK.
Настройки уравнения
Определения всех стилей, размеров и интервалов, используемых в уравнении, вместе называются «предпочтениями уравнения». См. Подменю Equation Preferences для получения более подробной информации.
Прикрепите настройки уравнения к документу Word
Вернувшись в Word, выберите команду Equation Preferences в группе Format на вкладке MathType. Убедитесь, что выбран параметр «MathType’s ‘New Equation’». Это означает, что всякий раз, когда вы создаете новое уравнение с помощью команд в группе «Вставить уравнения», настройки MathType, которые в настоящее время заданы для использования для новых уравнений, являются теми, которые будут использоваться.Щелкните ОК, чтобы закрыть это диалоговое окно.
Примечание:
Вы не можете всегда захотеть полагаться на предпочтения MathType «Новое уравнение». Если вы часто меняете определения размера и стиля MathType, вы можете создать файл настроек MathType, а затем выбрать этот файл в диалоговом окне «Установить настройки уравнения». Это скопирует настройки файла в ваш документ Word, так что независимо от того, какие изменения вы вносите в MathType, уравнения, созданные в вашем документе, всегда будут использовать эти настройки.
Создайте новый стиль
Теперь мы быстро создадим стиль Word для тела документа. Если вы используете Mac, см. Ниже, но , если вы используете Windows, щелкните панель запуска диалогового окна в правом нижнем углу группы стилей на вкладке Главная:
В нижнем левом углу диалогового окна Стили нажмите Новый стиль:
Если вы используете Mac, щелкните Панель стилей на вкладке Главная:. Теперь нажмите кнопку New Style .
И Windows, и Mac: в диалоговом окне Создать новый стиль из форматирования (Mac: Новый стиль ) назовите новый стиль «body». Вы, вероятно, основываете его на встроенном в Word обычном стиле. Установите шрифт нового стиля Times New Roman 10pt, сделав соответствующий выбор в разделе «Форматирование» диалогового окна. Пока не нажимайте ОК.
Параметры абзаца
Откройте список Format в нижнем левом углу диалогового окна.Выберите Абзац. На вкладке Отступы и интервалы диалогового окна измените параметр Межстрочный интервал на Одинарный. Щелкните ОК, чтобы закрыть диалоговое окно.
Закройте диалоги
Нажмите OK, чтобы закрыть диалоговое окно «Новый стиль», а затем нажмите X (Windows) или красный «стоп-сигнал» (Mac), чтобы закрыть диалоговое окно «Стили», если оно не закреплено, или нажмите X, чтобы закрыть панель «Стили», если оно закреплено.
Теперь вы настроили Word и MathType для использования тех же определений шрифта и размера, что сделает уравнения максимально похожими на внешний вид остальной части документа.Вперед, введите пару строк текста и вставьте простое уравнение.
Теперь предположим, что вам нужно изменить шрифт документа на Garamond. Чтобы не усложнять этот пример, мы не будем изменять размер точки, но вы бы выполнили те же действия, если бы это было так.
Вот те изменения, которые нам нужно внести:
Измените стиль «тела» Word, чтобы использовать Garamond вместо Times New Roman.
Измените стили MathType, чтобы использовать Garamond вместо Times New Roman.
Обновите существующие уравнения в документе, чтобы использовать новый шрифт.
Первые два шага очень похожи на то, как мы изначально создавали стили и добавляли их в документ Word, поэтому мы не будем их подробно рассматривать. Первый шаг включает использование диалогового окна «Стиль» Word (щелкните правой кнопкой мыши «Тело» в группе «Стили» и выберите «Изменить»), для второго шага потребуется диалоговое окно «Определить стили» MathType.
Третий шаг включает команду «Форматировать уравнения» на вкладке MathType на ленте Word.
Открыть
Форматировать уравнения диалоговое окно
Выберите команду «Форматировать уравнения», откроется диалоговое окно «Форматировать уравнения». Это диалоговое окно позволяет вам переформатировать уравнения в документе и предоставляет несколько способов определения применяемых предпочтений уравнения. Возможны следующие варианты:
Предпочтения уравнения уже сохранены в этом документе.
Текущие настройки уравнения MathType для новых уравнений.
Параметры уравнения, содержащиеся в уравнении MathType, которое вы скопировали в буфер обмена.
Параметры уравнения, содержащиеся в файле предпочтений MathType.
В этом примере нажмите кнопку «Настройки MathType ‘New Equation’». Вы можете нажать Preview, чтобы получить список фактических предпочтений.
Дополнительные сведения о других параметрах см. В диалоговом окне «Установить параметры уравнения».
Начать форматирование уравнения
Нажмите ОК, и начнется процесс форматирования.Это может занять от нескольких секунд до нескольких минут в зависимости от скорости вашего компьютера и количества уравнений в вашем документе. Ход выполнения команды отображается в строке состояния Word. По завершении операции убедитесь, что уравнения были обновлены.
Форматирование с вкладками
В этом примере мы покажем вам, как система вкладок MathType обеспечивает дополнительную гибкость для форматирования уравнений. Мы собираемся создать уравнение:
а затем отформатируйте его несколькими способами.Действуем следующим образом:
Создайте левую часть уравнения
Создайте выражение слева от знака равенства. Как вы уже знаете, вы можете выбрать шаблон или нажать Ctrl + L / ⌘ + L , чтобы прикрепить нижний индекс к c .
Добавить одинарную левую скобку
Выберите шаблон из палитры, чтобы вставить раскрывающуюся левую скобку. Теперь у вас должно быть следующее:
Введите «кусок» # 1
Введите верхнее выражение в фигурной скобке до x включительно, а затем нажмите Ctrl + Tab (нажмите клавишу Tab , удерживая нажатой клавишу Ctrl , Mac или Windows).Если вы нажмете только клавишу Tab , это переместит точку вставки, а не вставит символ табуляции.
Выбор стилей
Другой способ выбрать стиль — это щелкнуть правой кнопкой мыши на панели «Стиль» в строке состояния и выбрать стиль из появившегося контекстного меню.
Введите первое условие
Выберите стиль текста в меню «Стиль» и введите , если n равно . Пока вы используете текстовый стиль, пробел активен, поэтому вы можете вводить пробелы так же, как в текстовом редакторе.Выберите «Показать все» в меню «Просмотр», если он еще не отмечен, чтобы вы могли видеть свой символ табуляции, который отображается в виде небольшого ромба. Кроме того, выберите «Линейка» в меню «Вид», если она еще не отмечена. Ваше уравнение должно выглядеть так:
Обратите внимание, что символ табуляции приводит к тому, что фраза «когда n четно» выстраивается под первой по умолчанию табуляцией справа от x . Позиции табуляции по умолчанию (обозначенные маленькими перевернутыми буквами Ts вдоль шкалы линейки) расположены с полудюймовыми интервалами, начиная с левой стороны текущего слота.Поскольку в настоящее время мы находимся в основном слоте шаблона, интервалы в полдюйма измеряются от левого края этого слота, то есть чуть левее.
Линейки
По умолчанию единицы измерения деления линейки — дюймы. Если вы предпочитаете работать в сантиметрах, точках или пиках, дважды щелкните панель линейки , чтобы открыть диалоговое окно «Единицы измерения линейки». Выберите единицы линейки и нажмите OK.
Введите вторую часть функции
Нажмите Введите , чтобы начать новую строку под первой, и введите ее содержимое.Вы должны вернуться к математическому стилю и ввести 14,3x . Вставьте символ табуляции ( Ctrl + Tab ) после x , как в первой строке. Теперь снова вернитесь к тексту и введите , если n нечетное . Теперь у нас есть:
Опять же, текстовая фраза выравнивается по первой позиции табуляции по умолчанию справа от x . Обратите внимание, что вы создали в шаблоне двухстрочный ворс. Каждая стопка в MathType имеет свои позиции табуляции.
Изменить
n на математический
Выберите n в первой строке и выберите Math в меню Style.Это заставляет MathType интерпретировать n как математическую величину (т. Е. Переменную) и поэтому применяет стиль Variable (обычно курсив). Проделайте то же самое с n во второй строке.
Установить позицию табуляции
Поместите точку вставки где-нибудь в пределах одной из двух линий в правой части уравнения, щелкните область табуляции, а затем щелкните панель табуляции на линейке примерно на отметке 1½ дюйма, чтобы установить левую позицию табуляции. Это удалит все позиции табуляции по умолчанию слева от новой позиции табуляции.Теперь ваше уравнение должно быть выровнено следующим образом:
Если мы хотим, чтобы уравнение было отформатировано таким образом, то наша работа завершена. Однако есть несколько других вариантов, которые стоит изучить.
Совместите две линии на
x
Сначала мы собираемся выровнять x в 2 линиях. Вставьте символ табуляции ( Ctrl + Tab ) в начале каждой из двух строк. Это приведет к смещению каждой строки так, чтобы ее левая сторона выровнялась с левой табуляцией.Текстовая фраза в каждой строке, поскольку она разделена другим символом табуляции, будет выровнена с первой доступной табуляцией по умолчанию справа от x .
Выровняйте переменную
x
Затем щелкните вкладку, а затем щелкните линейку слева от предыдущей позиции табуляции. Это должно дать следующие результаты:
Теперь вы можете легко изменить форматирование, просто перетащив табуляторы на панель вкладок линейки.
Совместите две линии с десятичными знаками
Теперь мы собираемся выровнять две десятичные точки. Чтобы подготовиться к этому, сначала удалите, перетащив его вниз от линейки, а затем отпустив кнопку мыши. Щелкните углубление для табуляции, а затем щелкните линейку на отметке в один дюйм, чтобы установить десятичную позицию табуляции. Ваше уравнение должно выглядеть так:
Это все для этого урока, поэтому удалите свое уравнение, чтобы быть готовым к следующему уроку.
Вставка символов, которых нет на палитрах
В этом руководстве вы узнаете, как использовать диалоговое окно «Вставить символ» в MathType, чтобы находить и использовать символы, которые не всегда доступны во встроенных палитрах.Предположим, например, что вы собираетесь написать документ о некоторых недавно изобретенных операциях над множествами, которые аналогичны обычным объединениям и пересечениям. Вы захотите найти символы для представления ваших новых операций над множеством, и было бы неплохо, если бы они были похожи на обычные символы ∪ и ∩. Ваша первая попытка может заключаться в использовании полужирных версий обычных символов для представления ваших новых операций, например:
К сожалению, жирные символы слишком похожи на обычные, поэтому мы постараемся найти лучшее решение.
Создайте уравнения
Создайте уравнения, как показано выше.
Открыть диалоговое окно
Вставить символ
В меню «Правка» MathType выберите «Вставить символ». Появится следующий диалог:
Это диалоговое окно в некоторой степени похоже на диалоговое окно Microsoft Word, приложения «Карта символов Windows» и средства просмотра символов Mac, по крайней мере, один из которых вы, возможно, уже знаете, как использовать.
Вы можете использовать диалоговое окно «Вставить символ», чтобы просмотреть все шрифты, доступные на вашем компьютере, и выяснить, знает ли MathType о них.В частности, вы можете:
Вставьте в уравнение определенный символ или математический символ.
Добавить часто используемый символ на панель инструментов.
Добавьте сочетание клавиш для часто используемого символа.
Найдите символ, сопоставив слова в его описании.
Символ шрифт
Первое место, где нужно искать пригодные для использования символы, — это шрифт Symbol, поэтому выберите Symbol из списка шрифтов в верхней части диалогового окна Insert Symbol.Быстрый способ найти шрифт — щелкнуть список, а затем ввести первую или две буквы имени шрифта. Выбрав нужный шрифт, вы можете прокручивать большую сетку символов в центре диалогового окна в поисках потенциальных клиентов.
Отображение большего символа
Чтобы увеличить символы в диалоговом окне «Вставить символ», выберите «Настройки рабочего пространства» в меню «Настройки» MathType и установите для размера панели инструментов значение «Средний» или «Большой».
Другие символьные шрифты
Вы также можете посмотреть шрифты Euclid Symbol и Wingdings.Обратите внимание, что в диалоговом окне «Вставить символ» сообщается, что символ и символ Евклида имеют одинаковую «кодировку» (расположение символов). Итак, если вы не найдете нужных символов в одном из этих двух шрифтов, вы не найдете их и в другом.
Найдите символ
Диалоговое окно «Вставить символ» на самом деле предоставляет более интеллектуальный способ поиска нужных символов, а не просто просмотр шрифтов. В поле Просмотр по выберите Описание. Нажмите кнопку «Новый поиск», введите слово union и нажмите «ОК».Сетка символов теперь покажет вам несколько символов, подобных объединению.
Когда их слишком много, чтобы показать
В диалоговом окне «Вставить символ» снимите флажок «Показать по одному», чтобы увидеть все символы на вашем компьютере, о которых знает MathType, и имена которых содержат слово «объединение». В зависимости от того, какие шрифты вы установили, таких символов может быть несколько десятков. Если вас ошеломило огромное количество показанных символов, нажмите «Показать по одному», чтобы уменьшить количество.Это заставляет диалоговое окно отображать только один символ (из первого шрифта, который его содержит) для каждого описания, соответствующего критериям поиска.
Найдите подходящий символ для соединения
Щелкните несколько многообещающих символов объединения, чтобы узнать, что MathType может рассказать вам о них. Помимо прочего, MathType предоставит вам описание символа, шрифт, в котором он был найден, и соответствующее нажатие клавиши.
Попробуйте символ двойного союза
Один из символов, который вы должны увидеть, взят из шрифта Euclid Math Two.Предположим, мы хотим использовать это, если мы можем найти соответствующий символ для пересечения.
Теперь подходящий символ для перекрестка
Используя описанные выше методы, найдите символы, в названии которых есть слово «пересечение». Вы должны найти, опять же, шрифт Euclid Math Two.
Переключить шрифты
В списке «Просмотр по» выберите «Шрифт», затем выберите «Евклид Математический 2» из списка шрифтов в верхней части диалогового окна «Вставить символ». Прокрутите вниз до нижней части таблицы символов, пока не увидите символы и.Рядом в таблице символов вы увидите квадратные символы объединения и пересечения, а также. Наш поиск не нашел их, потому что их имена получены из стандарта Unicode, который называет их «квадратная чашка» и «квадратная крышка» соответственно.
Сочетания клавиш
Диалоговое окно «Вставить символ» позволяет назначить сочетание клавиш для любого символа любого шрифта.
Сохраните новые символы на панели инструментов
Вы можете нажать «Вставить», чтобы вставить символы непосредственно из диалогового окна «Вставить символ».Однако, если вы собираетесь использовать их неоднократно, вам нужно разместить их на одной из панелей MathType для облегчения доступа. Нажмите и удерживайте Alt (Mac: ⌘ ) и перетащите символ из сетки в диалоговом окне «Вставить символ» на маленькую полосу. Затем проделайте то же самое с символом. См. Раздел Использование панели инструментов MathType для получения дополнительной информации о работе с панелями инструментов MathType.
Теперь используйте новые символы
Измените свои уравнения, чтобы использовать новые символы:
MathType знает все о шрифте Euclid Math Two, поэтому он понимает, что символы и являются бинарными операторами, как ∪ и ∩, и автоматически устанавливает правильный интервал вокруг них.Если вы используете символы из более непонятных шрифтов, вам придется предпринять несколько дополнительных шагов, чтобы этот автоматический интервал заработал. Чтобы узнать больше о знаниях MathType о шрифтах и о том, как их расширить, см. Добавление к знаниям о шрифтах и символах MathType.
Настройка клавиатуры
MathType имеет встроенные сочетания клавиш для многих своих команд, а также наиболее часто используемые символы и шаблоны. Однако вы можете изменить любой из ярлыков MathType, а также можете назначить свои собственные ярлыки для любых элементов, которые вы размещаете на панели инструментов.См. Сочетания клавиш для получения полного списка встроенных сочетаний клавиш.
Наблюдать за строкой состояния Когда вы наводите указатель мыши на элементы на палитрах, в строке состояния MathType — в самом низу окна MathType — отображается краткое описание текущего элемента, включая его сочетание клавиш, если оно было определено.
Мы начнем с определения ярлыка для шаблона, у которого его еще нет.
Использование одного и того же шаблона несколько раз
Предположим, вам нужно создать несколько уравнений, включающих шаблон (открытые скобки).MathType не определяет ярлык для этого шаблона. Чтобы назначить его, сначала выберите команду «Настроить клавиатуру» в меню «Настройки».
Настройка клавиатуры диалоговое окно
Появится диалоговое окно «Настроить клавиатуру». Панель под названием «Команда»: содержит иерархический список всех команд MathType, которым можно назначить сочетания клавиш. Мы хотим назначить один элемент панели инструментов, поэтому щелкните значок + рядом с категорией «Команды панели инструментов». Список с отступом появится под командами панели инструментов.Нажмите на + рядом с шаблонами в этом списке, а затем на + рядом с шаблонами ограждений.
Найти
Раскрыть скобки
Выберите Открытые скобки (obrack) из списка (возможно, вам придется прокрутить список немного вниз, чтобы этот элемент появился).
Шаблон появится на панели рядом с описанием, чтобы вы могли подтвердить, что выбрали правильный шаблон.
Ярлыки
Щелкните внутри текстового поля с надписью «Введите новые сочетания клавиш».
Создать ярлык
Введите Ctrl + T , затем [. Обратите внимание, что под полем появляется сообщение о том, что этот ярлык уже назначен команде «Левая скобка». Если бы мы назначили эту комбинацию шаблону «Открытые скобки», она была бы удалена из команды «Левая скобка». При назначении новых ярлыков всегда проверяйте, не перезаписали ли вы случайно существующий ярлык.
Несколько ярлыков
Вы можете назначить более одного ярлыка для одного символа, шаблона или команды меню, если хотите.
Назначьте другой ярлык
Один раз нажмите клавишу Backspace и введите Alt + [. На этот раз нет текущего задания. Теперь нажмите кнопку «Назначить», и вы увидите, что ярлык появится в списке «Текущие ключи», а также добавлен к элементу «Открытые скобки» в списке команд.
Попробуйте ярлык
Щелкните Закрыть, чтобы закрыть диалоговое окно, затем введите Ctrl + T , а затем Alt + [.Вы увидите, что шаблон открытых скобок появится в окне уравнения.
Настроить клавиатуру
Диалоговое окно «Настроить клавиатуру» позволяет сбросить для ярлыка команды значение по умолчанию, выбрав его и нажав «Сбросить выделение». Нажмите «Сбросить все», чтобы сбросить ярлыки каждой команды к исходным настройкам.
Поскольку в MathType доступно так много команд, поддерживаются как одноклавишные, так и двухклавишные сочетания клавиш. MathType определяет ярлыки для многих шаблонов, используя форму Ctrl + T , за которой следует другой символ, поэтому мы использовали именно эту комбинацию.Конечно, вы можете определять свои собственные схемы по своему усмотрению.
Сочетания двух клавиш
Когда MathType отображает сочетание клавиш с двумя клавишами, оно будет в виде первой клавиши, запятой и второй клавиши. Для ярлыка, созданного на шаге 7 выше, мы бы показали, что как Ctrl + T , Alt + [. Другими распространенными двухклавишными сочетаниями клавиш являются греческие буквы: Ctrl + G , A для букв нижнего регистра или Ctrl + G , Shift + S для заглавной сигмы, например.С того момента, как вы отпустите первую клавишу или комбинацию клавиш, у вас будет четыре секунды, чтобы нажать вторую клавишу или комбинацию клавиш.
Назначение ярлыка выражению панели инструментов
Пользовательские элементы панели инструментов
Убедитесь, что небольшая панель с вкладками видна, и щелкните вкладку «Алгебра». Мы собираемся назначить ярлык для выражения, которое должно быть последним элементом на панели, если вы не изменили содержимое.
Свойства выражения диалоговое окно
Щелкните элемент правой кнопкой мыши и выберите команду «Свойства» (Mac: свойства выражения) в появившемся контекстном меню.В открывшемся диалоговом окне «Свойства выражения» (Mac: Свойства шаблона) вы увидите те же элементы сочетания клавиш, которые мы видели в диалоговом окне «Настройка клавиатуры».
Введите ярлык
Введите для этого выражения ярлык Alt + R и закройте диалоговое окно.
Попробуйте ярлык
Введите Alt + R , и он будет вставлен в окно уравнения.
Мы могли бы назначить ярлык для этого выражения с помощью диалогового окна «Настройка клавиатуры», но для поиска команды нужно было бы щелкнуть «Команды панели инструментов», «Вкладки», «Вкладка 1», «Маленькая полоса», «Выражение 14».Щелчок правой кнопкой мыши по выражению выполняется намного быстрее!
Работа с TeX, LaTeX и MathML
В этом руководстве вы узнаете, как преобразовать уравнения MathType в текстовые языки разметки, такие как TeX, LaTeX и MathML. Наше основное внимание будет уделено LaTeX, но методы для других языков очень похожи.
Мы предполагаем, что при создании документа LaTeX вы будете запускать MathType одновременно с вашей обычной системой TeX.
Ни процессор TeX, ни редактор TeX / MathML.
MathType использует систему трансляторов для преобразования уравнения MathType в код TeX / LaTeX / MathML.Он не создает полный документ TeX и не является редактором TeX или MathML. Как и в случае с устными языками, каждый раз, когда требуется перевод, существует риск того, что что-то будет переведено неоптимально или, возможно, даже неправильно. Если вы столкнетесь с подобными случаями, сообщите нам об этом по электронной почте в наш отдел технической поддержки.
Предположим, вы хотите создать следующий абзац в своем документе LaTeX:
Вот как это сделать:
Начало документа
Введите в квадратную формулу в текстовом редакторе или системе TeX.
Открыть MathType
Запустите MathType, выбрав его из меню «Пуск», меню «Программы», папки «Приложения» и т. Д. (Другими словами, не запускайте его, открывая его из Word, Pages или другого приложения).
Параметры вырезания и копирования диалоговое окно
В меню настроек MathType выберите Настройки вырезания и копирования . В появившемся диалоговом окне установите параметры, как показано ниже, а затем нажмите OK.
Типовая формула
Создайте квадратную формулу в MathType.{2} — 4ac}}} {{2a}} \]
Если вы знакомы с LaTeX, вы узнаете в нем исходный код LaTeX для формулы квадратичного уравнения.
Продолжить ввод текста документа
Продолжайте вводить дискриминант , затем снова переключитесь на MathType.
Другое выражение MathType
Создайте дискриминантный термин.
Встроенное уравнение
В меню Формат MathType выберите Inline Equation .{2} — 4ac} $ — самый важный термин.
Опции переводчика
Во многих ситуациях полезно иметь возможность переносить старые уравнения из документа TeX обратно в MathType для редактирования или повторного использования. Обычно это возможно, независимо от того, были ли уравнения изначально созданы в MathType или нет. Однако, если вы создаете уравнения TeX с помощью MathType и есть вероятность, что вам или кому-то еще может понадобиться перевести их обратно в MathType в будущем, полезно ознакомиться с параметрами переводчика.
Чтобы понять этот подход, выберите «Вырезать и скопировать настройки» в меню «Настройки MathType» и установить флажок «Включить данные MathType в перевод». Теперь снова создайте квадратную формулу, скопируйте и вставьте ее в текстовый документ. 2} — 4ac}}} {{2a}} \]
Первые девять строк текста (те, которые начинаются со знака%) — это комментарий TeX, содержащий собственное частное представление MathType вашего уравнения.Вы должны выбрать этот комментарий, когда вставляете его обратно в MathType, чтобы он был точно преобразован обратно в обычное уравнение MathType. Если вы каким-либо образом измените комментарий, возврат в MathType не состоится. Комментарии TeX игнорируются в процессе набора, поэтому они не повлияют на ваш окончательный результат.
Что не вошло в перевод?
Обратите внимание: если вы скопируете только код TeX и вставите его в MathType (без данных MathType), уравнение обычно будет отображаться нормально.Но предположим, что вы скопировали это уравнение из документа Word для перевода в TeX, и теперь вы хотите вставить его обратно в MathType для использования в PowerPoint. MathType допускает множество корректировок внешнего вида уравнения, которые не переносятся в перевод TeX. Если вы внесли изменения в цвет уравнения, начертание шрифта, размер шрифта или некоторые корректировки интервалов, они не появятся в коде TeX, но будут сохранены в коде MathType. Следовательно, сохранение кода MathType вместе с уравнением гарантирует, что вы сможете вставить уравнение обратно в MathType точно так, как оно было при первоначальном создании.
В диалоговом окне MathType «Параметры вырезания и копирования» также есть опция «Включить имя переводчика в перевод», которая помогает очерчивать и идентифицировать уравнения в ваших документах. Это может быть полезно, если вы хотите писать программы, которые ищут в ваших исходных файлах TeX уравнения и обрабатывают их каким-либо образом.
Другие переводчики
MathType включает переводчики для нескольких диалектов TeX (Plain TeX, AMS-TeX, LaTeX и AMS-LaTeX). Эти диалекты соответствуют различным пакетам макросов TeX, которые вы должны загрузить перед набором документа.Например, чтобы набрать код AMS-LaTeX, вы должны включить команды \ documentclass {amsart} или \ usepackage {amsmath} или их эквивалент где-нибудь в преамбуле вашего документа. Пожалуйста, обратитесь к документации TeX или LaTeX для получения более подробной информации.
Википедия и многие другие блоги, вики и веб-сайты представляют математику на языке под названием Texvc, который, по сути, является подмножеством математики TeX. MathType включает переводчик Texvc, настроенный для использования с Википедией, и второй общий переводчик Texvc, который работает со многими другими сайтами, использующими TeX.Поскольку Texvc несколько проще, чем другие диалекты TeX, один из этих переводчиков часто является хорошим выбором, если вы будете редактировать уравнение вручную. MathType имеет функцию Toggle TeX, которая позволяет переключаться между видами Texvc и MathType уравнения в Microsoft Word.
MathType также включает переводчики для использования MathType с рядом других приложений и веб-сайтов, включая Maple, Mathematica, Physics Forum, Wikipedia и Wolfram | Alpha. Ищите эти приложения по имени в разделе Equation for application или на веб-сайте диалогового окна.
Список доступных переводчиков постоянно растет. См. Раздел Использование MathType с приложениями и веб-сайтами для получения дополнительной информации.
MathML
Мы также поставляем переводчики для MathML, языка разметки на основе XML (расширяемого языка разметки) для кодирования математики. Текущая версия MathML — MathML 3.0, но у MathType пока нет переводчиков для дополнительных возможностей, предоставляемых MathML 3. MathType поставляется с тремя трансляторами MathML 2.0, которые отличаются только пространством имен, в котором размещен MathML.Какой из них выбрать, определяется используемым средством визуализации MathML — либо добавленным инструментом визуализации (например, MathJax), либо браузером со встроенной поддержкой MathML (Firefox и, в меньшей степени, Safari и, возможно, другие).
Создание и изменение переводчиков
Если наши стандартные переводчики не соответствуют вашим потребностям, вы можете изменить одного из них или написать новый собственный. Каждый переводчик управляется файлом перевода, написанным на нашем языке определения переводчика (TDL).Вы найдете несколько файлов TDL в папке «Переводчики» MathType, и вы можете отредактировать их в соответствии со своими потребностями или написать совершенно новые.
Экспорт уравнений в Microsoft Word
В этом руководстве мы покажем вам, как экспортировать все уравнения в документе Word в отдельные графические файлы. Вы можете экспортировать их как файлы GIF, EPS, WMF, PICT (Mac) или PDF (Mac), а также управлять расположением и именами файлов. У вас также есть возможность заменить каждое уравнение именем соответствующего файла.Эта функция может быть полезна при импорте документов Word в программы настольных издательских систем. Некоторое программное обеспечение не очень хорошо импортирует встроенные уравнения, предпочитая отдельные файлы уравнений. Команда «Экспорт уравнений» значительно упрощает этот процесс.
Запустите Microsoft Word
Запустите Word и создайте документ, содержащий пару уравнений.
Экспорт уравнений диалоговое окно
Выберите команду «Экспорт уравнений» в меню Word MathType или в группе «Опубликовать» на вкладке MathType Word.Появится диалоговое окно «Экспорт уравнений».
Куда сохранять изображения?
Введите местоположение в поле «Папка». Вы можете ввести имя папки или нажать кнопку «Обзор» и выбрать папку. Если вы введете имя несуществующей папки, вас спросят, хотите ли вы ее создать. Установите флажок «Удалить все файлы одного типа в папке», если вы хотите, чтобы все файлы с одинаковым расширением были удалены из этой папки перед экспортом. Будьте осторожны, выбирая этот вариант; если вы экспортируете как файлы GIF в папку C: \ My Documents, то все файлы GIF в этой папке будут удалены.Обычно безопаснее создать новую папку для каждого набора экспортируемых файлов уравнений.
Какой формат изображения?
Выберите формат экспортируемых файлов уравнений. Вы также можете установить шаблон имени файла и начальный номер. В приведенном выше примере будут созданы файлы Eqn001.gif, Eqn002.gif и т. Д. Установка шаблона на «PhysIntro ###» и первое число 50 создаст файлы PhysIntro050.eps, PhysIntro051.eps и т. Д. Вы можете захотеть экспериментируйте с разными узорами и числами.
Заменить уравнение именем файла
Установите флажок «Заменить уравнение именем файла», если вы хотите заменить каждое уравнение, экспортированное из документа, соответствующим именем файла. Например, указанные выше настройки вставят текст << Eqn001.gif >> вместо первого экспортированного уравнения. Снимите этот флажок, если вы хотите оставить уравнения в документе без изменений.
«Весь документ»?
Выберите вариант «Весь документ», если вы хотите экспортировать все уравнения в документе.Параметр «Текущий выбор» доступен только в том случае, если вы выбираете часть документа перед запуском команды «Экспорт уравнений».
Экспорт уравнений
Щелкните OK, чтобы начать процесс экспорта. Когда процесс будет завершен, появится диалоговое окно, показывающее, сколько уравнений было экспортировано.
Упрощение рациональных выражений путем деления общих множителей
Довольно часто в математике необходимо разметить член в выражении, чтобы показать заимствование в задаче на вычитание, разделить общие множители в рациональном выражении и т. Д.С карандашом и бумагой выполнить такое «зачеркивание» — нетрудно, но когда вы пишете документ в текстовом редакторе, это другое дело. В этом руководстве показано, как создавать такие аннотации с помощью MathType. Предположим, вы готовите рабочий лист, показывающий, как упростить рациональное выражение:
Мы хотим показать студентам, как разделить общие факторы, поэтому воспользуемся зачеркнутыми шаблонами MathType.
Начать уравнение
Создайте первую дробь, показанную выше, затем введите = и вставьте второй шаблон дроби:
Зачеркнутый шаблон
Перед вводом числителя выберите шаблон «Зачеркнутый (нижний левый верхний правый)» из палитры шаблонов «Нижняя и верхняя полосы»:
Введите выражение внутри зачеркнутого шаблона
Внутри зачеркнутого шаблона введите первый множитель в числителе.Нажмите Tab, чтобы выйти из зачеркнутого шаблона, затем введите второй фактор:
Толщина зачеркивания
Если линия зачеркивания недостаточно отчетлива при ее печати или проецировании, вы можете увеличить ее толщину. В меню «Формат» выберите «Определить интервал». Прокрутите вниз в самом низу списка, пока не найдете Толщина зачеркивания. Увеличьте толщину до значения, при котором штриховка будет более яркой. Нет необходимости нажимать «Применить» перед тем, как нажать «ОК», но это позволит вам попробовать различные значения толщины, прежде чем выбрать тот, который вам больше всего нравится.
Повторить для знаменателя
Повторите эти шаги для знаменателя.
Зачеркнутый цвет
Хороший способ привлечь внимание к части выражения — это создать ее контрастным цветом. Если вы распечатываете свой рабочий лист в цвете или вставляете зачеркивание в презентацию PowerPoint, выберите цвет зачеркивания перед выбором шаблона, а затем выберите шаблон зачеркивания. Если вы хотите, чтобы содержимое было черным, вернитесь к черному цвету, прежде чем вводить содержимое.
Введите вторую строку для завершения
Если вы хотите выполнить шаги решения, нажмите Enter, когда закончите со второй дробью. Введите еще = , затем введите конечную дробь в упрощенном виде. Чтобы выровнять две линии по символам =, выберите команду «Выровнять по =» в меню «Формат». Окончательное решение проблемы должно выглядеть так:
Длина зачеркивания
Если вам кажется, что зачеркивание слишком длинное, вы можете отрегулировать длину, аналогично тому, как мы описали регулировку толщины зачеркивания выше.В диалоговом окне «Определить интервал» прокрутите вниз и найдите значение «Радикальный зазор (вертикальный)». Меньшее значение этого параметра приведет к более короткому перечеркнутому изображению. Однако имейте в виду, что это также будет иметь очевидный дополнительный эффект, который может быть нежелательным. (То есть это также повлияет на расстояние по вертикали между подкоренным выражением и радикальной чертой над ним.)
Что делать дальше
На этом мы завершаем последний урок. Конечно, мы не рассмотрели все, что может MathType, но если все прошло хорошо, то вы усвоили основные принципы.Использование MathType с приложениями и веб-сайтами содержит дополнительную информацию об использовании MathType с другими приложениями. Создание веб-страниц с помощью MathPage знакомит с технологией MathPage MathType и показывает, как можно создавать великолепно выглядящие веб-страницы из документов Word.
Раздел меню «Стиль» охватывает стили MathType и расширенное форматирование. Необязательно сразу читать эти разделы, но как только вы перейдете к созданию простых уравнений, вы обнаружите, что их стоит прочитать.Если вы застряли, свяжитесь с нами — наша контактная информация указана на нашем сайте.
.

Палитра или панель	Windows	Mac
Палитра символов	`F5`	`⌘` + `F5`
Палитра шаблонов	`F6`	`⌘` + `F6`
Малый стержень	`F7`	`⌘` + `F7`
Бар с большими выступами	`F8`	`⌘` + `F8`
Стержень с малыми выступами	`F9`	`⌘` + `F6`