Число \(n\) при этом называют показателем корня.
Если \(n=2\), то перед вами корень 2-й степени или обычный квадратный корень.
Если \(n=3\), то корень 3-й степени и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.
Пример 1 $$ \sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2 $$ \sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3 $$ \sqrt[3]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4 $$ \sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим \(2,668…\) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть \(\sqrt[3]{19}\).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:
$$ \sqrt[3]{8} \le \sqrt[3]{19} \le \sqrt[3]{27} $$ $$ 2 \le \sqrt[3]{19} \le 3 $$Получается, что наш корень лежит между числами 2 и 3.
Корень четной и нечетной степени
Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 5 $$ \sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.
Как Навальный и другие политзаключенные невольно помогают российскому обществу понять весь ужас системы ФСИН
Все события вокруг массовых арестов по итогам январских митингов, а также попытка общественности выследить, где и в каких условиях сидит Алексей Навальный вкупе с его отчетами из мест пребывания приближает нас к ситуации «не было бы счастья, да несчастье помогло». Счастья в этом смысле у нас пока нет, и неизвестно, когда будет, но несчастье привело к тому, что общественность хотя бы заглядывает внутрь системы федеральной службы исполнения наказаний и закономерно ужасается тому, что там сквозь немногочисленные щелочки приходится наблюдать.
Этот процесс начался не вчера и закончится не завтра. Но он явно идет, и многочисленные известные и не очень сидельцы, если так угодно, своей невольной жертвой помогают нам разобраться в том аду, который именуется империей российской ФСИН.
Будем откровенны, все последние десятилетия (да что уж там, куда больше) кто-нибудь сомневался, что в российских тюрьмах совершенно скотские условия содержания, а отношение к арестантам чаще всего – еще хуже, чем к скоту? Никто не сомневался. Но почему-то, когда российское общество стало получать живые свидетельства и видеозаписи рутинных тюремных процедур, где охранники разнообразными способами причиняют боль заключенным, начали звучать голоса возмущения.
Конечно, разнообразные людоеды (которые сейчас толпой набегут в комментарии, я уже вижу, как там раскрываются врата бездны) говорят, типа: «Так им и надо! Пусть эти убийцы и насильники (несмотря на то, что убийц и насильников в российских тюрьмах в процентном отношении не так много – прим. авт.) страдают», и многие пока с ними соглашаются. Но все больше становится тех, кто задает резонный вопрос: «Этот человек, которому палкой бьют по пяткам – его приговаривали к лишению свободы и пыткам? Или просто к лишению свободы? Тогда почему к нему применяются пытки?»
Людоедам,
ликующим от того, что вроде как преступники (вроде как – потому что сколько там
сидит народу, которому элементарно подбросили наркотики – не счесть) страдают,
невдомек, что по итогам скотских условий содержания 70 процентов вышедших на
свободу из системы ФСИН возвращаются обратно. Не просто так, а по пути совершив
преступление. Поэтому фактически это не служба «исправления» преступников, а
служба создания рецидивистов.
Не просто так, а по пути совершив
преступление. Поэтому фактически это не служба «исправления» преступников, а
служба создания рецидивистов.
На изменение такой нормы и кардинальную реформацию системы ФСИН у нашей страны, скорее всего, уйдут многие годы. Возможно, пока кто-нибудь, отсидевший там по политическому делу, не войдет в число руководителей страны и не возьмется за перестройку тех концлагерей, через которые прошли миллионы россиян.
Заранее отвечу
умникам, которые сейчас будут говорить, что
Еще раз. Задача государства и общества – не отомстить преступникам, не заставить их страдать, а временно изолировать и перевоспитать, дав инструментарий для мирной и продуктивной (хотя бы не деструктивной) жизни на воле, дабы максимально снизить шанс, что этот человек снова что-то украдет или кого-то прибьет.
√ 0,16
кв. (0,16). Найдите квадратный корень из 0,16 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: √ 0,16 или каков квадратный корень из 0,16? Используйте калькулятор квадратного корня ниже, чтобы найти квадратный корень любого действительного числа, положительного или отрицательного. См. Также на этой странице таблицу квадратного корня от 1 до 100.
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа «x» — это такое число y, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 5 — это квадратный корень из 25, потому что 5 2 = 5 • 5 = 25, -5 — квадратный корень из 25, потому что (-5) 2 = (-5) • (-5) = 25. При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Например, 5 — это квадратный корень из 25, потому что 5 2 = 5 • 5 = 25, -5 — квадратный корень из 25, потому что (-5) 2 = (-5) • (-5) = 25. При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как знак корня или основание.
Квадратный корень Таблица 1-100
Квадратные корни от 1 до 100 с округлением до тысячных.
| число | квадрат | квадрат корень |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1,414 |
| 3 | 9 | 1,732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2,236 |
| 6 | 36 | 2,449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2,828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3,162 |
| 11 | 121 | 3,317 |
| 12 | 144 | 3,464 |
| 13 | 169 | 3,606 |
| 14 | 196 | 3,742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4,123 |
| 18 | 324 | 4,243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4,472 |
| 21 | 441 | 4,583 |
| 22 | 484 | 4,690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4,899 |
| 25 | 625 | 5. 000 000 |
| число | квадрат | квадрат корень | |||
|---|---|---|---|---|---|
| 26 | 676 | 5,099 | |||
| 27 | 729 | 5,196 | |||
| 28 | 784 | 5,292 | |||
| 29 | 841 | ||||
| 30 | 900 | 5,477 | |||
| 31 | 961 | 5,568 | |||
| 32 | 1,024 | 5,657 | |||
| 33 | 1,089 | 5,745 | |||
| 34 | 1,156 | 5,831 | |||
| 35 | 1,225 | 5,916 | |||
| 36 | 1,296 | 6.000 | |||
| 37 | 1,369 | 6.083 | |||
| 38 | 1,444 | 6,164 | |||
| 39 | 1,521 | 6,245 | |||
| 40 | 1,600 | 6,325 | |||
| 41 | 1,681 | 6,403 | |||
| 42 | 1,764 | 6,481 | |||
| 43 | 1,849 | 6,557 | |||
| 44 | 1,936 | 6,633 | |||
| 45 | 2,025 | 6.708 | |||
| 46 | 2116 | 6,782 | |||
| 47 | 2,209 | 6,856 | |||
| 48 | 2,304 | 6,928 | |||
| 49 | 2,401 | 7.000 | 49 | 2,401 | 7.000 | 2,500 | 7,071 |
| число | квадрат | квадрат корень |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2704 | 7,211 |
| 53 | 2,809 | 7,280 |
| 54 | 2,916 | 7,348 |
| 55 | 3025 | 7,416 |
| 3,136 | 7,483 | |
| 57 | 3,249 | 7,550 |
| 58 | 3,364 | 7,616 |
| 59 | 3,481 | 7.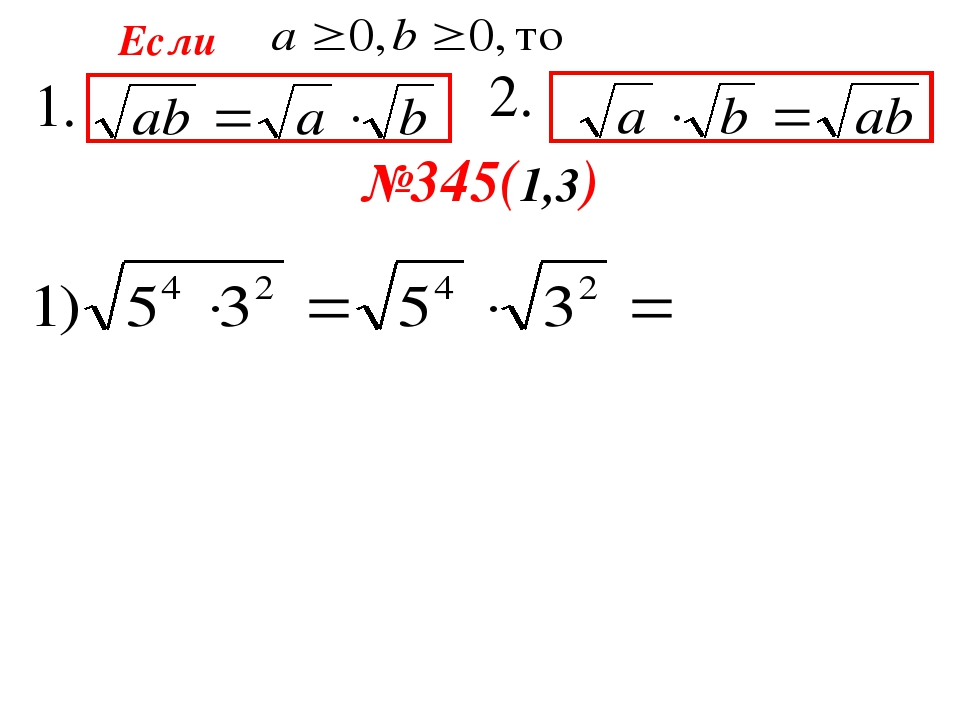 681 681 |
| 60 | 3,600 | 7,746 |
| 61 | 3,721 | 7,810 |
| 62 | 3,844 | 7,874 |
| 63 | 3,969 | 7,937 |
| 4096 | 8,000 | |
| 65 | 4,225 | 8,062 |
| 66 | 4,356 | 8,124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8,246 |
| 69 | 4,761 | 8,307 |
| 70 | 4,900 | 8,367 |
| 71 | 5,041 | 8,426 |
| 5,184 | 8,485 | |
| 73 | 5,329 | 8,544 |
| 74 | 5,476 | 8,602 |
| 75 | 5,625 | 8.660 |
| число | квадрат | квадрат корень | ||
|---|---|---|---|---|
| 76 | 5,776 | 8,718 | ||
| 77 | 5,929 | 8,775 | ||
| 78 | 6,084 | 8,832 | ||
| 79 | 6,241 | 8,888 | ||
| 6,241 | 8,888 | |||
| 8,944 | ||||
| 81 | 6,561 | 9.000 | ||
| 82 | 6,724 | 9,055 | ||
| 83 | 6,889 | 9,110 | ||
| 84 | 7,056 | 9,165 | ||
| 85 | 7,225 | 9,220 | 867,396 | 9,274 |
| 87 | 7,569 | 9,327 | ||
| 88 | 7,744 | 9,381 | ||
| 89 | 7921 | 9.434 | ||
| 90 | 8100 | 9,487 | ||
| 91 | 8,281 | 9,539 | ||
| 92 | 8,464 | 9,592 | ||
| 93 | 8,649 | 9,644 | 8,836 | 9,695 |
| 95 | 9,025 | 9,747 | ||
| 96 | 9216 | 9,798 | ||
| 97 | 9,409 | 9. 849 849 | ||
| 98 | 9,604 | 9,899 | ||
| 99 | 9,801 | 9,950 | ||
| 100 | 10,000 | 10.000 |
Квадратный корень из значений около 0,16
| Число | Sqrt |
|---|---|
| 0,26 | 0,510 |
| 0,36 | 0,600 |
| 0,46 | 0,678 |
| 0.56 | 0,748 |
| 0,66 | 0,812 |
| 0,76 | 0,872 |
| 0,86 | 0,927 |
| 0,96 | 0,980 |
| 1,16 | 1,030 |
| 1,16 | 1,030 |
| 1.077 |
Примеры квадратного корня
Калькулятор квадратного корняИспользование калькулятора
Используйте этот калькулятор, чтобы найти главный квадратный корень и корни действительных чисел.Входные данные для подкоренного выражения x могут быть положительными или отрицательными действительными числами. Ответ также скажет вам, вошли ли вы в идеальный квадрат.
Ответ покажет вам комплексные или мнимые решения для квадратных корней из отрицательных действительных чисел. Также Упростите калькулятор радикальных выражений, чтобы упростить радикалы вместо поиска дробных (десятичных) ответов.
квадратного корня, четное и нечетное:
Для любого положительного действительного числа существует 2 возможных корня.Положительный корень и отрицательный корень. Учитывая число x , квадратный корень из x — это число на , такое, что a 2 = x . Квадратные корни — это особая форма нашего общего
калькулятор корней.
«Обратите внимание, что любое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. Например, квадратные корни из 9 равны -3 и +3, поскольку (-3) 2 = (+3) 2 = 9.Любое неотрицательное действительное число x имеет уникальный неотрицательный квадратный корень r; это называется главным квадратным корнем ………. Например, главный квадратный корень из 9 равен sqrt (9) = +3, а другой квадратный корень из 9 равен -sqrt (9) = — 3. В обычном использовании, если не указано иное, «квадратный корень обычно означает главный квадратный корень» [1].
Калькулятор идеального квадрата
Этот калькулятор также подскажет, является ли введенное вами число идеальным квадратом или нет.Идеальный квадрат — это число x , где квадратный корень из x — это число на , такое, что a 2 = x , а a — целое число. Например, 4, 9 и 16 являются полными квадратами, поскольку их квадратные корни 2, 3 и 4, соответственно, являются целыми числами.
Пример квадратного корня:
- Второй корень из 81, или 81, корень 2, или квадратный корень из 81 записывается как \ (\ sqrt [2] {81} = \ sqrt [] {81} = \ pm 9 \).
- Корень 2-й степени из 25, или 25 корень 2, или квадратный корень из 25 записывается как \ (\ sqrt [2] {25} = \ sqrt [] {25} = \ pm 5 \).
- Второй корень из 100, или 100, радикал 2, или квадратный корень из 100 записывается как \ (\ sqrt [2] {100} = \ sqrt [] {100} = \ pm 10 \).
- Второй корень из 10, или 10, радикал 2, или квадратный корень из 10 записывается как \ (\ sqrt [2] {10} = \ sqrt [] {10} = \ pm 3.
 {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$Квадратный корень записывается с помощью символа корня √, а число или выражение внутри символа корня, обозначенное ниже a, называется подкоренным выражением.
$$ \ sqrt {a} $$
Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренной части, мы помещаем символ ± (читается как плюс минус) перед корнем.
$$ \ pm \ sqrt {9} = \ pm 3 $$
У нуля один квадратный корень, равный 0.
$$ \ sqrt {0} = 0 $$
Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положительный, либо 0.
Если квадратный корень целого числа является другим целым числом, квадрат называется полным квадратом.Например, 25 — это идеальный квадрат, так как
$$ \ pm \ sqrt {25} = \ pm 5 $$
Если подкоренное выражение не является точным квадратом, то есть квадратный корень не является целым числом, вам нужно приблизительно вычислить квадратный корень
$$ \ pm \ sqrt {3} = \ pm 1.73205 … \ приблизительно \ pm 1,7 $$
Квадратные корни из чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел. Десятичная форма иррационального числа не прерывается и не повторяется.Иррациональные числа вместе с рациональными числами составляют действительные числа.
Пример
$$ иррационально \: number \ Rightarrow \ sqrt {19} \ приблизительно 4,35889 … $$
$$ рациональное \: число \ Rightarrow 0.5 = \ frac {1} {2} $$
ВидеоурокиРешить
Определите, являются ли эти числа рациональными или иррациональными
чисел — квадратные корни — глубина
Многие математические операции имеют обратную или противоположную операцию. Вычитание противоположное
сложения, деление — это обратное умножение и т. д. Квадрат,
о котором мы узнали на предыдущем уроке (экспоненты),
есть и обратное, называемое «нахождение квадратного корня». Помните, что
квадрат числа — это число, умноженное на само число. Идеальные квадраты — это
квадраты целых чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Вычитание противоположное
сложения, деление — это обратное умножение и т. д. Квадрат,
о котором мы узнали на предыдущем уроке (экспоненты),
есть и обратное, называемое «нахождение квадратного корня». Помните, что
квадрат числа — это число, умноженное на само число. Идеальные квадраты — это
квадраты целых чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100Квадратный корень числа n написано
это число, которое дает n при умножении на себя.Например,
потому что 10 х 10 = 100
Примеры
Вот квадратные корни из всех полных квадратов от 1 до 100.
Нахождение квадрата корни чисел, которые не являются точными квадратами без калькулятора
1. Оценка — во-первых, подойдите как можно ближе, найдя два идеальных квадратных корня из ваших число находится между.
2.Разделять — разделите ваше число на один из этих квадратных корней.
3. Среднее — возьмите среднее значение результата шага 2 и корень.
4. Используйте результат шага 3, чтобы повторять шаги 2 и 3, пока не получите точное число достаточно для вас.
Пример: Вычислите квадратный корень из 10 () до 2 знаков после запятой.
1. Найти между двумя точными квадратами.
Решение:
3 2 = 9 и 4 2 = 16, поэтому находится между 3 и 4.2. Разделить 10 на 3. 10/3 = 3,33 (ответ можно округлить)
3. Среднее 3,33 и 3. (3,33 + 3) / 2 = 3,1667
Повторить шаг 2: 10 / 3,1667 = 3,1579
Повторите шаг 3: Среднее значение 3,1579 и 3,1667. (3,1579 + 3,1667) / 2 = 3,1623Попробуй ответ -> Это 3.1623 в квадрате равно 10? 3,1623 x 3,1623 = 10,0001
Если это верно хватит тебе, можешь остановиться! В противном случае вы можете повторить шаги 2 и 3.

Примечание : Есть несколько способов вычислить квадратные корни без использования калькулятора. Это только один из них.
назад наверх
Как вычислить квадратный корень в Python? · Kodify
Квадратный корень из числа — это значение, которое при умножении на себя дает исходное число.Python может вычислить квадратный корень несколькими способами. Давайте взглянем.
# Получение квадратного корня в Python: три варианта
Квадратный корень числа — это некоторое значение, которое при умножении само на себя возвращает то же самое число (Wikipedia, 2019). Например, 5 x 5 = 25, поэтому квадратный корень 25 равен 5. Но -5 x -5 тоже 25, поэтому -5 также является квадратным корнем из 25.
Символ, который мы используем для получения квадратного корня, √, однако, всегда означает положительный квадратный корень. Итак, √16 равно 4 (а не -4).
Python имеет три способа получить положительный квадратный корень из числа:
- Функция
math.sqrt ()возвращает квадратный корень как точное значение с плавающей запятой. (Эта функция — то, что вам нужно в 95% случаев.) - Функция
math.isqrt ()возвращает квадратный корень в виде целого числа (то есть с округлением до целого числа в меньшую сторону). - И, когда мы возводим число в степень
0,5, мы также получаем квадратный корень. Для этого мы можем использовать оператор экспоненты Python (**) или функциюpow ().
Давайте посмотрим, как каждый подход работает в Python.
# Получение точного квадратного корня: функция Python
math.sqrt ()Функция
math.sqrt ()возвращает точный квадратный корень из своего аргумента (Python Docs, n.d.). Итак, чтобы получить квадратный корень, мы просто передаем значение функцииmath.sqrt ().
Например:
импорт математики math.sqrt (12) # Возвращает: 3,464101615137755Python
math.Функция sqrt ()требует положительного значения. Если мы используем отрицательное значение, функция генерирует исключениеValueError. С помощью функцииabs ()вы можете убедиться, что функция работает с положительным значением.# Пример: получить квадратный корень в Python с помощью
math.sqrt ()Итак, чтобы получить квадратный корень, мы просто вызываем функцию
math.sqrt ()для значения. Вот небольшая программа на Python, которая показывает, как:import math # Некоторые значения значениеA = 16 значениеB = 81 значениеC = 8301.430 значениеD = -98,25 # Получить квадратный корень из этих значений sqrtA = math.sqrt (значениеA) sqrtB = math.sqrt (значениеB) sqrtC = math.sqrt (значениеC) sqrtD = math.sqrt (абс (значениеD)) # Вывести результаты print ("√", valueA, "=", sqrtA, sep = "") print ("√", значениеB, "=", sqrtB, sep = "") print ("√", valueC, "=", sqrtC, sep = "") print ("√", abs (значениеD), "=", sqrtD, sep = "")Сначала мы импортируем модуль
math. Это делает доступной функциюmath.sqrt (). Затем мы создаем четыре разные переменные, отvalueAдоvalueD.К ним относятся положительные и отрицательные, а также целые числа и значения с плавающей запятой.Затем мы вычисляем квадратный корень из каждого. Мы выполняем функцию
math.sqrt ()для каждой из переменных. Мы помещаем возвращенный квадратный корень в новую переменную для последующего использования (отsqrtAдоsqrtD). Мы используем функциюabs ()для отрицательной переменной. Таким образом,math.sqrt ()не ошибается.Затем мы отображаем как исходное значение, так и его квадратный корень.
 Для этого мы несколько раз вызываем функцию Python
Для этого мы несколько раз вызываем функцию Python print (). Вот что отображается:√16 = 4,0 √81 = 9,0 √8301,43 = 91,11218359802382 √98,25 = 9,3800799505Квадратный корень — это все равно что спросить себя: «Какое значение мы можем умножить само на себя, чтобы получить такой результат?». Это умножение само по себе также называется возведением в квадрат. Другими словами, 3 в квадрате равно 9, и поэтому квадрат корень из 9 равен 3. Подробнее см. квадратные значения в Python
# Получение целочисленного квадратного корня: математика Python
.isqrt ()Другой способ вычисления квадратного корня — использование функции
math.isqrt (). Эта функция всегда возвращает целое число квадратный корень (Python Docs, n.d.). То есть функция возвращает квадратный корень значения, округленный до целого числа.Для функции нужен один аргумент: значение, из которого мы хотим получить целочисленный квадратный корень. Например:
импорт математики math.isqrt (12) # Возвращает: 3 (а не 3,464101615137755)Python
math.isqrt ()требует аргумента, значение которого равно нулю или больше (Python Docs, n.d.). При отрицательном аргументе получаем ошибку Python. Используйте функцию Pythonabs (), чтобы убедиться, чтоmath.isqrt ()работает с неотрицательным значением.# Пример: вычисление целочисленного квадратного корня в Python
Чтобы наша программа извлекала целочисленный квадратный корень, мы просто вызываем функцию
math.isqrt ()для числового значения. Вот как это работает на практике:import math # Некоторые значения значениеA = 16 значениеB = 81 значениеC = 8301.430 значениеD = -98,25 # Получить целочисленный квадратный корень из этих значений isqrtA = math.isqrt (значениеA) isqrtB = math.isqrt (значениеB) isqrtC = math. isqrt (значениеC)
isqrtD = math.isqrt (абс (значениеD))
# Вывести результаты
print ("√", valueA, "=", isqrtA, sep = "")
print ("√", значениеB, "=", isqrtB, sep = "")
print ("√", значениеC, "=", isqrtC, sep = "")
print ("√", abs (значениеD), "=", isqrtD, sep = "")
isqrt (значениеC)
isqrtD = math.isqrt (абс (значениеD))
# Вывести результаты
print ("√", valueA, "=", isqrtA, sep = "")
print ("√", значениеB, "=", isqrtB, sep = "")
print ("√", значениеC, "=", isqrtC, sep = "")
print ("√", abs (значениеD), "=", isqrtD, sep = "")
Сначала мы импортируем модуль
math. Затем мы создаем четыре переменные со случайными значениями (отvalueAдоvalueD).Здесь бывают целые числа и значения с плавающей запятой, а также положительные и отрицательные.Затем мы получаем квадратный корень целого числа из этих значений. Для этого мы вызываем функцию
math.isqrt ()для каждой переменной. Возвращенный квадратный корень — это то, что мы сохраняем в новых переменных отisqrtAдоisqrtD.Поскольку
math.isqrt ()не работает с отрицательными значениями, мы сначала оборачиваем переменнуюvalueDвнутри функцииabs ().Это извлекает квадратный корень из абсолютного положительного значения.Последний бит программы выводит исходный и целочисленный квадратный корень с помощью функции
print (). Вот что это дает:√16 = 4 √81 = 9 √8301,43 = 91 √98,25 = 9# Вычислить квадратные корни из значений списка Python
До сих пор мы вычисляли квадратный корень только для одного значения. Но, конечно, у нас также может быть список ценностей. Как нам получить из них квадратный корень? Давай выясним.
# Получение квадратного корня с пониманием списка
Так называемое понимание списка — это первый способ получить квадратный корень из списка. Эти эффективные конструкции кода могут управлять целым списком значений с помощью одной строчки кода.
Вот пример:
импорт математики # Некоторые случайные положительные значения значения = [ 33, 81, 4,25, 16, 55, 12 ] # Создать новый список с квадратными корнями squareRoots = [math. sqrt (число) для числа в значениях]
# Выходные данные
print ("Исходные значения: \ n", значения)
print ("Их квадратные корни: \ n", squareRoots)
sqrt (число) для числа в значениях]
# Выходные данные
print ("Исходные значения: \ n", значения)
print ("Их квадратные корни: \ n", squareRoots) Сначала мы импортируем модуль
math.Это делает доступной функциюmath.sqrt (). Затем мы составляем список (значений,) со случайными числами.Затем мы составляем еще один список с именем
squareRoots. Значения этого списка являются квадратными корнями из списказначений, и мы генерируем эти значения с пониманием списка. Этот код вызывает функциюmath.sqrt ()для каждой переменнойnumber.Переменная генерируется встроенным
для выражения цикла:для числа в значениях.Это выполняет итерацию по всем элементам в спискезначенийи делает по одному доступным через переменнуюnumber.Когда понимание этого списка завершено, список
squareRootsсодержит квадратный корень для каждого числа в исходном спискезначений. Чтобы проверить, мы выводим оба списка с помощью функции Pythonprint (). Вот что отображается:Исходные значения: [33, 81, 4,25, 16, 55, 12] Их квадратные корни: [5.744562646538029, 9,0, 2,0615528128088303, 4,0, 7,416198487095663, 3,4641016151377544]Может ли ваш список содержать отрицательные значения? Тогда неплохо было бы также использовать функцию
abs (). Таким образом вы предотвратите появление ошибкиmath.sqrt (). В этом случае список становится понятным:# Создать новый список с квадратным корнем из каждого числа squareRoots = [math.sqrt (abs (число)) для числа в значениях]Кстати, если вам не нужно сохранять исходный список, вы также можете перезаписать его значения квадратными корнями.Для этого просто установите значение списка на результат понимания списка.
 Например:
Например:# Извлеките квадратный корень из каждого значения в 'values' # list, перезаписывая исходный список values = [math.sqrt (значение) для значения в значениях]# Получение квадратного корня с помощью обычного
для циклаВторой вариант получения квадратного корня из списка — это цикл Python
для. По сравнению с пониманием списка, циклдлятребует немного больше кода.Но он также более гибкий и его легче читать, когда код становится сложным.Вот как цикл
дляизвлекает квадратный корень из списка:import math # Некоторые случайные значения числа = [ 12, 36, 45, 81, 122, 234, 450, 992 ] # Создать новый список sqrtNumbers = [] # Прокрутите список, извлеките квадратный корень из каждого # значение, округленное до 2 знаков после запятой для числа в числах: sqrtNumbers.append (круглый (math.sqrt (число), 2)) # Выходные данные print ("Исходные значения: \ n", числа) print ("Значения квадратного корня: \ n", sqrtNumbers)Сначала мы импортируем модуль
math, чтобы получитьmath.sqrt ()функция. Затем мы составляем список со случайными целыми числами. Этот списокчисел— это то, из чего мы хотим получить квадратные корни.Прежде чем мы это сделаем, мы сначала составим список, который будет содержать эти квадратные корни. Этот список
sqrtNumbersизначально пуст ([]).Затем мы обрабатываем список
номеровцикломдля. Во время каждого цикла цикла переменнаяnumberссылается на одно значение из этого списка.Внутри цикла мы добавляем новое значение в список
sqrtNumbersс его методомappend ().Это значение является квадратным корнем из переменнойnumber, вычисленной с помощью функцииmath.. Но прежде чем добавить это значение в список, мы сначала округляем его до двух десятичных знаков с помощью функции sqrt ()
sqrt () round ().После того, как цикл выполнил эти задачи, у нас есть два списка: один с исходными значениями и квадратными корнями. Мы выводим оба значения с помощью функции
print ():Исходные значения: [12, 36, 45, 81, 122, 234, 450, 992] Значения квадратного корня: [3.46, 6,0, 6,71, 9,0, 11,05, 15,3, 21,21, 31,5]Не нужно хранить исходный список? В этом случае вы можете перезаписать список его квадратными корнями. Полезной функцией для этого является функция Python
enumerate (), которая генерирует как значение списка, так и его значение индекса. Например:# Просмотрите исходный список номеров и # заменяем каждое число его квадратным корнем для индекса, число в перечислении (числа): числа [индекс] = math.sqrt (число)# Бонус: получить квадратный корень через возведение в степень
Математика Python
.Функция sqrt ()— это стандартный способ получения квадратного корня. Но знаете ли вы, что возведение значения в степень0,5также возвращает квадратный корень? Давайте взглянем.# Получение квадратного корня в Python: оператор экспоненты (
**)Первый способ поднять значение — использовать оператор экспоненты Python (
**). Когда мы вычисляем значение в степени0,5, результатом является квадратный корень. Например:12 ** 0.5 # Возвращает: 3,464101615137755Выражение
** 0,5возвращает квадратный корень, только если основание возведения в степень неотрицательно. (В противном случае вместо этого мы получим комплексное число.) Используйте функцию Pythonabs (), чтобы получить абсолютное положительное значение числа.
# Пример: вычисление квадратных корней с помощью оператора экспоненты
Итак, чтобы получить квадратный корень, мы просто возводим значение в степень
0,5. Вот пример быстрой программы на Python:# Некоторые значения значениеA = 16 значениеB = 81 значениеC = 8301.430 значениеD = -98,25 # Получить квадратный корень из этих значений sqrtA = значениеA ** 0,5 sqrtB = значениеB ** 0,5 sqrtC = значениеC ** 0,5 sqrtD = abs (значениеD) ** 0,5 # Вывести результаты print ("√", valueA, "=", sqrtA, sep = "") print ("√", значениеB, "=", sqrtB, sep = "") print ("√", valueC, "=", sqrtC, sep = "") print ("√", abs (значениеD), "=", sqrtD, sep = "")Сначала мы создадим здесь четыре разные переменные (от
valueAдоvalueD). Каждому присваивается случайное значение. У нас есть положительные и отрицательные, а также целые числа и значения с плавающей запятой.Затем мы получаем квадратный корень из каждого. Для этого мы возводим каждое значение в степень
0,5. Поскольку значениеvalueDотрицательно, мы сначала получаем абсолютное значение и , затем возведение в степень. В противном случае мы получили бы комплексное число, а не квадратный корень. Мы сохраняем результаты в четырех новых переменных (отsqrtAдоsqrtD).Последний бит кода выводит результаты. Для этого мы несколько раз вызываем функцию Python
print ().Вот как выглядит этот вывод:√16 = 4,0 √81 = 9,0 √8301,43 = 91,11218359802382 √98,25 = 9,3800799505# Вычислить квадратный корень в Python: функция
pow ()Другой способ поднять значение до определенной степени — использовать функцию Python
pow (). Эта функция принимает два аргумента: основание и показатель степени. Когда второй равен0,5,pow ()возвращает квадратный корень. Например:
Например:pow (12, 0.5) # Возвращает: 3,464101615137755# Пример: вычисление квадратных корней с помощью функции
pow ()Итак, для получения квадратного корня мы возводим в степень
0,5с помощьюpow (). Вот как это работает в программе Python:# Некоторые значения значениеA = 16 значениеB = 81 значениеC = 8301,430 значениеD = -98,25 # Получить квадратный корень из этих значений sqrtA = pow (значениеA, 0,5) sqrtB = pow (значениеB, 0,5) sqrtC = pow (значениеC, 0,5) sqrtD = pow (значениеD, 0.5) # Вывести результаты print ("√", valueA, "=", sqrtA, sep = "") print ("√", значениеB, "=", sqrtB, sep = "") print ("√", valueC, "=", sqrtC, sep = "") print ("√", abs (значениеD), "=", abs (sqrtD), sep = "")Сначала мы делаем четыре переменные. Мы называем эти значения
A отдозначениемD.Затем мы получаем квадратный корень из них. Для этого мы вызываем функцию
pow ()с двумя аргументами. Первая — это переменная, из которой мы хотим получить квадратный корень. Второй —0.5. Мы помещаем результаты этого возведения в степень в переменных отsqrtAдоsqrtD.Третья часть отображает как исходный, так и квадратный корень. Для этого мы многократно выполняем функцию
print (). Вот как выглядит этот вывод:√16 = 4,0 √81 = 9,0 √8301,43 = 91,11218359802382 √98,25 = 9,3800799505# Сводка
Квадратный корень из числа — это некоторое значение, которое при умножении само на себя возвращает это число.В Python есть несколько способов сделать это.
Первым и наиболее простым вариантом является функция
math.sqrt (), которая возвращает квадратный корень из своего аргумента. Эта функция выдает ошибку с отрицательными значениями. В этих случаях мы вызываем функцию
В этих случаях мы вызываем функцию abs (), чтобы сначала получить абсолютное значение.Мы также можем вычислить квадратный корень, возведя число в степень
0,5. Для этого возведения в степень мы используем функцию Pythonpow ()или оператор экспоненты (**).Чтобы извлечь квадратный корень из каждого значения в списке (или массиве), мы либо используем понимание списка, либо
Опубликован . «Все математические статьи Pythonдля цикла. Первый компактный, второй более гибкий и читаемый.Квадрат, куб, квадратный корень и кубический корень
Калькулятор квадрата, куба, квадратного корня и кубического корня
Квадрат, куб, квадратный корень и кубический корень для ранжирования чисел 0-100
Число
xКвадрат
x 2Куб
x 3Квадратный корень
x 1/2Кубический корень
x 1/31 1 1 1.000 1.000 2 4 8 1,414 1,260 3 9 27 1,732 1.442 4 16 64 2.000 1,587 5 25 125 2,236 1,710 6 36 216 2.449 1,817 7 49 343 2,646 1,913 8 64 512 2,828 2.000 9 81 729 3.000 2.080 10 100 1000 3.162 2.154 11 121 1331 3.  317
3172,224 12 144 1728 3,464 2,289 13 169 2197 3,606 2,351 14 196 2744 900 3,742 2,410 15 225 3375 3,873 2,466 16 256 4096 4.000 2,520 17 289 4913 4,123 2,571 18 324 5832 4,243 2,621 19 361 6859 4,359 2,668 20 400 8000 4,472 2,714 21 441 9261 4.583 2,759 22 484 10648 4,690 2,802 23 529 12167 4,796 2,844 24 576 4,899 2,884 25 625 15625 5.000 2,924 26 676 17576 5.099 2,962 27 729 19683 5,196 3.000 28 784 21952 5.292 3,037 29 841 5,385 3,072 30 900 27000 5,477 3,107 31 961 29791 5.568 3,141 32 1024 32768 5,657 3,175 33 1089 35937 5,745 3,208 34 11564 5,831 3,240 35 1225 42875 5,916 3,271 36 1296 46656 6.  000
0003.302 37 1369 50653 6.083 3.332 38 1444 54872 6.164 3.362 39 1521 6,245 3,391 40 1600 64000 6,325 3,420 41 1681 68921 6.403 3,448 42 1764 74088 6,481 3,476 43 1849 79507 6,557 3,503 44 1936 6,633 3,530 45 2025 6,708 3,557 46 2116 97336 6.782 3,583 47 2209 103823 6,856 3,609 48 2304 110592 6,928 3,634 49 2401 7.000 3.659 50 2500 125000 7.071 3.684 51 2601 132651 7.141 3,708 52 2704 140608 7,211 3,733 53 2809 148877 7,280 3,756 54 2916 7,348 3,780 55 3025 166375 7,416 3,803 56 3136 175616 7.483 3,826 57 3249 185193 7,550 3,849 58 3364 195112 7,616 3481 59 3481 59 3481 900 7,681 3,893 60 3600 216000 7,746 3,915 61 3721 226981 7.  810
8103,936 62 3844 238328 7,874 3,958 63 3969 250047 7,937 3,979 4096 8.000 4.000 65 4225 274625 8.062 4.021 66 4356 287496 8.124 4,041 67 4489 300763 8,185 4,062 68 4624 314432 8,246 4,082 69 4761 69 4761 50 8,307 4,102 70 4900 343000 8,367 4,121 71 5041 357911 8.426 4,141 72 5184 373248 8,485 4,160 73 5329 389017 8,544 4,179 74 547624 8,602 4,198 75 5625 421875 8,660 4,217 76 5776 438976 8.718 4,236 77 5929 456533 8,775 4,254 78 6084 474552 8,832 4,273 79 6241 8,888 4,291 80 6400 512000 8,944 4,309 81 6561 531441 9.000 4,327 82 6724 551368 9,055 4,344 83 6889 571787 9,110 4,362 84 70562 9,165 4,380 85 7225 614125 9,220 4,397 86 7396 636056 9.  274
2744,414 87 7569 658503 9,327 4,431 88 7744 681472 9,381 4,448 89 7921 9,434 4,465 90 8100 729000 9,487 4,481 91 8281 753571 9.539 4,498 92 8464 778688 9,592 4,514 93 8649 804357 9,644 4,531 94 8830 8830 9,695 4,547 95 9025 857375 9,747 4,563 96 9216 884736 9.798 4,579 97 9409 3 9,849 4,595 98 9604 941192 9,899 4,610 99 980 980 9,950 4,626 100 10000 1000000 10.000 4,642 Загрузите и распечатайте квадрат, куб, квадратный корень и кубический корень
Добавьте кубические линии в свой эскиз 3D-модель
Используйте расширение Engineering ToolBox Sketchup — для добавления кубических линий в модели Sketchup.
Браунов — это команда, которая будет болеть за
ЗАКРЫТЬЭто «Утренняя победа» Энди Несбитта.
Что касается плей-офф НФЛ в этом году, у меня действительно нет команды. Я имею в виду, что я из Бостона, и мне нравятся Патриоты (которые воняют в этом году), поэтому я надеюсь на еще одну поездку на Суперкубок для Тома Брэди. Но есть еще одна команда, которая, я надеюсь, добьется определенного успеха и сыграет важную роль .
 .. и это Cleveland Browns.
.. и это Cleveland Browns.Я знаю, я тоже не могу поверить, что сказал это.Но вот в 2021 году я надеюсь на новый старт, и сейчас нет лучшего нового старта в НФЛ, чем Браунс, которые вышли в плей-офф в этом году впервые за 18 лет.
18 лет!
Многие из тех лет тоже были ужасными. Типа, ДЕЙСТВИТЕЛЬНО некрасиво. Шестнадцать из этих сезонов оказались проигрышными. С 2015 по 2017 год они выиграли в общей сложности ЧЕТЫРЕ игры, три из которых — в 2015 году! В 2016 году они набрали 1–15 очков, а в 2017 году они упали на дно, когда они опустились до 0–16.
Я пытаюсь сказать, что Брауны были одним из самых больших посмешищ во всех видах спорта в течение довольно долгого времени, но теперь это время прошло, и если у вас нет собаки в этой битве, вы можете Предлагаю болеть за… Браунов?
Дикий, да?
Бейкер Мэйфилд и компания едут в Питтсбург, чтобы встретиться с Стилерс в воскресенье вечером, командой, которую они обыграли на 17-й неделе, но Биг Бен не сыграл на этой неделе, и Браунам пришлось сдерживать их на отрезке, чтобы получить W .
Что безумно в этом матче, так это то, что последней командой Браунов в плей-офф была…. Питтсбург Стилерс. Келли Холкомб бросила 429 ярдов и 3 TD в этой игре за Браунс, но этого было недостаточно, чтобы победить Томми Мэддокса и Стилерс, выигравших триллер со счетом 36–33.
До этого «Браунс» не выходили в плей-офф с 1994 года, когда они обыграли «Патриотов» в раунде «уайлд-кард», а затем проиграли… «Питтсбург Стилерз».
Теперь они получают еще один удар по своим соперникам из AFC North, и трудно не бороться команде и городу, который за эти годы пережил столько неудач.Было весело наблюдать, как в воскресенье стадион в Кливленде раскачивался, когда команда покинула поле после того, как заняла место в плей-офф. Болельщики, которым разрешили войти, никогда не забудут этот момент.
Теперь у них еще один момент плей-офф, и вы знаете, что никто в Кливленде не принимает это как должное.

- Функция

 {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$ Вычитание противоположное
сложения, деление — это обратное умножение и т. д. Квадрат,
о котором мы узнали на предыдущем уроке (экспоненты),
есть и обратное, называемое «нахождение квадратного корня». Помните, что
квадрат числа — это число, умноженное на само число. Идеальные квадраты — это
квадраты целых чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Вычитание противоположное
сложения, деление — это обратное умножение и т. д. Квадрат,
о котором мы узнали на предыдущем уроке (экспоненты),
есть и обратное, называемое «нахождение квадратного корня». Помните, что
квадрат числа — это число, умноженное на само число. Идеальные квадраты — это
квадраты целых чисел: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100

 Для этого мы несколько раз вызываем функцию Python
Для этого мы несколько раз вызываем функцию Python  isqrt (значениеC)
isqrtD = math.isqrt (абс (значениеD))
# Вывести результаты
print ("√", valueA, "=", isqrtA, sep = "")
print ("√", значениеB, "=", isqrtB, sep = "")
print ("√", значениеC, "=", isqrtC, sep = "")
print ("√", abs (значениеD), "=", isqrtD, sep = "")
isqrt (значениеC)
isqrtD = math.isqrt (абс (значениеD))
# Вывести результаты
print ("√", valueA, "=", isqrtA, sep = "")
print ("√", значениеB, "=", isqrtB, sep = "")
print ("√", значениеC, "=", isqrtC, sep = "")
print ("√", abs (значениеD), "=", isqrtD, sep = "")
 sqrt (число) для числа в значениях]
# Выходные данные
print ("Исходные значения: \ n", значения)
print ("Их квадратные корни: \ n", squareRoots)
sqrt (число) для числа в значениях]
# Выходные данные
print ("Исходные значения: \ n", значения)
print ("Их квадратные корни: \ n", squareRoots)  Например:
Например: sqrt ()
sqrt () 
 Например:
Например: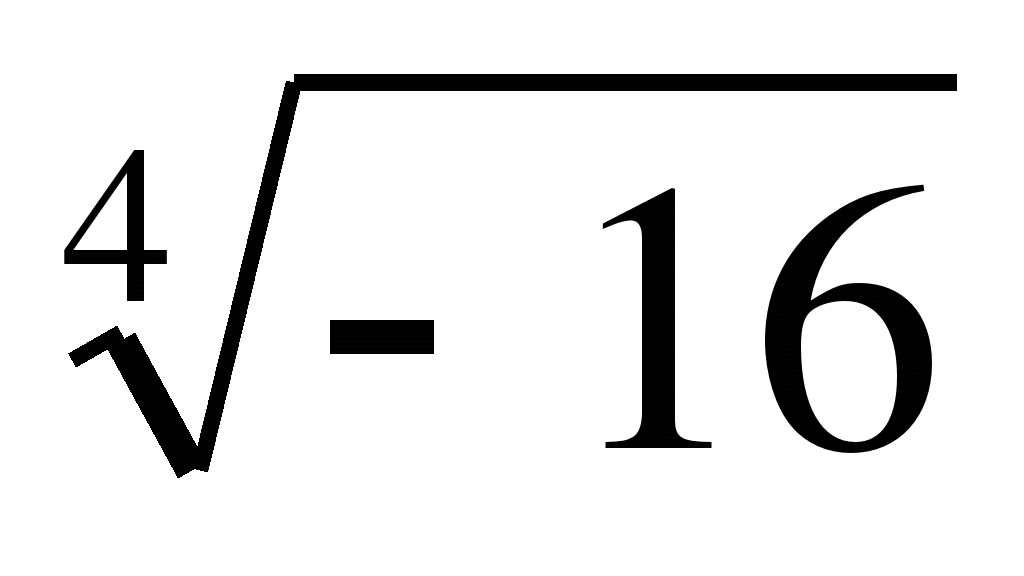 В этих случаях мы вызываем функцию
В этих случаях мы вызываем функцию  317
317 000
000 810
810 274
274 .. и это Cleveland Browns.
.. и это Cleveland Browns.