| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) ) |
|
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | cos(pi/2) | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.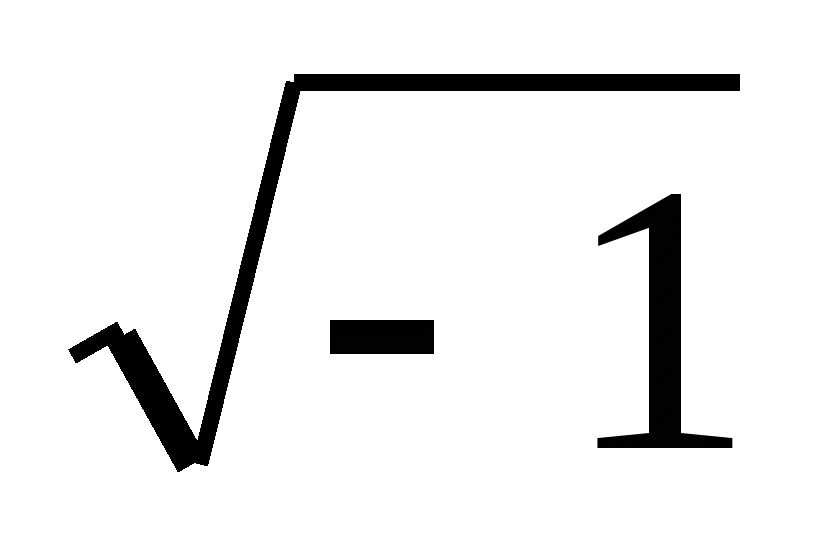 ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
1.1.5 Корень степени n > 1 и его свойства
Видеоурок 1: Степени и корни
Видеоурок 2: Свойства корня степени n > 1
Лекция: Корень степени n > 1 и его свойства
Корень
Предположим, Вы имеете уравнение вида:
Решением данного уравнения будет х1 = 2 и х2 = (-2). В качестве ответа подходят оба решения, поскольку числа с равными модулями при возведении в четную степень дают одинаковый результат.
Это был простой пример, однако, что мы можем сделать в том случае, если, например,
Давайте попробуем построить график функции y=x2. Её графиком является парабола:
На графике необходимо найти точки, которым соответствует значение у = 3. Данными точками является:
Это означает, что данное значение нельзя назвать целым числом, но можно представить в виде корня квадратного.
Любой корень — это иррациональное число. К иррациональным числам относятся корни, непериодические бесконечные дроби.
Квадратный корень — это неотрицательное число «а», подкоренное выражение которого равно данному числу «а» в квадрате.
Например,
То есть в результате мы получим только положительное значение. Однако в качестве решения квадратного уравнения вида
Решением будет х1 = 4, х2 = (-4).
Свойства квадратного корня
1. Какое бы значение не принимала величина x, данное выражение верно в любом случае:
2. Сравнение чисел, содержащих квадратный корень. Чтобы сравнить данные числа, необходимо и одно, и второе число внести под знак корня. То число будет больше, чье подкоренное выражение больше.
Вносим число 2 под знак корня
А теперь давайте внесем число 4 под знак корня. В результате этого получим
В результате этого получим
И только теперь два полученных выражения можно сравнить:
3. Вынесение множителя из под корня.
Если подкоренное выражение может разложиться на два множителя, один из которых можно вынести из под знака корня, то необходимо пользоваться данным правилом.
4. Существует свойство, обратное данному — внесение множителя под корень. Этим свойством мы заведомо воспользовались во втором свойстве:
Корень степени n > 1
Под корнем n-ой степени некоторого числа «a» понимают число, которое при возведении в степень «n» даст число «а».
Иными словами можно сказать, что это решение следующего уравнения:
Например,
Если под корнем некоторой степени стоит степень, то для вынесения данного числа из под знака корня следует показатель степени разделить на степень корня.
Вкладыш коренной Yamaha F80-115 красный Код товара: 67F114162000
Вкладыш коренной Yamaha F80-115 красный Код товара: 67F114162000 | Купить в интернет-магазине «R5»Корзина пуста
Код товара: 67F114162000
Этот товар не продаётся или закончился
Сообщить о поступленииОписание | |
| Артикул | 00010450 |
|---|---|
Информация о производителе | |
| Производитель | Yamaha |
|---|---|
Применимость
Yamaha F80-115
-
Тех.
 Поддержка
ПоддержкаКолл-центр 24 часа. Любые вопросы от тех. консультаций до помощи с оформлением заказа.
-
Гарантия на все товары
Гарантия на товары от 6 месяцев до 3 лет. В случае брака, меняем товар без лишних вопросов.
-
Безопасные способы оплаты
Оплачивайте банковской картой, PayPal, банковским переводом или наличными при получении.
-
Доставка по всей России
Вы можете выбрать доставку курьером, Почтой России или в пункте самовывоза.
-
Контроль доставки
Качественно упакуем, передадим в отправку и будем следить за заказом до вручения.
Александр Пыжиков «Корни сталинского большевизма» страница 115
злободневной на конференции металлистов Москвы и губернии, собравшей более тысячи делегатов. Здесь раздавались голоса о засилье евреев в главках и комитетах, звучали требования уничтожить привилегии, но, в первую очередь, рабочие выступали за уравнительное распределение пайков. Хотя роль спецов в организации производства не отрицалась, «обволакивание их в золотую вату» казалось неприемлемым.1 Выступающие говорили об оживлении советов, о насыщении их рабочими от станка и даже о возрождении рабочих советов непосредственно на фабриках и заводах, где руководящую роль должны играть коммунисты, избираемые на производстве.2 Отдельно обсуждали проблему кандидатского стажа: зачастую рекомендации в партию давались необдуманно, формально, без учета нравственных качеств человека, из-за чего партийные ряды засорялись случайными и даже чуждыми элементами. Интересно, что бороться с этим предлагалось с помощью религиозного института крестных. Как известно, обязанность крестных отцов и матерей — наблюдение за развитием крестника, участие в его воспитании; на них лежит ответственность за поведение новообращенных. Такова же была и задача «коммунистических крестных»: кандидат должен был не только получить от них некую сумму политических знаний, но и всем своим существом воспринять подлинный партийный дух. 3
3
Бурная профсоюзная активность серьезно взволновала руководство партии. На рубеже 1920-1921 годов на этой проблеме пришлось сконцентрироваться и В.И. Ленину. В набиравшей силу тенденции он ощутил внутреннюю угрозу, нависшую над большевизмом, и прямо констатировал, что опасность раскола с профсоюзным движением есть «наверняка гибель советской власти».4 Вождь не скупился на лестные характеристики профсоюзов, правда, перемежевывая реверансы с напоминаниями
1 Вышинский А. Уроки одной конференции (продовольственный вопрос у металлистов) // Правда. 1921. 08 фев.
2 Яковлев А. О возрождении рабочих советов // Правда. 1921. 09 фев.
3 Волин Б. «Крестные» и «крестники» // Правда. 1921. 10 фев.
4 Ленин В.И. Доклад о роли и задачах профессиональных союзов на заседании фракции съезда горнорабочих. 23 января 1921 года // Ленин В.И. Полн. собр. соч. T. 42. С. 249.
Резекция верхушки корня
Резекция верхушки корня – это хирургическая операция, проводящаяся с целью удаления очагов воспаления и инфекций на зубном корне, необходимая для сохранения функций зуба. Чаще всего операция проводится на клыках и резцах.
Основанием для проведения резекции корня зачастую служит наличие кисты, с гнойным воспалением, вызванной периодонтитом.
Киста, образующаяся у корней зубов, может вызвать воспалительный процесс и способствовать разрушению костной ткани. При обострении киста также способна стать причиной воспаления лимфатических узлов и привести к появлению сильной боли, свища в области больного зуба. Поэтому очень важно, обращаться в стоматологическую клинику за своевременным лечением вовремя во избежание серьезных осложнений.
Показания:
1) кисты и гранулёмы возле корня зуба больших размеров
2)невозможность проведения лечения зубных каналов, например, при их неправильном анатомическом расположении
Важным условием для проведения операции является наличие костной ткани не менее чем 0,5-1 см по толщине, в противном случае может произойти перелом кости во время удаления кисты или гранулемы.
Кроме того, резекция корня зуба окажется малоэффективной при хронических пародонтите и периодонтите, особенно с повышенной подвижностью зуба (в этом случае зуб лучше удалить полностью вместе с кистой или гранулёмой). Операцию не рекомендуется проводить в случае, если корень зуба сильно разрушен самой кистой или распространившейся в него гранулёмой – удаление также окажется более эффективным способом лечения.
Противопоказания к операции- плотное соприкосновение больных корней зубов со здоровыми,
- распространение кисты или гранулемы более чем на треть зуба – показано его полное удаление,
- разрушена верхушка зуба – в этом случае его нельзя будет восстановить или использовать как основу для фиксации протеза,
- сильная подвижность зуба,
- общие заболевания организма: нарушения сердечно-сосудистой, иммунной систем, сахарный диабет, психические расстройства, болезни кровеносной системы.
Сама операция обязательно проводится под местной анестезией, и пациент совершенно не чувствует никаких болевых ощущений. При сильном волнении и повышенной чувствительности возможно применение премедикации.
Суть операции сводится к проведению следующих этапов:
- удаление нерва зуба (при его наличии – но, как правило, кисты и гранулёмы появляются у основания ранее пролеченных зубов) и пломбирование каналов больного зуба – данная операция проводится за 1-2 дня до основного хирургического вмешательства,
- введение анестезии – укол ставится в область больного зуба,
- создание доступа к опухоли: для этого десна разрезается и отслаивается от зуба, также создается надрез в костной ткани – такого размера, чтобы можно было беспрепятственно добраться до кисты,
- удаление образования: из образовавшейся полости аккуратно извлекается опухоль, при этом при помощи бора отрезается кусочек корня зуба. При необходимости полость выскабливается – очень важно удалить все остатки инфицированных тканей, после чего проводится антисептическая обработка пространства,
- восстановление костной ткани: для того, чтобы на месте полости не осталось пустое пространство, оно заполняется искусственными синтетическими материалами – аналогами живой кости пациента, либо плазмой его собственной крови,
- наложение швов: на ранку накладывается специальная защитная мембрана, которая самостоятельно рассасывается через некоторое время, после чего десневой лоскут возвращается на место и тщательно ушивается.
 На 5-7 дней может быть также наложен бандаж, который будет защищать травмированную десну от механических воздействий.
На 5-7 дней может быть также наложен бандаж, который будет защищать травмированную десну от механических воздействий.
квадратный корень из 115 — Как найти квадратный корень из 115?
115 — нечетное составное число и полупростое число. Нахождение квадратов и квадратных корней — два процесса, обратных друг другу. Квадратный корень из 115 можно записать как 115 в степени половинной. В этом мини-уроке давайте узнаем о квадратном корне из 115 и научимся находить квадратный корень из 115 методом деления в столбик.
- Квадратный корень из 115 : √ 115 = 10,723
- Квадрат из 115: 115 2 = 13,225
Содержание
Что такое квадратный корень из 115?
- Квадратный корень из 115 может быть записан как √115 в его простейшей радикальной форме и (115) ½ в экспоненциальной форме.
- Это означает, что существует число a такое, что: a × a = 115. Теперь его также можно записать как: a 2 = 115 ⇒ a = √115.
- a — второй корень из 115 и a = ± 10,723.
Является ли квадратный корень из 115 рациональным или иррациональным?
Квадратный корень из 115 — это иррациональное число, в котором числа после десятичной точки увеличиваются до бесконечности. √115 = 10,72380529476361. √115 нельзя записать в виде p / q, поэтому это иррациональное число.
Как найти квадратный корень из 115?
Квадратный корень из 115 или любого числа можно вычислить разными способами. Два из них — это метод среднего и метод длинного деления.
Квадратный корень из 115 методом среднего
- Возьмем два точных квадратных числа, одно из которых чуть меньше 115, а другое чуть больше 115. Оно записывается как:
√100 <√115 <√121 ⇒ 10 <√ 115 <11 - Разделим 115 на 11
- Разделим на 8 ⇒ 115 ÷ 11 = 10.
 45
45 - Найдите среднее значение 10,45 и 11
- (10,45 + 11) / 2 = 21,45 ÷ 2 = 10,725
- Следовательно, √115 ≈ 10,725
Квадратный корень из 115 методом длинного деления
Метод деления в столбик помогает нам найти более точное значение квадратного корня из любого числа. Давайте посмотрим, как найти квадратный корень из 115 методом деления в длину.
- Шаг 1: Экспресс 115 как 115.000000 . Число попарно берем справа. Возьмите 1 в качестве дивиденда.
- Шаг 2: Теперь найдите частное, которое совпадает с делителем. Умножьте частное на делитель и вычтите результат из 1, и, как мы знаем, 1 × 1 = 1.
- Шаг 3: Теперь удвойте частное, полученное на шаге 2. Здесь 1 × 2 = 2. 2 0 становится новым делителем.
- Шаг 4: Вниз 15. У нас теперь 1500 в качестве дивиденда.Найдите (число + 2 0 ) × число ≤ 15. Мы не можем найти ни одного. Отсюда сбрасываем следующую пару нулей.
- Шаг 5: Нам нужно выбрать число, которое, прибавляя к 14 0 и умножая сумму на то же число, мы получаем число меньше 600. 2 0 + 4 = 144 и 16 4 × 4 = 576. Вычтем 576 из 600. Получаем 24. .
- Шаг 6: Запишите следующую пару нулей. 2400 — это новый дивиденд. Удвойте частное.Вот оно 148. Получите 148 0 . Теперь найдите число на месте единицы: 148 0 , умноженное на само себя, дает 2400 или меньше. Получаем, что 148 1 × 1 = 1481. Найдите остаток.
- Шаг 6: Повторяйте процесс, пока мы не получим остаток, равный нулю. Квадратный корень 115 с точностью до двух знаков получается методом деления в столбик. Таким образом, √115 = 7,416.
Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров.
Часто задаваемые вопросы о квадратном корне из 115
Что такое квадратный корень из 115?
Квадратный корень из 115 приблизительно равен 10,723.
Как записать квадратный корень из 115 в упрощенном виде?
Квадратный корень из 115 в упрощенном виде записывается как √115.
Является ли квадратный корень из 115 действительным?
Да, квадратный корень 115 является действительным.
Является ли √115 рациональным числом?
Нет, √115 — это иррациональное число, потому что значение √115 не является конечной десятичной дробью при вычислении.
Как найти квадратный корень из 115?
Существуют различные методы получения значения квадратного корня из 115. Наиболее точное значение √115 можно оценить с помощью метода деления в столбик.
Важные примечания
- Квадратный корень из 115 равен √115 в радикальной форме, 115 ½ в экспоненциальной форме и 10,723 в десятичной форме.
- √115 — иррациональное число.
Квадратный корень из 115 решенных примеров
Пример 1 : Вычислить: √115 + √345
Решение:
√115 = √ (5 × 23) и √345 = √ (15 × 23) = √ (5 × 3 × 23)
⇒ √115 + √343 = √ (5 × 23) + √ (5 × 3 × 23) = (√ (5 × 23)) (√3 + 1) = √115 (√3 + 1)
Следовательно, √115 + √345 = √115 (√3 + 1).
Пример 2: Если длина ковра вдвое больше его ширины, а его площадь составляет 230 квадратных ярдов, какой длины ковер? Примерно с точностью до сотых.
Решение:
Площадь ковра = длина × ширина, кв. Ярд
Дана длина = 2 × ширина ярдов
Таким образом, Площадь = (2 × ширина) × ширина
.
Площадь = 2 ширины 2
230 = 2 ширина 2
ширина 2 = 230 ÷ 2 = 115
ширина = √115 ярдов
ширина = √115 = 10.725 ярдов
⇒ длина = 2 × 10,725 ярда = 21,45 ярда.
Следовательно, длина ковра составляет 21,45 ярда с точностью до сотых.
Сложные вопросы
- Найти 1,15 2 × √1,15
- Вычислите квадратный корень 115 с точностью до 7 знаков после запятой.

Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Квадратный корень из 115, пошаговое решение
Калькулятор квадратного корня
Вот ответ на такие вопросы: Квадратный корень из 115, пошаговое решение или что такое квадратный корень из 115?
Воспользуйтесь калькулятором квадратного корня ниже, чтобы найти квадратный корень из любого мнимого или действительного числа.См. Также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод героя.
Вавилонский метод, также известный как метод героя
См. Ниже, как вычислить квадратный корень из 115, используя вавилонский метод , также известный как метод героя .
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это такое число x, что x 2 = a, другими словами, число x, квадрат которого равен a.Например, 10 — это квадратный корень из 100, потому что 10 2 = 10 • 10 = 100, -10 — квадратный корень из 100, потому что (-10) 2 = (-10) • (-10) = 100.
Квадратный корень Таблица 1-100
Квадратный корень от 1 до 100 с округлением до тысячных.
| число | квадрат | корень квадратный | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000 | |||||||||||
| 2 | 4 | 1.414 | |||||||||||
| 3 | 9 | 1.732 | |||||||||||
| 4 | 16 | 2.000 | |||||||||||
| 5 | 25 | 2,236 | |||||||||||
| 6 | 36 | ||||||||||||
| 64 | 2,828 | ||||||||||||
| 9 | 81 | 3,000 | |||||||||||
| 10 | 100 | 3,162 | |||||||||||
| 11 | 121 | 317||||||||||||
| 12 | 144 | 3,464 | |||||||||||
| 13 | 169 | 3,606 | |||||||||||
| 14 | 196 | 3,742 | |||||||||||
| 256 | 4. 000 000 | ||||||||||||
| 17 | 289 | 4,123 | |||||||||||
| 18 | 324 | 4,243 | |||||||||||
| 19 | 361 | 59 | |||||||||||
| 20 | 400 | 4,472 | |||||||||||
| 21 | 441 | 4,583 | |||||||||||
| 22 | 484 | 4,690 | |||||||||||
| 576 | 4.899 | ||||||||||||
| 25 | 625 | 5.000 |
| число | квадрат | корень квадратный | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 26 | 676 | 5.099 | |||||||||||
| 27 | 729 | 5,196 | |||||||||||
| 28 | 784 | 5,292 | |||||||||||
| 29 | 841 | 5,385 | 961 | 5,568 | |||||||||
| 32 | 1,024 | 5,657 | |||||||||||
| 33 | 1,089 | 5,745 | |||||||||||
| 34 | 1,156831 | ||||||||||||
| 35 | 1,225 | 5,916 | |||||||||||
| 36 | 1,296 | 6,000 | |||||||||||
| 37 | 1,369 | 6,083 | 1,403 | 1,521 | 6,245 | ||||||||
| 40 | 1,600 | 6,325 | |||||||||||
| 41 | 1,681 | 6,403 | |||||||||||
| 42 | 1,75481 | ||||||||||||
| 43 | 1,849 | 6,557 | |||||||||||
| 44 | 1,936 | 6,633 | |||||||||||
| 45 | 2025 | 6,708 | |||||||||||
| 2025 | 6,708 | ||||||||||||
| 2,209 | 6,856 | ||||||||||||
| 48 | 2,304 | 6,928 | |||||||||||
| 49 | 2,401 | 7.000 | |||||||||||
| 503 | 071
| число | квадрат | корень квадратный | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 51 | 2,601 | 7,141 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | 2,704 | 7,211 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | 2,809 | 7,280 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7,416 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | 3,136 | 7. 483 483 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | 3,249 | 7,550 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | 3,364 | 7,616 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | 3,481 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7,681 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7,681 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7,681 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,721 | 7,810 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | 3,844 | 7,874 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | 3,969 | 7,937 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 4 | .000||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | 4225 | 8,062 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | 4,356 | 8,124 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | 4,489 | 8,185 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4,761 | 8,307 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | 4,900 | 8,367 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | 5,041 | 8,426 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 5,1304 | 485||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | 5,329 | 8,544 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | 5,476 | 8,602 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | 5,625 | 8,660 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| число | квадрат | корень квадратный | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 76 | 5,776 | 8,718 | |||||||||||||
| 77 | 5,929 | 8,775 | |||||||||||||
| 78 | 6,084 | 8.832 | |||||||||||||
| 79 | 6,241 | 8,888 | |||||||||||||
| 80 | 6,400 | 8,944 | |||||||||||||
| 81 | 6,561 | ||||||||||||||
| 274 | |||||||||||||||
| 87 | 7,569 | 9,327 | |||||||||||||
| 88 | 7,744 | 9,381 | |||||||||||||
| 89 | 7,921 | 8,281 | 9,539 | ||||||||||||
| 92 | 8,464 | 9,592 | |||||||||||||
| 93 | 8,649 | 9,644 | |||||||||||||
| 94,8303 9,644695 | |||||||||||||||
| 95 | 9,025 | 9,747 | |||||||||||||
| 96 | 9,216 | 9,798 | |||||||||||||
| 97 | 9,409 | 9,849 | 9,801 | 9,950 | |||||||||||
| 100 | 10,000 | 10. 000 000 |
Заявление об ограничении ответственности
Несмотря на то, что прилагаются все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения или за результаты, полученные в результате использования этой информации.Вся информация на этом сайте предоставляется «как есть», без каких-либо гарантий полноты, точности, своевременности или результатов, полученных в результате использования этой информации.
Факторы квадратного корня из 115 (Факторы √115)
Здесь мы покажем вам, как получить множители квадратного корня из 115 (множители √115). Мы определяем множители квадратного корня из 115 как любые целое число (целое число) или квадратный корень, который можно равномерно разделить на квадратный корень из 115. Кроме того, если вы разделите √115 на коэффициент √115, получится приводят к другому коэффициенту √115.
Сначала мы найдем все квадратные корни, которые можно равномерно разделить на квадратный корень из 115. Мы делаем это, находя все делим 115 и добавляем к ним радикал (√) следующим образом:
√1, √5, √23 и √115
Затем мы найдем все целые числа, которые мы можем равномерно разделить на квадратный корень из 115. Мы делаем это, сначала определяя полные квадратные корни из приведенного выше списка:
√1
Затем мы извлекаем квадратный корень из совершенных квадратных корней, чтобы получить целые числа, которые мы можем равномерно разделить на квадратный корень из 115.
1
Множители квадратного корня из 115 — это два приведенных выше списка, вместе взятых. Таким образом, множители квадратного корня из 115 (квадратные корни и целые числа) следующие:
1, √1, √5, √23 и √115
Как мы уже говорили выше, квадратный корень 115, деленный на любой из его множителей, даст другой из его множителей. Следовательно, если разделить √115 на любой из
факторов, указанных выше, вы увидите, что это приводит к одному из других факторов.
Следовательно, если разделить √115 на любой из
факторов, указанных выше, вы увидите, что это приводит к одному из других факторов.
Что вы можете сделать с этой информацией? Во-первых, вы можете получить квадратный корень из 115 в простейшей форме.Квадратный корень из 115 упрощенное — это наибольший целочисленный множитель, умноженный на квадратный корень из 115, деленный на наибольший полный квадратный корень. Таким образом, вот математика для получения квадратного корня из 115 в его простейшей радикальной форме:
√115
= 1 × (√115 ÷ √1)
= √115
Калькулятор коэффициента квадратного корня
Нужен ли вам множители другого квадратного корня? Хорошо, введите квадратный корень в поле ниже.
Коэффициенты квадратного корня из 116
Надеемся, эта информация была полезной.Хотите узнать больше? Если это так, перейдите сюда, чтобы получить множители следующего квадратного корня в нашем списке.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
Корень квадратный из 115 | кв из 115
Факторинг 115 Решения
115√13225 = 13225
115√1520875 = 141822.325023
115√174
115√20113571875 = 16309567,3777
115√2313060765625 = 174
2√230 = 30,3315017762
2√460 = 42,8952211791
2√920 = 60.6630035524
2√1840 = 85,73581
2√3680 = 121,326007105
3√345 = 55,722526863
3√1035 = 96,5142476529
3√3105 = 167,167580589
3√9315 = 289,542742959
3√27945 = 501,502741767
Вопрос: Является ли 115 рациональным числом?.
Ответ: Да 115 рациональное число, потому что это целое и целое число. Все числа и целые числа являются рациональными числами.
Вопрос: Является ли 115 иррациональным числом?.
Ответ: Нет.
Вопрос: является ли sqrt 115 рациональным числом?
Ответ: Нет.
Этот калькулятор — два в одном, он вычисляет квадратные и кубические корни чисел. .
Квадратный корень из числа b — это такое число x, что x2 = b, что означает число x, квадрат которого является результатом умножения числа на себя, или x × x равен b.
Например, 5 и −5 являются квадратным корнем из 25, потому что 5² = (−5) ² = 25.
Каждое неотрицательное действительное число c имеет уникальный неотрицательный квадратный корень, называемый главным, который обозначается √c, где √ называется радикальным знаком или основанием системы счисления. Например, главный квадратный корень 36 равен 6, обозначается √36 = 6, потому что 6² = 6 × 6 = 36 и 6 неотрицательно. Нет, корень которого рассматривается, известен как подкоренное выражение. Подкоренное выражение — это число или выражение под знаком радикала, в этом примере 36.
Каждое положительное число a имеет два корня: √b, положительный, и −√b, отрицательный.Эти два корня обозначены ± √b. Главный корень положительного числа — это только один из двух квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного корня. Для положительного b главный квадратный корень можно также записать в экспоненциальной записи как b1 / 2.
Система счисления. Система счисления в математике устроена так, что 2 (два) — наименьшее четное простое число. это единственное простое число, за которым следует еще одно простое число 3 (тройка). Все четные и целые числа делятся на 2.Два — это третье число последовательности Фибоначчи. Готфрид Вильгельм Лейбниц открыл двойную систему счета (двоичную систему), в которой для представления чисел используются только две цифры. Это помогло в развитии цифровых технологий для распространения. По этой причине это самая известная и самая важная система счисления в дополнение к обычно используемой десятичной системе.
Нулевая цифра. Цифра ноль — это количество элементов в пустой коллекции объектов. Математически мощность пустого множества Zero зависит от контекста других по-разному определенных объектов. но его можно отождествить с другими, принадлежащими тому же объекту, который сочетает в себе несколько свойств, совместимых друг с другом. Поскольку кардинальные числа, то есть количество элементов в наборе, идентифицируются специальными порядковыми числами, нулевая цифра — это просто наименьшее кардинальное число. ноль выбирается первым порядковым номером. Как конечный кардинал и порядковый номер, это зависит от определения, которое часто считается среди натуральных чисел. Нулевая цифра является элементом идентичности для добавления во многие системы couting, такие как рациональные числа, комплексные числа и действительные числа, а также общее имя для нейтрального элемента во многих алгебраических процессах, даже если другие элементы не идентифицируются с общими числами .Нулевое значение — единственное действительное число, которое не является ни положительным, ни отрицательным.
но его можно отождествить с другими, принадлежащими тому же объекту, который сочетает в себе несколько свойств, совместимых друг с другом. Поскольку кардинальные числа, то есть количество элементов в наборе, идентифицируются специальными порядковыми числами, нулевая цифра — это просто наименьшее кардинальное число. ноль выбирается первым порядковым номером. Как конечный кардинал и порядковый номер, это зависит от определения, которое часто считается среди натуральных чисел. Нулевая цифра является элементом идентичности для добавления во многие системы couting, такие как рациональные числа, комплексные числа и действительные числа, а также общее имя для нейтрального элемента во многих алгебраических процессах, даже если другие элементы не идентифицируются с общими числами .Нулевое значение — единственное действительное число, которое не является ни положительным, ни отрицательным.
Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо контакту на нашем сайте.
Отказ от ответственности — этот сайт не гарантирует точность этой информации и, следовательно, не несет ответственности за содержание или то, как вы используете информацию на этом сайте. Вы несете полную ответственность за информацию, которую вы используете, и то, как вы ее используете.Пожалуйста, советуем использовать информацию здесь по своему усмотрению. Но мы постараемся поддерживать точный расчет на уровне программного обеспечения, которое мы используем.
115-летний дом Pioneer Era в Палм-Бич будет отремонтирован, расширен
Владельцы Кэти и Дэвид Брукер планируют капитальный ремонт и пристройку к 115-летнему каркасному дому.
Дом эпохи пионеров в одном из старейших районов Палм-Бич подвергается реконструкции.
Кэти и Дэвид Брукер, купившие в октябре двухэтажный каркасный дом по адресу 127 Root Trail в октябре за 1,5 миллиона долларов, планируют капитальный ремонт, включая пристройку, подвал, автомобильный лифт и лоджию.
115-летний дом, который находится на небольшом участке вдоль северной стороны Root Trail между North Ocean Boulevard и North County Road, является одним из немногих уцелевших жилых домов эпохи пионеров города, согласно Landmark Preservation Комиссия.
Он был построен на участке земли, принадлежащем Эноху Руту, художнику из Иллинойса, который построил на территории несколько небольших каркасных домиков для художников, а затем проложил Корневую тропу.
СВЯЗАННЫЙ: Битва за доступ к пляжу шириной 20 футов раскрывает вековую тайну в Палм-Бич
Дом Брукеров — самый большой из трех, которые они купили на участке размером 50×55 футов. Они снесли два других и сосредоточатся на ремонте и добавлении к основному строению, которое осталось в основном нетронутым.
Брукеры планируют обозначить дом площадью примерно 1200 квадратных футов и оставить его в том же месте на территории.
«Мы собираемся поставить надстройку примерно того же размера, что и существующая конструкция», — сказала Кэти Брукер.«Кроме того, мы собираемся устроить под ним подвал. Учитывая, что дом довольно компактен, участок довольно компактен, и мы действительно хотели в нем много упаковать, подвал позволит нам иметь автоподъемник.»
СВЯЗАННЫЙ: Нераскрытая тайна, но адвокат говорит, что Палм-Бич должен бороться за то, чтобы доступ к пляжу оставался открытым.
Комиссия по сохранению достопримечательностей одобрила план ремонта в среду на своем ежемесячном заседании.
«Это потрясающий проект, — сказал Рене Сильвин, председатель комиссии.«Я редко видел клиента, который был бы более чувствителен к архитектуре, чем Брукеры».
Ожидается, что строительство начнется после того, как городской совет одобрит запрос на отклонение от проекта. Следующее заседание совета назначено на 10 февраля.
«Мы хотели бы начать работу как можно скорее», — сказала Кэти Брукер. «Мы работаем над всеми строительными чертежами. Потом будет время, необходимое для получения разрешения. Мы определенно надеемся, что этой весной начнется строительство».
Мы определенно надеемся, что этой весной начнется строительство».
Брукер считает, что строительство может занять около года.Когда дом будет готов, он станет их основным местом проживания.
«Мы не можем ждать», — сказала она. «На днях мы были у нашего нового соседа — джентльмена, который живет к востоку от нас, на Коренной тропе. Мы болтали с ним, и это было так мило. Мы не можем дождаться, чтобы жить там».
@ JRWagner5
Congress.gov | Библиотека Конгресса
Секция записи Конгресса Ежедневный дайджест Сенат дом Расширения замечаний
Замечания участников
Автор: Any House Member Адамс, Альма С.[D-NC] Адерхольт, Роберт Б. [R-AL] Агилар, Пит [D-CA] Аллен, Рик У. [R-GA] Оллред, Колин З. [D-TX] Амодеи, Марк Э. [R -NV] Армстронг, Келли [R-ND] Аррингтон, Джоди К. [R-TX] Auchincloss, Jake [D-MA] Axne, Cynthia [D-IA] Бабин, Брайан [R-TX] Бэкон, Дон [R -NE] Бэрд, Джеймс Р. [R-IN] Балдерсон, Трой [R-OH] Бэнкс, Джим [R-IN] Барр, Энди [R-KY] Барраган, Нанетт Диас [D-CA] Басс, Карен [ D-CA] Битти, Джойс [D-OH] Бенц, Клифф [R-OR] Бера, Ами [D-CA] Бергман, Джек [R-MI] Бейер, Дональд С., младший [D-VA] Байс , Стефани И. [R-OK] Биггс, Энди [R-AZ] Билиракис, Гас М.[R-FL] Бишоп, Дэн [R-NC] Бишоп, Сэнфорд Д., младший [D-GA] Блуменауэр, Эрл [D-OR] Блант Рочестер, Лиза [D-DE] Боберт, Лорен [R-CO ] Бонамичи, Сюзанна [D-OR] Бост, Майк [R-IL] Bourdeaux, Carolyn [D-GA] Bowman, Jamaal [D-NY] Бойл, Брендан Ф. [D-PA] Брэди, Кевин [R-TX ] Брукс, Мо [R-AL] Браун, Энтони Г. [D-MD] Браунли, Джулия [D-CA] Бьюкенен, Верн [R-FL] Бак, Кен [R-CO] Бакшон, Ларри [R-IN ] Бадд, Тед [R-NC] Берчетт, Тим [R-TN] Берджесс, Майкл С. [R-TX] Буш, Кори [D-MO] Бустос, Cheri [D-IL] Баттерфилд, GK [D-NC ] Калверт, Кен [R-CA] Каммак, Кэт [R-FL] Карбаджал, Салуд О.[D-CA] Карденас, Тони [D-CA] Карл, Джерри Л. [R-AL] Карсон, Андре [D-IN] Картер, Эрл Л. «Бадди» [R-GA] Картер, Джон Р. [ R-TX] Картрайт, Мэтт [D-PA] Кейс, Эд [D-HI] Кастен, Шон [D-IL] Кастор, Кэти [D-FL] Кастро, Хоакин [D-TX] Cawthorn, Мэдисон [R- NC] Шабо, Стив [R-OH] Чейни, Лиз [R-WY] Чу, Джуди [D-CA] Cicilline, Дэвид Н. [D-RI] Кларк, Кэтрин М. [D-MA] Кларк, Иветт Д. . [D-NY] Кливер, Эмануэль [D-MO] Клайн, Бен [R-VA] Клауд, Майкл [R-TX] Клайберн, Джеймс Э. [D-SC] Клайд, Эндрю С. [R-GA] Коэн, Стив [D-TN] Коул, Том [R-OK] Комер, Джеймс [R-KY] Коннолли, Джеральд Э.[D-VA] Купер, Джим [D-TN] Корреа, Дж. Луис [D-CA] Коста, Джим [D-CA] Кортни, Джо [D-CT] Крейг, Энджи [D-MN] Кроуфорд, Эрик А. «Рик» [R-AR] Креншоу, Дэн [R-TX] Крист, Чарли [D-FL] Кроу, Джейсон [D-CO] Куэльяр, Генри [D-TX] Кертис, Джон Р. [R- UT] Дэвидс, Шарис [D-KS] Дэвидсон, Уоррен [R-OH] Дэвис, Дэнни К. [D-IL] Дэвис, Родни [R-IL] Дин, Мадлен [D-PA] ДеФазио, Питер А. [ D-OR] DeGette, Diana [D-CO] DeLauro, Rosa L. [D-CT] DelBene, Suzan K. [D-WA] Delgado, Antonio [D-NY] Demings, Val Butler [D-FL] DeSaulnier , Марк [D-CA] ДеДжарле, Скотт [R-TN] Дойч, Теодор Э.[D-FL] Диас-Баларт, Марио [R-FL] Дингелл, Дебби [D-MI] Доггетт, Ллойд [D-TX] Дональдс, Байрон [R-FL] Дойл, Майкл Ф. [D-PA] Дункан , Джефф [R-SC] Данн, Нил П. [R-FL] Эммер, Том [R-MN] Эскобар, Вероника [D-TX] Эшу, Анна Г. [D-CA] Эспайлат, Адриано [D-NY ] Эстес, Рон [R-KS] Эванс, Дуайт [D-PA] Фаллон, Пэт [R-TX] Feenstra, Рэнди [R-IA] Фергюсон, А. Дрю, IV [R-GA] Фишбах, Мишель [R -MN] Фицджеральд, Скотт [R-WI] Фитцпатрик, Брайан К. [R-PA] Флейшманн, Чарльз Дж. «Чак» [R-TN] Флетчер, Лиззи [D-TX] Фортенберри, Джефф [R-NE] Фостер, Билл [D-IL] Фокс, Вирджиния [R-NC] Франкель, Лоис [D-FL] Франклин, К.
[D-MD] Браунли, Джулия [D-CA] Бьюкенен, Верн [R-FL] Бак, Кен [R-CO] Бакшон, Ларри [R-IN ] Бадд, Тед [R-NC] Берчетт, Тим [R-TN] Берджесс, Майкл С. [R-TX] Буш, Кори [D-MO] Бустос, Cheri [D-IL] Баттерфилд, GK [D-NC ] Калверт, Кен [R-CA] Каммак, Кэт [R-FL] Карбаджал, Салуд О.[D-CA] Карденас, Тони [D-CA] Карл, Джерри Л. [R-AL] Карсон, Андре [D-IN] Картер, Эрл Л. «Бадди» [R-GA] Картер, Джон Р. [ R-TX] Картрайт, Мэтт [D-PA] Кейс, Эд [D-HI] Кастен, Шон [D-IL] Кастор, Кэти [D-FL] Кастро, Хоакин [D-TX] Cawthorn, Мэдисон [R- NC] Шабо, Стив [R-OH] Чейни, Лиз [R-WY] Чу, Джуди [D-CA] Cicilline, Дэвид Н. [D-RI] Кларк, Кэтрин М. [D-MA] Кларк, Иветт Д. . [D-NY] Кливер, Эмануэль [D-MO] Клайн, Бен [R-VA] Клауд, Майкл [R-TX] Клайберн, Джеймс Э. [D-SC] Клайд, Эндрю С. [R-GA] Коэн, Стив [D-TN] Коул, Том [R-OK] Комер, Джеймс [R-KY] Коннолли, Джеральд Э.[D-VA] Купер, Джим [D-TN] Корреа, Дж. Луис [D-CA] Коста, Джим [D-CA] Кортни, Джо [D-CT] Крейг, Энджи [D-MN] Кроуфорд, Эрик А. «Рик» [R-AR] Креншоу, Дэн [R-TX] Крист, Чарли [D-FL] Кроу, Джейсон [D-CO] Куэльяр, Генри [D-TX] Кертис, Джон Р. [R- UT] Дэвидс, Шарис [D-KS] Дэвидсон, Уоррен [R-OH] Дэвис, Дэнни К. [D-IL] Дэвис, Родни [R-IL] Дин, Мадлен [D-PA] ДеФазио, Питер А. [ D-OR] DeGette, Diana [D-CO] DeLauro, Rosa L. [D-CT] DelBene, Suzan K. [D-WA] Delgado, Antonio [D-NY] Demings, Val Butler [D-FL] DeSaulnier , Марк [D-CA] ДеДжарле, Скотт [R-TN] Дойч, Теодор Э.[D-FL] Диас-Баларт, Марио [R-FL] Дингелл, Дебби [D-MI] Доггетт, Ллойд [D-TX] Дональдс, Байрон [R-FL] Дойл, Майкл Ф. [D-PA] Дункан , Джефф [R-SC] Данн, Нил П. [R-FL] Эммер, Том [R-MN] Эскобар, Вероника [D-TX] Эшу, Анна Г. [D-CA] Эспайлат, Адриано [D-NY ] Эстес, Рон [R-KS] Эванс, Дуайт [D-PA] Фаллон, Пэт [R-TX] Feenstra, Рэнди [R-IA] Фергюсон, А. Дрю, IV [R-GA] Фишбах, Мишель [R -MN] Фицджеральд, Скотт [R-WI] Фитцпатрик, Брайан К. [R-PA] Флейшманн, Чарльз Дж. «Чак» [R-TN] Флетчер, Лиззи [D-TX] Фортенберри, Джефф [R-NE] Фостер, Билл [D-IL] Фокс, Вирджиния [R-NC] Франкель, Лоис [D-FL] Франклин, К. Скотт [R-FL] Фадж, Марсия Л. [D-OH] Фулчер, Расс [R-ID] Gaetz, Мэтт [R-FL] Галлахер, Майк [R-WI] Галлего, Рубен [D-AZ] Гараменди, Джон [D-CA] Гарбарино, Эндрю Р. [R-NY] Гарсия, Хесус Дж. «Чуй» [D-IL] Гарсия, Майк [R-CA] Гарсия, Сильвия Р. [D-TX] Гиббс, Боб [R-OH] Хименес, Карлос А. [R-FL] Гомерт, Луи [R-TX] Голден, Джаред Ф. [D-ME] Гомес, Джимми [D-CA] Гонсалес, Тони [R-TX] Гонсалес , Энтони [R-OH] Гонсалес, Висенте [D-TX] Гонсалес-Колон, Дженниффер [R-PR] Гуд, Боб [R-VA] Гуден, Лэнс [R-TX] Госар, Пол А. [R-AZ ] Gottheimer, Джош [D-NJ] Granger, Kay [R-TX] Graves, Garret [R-LA] Graves, Sam [R-MO] Green, Al [D-TX] Green, Mark E.[R-TN] Грин, Марджори Тейлор [R-GA] Гриффит, Х. Морган [R-VA] Гриджалва, Рауль М. [D-AZ] Гротман, Гленн [R-WI] Гость, Майкл [R-MS] Гатри, Бретт [R-KY] Хааланд, Дебра А. [D-NM] Хагедорн, Джим [R-MN] Хардер, Джош [D-CA] Харрис, Энди [R-MD] Харшбаргер, Диана [R-TN] Хартцлер, Вики [R-MO] Гастингс, Элси Л. [D-FL] Хейс, Джахана [D-CT] Херн, Кевин [R-OK] Херрелл, Иветт [R-NM] Эррера Бейтлер, Хайме [R-WA ] Хайс, Джоди Б. [R-GA] Хиггинс, Брайан [D-NY] Хиггинс, Клэй [R-LA] Хилл, Дж. Френч [R-AR] Хаймс, Джеймс А. [D-CT] Хинсон, Эшли [R-IA] Hollingsworth, Trey [R-IN] Horsford, Steven [D-NV] Houlahan, Chrissy [D-PA] Hoyer, Steny H.[D-MD] Хадсон, Ричард [R-NC] Хаффман, Джаред [D-CA] Хьюизенга, Билл [R-MI] Исса, Даррелл Э. [R-CA] Джексон, Ронни [R-TX] Джексон Ли, Шейла [D-TX] Джейкобс, Крис [R-NY] Джейкобс, Сара [D-CA] Jayapal, Pramila [D-WA] Джеффрис, Хаким С. [D-NY] Джонсон, Билл [R-OH] Джонсон, Дасти [R-SD] Джонсон, Эдди Бернис [D-TX] Джонсон, Генри К. «Хэнк» младший [D-GA] Джонсон, Майк [R-LA] Джонс, Mondaire [D-NY] Джордан, Джим [R-OH] Джойс, Дэвид П. [R-OH] Джойс, Джон [R-PA] Кахеле, Кайали [D-HI] Каптур, Марси [D-OH] Катко, Джон [R-NY] Китинг , Уильям Р.[D-MA] Келлер, Фред [R-PA] Келли, Майк [R-PA] Келли, Робин Л. [D-IL] Келли, Трент [R-MS] Кханна, Ро [D-CA] Килди, Дэниел Т. [D-MI] Килмер, Дерек [D-WA] Ким, Энди [D-NJ] Ким, Янг [R-CA] Кинд, Рон [D-WI] Кинзингер, Адам [R-IL] Киркпатрик, Энн [D-AZ] Кришнамурти, Раджа [D-IL] Кустер, Энн М.
Скотт [R-FL] Фадж, Марсия Л. [D-OH] Фулчер, Расс [R-ID] Gaetz, Мэтт [R-FL] Галлахер, Майк [R-WI] Галлего, Рубен [D-AZ] Гараменди, Джон [D-CA] Гарбарино, Эндрю Р. [R-NY] Гарсия, Хесус Дж. «Чуй» [D-IL] Гарсия, Майк [R-CA] Гарсия, Сильвия Р. [D-TX] Гиббс, Боб [R-OH] Хименес, Карлос А. [R-FL] Гомерт, Луи [R-TX] Голден, Джаред Ф. [D-ME] Гомес, Джимми [D-CA] Гонсалес, Тони [R-TX] Гонсалес , Энтони [R-OH] Гонсалес, Висенте [D-TX] Гонсалес-Колон, Дженниффер [R-PR] Гуд, Боб [R-VA] Гуден, Лэнс [R-TX] Госар, Пол А. [R-AZ ] Gottheimer, Джош [D-NJ] Granger, Kay [R-TX] Graves, Garret [R-LA] Graves, Sam [R-MO] Green, Al [D-TX] Green, Mark E.[R-TN] Грин, Марджори Тейлор [R-GA] Гриффит, Х. Морган [R-VA] Гриджалва, Рауль М. [D-AZ] Гротман, Гленн [R-WI] Гость, Майкл [R-MS] Гатри, Бретт [R-KY] Хааланд, Дебра А. [D-NM] Хагедорн, Джим [R-MN] Хардер, Джош [D-CA] Харрис, Энди [R-MD] Харшбаргер, Диана [R-TN] Хартцлер, Вики [R-MO] Гастингс, Элси Л. [D-FL] Хейс, Джахана [D-CT] Херн, Кевин [R-OK] Херрелл, Иветт [R-NM] Эррера Бейтлер, Хайме [R-WA ] Хайс, Джоди Б. [R-GA] Хиггинс, Брайан [D-NY] Хиггинс, Клэй [R-LA] Хилл, Дж. Френч [R-AR] Хаймс, Джеймс А. [D-CT] Хинсон, Эшли [R-IA] Hollingsworth, Trey [R-IN] Horsford, Steven [D-NV] Houlahan, Chrissy [D-PA] Hoyer, Steny H.[D-MD] Хадсон, Ричард [R-NC] Хаффман, Джаред [D-CA] Хьюизенга, Билл [R-MI] Исса, Даррелл Э. [R-CA] Джексон, Ронни [R-TX] Джексон Ли, Шейла [D-TX] Джейкобс, Крис [R-NY] Джейкобс, Сара [D-CA] Jayapal, Pramila [D-WA] Джеффрис, Хаким С. [D-NY] Джонсон, Билл [R-OH] Джонсон, Дасти [R-SD] Джонсон, Эдди Бернис [D-TX] Джонсон, Генри К. «Хэнк» младший [D-GA] Джонсон, Майк [R-LA] Джонс, Mondaire [D-NY] Джордан, Джим [R-OH] Джойс, Дэвид П. [R-OH] Джойс, Джон [R-PA] Кахеле, Кайали [D-HI] Каптур, Марси [D-OH] Катко, Джон [R-NY] Китинг , Уильям Р.[D-MA] Келлер, Фред [R-PA] Келли, Майк [R-PA] Келли, Робин Л. [D-IL] Келли, Трент [R-MS] Кханна, Ро [D-CA] Килди, Дэниел Т. [D-MI] Килмер, Дерек [D-WA] Ким, Энди [D-NJ] Ким, Янг [R-CA] Кинд, Рон [D-WI] Кинзингер, Адам [R-IL] Киркпатрик, Энн [D-AZ] Кришнамурти, Раджа [D-IL] Кустер, Энн М. [D-NH] Кустофф, Дэвид [R-TN] Лахуд, Дарин [R-IL] Ламальфа, Дуг [R-CA] Лэмб, Конор [D-PA] Лэмборн, Дуг [R-CO] Ланжевен, Джеймс Р. [D-RI] Ларсен, Рик [D-WA] Ларсон, Джон Б. [D-CT] Латта, Роберт Э. [R-OH ] Латернер, Джейк [R-KS] Лоуренс, Бренда Л.[D-MI] Лоусон, Эл, младший [D-FL] Ли, Барбара [D-CA] Ли, Сьюзи [D-NV] Леже Фернандес, Тереза [D-NM] Леско, Дебби [R-AZ] Левин , Энди [D-MI] Левин, Майк [D-CA] Лью, Тед [D-CA] Лофгрен, Зои [D-CA] Лонг, Билли [R-MO] Лоудермилк, Барри [R-GA] Ловенталь, Алан С. [D-CA] Лукас, Фрэнк Д. [R-OK] Люткемейер, Блейн [R-MO] Лурия, Элейн Г. [D-VA] Линч, Стивен Ф. [D-MA] Мейс, Нэнси [R -SC] Малиновски, Том [D-NJ] Маллиотакис, Николь [R-NY] Мэлони, Кэролин Б. [D-NY] Мэлони, Шон Патрик [D-NY] Манн, Трейси [R-KS] Мэннинг, Кэти Э. .[D-NC] Мэсси, Томас [R-KY] Маст, Брайан Дж. [R-FL] Мацуи, Дорис О. [D-CA] МакБэт, Люси [D-GA] Маккарти, Кевин [R-CA] МакКол , Майкл Т. [R-TX] Макклейн, Лиза К. [R-MI] МакКлинток, Том [R-CA] МакКоллум, Бетти [D-MN] МакИчин, А. Дональд [D-VA] Макговерн, Джеймс П. [D-MA] МакГенри, Патрик Т. [R-NC] МакКинли, Дэвид Б. [R-WV] МакМоррис Роджерс, Кэти [R-WA] Макнерни, Джерри [D-CA] Микс, Грегори В. [D- NY] Мейер, Питер [R-MI] Мэн, Грейс [D-NY] Meuser, Daniel [R-PA] Mfume, Kweisi [D-MD] Миллер, Кэрол Д. [R-WV] Миллер, Мэри Э. [ R-IL] Миллер-Микс, Марианнетт [R-IA] Мооленаар, Джон Р.[R-MI] Муни, Александр X. [R-WV] Мур, Барри [R-AL] Мур, Блейк Д. [R-UT] Мур, Гвен [D-WI] Морелль, Джозеф Д. [D-NY ] Моултон, Сет [D-MA] Мрван, Фрэнк Дж. [D-IN] Маллин, Маркуэйн [R-OK] Мерфи, Грегори [R-NC] Мерфи, Стефани Н. [D-FL] Надлер, Джерролд [D -NY] Наполитано, Грейс Ф. [D-CA] Нил, Ричард Э. [D-MA] Негусе, Джо [D-CO] Нелс, Трой Э. [R-TX] Ньюхаус, Дэн [R-WA] Ньюман , Мари [D-IL] Норкросс, Дональд [D-NJ] Норман, Ральф [R-SC] Нортон, Элеонора Холмс [D-DC] Нуньес, Девин [R-CA] О’Халлеран, Том [D-AZ] Обернолти, Джей [R-CA] Окасио-Кортес, Александрия [D-NY] Омар, Ильхан [D-MN] Оуэнс, Берджесс [R-UT] Палаццо, Стивен М.[R-MS] Паллоне, Фрэнк, младший [D-NJ] Палмер, Гэри Дж.
[D-NH] Кустофф, Дэвид [R-TN] Лахуд, Дарин [R-IL] Ламальфа, Дуг [R-CA] Лэмб, Конор [D-PA] Лэмборн, Дуг [R-CO] Ланжевен, Джеймс Р. [D-RI] Ларсен, Рик [D-WA] Ларсон, Джон Б. [D-CT] Латта, Роберт Э. [R-OH ] Латернер, Джейк [R-KS] Лоуренс, Бренда Л.[D-MI] Лоусон, Эл, младший [D-FL] Ли, Барбара [D-CA] Ли, Сьюзи [D-NV] Леже Фернандес, Тереза [D-NM] Леско, Дебби [R-AZ] Левин , Энди [D-MI] Левин, Майк [D-CA] Лью, Тед [D-CA] Лофгрен, Зои [D-CA] Лонг, Билли [R-MO] Лоудермилк, Барри [R-GA] Ловенталь, Алан С. [D-CA] Лукас, Фрэнк Д. [R-OK] Люткемейер, Блейн [R-MO] Лурия, Элейн Г. [D-VA] Линч, Стивен Ф. [D-MA] Мейс, Нэнси [R -SC] Малиновски, Том [D-NJ] Маллиотакис, Николь [R-NY] Мэлони, Кэролин Б. [D-NY] Мэлони, Шон Патрик [D-NY] Манн, Трейси [R-KS] Мэннинг, Кэти Э. .[D-NC] Мэсси, Томас [R-KY] Маст, Брайан Дж. [R-FL] Мацуи, Дорис О. [D-CA] МакБэт, Люси [D-GA] Маккарти, Кевин [R-CA] МакКол , Майкл Т. [R-TX] Макклейн, Лиза К. [R-MI] МакКлинток, Том [R-CA] МакКоллум, Бетти [D-MN] МакИчин, А. Дональд [D-VA] Макговерн, Джеймс П. [D-MA] МакГенри, Патрик Т. [R-NC] МакКинли, Дэвид Б. [R-WV] МакМоррис Роджерс, Кэти [R-WA] Макнерни, Джерри [D-CA] Микс, Грегори В. [D- NY] Мейер, Питер [R-MI] Мэн, Грейс [D-NY] Meuser, Daniel [R-PA] Mfume, Kweisi [D-MD] Миллер, Кэрол Д. [R-WV] Миллер, Мэри Э. [ R-IL] Миллер-Микс, Марианнетт [R-IA] Мооленаар, Джон Р.[R-MI] Муни, Александр X. [R-WV] Мур, Барри [R-AL] Мур, Блейк Д. [R-UT] Мур, Гвен [D-WI] Морелль, Джозеф Д. [D-NY ] Моултон, Сет [D-MA] Мрван, Фрэнк Дж. [D-IN] Маллин, Маркуэйн [R-OK] Мерфи, Грегори [R-NC] Мерфи, Стефани Н. [D-FL] Надлер, Джерролд [D -NY] Наполитано, Грейс Ф. [D-CA] Нил, Ричард Э. [D-MA] Негусе, Джо [D-CO] Нелс, Трой Э. [R-TX] Ньюхаус, Дэн [R-WA] Ньюман , Мари [D-IL] Норкросс, Дональд [D-NJ] Норман, Ральф [R-SC] Нортон, Элеонора Холмс [D-DC] Нуньес, Девин [R-CA] О’Халлеран, Том [D-AZ] Обернолти, Джей [R-CA] Окасио-Кортес, Александрия [D-NY] Омар, Ильхан [D-MN] Оуэнс, Берджесс [R-UT] Палаццо, Стивен М.[R-MS] Паллоне, Фрэнк, младший [D-NJ] Палмер, Гэри Дж. [R-AL] Панетта, Джимми [D-CA] Паппас, Крис [D-NH] Паскрелл, Билл, мл. [D -NJ] Пейн, Дональд М., младший [D-NJ] Пелоси, Нэнси [D-CA] Пенс, Грег [R-IN] Перлмуттер, Эд [D-CO] Перри, Скотт [R-PA] Питерс, Скотт Х. [D-CA] Пфлюгер, Август [R-TX] Филлипс, Дин [D-MN] Пингри, Челли [D-ME] Пласкетт, Стейси Э. [D-VI] Покан, Марк [D-WI] Портер, Кэти [D-CA] Поузи, Билл [R-FL] Прессли, Аянна [D-MA] Прайс, Дэвид Э. [D-NC] Куигли, Майк [D-IL] Радваген, Аумуа Амата Коулман [R- AS] Раскин, Джейми [D-MD] Рид, Том [R-NY] Решенталер, Гай [R-PA] Райс, Кэтлин М.[D-NY] Райс, Том [R-SC] Ричмонд, Седрик Л. [D-LA] Роджерс, Гарольд [R-KY] Роджерс, Майк Д. [R-AL] Роуз, Джон В. [R-TN ] Розендейл старший, Мэтью М. [R-MT] Росс, Дебора К. [D-NC] Роузер, Дэвид [R-NC] Рой, Чип [R-TX] Ройбал-Аллард, Люсиль [D-CA] Руис , Рауль [D-CA] Рупперсбергер, Калифорния Датч [D-MD] Раш, Бобби Л. [D-IL] Резерфорд, Джон Х. [R-FL] Райан, Тим [D-OH] Саблан, Грегорио Килили Камачо [ D-MP] Салазар, Мария Эльвира [R-FL] Санчес, Линда Т. [D-CA] Сан-Николас, Майкл FQ [D-GU] Сарбейнс, Джон П. [D-MD] Скализ, Стив [R-LA ] Скэнлон, Мэри Гей [D-PA] Шаковски, Дженис Д.[D-IL] Шифф, Адам Б. [D-CA] Шнайдер, Брэдли Скотт [D-IL] Шрейдер, Курт [D-OR] Шриер, Ким [D-WA] Швейкерт, Дэвид [R-AZ] Скотт, Остин [R-GA] Скотт, Дэвид [D-GA] Скотт, Роберт С. «Бобби» [D-VA] Сешнс, Пит [R-TX] Сьюэлл, Терри А. [D-AL] Шерман, Брэд [D -CA] Шерилл, Мики [D-NJ] Симпсон, Майкл К. [R-ID] Sires, Альбио [D-NJ] Slotkin, Элисса [D-MI] Смит, Адам [D-WA] Смит, Адриан [R -NE] Смит, Кристофер Х. [R-NJ] Смит, Джейсон [R-MO] Смакер, Ллойд [R-PA] Сото, Даррен [D-FL] Спанбергер, Эбигейл Дэвис [D-VA] Спарц, Виктория [ R-IN] Шпейер, Джеки [D-CA] Стэнтон, Грег [D-AZ] Стаубер, Пит [R-MN] Стил, Мишель [R-CA] Стефаник, Элиза М.[R-NY] Стейл, Брайан [R-WI] Steube, В. Грегори [R-FL] Стивенс, Хейли М. [D-MI] Стюарт, Крис [R-UT] Стиверс, Стив [R-OH] Стрикленд , Мэрилин [D-WA] Суоззи, Томас Р. [D-NY] Swalwell, Эрик [D-CA] Такано, Марк [D-CA] Тейлор, Ван [R-TX] Тенни, Клаудия [R-NY] Томпсон , Бенни Г.
[R-AL] Панетта, Джимми [D-CA] Паппас, Крис [D-NH] Паскрелл, Билл, мл. [D -NJ] Пейн, Дональд М., младший [D-NJ] Пелоси, Нэнси [D-CA] Пенс, Грег [R-IN] Перлмуттер, Эд [D-CO] Перри, Скотт [R-PA] Питерс, Скотт Х. [D-CA] Пфлюгер, Август [R-TX] Филлипс, Дин [D-MN] Пингри, Челли [D-ME] Пласкетт, Стейси Э. [D-VI] Покан, Марк [D-WI] Портер, Кэти [D-CA] Поузи, Билл [R-FL] Прессли, Аянна [D-MA] Прайс, Дэвид Э. [D-NC] Куигли, Майк [D-IL] Радваген, Аумуа Амата Коулман [R- AS] Раскин, Джейми [D-MD] Рид, Том [R-NY] Решенталер, Гай [R-PA] Райс, Кэтлин М.[D-NY] Райс, Том [R-SC] Ричмонд, Седрик Л. [D-LA] Роджерс, Гарольд [R-KY] Роджерс, Майк Д. [R-AL] Роуз, Джон В. [R-TN ] Розендейл старший, Мэтью М. [R-MT] Росс, Дебора К. [D-NC] Роузер, Дэвид [R-NC] Рой, Чип [R-TX] Ройбал-Аллард, Люсиль [D-CA] Руис , Рауль [D-CA] Рупперсбергер, Калифорния Датч [D-MD] Раш, Бобби Л. [D-IL] Резерфорд, Джон Х. [R-FL] Райан, Тим [D-OH] Саблан, Грегорио Килили Камачо [ D-MP] Салазар, Мария Эльвира [R-FL] Санчес, Линда Т. [D-CA] Сан-Николас, Майкл FQ [D-GU] Сарбейнс, Джон П. [D-MD] Скализ, Стив [R-LA ] Скэнлон, Мэри Гей [D-PA] Шаковски, Дженис Д.[D-IL] Шифф, Адам Б. [D-CA] Шнайдер, Брэдли Скотт [D-IL] Шрейдер, Курт [D-OR] Шриер, Ким [D-WA] Швейкерт, Дэвид [R-AZ] Скотт, Остин [R-GA] Скотт, Дэвид [D-GA] Скотт, Роберт С. «Бобби» [D-VA] Сешнс, Пит [R-TX] Сьюэлл, Терри А. [D-AL] Шерман, Брэд [D -CA] Шерилл, Мики [D-NJ] Симпсон, Майкл К. [R-ID] Sires, Альбио [D-NJ] Slotkin, Элисса [D-MI] Смит, Адам [D-WA] Смит, Адриан [R -NE] Смит, Кристофер Х. [R-NJ] Смит, Джейсон [R-MO] Смакер, Ллойд [R-PA] Сото, Даррен [D-FL] Спанбергер, Эбигейл Дэвис [D-VA] Спарц, Виктория [ R-IN] Шпейер, Джеки [D-CA] Стэнтон, Грег [D-AZ] Стаубер, Пит [R-MN] Стил, Мишель [R-CA] Стефаник, Элиза М.[R-NY] Стейл, Брайан [R-WI] Steube, В. Грегори [R-FL] Стивенс, Хейли М. [D-MI] Стюарт, Крис [R-UT] Стиверс, Стив [R-OH] Стрикленд , Мэрилин [D-WA] Суоззи, Томас Р. [D-NY] Swalwell, Эрик [D-CA] Такано, Марк [D-CA] Тейлор, Ван [R-TX] Тенни, Клаудия [R-NY] Томпсон , Бенни Г. [D-MS] Томпсон, Гленн [R-PA] Томпсон, Майк [D-CA] Тиффани, Томас П. [R-WI] Тиммонс, Уильям Р. IV [R-SC] Титус, Дина [ D-NV] Тлаиб, Рашида [D-MI] Тонко, Пол [D-NY] Торрес, Норма Дж. [D-CA] Торрес, Ричи [D-NY] Трахан, Лори [D-MA] Трон, Дэвид Дж. .[D-MD] Тернер, Майкл Р. [R-OH] Андервуд, Лорен [D-IL] Аптон, Фред [R-MI] Валадао, Дэвид Г. [R-CA] Ван Дрю, Джефферсон [R-NJ] Ван Дайн, Бет [R-Техас] Варгас, Хуан [D-CA] Визи, Марк А. [D-TX] Вела, Филемон [D-TX] Веласкес, Нидия М. [D-Нью-Йорк] Вагнер, Энн [R -MO] Уолберг, Тим [R-MI] Валорски, Джеки [R-IN] Вальс, Майкл [R-FL] Вассерман Шульц, Дебби [D-FL] Уотерс, Максин [D-CA] Уотсон Коулман, Бонни [D -NJ] Вебер, Рэнди К., старший [R-TX] Вебстер, Дэниел [R-FL] Велч, Питер [D-VT] Венструп, Брэд Р. [R-OH] Вестерман, Брюс [R-AR] Векстон, Дженнифер [D-VA] Уайлд, Сьюзан [D-PA] Уильямс, Nikema [D-GA] Уильямс, Роджер [R-TX] Уилсон, Фредерика С.[D-FL] Уилсон, Джо [R-SC] Виттман, Роберт Дж. [R-VA] Womack, Стив [R-AR] Райт, Рон [R-TX] Ярмут, Джон А. [D-KY] Янг , Дон [R-AK] Зельдин, Ли М. [R-NY] Любой член Сената Болдуин, Тэмми [D-WI] Баррассо, Джон [R-WY] Беннет, Майкл Ф. [D-CO] Блэкберн, Марша [ R-TN] Блюменталь, Ричард [D-CT] Блант, Рой [R-MO] Букер, Кори А. [D-NJ] Бузман, Джон [R-AR] Браун, Майк [R-IN] Браун, Шеррод [ D-OH] Берр, Ричард [R-NC] Кантуэлл, Мария [D-WA] Капито, Шелли Мур [R-WV] Кардин, Бенджамин Л. [D-MD] Карпер, Томас Р. [D-DE] Кейси , Роберт П., Младший [D-PA] Кэссиди, Билл [R-LA] Коллинз, Сьюзан М. [R-ME] Кунс, Кристофер А. [D-DE] Корнин, Джон [R-TX] Кортез Масто, Кэтрин [D -NV] Коттон, Том [R-AR] Крамер, Кевин [R-ND] Крапо, Майк [R-ID] Круз, Тед [R-TX] Дейнс, Стив [R-MT] Дакворт, Тэмми [D-IL ] Дурбин, Ричард Дж. [D-IL] Эрнст, Джони [R-IA] Файнштейн, Dianne [D-CA] Фишер, Деб [R-NE] Гиллибранд, Кирстен Э. [D-NY] Грэм, Линдси [R -SC] Грассли, Чак [R-IA] Хагерти, Билл [R-TN] Харрис, Камала Д. [D-CA] Хассан, Маргарет Вуд [D-NH] Хоули, Джош [R-MO] Генрих, Мартин [ D-NM] Гикенлупер, Джон В.[D-CO] Хироно, Мази К. [D-HI] Хувен, Джон [R-ND] Хайд-Смит, Синди [R-MS] Инхоф, Джеймс М.
[D-MS] Томпсон, Гленн [R-PA] Томпсон, Майк [D-CA] Тиффани, Томас П. [R-WI] Тиммонс, Уильям Р. IV [R-SC] Титус, Дина [ D-NV] Тлаиб, Рашида [D-MI] Тонко, Пол [D-NY] Торрес, Норма Дж. [D-CA] Торрес, Ричи [D-NY] Трахан, Лори [D-MA] Трон, Дэвид Дж. .[D-MD] Тернер, Майкл Р. [R-OH] Андервуд, Лорен [D-IL] Аптон, Фред [R-MI] Валадао, Дэвид Г. [R-CA] Ван Дрю, Джефферсон [R-NJ] Ван Дайн, Бет [R-Техас] Варгас, Хуан [D-CA] Визи, Марк А. [D-TX] Вела, Филемон [D-TX] Веласкес, Нидия М. [D-Нью-Йорк] Вагнер, Энн [R -MO] Уолберг, Тим [R-MI] Валорски, Джеки [R-IN] Вальс, Майкл [R-FL] Вассерман Шульц, Дебби [D-FL] Уотерс, Максин [D-CA] Уотсон Коулман, Бонни [D -NJ] Вебер, Рэнди К., старший [R-TX] Вебстер, Дэниел [R-FL] Велч, Питер [D-VT] Венструп, Брэд Р. [R-OH] Вестерман, Брюс [R-AR] Векстон, Дженнифер [D-VA] Уайлд, Сьюзан [D-PA] Уильямс, Nikema [D-GA] Уильямс, Роджер [R-TX] Уилсон, Фредерика С.[D-FL] Уилсон, Джо [R-SC] Виттман, Роберт Дж. [R-VA] Womack, Стив [R-AR] Райт, Рон [R-TX] Ярмут, Джон А. [D-KY] Янг , Дон [R-AK] Зельдин, Ли М. [R-NY] Любой член Сената Болдуин, Тэмми [D-WI] Баррассо, Джон [R-WY] Беннет, Майкл Ф. [D-CO] Блэкберн, Марша [ R-TN] Блюменталь, Ричард [D-CT] Блант, Рой [R-MO] Букер, Кори А. [D-NJ] Бузман, Джон [R-AR] Браун, Майк [R-IN] Браун, Шеррод [ D-OH] Берр, Ричард [R-NC] Кантуэлл, Мария [D-WA] Капито, Шелли Мур [R-WV] Кардин, Бенджамин Л. [D-MD] Карпер, Томас Р. [D-DE] Кейси , Роберт П., Младший [D-PA] Кэссиди, Билл [R-LA] Коллинз, Сьюзан М. [R-ME] Кунс, Кристофер А. [D-DE] Корнин, Джон [R-TX] Кортез Масто, Кэтрин [D -NV] Коттон, Том [R-AR] Крамер, Кевин [R-ND] Крапо, Майк [R-ID] Круз, Тед [R-TX] Дейнс, Стив [R-MT] Дакворт, Тэмми [D-IL ] Дурбин, Ричард Дж. [D-IL] Эрнст, Джони [R-IA] Файнштейн, Dianne [D-CA] Фишер, Деб [R-NE] Гиллибранд, Кирстен Э. [D-NY] Грэм, Линдси [R -SC] Грассли, Чак [R-IA] Хагерти, Билл [R-TN] Харрис, Камала Д. [D-CA] Хассан, Маргарет Вуд [D-NH] Хоули, Джош [R-MO] Генрих, Мартин [ D-NM] Гикенлупер, Джон В.[D-CO] Хироно, Мази К. [D-HI] Хувен, Джон [R-ND] Хайд-Смит, Синди [R-MS] Инхоф, Джеймс М. [R-OK] Джонсон, Рон [R-WI ] Кейн, Тим [D-VA] Келли, Марк [D-AZ] Кеннеди, Джон [R-LA] Кинг, Ангус С., младший [I-ME] Klobuchar, Amy [D-MN] Ланкфорд, Джеймс [ R-OK] Лихи, Патрик Дж. [D-VT] Ли, Майк [R-UT] Леффлер, Келли [R-GA] Лухан, Бен Рэй [D-NM] Ламмис, Синтия М. [R-WY] Манчин , Джо, III [D-WV] Марки, Эдвард Дж. [D-MA] Маршалл, Роджер В. [R-KS] МакКоннелл, Митч [R-KY] Менендес, Роберт [D-NJ] Меркли, Джефф [D -ИЛИ] Моран, Джерри [R-KS] Мурковски, Лиза [R-AK] Мерфи, Кристофер [D-CT] Мюррей, Пэтти [D-WA] Оссофф, Джон [D-GA] Падилья, Алекс [D-CA ] Пол, Рэнд [R-KY] Питерс, Гэри К.[D-MI] Портман, Роб [R-OH] Рид, Джек [D-RI] Риш, Джеймс Э. [R-ID] Ромни, Митт [R-UT] Розен, Джеки [D-NV] Раундс, Майк [R-SD] Рубио, Марко [R-FL] Сандерс, Бернард [I-VT] Sasse, Бен [R-NE] Schatz, Брайан [D-HI] Шумер, Чарльз Э. [D-NY] Скотт, Рик [R-FL] Скотт, Тим [R-SC] Шахин, Жанна [D-NH] Шелби, Ричард К. [R-AL] Синема, Кирстен [D-AZ] Смит, Тина [D-MN] Стабеноу, Дебби [D-MI] Салливан, Дэн [R-AK] Тестер, Джон [D-MT] Тьюн, Джон [R-SD] Тиллис, Том [R-NC] Туми, Пэт [R-PA] Тубервиль, Томми [R -AL] Ван Холлен, Крис [D-MD] Уорнер, Марк Р.[D-VA] Варнок, Рафаэль Г. [D-GA] Уоррен, Элизабет [D-MA] Уайтхаус, Шелдон [D-RI] Уикер, Роджер Ф. [R-MS] Уайден, Рон [D-OR] Янг , Тодд [R-IN]
[R-OK] Джонсон, Рон [R-WI ] Кейн, Тим [D-VA] Келли, Марк [D-AZ] Кеннеди, Джон [R-LA] Кинг, Ангус С., младший [I-ME] Klobuchar, Amy [D-MN] Ланкфорд, Джеймс [ R-OK] Лихи, Патрик Дж. [D-VT] Ли, Майк [R-UT] Леффлер, Келли [R-GA] Лухан, Бен Рэй [D-NM] Ламмис, Синтия М. [R-WY] Манчин , Джо, III [D-WV] Марки, Эдвард Дж. [D-MA] Маршалл, Роджер В. [R-KS] МакКоннелл, Митч [R-KY] Менендес, Роберт [D-NJ] Меркли, Джефф [D -ИЛИ] Моран, Джерри [R-KS] Мурковски, Лиза [R-AK] Мерфи, Кристофер [D-CT] Мюррей, Пэтти [D-WA] Оссофф, Джон [D-GA] Падилья, Алекс [D-CA ] Пол, Рэнд [R-KY] Питерс, Гэри К.[D-MI] Портман, Роб [R-OH] Рид, Джек [D-RI] Риш, Джеймс Э. [R-ID] Ромни, Митт [R-UT] Розен, Джеки [D-NV] Раундс, Майк [R-SD] Рубио, Марко [R-FL] Сандерс, Бернард [I-VT] Sasse, Бен [R-NE] Schatz, Брайан [D-HI] Шумер, Чарльз Э. [D-NY] Скотт, Рик [R-FL] Скотт, Тим [R-SC] Шахин, Жанна [D-NH] Шелби, Ричард К. [R-AL] Синема, Кирстен [D-AZ] Смит, Тина [D-MN] Стабеноу, Дебби [D-MI] Салливан, Дэн [R-AK] Тестер, Джон [D-MT] Тьюн, Джон [R-SD] Тиллис, Том [R-NC] Туми, Пэт [R-PA] Тубервиль, Томми [R -AL] Ван Холлен, Крис [D-MD] Уорнер, Марк Р.[D-VA] Варнок, Рафаэль Г. [D-GA] Уоррен, Элизабет [D-MA] Уайтхаус, Шелдон [D-RI] Уикер, Роджер Ф. [R-MS] Уайден, Рон [D-OR] Янг , Тодд [R-IN]
Калькулятор кубического корня — Калькулятор капитана
Калькулятор кубического корня
Обратите внимание: для работы этого калькулятора требуется JavaScript.Определение — Что такое кубический корень?
Кубический корень числа — это число, которое при трехкратном умножении на само себя (число x число x число) дает исходное число.
Например, кубический корень из 27 равен 3, так как 3 x 3 x 3 = 27.
Кубический корень из 125 равен 5, так как 5 x 5 x 5 = 125.
В отличие от квадратного корня, кубический корень всегда положителен.
Корень, противоположный кубу, вычисляется в кубе (степень 3).
В геометрии кубический корень может использоваться, чтобы найти длину стороны куба, когда объем известен.
— Как вычислить кубический корень числа
Нет быстрой формулы для вычисления кубического корня.Большинство калькуляторов используют метод проб и ошибок.
Пробная версия и ошибка
Большинство калькуляторов используют метод проб и ошибок, чтобы найти кубический корень. Метод проб и ошибок хорошо работает для идеальных кубиков. Для несовершенных кубов это может занять очень много времени из-за большого количества десятичных знаков.
Чтобы найти кубированный корень методом проб и ошибок:
- Угадайте число, которое, по вашему мнению, может быть кубическим корнем.
- Умножьте число x число x число.
- Если результат слишком низкий, угадайте другое большее число.Если результат слишком высокий, угадайте другое меньшее число.
- Повторяйте, пока не найдете кубический корень.
Пример. Методом проб и ошибок найти кубический корень из 512:
- Попробуйте число — 5: 5 x 5 x 5 = 125 (слишком мало)
- Попробуйте число больше 5-10-10 x 10 x 10 = 1000 (слишком большое)
- Попробуйте число от 5 и 10-8-8 x 8 x 8 = 512 (ответ)
Метод 2 — Быстрое нахождение корней из чисел идеального куба
Этот метод позволяет быстрее найти корень идеального числа куба.Однако, если число не является числом идеального кубического корня, этот метод не даст ответа.
Как вводить кубический корень?
- На клавиатуре Windows введите 3. Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный». Затем откройте карту символов, найдите символ квадратного корня и скопируйте / вставьте его в документ.
- На клавиатуре Mac введите 3.
 Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный.Затем нажмите option + v для символа квадратного корня.
Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный.Затем нажмите option + v для символа квадратного корня. - В HTML или веб-документе заключите «3» в теги ( 3 ). После 3 используйте символ квадратного корня √.
Таблица чисел кубического корня — Perfect Cubes
- 3 √1 = 1, как 1 x 1 x 1 = 1
- 3 √8 = 2, как 2 x 2 x 2 = 8
- 3 √27 = 3, как 3 x 3 x 3 = 27
- 3 √64 = 4, поскольку 4 x 4 x 4 = 64
- 3 √125 = 5, поскольку 5 x 5 x 5 = 125
- 3 √216 = 6, как 6 x 6 x 6 = 216
- 3 √343 = 7, как 7 x 7 x 7 = 343
- 3 √512 = 8, как 8 x 8 x 8 = 4096
- 3 √ 729 = 9, поскольку 9 x 9 x 9 = 729
- 3 √1000 = 10, поскольку 10 x 10 x 10 = 1000
- 3 √1331 = 11, поскольку 11 x 11 x 11 = 1,331
- 3 √1728 = 12, поскольку 12 x 12 x 12 = 1,728
- 3 √3375 = 15, поскольку 15 x 15 x 15 = 3,375
- 3 √4913 = 17, как 17 x 17 x 17 = 4,913
- 3 √8000 = 20, поскольку 20 x 20 x 20 = 8000
- 3 √15625 = 25, поскольку 25 x 25 x 25 = 15,625
- 3 √27000 = 30, как 30 Икс 30 x 30 = 27000
- 3 √35936 = 33, так как 33 x 33 x 33 = 35,936
- 3 √
= 45, так как 45 x 45 x 45 = 91,125 - 3 √125000 = 50 , как 50 x 50 x 50 = 125,000
- 3 √216000 = 60, как 60 x 60 x 60 = 216,000
- 3 √421875 = 75, как 75 x 75 x 75 = 421,875
- 3 √1000000 = 100, так как 100 x 100 x 100 = 1000000
Таблица кубических корневых номеров
Обратите внимание: для работы этой таблицы требуется JavaScript.Источники и другие ресурсы
.

 Поддержка
Поддержка На 5-7 дней может быть также наложен бандаж, который будет защищать травмированную десну от механических воздействий.
На 5-7 дней может быть также наложен бандаж, который будет защищать травмированную десну от механических воздействий. 45
45
 Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный.Затем нажмите option + v для символа квадратного корня.
Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный.Затем нажмите option + v для символа квадратного корня.