Опубликовано 1.2. Корень n-й степени
1.2. Корень n-й степениВ 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).
Перейдем к изучению корней степени n для произвольного натурального числа n≥2.
Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .
Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.
Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.
Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается
Например, 1253=5,−1287=−2,07=0.
Стр. 11Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.
Согласно определению, когда n нечетное, то при любом значении а верно равенство
(an)n=a.
Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.
Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому
при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.
Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.
Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается
Например, 814=3,646=2.
Утверждение о существовании корня четной степени из любого положительного
числа мы принимаем без доказательства.
Согласно определению, когда n четное, то при любом положительном значении а верно
равенство
(an)n=a.
Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.
Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то
Стр. 12не существует корня четной степени из отрицательного числа.
Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .
При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении
записи an слово «арифметический» обычно пропускают).
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень n-й степени из числа a — это значит найти значение выражения an.
Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.
Например, не имеют смысла выражения −814 и −646.
Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство
1
1 (an)n=a.
1
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования
в алгебраическую символику. В частности, знаком корня служил символ Rx (от латинского слова radix — корень).
Так,
выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.
Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
Знак еще называют радикалом.
Стр. 13Пример 1. Верно ли, что:
а) (−2)44=−2;
б) (−2)77=−2?
Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.
Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.
б) По определению корень n-й степени из числа
а (n — нечетное
число) является числом, n-я степень которого равна
подкоренному выражению а.
Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.
Пример 2. Решить уравнение:
а) x3=7;
б) x4=5.
Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т. е. x=±54.
Ответ: а) 73; б) ±54.
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение: x4=5 ⇔ x=±54.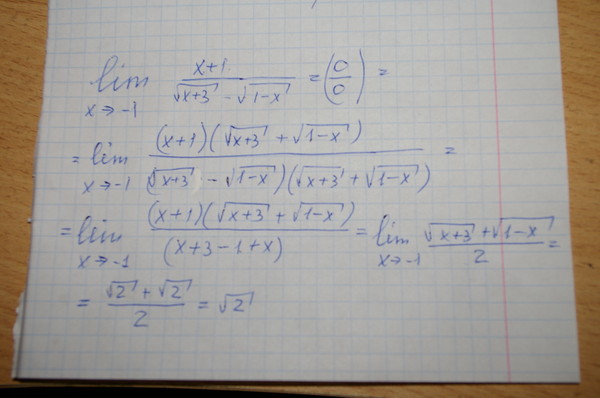
Ответ: ±54.
Пример 3. Решить уравнение:
а) (x8)8=x;
б) (x13)13=x.
Стр. 14Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.
Ответ: а) [0;+∞); б) R.
Пример 4. Решить уравнение
x12−63×6−64=0.
Решение. Обозначим x6=t, тогда получим уравнение
t2−63t−64=0.
Корни этого уравнения
t1=64,t2=−1.
Таким образом, имеем
x6=64 или x6=−1,
откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).
Ответ: ±2.
1
1Какое число называется корнем n-й степени из числа а?
1
2
2Сколько существует корней четной степени n из положительного числа а?
2
3
3Корень какой степени существует из любого числа а?
3
4
4Какой корень n-й степени из числа а называется арифметическим?
4
5
5При каких значениях а верно равенство (an)n=a, если:
а) n — нечетное число;
б) n — четное число?
5
Упражнения
1.24°
1.24°Используя определение арифметического корня n-й степени, докажите, что:
1) 2564=4;
2) 102410=2;
3) 7296=3;
4) 65618=3;
5) 409612=2;
6) 14 6414=11.
1.24°
Стр. 151.25°
1.25°Верно ли, что:
1) число −4 является корнем четвертой степени из числа 256;
2) число −0,3 является корнем четвертой степени из числа −0,0081?
1.25°
1.26°
1.26°Верно ли, что:
1) −17283=−12;
2) −33753=15;
3) −16 8075=7;
4) −77765=−6?
1.26°
1.27°
1.27°Найдите арифметический квадратный корень из числа:
1) 16;
2) 49;
3) 0;
4) 1;
5) 0,81;
6) 0,25;
7) 2,25;
8) 1,21;
9) 36169;
10) 144289;
11) 169100;
12) 81256.
1.27°
1.28°
1.28°Найдите кубический корень из числа:
1) 1;
2) 0;
3) 343;
4) 8;
5) 127;
6) 0,027;
7) 0,001;
8) 64125.
1.28°
1.29°
1.29°Найдите арифметический корень четвертой степени из числа:
1) 0;
2) 1;
3) 16;
4) 0,0016;
5) 1681;
6) 256625;
7) 0,0001;
8) 0,1296.
1.29°
Вычислите (1.30—1.42).
1.30°
1.30°1) 9,16,25,49,81,100;
2) 0,16,0,09,0,01,0,04,0,0025,0,0001;
3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;
4) 164,6254,10 0004,0,00814,0,000000164,24014;
5) 325,10245,2435,0,031255,100 0005,0,000015;
6) 646,7296,15 6256,40966,0,0466566,1 000 0006.
1.30°
1.31°
1.31°1) −10003;
2) −115;
3) −643;
4) −10245;
5) −1273;
6) −3433;
7) −272163;
8) −31255;
9) −0,000325.
1.31°
Стр. 161.32
1.321) ⎛⎝−33⎞⎠3;
2) ⎛⎝−145⎞⎠5;
3) ⎛⎝−307⎞⎠7;
4) ⎛⎝−1511⎞⎠11;
5) ⎛⎝−69⎞⎠9;
6) ⎛⎝−9915⎞⎠15.
1.32
1.33
1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;
2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.
1.33
1.34
1.341) ⎛⎝53⎞⎠6;
2) ⎛⎝0,14⎞⎠12;
3) ⎛⎝1125⎞⎠10;
4) ⎛⎝2136⎞⎠18;
5) ⎛⎝567⎞⎠21;
6) ⎛⎝239⎞⎠36.
1.34
1.35
1.351) ⎛⎝35⎞⎠10;
2) ⎛⎝534⎞⎠48;
3) ⎛⎝7610⎞⎠120;
4) ⎛⎝643⎞⎠12;
5) ⎛⎝108⎞⎠16;
6) ⎛⎝1294⎞⎠36.
1.35
1.36°
1.36°1) ⎛⎝10⎞⎠2;
2) ⎛⎝53⎞⎠3;
3) ⎛⎝−124⎞⎠4;
4) −1244;
5) ⎛⎝−35⎞⎠5;
6) ⎛⎝323⎞⎠3;
7) ⎛⎝−444⎞⎠4;
8) ⎛⎝−157⎞⎠7;
9) −5555;
10) ⎛⎝−36⎞⎠6;
11) ⎛⎝−229⎞⎠9;
12) −488.
1.36°
1.37°
1.37°1) 325+−83;
2) 6254−−1253;
3) 12−60,1253;
4) 1+100,00814;
5) 3164−4273;
6) −3383+2,25;
7) 83−643;
8) 164−643.
1.37°
1.38°
1.38°1) 9+4;
2) 36−164;
3) 0,81+0,0013;
4) 0,0273−0,04;
5) 5−2564;
6) 7+83;
7) −325+164;
8) −273+814.
1.38°
1.39°
1.39°1) (1−2)⎛⎝1+2⎞⎠;
2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;
3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;
4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;
5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;
6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.
1.
39°
1.40
1.401) 1225244⋅15−1382−2323;
2) 58+442−26235;
3) 90+31⎛⎝572−262⎞⎠83;
4) 2364+⎛⎝482−3225⎞⎠−13.
1.40
1.41
1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;
2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;
3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;
4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).
1.41
1.42
1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;
2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;
3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;
4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.
1.42
Найдите естественную область определения выражения (1.43—1.44).
1.43
1.431) x+4;
2) −9+2×4;
3) 5×2−6×10;
4) 8x−4×212;
5) x+33;
6) x−75;
7) x2−47;
8) 2×2−329.
1.43
1.44
1.441) 34x−112;
2) −48x−314;
3) 2−59−5×8;
4) 3−1016−7×6;
5) 2+x4−2(8−6x)3;
6) 12−6×2−7x+(3x−1)·25;
7) −x22(x−2)−5⎛⎝1−3x)−24;
8) 3(x+4)−6(2−x)+9×428.
1.44
Стр. 181.45
1.45Найдите длину ребра куба, если его объем равен:
1) 27 см3;
2) 64 мм3;
3) 0,125 дм3;
4) 0,216 м3.
1.45
Решите уравнение (1.46—1.54).
1.46°
1.46°1) x2=0,49;
2) x2=121;
3) x3=0,008;
4) x3=1000;
5) x3=−64 000;
6) x3=216;
7) x4=0,0625;
8) x4=−16.
1.46°
1.47
1.471) x3=−27;
2) x5=−132;
3) x7=−1;
4) x9=−512;
5) x3=−0,027;
6) x11=0.
1.47
1.48°
1.48°1) x2=11;
2) x4=19;
3) x8=27;
4) x3=25;
5) x7=38;
6) x9=−2;
7) x15=−6;
8) x17=4;
9) x13=−13.
1.48°
1.49
1.491) x2=25 600;
2) x2=0,0196;
3) x2+1=1,0016;
4) 5×2−20=0;
5) x2+25=0;
6) x2+179=0;
7) x2·4=0;
8) −6×2=0;
9) 113×2−12=0;
10) 13×2−1=0.
1.49
1.50
1.501) 4×3+4125=0;
2) 8×3+27=0;
3) −0,1×4=−0,00001;
4) 16×4−81=0;
5) 12×5+16=0;
6) 132×6−2=0.
1.50
1.51
1.511) x4+2=7;
2) x5−3=30;
3) x6−7=19;
4) x3+5=5.
1.51
1.52
1.521) (x+1)4=16;
2) (x−2)6=64;
3) (2x+1)3=27;
4) (3x−1)5=32.
1.52
1.53
1.531) x10−31×5−32=0;
2) x8−15×4−16=0;
3) x4−12×2+27=0;
4) x6−7×3−8=0;
5) x8−82×4+81=0;
6) x4+2×2−15=0.
1.53
Стр. 191.54
1.541)° (x6)6=x;
2)° (x10)10=x;
3)° (x3)3=x;
4)° (x5)5=x;
5) ⎛⎝x−14⎞⎠4=x−1;
6) ⎛⎝x+212⎞⎠12=x+2;
7) ⎛⎝1×7⎞⎠7=1x;
8) ⎛⎝1x−211⎞⎠11=1x−2.
1.54
3-8Кубический корень из 9 — Как найти кубический корень из 9? [Решено]
Значение кубического корня из 9, округленное до 4 знаков после запятой, равно 2,0801.
Это действительное решение уравнения x 3 = 9. Кубический корень из 9 выражается как ∛9 в радикальной форме и как (9) ⅓ или (9) 0,33 в экспоненциальной форме. Простая факторизация 9 равна 3 × 3, поэтому кубический корень из 9 в его низшей радикальной форме выражается как ∛9.
- Кубический корень из 9: 2,080083823
- Кубический корень из 9 в экспоненциальной форме: (9) ⅓
- Кубический корень из 9 в радикальной форме: ∛9
| 1. | Что такое кубический корень из 9? |
| 2. | Как вычислить кубический корень из 9? |
| 3. | — кубический корень из 9Иррациональный? |
| 4. | Часто задаваемые вопросы о кубическом корне из 9 |
Что такое кубический корень из 9?
Кубический корень из 9 — это число, которое при трехкратном умножении само на себя дает произведение 9.
Так как 9 можно выразить как 3 × 3. Следовательно, кубический корень из 9 = ∛(3 × 3) = 2,0801.
☛ Проверить: Калькулятор кубического корня
Как вычислить значение кубического корня из 9?
Кубический корень из 9 по методу Галлея
Его формула ∛a ≈ x ((x 3 + 2a)/(2x 3 + a))
где,
a = число, для которого вычисляется кубический корень
x = целочисленное предположение его кубического корня.
Здесь а = 9
Предположим, что x равен 2
.
[∵ 2 3 = 8 и 8 — ближайший совершенный куб, который меньше 9]
⇒ х = 2
Следовательно,
∛9 = 2 (2 3 + 2 × 9)/(2 × 2 3 + 9)) = 2,08
⇒ ∛9 ≈ 2,08
Следовательно, кубический корень из 9 примерно равен 2,08.
Является ли кубический корень из 9 иррациональным?
Да, потому что ∛9 = ∛(3 × 3) и его нельзя выразить в виде p/q, где q ≠ 0. Следовательно, значение кубического корня из 9 является иррациональным числом.
☛ Также проверьте:
- Кубический корень из 26
- Кубический корень из 800
- Кубический корень из 8000
- Кубический корень из 36
- Кубический корень из 57
- Кубический корень из 11
- Кубический корень из 197
Кубический корень из 9 решенных примеров
Пример 1. Найдите действительный корень уравнения x 3 − 9 = 0.
Решение:
x 3 − 9 = 0, т.е. x 908 911 2 909 Решение для x дает нам,
x = ∛9, x = ∛9 × (-1 + √3i))/2 и x = ∛9 × (-1 — √3i))/2
где я называется мнимой единицей и равен √-1.
Игнорирование мнимых корней,
х = ∛9
Следовательно, действительный корень уравнения x 3 − 9 = 0 равен x = ∛9 = 2,0801.Пример 2. Чему равно ∛9 + ∛(-9)?
Решение:
Кубический корень из -9 равен минусу кубического корня из 9.
то есть ∛-9 = -∛9Следовательно, ∛9 + ∛(-9) = ∛9 — ∛9 = 0
Пример 3: Объем сферического шара равен 9π в 3 . Каков радиус этого шара?
Решение:
Объем сферического шара = 9π в 3
= 4/3 × π × R 3
⇒ R 3 = 3/4 × 9
⇒ R = ∛(3/4 × 9) = ∛(3/4) × ∛9 = 0,× 2,08008 (∵ ∛(3/4) = 0, и ∛9 = 2,08008)
⇒ R = 1,88988 в 3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о кубическом корне из 9
Каково значение кубического корня из 9?
Мы можем выразить 9 как 3 × 3, т.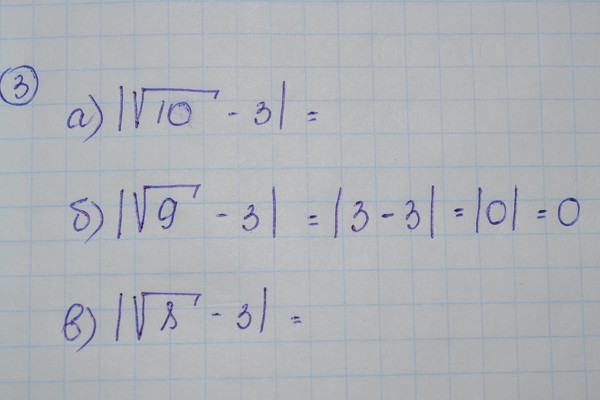
е. ∛9 = ∛(3 × 3) = 2,08008. Следовательно, значение кубического корня из 9 равно 2,08008.
Почему значение кубического корня из 9 иррационально?
Значение кубического корня из 9 не может быть выражено в виде p/q, где q ≠ 0. Следовательно, число ∛9 иррационально.
Является ли число 9 идеальным кубом?
Число 9 при разложении на простые множители дает 3 × 3. Здесь простой делитель 3 не находится в степени 3. Следовательно, кубический корень из 9 иррационален, следовательно, 9не идеальный куб.
Что такое кубический корень из -9?
Кубический корень из -9 равен отрицательному значению кубического корня из 9. Следовательно, ∛-9 = -(∛9) = -(2,08) = -2,08.
Что такое куб кубического корня из 9?
Куб кубического корня из 9 — это само число 9, т.е. (∛9) 3 = (9 1/3 ) 3 = 9.
Каково значение 4 плюс 8 кубического корня 9?
Значение ∛9 равно 2,08. Итак, 4 + 8 × ∛9 = 4 + 8 × 2,08 = 20,64.