Косинус в квадрате калькулятор: Теорема косинусов. Онлайн калькулятор.

{2} \alpha=1 \]

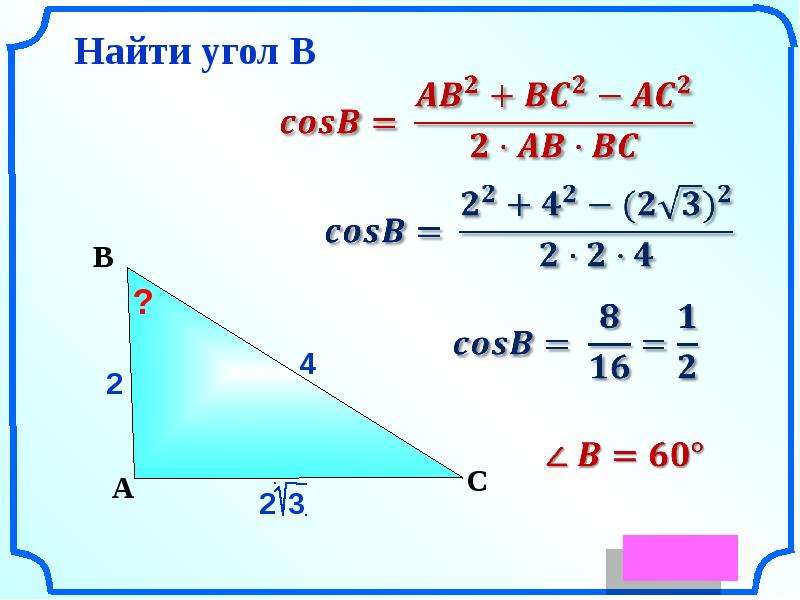
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \]

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой \( \dfrac{y}{x}=\dfrac{\sin \alpha}{\cos \alpha} \), а отношение \( \dfrac{x}{y}=\dfrac{\cos \alpha}{\sin \alpha} \) — будет являться котангенсом.

Добавим, что только для таких углов \( \alpha \), при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества \( tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} \), \( ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \).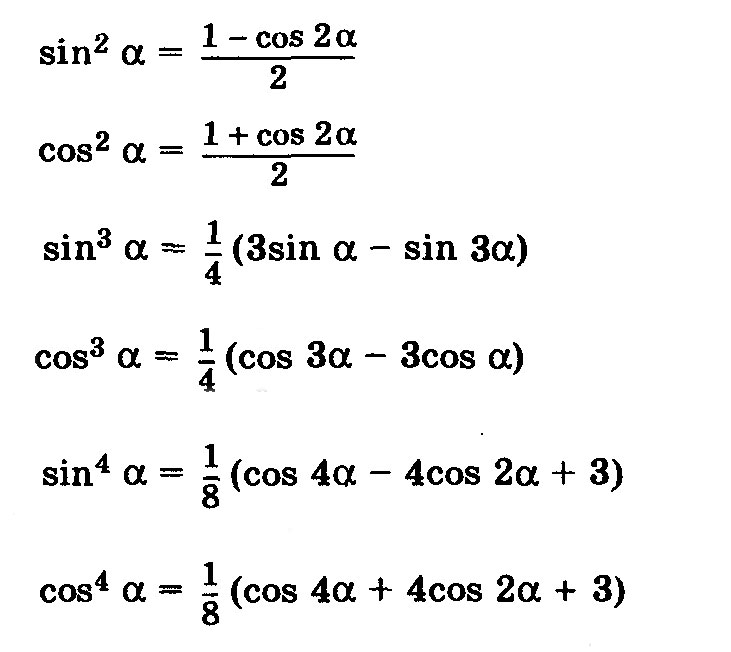

Например: \( tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} \) является справедливой для углов \( \alpha \), которые отличны от \( \dfrac{\pi}{2}+\pi z \), а \( ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \) — для угла \( \alpha \), отличного от \( \pi z \), \( z \) — является целым числом.

Зависимость между тангенсом и котангенсом

\[ tg \alpha \cdot ctg \alpha=1 \]

Данное тождество справедливо только для таких углов \( \alpha \), которые отличны от \( \dfrac{\pi}{2} z \). Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что \( tg \alpha = \dfrac{y}{x} \), а \( ctg \alpha=\dfrac{x}{y} \). Отсюда следует, что \( tg \alpha \cdot ctg \alpha = \dfrac{y}{x} \cdot \dfrac{x}{y}=1 \). Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

\( tg^{2} \alpha + 1=\dfrac{1}{\cos^{2} \alpha} \) — сумма квадрата тангенса угла \( \alpha \) и \( \alpha \), отличных от \( \dfrac{\pi}{2}+ \pi z \).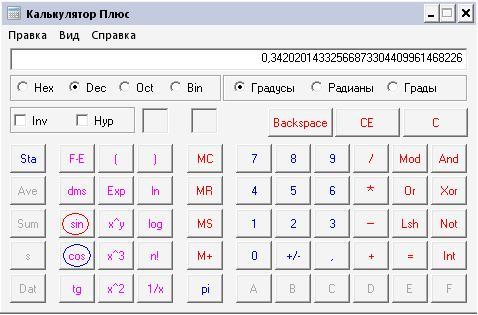 {2}\alpha} \) — сумма \( \alpha \), равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \( \alpha \), отличного от \( \pi z \).

Формулы приведения

sinα+2πz=sinα,cosα+2πz=cosαtgα+2πz=tgα,ctgα+2πz=ctgαsin-α+2πz=-sinα,cos-α+2πz=cosαtg-α+2πz=-tgα,ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα,cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα,ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα,cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα,ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα,cosπ+α+2πz=-cosαtgπ+α+2πz=tgα,ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα,cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα,ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα,cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα,ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα,cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα,ctg3π2-α+2πz=tgα

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Кнопки калькулятора онлайн

Калькулятор онлайн может стать верным помощником предпринимателям и их сотрудникам, профессионально занимающихся финансовыми расчетами. Наш калькулятор может стать палочкой-выручалочкой для бухгалтера или финансиста. В любом случае, если ваш бизнес или трудовая деятельность напрямую или косвенно связаны с постоянными вычислениями и расчетами, то стоит испытать предлагаемый бесплатный калькулятор, оценить степень его точности и функциональности для нужд конкретного дела.

В таблице ниже указаны все кнопки калькулятора онлайн (виртуальные клавиши) и выполняемые ими операции.

Клавиша	Символ	Операция
pi	pi	Постоянная pi
е	е	Число Эйлера
%	%	Процент
( )	( )	Открыть/Закрыть скобки
,	,	Запятая
sin	sin(α)	Синус угла
cos	cos(β)	Косинус
tan	tan(y)	Тангенс
sinh	sinh()	Гиперболический синус
cosh	cosh()	Гиперболический косинус
tanh	tanh()	Гиперболический тангенс
sin-1	asin()	Обратный синус
cos-1	acos()	Обратный косинус
tan-1	atan()	Обратный тангенс
sinh-1	asinh()	Обратный гиперболический синус
cosh-1	acosh()	Обратный гиперболический косинус
tanh-1	atanh()	Обратный гиперболический тангенс
x2	^2	Возведение в квадрат
х3	^3	Возведение в куб
xy	^	Возведение в степень
10x	10^()	Возведение в степень по основанию 10
ex	exp()	Возведение в степень числа Эйлера
√x	sqrt(x)	Квадратный корень
3√x	sqrt3(x)	Корень 3-ей степени
y√x	sqrt(x,y)	Извлечение корня
log2x	log2(x)	Двоичный логарифм
log	log(x)	Десятичный логарифм
ln	ln(x)	Натуральный логарифм
logyx	log(x,y)	Логарифм
I / II		Сворачивание/Вызов дополнительных функций
Unit		Конвертер величин
Matrix		Матрицы
Solve		Уравнения и системы уравнений
		Построение графиков
Дополнительные функции (вызов клавишей II)
mod	mod	Деление с остатком
!	!	Факториал
i / j	i / j	Мнимая единица
Re	Re()	Выделение целой действительной части
Im	Im()	Исключение действительной части
|x|	abs()	Модуль числа
Arg	arg()	Аргумент функции
nCr	ncr()	Биноминальный коэффициент
gcd	gcd()	НОД
lcm	lcm()	НОК
sum	sum()	Суммарное значение всех решений
fac	factorize()	Разложение на простые множители
diff	diff()	Дифференцирование
Deg		Градусы
Rad		Радианы

 

На этом предлагаем закончить изучение кнопок онлайн калькулятора и перейти к рассмотрению его функций. Функции онлайн калькулятора >>

Правила ввода функций в онлайн калькуляторах.

На данной странице описаны правила ввода функций, которых следует придерживаться в онлайн калькуляторах, созданных на базе виждетов WolframAlpha Mathematica.

Не забывайте проверять правильность написания формул. Неточность и ошибки в написании, приводят к невернному ответу и ситуациям при которых калькулятор отказывается проводить вычисления.

Оператор	Описание
Простейшие математические операции
+ — * / ()	Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * — необязателен: выражение 2sin(3 x ) еквивалентно 2*sin(3* x ). Cкобки используются для группирования выражений.
0. x
Тригонометрические функции
	Синус от x
	Косинус от x
	Тангенс от x . Можно вводить tg( x ) или tan( x )
	Котангенс от x . Можно вводить ctg( x ) или cot( x )
	Секанс от x , определяется как 1/cos( x )
	Косеканс от x , определяется как 1/sin( x )
	Арксинус от x . Можно вводить arcsin( x ) или asin( x )
	Арккосинус от x . Можно вводить arccos( x ) или acos( x )
	Арктангенс от x . Можно вводить arctg( x ) или atan( x )
	Арккотангенс от x . Можно вводить arcctg( x ) или acot( x )
	Арксеканс от x
	Арккосеканс от x
Некоторые константы
	Число Эйлера e = 2.718281828459045…
	Число π = 3.141592653589793…

Калькулятор косинуса онлайн — Расчет cos — производная — первообразная

Резюме:

Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.

потому что онлайн

---

Описание:

Калькулятор позволяет использовать большинство тригонометрических функций , можно рассчитать косинус , синус и касательная угла через одноименные функции. .

Тригонометрическая функция косинус отмечен cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, градианы и радианы, которые являются угловыми единицами по умолчанию.

Расчет косинуса

Косинус для вычисления угла в радианах

Калькулятор косинуса позволяет через функцию cos вычислить

онлайн косинус угла в радианах, сначала необходимо выберите желаемую единицу измерения, нажав кнопку параметров модуля расчета.После этого можно приступать к расчетам.

Чтобы вычислить косинус онлайн «пи / 6», введите cos (`pi / 6`), после вычисления результат sqrt (3) / 2 возвращается.

Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и делать расчеты со специальными связанными значениями в точной форме.

Вычислить косинус угла в градусах

Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу нажав кнопку опций модуля расчета.После этого вы можете приступить к расчету.

Чтобы вычислить косинус 90, введите cos (90), после вычисления restults 0 возвращается.

Вычислить косинус угла в градусах

Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать желаемую единицу измерения. нажав кнопку опций модуля расчета. После этого вы можете приступить к расчету.

Чтобы вычислить косинус 50, введите cos (50), после вычисления возвращается результат sqrt (2) / 2.

Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и выполнять исчисление со специальными связанными точными значениями.

Специальные значения косинуса

Косинус допускает некоторые особые значения, которые калькулятор может определять в точной форме. Вот список специальные значения косинуса

:

Производная косинуса

Производная косинуса равна -sin (x).

Первообразная косинуса

Первообразная косинуса равна sin (x).

Свойства функции косинуса

Функция косинуса является четной функцией, для e

Online Scientific Calculator

Для получения справки см. Руководство по эксплуатации и записи блога онлайн-научного калькулятора.

Это калькулятор формул . Введите выражения в том же порядке, что и на бумаге . Затем нажмите ‘=’, чтобы отобразить результат.

Используйте круглые скобки, чтобы изменить порядок операций или указать параметры функции.

Пример допустимого выражения:

(-3 + sqrt (16/4)) / 4

Результаты отображаются как дроби , когда это возможно, а также в приближении с плавающей запятой.

Этот калькулятор поддерживает следующие операторы, функции и константы:

Операторы

• + — * / : Сложение, вычитание, умножение и деление
• cis : используется для ввода комплексных чисел в полярной форме (см. Комплексные числа)

Тригонометрические функции

• sin : синус
• asin : обратный синус (sin ^-1 )
• sinh : гиперболический синус
• cos : косинус
• acos : Обратный косинус (cos ^-1 )
• cosh : гиперболический косинус
• загар : касательная
• atan : арктангенс (tan ^-1 )

Константы

• e : Постоянная e
• i : Мнимая единица (для получения дополнительной информации см.
  Комплексные числа)
• pi : постоянная PI (& pi)

Статистические функции

• ! : Факториал
• пермь : перестановки
• гребень : Комбинации

Логарифмы

• ln : натуральный логарифм (основание e)
• журнал : основание логарифма 10

Прочие функции

• абс : Абсолютное значение
• и : результат предыдущего выражения
• gcd : Наибольший общий делитель (см. GCD)
• int : целая часть числа (см. INT)
• lcm : наименьшее общее кратное (дополнительную информацию см. В LCM)
• rand : возвращает случайное число от 0 до 1 (информацию о том, как использовать эту функцию, см. В rand и о том, как использовать функцию random).
• округление : округление числа до ближайшего целого (см. Примеры округления)
• sqrt : квадратный корень

Этот калькулятор позволяет вам определять свои собственные функции для использования в выражениях . Чтобы определить тип функции, введите его в следующем формате: <имя функции> (<аргументы, разделенные запятыми>) = <тело>. Пример: площадь (x, y) = x * y.

Вы также можете выбрать отображение результатов в другом формате. Выберите между фиксированным , с плавающей точкой , научным или инженерной нотацией . См. Дополнительную информацию в обозначениях калькулятора.

Вы можете вводить выражения прямо в поле ввода калькулятора или использовать онлайн-клавиатуру.

Калькулятор тригонометрии | Пошаговый калькулятор

Математика определенно входит в число главных опасений студентов во всем мире. Хотя образовательная система предоставляет учащимся многочисленные возможности для развития новых навыков, достижений в спорте и практики публичных выступлений, кажется, что ничего не работает, когда дело доходит до математики.

Почему, спросите вы? Смотря как.

Во-первых, нашей образовательной системе не хватает интуитивного и интерактивного обучения.

Как вы ожидаете, что студенты получат удовольствие от изучения определенного предмета, если им даже не нравятся занятия?

Хотя есть некоторые исключения, большинство учителей математики не предлагают (или, возможно, не могут) предлагать активные уроки. Студенты, особенно в наши дни, предпочитают взаимодействие, а не пассивное обучение. Но кто здесь виноват? Учителя такие, потому что их учителя были такими, и то же самое происходит с теми, кто находится в непрерывном цикле недостатков, управляющих системой.

С другой стороны, студенты недостаточно ценят математику, чтобы выкладываться на полную. Всегда возникает вопрос: «Когда я когда-нибудь собираюсь использовать это в реальной жизни?», Особенно когда речь идет о конкретных областях математики, таких как алгебра и тригонометрия.

Они мало знают, что более глубокое понимание математики как предмета может помочь им лучше понять вашу среду и мир вокруг нас. Математика — это основной фактор, отвечающий за развитие вашего критического мышления и улучшение навыков решения проблем в зрелом возрасте.

Как правило, люди, которые мыслят математически, думают намного быстрее, чем те, кто использует творческий или художественный подход, когда им нужно решить проблему.

В то время как любители математики более реалистичны и вдумчивы, любители искусства, как правило, живут моментом и забывают о будущем и о том, что оно может предложить.

Тригонометрия — это исследование свойств треугольников, в основном взаимосвязи между углами и длиной разных сторон.

Треугольники, вероятно, одна из самых основных геометрических фигур. Несмотря на это, тригонометрия открыла множество приложений с множеством практических применений в реальной жизни, включая, помимо прочего, оценку пеленгов и точных расстояний.

Для проверки расчетов и выполнения операций в тригонометрии используются три основные функции: косинус, синус и тангенс. В принципе, если вы знаете размеры двух сторон или углов, вы можете легко определить размеры остальных.

Когда вы говорите тригонометрия, вы говорите теорему Пифагора; формула, которая используется для вычисления длины разных сторон треугольника.

В треугольнике гипотенуза относится к самой длинной стороне, обращенной к прямому углу. Остальные стороны называются перпендикуляром и основанием.

Теорема Пифагора может быть возобновлена ​​в H² = B² + P², где H относится к гипотенузе, B — к основанию, а P — к перпендикуляру (да!).

Многие формулы или тождества могут быть выведены из теоремы, которую мы подробно рассмотрим ниже.

Если вам сложно осмыслить эти концепции, не волнуйтесь, наш калькулятор триггеров поможет вам сделать эти вычисления намного быстрее и проще.

Пифагорейские тождества в тригонометрии

Все тригонометрические производные и значения основаны на пифагорейских тождествах. Хотя они могут показаться трудными для запоминания и понимания, на самом деле они совершенно противоположны, поскольку вам нужно попрактиковаться только в нескольких вопросах, чтобы понять их суть.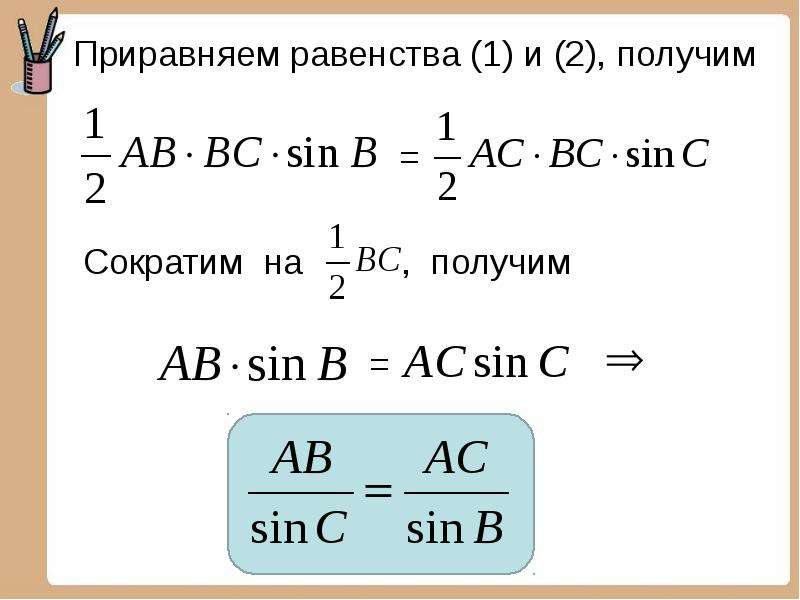 Как только вы это сделаете, применение этих идентичностей в различных задачах станет куском пирога.

Есть 6 основных идентичностей, которым вы должны научиться, чтобы овладеть тригонометрией. Эти идентификаторы могут оказаться полезными в нескольких ситуациях, будь то в школе или за ее пределами, и это:

1. sin² + cos² = 1² (обратите внимание, что 1 в квадрате = 1)
2. tan² + 1² = sec²
3. детская кроватка² + 1² = cosec²
4. tan = sin / cos = 1 / детская кроватка
5. sin = tan / sec = 1 / cosec, если вы просто это означает, что sin равен разделенному cosec
6. cosec = 1 / sec = детская кроватка / cosec

Как и в случае с любым другим предметом, все дело в практике, поэтому не забывайте уделять хотя бы 30 минут каждый день решению задач тригонометрии, если вы хотите овладеть этим предметом.Если вы обнаружите препятствие, которое не можете обойти самостоятельно, попробуйте наш онлайн-калькулятор тригонометрии, чтобы попрактиковаться и ознакомиться с расчетами.

Несмотря на широко распространенное мнение, что математические правила можно использовать только в школе и на экзаменах, математика, в частности тригонометрия, имеет различные практические применения практически в любой отрасли, например, в развитии бизнеса, физике, дизайне и т. Д.

Трудно в это поверить? Вот пара карьерных путей, не связанных с математикой, в которых вы сможете найти отличное применение своим тригонометрическим навыкам.

Музыка и тригонометрия

Как ни странно это может показаться, музыка на самом деле связана с математикой. Но как?

Проще говоря, звук распространяется волнами, которые напоминают графическое представление функций косинуса и синуса. Другими словами, то, что вы слышите каждый день, когда идете в школу, — не что иное, как реальное представление этих тригонометрических функций. Я имею ввиду, как это круто?

Использование калькулятора тригонометрии sin cos tan позволяет инженерам и продюсерам управлять звуком, изменяя шаблоны звуковых волн для различных переменных, таких как высокие частоты, громкость и база, чтобы получить мелодии, которые нравятся слушателям.

Вы, наверное, знакомы с T-pain и автонастройкой. Известный американский рэпер и певец сообщил, что пару лет ИЗУЧИЛ автонастройку, прежде чем начать использовать ее в своей музыке.

Видеоигры и тригонометрия

Взгляните на такие игры, как Battlefield, Call of Duty, Far Cry и God of War, и вы заметите, что с каждым выпуском они становятся все более реалистичными. Тени, эффекты движения, рендеринг графики и все другие элементы игры никогда не были лучше.

Почему мы наблюдаем такое улучшение? Потому что разработчики делают все возможное, чтобы улучшить физические движки, графику, программное обеспечение и программирование, сосредоточив внимание на свойствах тригонометрии. Сногсшибательно, да?

Другими словами, если вы занимаетесь разработкой игр и хотите сделать карьеру в этой области, пора начать заниматься математикой и тригонометрией.

Пространство и тригонометрия

Вы когда-нибудь смотрели запуск ракеты? Нет? Тогда посмотрите их на YouTube, они потрясающие.

Тригонометрия имеет первостепенное значение при отправке оборудования, такого как ракеты и спутники, в космическое пространство, поскольку такие операции требуют точных расчетов скорости и пеленга. Малейший просчет в этой области может привести к катастрофическим результатам и неудачам, и даже к человеческим жертвам, поэтому здесь нет места ошибкам.

Итак, если работа с Илоном Маском — это ваша фантазия, вам лучше начать заниматься тригонометрией.

Цифровая визуализация и тригонометрия

Мы живем в цифровом мире, где все определяется творческими визуальными эффектами, и когда дело доходит до них, никто не может отрицать важность тригонометрии.

Цифровые изображения — это то, что стоит за компьютерами и визуализацией, и это все измерения, вычисления и геометрические узоры, которые определяют, как каждый пиксель отображается на вашем экране.

Другими словами, если вы хотите окунуться в мир цифровых изображений и творчества в ближайшие годы, вы не можете игнорировать математику и тригонометрию.

Современная архитектура и тригонометрия

Каждая структура, кривая и расчет в современной архитектуре точно определяется с помощью различных математических формул, в том числе тригонометрических.Как вы думаете, эти небоскребы в Дубае добрались до облаков самостоятельно? Нет, глупый. Это результат бесчисленных часов вычислений и измерений.

Дизайн интерьера и тригонометрия

Как и в архитектуре, в дизайне интерьера также используются математические и тригонометрические формулы, которые определяют, что подходит, а что нет, чтобы создать гармоничный дизайн повсюду.

Итак, вот они, некоторые карьерные пути, которые регулируются тригонометрией, несмотря на то, что они не имеют прямого отношения к математике.Если вы хотите получить работу в любой из упомянутых областей, у вас нет другого выбора, кроме как приложить все усилия и подготовиться к занятиям по математике.

Как бы сложно это ни казалось, но изучение тригонометрии может быть интересным. Все, что вам нужно, — это немного решимости и целеустремленности, и вы уже опережаете 99% студентов.

Если вы хотите правильно изучить тригонометрию, вы можете следовать этому простому плану, чтобы добиться успеха:

1. Начните с простых понятий

Из крошечного желудя вырастает могучий дуб, а из простых понятий вырастают более крупные теоремы.Начните свой путь к мастерству тригонометрии с изучения и практики простых понятий, чтобы познакомиться с основами. К ним относятся шесть основных тождеств, упомянутых выше, и их простые приложения, а также теорема Пифагора и ее использование.

2. Практика извлечения

Как только вы поймете суть основ, вам нужно начать практиковаться в выводе. Таким образом, вам не нужно будет запоминать каждую личность или формулу, так как вы сможете вывести их самостоятельно.Делайте это неоднократно, и происхождение и идентичность станут второй натурой в кратчайшие сроки.

Практикуйте разные типы задач

После того, как вы освоите деривацию, вам нужно пойти дальше и перейти к более сложным задачам.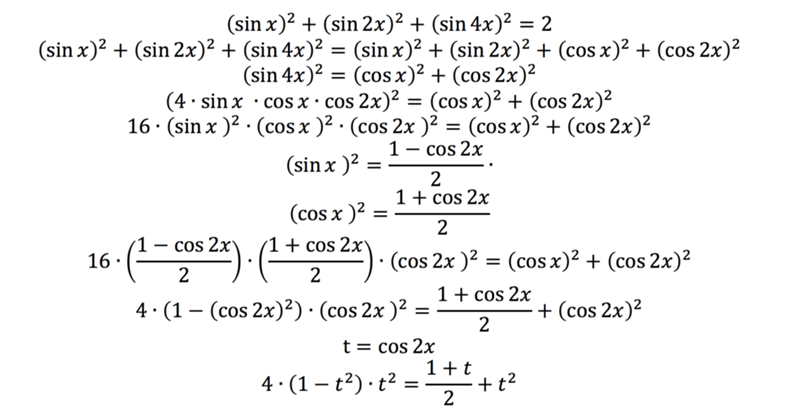 Таким образом, вы не только сможете запоминать формулы, но и поймете, как переходить от одной концепции к другой и как использовать каждую из них, не беспокоясь.

3. Продолжайте практиковать

Вы знаете, как выполнять сложение и вычитание? Конечно, у вас.Вы делаете это всю свою жизнь. Итак, если вы хотите, чтобы тригонометрия также стала вашей второй натурой, вам нужно постоянно практиковать ее, следуя президентскому плану обучения. Мы настоятельно рекомендуем распределить вашу практику на всю неделю, а не втискивать несколько часов в один день. Так вы избежите скуки и в то же время сможете чаще заниматься.

4. Организация исследовательских комиссий

Когда вы находитесь в группе, вы всегда стараетесь изо всех сил, чтобы не показаться самым слабым, что делает учебные группы отличным способом проявить себя во время занятий тригонометрией.Кроме того, вы получите большую пользу от словесного обмена во время сеанса.

5. Если вам нужна помощь, не стесняйтесь спрашивать

Если вы застряли при попытке решить конкретную проблему, не стесняйтесь обратиться за помощью к своему учителю или инструктору. Если они недоступны, вы можете воспользоваться нашим калькулятором тригонов, поскольку он может показать вам пошаговый процесс, который приводит к каждому результату.

Есть много причин, почему вам следует использовать наш калькулятор для построения тригонометрических графиков.Во-первых, им очень легко пользоваться, и вам не придется часами пытаться понять, что делает каждая кнопка, как это бывает при использовании стандартного научного или графического калькулятора.

Мы настоятельно рекомендуем использовать калькулятор тригонометрических треугольников Mathway, если:

• Вы ищете приложение для калькулятора тригонометрии

Мы поняли. Вы не хотите использовать графические калькуляторы, потому что их будет немного неудобно носить с собой.В конце концов, зачем вам это делать, если вы можете просто использовать приложение на своем телефоне?

Проблема с приложениями в том, что они занимают место на вашем смартфоне или планшете и могут немного тормозить ваше устройство. Если вы предпочитаете держаться подальше от подобных вопросов, вы можете просто использовать наш онлайн-инструмент, который считается лучшим калькулятором для тригонометрии. Почему? Потому что он совместим с любым электронным устройством, что делает его лучше приложений, которые вам нужно скачать и установить. С помощью нашего калькулятора треугольной тригонометрии вы сможете решить свои математические задачи всего за несколько кликов.

Также — это приложение для онлайн-калькулятора триггеров.

• Вам нужен калькулятор тригонометрии с шагом

Вы застряли и не можете найти способ решить домашнее задание, которое вам дал учитель? Не можете найти репетитора, который укажет вам путь? Нет проблем, просто зарегистрируйтесь в Mathway, и калькулятор тригонометрии прямоугольного треугольника покажет вам, как решить любую проблему шаг за шагом.

SolveMathPorblems может не только решить любую проблему, с которой вы столкнулись, но и показать шаги, которые привели к результату. Таким образом, вы сможете выявить свои ошибки и исправить их, чтобы улучшить и вывести свои навыки тригонометрии на новый уровень.

Помните, не проверяйте результат, пока не попытаетесь решить проблему и сами не ответите на вопросы. В противном случае вы обманываете только себя. Математика заключается не в том, чтобы заставить учителя поверить в то, что вы сделали отличную работу, а в том, чтобы выявить свои ошибки и поработать над своими недостатками. Вот почему у нас есть триггерный расчет.

• Требуется тригонометрический калькулятор для упрощения

Кто сказал, что математика сложна? Математика на самом деле не усложняет вещи; речь идет об упрощении сложных проблем и их разбиении на небольшие части, которые можно решать по шагам.Зная, что то, что применимо к математике в целом, относится и к тригонометрии, вы будете довольны, узнав, что наш онлайн-калькулятор тригонометрии может упростить сложные задачи и решить их простейшими способами, таким образом обучая вас логическому процессу, лежащему в основе каждого решения. .

• У вас нет научного калькулятора для тригонометрии

Без научного калькулятора можно оказаться по разным причинам

Являясь онлайн-приложением, наш калькулятор тригонометрии не только может работать на любом устройстве без загрузки или установки, но его также можно использовать в любом месте и в любое время.Таким образом, вы можете практиковаться в решении проблем, когда захотите, не нося с собой громоздкий научный калькулятор, куда бы вы ни пошли.

В этом мире есть всего несколько вещей, которые каждый из нас может считать бесценными. Знание определенно является одним из них. Сегодня студенты во всем мире, особенно в научных областях, нуждаются в помощи, чтобы хорошо усвоить основные и базовые навыки и инструменты, необходимые для их обучения.

Итак, когда дело доходит до всего, что связано с математикой и тригонометрией, мы хотели бы предложить как можно больше помощи.Что касается того, что у нас есть под рукой, мы думаем, что, предоставив этот калькулятор триггеров (с его руководством по использованию) всем студентам по всему миру, мы сможем сделать все, что в наших силах, в нашем стремлении донести знания до всех. наиболее подходящим способом. Кстати, мы бесплатно раздаем этот калькулятор триггеров онлайн.

Надеюсь, ваш поиск бесплатного калькулятора тригонометрии завершится тем, что мы можем предложить. Держите деньги в кармане и получайте удовольствие от обучения с помощью нашего бесплатного сервиса.

В принципе, много всего. Некоторые могут прийти с предположением, что, поскольку это интернет-сервис, он не может обеспечить такой же уровень универсальности, как обычный калькулятор. Но это было бы неправильно. Этот онлайн-калькулятор триггеров с шагами может предоставить несколько утилит, которые удовлетворят все ваши математические потребности, независимо от вашего уровня. Наше приложение может работать как:

• Калькулятор аналитической тригонометрии
• Калькулятор для тригонометрии под прямым углом
• Калькулятор решений тригонометрии
• Калькулятор тригонометрического графика
• Калькулятор тригонометрических уравнений
• Калькулятор тригонометрических формул
• Калькулятор сферической тригонометрии

Это не просто хороший калькулятор триггеров; это лучший калькулятор тригонометрии.

Если вы продолжите и посмотрите, что может предложить интерфейс нашего калькулятора, вы обнаружите, что он включает в себя большое количество символов. Теперь вы можете увидеть некоторые из них в любом стандартном калькуляторе, но некоторые другие характерны только для нашего калькулятора.

Среди прочего вы найдете такие символы, как знак деления, прямоугольная пирамида, цилиндр, трапеция, треугольник, равный или меньший, квадратные корни, показатели степени, дроби, абсолютное значение и скобки. По этой причине мы достаточно уверены, чтобы сказать, что этот калькулятор не только лучший калькулятор значений тригонометрии, но и лучший калькулятор обратной тригонометрии.

Универсальность, которую дает этот калькулятор, делает его идеальным для всего, от работы в колледже, домашних заданий, тестирования и проверки ответов. Допустим, у вас есть свободное время: вы можете достать смартфон из кармана, зайти на веб-сайт и отточить свои навыки тригонометрии, решая проблемы. Даже если в вашем распоряжении нет проблем, вы можете выбрать их из уже существующего списка примеров.

Если вы будете искать руководство по использованию калькулятора для тригонометрии, вы, вероятно, не найдете ничего полезного.Мы постараемся избавить вас от бесполезных поисков таких вещей в Интернете и дадим вам простое объяснение того, как пользоваться калькулятором, чтобы вы могли сразу приступить к выполнению своей домашней работы. Вот как это делается:

1. Введите свою проблему с помощью предоставленных символов или используя существующие примеры
2. Когда вы нажимаете кнопку «Показать», написанное вами выражение будет отображаться в обычной математической форме. Знак «?» Кнопка доступна для вас, если вы столкнулись с определенной проблемой.
3. Калькулятор автоматически настраивается на определение типа проблемы, с которой вы имеете дело, на основе введенных вами данных. Но в случае выбора неподходящего выбора всегда можно исправить вручную.
4. Нажмите «Ответить» и подождите, пока приложение выполнит свои вычисления.
5. После отображения ответа вы можете сравнить его с решением, которое вы придумали.

Если вы сделали ошибку, запишите ее и потренируйтесь избегать ее в будущем.Если вы чувствуете, что вам нужно увидеть подробные инструкции, все, что вам нужно сделать, это зарегистрироваться в Mathway.

Блестящая работа, проделанная для того, чтобы воплотить в жизнь это великолепное приложение, исходит от умы сотрудников Mathway. Это только здесь, на нашем веб-сайте, чтобы упростить доступ к нему для всех во всем мире. Если вы хотите использовать весь потенциал этого приложения, вам необходимо зарегистрироваться. Но не позволяйте этому сдерживать вас; на самом деле это довольно просто и быстро. Просто убедитесь, что у вас есть одобрение родителей, если вы несовершеннолетний.

Это приложение, которое вам нужно в вашем арсенале, если вы хотите подтолкнуть себя и улучшить свои навыки решения проблем. Это бесплатный и полезный калькулятор, в котором есть все необходимое для решения любой задачи тригонометрии. От синуса и косинуса до фундаментальной теоремы Пифагора — это инструмент, который вам захочется иметь под рукой, а точнее, в кармане.

Тригонометрия, изучающая размер треугольников, выводит алгебру на новый уровень. Его наиболее известные особенности включают теорему Пифагора и отношения синуса, косинуса и тангенса.Наш калькулятор триггеров может помочь вам проверить проблемы, связанные с этими отношениями, а также со многими другими. Просто введите свою задачу в этот продвинутый калькулятор, чтобы убедиться, что вы правильно с ней справились.

Примечание. Приложение Mathway поможет вам, шаг за шагом показывая, как решать каждую задачу, которую вы вставляете в калькулятор. Если вы не можете найти свою ошибку, это определенно инструмент для вас. Чтобы зарегистрироваться, просто нажмите «Просмотреть шаги» на экране ответа. [/ Note]

Этот усовершенствованный калькулятор не только проверяет ответы, но и предоставляет дополнительные практические задания, которые помогут отточить свои навыки при подготовке к тестам и викторинам. Чтобы использовать эту функцию, найдите тип задачи, которую вы хотите отработать, в разделе «Примеры». Щелкните нужную тему, и на экране калькулятора появится пример задачи. Нажмите кнопку «Показать», чтобы увидеть проблему в стандартном формате или, если возможно, в виде изображения. Решите проблему и нажмите «Ответить», чтобы убедиться, что вы правы.

Теорема Пифагора

Триггерные отношения

Закон синуса

Закон косинусов

Справочные треугольники

• • Знай свои формулы: Время, потраченное на изучение формул, определений и закономерностей, определенно окупится.Таким образом, когда вы подойдете к проблеме, у вас будут инструменты, необходимые для ее решения. В противном случае вы можете запутаться, и ваша работа может быстро превратиться в беспорядок. Вы можете использовать уловки с памятью, такие как SOH CAH TOA, чтобы вам помочь. SOH CAH TOA помогает запоминать триггерные отношения. SOH означает синус = противоположность по гипотенузе, COH означает косинус = смежный по сравнению с гипотенузой, а TOA помогает вам помнить, что касательная = противоположная по сравнению с соседним.

• • Не торопитесь: По мере того, как вы углубляетесь в математику, задачи становятся длиннее и сложнее.Не позволяйте этому запугать вас и не спешите с завершением. Тщательно и методично прорабатывайте каждую проблему шаг за шагом, и вы устраните множество неосторожных ошибок.

• • Проверьте свои ответы: Если вы практикуете неправильно, практика не принесет особой пользы, поэтому проверьте свои ответы, чтобы убедиться, что вы на правильном пути. Наш калькулятор триггеров поможет вам с домашним заданием, но если у вас есть время, вы также захотите вернуться и проверить свои ответы на тесты и викторины.Вы удивитесь, сколько ошибок вы поймаете и сколько очков это сэкономит вам.

• Определите свои ошибки: Многие студенты в конечном итоге повторяют одни и те же ошибки снова и снова, потому что они не обращают внимания на то, что пошло не так, когда они пропускают вопрос. Ошибки — это часть процесса обучения, но их нужно выявлять и исправлять. Каждый раз, когда вы ошибаетесь в проблеме, старательно ищите свою ошибку и выясняйте, что вам следовало бы сделать вместо этого.Если вы не можете найти свою ошибку, обратитесь за помощью к учителю или другу. Или зарегистрируйтесь в Mathway, который покажет вам шаги для решения любой проблемы, которую вы вводите в калькулятор.

1. Введите задачу в калькулятор, начав с примера или используя символы.
2. Нажмите кнопку Показать рядом с Math Format , чтобы убедиться, что вы правильно ввели задачу. Если это выглядит неправильно и вам нужна дополнительная помощь, нажмите ? Поле рядом с полем Укажите проблему.
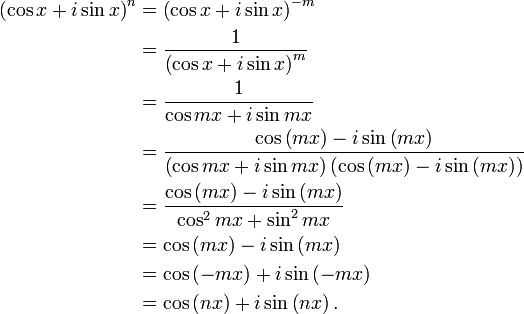
3. В раскрывающемся списке Select Topic выберите правильный вариант для типа проблемы, которую вы пытаетесь решить.
4. Щелкните Ответ , чтобы просмотреть ответ.
5. Чтобы увидеть шаги, зарегистрируйтесь на Mathway .

Начиная с примера

Прокрутите темы, чтобы найти тип проблемы, которую вы хотите проверить или отработать. Это предоставит пример в калькуляторе, чтобы вы могли видеть, как он отформатирован.Затем вы можете изменить числа или переменные в соответствии с проблемой, которую вы пытаетесь проверить.

Круглые скобки — Они указывают на умножение или на то, что операция внутри должна быть выполнена первой.

Скобки — Используйте квадратные скобки, если вам нужна скобка внутри скобок — Скобки выходят наружу, как показано в этом примере: [3 + 2 (10 -1)] ÷ 7.

Абсолютное значение — Абсолютное значение показывает, насколько далеко число от нуля.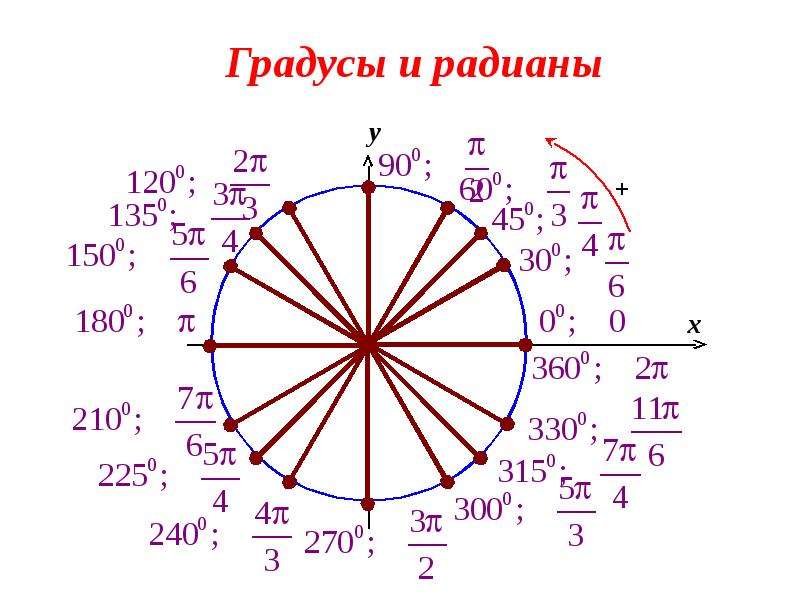 Это всегда одно и то же число, но положительное.(2) для. Помните, что показатель степени показывает, сколько раз основание умножается само на себя.

Нижние индексы — Ваша переменная выходит за пределы скобок, а нижний индекс входит внутрь. Например, x ₁ будет x [1].

Квадратные корни — Введите подкоренное выражение (число внутри символа квадратного корня) в скобках. Квадратные корни находят, сколько раз само число равно подкоренному выражению. Например, квадратный корень из 49 равен 7, потому что 7 * 7 = 49.

Другие корни — Введите индекс после символа √ и подкоренного выражения в скобках. Например, используйте √3: (8) для. Помните, что другой индекс означает, что ответ должен быть умножен сам на себя столько раз, чтобы получить подкоренное выражение. В нашем примере 2 * 2 * 2 = 8, поэтому 2 будет ответом, потому что 2 раза сам 3 (индекс) раз равен 8.

Примечание. Если индекс не указан, предполагается, что он равен двум, и это просто называется квадратным корнем.

Координаты — Введите координату, как обычно, например (1,5).

Больше или равно — Если вам нужно использовать только знак «больше» (>), просто введите его с клавиатуры. (Нажмите Shift, затем точку).

Меньше или равно — Если вам нужно использовать только знак «больше» (>), просто введите его с клавиатуры. (Нажмите Shift, затем точку).

Функциональная нотация — Введите функциональную нотацию, как обычно. Помните, что f (x) произносится как « f из x » и обычно заменяет y в уравнении.

Натуральный логарифм — введите число в скобках. Помните, что натуральный логарифм отвечает на следующий вопрос: e в какой степени равно данному числу? Константа е приблизительно равна 2,718.

Логарифм — введите число в скобках. Логарифм без нижнего индекса (например, тот, что показан здесь) отвечает на вопрос: «В какой степени 10 равно заданному числу?» Например, ответ на log 100 будет 2, потому что 10 во второй степени равно 100.

Логарифм с другим основанием — Введите основание (маленькое число) внутри скобок и аргумент (число обычного размера) внутри скобок. Например, будет записано как log [2] (8). Когда вы меняете индекс логарифма, вы меняете основание. В этом примере задается следующий вопрос: в какой степени 2 равно 8? Ответ, конечно, будет 3.

Примечание : Если нижний индекс (основание) не указан, предполагается, что основание равно 10.

Правые треугольники — Введите имеющуюся у вас информацию в скобках. Обязательно используйте правильный порядок, а именно: [угол, 90 °, угол, отрезок, отрезок, гипотенуза]. Щелкните Показать, чтобы еще раз убедиться, что вы ввели свою информацию в соответствующее место.

Синус — введите значение угла в скобках.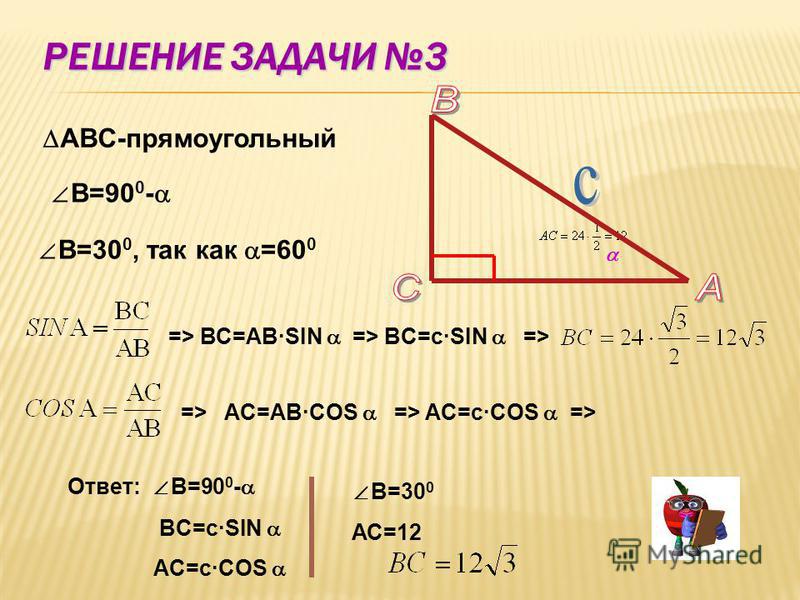 Синус угла противоположен гипотенузе.

Косинус — Косинус равен смежному по гипотенузе.

Касательная — Касательная противоположна смежной.

Секанс — Секанс является обратным косинусу и равен гипотенузе над смежными.

Косеканс — Косеканс находится путем инвертирования синуса и равен гипотенузе над противоположным.

Котангенс — Котангенс, обратный касательной, находится путем наложения смежного на противоположное.

Знак деления — Для умножения используйте кнопку со звездочкой на клавиатуре.(Нажмите Shift, затем 8.)

Пи — Пи — это уникальное число, которое можно найти, разделив длину окружности любого круга на его диаметр. Пи примерно равно 3,14.

Градусы — Используйте символ градуса, когда необходимо указать градусы.

Theta — греческая буква Theta используется в тригонометрии для обозначения неизвестного угла.

Инструмент Me Now

Математические калькуляторы
• градусов в радианы
• радиан в градусах
• Калькулятор квадратного корня
• Калькулятор журнала
• Ln Калькулятор
• Факториальный калькулятор
• Калькулятор округления
• Калькулятор Фибоначчи
• Калькулятор возведения в степень
• Проверка простых чисел
Тригоновые функции
• Калькулятор косинусов
• Калькулятор синусов
• Калькулятор тангенса
• Калькулятор Arccos
• Калькулятор Arcsin
• Калькулятор Arctan
• Калькулятор Arcsec
• Калькулятор Arccsc
• Калькулятор Arccot ​​
Базовые преобразователи
• Десятичное в двоичное
• Десятичное в шестнадцатеричное
• десятичное в восьмеричное
• Из двоичного в десятичный
• Двоичное в шестнадцатеричное
• Двоичное преобразование в восьмеричное
• из шестнадцатеричного в десятичный
• из шестнадцатеричного в двоичный
• от шестнадцатеричного до восьмеричного
• Восьмеричное в десятичное
• Восьмеричное в двоичное
• Восьмерично-шестнадцатеричное
Текстовые инструменты
• Преобразователь прописных
• Преобразователь в нижний регистр
• Правильный преобразователь корпуса
• Длина текста
• Повторитель текста
• Добавить текст к строкам
• Счетчик слов
• Счетчик линий
• Обратный текст
• Удалить пробелы
• Удалить пустые строки
• Конвертер текста в Unicode
• Конвертер Unicode в текст
• URL для конвертера ссылки
• Кодировщик URL
• URL-декодер
Генераторы
• Генератор случайных чисел
• Генератор случайных букв
• Генератор случайных чисел
• Генератор MAC-адресов
• Генератор случайных цветов
• Генератор паролей
• Валик для игры в кости
Температура
• Фаренгейта в Цельсия
• Фаренгейта Кельвина
• по Фаренгейту К Ранкина
• градусов по Фаренгейту
• Цельсия в Кельвин
• Цельсия к Ранкина
• Кельвин в градус по Фаренгейту
• Кельвин по Цельсию

Как вычислить синус, косинус, тангенс числа пи / 4 без использования калькулятора?

Тригонометрия

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде

.