Таблица квадратов натуральных чисел.
Таблица квадратов натуральных чисел.Таблица квадратов натуральных чисел от 1 до 100. Квадрат числа определение: квадратом числа называется результат умножения числа на точно такое число. Говорят, что для того, чтобы возвести число в квадрат, нужно это число умножить само на себя. За математическую точность приведенных определений я ответственности не несу, написал, как понимаю. Для бюрократов от математики советую воспользоваться учебником и выучить определение оттуда. Таблица квадратов натуральных чисел представляет собой натуральные числа от 1 до 100 в степени 2. Все результаты возведения натуральных чисел в квадрат или в степень 2 сведены в таблицу, эту таблицу квадратов натуральных чисел любой желающий может скачать бесплатно.
В таблице квадратов натуральных чисел числа представлены по десяткам, как в таблице умножения. В первом квадратике вы найдете квадраты однозначных чисел до 10 включительно.
Степень 2 для любого числа показывает, что это число умножается само на себя. Любое отрицательное число в степени 2 дает положительный результат потому, что минус на минус при умножении дает плюс. Поэтому приведенная выше таблица является также таблицей квадратов целых чисел. Если вам нужно найти результат возведения отрицательного числа в степень 2, то смело отбрасывайте знак минус перед числом и результат ищите по таблице — он всегда будет положительным. Формулы возведения положительного и отрицательного числа в квадрат или в степень 2 будут выглядеть так:
a² = a · a
(-a)² = (-a) · (-a) = a · a
Рассмотрим несколько примеров. Начинается таблица с единицы. 1 в квадрате или единица во второй степени равняется единице. Минус единица -1 в квадрате так же равняется единице.
1² = 1 · 1 = 1
(-1)² = (-1) · (-1) = 1
2 в квадрате или 2 в степени 2 будет равно четырем. Если двойка отрицательная возводится во 2 степень, -2 в квадрате, это тоже равно четыре. Дважды два равно четыре — эта классика детской математики показывает результат возведения числа 2 в квадрат.
2² = 2 · 2 = 4
(-2)² = (-2) · (-2) = 4
Квадрат числа три или 3 в степени 2 равняется девяти. Трижды три равно девять. Минус три в квадрате равно девять. Не забываем, что минус умножить на минус дает плюс.
3² = 3 · 3 = 9
(-3)² = (-3) · (-3) = 9
Квадрат числа четыре или 4 в степени 2 равняется шестнадцати. Четырежды четыре равно шестнадцать. Минус четыре во второй степени тоже дает шестнадцать.
4² = 4 · 4 = 16
(-4)² = (-4) · (-4) = 16
Квадрат числа пять или 5 в степени 2 равняется двадцати пяти. Пять у пять — двадцать пять. Минус пять в степени два дает опять двадцать пять.
Пять у пять — двадцать пять. Минус пять в степени два дает опять двадцать пять.
5² = 5 · 5 = 25
(-5)² = (-5) · (-5) = 25
27 ноября 2010 года — 22 сентября 2019 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
Таблица квадратов чисел от 1 до 210
Таблица квадратов чисел от 1 до 210| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 |
| 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 |
| 841 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | 1600 | 1681 | 1764 |
| 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 |
| 3249 | 3364 | 3481 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | 4900 |
| 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | 6400 | 6561 | 6724 | 6889 | 7056 |
| 7225 | 7396 | 7569 | 7744 | 7921 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 |
| 9801 | 10000 | 10201 | 10404 | 10609 | 10816 | 11025 | 11236 | 11449 | 11664 | 11881 | 12100 | 12321 | 12544 |
| 12769 | 12996 | 13225 | 13456 | 13689 | 13924 | 14161 | 14400 | 14641 | 14884 | 15129 | 15376 | 15625 | 15876 |
| 16129 | 16384 | 16641 | 16900 | 17161 | 17424 | 17689 | 17956 | 18225 | 18496 | 18769 | 19044 | 19321 | 19600 |
| 19881 | 20164 | 20449 | 20736 | 21025 | 21316 | 21609 | 21904 | 22201 | 22500 | 22801 | 23104 | 23409 | 23716 |
| 24025 | 24336 | 24649 | 25281 | 25600 | 25921 | 26244 | 26569 | 26896 | 27225 | 27556 | 27889 | 28224 | |
| 28561 | 28900 | 29241 | 29584 | 29929 | 30276 | 30625 | 30976 | 31329 | 31684 | 32041 | 32400 | 32761 | 33124 |
| 33489 | 33856 | 34225 | 34596 | 34969 | 35344 | 35721 | 36100 | 36481 | 36864 | 37249 | 37636 | 38025 | 38416 |
| 38809 | 39204 | 39601 | 40000 | 40401 | 40804 | 41209 | 41616 | 42025 | 42436 | 42849 | 43264 | 43681 | 44100 |
— версия для печати
- Пояснение к таблице:
2209 — квадрат числа [47] — само число
- Определение
- Квадрат числа — результат умножения числа на самого себя.
 Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
- Пример:
- 972 = 97×97 = 9409
- Дополнительно:
- Таблица квадратов двузначных чисел
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Таблица квадратов
Таблица квадратов| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
— версия для печати
- Определение
- Квадрат числа — результат умножения числа на себя.

- Пример:
- 92 = 9×9 = 81
- Дополнительно:
- Расширенная таблица квадратов (числа от 1 до 210)
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Квадрат суммы и квадрат разности, разность квадратов
Квадрат суммы
Выражение (a + b)2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b)2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что
Следовательно, из квадрата суммы мы можем сделать выводы, что
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:
(a + b)2 = a2 + 2ab + b2.
Многочлен a2 + 2ab + b2 называется разложением квадрата суммы.
Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.
Пример. Возвести в квадрат выражение 3x2 + 2xy.
Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(3x2 + 2xy)2 = (3x2)2 + 2(3x2 · 2xy) + (2xy)2.
Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:
(3x2)2 + 2(3x2 · 2xy) + (2xy)2 = 9x4 + 12x3y + 4x2y2.
Квадрат разности
Выражение (a — b)2 — это квадрат разности чисел a и b. Выражение (a — b)2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что
Выражение (a — b)2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:
(a — b)2 = a2 — 2ab + b2.
Многочлен a2 — 2ab + b2 называется разложением квадрата разности.
Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.
Пример. Представьте квадрат разности в виде трёхчлена:
(2a2 — 5ab2)2.
Решение: Используя формулу квадрата разности, находим:
(2a2 — 5ab2)2 = (2a2)2 — 2(2a2 · 5ab2) + (5ab2)2.
Теперь преобразуем выражение в многочлен стандартного вида:
(2a2)2 — 2(2a2 · 5ab2) + (5ab2)2 = 4a4 — 20a3b2 + 25a2b4.
Разность квадратов
Выражение a2 — b2 — это разность квадратов чисел a и b. Выражение a2 — b2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:
(a + b)(a — b) = a2 + ab — ab — b2 = a2 — b2.
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Из правила следует, что общая формула разности квадратов выглядит так:
a2 — b2 = (a + b)(a — b).
Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.
Пример. Преобразуйте произведение в двучлен:
(5a2 + 3)(5a2 — 3).
Решение:
(5a2 + 3)(5a2 — 3) = (5a2)2 — 32 = 25a4 — 9.
В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:
(a + b)(a — b) = a2 — b2.
На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.
Формулы сокращённого умножения. Неполный квадрат суммы и разности
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
a2 + b2 = (a + b)2 — 2ab — сумма квадратов;
a2 — b2 = (a + b)(a — b) — разность квадратов;
(a + b)2 = a2 + 2ab + b2 — квадрат суммы;
(a — b)2 = a2 — 2ab + b2 — квадрат разности;
a3 + b3 = (a + b)(a2 — ab + b2) — сумма кубов;
a3 — b3 = (a — b)(a2 + ab + b2) — разность кубов;
(a + b)3 = a3 + 3a2b + 3ab2 + b3 — куб суммы;
(a — b)3 = a3 — 3a2b + 3ab2 — b3 — куб разности.
Обратите внимание, что a
и b
в формулах сокращённого умножения могут быть как числами, так и выражениями.
Разложение формул сокращенного умножения
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.
Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
a2 + b2 = (a + b)2 — 2ab.
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)2 — 2ab = (a + b)(a + b) — 2ab = a2 + ab + ab + b2 — 2ab = a2 + b2.
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
a2 — b2 = (a + b)(a — b).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2.
Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
(a — b)2 = a2 — 2ab + b2.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.
Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
a3 + b3 = (a + b)(a2 — ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3.
Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
a3 — b3 = (a — b)(a2 + ab + b2).
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3.
Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
(a — b)3 = a3 — 3a2b + 3ab2 — b3.
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) = a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3.
Неполный квадрат суммы
Выражение:
a2 + 2ab + b2
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
a2 + ab + b2,
которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Выражение:
a2 — 2ab + b2
это квадрат разности, который также называется полным квадратом разности относительно выражения:
a2 — ab + b2,
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Возведение в степень: правила, примеры, дробная степень
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Пример 3Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи .
От основания степени это не зависит.
Пример 4Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Пример 5Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Возведите 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Пример 7Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Определение 2Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.
Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11Вычислите приближенное значение 2 в степени 1,174367. …
…
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Арифметические операции | MDN
Арифметические операции принимают в качестве операндов числовые значения (это может быть и литерал и переменная) и возвращают результат в виде одного числового значения. Стандартными арифметическими операциями являются сложение (+), вычитание (-), умножение (*) и деление (/).
Оператор сложения возвращает сумму числовых операндов или объединяет строки.
Синтаксис
Примеры
1 + 2
true + 1
false + false
5 + "foo"
"foo" + false
"foo" + "bar"
Оператор вычитания вычитает один операнд из другого и возвращает разницу.
Синтаксис
Примеры
Оператор деления производит деление его операндов, где левый операнд — делимый, а правый — делитель.
Синтаксис
Примеры
1 / 2
1 / 2
1.0 / 2.0
2.0 / 0
2.0 / 0.0
2.0 / -0.0 Оператор умножения возвращает произведение операндов.
Синтаксис
Примеры
2 * 2
-2 * 2
Infinity * 0
Infinity * Infinity
"foo" * 2
Оператор возвращает целый остаток от деления левого операнда на правый. Возвращаемое значение всегда получает знак делимого, а не делителя. Он использует встроенную функцию modulo, для получения результата, которая является целочисленным остатком деления var1 на var2 — например— var1 modulo var2. Есть предложение добавить оператор modulo в будущие версии ECMAScript, с той разницей, что оператор будет брать знак делителя, а не делимого.
Синтаксис
Оператор: var1 % var2
Примеры
12 % 5
-1 % 2
NaN % 2
1 % 2
2 % 3
-4 % 2
5. или **), оператор определён имеющим приоритет выше, чем у унарных операторов, таких как унарный + и унарный -, но есть несколько исключений. Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (
или **), оператор определён имеющим приоритет выше, чем у унарных операторов, таких как унарный + и унарный -, но есть несколько исключений. Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (+/-/~/!/delete/void/typeof) непосредственно перед базовым числом.
-2 ** 2;
-(2 ** 2);
Примеры
2 ** 3
3 ** 2
3 ** 2.5
10 ** -1
NaN ** 2
2 ** 3 ** 2
2 ** (3 ** 2)
(2 ** 3) ** 2
Изменим знак результата возведения в степень:
-(2 ** 2)
Насильная установка основания как отрицательного числа:
(-2) ** 2
Оператор инкремента увеличивает на единицу(инкрементирует) операнд и возвращает значение.
- Если операция используется как постфикс, с оператором после операнда (например, x++), значение операнда возвращается, а затем увеличивается на единицу.

- Если используется префиксная форма с оператором перед операндом (например, ++x), значение операнда возвращается увеличенным на единицу.
Синтаксис
Оператор: x++ или ++x
Примеры
var x = 3;
y = x++;
var a = 2;
b = ++a;
Операция декремента уменьшает на 1 (отнимает единицу) свой операнд и возвращает значение.
- Если операция используется как постфикс (например, x--), значение операнда возвращается, а затем уменьшается на единицу.
- Если используется префиксная форма (например, --x), значение операнда возвращается уменьшенным на единицу.
Синтаксис
Оператор: x-- или --x
Примеры
var x = 3;
y = x--;
var a = 2;
b = --a;
Унарный минус ставится перед своим операндом и возвращает его математическое отрицание.
Синтаксис
Примеры
Оператор унарный плюс предшедствует своему операнду и оценивает его, пытается преобразовать его в число, если он им не является. Хотя, унарное отрицание (-) также конвертирует не числа, унарный плюс - быстрейший и предпочитаемый способ конвертирования чего-либо в число потому, что он не выполняет каких-либо операций с числом. Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения
Хотя, унарное отрицание (-) также конвертирует не числа, унарный плюс - быстрейший и предпочитаемый способ конвертирования чего-либо в число потому, что он не выполняет каких-либо операций с числом. Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения true, false и null. Поддерживаются числа в десятичном и шестнадцатиричном (с префиксом "0x") формате. Отрицательные числа тоже поддерживаются (но не 16-ричные). Если он не может вычислить конкретное значение, выполнится как NaN.
Синтаксис
Примеры
+3
+"3"
+true
+false
+null
Квадратное вычитание
Было отправлено решений на сумму около 80 долларов! У них было много примеров, на которые были даже ответы. Мы действительно предложили вам пойти немного дальше, и у нас есть несколько идей.
Первый от Оуэна из Монтессори школы Вустера, Огайо, США
Квадратное число, вычитаемое из самого себя (X в квадрате - X), всегда должно быть четным. Это всегда будет четное число, потому что четное число, умноженное на нечетное (3 x 3 = 3 x 2), всегда будет четным
Это всегда будет четное число, потому что четное число, умноженное на нечетное (3 x 3 = 3 x 2), всегда будет четным
(например,4 х 4-4 = 4 х 3 = 12, 5 х 5-5 = 4 х 5 = 20)
У Эми из начальной школы Клермонта в Великобритании были следующие мысли;
2 x 2 = 4
4-2 = 2 (четное)
Ответ четное с четным числом отправной точкой
3 x 3 = 9
9 - 3 = 6 (четное)
Ответ четное с нечетным числом отправной точкой
Поэтому ответ всегда четный. Почему?
Ответ всегда будет четным, потому что квадрат нечетного числа дает другое нечетное число.Четное число в квадрате дает четное число. И четное число, убрав другое четное число, сделает другое четное число. Но, как ни странно, нечетное число убирает другое нечетное число, также получается четное.
Жасмин, Арран, Ребекка и Томас из школы Святой Марии Шоубери в Англии, у нас возникла похожая мысль;
Ответ четный. Мы знаем это, потому что когда вы возводите в квадрат четное число, вы всегда получаете четное число, но когда вы убираете четное число из числа, которое у вас есть сейчас, вы все равно остаетесь четным числом, независимо от того, с какого числа вы начали.
Когда вы возводите в квадрат нечетное число, в результате должно получиться другое нечетное число, но когда вы вычитаете нечетное число из числа, которое у вас есть сейчас, оно будет четным.
например Четный квадрат = четный - четный = четный.
например Нечетный квадрат = нечетный - нечетный = четный.
Мы пробовали это с 1,2,3-значными числами, и все они заканчивались четными, мы также пробовали разные нечетные и четные числа и нашли тот же результат, все ответы были четными.
Олли из Академии Буртон-Мидоу в Англии написал;
Это всегда четно, потому что четное число, кратное четному
$ (2a) (2a + 1) = 6a,
долларов США. ) = 6a $
Наконец Виктор и Эллиот из школы Кенакена в Новой Зеландии;
$ X² - X = четный.Если $ X $ нечетное. $ X² $ - это странно. так что $ X² - X = даже $.
Если $ X $ четное. $ X² $ чётно. так что $ X² - X = даже $.
Сторона доказательства: как четное - четное = четное и нечетное - нечетное = четное:
Если n и e - произвольные целые числа, то even = $ 2n $ (я думаю, это означает, что вы можете записать четное число как $ 2n $), так что даже - четное $ = 2n - 2e = 2 (n - д) $. Тем самым даже - даже = даже.
Тем самым даже - даже = даже.
Итак, нечетный $ = 2n + 1 $. Итак, odd - odd = $ 2n + 1 - (2e + 1) = 2n - 2e + 1 - 1 = 2 (n- e) $.
Таким образом, нечетное минус нечетное = четное.
В конце месяца у нас было несколько предложений от Джека, Дэниела, Софи, Изобель и Райана из начальной школы Кейдмарк
Спасибо всем за вашу тяжелую работу и электронные письма.
Квадраты и квадратные корни в алгебре
Возможно, вы сначала захотите прочитать наше Введение в квадраты и квадратные корни.
Квадраты
Чтобы возвести число в квадрат, просто умножьте его само на себя
...
Пример: Что такое 3 в квадрате?
3 Квадратный = = 3 × 3 = 9
«В квадрате» часто записывают как две маленькие цифры:
Это говорит о том, что "4 в квадрате равно 16"
(маленькая 2 означает
число появляется дважды при умножении, поэтому 4 × 4 = 16)
Квадратный корень
Квадратный корень идет в другом направлении:
3 в квадрате равно 9, поэтому квадратный корень из 9 это 3
Это как спросить:
Что можно умножить на само по себе, чтобы получить это?
Определение
Вот определение:
Квадратный корень из x равен , число r , квадрат которого равен x:
r 2 = x
r квадратный корень из x
Символ квадратного корня
Это специальный символ, означающий "квадратный корень", это как галочка,
и фактически началось сотни лет
назад в виде точки с движением вверх.
Он называется радикалом и всегда делает математику важной!
Мы можем использовать это так:
мы говорим "квадратный корень из 9 равен 3"
Пример: Что такое √36?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Отрицательные числа
Мы также можем возводить в квадрат отрицательные числа.
Пример: Что такое
минус 5 в квадрате ? Но подождите... что означает «минус 5 в квадрате»?
- квадрат 5, тогда минус?
- или квадрат (−5)?
Непонятно! И получаем разные ответы:
- возвести в квадрат 5, затем вычислить минус: - (5 × 5) = −25
- квадрат (−5): (−5) × (−5) = +25
Итак, давайте проясним это с помощью «()».
Это было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительный результат .
То же, что и возведение положительного числа в квадрат:
Теперь помните наше определение квадратного корня?
Квадратный корень из x равен , число r , квадрат которого равен x:
r 2 = x
r квадратный корень из x
И мы только что обнаружили, что:
(+5) 2 = 25
(−5) 2 = 25
Итак, и +5, и −5 являются квадратными корнями из 25
. Два квадратных корня
Может быть положительный и отрицательный квадратный корень!
Это важно помнить.
Пример: Решите w
2 = a Ответ:
w = √a и w = −√a
Главный квадратный корень
Итак, если на самом деле есть два квадратных корня, почему люди говорят √25 = 5?
Потому что √ означает главный квадратный корень ... тот, который не является отрицательным!
- это два квадратных корня, но символ √ означает только главный квадратный корень .
Пример:
Квадратные корни из 36 равны 6 и −6
Но √36 = 6 (не −6)
Главный квадратный корень иногда называют положительным квадратным корнем (но он может быть нулевым).
Знак плюс-минус
± - специальный символ, означающий «плюс или минус»,
поэтому вместо записи: w = √a и w = −√a мы можем написать: w = ± √a
В двух словах
Когда имеем: r 2 = x
, тогда: r = ± √x
Почему это важно?
Почему этот «плюс-минус» важен? Потому что мы не хотим упустить решение!
Пример: Решить x
2 - 9 = 0 Начать с: x 2 - 9 = 0
Переместите 9 вправо: x 2 = 9
Квадратный корень: x = ± √9
Ответ: x = ± 3
Знак «±» говорит нам также включить ответ «−3».
Пример: найти x в (x - 3)
2 = 16 Начать с: (x - 3) 2 = 16
Квадратный корень: x - 3 = ± √16
Вычислить √16: x - 3 = ± 4
Добавьте 3 к обеим сторонам: x = 3 ± 4
Ответ: x = 7 или −1
Чек: (7−3) 2 = 4 2 = 16
Чек: (−1−3) 2 = (−4) 2 = 16
Квадратный корень xy
Когда два числа умножаются на на квадратный корень, мы можем разделить это на умножение двух квадратных корней следующим образом:
√xy = √x√y
, но только если x и y оба больше или равны 0
Пример: Что такое
√ (100 × 4) ? √ (100 × 4) = √ (100) × √ (4)
= 10 × 2
= 20
и √x√y = √xy :
Пример: Что такое
√8√2 ? √8√2 = √ (8 × 2)
= √16
= 4
Пример: Что такое
√ (−8 × −2) ? √ (−8 × −2) = √ (−8) × √ (−2)
= ???
Кажется, мы здесь попались в какую-то ловушку!
Мы можем использовать мнимые числа, но это приводит к неправильному ответу -4
Да, верно. ..
..
Правило работает, только если x и y оба больше или равны 0
Итак, мы не можем использовать это правило здесь.
Вместо этого просто сделайте это так:
√ (−8 × −2) = √16 = +4
Почему √xy = √x√y?
Мы можем использовать тот факт, что возведение квадратного корня в квадрат снова возвращает нам исходное значение:
(√a) 2 = a
Предположим, что , а не отрицательное!
Мы можем сделать это для xy: (√xy) 2 = xy
А также к x и y по отдельности: (√xy) 2 = (√x) 2 (√y) 2
Используйте 2 b 2 = (ab) 2 : (√xy) 2 = (√x√y) 2
Убрать квадрат с обеих сторон : √xy = √x√y
Показатель половины
Квадратный корень можно также записать в виде дробной степени от половины:
, но только для x больше или равно 0
Как насчет квадратного корня негативов?
Результат - мнимое число. .. прочтите эту страницу, чтобы узнать больше.
.. прочтите эту страницу, чтобы узнать больше.
разницы в квадратных числах | NZ Maths
В этом упражнении ученики ищут узоры в расположении квадратных плиток. Отображение различий с помощью плиток, многозвенных кубов или рисунков на бумаге в квадрате, вероятно, поможет учащимся увидеть различные узоры.
В вопросе 1 расположение плиток связано с различиями между последовательными номерами квадратов. Когда 32, представленное квадратом 3 на 3, сравнивается с 2 2 (квадрат 2 на 2), разница составляет 5 квадратов, представленных в виде буквы L.
Различия между двумя последовательными квадратными числами, например, 2 2 - 1 2 , 3 2 -2 2 или 4 2 - 3 2 , могут быть показаны следующим образом:
Рассматривая уравнения или диаграммы, ученики могут увидеть простое правило для этих вычислений, в котором разница между возведенными в квадрат числами равна 1. Правило: сложите два числа, которые возводятся в квадрат. Например, 7 2 -6 2 может быть представлено как 7 + 6 = 13, а 19 2 -18 2 как 19 + 18 = 37.Это правило
Правило: сложите два числа, которые возводятся в квадрат. Например, 7 2 -6 2 может быть представлено как 7 + 6 = 13, а 19 2 -18 2 как 19 + 18 = 37.Это правило
также может быть выражено алгебраически как: «Если b = a + 1 (где a и b - последовательные числа), то b 2 - a 2 = a + b». Приведенные выше диаграммы должны помочь учащимся геометрически понять, почему это правило работает. Например, 20 2 - 19 2 = 20 + 19 (что составляет b 2 - a 2 = a + b для значений a = 19, b = 20)
= 39
В вопросе 2 , образец различий между альтернативными квадратными числами может быть показан следующим образом:
Учащиеся могут увидеть простое правило для этих вычислений, в котором разница между числами, возведенными в квадрат, равна 2.Правило: удвойте сумму двух чисел, возведенных в квадрат. Так, например, 27 2 -25 2 = 2 x (27 + 25).
Еще раз, приведенные выше диаграммы помогут ученикам геометрически понять, почему это правило работает.
Алгебраически здесь действует правило: если b = a + 2, то b 2 - a 2 = 2 (a + b).
В вопросе 3 образец разницы между любым квадратным числом и третьим последующим квадратным числом может быть показан следующим образом:
Учащиеся могут увидеть простое правило для этих вычислений, в котором разница между числами, возведенными в квадрат, равна 3.Правило таково: утроить сумму двух возведенных в квадрат чисел. Так, например, 27 2 -24 2 = 3 x (27 + 24). Алгебраически правило здесь таково: если b = a + 3, то b 2 - a 2 = 3 (a + b).
Эти правила можно обобщить. В следующих таблицах приведены расчеты для вопросов с 1 по 3. Для каждой из этих таблиц кратчайший расчет всегда представляет собой разницу, умноженную на сумму двух возведенных в квадрат чисел. Обратите внимание, что в первой таблице ниже разница равна 1, поэтому мы можем написать 4 + 3 вместо 1 x (4 + 3) и так далее.
В общем, тогда правило: b в квадрате минус квадрат равняется разнице между b и a, умноженной на сумму b и a. Алгебраически мы можем записать это как:
b 2 - a 2 = (b - a) x (b + a)
= (b - a) (b + a).
Это правило будет работать для всех значений a и b. В следующей таблице показано, как можно использовать это правило:
Ответы на действие
1. а. 3 2 - 2 2 = 5 и 4 2 - 3 2 = 7
б.Разница между последовательными квадратными числами всегда нечетная. Разница - это сумма двух возведенных в квадрат чисел.
г. 19 + 18 = 37, поэтому 19 2 - 18 2 = 37
2. a. 42 - 22 = 12 и 52 - 32 = 16
б. Разница между альтернативными квадратными числами всегда четная; это удвоенная сумма двух возведенных в квадрат чисел.
с. 2 x (13 + 11) = 48, поэтому 13 2 - 11 2 = 48
3. a. 5 2 - 2 2 = 21 и 6 2 - 3 2 = 27
б. {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
Квадратный корень записывается с помощью символа корня √, а число или выражение внутри символа корня, обозначенное ниже a, называется подкоренным выражением.
$$ \ sqrt {a} $$
Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренной части, мы помещаем перед корнем символ ± (читается как плюс минус).
$$ \ pm \ sqrt {9} = \ pm 3 $$
У нуля один квадратный корень, равный 0.
$$ \ sqrt {0} = 0 $$
Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положительный, либо 0.
Если квадратный корень целого числа является другим целым числом, квадрат называется полным квадратом.Например, 25 - это идеальный квадрат, так как
$$ \ pm \ sqrt {25} = \ pm 5 $$
Если подкоренное выражение не является полным квадратом, то есть квадратный корень не является целым числом, тогда вам нужно приблизительно вычислить квадратный корень
$$ \ pm \ sqrt {3} = \ pm 1. 73205 ... \ приблизительно \ pm 1,7 $$
73205 ... \ приблизительно \ pm 1,7 $$
Квадратные корни из чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел. Десятичная форма иррационального числа не прерывается и не повторяется.Иррациональные числа вместе с рациональными числами составляют действительные числа.
Видеоурок Приблизительно квадратный корень из 250
Вычитание квадратного корня - математический класс (видео)
Вычитание с подобными подкоренными элементами
Квадратный корень состоит из трех частей:
- Дробный индекс
- Радикал или символ квадратного корня
- Родиканд, или число под радикальным символом
Для квадратных корней стандартная практика подразумевает, но не показывает индекс.
Чтобы вычесть квадратные корни, мы должны обращать внимание на их подкоренные выражения. Если подкоренные выражения совпадают, мы можем вычесть квадратные корни, комбинируя члены.
Здесь наш ответ представлен в виде числа, умноженного на квадратный корень. Это простейшая форма, которую может принять эта задача вычитания выборки, если мы ищем точный ответ.
Вычитание с использованием подкоренных выражений, отличных от подкоренных
Когда квадратные корни имеют непохожие подкоренные выражения, первым делом нужно проверить, можно ли разложить на множители какие-либо подкоренные выражения.
При этом следите за идеальными квадратами. Идеальный квадрат - это любое число, полученное в результате умножения другого числа на себя. Это означает, что мы можем упростить подкоренные выражения, извлекая квадратные корни из любого их точного квадратного множителя.
Как только квадратные корни уравнения имеют одинаковые подкоренные выражения, мы можем вычесть их таким же образом, как и в предыдущем разделе. Точный ответ для нашего уравнения уже есть в его простейшей форме.
Точный ответ для нашего уравнения уже есть в его простейшей форме.
Приближение и десятичные дроби
До сих пор мы работали только с целыми числами, набором чисел, состоящим из нуля и всех положительных целых чисел. При работе с десятичными знаками мы можем использовать калькулятор, чтобы получить приближение квадратного корня из неполных квадратных чисел.
Решение для квадратных корней позволяет использовать обычный порядок операций, как и в случае любой стандартной математической задачи.Даже решение проблемы в его простейшей форме может быть аппроксимировано десятичными знаками. Однако помните, что использование этого метода для вычитания квадратных корней всегда приводит к приближению, а не к точному ответу. Вот почему понимание правил вычитания квадратных корней, которые мы обсуждали ранее, по-прежнему важно.
Итоги урока
Давайте рассмотрим. Корень - это показатель степени в дробной форме. Квадратный корень состоит из трех частей:
Корень - это показатель степени в дробной форме. Квадратный корень состоит из трех частей:
- Дробный индекс, который обычно подразумевается
- Радикал или символ квадратного корня
- Родиканд, или число под радикальным символом
При вычитании квадратных корней с одинаковыми подкоренными элементами объедините члены.При вычитании квадратных корней с разными подкоренными выражениями посмотрите, можно ли еще больше упростить подкоренное выражение, найдя его идеальный квадрат или любое число, полученное в результате умножения другого числа на себя. Если результатом является уравнение с такими же подкоренными выражениями, вычтите, снова комбинируя члены. В отсутствие подобных подкоренных выражений вычитание не даст точного ответа. Если ответ на задачу вычитания квадратных корней дает приблизительный, а не точный ответ, используйте калькулятор, чтобы найти приблизительное значение квадратных корней.2} = \ pm xx2 = ± x
Почему некоторые люди говорят, что это правда: Это именно то, чему меня учили в школе: когда вы извлекаете квадратный корень, ответ всегда будет положительным или отрицательным.
Почему некоторые люди говорят, что это ложь: Когда вы возводите в квадрат x, x, x, оно становится положительным, независимо от того, что было раньше; тогда, когда вы извлекаете квадратный корень, он все равно положительный. Следовательно, ответ будет просто ∣x∣ | x | ∣x∣, а не ± x \ pm x ± x.
Выявите правильный ответ: \ color {# 20A900} {\ text {Выявите правильный ответ:}} Выявите правильный ответ:
Утверждение ложно \ color {# D61F06} {\ textbf {false}} ложно.
Пояснение:
В своей стандартной области неотрицательных действительных чисел x \ sqrt {x} x определяется как «неотрицательное действительное число, которое в квадрате равно x.x.x.» Например, 25 = 5 \ sqrt {25} = 525 = 5 , а не ± 5 \ pm 5 ± 5. x \ sqrt {x} x определяется таким образом, так что это функция.
Функция - это отношение или карта между набором входных значений (домен) и набором выходных значений (диапазон), которая имеет свойство, что каждый принятый вход соответствует ровно одному выходу. Парабола 2x2 не пройдет проверку вертикальной линии и не будет функцией.
Парабола 2x2 не пройдет проверку вертикальной линии и не будет функцией.
Расширение домена до всех действительных чисел и диапазона до комплексных чисел:
Поведение функции извлечения квадратного корня при расширении на область всех действительных чисел (положительные действительные числа, отрицательные действительные числа и 0) точно отражает приведенный выше аргумент. Квадратный корень отрицательного числа - это комплексное число. Но даже с расширенной областью определения x \ sqrt {x} x аналогичным образом определяется, так что это все еще функция.2}} {| x |} + 1, ∣x∣x2 +1,
, где xxx - ненулевое действительное число.
См. Также
Факторизация разницы двух квадратов
В какой-то момент вашего изучения алгебры вас попросят разложить на множители выражения, распознавая некоторые особые шаблоны. разность двух квадратов - одна из самых распространенных. Хорошая новость в том, что эту форму очень легко идентифицировать.
Хорошая новость в том, что эту форму очень легко идентифицировать.
Всякий раз, когда у вас есть бином, в котором каждый член возведен в квадрат (с показателем 2), и у них есть вычитание в качестве среднего знака, вы гарантированно получите случай разницы в два квадрата.
Приведенная ниже диаграмма должна обеспечить интуитивное понимание этой концепции.
Убедившись, что у вас есть разница в два квадрата, вы можете теперь разложить ее на множители как произведение двух биномов с чередующимися знаками в середине, положительным и отрицательным.
Формула разности двух квадратов
Это других способа записать формулу разности двух квадратов с использованием переменных. Научитесь распознавать их по-разному, чтобы точно знать, как с ними обращаться.
Примеры того, как множить разность двух идеальных квадратов
Давайте рассмотрим несколько примеров!
Пример 1: Разложите приведенный ниже бином на множители, используя метод разницы двух квадратов.
Первый член бинома определенно является полным квадратом, потому что переменная x возводится во вторую степень. Однако второй член двучлена не записывается в виде квадрата. Поэтому нам нужно переписать его таким образом, чтобы 9 выражалось некоторым числом с степенью 2.2}. Ясно, что у нас есть разница в два квадрата, потому что знак между двумя членами в квадрате - это вычитание.
В этом примере решение разбито всего на несколько шагов, чтобы выделить процедуру. Когда вы освоитесь с процессом, вы можете пропустить множество шагов. Фактически, вы можете сразу перейти от разницы двух квадратов к ее множителям.
Пример 2: Разложите на множители приведенный ниже бином.
На первый взгляд кажется, что это не разница в два квадрата.2}? Это должно быть 2x, так как
Для второго члена число при умножении на само себя дает 49, так как
Решение этой проблемы выглядит следующим образом:
Пример 3: Разложите на множители бином, приведенный ниже.
Эта задача немного отличается, потому что оба члена бинома содержат переменные. Если мы сможем показать, что это идеальные квадраты, тогда все будет в порядке!
- Первый член является точным квадратом, поскольку
- Более того, второй также является полным квадратом, потому что
Применяя формулу для разности двух квадратов, мы получаем:
Пример 4: Фактор бином ниже.2} = \ left ({2y} \ right) \ left ({2y} \ right) и, очевидно, 9 = \ left (3 \ right) \ left (3 \ right).
Это означает, что вам нужно еще раз применить формулу для разности двух квадратов.
Вот полное решение этой проблемы.
Пример 5: Разложите на множители приведенный ниже бином.
Обратите внимание, что у бинома есть только один вид переменной - «x». Основная стратегия, когда вы видите что-то похожее, состоит в том, чтобы исключить наибольший общий фактор (GCF) среди переменных.4}. Если вычесть это за скобки, получится
. Теперь мы можем разобраться с биномом в скобках. Фактически это разница в два квадрата, потому что мы можем выразить каждый член бинома как выражение со степенью 2.
Теперь мы можем разобраться с биномом в скобках. Фактически это разница в два квадрата, потому что мы можем выразить каждый член бинома как выражение со степенью 2.
Затем мы применим формулу для разности двух квадратов,
Готово? Неа! Вторая скобка по-прежнему означает разность двух квадратов. У нас нет выбора, кроме как еще раз вычленить это.
Просмотрите биномы еще раз, чтобы увидеть, сохраняется ли разница в два квадрата.2}, а второй член равен 4. Поскольку оба члена возведены в квадрат и разделены вычитанием, это действительно случай разности двух квадратов.
Вы можете сохранить его в этой форме в качестве окончательного ответа. Но лучший ответ - комбинировать одинаковые термины, добавляя или вычитая константы. Это также упрощает ответ, избавляясь от внутренних скобок.
Возможно, вас также заинтересует:
Факторинговая разность двух квадратов практических задач
Факторинговая сумма и разность двух кубов
Факторинговая сумма и разница двух кубов практические задачи
.

 Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
 или **), оператор определён имеющим приоритет выше, чем у унарных операторов, таких как унарный + и унарный -, но есть несколько исключений. Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (
или **), оператор определён имеющим приоритет выше, чем у унарных операторов, таких как унарный + и унарный -, но есть несколько исключений. Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (
 Хотя, унарное отрицание (-) также конвертирует не числа, унарный плюс - быстрейший и предпочитаемый способ конвертирования чего-либо в число потому, что он не выполняет каких-либо операций с числом. Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения
Хотя, унарное отрицание (-) также конвертирует не числа, унарный плюс - быстрейший и предпочитаемый способ конвертирования чего-либо в число потому, что он не выполняет каких-либо операций с числом. Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения  Это всегда будет четное число, потому что четное число, умноженное на нечетное (3 x 3 = 3 x 2), всегда будет четным
Это всегда будет четное число, потому что четное число, умноженное на нечетное (3 x 3 = 3 x 2), всегда будет четным
 Тем самым даже - даже = даже.
Тем самым даже - даже = даже.



 ..
.. .. прочтите эту страницу, чтобы узнать больше.
.. прочтите эту страницу, чтобы узнать больше. Правило: сложите два числа, которые возводятся в квадрат. Например, 7 2 -6 2 может быть представлено как 7 + 6 = 13, а 19 2 -18 2 как 19 + 18 = 37.Это правило
Правило: сложите два числа, которые возводятся в квадрат. Например, 7 2 -6 2 может быть представлено как 7 + 6 = 13, а 19 2 -18 2 как 19 + 18 = 37.Это правило 

 {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$ 73205 ... \ приблизительно \ pm 1,7 $$
73205 ... \ приблизительно \ pm 1,7 $$
 Точный ответ для нашего уравнения уже есть в его простейшей форме.
Точный ответ для нашего уравнения уже есть в его простейшей форме.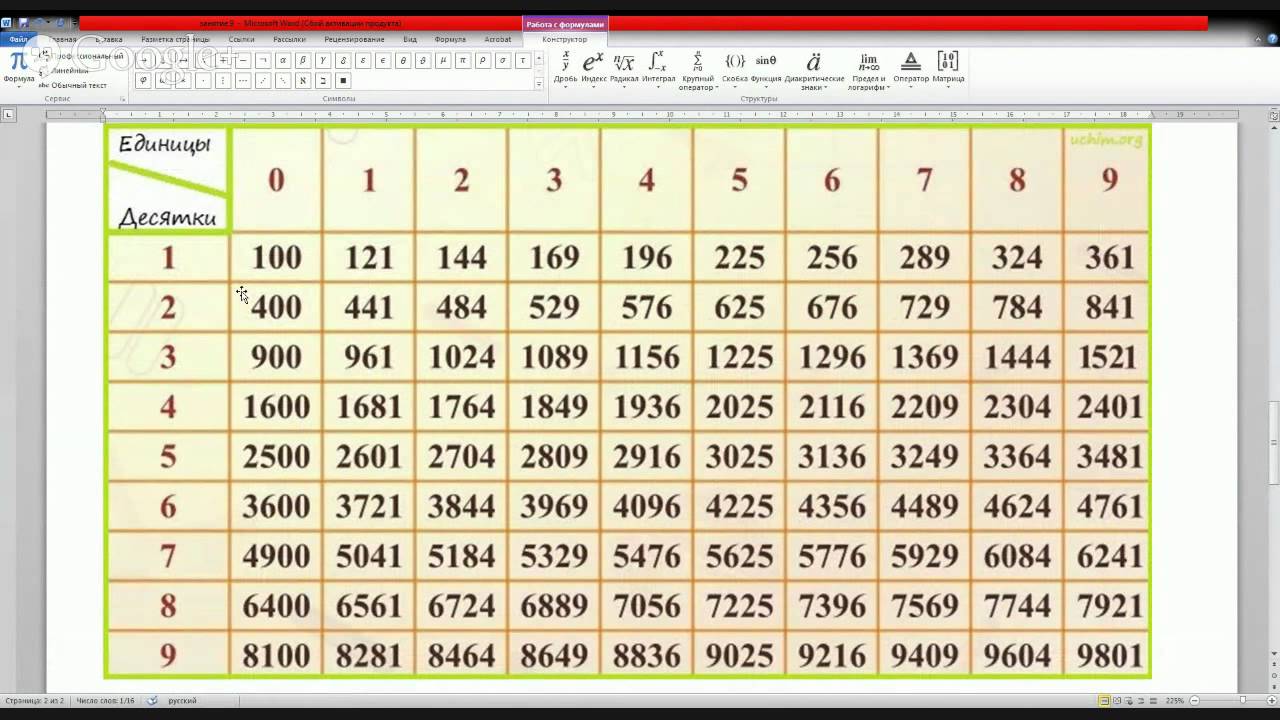 Корень - это показатель степени в дробной форме. Квадратный корень состоит из трех частей:
Корень - это показатель степени в дробной форме. Квадратный корень состоит из трех частей:
 Парабола 2x2 не пройдет проверку вертикальной линии и не будет функцией.
Парабола 2x2 не пройдет проверку вертикальной линии и не будет функцией. Хорошая новость в том, что эту форму очень легко идентифицировать.
Хорошая новость в том, что эту форму очень легко идентифицировать.

 Теперь мы можем разобраться с биномом в скобках. Фактически это разница в два квадрата, потому что мы можем выразить каждый член бинома как выражение со степенью 2.
Теперь мы можем разобраться с биномом в скобках. Фактически это разница в два квадрата, потому что мы можем выразить каждый член бинома как выражение со степенью 2.