Обратная функция онлайн калькулятор: Калькулятор Обратных Функций

2

Как найти обратную функцию — MathCracker.com

Алгебра Учебники

---

Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.

Прежде всего, вам нужно понять, что перед тем, как найти инверсию функции, вы должны убедиться, что такая инверсия существует.

Преимущество метода поиска обратного, который мы будем использовать, заключается в том, что мы найдем обратное и выясним, существует ли оно одновременно.

Готовый?? Тогда пристегнитесь.

Как узнать, есть ли у функции инверсия?

Технически функция имеет инверсию, когда она взаимно однозначна (инъективна) и сюръективна.

Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон своим собственным изображением.

Как узнать, что функция взаимно однозначна?

Что ж, есть как минимум пара способов.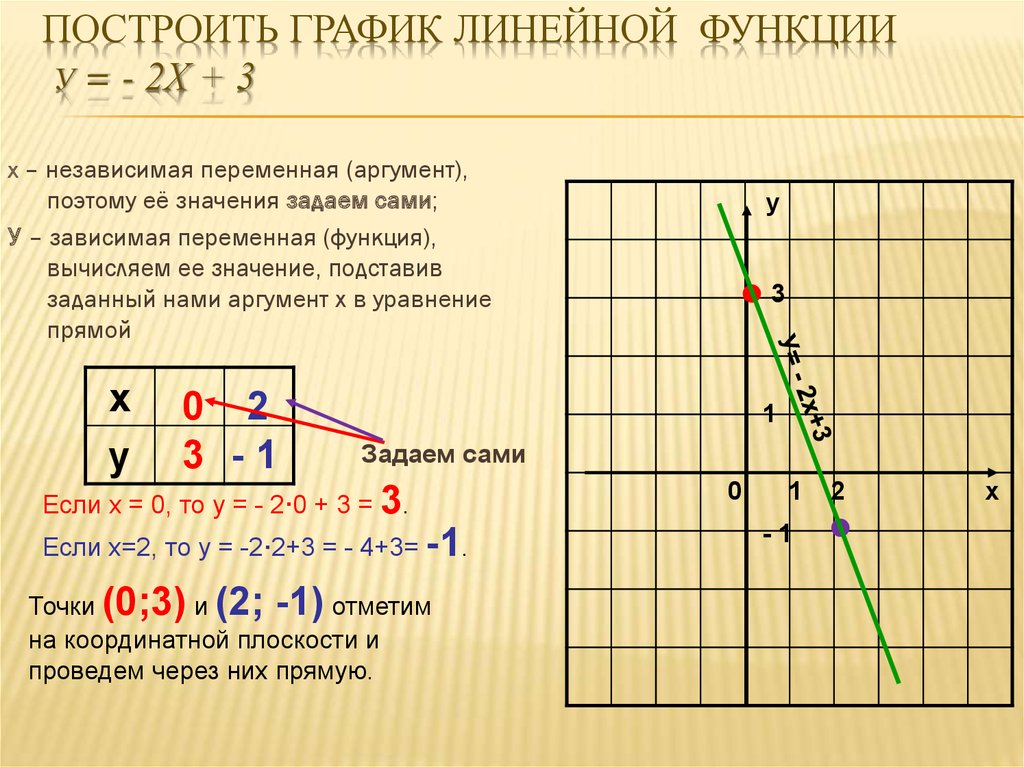 Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, да?)

Алгебраический путь

Для алгебраического подхода, чтобы функция \(f\) была взаимно однозначной, нам нужно доказать, что каждый раз, когда это \(f(x) = f(y)\), нам нужно иметь это \(x = y\).

Другими словами, нам нужно доказать, что

\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]

Графический способ

Для графического способа нам нужно использовать проверка горизонтальной линии

: Для любой горизонтальной линии, которую мы рисуем, график функции не более одного раза пересекает эту горизонтальную линию.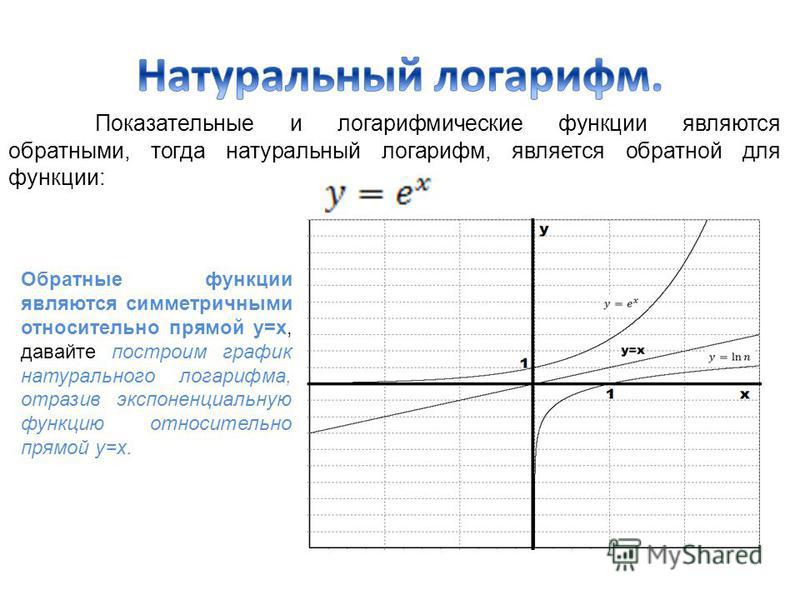

Графически:

Проходит тест горизонтальной линии

Не проходит тест горизонтальной линии

---

В поисках обратного

Чтобы найти обратную функцию для заданной функции \(f(x)\), необходимо решить уравнение.

Действительно, у вас есть уравнение \(f(x) = y\), вы берете \(y\) как заданное число, и вам нужно решить его для \(x\), и вам нужно убедиться, что решение УНИКАЛЬНО.

Это все. Легко, правда ??

Теперь о практических шагах:

Шаг 1: Для заданного \(y\) задайте уравнение:

\[f(x) = y\]

и решите его для \(x\). {-1}(x)\).

ПРИМЕР 1

Найдите обратную функцию \(f(x) = \sqrt x\)

ОТВЕЧАТЬ:

Итак, мы берем \(y\) как данное, и нам нужно решить \(f(x) = y\), что в данном случае соответствует решению

\[\sqrt x = y\]

Обратите внимание, что квадратный корень всегда неотрицателен, поэтому для решения нам понадобится \(y\ge 0\). 2\]

для \(x\ge 0\).

ПРИМЕР 2

Найдите обратную функцию \(f(x) = \displaystyle \frac{x}{x+1}\) для \(x > -1\)

ОТВЕЧАТЬ:

Опять же, мы берем \(y\) как дано, и теперь нам нужно решить для \(x\) уравнение \(f(x) = y\). Итак, у нас есть

\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x — yx = y\] \[\Rightarrow \,\, x(1 — y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]

Итак, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\), переключая имя переменной, мы получаем обратную функцию:

\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]

---

Подробнее о поиске обратной функции

Одним из важнейших свойств обратной функции \(f^{-1}(x)\) является то, что \(f(f^{-1}(x)) = x\).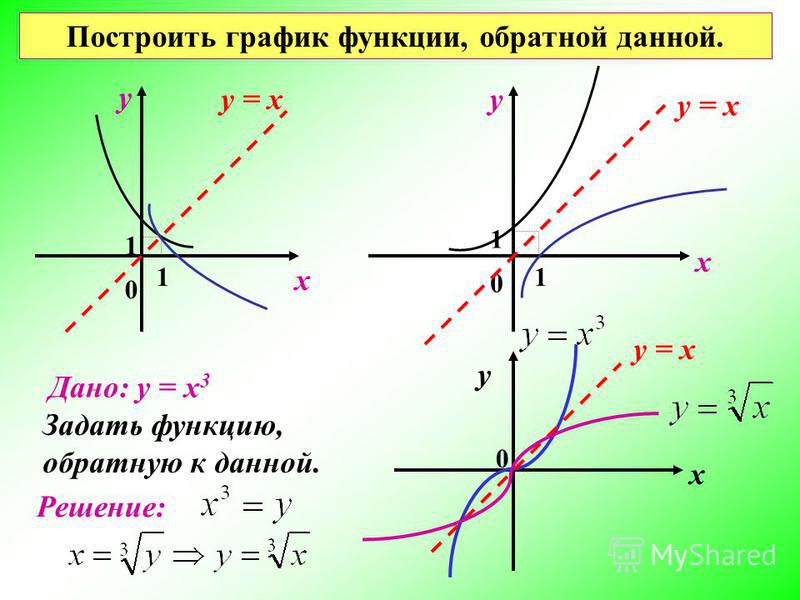

Подумайте, о чем это говорит. Что-то вроде: «Функция, вычисленная в обратном порядке, дает вам идентичность».

Или, другими словами, вычисление инверсии через функцию похоже на бездействие с аргументом.

Или, как некоторые любят говорить: функция может каким-то образом отменить обратное.

Вы выбираете свою версию.

Как найти обратную квадратичную функцию? Ты можешь?

Собственно, ответ таков: это зависит от обстоятельств. Это потому, что если мы рассмотрим квадратичную функцию по всей реальной линии , то это не один к одному, поскольку он не проходит тест горизонтальной линии, как вы можете видеть на диаграмме ниже:

Не пройдя тест горизонтальной линии, мы можем увидеть, что для данного \(y\) существует более одного значения \(x\), так что \(f(x) = y\), поэтому мы не можем «решить» для \(x\), поскольку существует более одного \(x\).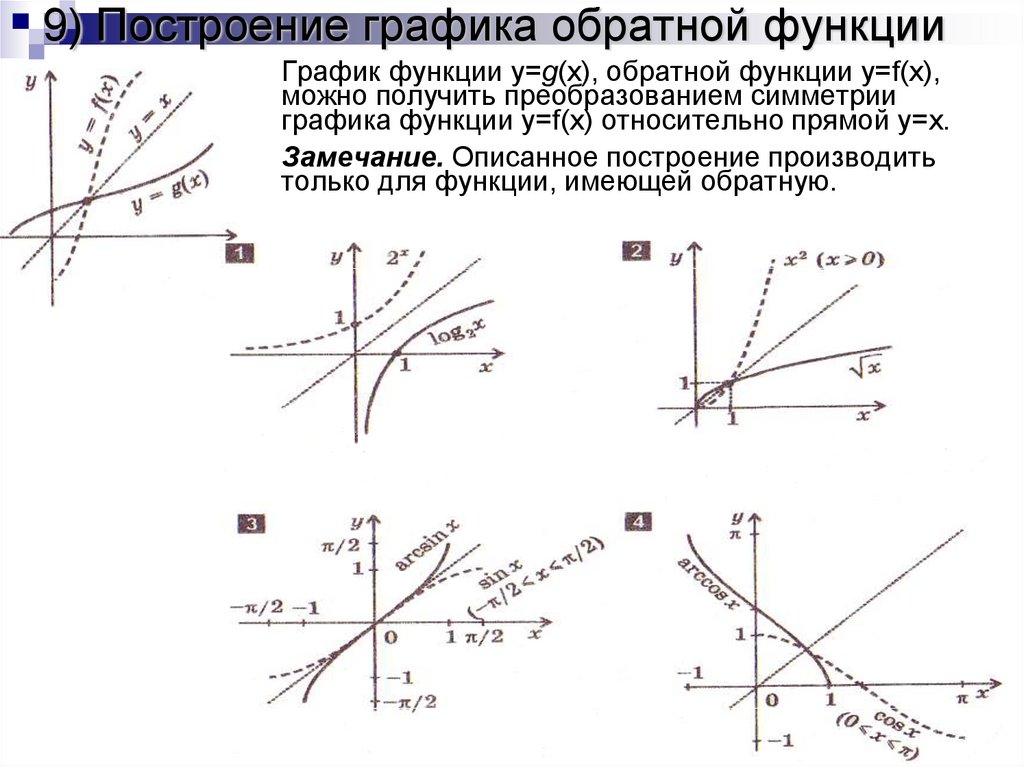

НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:

который проходит проверку горизонтальной линии, и, следовательно, квадратичная функция обратима.

НРАВСТВЕННОСТЬ ИСТОРИИ: Чтобы проверить, является ли что-то обратимым, речь идет НЕ только о функции. Речь идет о функции И ее домен и диапазон .

Как быстро построить график обратных функций

Всегда существует требование оценки, является ли функция \(f(x)\) обратимой или нет (проверяя, является ли она взаимно однозначной). {-1}(x) = \arcsin x\).

Другой способ увидеть это — использовать оригинал график и измените значение \(x\) на значение \(y\).

Есть ли способ сделать функцию обратной?

Да, это действительно возможно, но это происходит только для функции идентификации, то есть с \(f(x) = x\).

---

Учебник по алгебре Построение обратного Как найти обратную функцию Индивидуальные функции

Калькулятор обратной функции — Калькулятор обратной функции онлайн

Калькулятор обратной функции вычисляет обратное значение для заданной функции.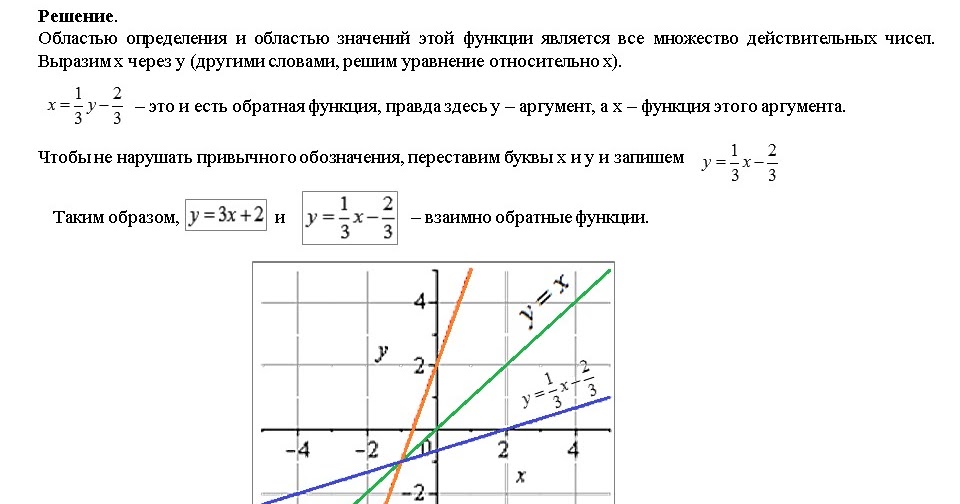 Функция, которая может обратить другую функцию, называется обратной этой функцией. Обратная функция, скажем, f, обычно обозначается как f ^-1 .

Что такое калькулятор обратной функции?

Калькулятор обратной функции — это онлайн-инструмент, который помогает найти обратную заданную функцию. Предположим, что g(x) является инверсией f(x). Затем f отображает элемент «a» в «b», а g отображает элемент «b» в «a». Чтобы использовать это Калькулятор обратной функции , введите функцию в поле ввода.

Калькулятор обратной функции

Как пользоваться калькулятором обратной функции?

Чтобы найти обратную функцию с помощью онлайн-калькулятора обратной функции, выполните следующие шаги:

• Шаг 1: Перейдите к онлайн-калькулятору обратной функции Cuemath.
• Шаг 2: Введите функцию в данное поле ввода калькулятора обратной функции.
• Шаг 3: Нажмите кнопку «Решить» , чтобы найти обратную заданную функцию.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поле и ввести новую функцию.

Как работает калькулятор обратной функции?

Если у нас есть функция f такая, что f: A→B. Тогда A называется доменом, а B — содоменом. В зависимости от типа отображения функции можно разделить на следующие три типа.

• Инъективная функция . Если функция сопоставляет каждый отдельный элемент своей области с каждым отдельным элементом своей совместной области, она называется инъективной функцией.
• Сюръективная функция . Если функция отображает один или несколько элементов своей области определения в один и тот же элемент своей области определения, она называется сюръективной функцией.
• Биективная функция — Биективная функция — это функция, которая одновременно является и сюръективной, и инъективной.

Обратная функция может существовать только в том случае, если она является биективной функцией. Шаги, указанные ниже, можно выполнить, чтобы найти обратную функцию y = f (x).

1. Поменять местами переменные x и y.
2. Решите уравнение относительно y.
3. Наконец, y заменяется на f ^-1 (x). Это дает обратную функцию.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе обратной функции

Пример 1:

Найдите обратную функцию y = f(x) = 4x — 9 и проверьте ее с помощью калькулятора обратной функции.

Решение:

Дано: Функция y = f(x) = 4x — 9

Чтобы найти обратную функцию,

Первая замена x и y, x = 4y — 9

И решить для y , y = (x + 9) / 4

Заменить y на f ^-1 (x) = (x + 9) / 4

Следовательно, обратная функция y = 4x — 9 равна (x + 9) / 4

Пример 2:

Найти обратную функции y = f(x) = 3x ²  + 2 и проверить ее с помощью калькулятора обратной функции.

Решение:

Дано: Функция y = f(x) = 3x ² + 2

Чтобы найти обратную функцию,

Первая замена x и y, x = 3y

3 2 + 90

И найдите y, y = √ [(x — 2)/3]

Замените y на f ^-1 (x) = √ [(x — 2)/3]

Следовательно, обратная величина заданная функция y = 3x ²  + 2 равна √ [(x — 2)/3]

Теперь попробуйте калькулятор обратной функции и найдите обратную для заданных функций:

• y = f(x) = 5x ³ + 6
• у = f (х) = (х + 5) / (2х — 7)

☛ Статьи по теме:

• Функции
• Обратные функции

☛ Математические калькуляторы:

Калькулятор обратной функции — вычисление обратной функции

Калькулятор обратной функции вычисляет обратное значение функции, заданной в качестве входных данных. Что касается определения, обратная функция — это функция, обращающая другую функцию. Она также известна как антифункция и обозначается как f(x) = y ⇔ f− 1(y) = x. Студенты, пытающиеся найти обратную функцию, могут использовать наш калькулятор обратных функций, чтобы найти точные ответы.

Калькулятор обратной функции — лучший рейтинг экспертов

Обратная функция обращает другую функцию. Однако большинству студентов трудно найти обратную функцию без калькулятора, потому что концепция им непонятна. Калькулятор обратной функции Myassignmenthelp.Com — это цифровой инструмент, который позволяет учащимся легко находить обратные функции. Если вы не знаете, как найти обратную функцию, воспользуйтесь нашим калькулятором обратных операций с шагами.

Решатель обратной функции Myassignmenthelp.Com разработан и разработан некоторыми компетентными математическими и программистскими гениями для упрощения сложных вычислений обратной функции. Инструмент быстрый, точный и рекомендован ведущими преподавателями предметов для получения правильных результатов с правильными шагами.

Да, верно! Наш обратный калькулятор функций даст вам правильные шаги для решения уравнений, чтобы вы могли обращаться к ним и практиковаться самостоятельно. И так, чего же ты ждешь? Используйте наш калькулятор уравнений обратных функций или специалистов по математике, чтобы упростить свои вычисления.

Get Instant Expert

Легкий доступ к решенным ключам, образцам и многому другому

Исследуйте нашу библиотеку, богатую справочными образцами, решенными вопросниками и исследовательскими заметками.

Поделиться Код курса

Как найти обратную функцию без калькулятора?

Решение математических задач, таких как уравнения обратной функции, без калькулятора может стать затруднительным, если концепция неясна. Следовательно, чтобы найти обратную функцию без калькулятора, вот что вы должны сделать:

• Возьмем одну функцию f(x) с x в качестве переменной
• Рассмотрим y как функцию для f(x)
• Измените переменные x и y, и результирующая функция будет вашей x
• Затем решите уравнение x относительно y
• Найдите значение y.

Не забудьте сначала заменить функциональную переменную другой, а затем решить другую переменную, заменив обе. Давайте рассмотрим несколько примеров, чтобы получить четкое представление о том же самом:

Пример 1: Найдите обратную функцию f(x) = y = 5x − 1

Решение:

Сначала замените f(x) с f(y).

Новое уравнение: y = 5x − 1,

x = 5y − 1

Решите для y,

y = (x + 1)/5

Таким образом, y = 5x − 1, обратное y = (x + 1)/5/

Давайте решим еще один пример обратной функции уравнение без калькулятора.

Пример 2: Найти обратную функцию y=x+6/3x+5

Решение:

Дана функция y=x+6/3x+5

Поменять местами переменные x и y

x=y+6/3y+5

x(3y+5)=y+6

3xy+5x-y=6

3xy-y=6-5x

y(3x-1)=6-5x

y=6-5x/3x-1

Таким образом, обратная функция x+6/3x+5 равна 6-5x/3x-1

Не уверен о вычислении обратной функции? Используйте калькулятор обратной функции спроса для мгновенных результатов. Вы также можете проверить наш репозиторий примеров, чтобы найти дополнительные примеры и образцы уравнений обратной функции спроса, которые можно решить без калькулятора.

Как определить калькулятор обратной функции с помощью шагов?

Средство поиска обратной функции вычислит обратную заданную функцию с необходимыми шагами. Решатель обратной функции сгенерирует уникальную обратную функцию, если функция является однозначной. Все еще не знаете, как найти обратный спрос с помощью калькулятора?

Давайте рассмотрим этапы нахождения обратной функции y= x+7/3x+5y с помощью калькулятора:

Чтобы найти обратную функцию, поменяйте местами x и y и решите уравнение относительно x.

В случае отсутствия начальной взаимно-однозначной функции увеличиваются шансы более чем на одну обратную.

Теперь переходим к шагам:

Поскольку переменные будут заменены местами, уравнение будет выглядеть примерно так:

Уравнение y=x+7/3x+5y станет x=y+7/3y+5

Теперь, чтобы решить уравнение: x=y+7/3y+5 для y

y=7−5x/3x−1

Следовательно, окончательный ответ: y=7−5x/3x−1

Калькулятор обратной функции может быть полезен, когда вам нужно быстро решить уравнения обратной функции. Используя наш калькулятор обратной функции, вы можете получить точные результаты из первых рук. Но в случае вопросов, не стесняйтесь обращаться к команде. Мы все уши 24×7.

Заказать сейчас

Как пользоваться калькулятором обратной функции спроса?

При нахождении производной обратной функции большинству учащихся часто не может быть и речи об использовании калькулятора. Вместо этого они предпочитают находить обратную функцию без калькулятора, следовать рекомендациям и обращаться к примерам из учебника.

К сожалению, этого нельзя сказать обо всех. Многие не понимают основ нахождения обратной функции и вместо этого используют калькуляторы для поиска сложных обратных функций. Использование калькулятора функций «один к одному» в любом случае лучше, чем сдача заданий с неправильными решениями.

Вы не можете просто полагаться на любой калькулятор случайных обратных функций, чтобы найти обратные. Не все онлайн-калькуляторы обратной функции являются подлинными или дают точные результаты с шагами. К счастью, калькулятор обратной функции MyAssignmenthelp.com обеспечивает оба этих фактора.

С нашим калькулятором обратного уравнения вы можете быть уверены в точных результатах с правильными шагами. Таким образом, если вы хотите использовать наш калькулятор обратной функции спроса, выполните следующие действия, чтобы начать работу:

Шаг 1:

Введите любую функцию в пустое поле после текста «Обратная функция».

Шаг 2:

Проверьте функцию и нажмите кнопку «Отправить».

Зачем беспокоиться о поиске сложных обратных функций, если наш калькулятор может сократить количество длинных шагов и давать 100% правильные результаты с помощью жизненно важных шагов? Используйте наш калькулятор обратной функции БЕСПЛАТНО и будьте вашим судьей.

Как работает калькулятор обратных функций?

Нельзя отрицать, что вы должны подкреплять свои ответы правильными шагами, чтобы получать хорошие оценки по математике. Итак, если вы недостаточно уверены в своих математических способностях, наш инструмент может очень помочь в вычислении обратной функции.

Но тогда почему наш калькулятор обратной функции самый лучший и как он работает?

Итак, наша обратная функция calc очень удобна и проста в использовании. Вам не нужно быть компьютерным экспертом или разбираться в технологиях, чтобы найти обратную функцию с помощью нашего калькулятора. На самом деле, вам нужно ввести функцию обратного калькулятора уравнения и отправить ее. Затем инструмент найдет инверсию(и) и сгенерирует результат с помощью шагов.

Что делает наш калькулятор обратной функции уникальным, спросите вы?

• За использование нашего онлайн-калькулятора обратной функции плата не взимается — это совершенно бесплатно, без каких-либо условий и подписки.
• Наш калькулятор обратной функции работает быстро и без проблем. Любой может использовать его, не полагаясь на руководство пользователя.
• Калькулятор обратной функции разработан с использованием новейшего алгоритма, чтобы гарантировать 100% точные результаты каждый раз.

Конечно, наш калькулятор обратной функции делает поиск обратной функции менее утомительным и экономит время. Но что, если вы хотите научиться основам у репетитора? домашнее задание по математике Не волнуйтесь! У нас есть и такой вариант.

Помимо нашего лучшего калькулятора обратной функции, у нас работают одни из лучших репетиторов по математике в городе. Каждый репетитор является настоящим гением математики и имеет многолетний опыт обучения своих котят. Студенты любят наших репетиторов за их уникальный способ преподавания и упрощения сложных математических сумм. В дополнение к индивидуальной помощи в обучении от доктора философии. специалисты, вам гарантировано:

• СВОЕВРЕМЕННОЕ решение проблем
• 100% статей без плагиата и ошибок
• БЕСПЛАТНЫЕ средства поддержки и доработки
• Гарантия возврата денег
• 100% анонимность и безопасность данных
• Непревзойденные цены с годовыми предложениями без каких-либо скрытых платежей

Тогда зачем ждать дальше? Используйте наш рекомендованный экспертами калькулятор обратной функции для быстрых расчетов. Если нет, учитесь у лучших репетиторов по математике, чтобы улучшить свои знания по предмету и повысить свои оценки по математике.

Нанять эксперта

Самые популярные вопросы, которые ищут студенты

Калькулятор обратной функции — это онлайн-инструмент, используемый для вычисления обратной заданной функции. Например, если e(x) является инверсией g(x), то g отображает элемент «a» в «b», а e отображает элемент «b» в «a». должен ввести функцию в поле ввода.

Чтобы найти обратную функцию, сначала запишите функцию y как функцию от x, т.е. y=f(x), а затем решите x как функцию от y. Вот пошаговый процесс поиска обратной функции:

1. Заменить f(x) на y
2. Заменить каждый y на x и наоборот
3. Решите уравнение для y
4. Заменить y на f-1(x)f -1(x)
5. Проверить, что (f∘f−1)(x)=x ( f ∘f − 1 ) ( x ) = x и (f−1∘f)(x)=x ( f − 1 ∘ f ) ( x ) = x оба верны.

Мультипликативное обратное число 5 равно 1/5, а аддитивное обратное число 5 равно -5.