| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвекторы величин |
| Конвертер единиц длины |
| Конвектор единиц скорости |
| Конвектор единиц ускорения |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
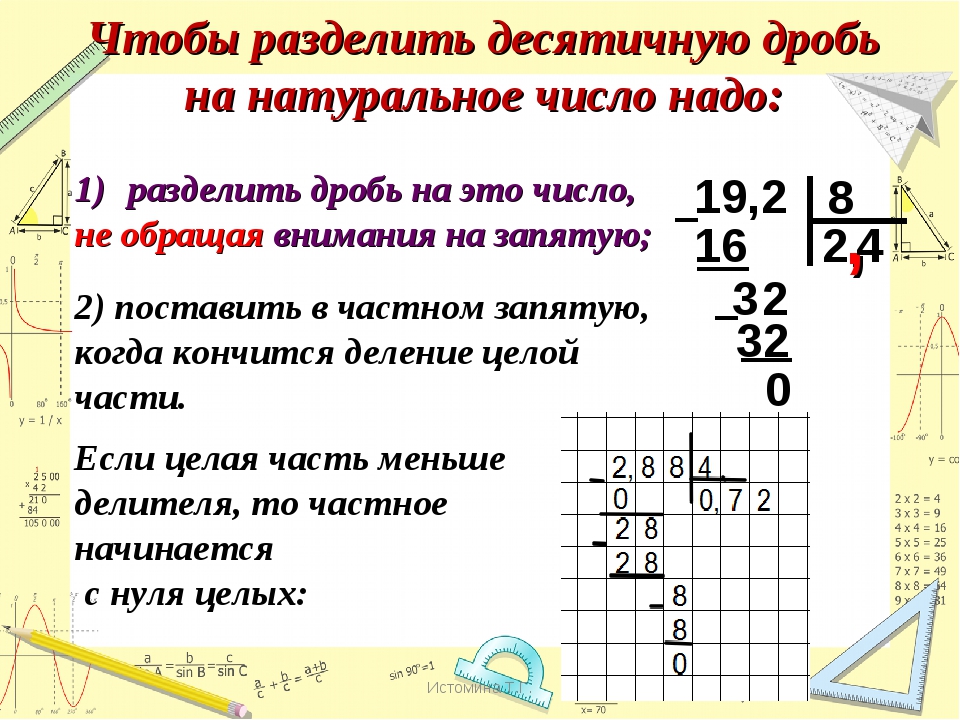
Деление столбиком
Калькулятор деление чисел столбиком
Рассчитать Очистить
\begin{align} \end{align}
Введите числа и калькулятор разделит числа столбиком и отобразит подробное решение.
Деление в столбик введение
Метод деления столбиком, позволяет упростить деления чисел.
Рассмотрим как делить в столбик на примере нахождения частного двух чисел 6344 ÷ 61.
- 1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное.
-
2 Найдем первую цифру частного, для этого
сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не
сформируем число большее или равное делителю.
 На первом шаге: 6 1 и ниже черты остаток от
деления 2=63-61.
На первом шаге: 6 1 и ниже черты остаток от
деления 2=63-61.
- 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 0.
-
4 Добавляем следующую не использованную цифру
равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли
третью цифру частного; записываем в частное 4=244 ÷ 61.
Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное
равно 104.

Ниже обозначены основные термины:
Пример Разделить столбиком число 558 на 18.
Вычитание столбиком. Онлайн калькулятор | Математика
Как вычитать столбиком
Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков – десятки и т. д. Результат вычитания записывают под чертой:
Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:
От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:
В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята
единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:
При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6
.
Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:
Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:
Занимаем единицу из разряда тысяч, получаем 10 сотен:
Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:
В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:
Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:
А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:
Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.
Калькулятор вычитания столбиком
Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку
Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить
.
Счет в столбик онлайн. Действия с десятичными дробями
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Выполнить сложение дробей путем сложения их числителей.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.

- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.

- Умножить числит
Умножение и деление десятичных дробей. Онлайн тренажер. — Kid-mama
Проверьте себя, как вы умеете умножать и делить десятичные дроби. Вспомните, как нужно умножать и делить дроби, а затем поработайте на нашем тренажёре. В нём всего 21 пример, но будьте внимательны!
Задания в тренажёре включают умножение и деление на 0,1; 0,01; 0,001; 0,0001 и т.д, а также умножение и деление десятичных дробей на 10, 100, 1000 и т.д. То есть мы учимся правильно переносить запятую.
Как умножать десятичные дроби на 10, 100, 1000, 10 000 и т. д.?
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Например:
8,963 · 10 = 89,63
0,062 · 1000 = 0062 = 62 (нули перед числом не пишутся)
2,9 · 10000 = 2,9000 · 10000 = 29000
Как умножать десятичные дроби на 0,1; 0,01; 0,001 и т. д.?
д.?
Умножить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).
Например:
54,3 · 0,1 = 54,3 : 10 = 5,43
0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001
Как делить десятичные дроби на 0,1; 0,01; 0,001 и т.д.?
Разделить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что умножить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в делимом на столько знаков вправо, сколько нулей стоит в делителе перед единицей (ноль перед запятой тоже считаем).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
Например:
54,87 : 0,1 = 548,7
34,56 : 0,0001 = 34,5600 : 0,0001 = 345600
24 : 0,001 = 24,000 : 0,001 = 24000
Как делить десятичные дроби на 10, 100, 1000 и т. д.?
д.?
Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.
При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.
Например:
374,5 : 100 = 3,745
5,021 : 1000 = 0005,021 : 1000 = 0,005021
0,1 : 100 = 000,1 : 100 = 0,001
В этом онлайн тренажере необходимо выбрать правильный ответ и нажать на него. В случае правильного ответа он загорится зеленым цветом, если ответ неверный — красным. В этом случае попробуйте найти правильный ответ, а затем нажмите кнопку «Дальше».
Онлайн тренажер по математике «Умножение и деление десятичных дробей.»
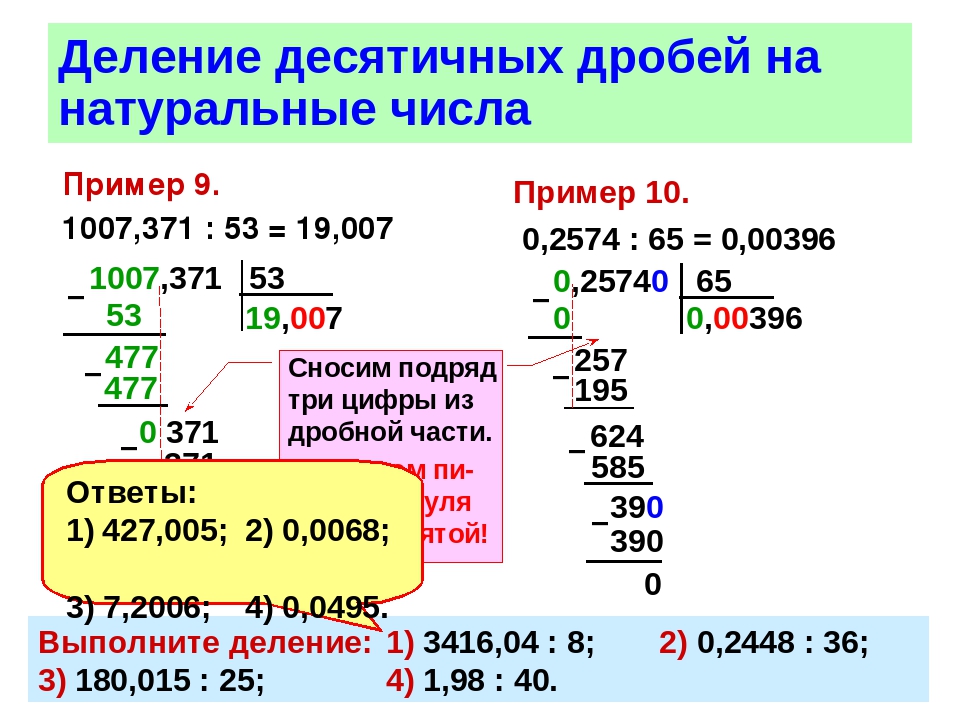
Деление десятичных дробей — Kid-mama
Деление десятичных дробей
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
В тесте 20 заданий. Выполните деление и введите ответ.
Выполните деление и введите ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
с десятичными знаками
Использование калькулятора
Сделайте долгое деление с десятичными числами и посмотрите пошаговые инструкции по расчету. Введите положительные или отрицательные десятичные числа для делителя и делимого и вычислите ответ частного.
Введите положительные или отрицательные десятичные числа для делителя и делимого и вычислите ответ частного.
Как сделать длинное деление с десятичными знаками
- Если число, на которое вы делите, имеет десятичную дробь, переместите десятичную точку до упора вправо, считая количество мест, на которые вы ее переместили.Затем переместите десятичную точку в числе, которое вы делите на такое же количество знаков вправо.
- Вставьте десятичную точку в поле частного (ответа) точно над десятичной точкой в числе под полосой деления.
- Делите, пока остаток не станет равен нулю или пока в вашем ответе не будет достаточно десятичных знаков. Вы также можете остановиться, если остаток повторяется, потому что это указывает на то, что ваш ответ является повторяющимся десятичным числом.
Вычислить десятичные разряды для частичного ответа
Как далеко вы хотите вычислить десятичные знаки для ответа? Вот несколько примеров:
- 31 разделить на 16 = 1.
 937500 с точностью до 6 знаков после запятой
937500 с точностью до 6 знаков после запятой - 31 разделить на 16 = 1,937 с точностью до 3 десятичных знаков
- 22 разделить на 15 = 1,466666666 с учетом 9 десятичных знаков
- 22 разделить на 15 = 1,466666 с учетом 6 знаков после запятой
- 22 разделить на 15 = 1,466 с точностью до 3 десятичных знаков
Обратите внимание, что это не то же самое, что округление до определенного числа десятичных знаков.Например, 22 разделить на 15 = 1,466, когда вычисляется до 3 десятичных разряда, потому что вы останавливаетесь, когда дойдете до третьего десятичного знака. С другой стороны, 22 делится на 15 = 1,467, когда округлено до 3 десятичных знака. Для округления до третьего знака после запятой необходимо вычислите до по крайней мере до четвертого десятичного знака, чтобы вы знали, как округлить третий десятичный знак. Смотрите наши
Калькулятор чисел округления для получения дополнительной информации.
Смотрите наши
Калькулятор чисел округления для получения дополнительной информации.
Также смотрите наши Длинное деление с остатками, чтобы увидеть, как работает длинное деление с остатками.
Части дивизиона
Для задачи деления 471 делится на 32:
- 471 — дивиденд
- 32 — делитель
- 14,718 — это частное, вычисленное до трех знаков после запятой
Как сделать длинное деление с десятичными знаками: пример
В этой задаче мы делим 4.71 на 3,2 до 3 знаков после запятой в ответе частного.
Устраните проблему с продольным кронштейном. Разместите делимое внутри скобки, а делитель снаружи слева.
Так как 3.2 не является целым числом, переместите десятичную точку на одну позицию вправо. 32 — целое число. Сделайте то же самое с делимым и переместите десятичную дробь на одну позицию вправо.
Так как мы решаем до 3 десятичных знаков, добавьте два конечных нуля к делимому.
Вставьте десятичную точку над полосой деления, прямо над новой десятичной позицией в делимом.
Разделите крайнее левое число делимого на делитель, в данном случае разделите 4 на 32. Поскольку 4, разделенное на 32, не является целым числом, первая цифра частного — 0.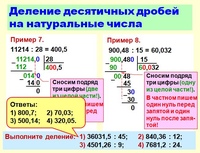
Умножьте делитель 32 на частное 0, чтобы получить произведение 0. Вычтите 0 из 4, чтобы получить остаток 4.
Затем убавьте 7 с дивиденда, чтобы получилось 47.
Как 47 делится на 32? Или, другими словами, сколько раз 32 переходит в 47? Один раз, с остатком.Вставьте 1 в частное. Чтобы найти остаток, умножьте делитель на 1 и вычтите произведение 32 из второго делимого 47. Остаток равен 15.
Опять же, уменьшите следующую цифру делимого, 1, и поместите ее в конец остатка.
Повторите шаги. Как 151 разделить на 32? Или сколько раз 32 входит в 151? 32 переходит в 151 четыре раза. Поставьте 4 на следующее место в частном и умножьте 32 на 4, чтобы получить 128.
Поставьте 4 на следующее место в частном и умножьте 32 на 4, чтобы получить 128.
Вычтем это произведение из 151, чтобы найти остаток от 23.
Опустите 0 из делимого и вставьте его после 23, чтобы получить 230.
Сколько 230 разделить на 32? 32 переходит в 230 семь раз. Поставьте 7 на следующее место в частном.32 умножить на 7 будет 224.
230 минус 224 остается остаток 6.
Теперь уменьшите следующий ноль из делимого и повторите шаги.
32 переходит в 60 только один раз. Поставьте 1 на следующее место в частном.
Поставьте 1 на следующее место в частном.32, умноженное на 1, равно 32.
При вычитании 32 из 60 остается 28.
Дополнительная литература
В Спросите доктора Математики вы можете найти Инструкции по длинному делению для простых и более сложных задач.
Википедия: Длинный дивизион
Калькулятор длинного деленияс остатками
Использование калькулятора
Разделите два числа, делимое и делитель, и найдите ответ как частное с остатком. Узнайте, как решать задачи деления в столбик с остатками, или попробуйте свои собственные задачи деления в столбик и используйте этот калькулятор, чтобы проверить свои ответы.
Деление в столбик с остатками — это один из двух методов ручного деления в столбик. Это несколько проще, чем решить задачу деления, найдя частный ответ с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш
Калькулятор длинного деления с десятичными знаками.
Это несколько проще, чем решить задачу деления, найдя частный ответ с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш
Калькулятор длинного деления с десятичными знаками.
Какие части подразделения
Для предложения деления 487 ÷ 32 = 15 R 7
- 487 — это дивиденд
- 32 — делитель
- 15 является частным от ответа
- 7 — это оставшаяся часть ответа
Как сделать длинное деление с остатками
Из приведенного выше примера разделим 487 на 32, показывая работу.
Задайте проблему деления с помощью символа деления или скобки с делением.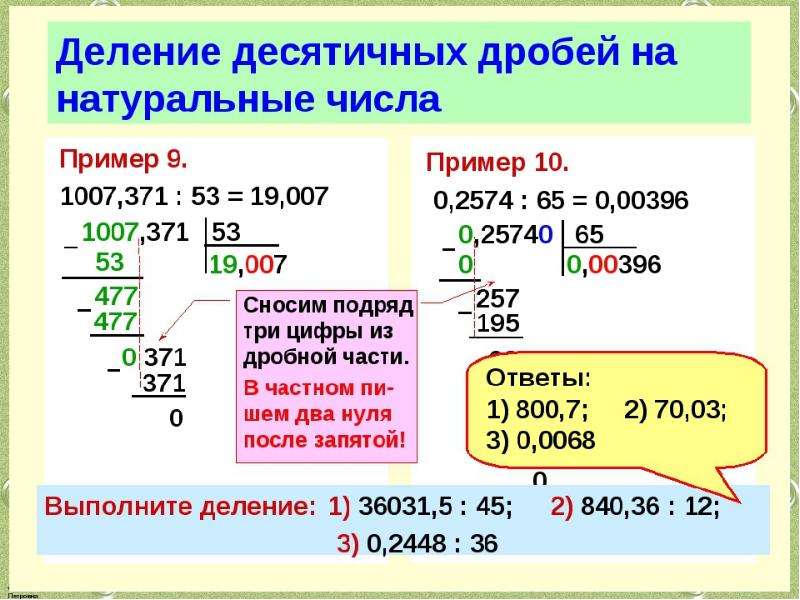
Поместите 487, делимое, на внутреннюю часть скобки. Дивиденд — это число, которое вы делите.
Поместите 32, делитель, на внешнюю сторону кронштейна. Делитель — это число, на которое вы делите.
делить 4 на 32 равно 0, а остаток равен 4. Остаток пока можно игнорировать.
Поместите 0 на верхнюю часть скобки деления.Это начало частного ответа.
Затем умножьте 0 на делитель 32 и вставьте результат 0 под первым числом делимого внутри скобок.
0 * 32 = 0
Проведите линию под 0 и вычтите 0 из 4.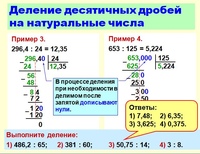
4 — 0 = 4
Введите следующее число делимого и вставьте его после 4, чтобы получилось 48.
Разделите 48 на делитель 32. Ответ: 1. Остаток пока можно проигнорировать.48 ÷ 32 = 1
Обратите внимание, что вы можете пропустить все предыдущие шаги с нулями и сразу перейти к этому шагу. Вам просто нужно понять, сколько цифр в дивиденде вам нужно пропустить, чтобы получить первое ненулевое значение в ответе на частное.В этом случае вы можете сразу разделить 32 на 48.
Поставьте цифру 1 вверху шкалы, справа от 0. Затем умножьте 1 на 32 и запишите ответ под 48.
Затем умножьте 1 на 32 и запишите ответ под 48.1 * 32 = 32
Проведите линию и вычтите 32 из 48.48 — 32 = 16
Выполните следующее число из делимого и вставьте его после 16, чтобы получилось 167.
Разделите 167 на 32. Видите возникающую закономерность?167 ÷ 32 равно 5 с остатком 7
Поместите цифру 5 вверху шкалы деления справа от единицы.Умножьте 5 на 32 и запишите ответ под 167.
5 * 32 = 160
Проведите линию и вычтите 160 из 167.167 — 160 = 7
Поскольку 7 меньше 32, деление в столбик выполнено.У вас есть свой ответ: частное равно 15, а остаток равен 7.Итак, 487 ÷ 32 = 15 с остатком 7
Для более длинных дивидендов вы должны продолжать повторять шаги деления и умножения, пока вы не уменьшите каждую цифру из divdend и не решите проблему.
Дополнительная литература
в Спросите доктораMath вы можете найти
Инструкции по длинному делению для простых и более сложных задач.
Math is Fun также предоставляет пошаговый процесс деления в столбик с Длинное деление с остатками.
Калькулятор дополнений по 1 и 2
- Home
- Engineering
- Цифровые вычисления
Калькулятор дополнения единиц и двоек — это онлайн-инструмент для цифровых вычислений, позволяющий найти дополнение единиц и двоек для заданного двоичного, шестнадцатеричного или десятичного числа.Дополнение до 1 двоичного числа — это число, которое можно получить, заменив все единицы на нули и все нули на единицы данного двоичного числа. В то время как дополнение до 2 — это двоичное число, которое может быть получено добавлением 1 к одному дополнению данного двоичного числа.
Как рассчитать дополнение до 1 двоичного числа?
Дополнение до 1 можно легко вычислить, инвертируя нули и единицы заданного двоичного числа.
Как рассчитать дополнение до единицы десятичного числа?
1.Найдите двоичный эквивалент данного десятичного числа.
2. Инвертирование нулей и единиц эквивалентного двоичного числа дает дополнение до единиц.
Как рассчитать дополнение до 2 двоичного числа?
1. Найдите дополнение до единицы, инвертируя нули и единицы заданного двоичного числа.
2. Добавление 1 к дополнению до одного дает дополнение до двух.
Как рассчитать дополнение до 2 десятичного числа?
1. Найдите двоичный эквивалент данного десятичного числа.
2. Найдите дополнение до единицы, инвертируя нули и единицы заданного двоичного числа.
3. Добавление 1 к дополнению до одного дает дополнение до двух.
Чтобы вычислить дополнение до 1 или 2 с помощью этого калькулятора для двоичного ввода, выберите переключатель Двоичный, просто введите двоичное число в текстовое поле и нажмите кнопку «Рассчитать», чтобы отобразить эквивалентное дополнение до 1 и 2 от заданного числа. .
.
Чтобы вычислить дополнение до единиц и двух с помощью этого калькулятора для ввода десятичных чисел, выберите переключатель «Десятичное число», просто введите десятичное число в текстовое поле и нажмите кнопку «Рассчитать», чтобы отобразить эквивалентное дополнение 1 или 2 для данного числа .Этот калькулятор может поддерживать и находить дополнение 1 и 2 для 8-битных, 16-битных и 32-битных двоичных чисел.
Калькулятор длинного деления— eMathHelp
Калькулятор разделит любые два числа (положительное или отрицательное, целое или десятичное) с указанными шагами. Введите делимое и делитель и получите частное с заданной точностью без остатка или частное с остатком.
Показать инструкции
- В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x».3 (х).
- Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
 -1 (x)
-1 (x)acoth (x) acosh (1 / x) asinh (x) asinh (1 / x) acsch (x) Калькулятор полиномиального деления в столбик — eMathHelp
Калькулятор выполняет деление полинома в столбик с указанием шагов.3 (х).
- Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
- Если вы получаете сообщение об ошибке, дважды проверьте свое выражение, добавьте скобки и знаки умножения, где это необходимо, и обратитесь к таблице ниже.
- Приветствуются все предложения и улучшения. Пожалуйста, оставьте их в комментариях.
В следующей таблице перечислены поддерживаемые операции и функции:
| Тип | Получить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Константы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| e | e | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | `pi` | i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a + b | a + b | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ab | ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a * b | `a * b` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a ^ b, a ** b | ` a ^ b` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sqrt (x), x ^ (1/2) | `sqrt (x)` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| корень (x, n), x ^ (1 / n) | ` root (n) (x) ` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x ^ (a / b) | ` x ^ (a / b) ` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x ^ a ^ b | ` x ^ (a ^ b) ` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| abs (x) | ` | x | ` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| e ^ x | `e ^ x` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (x), журнал (x) | ln (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ln (x) / ln (a) | `log_a (x)` | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тригонометрические функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin (x) | sin (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos (x) | cos (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan (x) | tan (x), tg (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кроватка (x) | кроватка (x), ctg ( x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sec (x) | sec (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| csc (x) | csc (x), cosec (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Обратные тригонометрические функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| asin , arcsin (x), sin ^ -1 (x) | asin (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| атан (x), arctan (x), tan ^ -1 (x) | atan (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| asec (x), arcsec (x), sec ^ -1 (x) | assec (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acsc (x), arccsc (x), csc ^ -1 (x) | 9 0250 acsc (x)|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Гиперболические функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sinh (x) | sinh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cosh (x) | cosh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| coth (x) | coth (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 / ch (x) | sech (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 / sinh (x) | csch (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Обратные гиперболические функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acoth (x), arccoth (x) , детская кроватка ^ -1 (x) | acoth (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| acosh (1 / x) | asinh (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| asinh (1 / x) | acsch (x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Добавить, Sub, Mul, Div, онлайн-преобразование
Шестнадцатеричное преобразование
Невозможно запомнить эту таблицу или нарисовать ее каждый раз, когда мы используем шестнадцатеричную систему, но мы можем легко преобразовать десятичную систему в шестнадцатеричную и наоборот. Если вы знаете, как преобразовать из двоичного в десятичный или из десятичного в двоичный, преобразование в шестнадцатеричный формат будет для вас очень простым, поскольку оно похоже на двоичное преобразование.
Если вы знаете, как преобразовать из двоичного в десятичный или из десятичного в двоичный, преобразование в шестнадцатеричный формат будет для вас очень простым, поскольку оно похоже на двоичное преобразование.
шестнадцатеричное в десятичное
Давайте начнем с преобразования шестнадцатеричного числа (в данном случае 4FD) в десятичное число. Для этого мы будем использовать разрядные значения. Начиная с правой стороны, D — наименьшее число, а 4 — наибольшее число. Итак, мы умножим наименьшее число на наименьшую степень 16.Наименьшая степень 16 равна 0. Затем умножьте следующее число (в данном случае F) на следующую наибольшую степень 16 (которая равна 1). Наконец, умножьте наибольшее число (в данном случае 4) на наибольшую степень 16 (здесь 2). Затем сложите все продукты, чтобы найти десятичный эквивалент 4FD. Получается, что это 1277. У нас также есть калькулятор возраста, который вы должны проверить, чтобы узнать свой точный возраст.
- Помните, что вы должны начинать с наименьшей мощности 0, но нет ограничений на наибольшую мощность.
 Если шестнадцатеричное число состоит из 4 цифр, максимальная степень будет 3.
Если шестнадцатеричное число состоит из 4 цифр, максимальная степень будет 3.
Пример:
4FD = (4 x 162) + (F x 161) + (D x160)
= (4 х 256) + (15 х 16) + (13 х 1)
= 1024 + 240 + 13
= 1277
Десятичное в шестнадцатеричное
Давайте вернем десятичное число 1277 обратно в шестнадцатеричное. Мы также будем точно знать, правильное ли наше преобразование, потому что мы знаем, что это должно быть 4FD.Мы будем использовать синтетическое деление для преобразования десятичного числа в шестнадцатеричное. Это означает, что мы будем непрерывно делить число на 16, если наше число не станет меньше 16. Этот процесс немного сложен, поэтому мы разделим его на шаги.
- Разделите десятичное число на 16. (1277/16 = 79,8125)
- Нам нужны только целые числа, поэтому мы вычтем целую часть из действительного числа.
 (79,8125 — 79 = 0,8125)
(79,8125 — 79 = 0,8125) - Теперь умножьте десятичную часть на 16, чтобы получить целое число.(0,8125 х 16 = 13)
- Теперь снова разделите число на 16. (79/16 = 4,9375)
- Повторите шаг 2 и вычтите всю часть. (4,9375 — 4 = 0,9375)
- Повторите шаг 3 и умножьте десятичную часть на 16. (0,9375 x 16 = 15)
- Так как 4 меньше 16. Мы больше не будем делить.
- Начиная с нижнего левого угла, наш ответ — внешние числа. (4, 15 и 13)
- В шестнадцатеричном формате 15 = F и 13 = D.
- Итак, 1233 в десятичной системе счисления равно 4FD в шестнадцатеричной системе.
Пример:
Добавление шестигранника
После того, как мы проясним преобразования, мы перейдем к арифметическим операциям с шестнадцатеричными числами. Добавление шестнадцатеричных чисел очень похоже на то, как мы это делаем в случае десятичных чисел.
- Начните с правой стороны, сложите два числа, добавив их десятичные значения.(А + В = 10 + 11 = 21)
- Затем преобразуйте сумму из десятичного числа в шестнадцатеричное. (21 в десятичном формате — 15 в шестнадцатеричном)
- Если ответ состоит из двух цифр, крайняя левая цифра переносится на следующие числа. (5 написано в ответе и 1 перенесено)
- Сложите следующие два числа и перенос. (D + 2 + 1 = 13+ 2+ 1 = 16)
- Повторите шаг 2. (16 в десятичной системе счисления — это 10 в шестнадцатеричной системе. Мы напишем 0 в ответе, и 1 будет передана в следующие числа.)
- Повторите шаги 4 и 2.(8 + 4 + 1 = 13, 13 в десятичной системе счисления — это D в шестнадцатеричной системе).
Пример:
.

 На первом шаге: 6 1 и ниже черты остаток от
деления 2=63-61.
На первом шаге: 6 1 и ниже черты остаток от
деления 2=63-61.


 д.?
д.? д.?
д.? 937500 с точностью до 6 знаков после запятой
937500 с точностью до 6 знаков после запятой -1 (x)
-1 (x)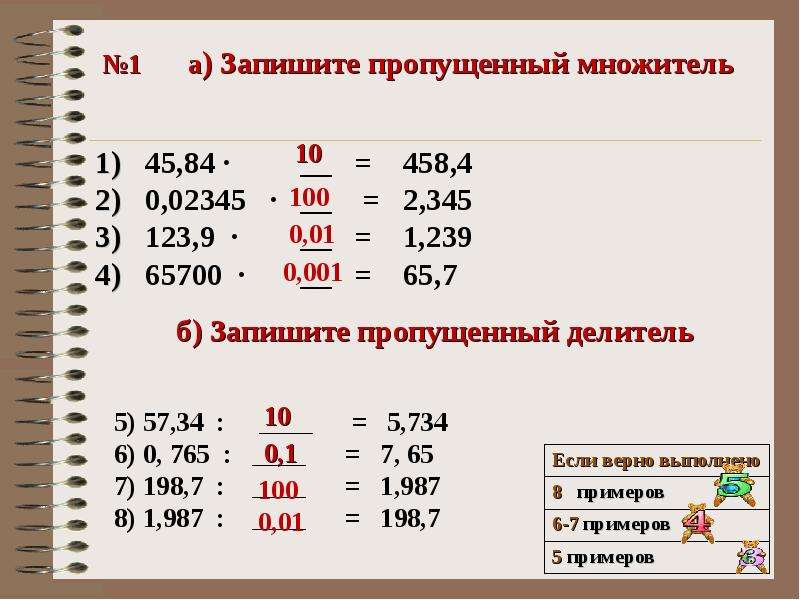 Если шестнадцатеричное число состоит из 4 цифр, максимальная степень будет 3.
Если шестнадцатеричное число состоит из 4 цифр, максимальная степень будет 3. (79,8125 — 79 = 0,8125)
(79,8125 — 79 = 0,8125)