Отрицательная степень калькулятор: Калькулятор степеней — возвести в степень онлайн

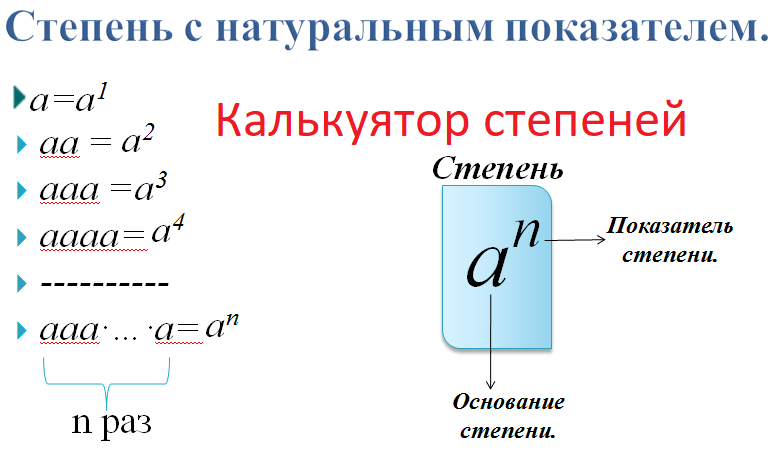
Возведение числа в степень — Онлайн калькулятор

Число Степень

Предлагаем вам простой и наглядный калькулятор степеней — удобное средство, которое позволяет возвести число в степень в режиме онлайн. Введите нужные значения в ячейки «Число» и «Степень» и нажмите кнопку «Вычислить». Результат сразу же появится внизу под кнопкой.

Число и степень могут быть любыми. Например, на калькуляторе возможно возведение в дробную степень, причем как положительных, так и отрицательных чисел. Главное, чтобы результат имел физический смысл.

Вопросы и ответы

Зачем нужен калькулятор со степенями?

Во-первых, с его помощью можно решать задачи по алгебре в 7 классе. А во-вторых, в жизни тоже есть немало случаев, когда может потребоваться возведение числа в степень. Например, при вычислении объема помещения или числа плиток на стенку.

Возможно ли возведение в степень отрицательного числа?

Да, но нужно быть осторожным. При попытке возвести отрицательное число в дробную степень с четным знаменателем онлайн-калькулятор выдаст ошибку, т.

к. эта операция не имеет смысла.

Что такое степень с дробным показателем?

Возведение в дробную степень обычно используется для вычисления корней. Например, чтобы посчитать корень третьей степени из числа, его можно возвести в степень 1/3.

Можно ли для возведения в степень использовать обычное умножение?

Можно, но это не всегда будет оптимальным решением. Проще открыть наш калькулятор и получить ответ за несколько секунд.

А возведение в степень комплексного числа здесь возможно?

Нет, наш калькулятор работает только со степенями и основаниями, выраженными действительными числами.

Каков смысл возведения в отрицательную степень?

Правило здесь такое: число в отрицательной степени равно единице, деленной на это число в степени с отброшенным минусом. Вручную посчитать такое выражение довольно сложно, а наш калькулятор степеней онлайн делает это мгновенно.

Мы изучаем возведение одночлена в степень, это алгебра, 8-й класс. Как сделать это на вашем калькуляторе?

На этом калькуляторе можно возвести в степень только число. Многочленов и одночленов он, к сожалению, не понимает.

Есть ли какие-то ограничения при возведении в степень действительных чисел?

Есть. Нельзя возводить отрицательное число в дробную степень с четным знаменателем. Нельзя также возводить ноль в отрицательную степень.

Приведите, пожалуйста, примеры использования калькулятора для вычисления выражений со степенями на практике.

Готовых примеров, к сожалению, нет, но попробуем. Допустим, вы строите бассейн размером 3,5х3,5 м и хотите вычислить площадь его дна. Она равна 3,52. Руками это можно посчитать только в виде произведения в столбик — долго и неудобно. А если его глубина также 3,5 м, а вам нужен объем воды, которую в него потребуется залить? Это будет уже 3,53. Для ручного подсчета совсем сложно, а калькулятор со степенями мгновенно покажет результат в режиме онлайн.

Каков порядок установки калькулятора на компьютер?

Ничего устанавливать не надо. Калькулятор работает прямо из браузера. Сохраните ссылку в ваших закладках, чтобы запускать его сразу же, как только он понадобится.

Комментарии

Смотрите также

Быстрое возведение в степень по модулю

УчебаМатематика

Калькулятор возводит большие числа в степень по модулю

Этот калькулятор можно использовать для возведения в степень целого числа по модулю. Калькулятор позволяет задать большие целые числа и в модуле, и в основании, и в показателе степени. Используется быстрый алгоритм, описанный сразу за калькулятором.

Возведение в степень по модулю

Основание

Показатель

Модуль

Результат

 

Если применять наивный способ возведения в степень — просто перемножить p-1 раз основание, нам потребуется на единицу меньше умножений, чем показатель степени. Несмотря на всю мощь современных компьютеров, такой способ нам не подходит, так как мы собираемся использовать для показателя числа даже большие, чем стандартные 64-битные целые. Например, в простом числе Мерсена: 618970019642690137449562111, уменьшая на единицу которое мы используем как значение показателя степени по-умолчанию, насчитывается 89 двоичных разрядов (см. Сколько бит занимает число).
Чтобы оперировать подобными показателями требуются алгоритмы быстрого возведения в степень.

В калькуляторе Возведение полинома в степень мы уже задействовали один быстрый алгоритм возведения в степень, основанный на дереве степеней, который позволяет свести к минимуму число операций умножения. Однако для огромных показателей реализация этого алгоритма с хранением в памяти всего дерева степеней не подходит из-за ограничений по ресурсам.
Поэтому в данном калькуляторе для вычисления степени мы применяем библиотеку bigInt, реализующую двоичный алгоритм, не требующий дополнительной памяти. Вариант этого алгоритма описан в той же статье, однако обработка двоичных разрядов показателя степени происходит там последовательно со старшего бита до младшего. В нашем случае это несколько неудобно, так как мы используем большие целые и не вдаваясь в реализацию хранилища целых, мы заранее не представляем, сколько разрядов они занимают в памяти.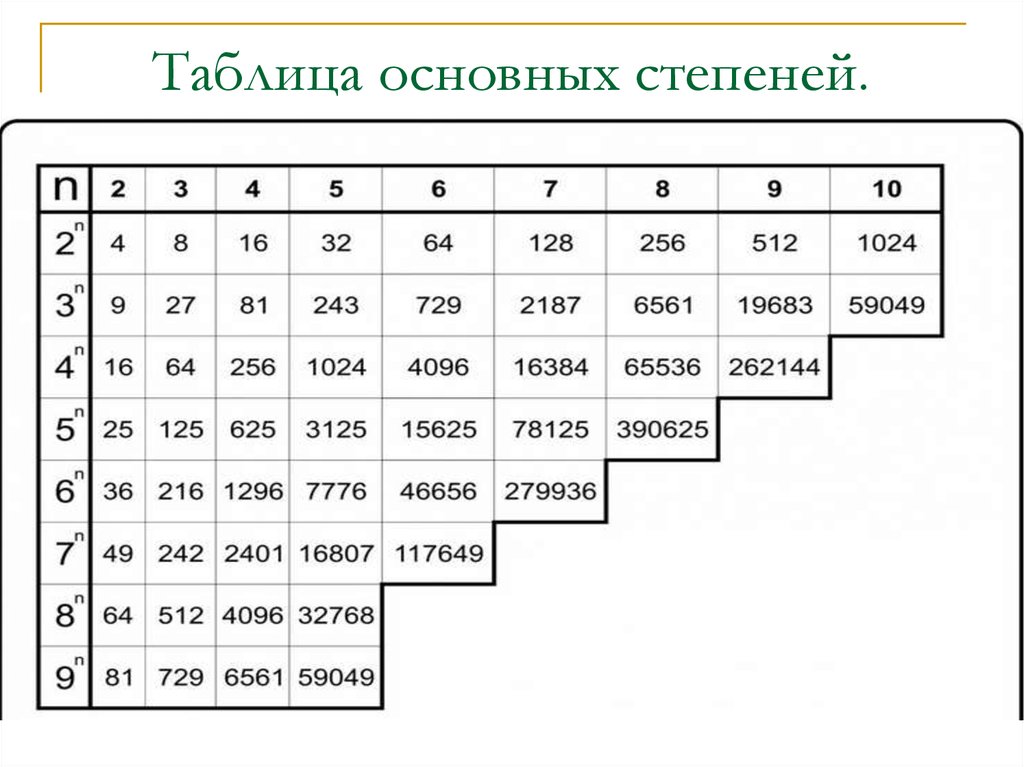

Двоичный алгоритм возведения в степень справа налево

Поэтому алгоритм обрабатывает двоичное представление показателя степени начиная с младшего бита и кончая старшим (слева направо), согласно следующему алгоритму:

a //основание степени
e //показатель степени
m //модуль
 //Вычисление степени
r ⟵ 1      
while (e!=0) {
            if (e mod 2 = 1) r ⟵ r * a mod m;
            e ⟵ e / 2;
            a = a*a mod m;
        }
output ⟵ r

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Модулярная арифметика
• • Решение сравнений по модулю
• • Обратный элемент в кольце по модулю
• • Простая дробь по модулю
• • Обратная матрица по модулю
• • Раздел: Математика ( 269 калькуляторов )

 Математика модуль по модулю степень Теория чисел

 PLANETCALC, Быстрое возведение в степень по модулю

Anton2020-11-10 14:37:45

‘; return ret; } }

Калькулятор котерминальных углов

| Формулы

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Джек Боуотер

Последнее обновление: 21 февраля 2023 г.

Содержание:

• Что такое котерминальный угол?
• Как найти котерминальные углы? Формула котерминальных углов
• Как найти котерминальный угол между 0 и 360° (или 0 и 2π)?
• Положительный и отрицательный котерминальные углы
• Что такое котерминальный угол…
• FAQ

Добро пожаловать в наш калькулятор котерминальных углов – инструмент, который решит многие ваши проблемы с котерминальными углами:

• Вы хотите найти котерминальный угол заданного угла , желательно в пределах [0,360°) [0, 360\градус)[0,360°) диапазон? Отличные новости: вы можете посмотреть здесь.
• Вы ищете положительных и отрицательных котерминальных углов ? Также здесь.
• Вы хотите проверить, являются ли два угла котерминальными ? Проверять! ✔️
• Вы ищете калькулятор котерминальных углов для радианов ? Хорошо для вас, наш инструмент работает как для π радиан, так и для градусов.
• Или, может быть, вы ищете определение котерминальных углов
  с некоторыми примерами ? Тогда вы не будете разочарованы этим калькулятором.
• Гарантирует ли инструмент получение проходного балла за контрольную по математике? ❌ Ну, наш инструмент универсален, но это на ваше усмотрение 🙂

Воспользуйтесь нашим калькулятором, чтобы решить проблемы с котерминальными углами, или прокрутите вниз, чтобы узнать больше.

Начнем с определения котерминальных углов.

Что такое котерминальный угол?

Котерминальные углы — это углы, которые разделяют конечную сторону угла, занимающего стандартное положение . Стандартное положение означает, что одна сторона угла закреплена вдоль положительной оси x, а вершина расположена в начале координат.

Другими словами, два угла являются котерминальными, когда сами углы различны, но их стороны и вершины совпадают . Также можно запомнить определение котерминального угла как углов, отличающихся целым числом полных окружностей .

Посмотрите на картинку ниже, и все должно быть понятно!

Итак, как мы сказали: все котерминальные углы начинаются с одной и той же стороны (исходной стороны) и имеют общую конечную сторону.

Иногда может сбивать с толку различие между определениями опорного угла и котерминального угла . Помните, что это не одно и то же — опорный угол — это угол между конечной стороной угла и осью x, и он всегда находится в диапазоне [0,90°][0, 90\градус][0 ,90°] (или [0,π/2][0, \pi/2][0,π/2]): чтобы узнать больше по теме, посетите наш калькулятор эталонного угла!

Как найти котерминальные углы? Формула котерминальных углов

Чтобы найти котерминальные углы к заданному углу, вам нужно прибавить или вычесть число, кратное 360° (или 2π, если вы работаете в радианах). Итак, чтобы проверить, являются ли углы α и β котерминальными, проверьте, согласуются ли они с формулой котерминальных углов:

а) Для углов, измеренных в градусах:

β=α±(360°×k)\beta=\alpha\pm(360\градус\k)β=α±(360°×k)

где kkk — целое положительное число.

b) Для углов, измеренных в радианах:

β=α±(2π×k)\beta = \alpha \pm(2\pi\times k)β=α±(2π×k)

здесь k — целое положительное число

Полезной особенностью является то, что при вычислении тригонометрических функций любые два котерминальных угла имеют точно такие же тригонометрические значения. Итак, если β\betaβ и α\alphaα котерминальны, то их синусы, косинусы и тангенсы равны.

При вычислении синуса, например, мы говорим:

sin⁡(α)=sin⁡(α±(360°×k))\sin(\alpha) = \sin(\alpha\pm(360\) градус \times k))sin(α)=sin(α±(360°×k))

Как найти котерминальный угол между 0 и 360° (или 0 и 2π)?

Чтобы определить котерминальный угол между 0°0\градусом 0° и 360°360\градусом 360°, все, что вам нужно сделать, это вычислить по модулю – другими словами, разделить полученный угол на 360°360\градус360° и проверить, что осталось.

Мы покажем вам, как это работает, на двух примерах, охватывающих как положительные, так и отрицательные углы. Мы хотим найти котерминальный угол с мерой θ\thetaθ такой, что 0°≤θ<360°0\градус \leq \theta < 360\степень0°≤θ<360°, для заданного угла, равного:

420°mod 360°=60°420\степень\текст{mod}\ 360\степень = 60\степень420°mod 360°=60°

Как это сделать вручную?

• Сначала разделим одно число на другое, округлив в меньшую сторону (рассчитываем функцию пола): ⌊420°/360°⌋=1\влево\lпол420\градус/360\градус\вправо\rпол = 1⌊420°/360 °⌋=1.

• Затем умножьте делитель на полученное число (называемое частным): 360°×1=360°360\градус\умножить на 1 = 360\градус360°×1=360°.

• Вычтите это число из исходного числа: 420°−360°=60°420\градус — 360\градус = 60\градус420°−360°=60°.

Подстановка этих углов в формулу котерминальных углов дает 420°=60°+360°×1420\градус = 60\градус + 360\градус\умножить на 1420°=60°+360°×1.

-858°

−858°mod 360°=222°-858\градус \text{mod}\ 360\степень = 222\градус −858°mod 360°=222°

Повторяем шаги, описанные выше:

• Рассчитать этаж: ⌊−858°/360°⌋=−3\влево\lпол-858\градус / 360\градус\вправо\rпол = -3⌊−858°/360°⌋=−3.
• Найдите общее количество полных окружностей: 360°×−3=−1080°360\градус \times -3 = -1080\степень360°×−3=−1080°.
• Вычислить остаток: -858°+1080°=222°-858\градус + 1080\градус = 222\градус-858°+1080°=222°.

Таким образом, формула котерминальных углов, β=α±360°×k\beta = \alpha \pm 360\степень \times kβ=α±360°×k, для нашего примера с отрицательным углом будет выглядеть следующим образом:

− 858°=222°−360°×3-858\градус = 222\градус — 360\градус\умножить на 3−858°=222°−360°×3

То же самое работает для [0,2π)[0 ,2\pi)[0,2π), все, что вам нужно изменить, это делитель — вместо 360°360\степень360° используйте 2π2\pi2π.

Теперь проверьте результаты с помощью нашего калькулятора котерминального угла

– он отображает котерминальный угол между 0°0\градусом 0° и 360°360\градусом 360° (или 000 и 2π2\pi2π), а также несколько образцовых положительных и отрицательные котерминальные углы.

Положительные и отрицательные котерминальные углы

Если вы хотите найти несколько положительных и отрицательных котерминальных углов , вам нужно вычесть или добавить несколько полных окружностей. Но сколько?

Один из методов состоит в том, чтобы найти котерминальный угол в диапазоне 0°0\градус 0° и 360°360\градус 360° (или диапазоне [0,2π)[0,2\pi)[0,2π)), как мы это сделали в предыдущем абзаце (если ваш угол уже находится в этом диапазоне, вам не нужно делать этот шаг). Затем просто добавьте или вычтите 360°360\градус 360°, 720°720\градус720°, 1080°1080\градус1080°… (2π2\pi2π,4π4\pi4π,6π6\pi6π…), чтобы получить положительное или отрицательное значение. котерминальные углы к заданному углу.

Например, если α=1400°\альфа = 1400\градусα=1400°, то котерминальный угол в диапазоне [0,360°)[0,360\градус)[0,360°) равен 320°320\градус320°, что равно уже один пример положительного котерминального угла.

• Другие положительные котерминальные углы равны 680°680\градус680°, 1040°1040\градус1040°…

• Другие отрицательные котерминальные углы: -40°-40\градус-40°, -400°-400\градус-400°, -760°-760\градус-760°…

Также можно просто складывать и вычитать число оборотов, если все, что вам нужно, это любой положительный и отрицательный котерминальный угол . Для нашего ранее выбранного угла α=1400°\alpha = 1400\градусα=1400° прибавим и вычтем 101010 оборотов (или 100100100, почему бы и нет):

• Положительный котерминальный угол: β=α+360°×10=1400°+3600°=5000°\бета = \альфа + 360\градус \умножить на 10 = 1400\градус + 3600\градус = 5000\градусβ=α+360 °×10=1400°+3600°=5000°.

• Отрицательный котерминальный угол: β=α−360°×10=1400°−3600°=−2200°\бета = \альфа — 360\градус\умножить на 10 = 1400\градус — 3600\градус = -2200\градусβ=α −360°×10=1400°−3600°=−2200°.

Число оборотов должно быть достаточно большим, чтобы изменить знак при сложении/вычитании. Например, одного оборота для нашего примерного α недостаточно, чтобы иметь как положительный, так и отрицательный котерминальный угол – мы получим два положительных, 1040°1040\градус1040° и 1760°1760\градус1760°.

Что такое котерминальный угол…

Если вам интересно, что такое котерминальный угол некоторого угла, не стесняйтесь использовать наш инструмент — он здесь, чтобы помочь вам!

Но если вы по каким-то причинам все же предпочитаете список примерных котерминальных углов (но мы действительно не понимаем почему . ..), то вот вам:

• Котерминальный угол 0°0\градус 0°: 360°360\градус 360°, 720°720\градус 720°, -360°-360\градус-360°, -720°-720\градус-720°.

• Котерминальный угол 1°1\градус 1°: 361°361\градус 361°, 721°721\градус 721° -359°-359\градус-359°, -719°-719\градус-719°.

• Котерминальный угол 5°5\градус 5°: 365°365\градус 365°, 725°725\градус 725°, -355°-355\градус-355°, -715°-715\градус-715°.

• Котерминальный угол 10°10\градус 10°: 370°370\градус 370°, 730°730\градус 730°, -350°-350\градус-350°, -710°-710\градус-710°.

• Котерминальный угол 15°15\градус 15°: 375°375\градус 375°, 735°735\градус 735°, -345°-345\градус-345°, -705°-705\градус-705°.

• Котерминальный угол 20°20\градус 20°: 380°380\градус 380°, 740°740\градус 740°, -340°-340\градус-340°, -700°-700\градус-700°.

• Котерминальный угол 25°25\градус 25°: 385°385\градус 385°, 745°745\градус 745°, -335°-335\градус-335°, -695°-695\градус-695°.

• Котерминальный угол 30°30\градус 30° (π/6\pi / 6π/6): 390°390\градус 390°, 750°750\градус 750°, -330°-330\градус-330°, -690° -690\градус-690°.

• Котерминальный угол 45°45\градус 45° (π/4\pi / 4π/4): 495°495\градус 495°, 765°765\градус 765°, -315°-315\градус-315°, -675° -675\градус-675°.

• Котерминальный угол 60°60\градус 60° (π/3\pi / 3π/3): 420°420\градус420°, 780°780\градус780°, −300°-300\градус−300°, −660° -660\градус-660°

• Котерминальный угол 75°75\градус75°: 435°435\градус435°, 795°795\градус795°,-285°-285\градус-285°, -645°-645\градус-645°

• Котерминальный угол 90°90\градус90° (π/2\pi / 2π/2): 450°450\градус450°, 810°810\градус810°, -270°-270\градус-270°, -630° -630\градус-630°.

• Котерминальный угол 105°105\градус 105°: 465°465\градус 465°, 825°825\градус 825°,-255°-255\градус-255°, -615°-615\градус-615°.

• Котерминальный угол 120°120\градус 120° (2π/32\pi/32π/3): 480°480\градус480°, 840°840\градус840°, -240°-240\градус-240°, -600° -600\градус-600°.

• Котерминальный угол 135°135\градус 135° (3π/43\pi / 43π/4): 495°495\градус 495°, 855°855\градус 855°, -225°-225\градус-225°, -585° -585\градус-585°.

• Котерминальный угол 150°150\градус 150° (5π/65\pi/65π/6): 510°510\градус510°, 870°870\градус870°, -210°-210\градус-210°, -570° -570\градус-570°.

• Котерминальный угол 165°165\градус 165°: 525°525\градус 525°, 885°885\градус 885°, -195°-195\градус-195°, -555°-555\градус-555°.

• Котерминальный угол 180°180\градус 180° (π\piπ): 540°540\градус540°, 900°900\градус900°, -180°-180\градус-180°, -540°-540\градус-540 °

• Котерминальный угол 195°195\градус 195°: 555°555\градус 555°, 915°915\градус 915°, -165°-165\градус-165°, -525°-525\градус-525°.

• Котерминальный угол 210°210\градус 210° (7π/67\pi / 67π/6): 570°570\градус570°, 930°930\градус930°, -150°-150\градус-150°, -510° -510\градус-510°.

• Котерминальный угол 225°225\градус 225° (5π/45\pi / 45π/4): 585°585\градус 585°, 945°945\градус 945°, -135°-135\градус-135°, -495° -495\градус-495°.

• Котерминальный угол 240°240\градус 240° (4π/34\pi / 34π/3: 600°600\градус600°, 960°960\градус960°, 120°120\градус120°, -480°-480\градус- 480°

• Котерминальный угол 255°255\градус 255°: 615°615\градус 615°, 975°975\градус 975°, -105°-105\градус-105°, -465°-465\градус-465°.

• Котерминальный угол 270°270\градус 270° (3π/23\pi / 23π/2): 630°630\градус630°, 990°990\градус990°, -90°-90\градус-90°, -450° -450\градус-450°.

• Котерминальный угол 285°285\градус 285°: 645°645\градус 645°, 1005°1005\градус 1005°, -75°-75\градус-75°, -435°-435\градус-435°.

• Котерминальный угол 300°300\градус300° (5π/35\pi / 35π/3): 660°660\градус660°, 1020°1020\градус1020°, −60°-60\градус−60°, −420° -420\градус-420°.

• Котерминальный угол 315°315\градус 315° (7π/47\pi / 47π/4): 675°675\градус 675°, 1035°1035\градус 1035°, -45°-45\градус-45°, -405° -405\градус-405°.

• Котерминальный угол 330°330\градус330° (11π/611\pi / 611π/6): 690°690\градус690°, 1050°1050\градус1050°, −30°-30\градус−30°, −390° -390\градус-390°.

• Котерминальный угол 345°345\градус345°: 705°705\градус705°, 1065°1065\градус1065°, -15°-15\градус-15°, -375°-375\градус-375°.

• Котерминальный угол 360°360\градус 360° (2π2\pi2π): 0°0\градус0°, 720°720\градус720°, -360°-360\градус-360°, -720°-720\градус-720 °.

Если вы не нашли свой запрос в этом списке, введите угол в наш калькулятор котерминального угла — вы получите ответ в мгновение ока!

Часто задаваемые вопросы

Каков котерминальный угол 1000° между 0° и 360°?

Ответ: 280° . Чтобы прийти к этому результату, вспомним формулу для котерминальных углов в 1000°:

1000° + 360° × k .

Очевидно, чтобы получить котерминальный угол между 0° и 360°, нам нужно использовать отрицательные значения k . При k=-1 получаем 640°, что слишком много. Итак, давайте попробуем k=-2: мы получим 280°, что находится между 0° и 360°, так что у нас есть ответ.

Как найти все котерминальные углы?

У данного угла бесконечно много котерминальных углов, поэтому вы не можете перечислить их все. Вы можете записать их с помощью формулы. Если ваш угол θ выражается в градусах, тогда котерминальные углы имеют вид θ + 360° × k , где k — целое число (может быть и отрицательное число!). Если θ выражено в радианах, то формула будет выглядеть так: θ + 2π × k .

Какие котерминальные углы равны 45°?

Котерминальные углы 45° имеют форму 45° + 360° × k , где k — целое число. Подставляя различные значения k , мы получаем разные котерминальные углы 45° . Перечислим некоторые из них:

45°, 405°, 765°, -315°, -675° .

Как проверить, являются ли два угла котерминальными?

Два угла, α и β , являются котерминальными, если их разность кратна 360° . То есть, если β - α = 360° × k для некоторого целого числа k .

Например, углы -170° и 550° являются котерминальными, потому что 550° - (-170°) = 720° = 360° × 2, Если ваши углы выражены в радианах, а не в градусах, то вы ищете кратных 2π , т. е. формула β - α = 2π × k для некоторого целого числа k .

Hanna Pamuła, PhD

Я хочу…

Угол в

Посмотреть 6 похожих калькуляторов углов 🕑 Калькулятор котерминального угла — TrigCalc.com

градус

/

радиан

минимум

угловая совмещенная с

(

)°

минимум

угловая совмещенная с

(

)

Решение:  

°

 или 

°

Требуется только два значения

Учебное пособие по котерминальному углу

Котерминальные углы — это углы, имеющие общие начальную и конечную стороны. Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам. Если вам нужно найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже. Максимальное количество раз, когда 360 градусов можно вычесть из 785 градусов и остаться положительным, находится путем деления заданного угла на 785 градусов и деления его на 360, но с округлением до целого числа в меньшую сторону. Это число равно 2. Как только это число найдено, оно умножается на 360 и вычитается из 785 градусов. Если бы сказали найти наименьший отрицательный котерминал угла с 526 градусами, был бы использован аналогичный процесс вычисления с той лишь разницей, что нужно сложить делимое данного угла и 360 градусов. Как только это число найдено, его нужно снова вычесть из заданного угла 526 градусов. Это дает вам наименьший отрицательный котерминальный угол. Таким же образом можно найти углы, котерминальные значениям в радианах. Если бы вам сказали найти котерминал наименьшего положительного угла с 32 пи радиан, вы бы использовали следующий процесс расчета: Поскольку при вычислении наименьшего положительного значения делимое данного радиана и 2pi должно быть округлено до целого числа в меньшую сторону. Это целое число нужно умножить на 2 пи и вычесть из заданного значения. Это приводит к решению, пи. Но ты Чтобы найти наименьший отрицательный угол, котерминальный другому углу, скажем, 78 пи, будет работать процесс вычисления, показанный ниже. В этом случае необходим наименьший отрицательный угол, что означает, что делимое 78 пи и 2 пи должно быть округлено до ближайшего целого числа. Затем это число нужно вычесть из 78 пи, чтобы найти решение.