Функция ATAN — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ATAN в Microsoft Excel.
Описание
Возвращает арктангенс числа. Арктангенс числа — это угол, тангенс которого равен числу. Угол определяется в радианах в диапазоне от -пи/2 до пи/2.
Синтаксис
ATAN(число)
Аргументы функции ATAN описаны ниже.
Замечания

Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=ATAN(1) |
Арктангенс числа 1 в радианах, пи/4 (0,785398) |
0,785398163 |
|
=ATAN(1)*180/ПИ() |
Арктангенс числа 1 в градусах |
45 |
|
=ГРАДУСЫ(ATAN(1)) |
Арктангенс числа 1 в градусах |
45 |
Чему равен arctg 3.
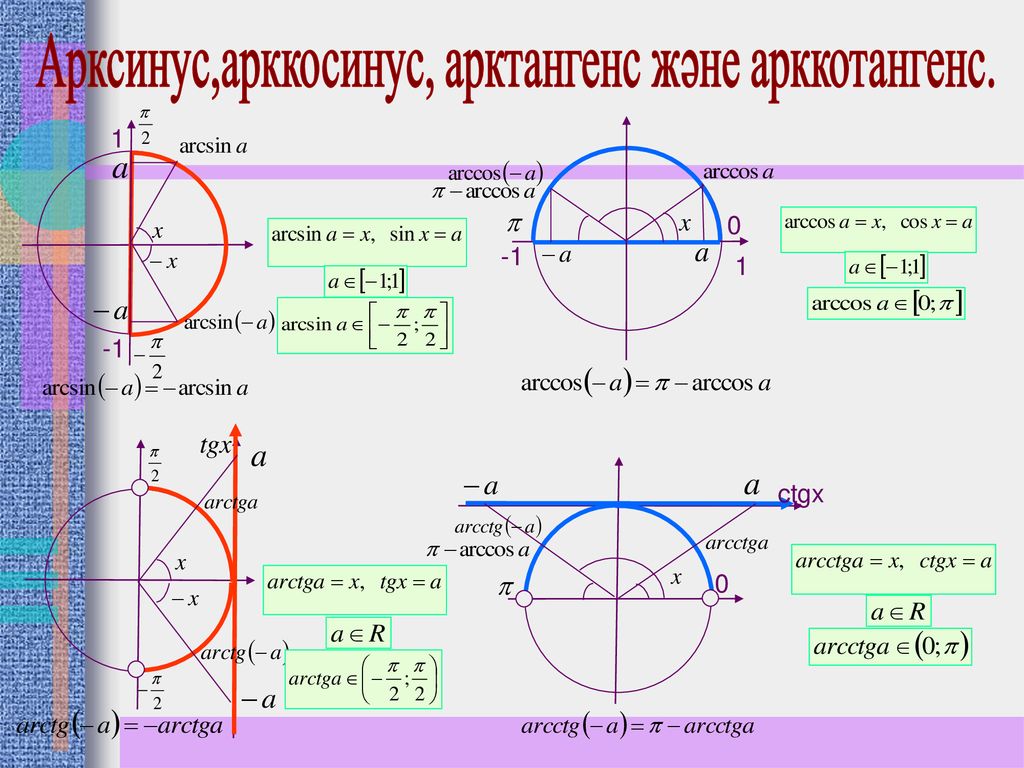
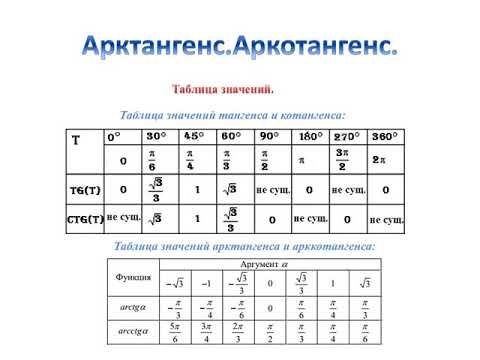 Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса. Разложение в ряд
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса. Разложение в рядЧто такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5.
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус.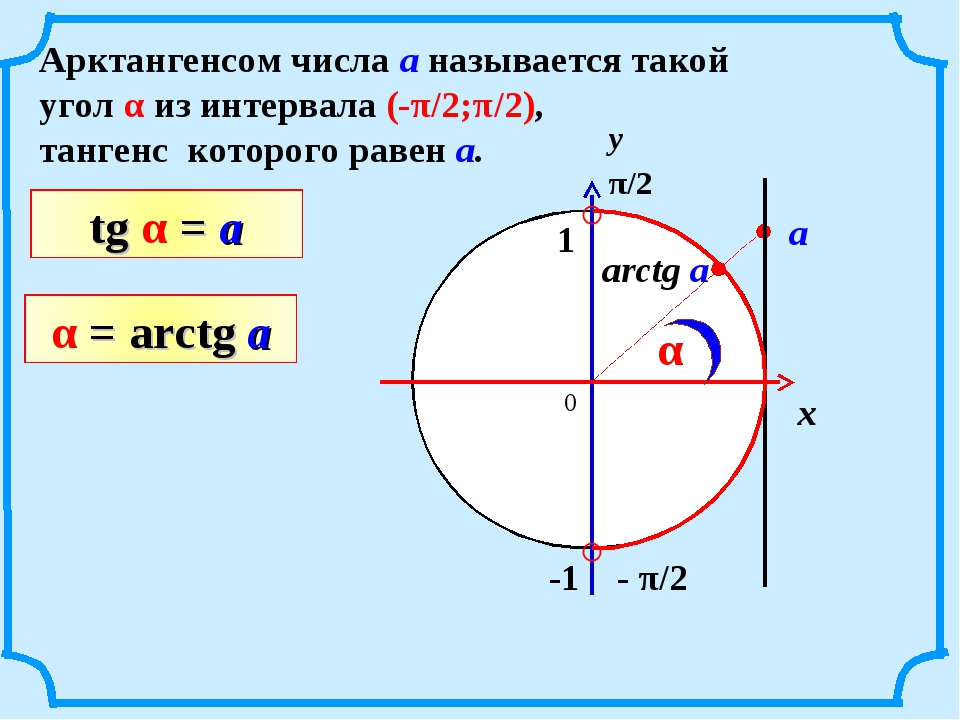 .. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
.. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения.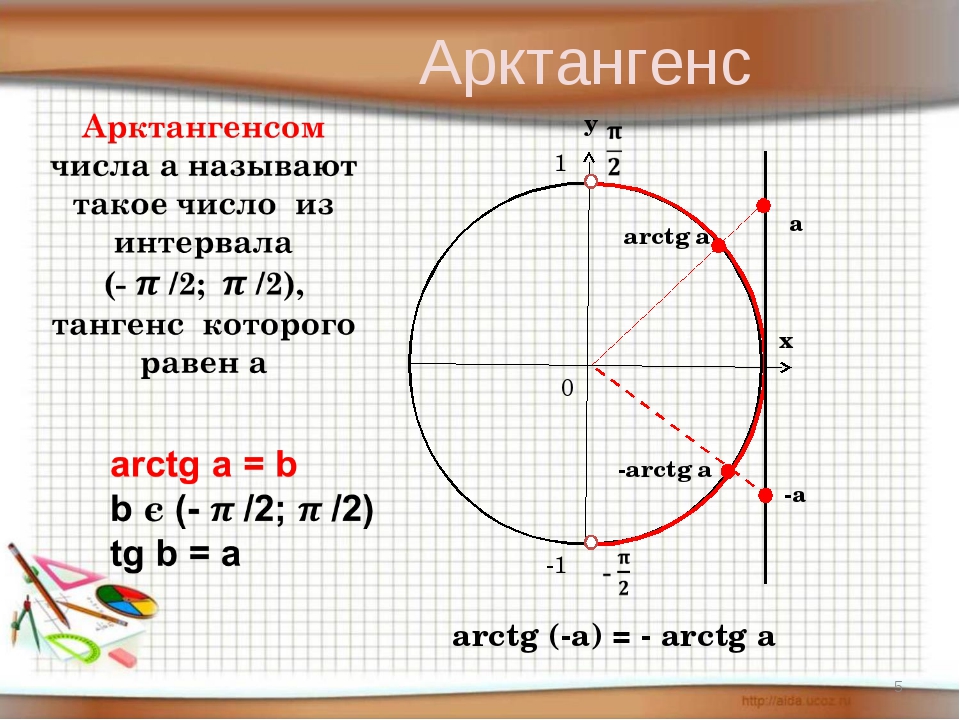 Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
И не только по тригонометрии. Очень помогает.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».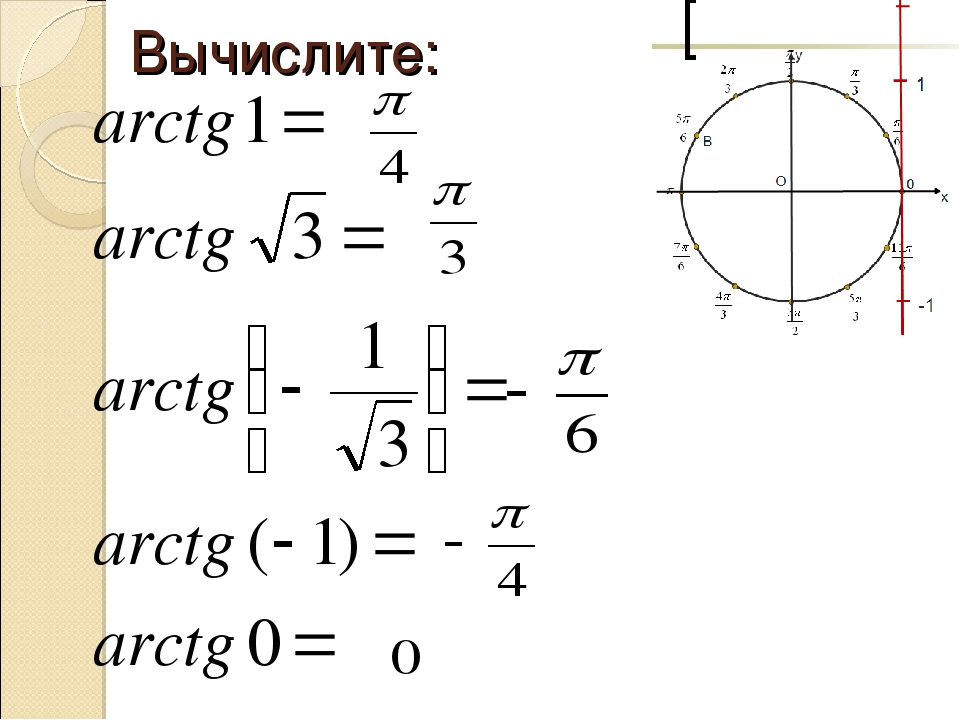
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a
равен π/10
, и нужно вычислить значение арктангенса этого числа a
. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.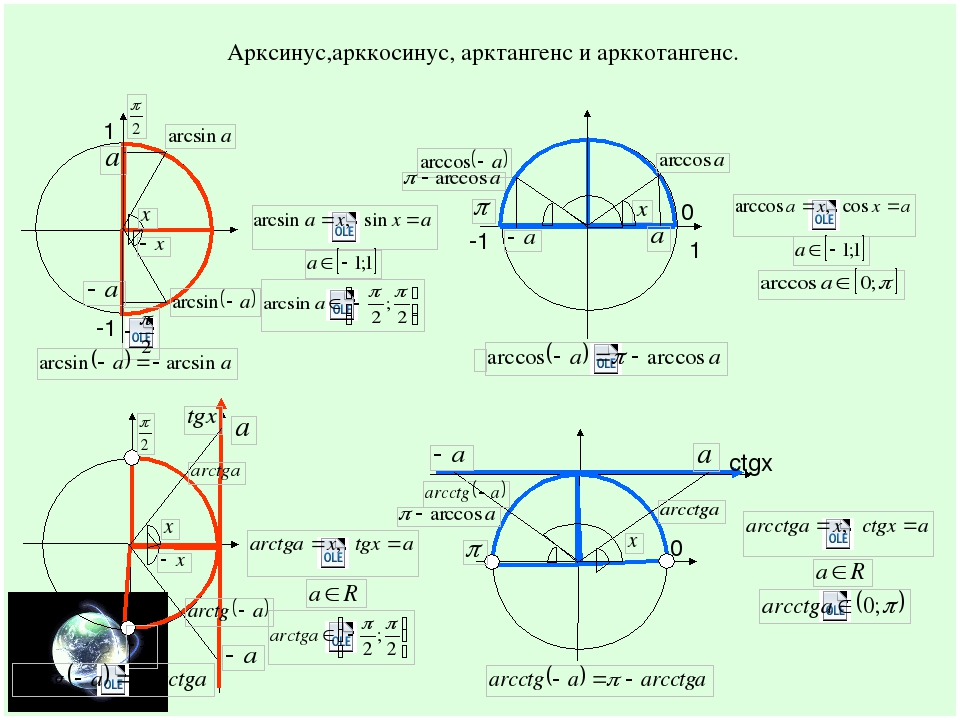
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П.
 Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
Определение.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т. к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
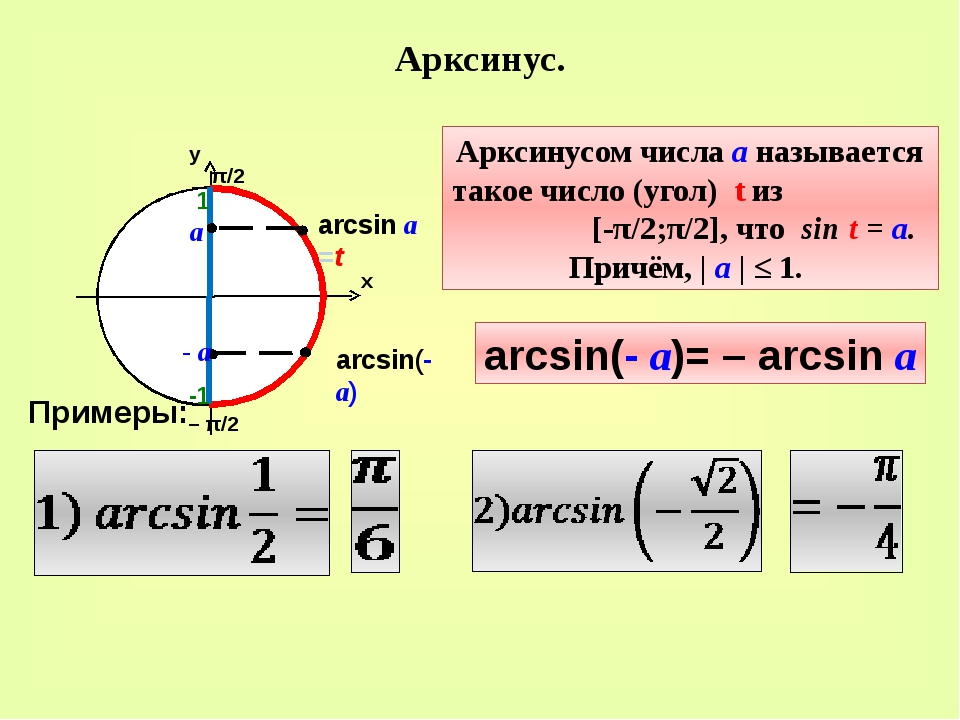
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
tg(arctg
x)
= x
arctg(tg
x)
= x
Арктангенс обозначается так:
.
График функции арктангенс
График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
). Он имеет область определения и множество значений .
ctg(arcctg
x)
= x
arcctg(ctg
x)
= x
Арккотангенс обозначается так:
.
График функции арккотангенс
График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат.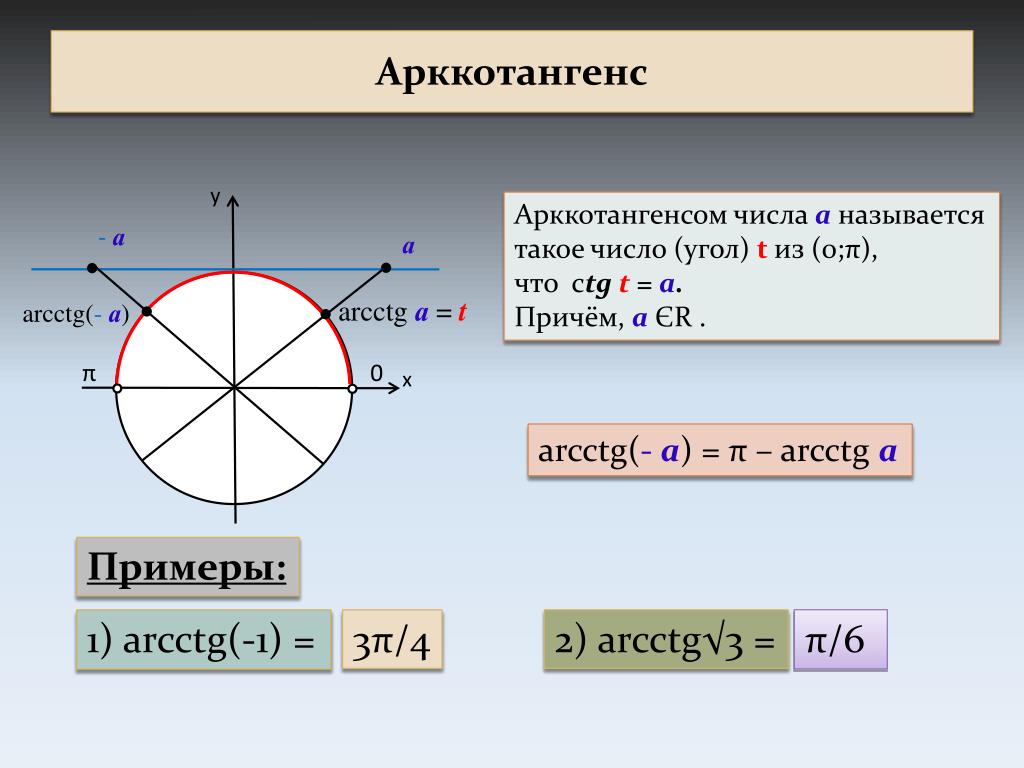 Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
Функция арккотангенс не является четной или нечетной:
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x ≠ ± arcctg
x
.
Свойства — экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| — | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| — ∞ | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — 1 | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
Формулы суммы и разности
при
при
при
при
при
при
Выражения через логарифм, комплексные числа
,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков :
Пусть .
Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть .
Тогда
;
.
Интегралы
Делаем подстановку x = tg
t
и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс , соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg
x)
= x
ctg(arcctg
x)
= x
.
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Функция арктангенса в Excel
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Синтаксис принимает следующую форму:
=ATAN(число)
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
=ATAN(число)Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
=ATAN(4)Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
- Для вывода результатов расчета на экран нажимаем на кнопку Enter.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.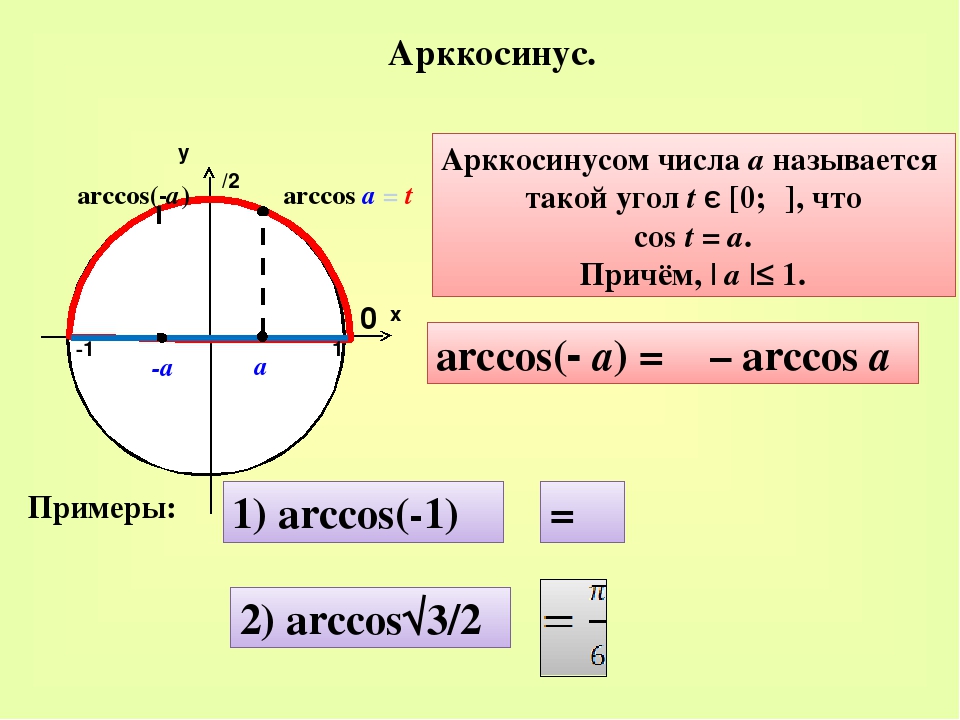
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
- Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
- После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов.
 Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Затем, как и в предыдущем варианте, жмем на кнопку «OK». - После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.
Урок: Мастер функций в Excel
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТswift тригонометрических функций (COS, загар, арксинуса, Аркос, равенства arctg)
Здравствуйте, я должен различать вычисления в градусах, и у меня есть следующий код, но я не возвращаю мне точные значения.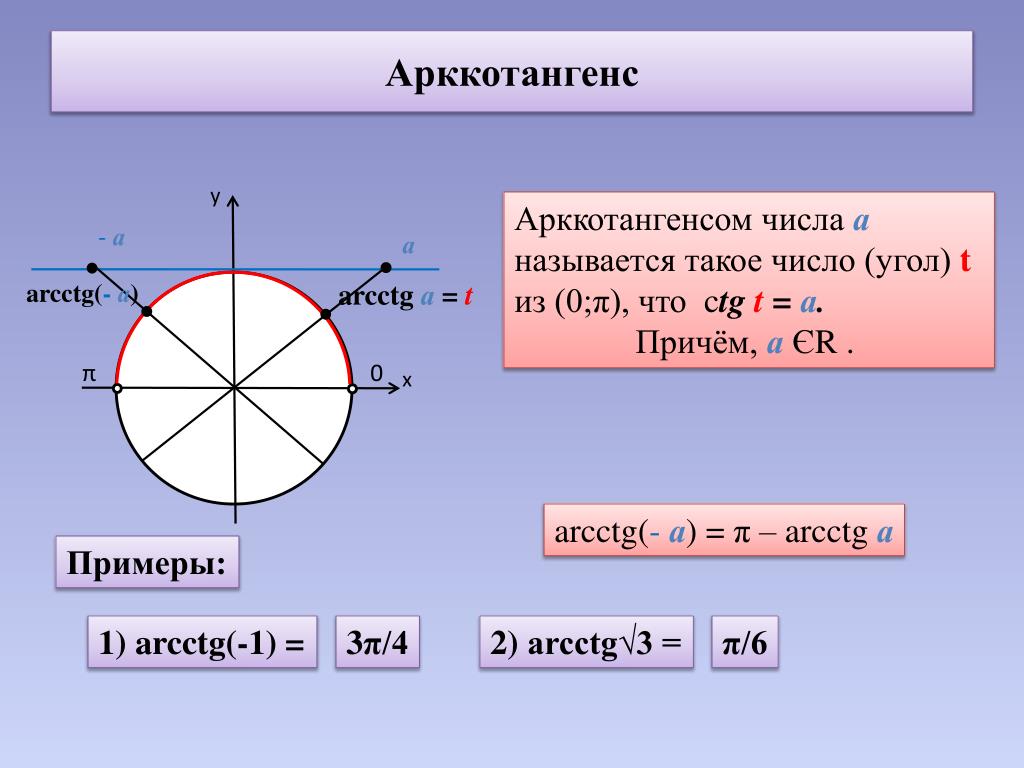 2), поэтому формула должна иметь Атан х, а не инструмент atan2 х, когда мы преобразуем формулу от арксинуса, чтобы равенства arctg. θ = 2 arcsin(sqrt (a)) = 2 arctan(sqrt (a)/(sqrt (1-a))) Но в большинстве…
2), поэтому формула должна иметь Атан х, а не инструмент atan2 х, когда мы преобразуем формулу от арксинуса, чтобы равенства arctg. θ = 2 arcsin(sqrt (a)) = 2 arctan(sqrt (a)/(sqrt (1-a))) Но в большинстве…
В Python 2.6 я обнаружил, что Decimal эквивалент sqrt(pi) Decimal(pi).sqrt() Есть ли что-нибудь подобное для sin, cos или других (обратных) тригонометрических функций? В документах упоминается только то, как вычислить cos и sin вычислительно. Decimal(pi).cos() не существует, как и from decimal…
30
Это скорее математическая задача, чем задача Swift:
let sinus = sin(90.0 * Double.pi / 180)
print("Sinus \(sinus)")
let cosinus = cos(90 * Double.pi / 180)
print("Cosinus \(cosinus)")
let tangent = tan(90 * Double.pi / 180)
print("Tangent \(tangent)")
печать
Sinus 1. 0
Cosinus 6.12323399573677e-17
Tangent 1.63312393531954e+16
0
Cosinus 6.12323399573677e-17
Tangent 1.63312393531954e+16
Синус 90 градусов равен 1 (Правильно)
Косинус 90 градусов равен 0. Значение 6e-17-это очень маленькое значение, любое разумное округление будет считать его равным нулю (правильно). Тот факт, что вы не можете получить ровно ноль, объясняется ошибками округления в вычислении.
Тангенс 90 градусов не определен (sin/tan = 1/0, деление на ноль не определено). Если бы у нас были точные расчеты, вы, вероятно, получили бы бесконечность. В этом случае мы имеем 1 , деленное на 6e-17, что становится большим числом 1.6e16 . Результат правильный.
Что касается обратных функций, обратите внимание на одно — их параметры не выражены ни в градусах, ни в радианах. Например, их результат находится в degrees/radians,:
let arcsinus = asin(1.0) * 180 / Double.pi
print("Arcsinus \(arcsinus)")
печать
Arcsinus 90. 0
0
Поделиться Sulthan 03 марта 2016 в 12:14
9
Swift 4 работает с измененным синтаксисом:
let sinus = sin(90.0 * Double.pi / 180)
let cosinus = cos(90 * Double.pi / 180)
let tangent = tan(90 * Double.pi / 180)
let arcsinus = asin(1) * 180/ Double.pi
let arcosinus = acos(0) * 180/ Double.pi
let arctangent = atan(1) * 180/ Double.pi
Поделиться Darius Miliauskas 18 июня 2018 в 11:04
Похожие вопросы:
Быстрая реализация тригонометрических функций для c++
Короткая версия: я хотел бы знать, существуют ли реализации стандартных тригонометрических функций, которые быстрее, чем те, которые включены в math.h . Длинная версия: у меня есть программа,…
Вычислительная стоимость тригонометрических функций
Возможный Дубликат : Как работают тригонометрические функции? Что на самом деле входит в вычисление тригонометрических функций, таких как Sin, Cos, Tan и Atan? Я думаю, что нашел оптимизацию в своем. 2), поэтому формула должна иметь Атан х, а не инструмент atan2 х, когда мы преобразуем формулу от…
2), поэтому формула должна иметь Атан х, а не инструмент atan2 х, когда мы преобразуем формулу от…
Sin, cos и т. д. Для Python 2 Decimal?
В Python 2.6 я обнаружил, что Decimal эквивалент sqrt(pi) Decimal(pi).sqrt() Есть ли что-нибудь подобное для sin, cos или других (обратных) тригонометрических функций? В документах упоминается…
Проверка математического уравнения regex для javascript
Я хочу получить подтверждение для моих математических уравнений Предположим, что у меня есть следующие уравнения: 1) x + y = e // допустимое уравнение 2) x + sin(x) = Y //valid уравнение 3) a + wq =…
Python3-Sympy: расширьте произведения тригонометрических функций
Я не могу найти способ, чтобы SymPy расширял произведения, подобные cos(a)*cos(b) , в сумму тригонометрических функций суммы углов. from sympy import * init_printing() wrf,wlo,t = symbols(‘\omega_RF…
Производная тригонометрических функций python
Я работаю над небольшим сайд-проектом и создаю калькулятор для различных методов численного анализа. То, с чем я борюсь, — это вычисление производных тригонометрических функций. Для расчетов…
То, с чем я борюсь, — это вычисление производных тригонометрических функций. Для расчетов…
Построение тригонометрических функций в R
Я новичок в R, и мне нужна помощь в построении тригонометрических функций. Если быть точным, то речь идет о x-лимитах. У меня есть следующий код. coz<-function(x) {cos(x)} plot(coz, 0, 2*pi, bty…
Использование symbolic toolbox для упрощения выражений известных функций (например, тригонометрических функций)
Я хотел бы использовать matlab для упрощения выражений, например, тригонометрических функций для меня. Например, я попробовал это: syms x; simplify(sin(x)/cos(x)) Мой ожидаемый результат был бы…
Чему равен arctg 3. Урок «Арктангенс и арккотангенс
Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.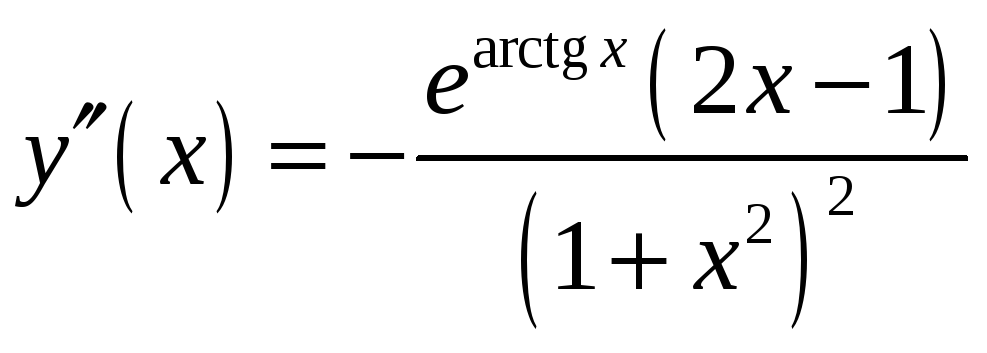
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x 1 + πk. Значение x 1 — это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = — 3. По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от -π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от -π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от -π/2 до π/2.
Пример 2 — вычислить арктангенс отрицательного числа. Используя равенство arctg (- a) = — arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = — 4,1. В данном случае x = arctg (- 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (- 4,1) + πk.
В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk
Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
В конце видеоурока делается еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим решение уравнений tg х = 3 и tg х= — 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде
х = х 1 + πk, где х 1 — это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение
arctg 3 (арктангенс трех).
Как же понимать arctg 3?
Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ;). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.
Аналогично решение уравнения tg х = — 3 можно записать в виде х = х 2 + πk, где х 2 — это абсцисса точки пересечения прямой у = — 3 с главной ветвью тангенсоиды (рис. 1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.
1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.
Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (-;), тангенс которого равен а.
Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.
Зная определение арктангенса, сделаем общий вывод о решении уравнения
tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.
Рассмотрим примеры.
ПРИМЕР 1.Вычислить arctg.
Решение. Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Итак, arctg =.
ПРИМЕР 2. Вычислить arctg (-).
Решение. Используя равенство arctg(- а) = — arctg а, запишем:
arctg(-) = — arctg . Пусть — arctg = х, тогда — tgх = и хϵ (- ;). Следовательно, х =, так как tg = и ϵ (- ;). Показать таблицу значений
Значит — arctg=- tgх= — .
ПРИМЕР 3. Решить уравнение tgх = 1.
1. Запишем формулу решений: х = arctg 1 + πk.
2. Найдем значение арктангенса
так как tg = . Показать таблицу значений
Значит arctg1= .
3. Поставим найденное значение в формулу решений:
ПРИМЕР 4. Решить уравнение tgх = — 4,1(тангенс икс равно минус четыре целые одна десятая).
Решение. Запишем формулу решений: х = arctg (- 4,1) + πk.
Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.
ПРИМЕР 5. Решить неравенство tgх 1.
Решение. Будем решать графически.
- Построим тангенсоиду
у= tgх и прямую у = 1(рис.2). Они пересекаются в точках вида х = + πk.
2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1. Это интервал (;).
3. Используем периодичность функции.
Своийство 2. у=tg х — периодическая функция с основным периодом π.
Учитывая периодичность функции у= tgх, запишем ответ:
(;). Ответ можно записать в виде двойного неравенства:
Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).
Графики функций у= ctg х и у =а а также
у= ctg х и у=-а
имеют бесконечно много общих точек, абсциссы которых имеют вид:
х = х 1 + , где х 1 — это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и
х 1 = arcсtg а;
х = х 2 + , где х 2 — это абсцисса точки пересечения прямой
у = — а с главной ветвью тангенсоиды и х 2 = arcсtg (- а).
Заметим, что х 2 = π — х 1 . Значит, запишем важное равенство:
arcсtg (-а) = π — arcсtg а.
Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.
Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .
Обратим внимание, что уравнение ctg х = a можно преобразовать к виду
tg х = , за исключение, когда а = 0.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки.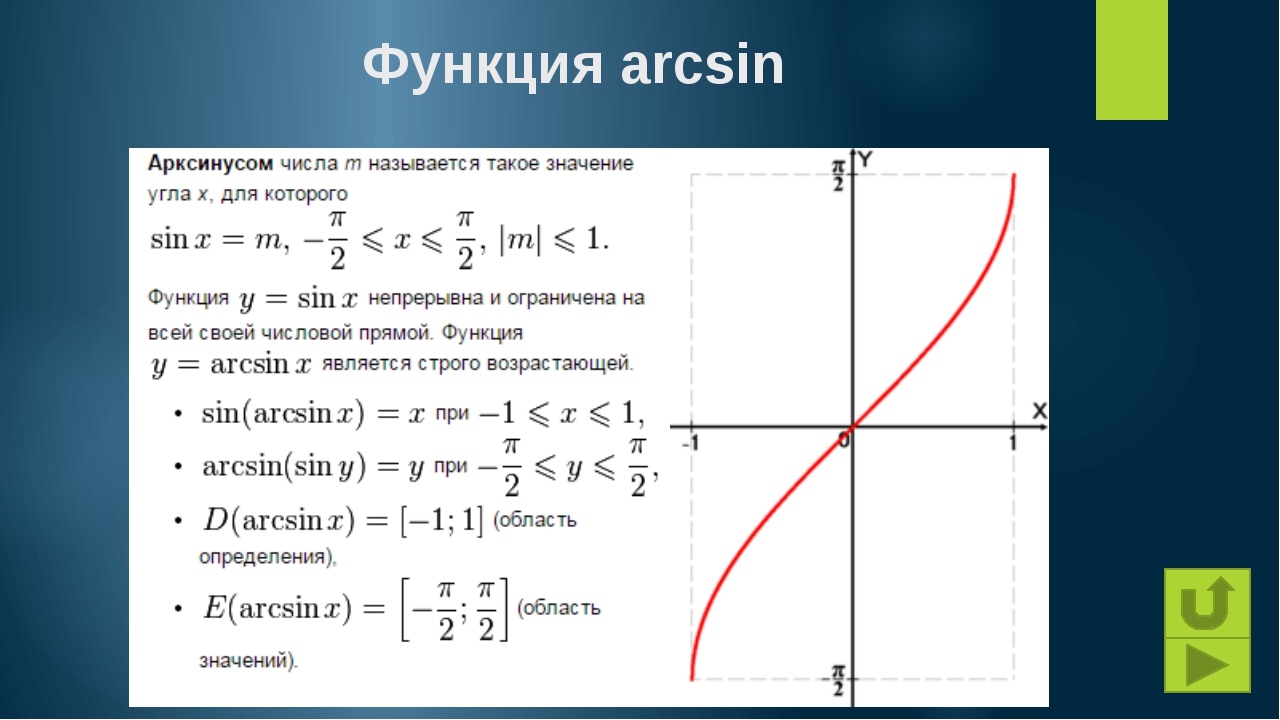 Чтобы печатать меньше.)
Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус. .. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
.. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
И не только по тригонометрии. Очень помогает.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии.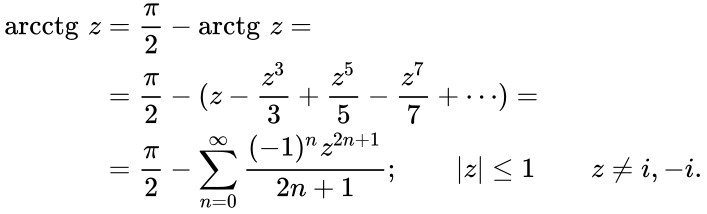 Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса.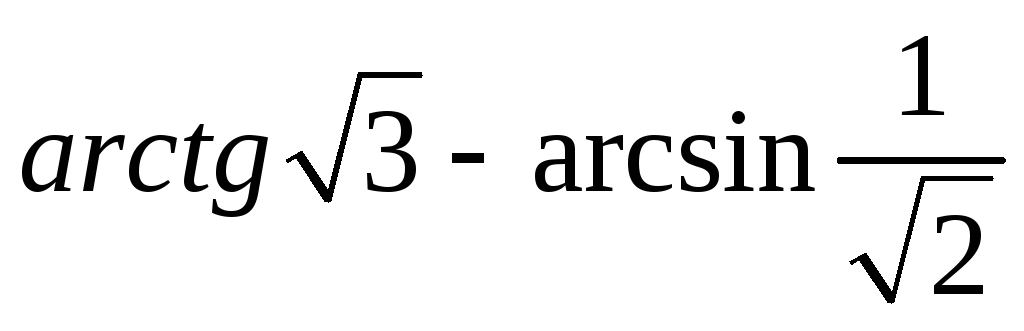 Будем это делать на примерах.
Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a
требуется найти значение арктангенса или арккотангенса этого числа a
или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н.
 Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1 и множество значений -π/2 ≤
y ≤ π/2 .
sin(arcsin
x)
= x
arcsin(sin
x)
= x
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1 и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
arccos(cos
x)
= x
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2 ,
cos
t ≥ 0 :
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К. А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Значение arctg 1 3. Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? График функции арксинус
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.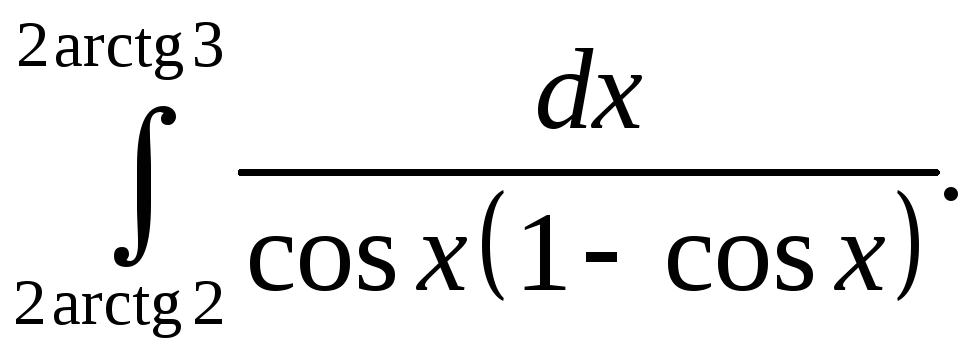
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис. 2 — 1.
2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже).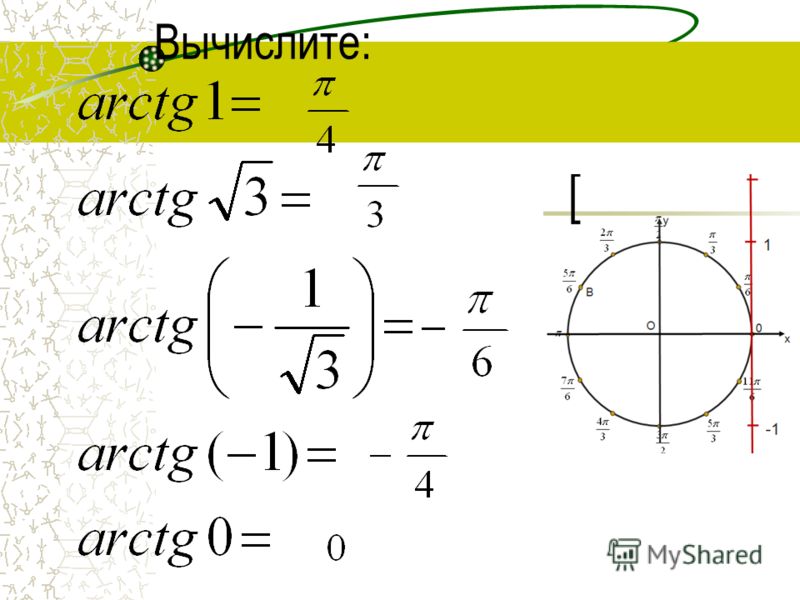 Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a
равен π/10
, и нужно вычислить значение арктангенса этого числа a
. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл.
 сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1 и множество значений -π/2 ≤
y ≤ π/2 .
sin(arcsin
x)
= x
arcsin(sin
x)
= x
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1 и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
arccos(cos
x)
= x
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2 ,
cos
t ≥ 0 :
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К. А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x 1 + πk. Значение x 1 — это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = — 3. По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk.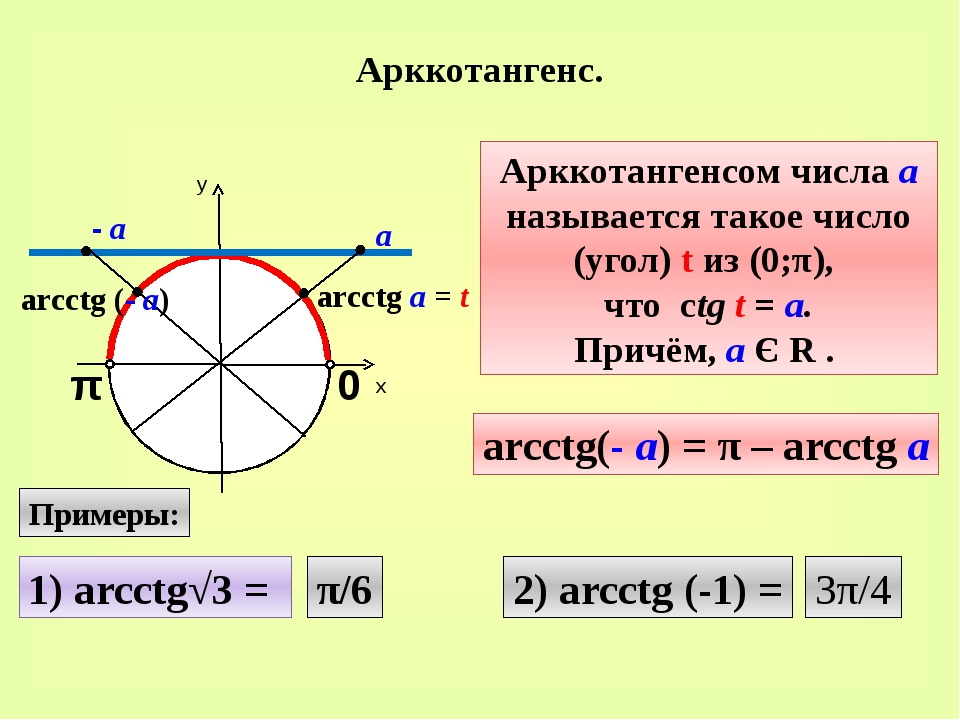 С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от -π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от -π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от -π/2 до π/2.
Пример 2 — вычислить арктангенс отрицательного числа. Используя равенство arctg (- a) = — arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Ответом уравнения будет — π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = — 4,1. В данном случае x = arctg (- 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (- 4,1) + πk.
В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk
Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
В конце видеоурока делается еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим решение уравнений tg х = 3 и tg х= — 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде
х = х 1 + πk, где х 1 — это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение
arctg 3 (арктангенс трех).
Как же понимать arctg 3?
Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ;). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.
Аналогично решение уравнения tg х = — 3 можно записать в виде х = х 2 + πk, где х 2 — это абсцисса точки пересечения прямой у = — 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.
Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (-;), тангенс которого равен а.
Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.
Зная определение арктангенса, сделаем общий вывод о решении уравнения
tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.
Рассмотрим примеры.
ПРИМЕР 1.Вычислить arctg.
Решение. Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Итак, arctg =.
ПРИМЕР 2. Вычислить arctg (-).
Решение. Используя равенство arctg(- а) = — arctg а, запишем:
Используя равенство arctg(- а) = — arctg а, запишем:
arctg(-) = — arctg . Пусть — arctg = х, тогда — tgх = и хϵ (- ;). Следовательно, х =, так как tg = и ϵ (- ;). Показать таблицу значений
Значит — arctg=- tgх= — .
ПРИМЕР 3. Решить уравнение tgх = 1.
1. Запишем формулу решений: х = arctg 1 + πk.
2. Найдем значение арктангенса
так как tg = . Показать таблицу значений
Значит arctg1= .
3. Поставим найденное значение в формулу решений:
ПРИМЕР 4. Решить уравнение tgх = — 4,1(тангенс икс равно минус четыре целые одна десятая).
Решение. Запишем формулу решений: х = arctg (- 4,1) + πk.
Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.
ПРИМЕР 5. Решить неравенство tgх 1.
Решение. Будем решать графически.
- Построим тангенсоиду
у= tgх и прямую у = 1(рис.2). Они пересекаются в точках вида х = + πk.
2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1.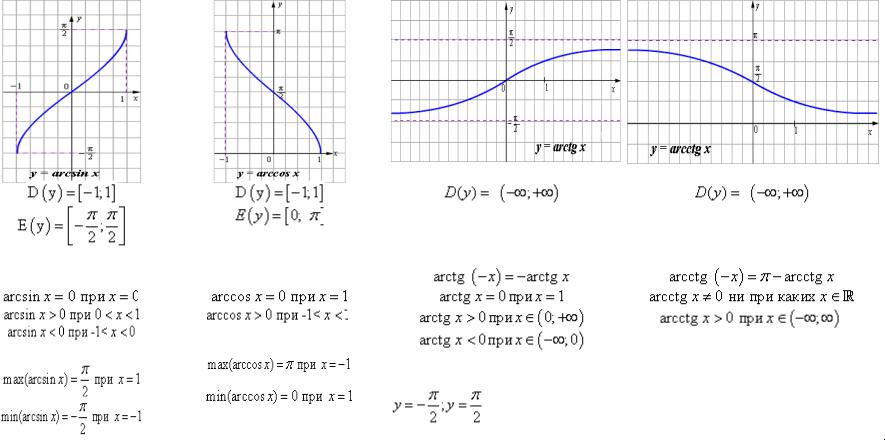 Это интервал (;).
Это интервал (;).
3. Используем периодичность функции.
Своийство 2. у=tg х — периодическая функция с основным периодом π.
Учитывая периодичность функции у= tgх, запишем ответ:
(;). Ответ можно записать в виде двойного неравенства:
Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).
Графики функций у= ctg х и у =а а также
у= ctg х и у=-а
имеют бесконечно много общих точек, абсциссы которых имеют вид:
х = х 1 + , где х 1 — это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и
х 1 = arcсtg а;
х = х 2 + , где х 2 — это абсцисса точки пересечения прямой
у = — а с главной ветвью тангенсоиды и х 2 = arcсtg (- а).
Заметим, что х 2 = π — х 1 . Значит, запишем важное равенство:
arcсtg (-а) = π — arcсtg а.
Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.
Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .
Обратим внимание, что уравнение ctg х = a можно преобразовать к виду
tg х = , за исключение, когда а = 0.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. .. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
.. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т. к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°.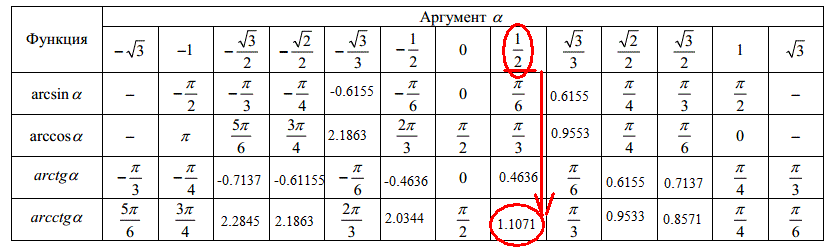 Можно смело записать:
Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость. )
)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Чему равен arctg бесконечности
Арктангенс, arctg
Определение и обозначения
Арктангенс обозначается так:
.
График функции арктангенс
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
Арккотангенс обозначается так:
.
График функции арккотангенс
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ | – ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
| – | π | |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0° | 90° | |||
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | ||
Формулы
Формулы суммы и разности
при
при 0,;xy > 1″>
при 1″>
при -1″>
при 0,;xy
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x ) = x
ctg(arcctg x ) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x ) = x при
arcctg(ctg x ) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 14-07-2014 Изменено: 23-12-2018
Чётность и возрастание
Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.
Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.
В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.
Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:
- косинус: cos (arccos a)=a;
- тангенс: tg (arctg a)=a;
- катангенс: ctg (arcctg a)=a.
В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.
Противоположные числа
Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).
Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.
На основе свойств неравенств, выполняется умножение составных частей на -а. Заменив знаки неравенств на противоположные, можно произвести умножение на -1: −π/2≤−arcsin a≤π/2.
Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.
Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.
Используя свойства неравенств, перемножаются поочерёдно его части на -1, сменяются знаки. Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.
Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.
Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.
Сложение величин
Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.
Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.
С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.
Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.
Примеры и задачи
Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:
Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.
Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса.
Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
Известно, аrcsin sin (-15)= -15 град., arccos (cos (2π/3))=2π/3, arctg (tg (0,2))=0,2. Нужно отметить, что выражение arcsin (sin α) справедливо на отрезке −π/2≤α≤π/2. Но равенство arcsin (sin α)=α имеет смысл только при соблюдении этого условия. Нельзя утверждать, что arcsin (sin (7π/4))=7π/4, так как 7π/4 не принадлежит указанному интервалу (−π/2-π/2).
Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).
Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.
Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .
· Область значений функции y = arcsin(x): .
· Функция арксинус — нечетная, так как .
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: .
· Область значений функции y = arccos(x): .
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба .
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x): .
· Область значений функции арктангенс: .
· Функция арктангенс — нечетная, так как .
· Функция возрастает на всей области определения, то есть, при .
· Функция арктангенс вогнутая при , выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел: .
· Область значений функции y = arcctg(x): .
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба .
· Горизонтальными асимптотами являются прямые при (на чертеже показана зеленым цветом) и y = 0 при .
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8774 — | 7582 — или читать все.
Калькулятор— arctan (0) — Solumaths
Описание:
Функция арктангенса позволяет вычислять арктангенс числа. Функция арктангенса — это функция, обратная функции касательной.
арктанОписание:
arctan функция является обратной функцией касательная функция, Он вычисляет арктангенс числа онлайн .
- Вычисление арктангенса
- Пределы арктангенса Пределы арктангенса существуют в точках `-oo` (минус бесконечность) и` + oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените arctan функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите
arctan (`10`) или прямо 10, если
Кнопка arctan уже появляется, возвращается результат 1. 4711276743.2) `.
4711276743.2) `.
- Функция арктангенса имеет ограничение в `-oo`, которое равно` pi / 2`.
- Функция арктангенса имеет предел в` + oo`, который равен `-pi / 2`.
- `lim_ (x -> — oo) arctan (x) = pi / 2`
- `lim_ (x -> + oo) arctan (x) = — pi / 2`
Функция arctan позволяет вычислять арктангенс числа.Функция арктангенса — это функция, обратная функции касательной.
Синтаксис:
arctan (x), x — это число.
Иногда используются другие обозначения: atan
Примеры:
arctan (`0`) возвращает 0Производный арктангенс:
Чтобы дифференцировать арктангенс функции онлайн, можно использовать калькулятор производных, который позволяет вычислить производную функции арктангенса
Производная от arctan (x) — это производная_вычислителя (`» arctan «(x)`) = `1 / (1+ (x) ^ 2)`
Первообразный арктангенс:
Калькулятор первообразной функции арктангенса позволяет вычислить первообразную. 2) `
2) `
Предельный арктангенс:
Калькулятор пределов позволяет вычислять пределы функции арктангенса.
Предел для arctan (x) равен limit_calculator (`» arctan (x) `)
Арктангенс обратной функции:
Функция, обратная арктангенсу , является тангенциальной функцией, обозначенной как tan.
Графический арктангенс:
Графический калькулятор может построить функцию арктангенса в интервале ее определения.
Свойство арктангенса функции:
Функция арктангенса — это нечетная функция.
Расчет онлайн с арктангенсом (арктангенс)
номеров.arctan () в Python — GeeksforGeeks
numpy.arctan () в Python
numpy.arctan (x [, out]) = ufunc ‘arctan’): Эта математическая функция помогает пользователю вычислить арктангенс для всех x (являющихся элементами массива).
Параметры:
array: [array_like] элементы указаны в радианах. out: [array_like] массив такой же формы, как x.
Примечание:
2pi Радианы = 360 градусов
По соглашению возвращается угол z, действительная часть которого лежит в [-pi / 2, pi / 2].
Возврат:
Массив с арктангенсом x для всех x, т.е. элементов массива. Значения находятся в закрытом интервале [-pi / 2, pi / 2].
Код # 1: Рабочий
|
Выход:
Входной массив: [0, 1, 0.3, -1] Значения обратной касательной: [0.0,78539816 0,2
79 -0,78539816]
Код # 2: Графическое представление
|
Выход:
in_array: [-3.14159265 -2.57039399 -1.99919533 -1.42799666 -0.856798 -0.28559933 0,28559933 0,856798 1,42799666 1,99919533 2.57039399 3,14159265] out_array с загаром: [1.22464680e-16 6.42660977e-01 2.18969456e + 00 -6.95515277e + 00 -1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00 6.95515277e + 00 -2.18969456e + 00 -6.42660977e-01 -1.22464680e-16] out_arraywith arctan: [1.22464680e-16 6.42660977e-01 2.18969456e + 00-6.95515277e + 00 -1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00 6.95515277e + 00 -2.18969456e + 00-6.42660977e-01-1.22464680e-16]
Ссылки:
https://docs.scipy.org/doc/numpy-dev/reference/generated/numpy.arcsin.html#numpy.arccos
.
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовка к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .
номеров.arctan — NumPy v1.20 Руководство
Тригонометрический арктангенс, поэлементно.
Обратная величина tan, так что если y = tan (x) , то x = arctan (y) .
- Параметры
- x array_like
- из ndarray, None или кортеж из ndarray и None, необязательно
Местоположение, в котором сохраняется результат. Если предусмотрено, он должен иметь форма, на которую транслируются входы. Если не указано или Нет, возвращается только что выделенный массив.Кортеж (возможно только как аргумент ключевого слова) должен иметь длину, равную количеству выходов.
- , где array_like, необязательно
Это условие транслируется по входу. В местах, где Условие равно True, массив out будет установлен в результат ufunc. В другом месте массив из сохранит свое исходное значение. Обратите внимание, что если неинициализированный массив из создается по умолчанию
out = None, местоположения внутри него, где условие False будет оставаться неинициализированным.
- ** kwargs
Для других аргументов, содержащих только ключевые слова, см. ufunc docs.
- Возвращает
- out ndarray или скаляр
Out имеет ту же форму, что и x . Его настоящая часть находится в
[-pi / 2, pi / 2](arctan (+/- inf)возвращает+/- pi / 2). Это скаляр, если x — скаляр.
См. Также
-
arctan2 «Четырехквадрантный» арктан угла, образованный ( x , y ) и положительной осью x .
-
угол Аргумент комплексных значений.
Банкноты
arctan — многозначная функция: на каждые x приходится бесконечно
много чисел z таких, что tan ( z ) = x . Конвенция — вернуться
угол z , действительная часть которого лежит в [-pi / 2, pi / 2].
Для типов входных данных с действительным знаком arctan всегда возвращает действительный вывод.{-1}.
Список литературы
Абрамовиц М., Стегун И. А., Справочник по математическим функциям , 10-е издание, Нью-Йорк: Довер, 1964, стр.79. http://www.math.sfu.ca/~cbm/aands/
Примеры
Мы ожидаем, что arctan 0 будет 0, а 1 — пи / 4:
>>> np.arctan ([0, 1]) массив ([0., 0.78539816])
>>> np.pi / 4 0,78539816339744828
Площадь участка:
>>> import matplotlib.pyplot как plt
>>> x = np.linspace (-10, 10)
>>> plt.plot (x, np.arctan (x))
>>> plt.axis ('плотно')
>>> plt.show ()
Использование серии arctan Power для вычисления числа Пи »Рекурсивный процесс
(Примечание: этот пост является расширением для вычисления числа Пи с помощью сообщения Python, написанного пару лет назад. Также есть еще один способ неэффективного вычисления числа Пи вычисления числа Пи с помощью игл Буффона.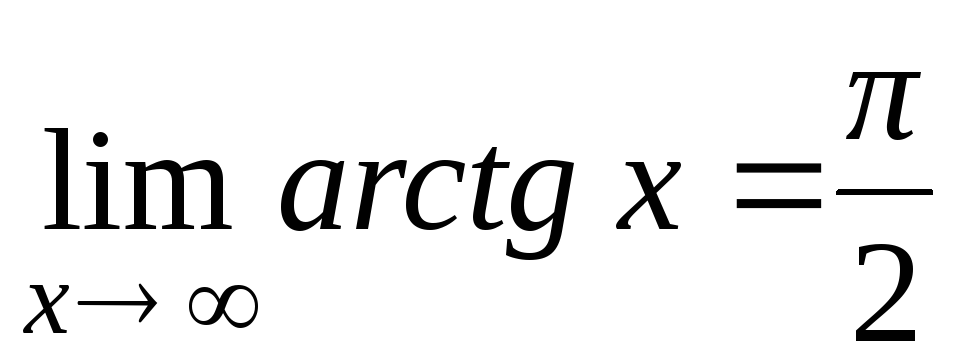 )
)
В настоящее время мы работаем с рядами Power и Taylor в Calculus. 5
Одна особенность, довольно производная от серии для к серии для
Еще лучше, вы можете использовать эту формулу для вычисления числа пи, поскольку, так.
Как быстро это сходится к пи? Давай выясним.
Вот первые десять частичных сумм:
n = 0, а частичная сумма равна 4,0
n = 1, а частичная сумма равна 2,6666666666667
n = 2, а частичная сумма равна 3,466666666666667
n = 3, а частичная сумма равна 2,8952380952380956.
n = 4, а частичная сумма равна 3.3396825396825403
n = 5, а частичная сумма равна 2,9760461760461765
n = 6, а частичная сумма равна 3,2837384837384844
n = 7, а частичная сумма равна 3,017071817071818
n = 8, а частичная сумма равна 3,2523659347188767
n = 9, а частичная сумма равна 3.0418396189294032
n = 10, а частичная сумма равна 3.232315809405594
Хорошо, это медленно.
Вот первые 100 членов:
n = 0, а частичная сумма равна 4,0
n = 10, а частичная сумма равна 3,232315809405594
n = 20, а частичная сумма равна 3. 189184782277596
189184782277596
n = 30, а частичная сумма равна 3,1738423371
n = 40, а частичная сумма равна 3,1659792728432157
n = 50, а частичная сумма равна 3,1611986129870506
n = 60, а частичная сумма равна 3,157984995168666
n = 70, а частичная сумма равна 3,155676462307475
n = 80, а частичная сумма равна 3,1539378622726155
n = 90, а частичная сумма равна 3,1525813328751204
n = 100, а частичная сумма равна 3,1514934010709914
Все еще не до 3,14 даже после добавления 100 членов этой последовательности?
Вот первые 10 000 членов:
n = 0, а частичная сумма равна 4.0
n = 1000, а частичная сумма равна 3,1425916543395442
n = 2000, а частичная сумма равна 3,1420924036835256
n = 3000, а частичная сумма равна 3,1419258758397897
n = 4000, а частичная сумма равна 3,1418425
n = 5000, а частичная сумма равна 3,1417926135957908
n = 6000, а частичная сумма равна 3,1417592924821482
n = 7000, а частичная сумма равна 3,1417354666 6
n = 8000, а частичная сумма равна 3,1417176379662446
n = 9000, а частичная сумма равна 3,14170375 235 1000062383, а частичная сумма равна 3. 1416926435
1416926435
Два множителя на десять больше, чем последний набор, и все же не с точностью до 5 знаков?
Наконец, вот первые десять миллионов приближений:
n = 0, а частичная сумма равна 4,0
n = 1000000, а частичная сумма равна 3,1415936535887745
n = 2000000, а частичная сумма равна 3,1415931535894743
n = 3000000, а частичная сумма равно 3,1415929869229293
n = 4000000, а частичная сумма равна 3,14159295926
n = 5000000, а частичная сумма равна 3.1415928535897395
n = 6000000, а частичная сумма равна 3,141592820256488
n = 7000000, а частичная сумма равна 3,1415927964468655
n = 8000000, а частичная сумма равна 3,141592778589681
n =00, а частичная сумма равна 3,141592764700862, а частичная сумма равна 3,141592764700862. 3,1415927535897814
Я действительно не хочу вычислять это вручную, если после 10 000 000 сложений у нас будет только 7 цифр точности.
(Вопрос: почему все эти четные значения являются завышенной оценкой числа Пи?)
График первых 1000 частичных сумм:
Сравним это с алгоритмом Чудновского:
Чудновский
n = 1 3. 14159265358973420766845352983407622332609156
14159265358973420766845352983407622332609156
п = 2 3.1415926535897932384626433835873506884758663459963
п = 3 3.1415926535897932384626433832795028841971676788547
п = 4 3.1415926535897932384626433832795028841971693993750
п = 5 3.1415926535897932384626433832795028841971693993750
п = 6 3.1415926535897932384626433832795028841971693993750
п = 7 3.1415926535897932384626433832795028841971693993750
Вау, этот алгоритм достиг максимальной точности до 51 цифры после 4 итераций.(2n + 1)) / (2n + 1) # Итак, чтобы вычислить число Пи, вычислите (arctan (1)) = Пи / 4 = 1 - 1/3 + 1/5 - 1/7 + ... четвертьpi = десятичный (0) п = 0 в то время как True: четверть пи = четверть пи + десятичное (-1) ** n / (десятичное (2 * n + 1)) # эта строка позволяет коду печатать только каждые 10 строк, увеличьте это число # для ускорения расчетов и сокращения печати если (n% 10 == 0): печать ((четверть на дюйм * десятичное (4))) п + = 1
А вот код чудновского питона:
из десятичного импорта * # Устанавливает десятичную дробь с точностью до 50 цифр getcontext ().Prec = 50 def factorial (n): если п
Excel ATAN Function
На главную »Встроенные функции Excel» Математические функции Excel »Excel-функция Атана
Арктангенс
Арктангенс является обратным касательной.
Следовательно, для простого прямоугольного треугольника ниже арктангенс противоположной стороны o, деленный на соседнюю сторону, a, равен углу θ.
Т.е. для треугольника выше
The Inverse trig.Функции обсуждаются далее в Википедии. Обратные тригонометрические функции. СтраницаОписание функции
Функция Excel ATAN вычисляет арктангенс (т.е. арктангенс) заданного числа и возвращает угол в радианах между -π / 2 и + π / 2.
Синтаксис функции:
ATAN (число)
Где числовой аргумент - это значение, для которого вы хотите вычислить арктангенс.
Преобразование из радианов в градусы
Если вы хотите, чтобы угол, возвращаемый функцией Atan, выражался в градусах, вы можете преобразовать его с помощью функции Excel Degrees:
= DEGREES ( радиан )
Пример этого представлен ниже.
Примеры функции Атана в Excel
В следующей таблице показана функция Атана в Excel, используемая для вычисления арктангенса четырех различных значений.
Формулы:
| Результаты:
|
Обратите внимание, что в ячейке A4 функция Excel Degrees используется для преобразования вычисленного угла из радианов в градусы.
Дополнительные сведения и примеры функции Excel Atan см. На веб-сайте Microsoft Office.
На веб-сайте Microsoft Office.
Ошибка функции Атана
Если вы получаете сообщение об ошибке из функции Атана Excel, скорее всего, это #VALUE! error:
Common Error
| #VALUE! | - | Происходит, если предоставленный числовой аргумент не является числовым. |
Вернуться к списку всех встроенных функций Excel
Arcsin, Arccos, Arctan - Тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.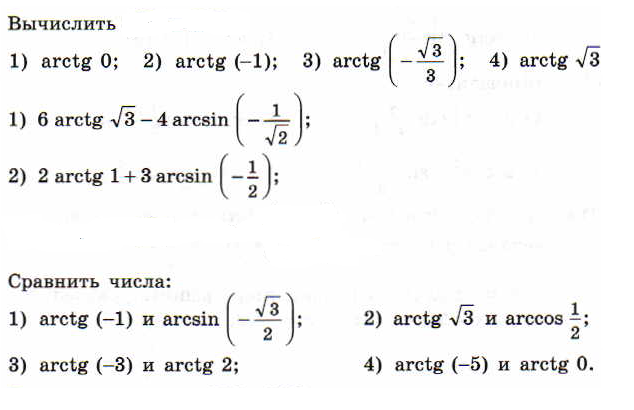
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса - изображению, ссылке, тексту и т.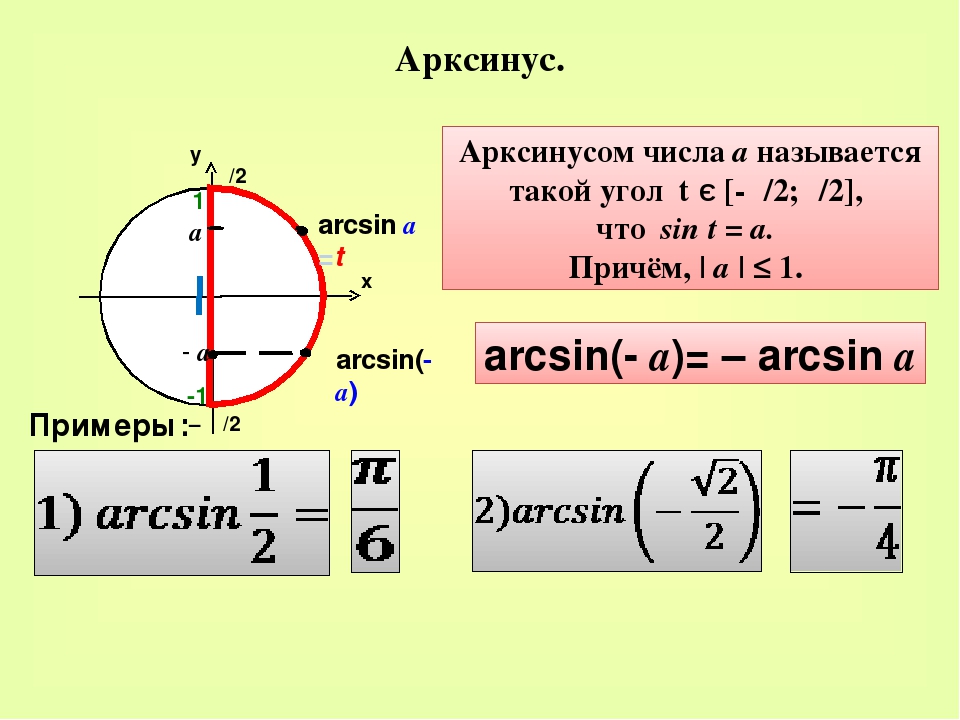 д. - относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. - относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Функции арксинуса, арккосинуса и арктангенса
Функции арксинуса, арккосинуса и арктангенсаФункция арксинуса
Справочная информация: Арксинусная функция - это , обратный синусоидальной функции. (до тех пор, пока функция синуса ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.
(до тех пор, пока функция синуса ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.Напомним, что функция синуса принимает угол x на входе и возвращает синус этого угла на выходе:
Например, если вход 30 °, то выход 0,5. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 на входе и вернуть 30 ° на выходе. Но есть проблема. Обратите внимание, что есть много углов с синусом 0,5: Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное отображение будет один ко многим и, следовательно, не будет удовлетворять Требование "одно значение диапазона" чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется Arcsine (с заглавной A и сокращением Arcsin), а функция называется arcsine (со строчной буквой «а» и сокращением arcsin). Вот как они определены:Определение: Арксинус x , обозначенный как Arcsin ( x ), определяется как « набор всех углов , синус которых равен x ».
 Это отношение «один ко многим». Вот пример: Определение: Арксинус x , обозначенный arcsin ( x ), определяется как определяется как
‘ один угол между −π / 2 и + π / 2 радиан
(или от -90 ° до + 90 °), синус которого равен x ’.
Это взаимно однозначная функция . Вот пример: Определение: Из всех значений, возвращаемых отношением Арксинус,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения Арксинуса.(Примером может служить значение 30 °, показанное выше красным.)
Это отношение «один ко многим». Вот пример: Определение: Арксинус x , обозначенный arcsin ( x ), определяется как определяется как
‘ один угол между −π / 2 и + π / 2 радиан
(или от -90 ° до + 90 °), синус которого равен x ’.
Это взаимно однозначная функция . Вот пример: Определение: Из всех значений, возвращаемых отношением Арксинус,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения Арксинуса.(Примером может служить значение 30 °, показанное выше красным.)График: Красная кривая на графике справа - это функция арксинуса. Обратите внимание, что для любых x между -1 и +1 он возвращает один значение от −π / 2 до + π / 2 радиан.
Если мы добавим серую кривую к красной кривой, мы получим график
Отношение арксинуса. Вертикальная линия, проведенная где-то между x =
−1 и +1 коснутся этой кривой во многих местах, и это означает, что
отношение Арксинус вернет много значений.
На этом графике угол y измеряется в радианах. Если вы хотите измерить y в градусе , тогда просто измените вертикальный масштаб, чтобы что y изменяется от −360 ° до 360 ° вместо от От −2π до 2π радиан; в остальном форма графика не изменится.
Если сравнить график арксинуса с графиком синуса тогда вы видите, что одно можно получить от другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арксинуса составляет от -1 до +1 включительно, а диапазон - от От −π / 2 до π / 2 радиан включительно (или от −90 ° до 90 °).
Функция арксинуса может быть распространяется на комплексные числа, в которых если домен состоит из комплексных чисел.
Специальные значения функции арксинуса (Нажмите здесь, чтобы узнать больше)
Решение уравнения sin ( θ ) = c для θ с помощью арксинуса и Arcsin e
Предположим, что угол θ неизвестен, но его синус известен
быть c . Тогда для определения этого угла необходимо решить это уравнение
для θ :
Тогда для определения этого угла необходимо решить это уравнение
для θ :
sin ( θ ) = cЕсли это, скажем, простая задача прямоугольного треугольника, и мы знаем, что угол θ должен быть где-то между 0 и 90 °, тогда решение - это единственное значение:
θ = arcsin ( c )С другой стороны, если это более сложная проблема, и нам нужно найти все возможные углы , синус которых равен c , тогда решение это весь набор значений:
θ = Арксин ( c )Решения в этих двух случаях следуют непосредственно из определения функции арксинуса и отношения арксинус.Обратите внимание: если c больше 1 или меньше -1, то есть нет реальных решений. Однако есть сложные решения.
Оценка Arcsin ( c )
Если c - число, тогда весь набор значений Arcsin ( c ) можно найти, используя следующую процедуру.
 См. График справа
где точки - желаемые значения.
См. График справа
где точки - желаемые значения.- Первое значение (главное значение), обозначенное θ PV , находится как вычисление arcsin ( c ) с помощью калькулятора или Algebra Coach.
- Второе значение, называемое θ 2 , находится по
используя симметрию кривой арксинуса. Обратите внимание, что две синие стрелки на
граф имеют одинаковую длину. Это означает, что θ 2 настолько же меньше π, сколько θ PV больше нуля. В форме формулы:
θ 2 = π - θ PV
(Щелкните здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Все остальные значения выше и ниже этих двух значений можно найти из этих двух значений, добавив или вычитая кратные 2π. Если мы используем целое число n для подсчета которое кратно другим значениям можно получить из этой формулы: Например, если мы положим n = −1, то получим значения для две самые низкие точки на графике.
- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арксинуса в Algebra Coach
- Введите arcsin (x) в текстовое поле, где x - аргумент.Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan . (Параметр возвращает главное значение Параметр возвращает одно значение; не оценивает параметр полезен, если вам нужны все значения отношения Arc - но вам придется вычислить их самостоятельно.)
- Установите опцию с точной / плавающей запятой .(Точный режим позволяет используйте специальные значения.)
- Установите режим градус / радиан .
- Установить p не представляет собой вариант π. (Если вы хотите, чтобы арксинус возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексное число , если вы хотите иметь возможность оценивать арксинус комплексного числа или числа больше 1.
- Нажмите кнопку «Упростить».
Алгоритм для функции арксинуса
Нажмите здесь чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арксинуса.
Функция арккосинуса
Справочная информация: Функция арккосинуса - это , обратный функции косинуса. (при условии, что функция косинуса ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.Напомним, что функция косинуса принимает угол x на входе и возвращает косинус этого угла на выходе:
Например, если вход 60 °, то выход 0,5. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 на входе и вернуть 60 ° в качестве вывода. Но есть проблема. Обратите внимание, что есть много углов, косинус которых равен 0,5: Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное отображение будет один ко многим и, следовательно, не будет удовлетворять Требование "одно значение диапазона" чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется Arccosine (с заглавной A и аббревиатурой Arccos), а функция называется arccosine (со строчной буквой «а» и сокращением arccos). Вот как они определены:Определение: Арккосинус x , обозначаемый Arccos ( x ), определяется как ‘ набор всех углов , косинус которых равен x ’.Это отношение «один ко многим». Вот пример: Определение: Арккосинус x , обозначенный arccos ( x ), определяется как ‘ один угол между 0 и π радиан (или от 0 ° до 180 °), косинус которого равен x ’. Это взаимно однозначная функция . Вот пример: Определение: Из всех значений, возвращаемых отношением Арккосинус, тот, который совпадает со значением, возвращаемым функцией arccosine называется главным значением отношения Арккосинуса.(Пример - значение 60 °, показанное выше красным.)
График: Красная кривая на графике справа - это функция арккосинуса. Обратите внимание, что для любых x между -1 и +1 он возвращает один значение от 0 до + π радиан.
Если мы добавим серую кривую к красной кривой, мы получим график Отношение арккосинуса. Вертикальная линия, проведенная где-то между x = −1 и +1 коснутся этой кривой во многих местах, и это означает, что отношение Арккосинус вернет много значений.
На этом графике угол y измеряется в радианах. Если вы хотите измерить y в градусе , тогда просто измените вертикальный масштаб, чтобы что y изменяется от −360 ° до 360 ° вместо от От −2π до 2π радиан; в остальном форма графика не изменится.
Если сравнить график арккосинуса с графиком косинуса тогда вы видите, что одно можно получить от другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область функции арккосинуса составляет от -1 до +1 включительно, а диапазон - от От 0 до π радиан включительно (или от 0 ° до 180 °).
Функция арккосинуса может быть распространяется на комплексные числа, в которых если домен состоит из комплексных чисел.
Специальные значения функции арккосинуса (Щелкните здесь, чтобы узнать больше)
Решение уравнения cos ( θ ) = c для θ с помощью арккосинуса и Arccos ine
Предположим, что угол θ неизвестен, но известен его косинус быть c .Тогда для определения этого угла необходимо решить это уравнение для θ :
cos ( θ ) = cЕсли это, скажем, простая задача прямоугольного треугольника, и мы знаем, что угол θ должен быть где-то между 0 и 90 °, тогда решение - это единственное значение:
θ = arccos ( c )С другой стороны, если это более сложная проблема, и нам нужно найти все возможные углы , косинус которых равен c , тогда решение это весь набор значений:
θ = Arccos ( c )Решения в этих двух случаях следуют непосредственно из определения функции арккосинуса и отношения арккосинуса.Обратите внимание: если c больше 1 или меньше -1, то есть нет реальных решений. Однако есть сложные решения.
Оценка Arccos ( c )
Если c - число, то весь набор значений Arccos ( c ) можно найти, используя следующую процедуру. См. График справа где точки - желаемые значения.
- Первое значение (главное значение), обозначенное θ PV , находится как оценка arccos ( c ) с помощью калькулятора или Algebra Coach.
- Второе значение, называемое θ 2 , находится по
используя симметрию кривой Арккосинуса. Обратите внимание, что две синие стрелки на
граф имеют одинаковую длину. Это означает, что θ 2 настолько же меньше 2π, сколько θ PV больше нуля. В форме формулы:
θ 2 = 2 π - θ PV
(Щелкните здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Все остальные значения выше и ниже этих двух значений можно найти из этих двух значений, добавив или вычитая кратные 2π. Если мы используем целое число n для подсчета которое кратно другим значениям можно получить из этой формулы: Например, если мы положим n = −1, то получим значения для две самые низкие точки на графике.
- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арккосинуса в Algebra Coach
- Введите arccos (x) в текстовое поле, где x - аргумент.Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan . (Параметр возвращает главное значение Параметр возвращает одно значение; не оценивает параметр полезен, если вам нужны все значения отношения Arc - но вам придется вычислить их самостоятельно.)
- Установите опцию с точной / плавающей запятой .(Точный режим позволяет используйте специальные значения.)
- Установите режим градус / радиан .
- Установить p не представляет собой вариант π. (Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексное число , если вы хотите иметь возможность оценивать арккозин комплексного числа или числа больше 1.
- Нажмите кнопку «Упростить».
Алгоритм для функции арккосинуса
Нажмите здесь чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арккосинуса.
Функция арктангенса
Фон: Функция арктангенса - это , обратный функции тангенса (при условии, что касательная функция ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.Напомним, что функция тангенса принимает угол x в качестве входных данных и возвращает тангенс этого угла в качестве выходных данных:
Например, если на входе 45 °, то на выходе будет 1,0. Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и вернуть 45 ° в качестве вывода. Но есть проблема. Обратите внимание, что существует много углов, тангенс которых равен 1,0: Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное отображение будет один ко многим и, следовательно, не будет удовлетворять Требование "одно значение диапазона" чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арктангенсом (с заглавной буквы A и сокращением арктангенс), а функция называется арктангенсом (со строчной буквой «а» и аббревиатурой arctan). Вот как они определяются:Определение: Арктангенс x , обозначаемый Arctan ( x ), определяется как ‘ набор всех углов , тангенс которых равен x ’.Это отношение «один ко многим». Вот пример: Определение: Арктангенс x , обозначаемый arctan ( x ), определяется как ‘ один угол между −π / 2 и + π / 2 радиан (или от -90 ° до + 90 °), касательная которого составляет x ’. Это взаимно однозначная функция . Вот пример: Определение: Из всех значений, возвращаемых отношением арктангенса, тот, который совпадает со значением, возвращаемым функцией арктангенса называется главным значением отношения арктангенса.(Пример - значение 45 °, показанное выше красным.)
График: Красная кривая на графике справа - это функция арктангенса. Обратите внимание, что для любых x он возвращает один значение от −π / 2 до + π / 2 радиан.
Если мы добавим серые кривые к красной кривой, мы получим график Отношение арктангенса. Вертикальная линия, проведенная в любом месте коснется этого набора кривых во многих местах, и это означает, что отношение арктангенса вернет много значений.
На этом графике угол y измеряется в радианах. Если вы хотите измерить y в градусе , тогда просто измените вертикальный масштаб, чтобы что y изменяется от -180 ° до 180 ° вместо От −π до π радиан; в остальном форма графика не изменится.
Если сравнить график арктангенса с графиком касательного тогда вы видите, что одно можно получить от другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область функции арктангенса - все действительные числа, а диапазон - от От −π / 2 до π / 2 без учета радиан (или от −90 ° до 90 °).
Функция арктангенса может быть распространяется на комплексные числа, в которых если домен состоит из комплексных чисел.
Специальные значения функции арктангенса (Щелкните здесь, чтобы получить более подробную информацию)
Решение уравнения tan ( θ ) = c для θ с использованием арктангенса и арктангенса
Предположим, что угол θ неизвестен, но известен его тангенс. быть c .Тогда для определения этого угла необходимо решить это уравнение для θ :
tan ( θ ) = cЕсли это, скажем, простая задача прямоугольного треугольника, и мы знаем, что угол θ должен быть где-то между 0 и 90 °, тогда решение - это единственное значение:
θ = арктангенс ( c )С другой стороны, если это более сложная проблема, и нам нужно найти все возможные углы , тангенс которых равен c , тогда решение это весь набор значений:
θ = Арктангенс ( c )Решения в этих двух случаях непосредственно следуют из определений функции арктангенса и отношения арктангенса.
Оценка Arctan ( c )
Если c - число, то весь набор значений Arctan ( c ) можно найти, используя следующую процедуру. См. График справа где точки - желаемые значения.
- Первое значение (главное значение), обозначенное θ PV , находится как оценка arctan ( c ) с помощью калькулятора или Algebra Coach.
- Все остальные значения выше и ниже этого значения можно найти
используя тот факт, что соседние значения удалены друг от друга на расстояние π.Если мы используем целое число n для подсчета числа, кратного π, то другое
значения могут быть получены из этой формулы:
θ = θ PV + π n
(Щелкните здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:
θ = θ PV + 180 ° · n
Как использовать функцию арктангенса в Algebra Coach
- Введите arctan (x) в текстовое поле, где x - аргумент.Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan . (Параметр возвращает главное значение Параметр возвращает одно значение; не оценивает параметр полезен, если вам нужны все значения отношения Arc - но вам придется вычислить их самостоятельно.)
- Установите опцию с точной / плавающей запятой .(Точный режим позволяет используйте специальные значения.)
- Установите режим градус / радиан .
- Установить p не представляет собой вариант π. (Если вы хотите, чтобы арктангенс возвращал специальные значения в радианах затем включите это.)
- Включите комплексное число , если вы хотите иметь возможность оценивать арктангенс комплексного числа.
- Нажмите кнопку «Упростить».
Алгоритм для функции арктангенса
Нажмите здесь чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арктангенса.

 Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
 Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Затем, как и в предыдущем варианте, жмем на кнопку «OK». 0
Cosinus 6.12323399573677e-17
Tangent 1.63312393531954e+16
0
Cosinus 6.12323399573677e-17
Tangent 1.63312393531954e+16
 0
0

 Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
 0,78539816 0,2
0,78539816 0,2 участок (in_array, out_array1,
участок (in_array, out_array1,  22464680e-16 6.42660977e-01 2.18969456e + 00 -6.95515277e + 00
-1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00
6.95515277e + 00 -2.18969456e + 00 -6.42660977e-01 -1.22464680e-16]
out_arraywith arctan: [1.22464680e-16 6.42660977e-01 2.18969456e + 00-6.95515277e + 00
-1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00
6.95515277e + 00 -2.18969456e + 00-6.42660977e-01-1.22464680e-16]
22464680e-16 6.42660977e-01 2.18969456e + 00 -6.95515277e + 00
-1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00
6.95515277e + 00 -2.18969456e + 00 -6.42660977e-01 -1.22464680e-16]
out_arraywith arctan: [1.22464680e-16 6.42660977e-01 2.18969456e + 00-6.95515277e + 00
-1.15406152e + 00 -2.93626493e-01 2.93626493e-01 1.15406152e + 00
6.95515277e + 00 -2.18969456e + 00-6.42660977e-01-1.22464680e-16] 
 Prec = 50
def factorial (n):
если п
Prec = 50
def factorial (n):
если п