Опубликовано Как посчитать арксинус
Арксинус относится к группе обратных тригонометрических функций. При измерении плоских углов его максимальное значение не может быть больше 90°, что соответствует половине числа Пи, если измерять угол в радианах. Нижняя граница области значений соответствует -90° или половине числа Пи в отрицательную сторону. Область определений (это все допустимые аргументы функции) ограничивается значениями от -1 до +1.Используйте, например, поисковую систему Nigma для вычисления значения арксинуса. Этот поисковик имеет встроенный калькулятор, сопряженный с конвертером единиц измерений. Чтобы вычислить, например, значение арксинуса от числа 0.387, перейдите по адресу http://nigma.ru и введите в поле поискового запроса «(arcsin 0.387) в градусах». После отправки запроса поисковик покажет результат вычисления. Если этот же результат нужно получить в радианах, то единицы измерения указывать не нужно: «arcsin 0.387». Поисковая система Google имеет схожий калькулятор, но при необходимости получить значение арксинуса в градусах эту операцию придется производить в два шага — сначала выяснить значение в радианах, затем попросить Google перевести полученное число из радиан в градусы.
Воспользуйтесь встроенным в операционную систему программным калькулятором, если не доверяете поисковикам или не имеете доступа в интернет. Этот калькулятор проще всего открыть через диалог запуска программ — раскройте меню на кнопке «Пуск», выберите пункт «Выполнить», введите команду calc и щелкните кнопку «OK».
Переключите интерфейс калькулятора в «Инженерный» или «Научный» вариант, раскрыв в его меню раздел «Вид» и выбрав соответствующий пункт. Это необходимо сделать, так как в базовом варианте интерфейса нет кнопок для работы с тригонометрическими функциями.
Введите значение аргумента функции, а затем выберите единицы измерения, в которых должен быть получен результат вычисления. Для этого надо поставить отметку в одном из трех полей (градусы, радианы, рады) под окном ввода числового значения.
Поставьте отметку в чекбоксе с надписью Inv и щелкните кнопку с меткой sin — в стандартных вычислениях она соответствует функции «синус», но при активированной установке Inv все тригонометрические функции заменяются обратными.
Калькулятор рассчитает и отобразит значение арксинуса от веденного вами аргумента.
Функция ASIN — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ASIN в Microsoft Excel.
Описание
Возвращает арксинус числа. Арксинус числа — это угол, синус которого равен числу. Угол определяется в радианах в диапазоне от -пи/2 до пи/2.
Синтаксис
ASIN(число)
Аргументы функции ASIN описаны ниже.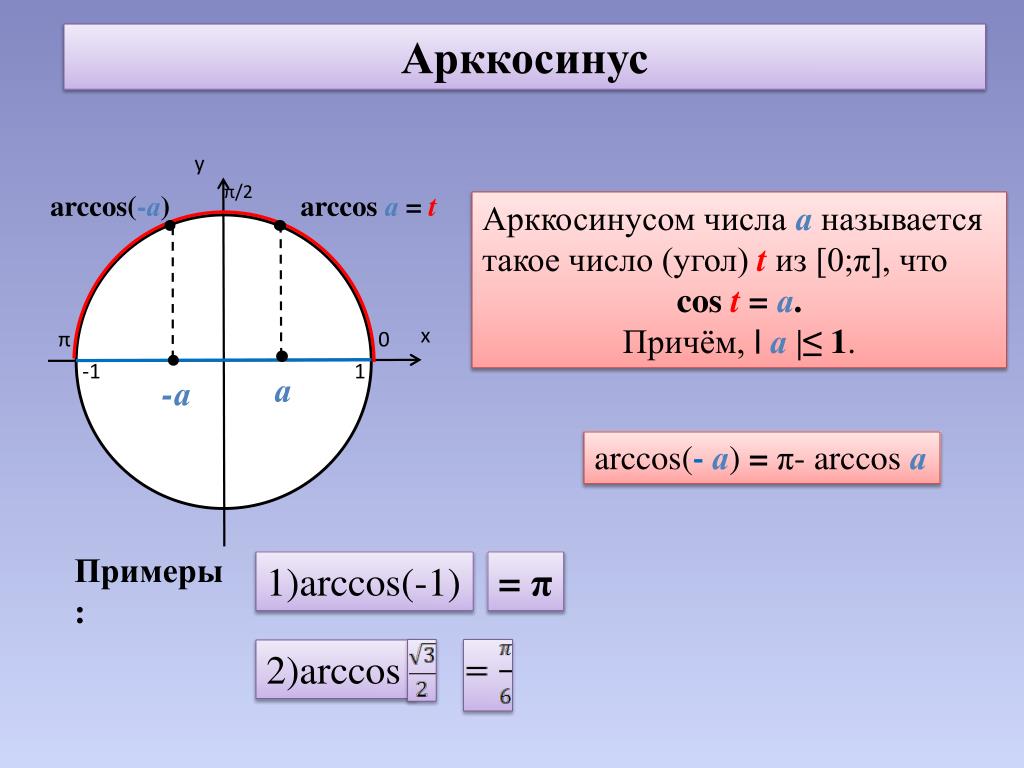
Замечания
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=ASIN(-0,5) |
Арксинус числа -0,5 в радианах, -пи/6 (-0,5236) |
-0,523598776 |
|
=ASIN(-0,5)*180/ПИ() |
Арккосинус числа -0,5 в градусах |
-30 |
|
=ГРАДУСЫ(ASIN(-0,5)) |
Арккосинус числа -0,5 в градусах |
-30 |
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Арксинус.
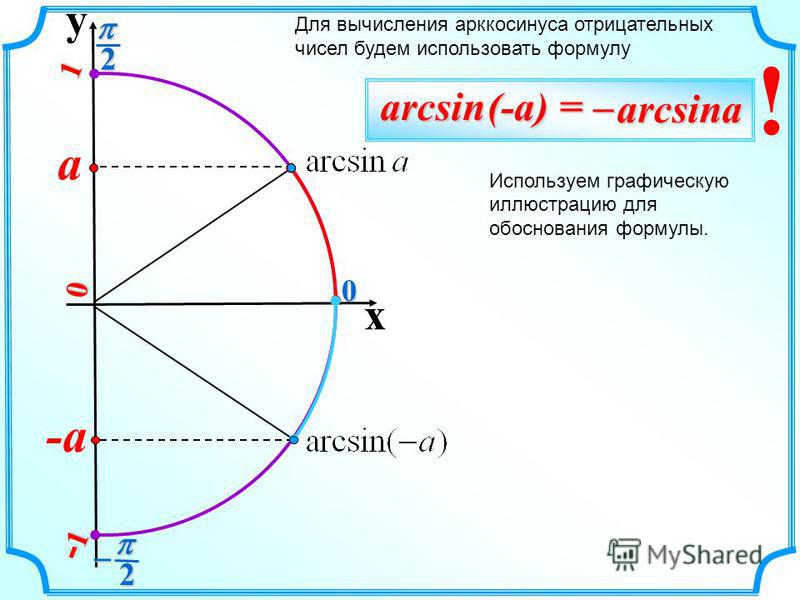Решение простейших уравнений с синусом. Часть 2 Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т.е.
\(\arcsin a=x\) \(<=>\) \(\sin x=a\)
Примеры:
\(\arcsin{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin \frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)
\(\arcsin 1=\frac{π}{2}\) потому что \(\sin\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)
\(\arcsin 0=0\) потому что \(\sin 0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)
\(\arcsin\sqrt{3}\) – не определен, потому что \(\sqrt{3}>1\)
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:
Как вычислить арксинус?
Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?
Например, вычислите значение арксинуса:
а) \(\arcsin(-\frac{1}{2})\)
б) \(\arcsin(\frac{\sqrt{3}}{2})\)
в) \(\arcsin(-1)\)
а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\).
Ответ очевиден:
\(\arcsin(-\frac{1}{2})=-\frac{π}{6}\)
б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).
\(\arcsin(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)
в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin x=-1\), \(x=\) ?
\(\arcsin(-1)=-\frac{π}{2}\)
Тригонометрический круг со всеми стандартными арксинусами:
Зачем нужен арксинус? Решение уравнения \(\sin x=a\)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin x=\frac{1}{2}\).
Это не вызывает затруднений:
\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)
Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.
А теперь решите уравнение: \(\sin x=\frac{1}{3}\).
Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin\frac{1}{3}\).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right.\) Без арксинусов решить уравнение \(\sin x=\frac{1}{3}\) не получилось бы.
Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{3}}\).
Решение:
Ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{2}}\).
Решение:
Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента.
\(\arcsin \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)
Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).
Ответ: \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{7}{6}\).
Решение:
И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса.
Ответ: решений нет.
Думаю, вы уловили закономерность.
Если \(\sin x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
\(\arcsin({-a})=-\arcsin a\)
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:
Примеры:
\(\arcsin(-0,7)=-\arcsin 0,7\)
\(\arcsin(-\frac{\sqrt{3}}{2})=-\arcsin\frac{\sqrt{3}}{2}=-\frac{π}{6}\)
\(\arcsin(-\frac{\sqrt{7}}{2}) \neq -\arcsin\frac{\sqrt{7}}{2}\)
Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).
Пример. Решите тригонометрическое уравнение: \(\sin x=-\frac{1}{\sqrt{3}}\).
Решение:
Можно воспользоваться готовой формулой и написать:
\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
Но я фанатка круга, поэтому:
Ответ: \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.
Смотрите также:
Синус
Тригонометрические уравнения
Арксинус, формула, график функции арксинус, урок и презентация
Дата публикации: .
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения. Арксинус (PPTX)
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арксинуса.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G.
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.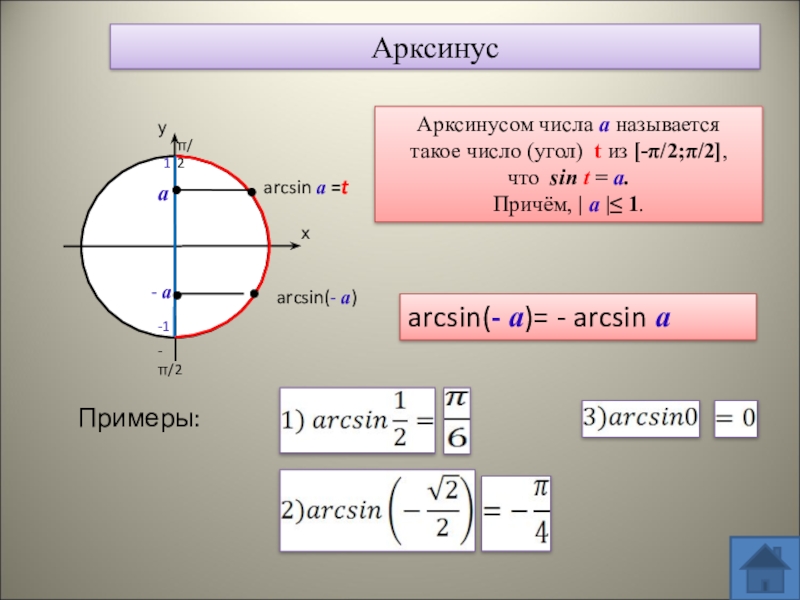
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Таблица значений арксинуса
Таблица значений синуса
Таблица значений арксинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2 ) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2 )= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1)n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности.
Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
дифференциал / Вычислить arcsin / Математика
Приближённые вычисления через дифференциал — вещь достаточно распространённая, и не слишком сложная. Хорошо, что Вы вовремя «спохватились» и уточнили смысл задания, а то бы вам рассказали о сложных методах, которые в данном случае не нужны.
Не очень хорошо здесь то, что не задана требуемая точность приближения. Ведь для «малых» величин имеет место приближённое равенство $%\arcsin x\approx x$%, и точность здесь достаточно неплохая (примерно 0.
005). Возможно, оно здесь и имелось в виду, но об этом чуть позже.
Для начала — описание самой идеи. У нас есть функция, мы знаем её значение в какой-то точке $%x_0$%, и хотим узнать значение в «близкой» точке $%x+\Delta x$%, где $%\Delta x$% — маленькая величина. Поскольку производная является пределом отношения приращения функции к приращению аргумента, то при «малых» значениях $%\Delta x$% имеет место приближённое равенство $%\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\approx f'(x_0)$%. Это даёт приближённую формулу для значения функции в точке: $%f(x_0+\Delta x)\approx f(x_0)+f'(x_0)\Delta x$%.
Вместо $%\Delta x$% часто пишут $%dx$%, и формулу записывают как $%\Delta f\approx df$%: приращение функции для малых значений аргумента приближённо равно дифференциалу функции. Под которым, по определению, понимается произведение производной функции на дифференциал аргумента: $%df=f’\,dx$%. Впрочем, всё это есть в учебниках (у нас было даже в школьном).
Приведу пример, как можно пользоваться приближённой формулой.
2}}$%; в нуле это даёт $%f'(x_0)=1$%. Тогда $%\arcsin0.3=f(0.3)=f(x_0+\Delta x)\approx f(x_0)+f'(x_0)\Delta x=0+1\cdot0.3=0.3$%. Это чуть менее интересно нежели в предыдущем примере, то точность и здесь неплохая.
отвечен 5 Дек ’16 0:37
Вывод формул обратных тригонометрических функций
Основные формулы
Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых.
Свойства обратных функций можно разбить на две группы.
В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x (–∞ < x < +∞)
ctg(arcctg x) = x (–∞ < x < +∞)
Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin x) = x при
arccos(cos x) = x при
arctg(tg x) = x при
arcctg(ctg x) = x при
Если переменная x не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n — целое):
sin x = sin(–x–π); sin x = sin(π–x); sin x = sin(x+2πn);
cos x = cos(–x); cos x = cos(2π–x); cos x = cos(x+2πn);
tg x = tg(x+πn); ctg x = ctg(x+πn)
Например, если известно, что то
arcsin(sin x) = arcsin(sin( π — x )) = π — x .
Легко убедиться, что при π – x попадает в нужный интервал.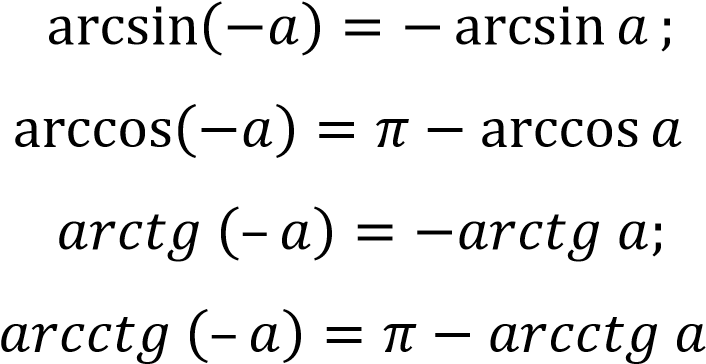
Для этого умножим на –1: и прибавим π: или Все правильно.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Поскольку то умножив на –1, имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x
Выражение арксинуса через арккосинус и арктангенса через арккотангенс
Выразим арксинус через арккосинус.
Формула справедлива при Эти неравенства выполняются, поскольку
Чтобы убедиться в этом, умножим неравенства на –1: и прибавим π/2: или Все правильно.
Итак,
Аналогично выражаем арктангенс через арккотангенс.
Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот
Поступаем аналогичным способом.
Формулы суммы и разности
Аналогичным способом, получим формулу суммы арксинусов.
Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin x, Y = arcsin y. Формула применима при
. Далее замечаем, что, поскольку arcsin(–x) = – arcsin x, arcsin(–y) = – arcsin y, то при разных знаках у x и y, X и Y также разного знака и поэтому неравенства выполняются. Условие различных знаков у x и y можно написать одним неравенством: . То есть при формула справедлива.
Теперь рассмотрим случай x > 0 и y > 0, или X > 0 и Y > 0. Тогда условие применимости формулы заключается в выполнении неравенства: . Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0, до π, то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ; то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin X = sin arcsin x = x:
;
;
;
.
Итак, полученная формула справедлива при или .
Теперь рассмотрим случай x > 0, y > 0 и x2 + y2 > 1. Здесь аргумент синуса принимает значения: . Его нужно привести к интервалу области значения арксинуса :
.
Итак,
при и.
Заменив x и y на – x и – y, имеем
при и.
Выполняем преобразования:
при и.
Или
при и.
Итак, мы получили следующие выражения для суммы арксинусов:
при или ;
при и ;
при и .
Аналогичным способом получаются остальные формулы:
при или ;
при и ;
при и ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при .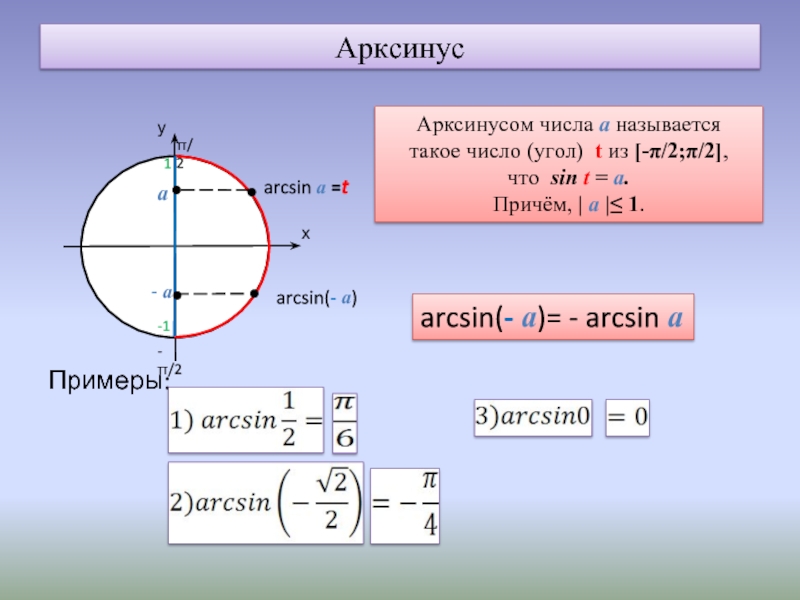
Автор: Олег Одинцов. Опубликовано:
КалькуляторArcsin. Нахождение обратной функции синуса.
С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной.И так, чего же ты ждешь?
Что такое арксинус?
Арксинус — это функция, обратная синусоиде. Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале.
Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0.Следовательно, если кто-то хочет вычислить arcsin (0), ответ может быть 0, 2π (360 °) или -π (-180 °), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением .
| Аббревиатура | Определение | Домен arcsin x для реального результата | Диапазон обычных основных значений |
|---|---|---|---|
| arcsin (x) sin -1 x, asin | х = грех (у) | -1 ≤ х ≤ 1 | -π / 2 ≤ y ≤ π / 2 -90 ° ≤ y ≤ 90 ° |
Arcsin (x) — наиболее распространенное обозначение, так как sin -1 x может привести к путанице (потому что sin -1 x ≠ 1 / sin (x)).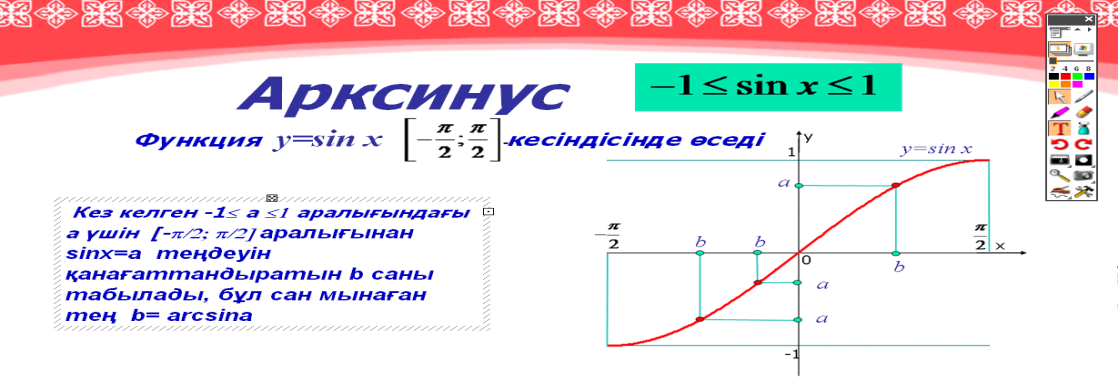
Аббревиатура asin обычно используется в языках программирования.
График arcsin x
Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса:
| х | arcsin (x) | График | |
|---|---|---|---|
| ° | рад | ||
| -1 | -90 ° | -π / 2 | Компьютерщик 3, CC BY-SA 4. 0 через Wikimedia Commons |
| -√3 / 2 | -60 ° | -π / 3 | |
| -√2 / 2 | -45 ° | -π / 4 | |
| -1/2 | -30 ° | -π / 6 | |
| 0 | 0 ° | 0 | |
| 1/2 | 30 ° | π / 6 | |
| √2 / 2 | 45 ° | π / 4 | |
| √3 / 2 | 60 ° | π / 3 | |
| 1 | 90 ° | π / 2 | |
Хотите знать, откуда взялся этот график arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x:
Jaro.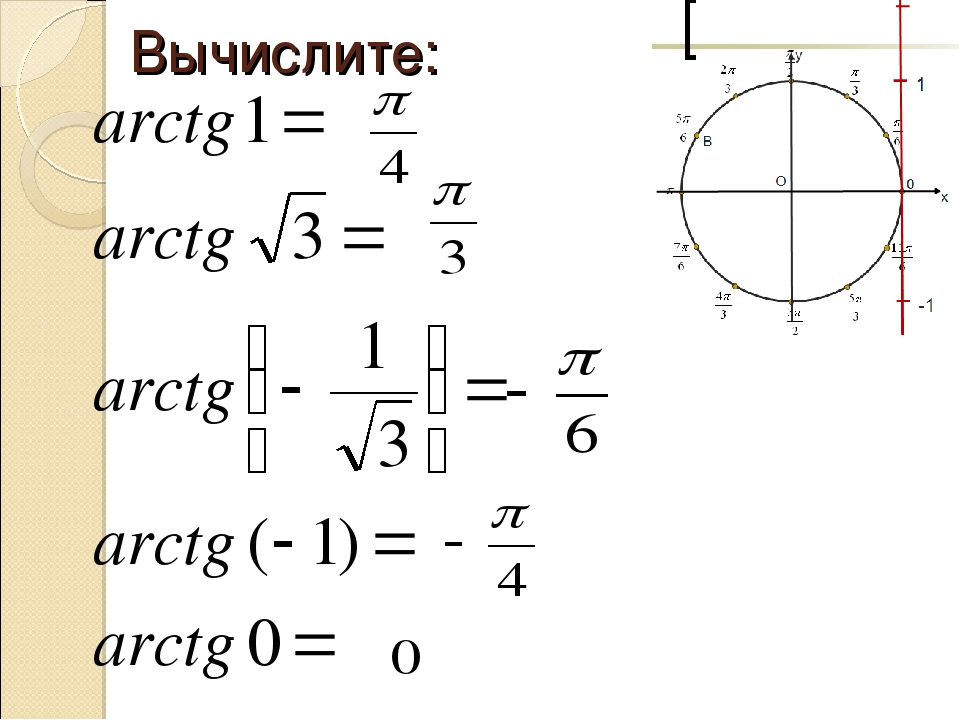
p CC BY-SA 3.0, через Wikimedia Commons Обратный синус, тригонометрические функции и другие отношения
Связь между тригонометрическими функциями и арксинусом может помочь вам еще лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка.
Просто быстрое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, принимает отношение противоположности / гипотенузы (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что:
- Синус:
sin (arcsin (x)) = x - Косинус:
cos (arcsin (x)) = √ (1-x²) - Касательная:
tan (arcsin (x)) = x / √ (1-x²)
Другие полезные отношения с арксинусом:
-
arcsin (x) = π / 2 - arccos (x) -
arcsin (-x) = -arcsin (x)
Иногда также нужны интеграл и производная от arcsin:
интеграл от arcsin:
arcsin (x) dx = x arcsin (x) + √ (1 - x²) + Cпроизводная от arcsin:
d / dx arcsin (x) = 1 / √ (1 - x²)где x ≠ -1, 1
Пример использования калькулятора arcsin
Арксинус — полезная функция e.
грамм. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус:
- для α:
sin (α) = a / c, поэтому α = arcsin (a / c) - для β:
sin (β) = b / c, поэтому β = arcsin (b / c)
Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:
- Введите значение, по которому вы хотите найти арксинус .В нашем случае это 6/10. Таким образом, вы можете ввести значение 0,6, но форма 6/10 также будет работать. Просто помните, что значение должно быть от -1 до 1.
- И … все! Калькулятор arcsin выполнил свою работу, и вы нашли арксинус своего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °
Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника.
Тригонометрическая функция arcsin () — обратный синус — определение математического слова
Тригонометрическая функция arcsin () — обратный синус — определение математического слова — Math Open Reference Функция arcsin является обратной функцией синуса.
Возвращает угол, синус которого является заданным числом.
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arcsin может быть помечена как asin, а иногда sin -1 .) Итак, обратное к греху — это arcsin и т. Д. Когда мы видим «arcsin A», мы понимаем его как «угол, грех которого равен A».
| sin30 = 0,5 | Означает: синус 30 градусов равен 0,5 |
| arcsin 0,5 = 30 | Означает: Угол, грех которого равен 0,5, равен 30 градусам. |
См. Также Обратные функции — тригонометрия
Пример — использование arcsin для нахождения угла
На рисунке выше нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, грех которого равен 0,5, или формально: Используя калькулятор, чтобы найти arcsin 0,5, мы находим, что это 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же синус. Например, 45 ° и 360 + 45 ° будут иметь одинаковый синус. Подробнее об этом см. Обратные тригонометрические функции.
Чтобы решить эту проблему,
диапазон
обратных триггерных функций ограничены
таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и область значений arcsin
Напомним, что область определения функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.
Для y = arcsin x:
По соглашению диапазон arcsin ограничен от -90 ° до + 90 °. Итак, если вы используете калькулятор для решения, скажем, arcsin 0,55, из бесконечного числа возможностей он вернет 33,36 °, тот, который находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «Сброс» и «Скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arcsin, вычислите значение угла C из длин сторон
- Нажмите «показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор арксинуса онлайн — Расчет арксинуса — производная — первообразная
Описание:
Функция arcsin позволяет вычислять арксинус числа.Функция арксинуса является обратной функцией функции синуса.
arcsin онлайнОписание:
Функция arcsine является обратной функцией синусоидальная функция, это позволяет вычислить арксинус из числа онлайн .
Число, к которому вы хотите применить функцию арксинуса, должно принадлежать диапазону [-1,1].
- Расчет арксинуса
Чтобы вычислить арксинус числа, просто введите число и примените функция arcsin .2) `.
Функция arcsin позволяет вычислять арксинус числа. Функция арксинуса является обратной функцией функции синуса.
2)`Первообразная арксинус:
Калькулятор первообразной функции арксинуса.2) `
Предел арксинуса:
Калькулятор пределов позволяет вычислять пределы функции арксинуса.
Предел для arcsin (x) равен limit_calculator (`» arcsin «(x)`)
Арксинус обратной функции:
Функция, обратная арксинусу , является синусоидальной функцией, отмеченной как sin.
Графический арксинус:
Графический калькулятор может строить функцию арксинуса в интервале ее определения.
Свойство функции arcsine:
Функция арксинуса — нечетная функция.
Расчет онлайн с помощью arcsin (арксинус) Алгоритм вычисления
Arcsin — Техническое обсуждение
ТЕПЕРЬ мы обсуждаем!
Я полностью согласен с Dr.Джо — ВРЕМЯ играет ключевую роль в этих соревнованиях. Любой инженерный проект зависит от контроля всех четырех аспектов: методов, материалов, денег и людей. Когда время = деньги (или ресурсы — время ЦП, наличные деньги, пространство и т. Д.), Невозможно добиться успеха, если слишком большая часть ограниченного ресурса расходуется непродуктивными способами.
При этом, возможно, было бы интересным интеллектуальным упражнением (сейчас октябрь, а до новой игры осталось два месяца) посмотреть, МОЖЕТ ли этот алгоритм быть реализован, и КАК это можно сделать.Затем каждая команда может решить, стоит ли им это делать?
Во-первых, позвольте мне указать, что метод Ньютона не использует никаких расширений в ряды — это исключено для вычислений arcsin!
Я провел быстрый тест, чтобы увидеть, сколько циклов потребуется алгоритму, чтобы сойтись при различных значениях синуса от -1 до +1.
При +/- 1 четыре петли находятся с точностью до 0,001 от точного значения угла и десять петель с точностью до 1E-6.
При +/- 0.7, две петли сходились в пределах 2E-5.
Вблизи нуля алгоритм сходится почти к точному значению после первого цикла (как и следовало ожидать).
Значение в пределах 0,001 будет достаточно близким для любого соревнования — может быть, слишком близким. Какой механизм кто-то собирается изобрести, требуя большей точности, чем эта? Вы можете реализовать версию, которая просто проходит дважды, называет ее выполненной и каждый раз все равно приближается к цели. Я не знаю, что связано с функцией поиска с точки зрения использования ЦП, и как это можно сравнить с двухпетлевым вычислением.
А теперь самое интересное — как Pbasic реализует функции синуса и косинуса. Согласно BASIC Stamp Programming Manual 2.0c, операторы SIN и COS используют метод, который немного необычен — по крайней мере, для меня. Эти операторы принимают аргумент не в градусах или радианах, а в «двоичных радианах», иногда называемых «скобками».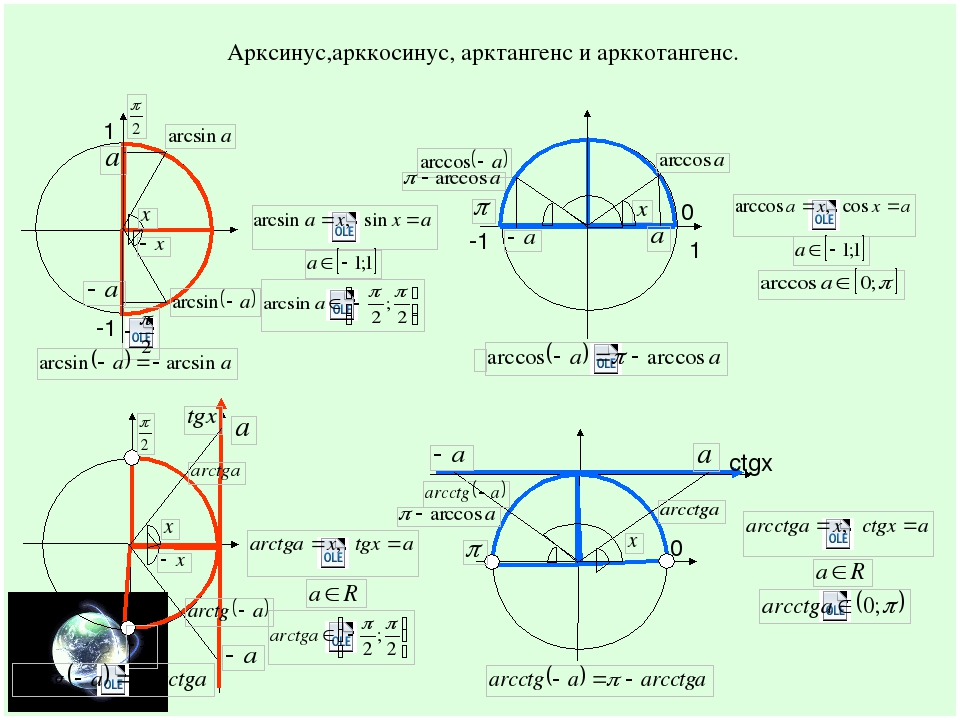
То есть они разбивают круг на 0–255 единиц (скобок), каждая из которых соответствует 1,406 градусам. Таким образом, аргумент, переданный функции SIN, представляет собой угол в скобках, выраженный целым числом от 0 до 255.
Значение, возвращаемое функцией, основано не на единичном круге, как в обычных значениях синуса в наших калькуляторах, а на круге радиуса 127. Мы часто видим это число на этом языке, не так ли? Результаты представлены в виде дополнения до двух для учета отрицательных значений. Функции возвращают целочисленные значения от -127 до +127.
Итак, при нулевом градусе получаем sin (0 brads) = 0; при 45 градусах sin (32 стержня) = 90. При 90 градусах sin (64 стержня) = 127; при 180 градусах sin (128 штифтов) = 0; а при 270 градусах sin (192 штифта) = -127.
Штифты X (180/128) = градусы и градусы X (128/180) = штифты.
Теперь, стоит ли применять этот метод — это еще раз другое. Похоже, это сработает, но это лишь 1/4 общей инженерной проблемы.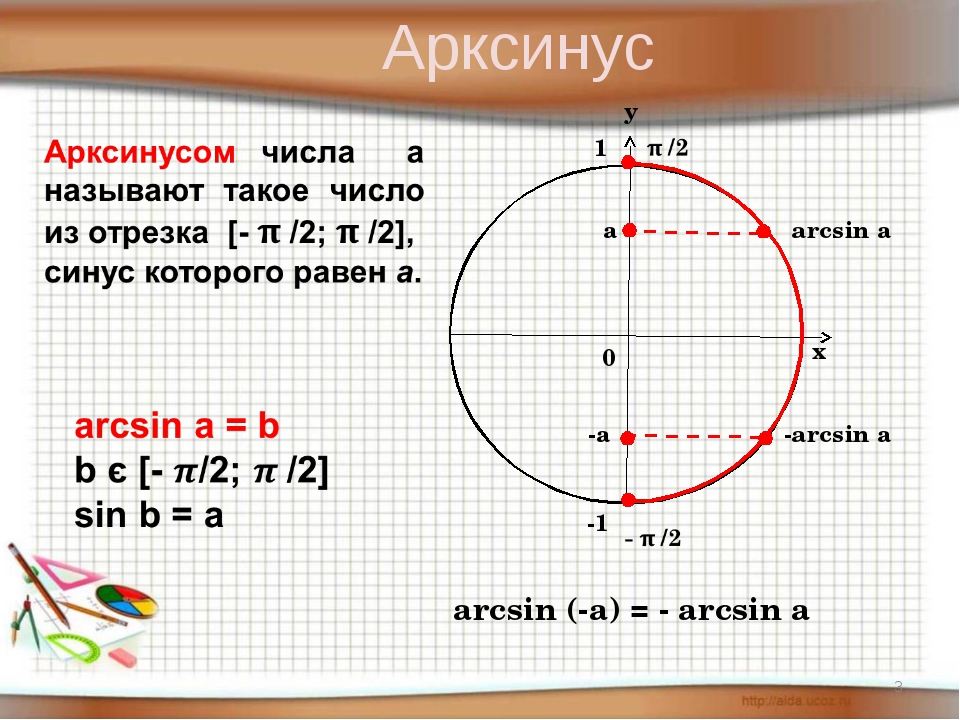
Есть ли у вашей команды люди, необходимые для этого, есть ли время, чтобы это сделать, дизайн, который может извлечь из этого выгоду? Не знаю — вы мне скажите.
Но разве вам не кажется, что умственное упражнение полезно? У этой проблемы много, и успешная реализация, по крайней мере, удовлетворит человека, который действительно ее выполнил.Это тоже часть ПЕРВОГО опыта, не так ли?
Это только мое очень скромное мнение. Если вы действительно хотите построить робота, который вовремя выйдет на поле, следуйте совету доктора Джо. Но, если в межсезонье вы ищете достойного интеллектуального соперника, попробуйте…
Опять же, дайте мне знать, как дела, и удачи.
Arcsin Calculator — Калькулятор обратного синуса
Введите значение от -1 до 1. Нажмите кнопку Calculate , чтобы получить арксинус с помощью калькулятора обратного синуса.
Калькулятор Arcsin находит угол треугольника в градусах и радианах для заданного значения.
Однако значение должно быть между -1 и 1 , чтобы получить арксин в градусах. Он преобразует синус в обратный, чтобы найти угол треугольника.
Что такое арксинус?
Арксинус x определяется как функция, обратная синусу x , когда -1≤x≤1. Это обратная тригонометрическая функция синуса.
Когда синус y равен x:
sin y = x
Тогда арксинус x равен обратной функции синуса x , что равно y:
arcsin x = sin -1 x = y
Как найти arcsin?
Чтобы вычислить арксинус треугольника, следуйте приведенному ниже примеру.
Пример:
x = 0,5
Arcsin (x) =?
Решение:
Шаг 1: Поместите значение x в функцию арксинуса.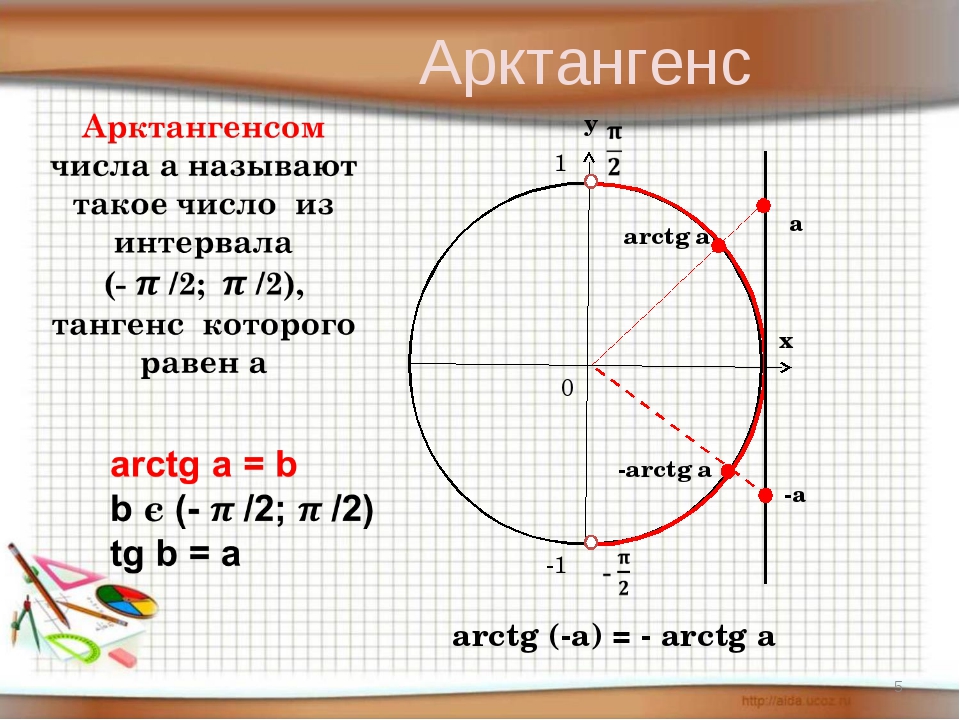
Arcsin (0,5)
Шаг 2: Возьмите sin -1 из 0,5 в калькуляторе (научный).
Arcsin (0,5) = sin -1 (0,5) = 30 °
Примечание: Arcsin 0 004 составляет
0 9023 °.
Таблица Arcsin
x | arcsin (x) в градусах | arcsin (x) в радианах |
| -1 02 90 ° | -π / 2 | |
-√3 / 2 | -60 ° | -π / 3 |
-√2 / 2 | -45 ° | -π / 4 |
-1/2 | -30 ° | -π / 6 |
0 | 0 ° | 0 |
1/2 | 30 ° | π / 6 |
√2 / 2 | 45 ° | π / 4 |
√3 / 2 | 60 ° | π / 3 |
1 | 90 ° | 20002 |
Arcsin бесплатный онлайн-калькулятор | Justfreetools
Тогда арксинус x равен функции обратного синуса x, которая равна y:
В настоящее время у нас есть около 940 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.
На этой странице Вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитования и лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и инструментах (как писать смайлы в Интернете и т. Д.)
В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Это наиболее часто используемые пользователями по всему миру.
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите даже малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Оценка обратной синусоидальной функции
Определения
Общие
Обратная синусоидальная функция, в современных обозначениях, записанная как arcsin (x), дает угол θ, так что:
\ sin \ theta = x
Поскольку значения синусоидальной функции находятся в диапазоне от -1 до 1, область аргумента x в функции arcsin ограничена тем же диапазоном: [-1,1].