Урок по теме «Угол. Прямой угол». 1-й класс
Вид урока: урок изучения и первичного закрепления новых знаний.
Цель: формирование общего понятия об угле, прямой угол.
Задачи:
Образовательная:
– учить различать прямой;
– учить строить прямой угол;
Развивающая:
– развивать познавательный интерес, умение сопоставлять и сравнивать, обобщать;
– развивать творческое мышление, внимание, воображение учащихся, интерес к
математике.
Воспитывающая – воспитание аккуратности, сплоченности, добросовестного отношения к труду.
Оборудование: таблички со словами: “геометрия, луч, вершина, сторона, прямой угол”; рисунки домиков, выставка книг Житомирский, Шеврин “Путешествие по стране Геометрии”, “Все обо всем”; для учеников: угольник, лист бумаги, компьютер; презентация Power Point.
Ход урока
I. Организационный момент.
Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте, Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
От кроем тетради и запишем число.
1) Минутка чистописания “Гусеница-растеряша”.
– Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это четные числа; каждое последующее число на 2 больше предыдущего). Допишите.
– Какие же числа растеряла гусеница? (2, 4, 6, 8, 10, 12, 14, 16 и т. д.)
II. Устный счет.
1) Индивидуальная работа по карточкам.
2) Игра “Математический баскетбол”.
– Любой из вас забьет гол, если правильно решит пример. (Дети по цепочке
решают примеры.
30 + 7
25 + 5
32 – 12
66 + 4
80 – 7
28 – 10
45 – 45
53 + 7
59 – 9
90 + 9
3) Решение задач.
– В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых деревьев росло в саду?
– Сестре 9 лет, брату 3 года. На сколько сестра будет старше брата через 5 лет?
– Посмотрите на фигуры. Как назвать их одним словом? Почему? (Геометрические фигуры.)
– Вы сказали “геометрические”? А от какого слово оно произошло? (Геометрия.)
– А что такое геометрия?
| ГЕОМЕТРИЯ |
– Табличка с этим словом вывешивается на доске.
– Слово геометрия пришло из греческого языка. “Ге” – земля “метрио” – мерить.
Геометрия – это раздел математики, в котором изучают фигуры, их
формы, положение предметов в пространстве.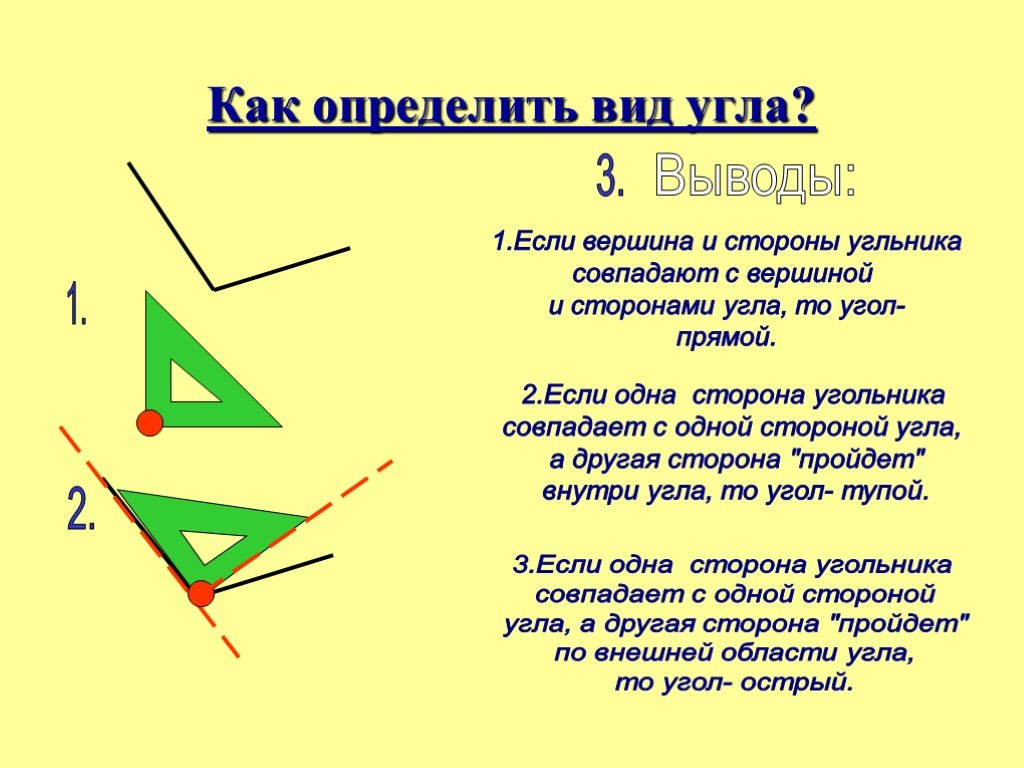
– На какие группы можно разделить все фигуры?
(В первую группу фигуры 1, 3, 5; во вторую – фигуры 2, 4.)
– Что общего между фигурами каждой группы? (I группа – есть углы; II группа – нет углов.)
III. Работа над новым материалом
Как вы думаете, о чем мы сегодня будем говорить?
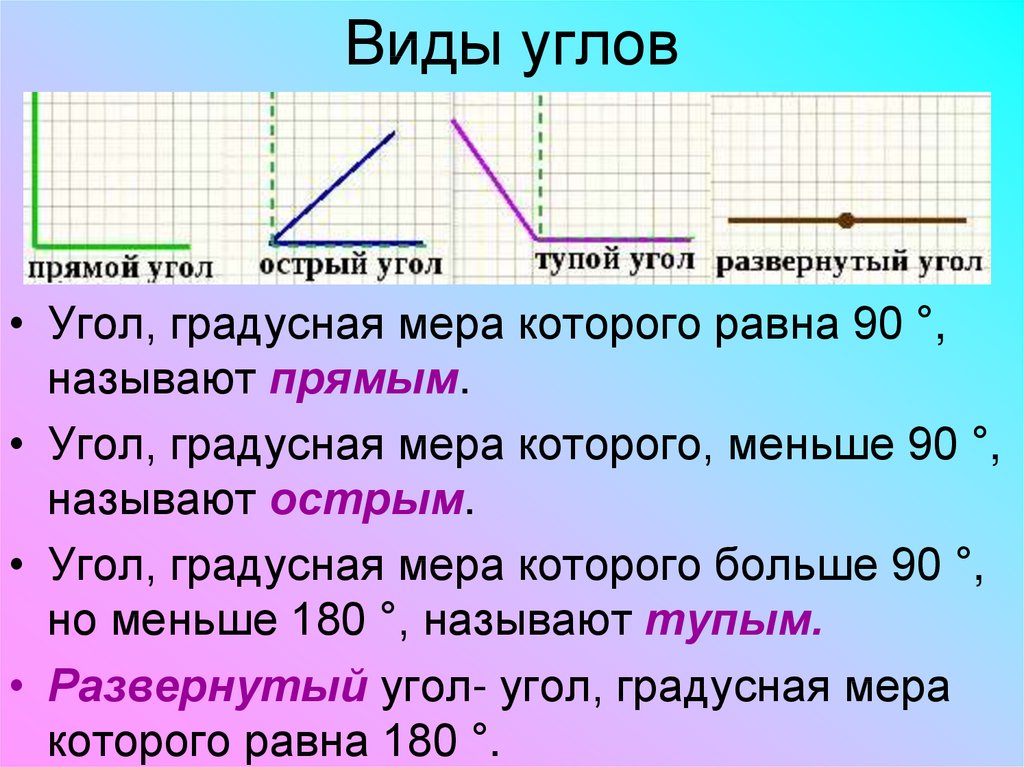
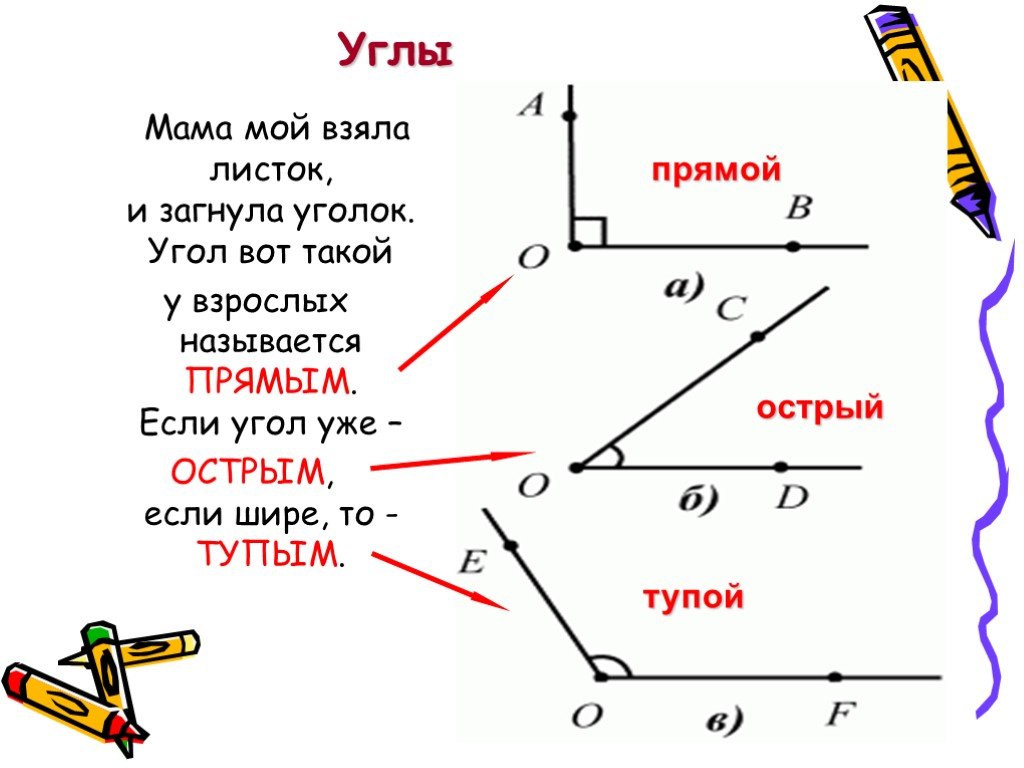
Сегодня на уроке мы поговорим об углах, познакомимся с прямым углом, их свойствами, научимся их обозначать буквами. Все ли углы в фигурах первой группы одинаковы? (Нет.)
1) Практическая работа. Построение модели прямого угла.
Какие бывают углы? Углы бывают разные, но сначала мы познакомимся с самым главным углом. Сейчас мы сложим модель угла, а вы скажите какой это угол.
Возьмет лист бумаги, который лежит на парте.
Согните лист, как на рисунке 1. Согните еще раз, как на рисунке 2. Получилась модель прямого угла.
рис. 1
рис.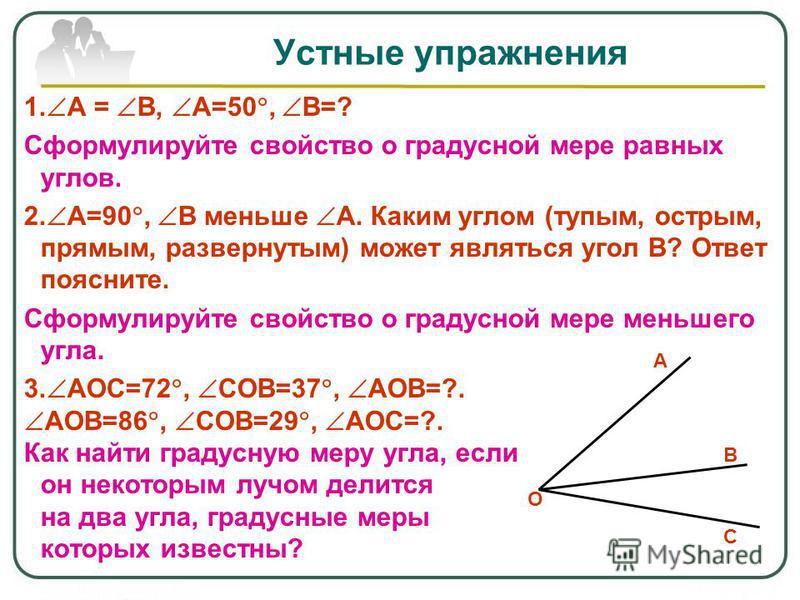 2
2
рис.3
рис.4
Обведите линии сгиба карандашом. На сколько частей прямые линии разделили плоскость? (На четыре.)
– Сколько углов получилось? (Четыре.)
– Это особенные углы.
– На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол буквами. Заштрихуйте цветным карандашом его внутреннюю часть.
Может быть, кто-то знает название этих углов? (Эти углы прямые.)
Покажите стороны прямого угла и вершину.
Дети показывают.
| ВЕРШИНА СТОРОНА |
Где в жизни мы встречаемся с прямыми углами?
Моделью прямого угла является также прямой угол чертежного треугольника. Найдите на нем с помощью своей модели прямой угол.
Прямой угол на чертежном треугольнике – это модель прямого угла.
2) Знакомство с угольником.
Рассмотрите чертежный треугольник.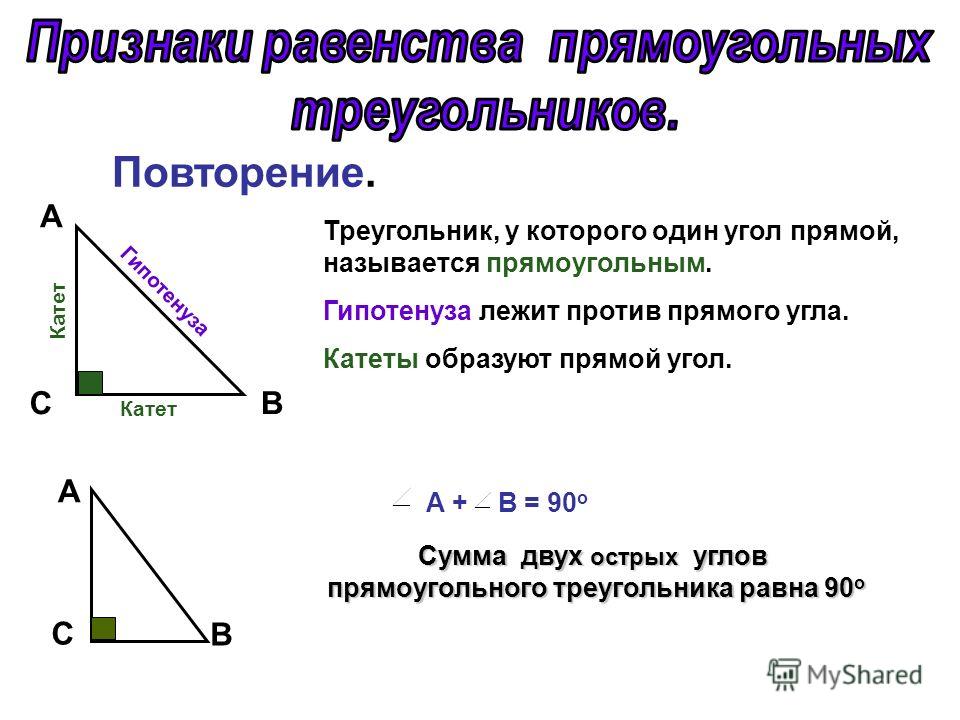 Вы уже убедились, что у него один угол
прямой.
Вы уже убедились, что у него один угол
прямой.
С помощью модели прямого угла узнайте, будут ли прямыми остальные углы этого треугольника.
Какие у вас получились углы? (Меньше прямого.)
Работа в тетради.
С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол в тетради, каждый сам назовет его тремя буквами.
(Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется взаимопроверка в парах.)
Что есть у угла? (Вершина, две стороны.)
– С помощью линейки-угольника проверьте работу друг друга в парах. Определить угол сначала “на глаз”, потом проверить с помощью угольника. Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике.
– Как вы думаете, как образовались углы? Как отличить два угла друг от друга?
Давайте сформулируем правило.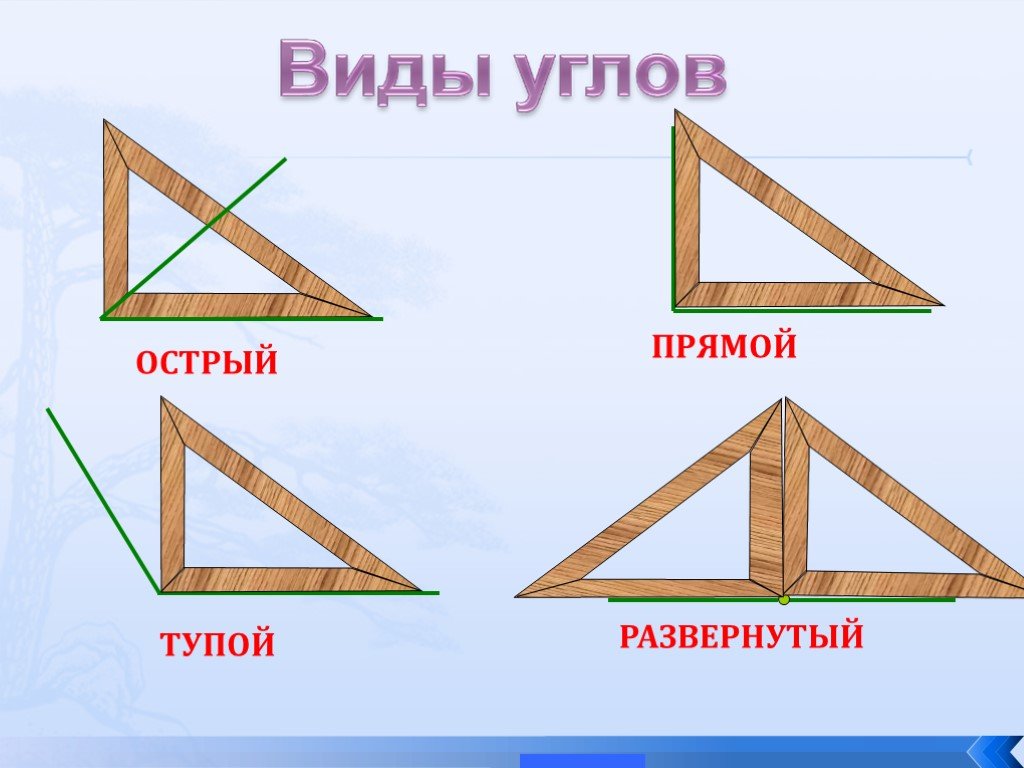 Что такое угол?
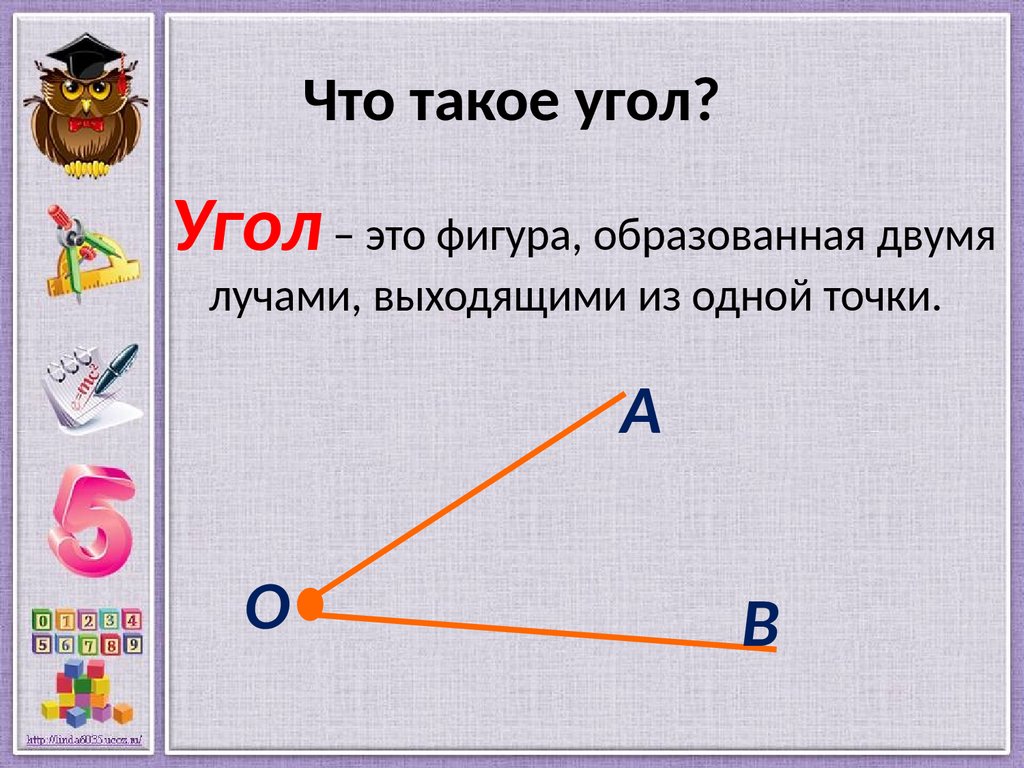
Что такое угол?
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
– Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда?
– В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идет речь. Что этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около нее букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.
Обратите внимание угол выделяется дугой.
IV. Актуализация знаний. Повторение изученного.
1) Работа по учебнику. Стр.38 № 2. Запиши различное название углов. Назови их вершины и стороны.
– Рассмотрите рисунки. Какое правило работы важно помнить, при определении
вида угла с помощью линейки-угольника? (Нужно совмещать вершину и одну сторону
угла с вершиной и стороной прямого угла на линейке-угольнике. )
)
V. динамическая пауза.
Физкультминутка “Буратино”.
Буратино потянулся, раз нагнулся, два нагнулся
Руки в стороны развел, ключик, видно не нашел.
Чтобы ключик нам достать, нужно на носочки встать.
2) Работа в учебнике.
Стр. 40 № 8.
1) Игра “Самый внимательный”.
– Посмотрите внимательно на рисунок, части всех предметов похожи на какие-то геометрические фиуры.
– Самый внимательный из вас найдет на рисунке нужные предмет. Подсказку ищите в верхнем правом углу. (Дети указкой показывают треугольник в квадрате.)
А кто подскажет, если здесь прямые углы?
VI. Итог урока. Рефлексия.
– Кто доволен своей работой на уроке? Прикрепите на нашей полянке красный цветочек.
– Кто считает, что работал не во всю силу и хотел бы на следующий раз работать лучше – желтый цветочек.
– Кто не доволен своей работой – синий цветочек.
– Посмотрите, какая полянка у нас получилась. Я вижу, что в основном дети старались и работали хорошо.
Д/з. Стр. 40 № 11. Придумайте и нарисуйте различные предметы, используя круги, овалы, точки, лучи и углы.
– Что вы узнали нового, интересного? С чем познакомились? Выставить оценки.
– Какое задание понравилось больше всего?
Спасибо за урок.
Соблюдайте правило прямого угла. Камасутра общения. Магия слов и жестов
Соблюдайте правило прямого угла. Камасутра общения. Магия слов и жестовВикиЧтение
Камасутра общения. Магия слов и жестов
Ром Наталья
Содержание
Соблюдайте правило прямого угла
Важную информацию о взаимоотношениях людей дает не только расстояние между ними, но и то, под каким углом они стоят или сидят по отношению друг к другу.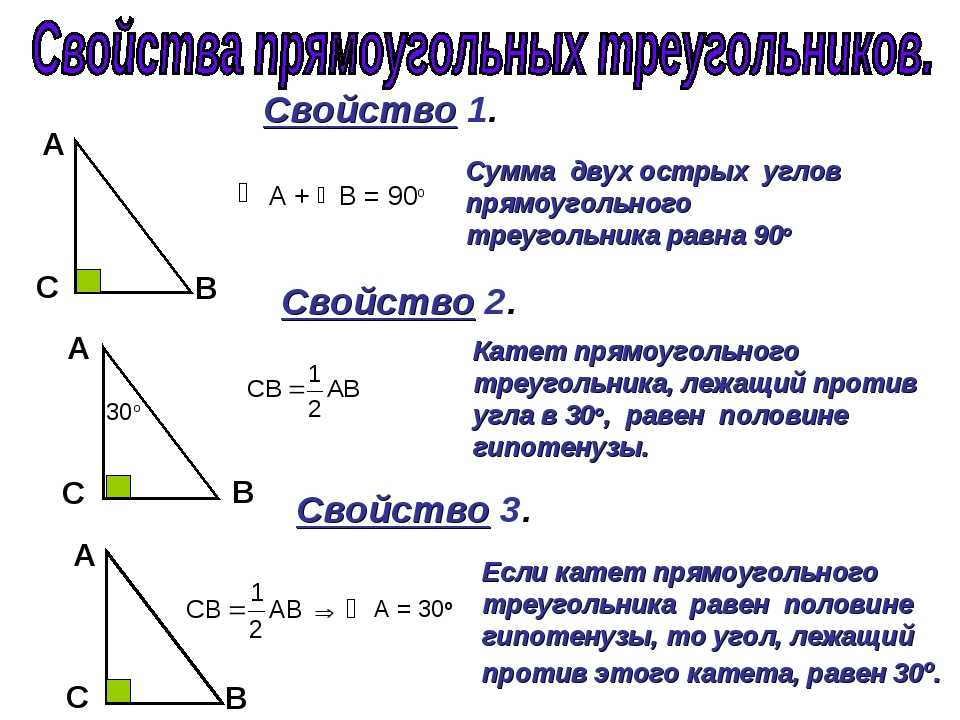
Правило прямого угла
Мысленно нарисуйте прямоугольный треугольник и представьте, что вы с собеседником стоите на его катетах лицом в центр треугольника. Это открытая позиция. Вы повернуты друг к другу, но перед вами остается свободное пространство для «маневра». Общаясь и постепенно узнавая друг друга, вы сможете доверительно развернуться уже лицом к лицу.
Этот прием всем мужчинам рекомендую использовать при знакомстве с женщиной! Вы должны подойти к ней не лицом к лицу, а сбоку, чтобы между вами образовался угол в 90 градусов. Затем, в процессе беседы, вы можете постепенно разворачивать корпус, чтобы оказаться лицом к лицу, и при этом уменьшать дистанцию между вами. Но только постепенно! Если вы поторопитесь, женщина воспримет это как наглое домогательство. А если будете терпеливы – у вас появится хороший шанс пригласить ее на свидание!
Объяснить действие правила прямого угла проще всего на конкретном примере.
Данный текст является ознакомительным фрагментом.
Соблюдайте закон духовной десятины (1)
Соблюдайте закон духовной десятины (1) Кем бы вы ни были – миллионером или обычным служащим, студентом или пенсионером, не стоит забывать о законе духовной десятины. Как пишет Рэнди Гейдж, мультимиллионер, автор бестселлеров: «Когда я не платил десятину, я был бедным,
Соблюдайте закон духовной десятины (2)
Соблюдайте закон духовной десятины (2) Мы отдаем десятину Богу не потому, что хотим что-то получить, а потому что мы благодарим за то, что имеем сегодня. У Сан Лайта есть замечательная аффирмация: «Моя радость получать, моя радость отдавать». Мы получаем деньги с радостью и
Закидывание Ноги на Ногу с Образованием Угла
Закидывание Ноги на Ногу с Образованием Угла
Этот способ закидывания ноги на ногу свидетельствует о том, что здесь присутствует дух соперничества и противоречия.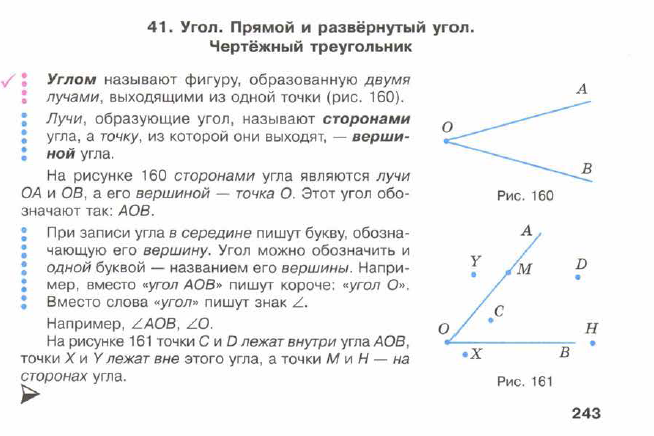 Эта манера сидеть очень популярна среди американцев мужского пола, имеющих бойцовый характер. Поэтому, имея
Эта манера сидеть очень популярна среди американцев мужского пола, имеющих бойцовый характер. Поэтому, имея
Первое правило (правило Гомера)
Первое правило (правило Гомера) Очередность приводимых аргументов влияет на их убедительность Наиболее убедителен следующий порядок аргументов: сильные – средние – один самый сильный. Из этого правила вытекает, что слабыми аргументами лучше не пользоваться: обнаружив
Третье правило (правило Паскаля)
Третье правило (правило Паскаля) Не загоняйте собеседника в угол. Дайте ему возможность сохранить лицо. Часто собеседник не соглашается с нами только потому, что согласие ассоциируется в его сознании с потерей своего достоинства.Например, открытая угроза воспринимается
3. Соблюдайте ваши планы — даже если они касаются только вас
3. Соблюдайте ваши планы — даже если они касаются только вас
Нельзя чувствовать вину за то, что вы отказываетесь от приглашения в пользу времени, которое хотите посвятить исключительно себе. Хотя отношения с окружающими являются важным аспектом жизни каждого из нас, это
Соблюдайте ваши планы — даже если они касаются только вас
Нельзя чувствовать вину за то, что вы отказываетесь от приглашения в пользу времени, которое хотите посвятить исключительно себе. Хотя отношения с окружающими являются важным аспектом жизни каждого из нас, это
Правило № 18 Соблюдайте правила ведения деловой беседы
Правило № 18 Соблюдайте правила ведения деловой беседы Что такое деловая беседа? В самом широком смысле – это беседа, имеющая цель, заранее сформулированную и определяющую логику общения. Существует распространенное мнение, что деловая беседа используется только в
Приемы отражения прямого давления, агрессии и манипуляций
Приемы отражения прямого давления, агрессии и манипуляций Психологическое влияние осуществляется для достижения следующих целей:1) удовлетворения своих потребностей с помощью других;2) подтверждения факта своего существования и значимости этого факта;3) преодоления
Соблюдайте баланс
Соблюдайте баланс
Вам предстоит исследовать величайшую силу в природе. Однако не сосредотачивайте свою жизнь только на этом и не забрасывайте свои текущие дела. Не стремитесь к контакту с Единым сознанием в ущерб работе своего сознательного мышления, ищите правильный
Однако не сосредотачивайте свою жизнь только на этом и не забрасывайте свои текущие дела. Не стремитесь к контакту с Единым сознанием в ущерб работе своего сознательного мышления, ищите правильный
— формула, свойства
Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°. Угол в 90 градусов называется прямым углом, поэтому треугольник с прямым углом называется прямоугольным треугольником . Кроме того, на основании других значений углов прямоугольные треугольники классифицируются как равнобедренные прямоугольные треугольники и разносторонние прямоугольные треугольники. Давайте узнаем больше о свойствах прямоугольного треугольника , о частях прямоугольного треугольника вместе с примерами прямоугольных треугольников в этой статье.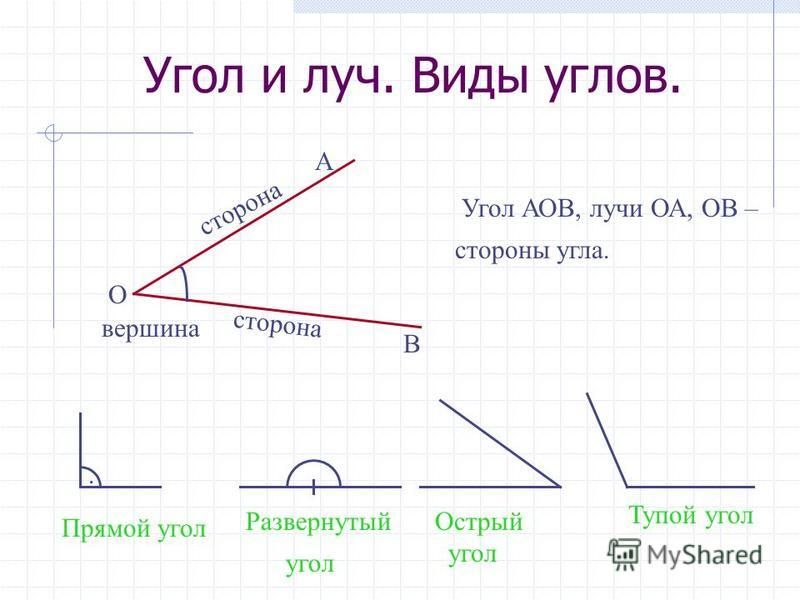
| 1. | Что такое прямоугольный треугольник? |
| 2. | Формула прямоугольного треугольника |
| 3. | Периметр прямоугольного треугольника |
| 4. | Площадь прямоугольного треугольника |
| 5. | Свойства прямоугольного треугольника |
| 6. | Типы прямоугольных треугольников |
| 7. | Часто задаваемые вопросы о прямоугольном треугольнике |
Что такое прямоугольный треугольник?
Прямоугольный треугольник — это треугольник, в котором один угол равен 90°. В этом треугольнике отношения между различными сторонами можно легко понять с помощью теоремы Пифагора. Сторона, противоположная прямому углу, является наибольшей стороной и называется гипотенузой. Обратите внимание на прямоугольный треугольник ABC, приведенный ниже, который показывает основание, высоту и гипотенузу. Здесь АВ — основание, АС — высота, ВС — гипотенуза.
Здесь АВ — основание, АС — высота, ВС — гипотенуза.
Определение прямоугольного треугольника
Определение прямоугольного треугольника гласит, что если один из углов треугольника является прямым углом — 90º, такой треугольник называется прямоугольным треугольником или прямоугольным треугольником.
Теперь давайте разберемся в отличительных чертах прямоугольного треугольника, относящегося к треугольнику ABC, приведенному выше.
- AC высота, высота или перпендикуляр
- AB является базовым
- АС ⊥ АВ
- ∠А = 90º
- Сторона ВС, противоположная прямому углу, называется гипотенузой и является наибольшей стороной прямоугольного треугольника.
Примерами прямоугольных треугольников в нашей повседневной жизни являются треугольный кусок хлеба, квадратный лист бумаги по диагонали или треугольная шкала 30-60-90 в геометрической коробке.
Формула прямоугольного треугольника
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других катетов. Используя это правило, формулу прямоугольного треугольника можно представить следующим образом: Квадрат гипотенузы равен сумме квадрата основания и квадрата высоты .
Используя это правило, формулу прямоугольного треугольника можно представить следующим образом: Квадрат гипотенузы равен сумме квадрата основания и квадрата высоты .
(Гипотенуза) 2 = (Основание) 2 + (Высота) 2
Тройки Пифагора : Три числа, которые удовлетворяют приведенному выше уравнению, известны как тройки Пифагора. Например, (3, 4, 5) является пифагорейской тройкой, потому что мы знаем, что 3 2 = 9, 4 2 = 16 и 5 2 = 25 и 9 + 16 = 25. Следовательно, 3 2 + 4 2 = 5 2 . Любые три числа, которые удовлетворяют этому условию, называются пифагорейскими тройками, такими как 3, 4 и 5. Некоторые другие примеры пифагорейских троек: (6, 8, 10) и (12, 5, 13).
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника равен сумме мер всех трех сторон. Это сумма основания, высоты и гипотенузы прямоугольного треугольника. Обратите внимание на показанный ниже прямоугольный треугольник, в котором периметр равен сумме сторон BC + AC + AB = (a + b + c). Периметр является линейной величиной и представлен линейными единицами, такими как см, дюймы, ярды и т. д.
Обратите внимание на показанный ниже прямоугольный треугольник, в котором периметр равен сумме сторон BC + AC + AB = (a + b + c). Периметр является линейной величиной и представлен линейными единицами, такими как см, дюймы, ярды и т. д.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника — это пространство, занимаемое треугольником. Он равен половине произведения основания и высоты треугольника. Это двумерная величина и поэтому представлена в квадратных единицах. Две стороны, необходимые для нахождения площади прямоугольного треугольника, — это основание и высота.
Площадь прямоугольного треугольника рассчитывается по формуле: Площадь прямоугольного треугольника = (1/2 × основание × высота)
Свойства прямоугольного треугольника
Первое свойство прямоугольного треугольника состоит в том, что один из его углов равен 90º. Угол 90º является прямым углом и наибольшим углом прямоугольного треугольника.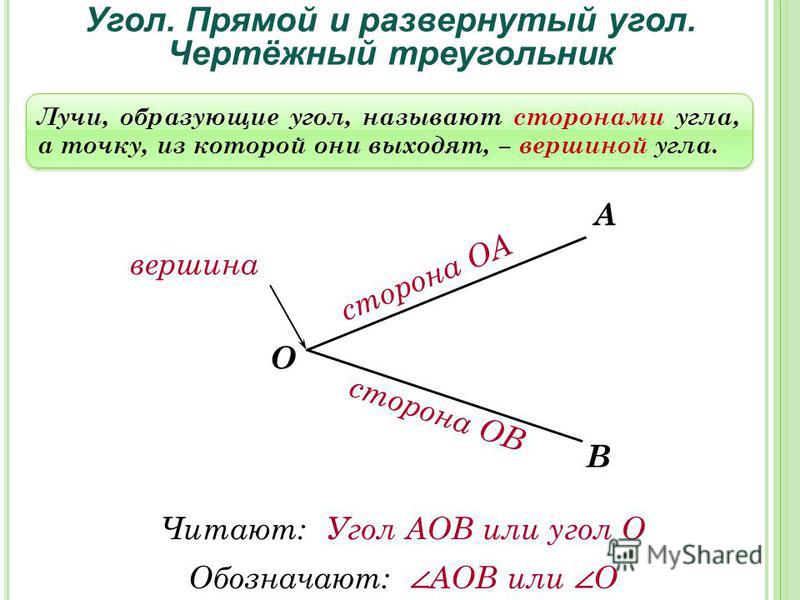 Кроме того, два других угла меньше 90º и называются острыми углами. Свойства прямоугольного треугольника перечислены ниже:
Кроме того, два других угла меньше 90º и называются острыми углами. Свойства прямоугольного треугольника перечислены ниже:
- Наибольший угол прямоугольного треугольника всегда равен 90º.
- Самая большая сторона прямоугольного треугольника называется гипотенузой, которая всегда является стороной, противоположной прямому углу.
- Стороны измеряются по правилу Пифагора.
- У него не может быть тупого угла.
Типы прямоугольных треугольников
Мы узнали, что один из углов прямоугольного треугольника равен 90º. Это означает, что два других угла в треугольнике будут острыми углами. Есть несколько особых прямоугольных треугольников, таких как равнобедренных прямоугольных треугольника и разносторонних прямоугольных треугольников . Треугольник, в котором один угол равен 90º и два других угла равны, называется равнобедренным прямоугольным треугольником, а треугольник, в котором два других угла имеют разные значения, называется разносторонним прямоугольным треугольником.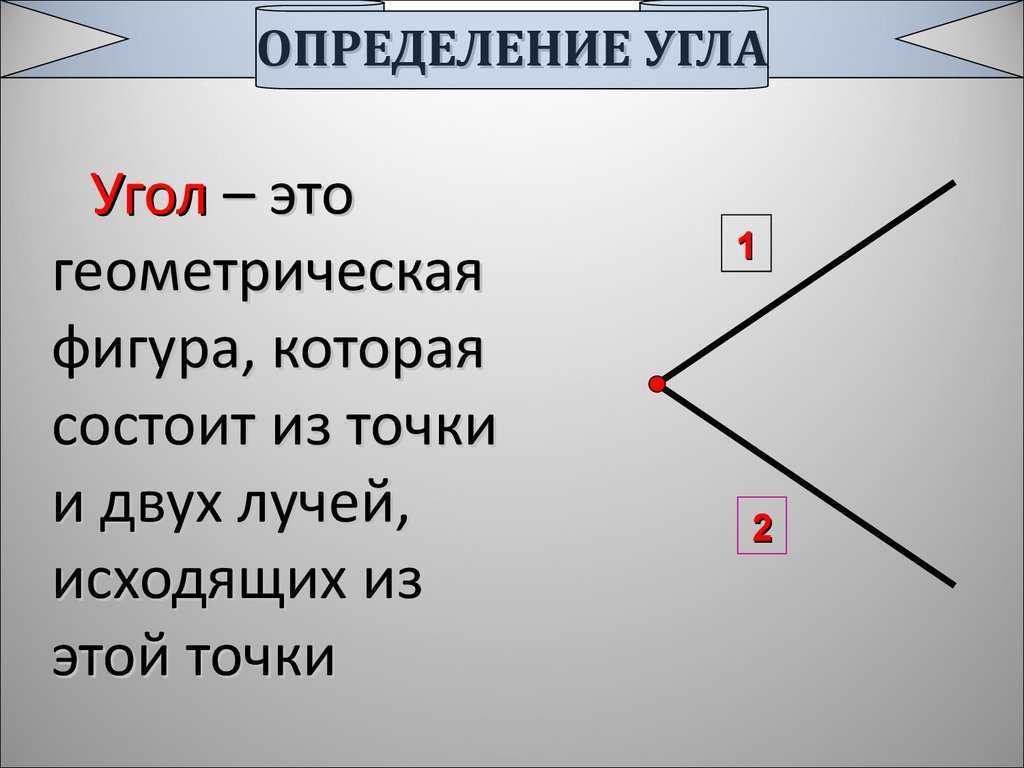
Равнобедренный прямоугольный треугольник
Равнобедренным прямоугольным треугольником называется треугольник с углами 90º-45º-45º. Обратите внимание на приведенный ниже треугольник ABC, в котором угол A = 90º, и мы увидим, что AB = AC. Поскольку две стороны равны, треугольник также является равнобедренным. Мы знаем, что сумма углов треугольника равна 180º. Следовательно, сумма углов при основании равна 9.0º, что означает, что они по 45º каждая. Итак, в равнобедренном прямоугольном треугольнике углы всегда равны 90°-45°-45°.
Разносторонний прямоугольный треугольник
Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90°, а два других угла имеют разные измерения. В приведенном ниже треугольнике PQR ∠Q = 90º, следовательно, это прямоугольный треугольник. PQ не равен QR, следовательно, это разносторонний треугольник. Существует также особый случай разностороннего треугольника 30º-60º-90º, который также является прямоугольным треугольником, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2: 1. Сторона, противоположная углу 30º, является самой короткой стороной.
Сторона, противоположная углу 30º, является самой короткой стороной.
Советы и рекомендации
Здесь перечислены некоторые важные советы и рекомендации, связанные с прямоугольным треугольником.
- Длины сторон прямоугольного треугольника всегда удовлетворяют теореме Пифагора.
- В прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
- Две другие ноги перпендикулярны друг другу; один — основание, а другой — высота.
Важные примечания
- В прямоугольном треугольнике (гипотенуза) 2 = (основание) 2 + (высота) 2
- Площадь прямоугольного треугольника рассчитывается по формуле Площадь прямоугольного треугольника = 1/2 × основание × высота
- Периметр прямоугольного треугольника равен сумме мер всех трех сторон.
- Равнобедренные прямоугольные треугольники имеют углы 90º, 45º, 45º.

☛ Похожие темы
- Гипотенуза
- Пифагорейские тройки
- Формула гипотенузы
Примеры прямоугольных треугольников
Пример 1: Может ли прямоугольный треугольник иметь размеры 11 дюймов, 60 дюймов и 61 дюйм?
Решение:
Если числа 11, 60 и 61 — пифагоровы тройки, они образуют прямоугольный треугольник. 11 2 = 121; 60 2 = 3600; 61 2 = 3721. Мы видим, что: 121 + 3600 = 3721. Следовательно, данные числа являются пифагоровыми тройками и могут быть размерами прямоугольного треугольника. Следовательно, 11 дюймов, 60 дюймов и 61 дюйм могут образовать прямоугольный треугольник.
Пример 2: Найдите площадь прямоугольного треугольника, основание которого равно 12 единицам, а высота 5 единицам.
Решение:
Формула площади треугольника равна 1/2 × b × h.
 Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.
Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.Пример 3: Укажите истинное или ложное значение прямоугольного треугольника.
а.) В прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
б.) Прямоугольный треугольник может иметь один тупой угол.
Решение:
а.) Верно, что в прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
б.) Неверно, в прямоугольном треугольнике не может быть тупых углов.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.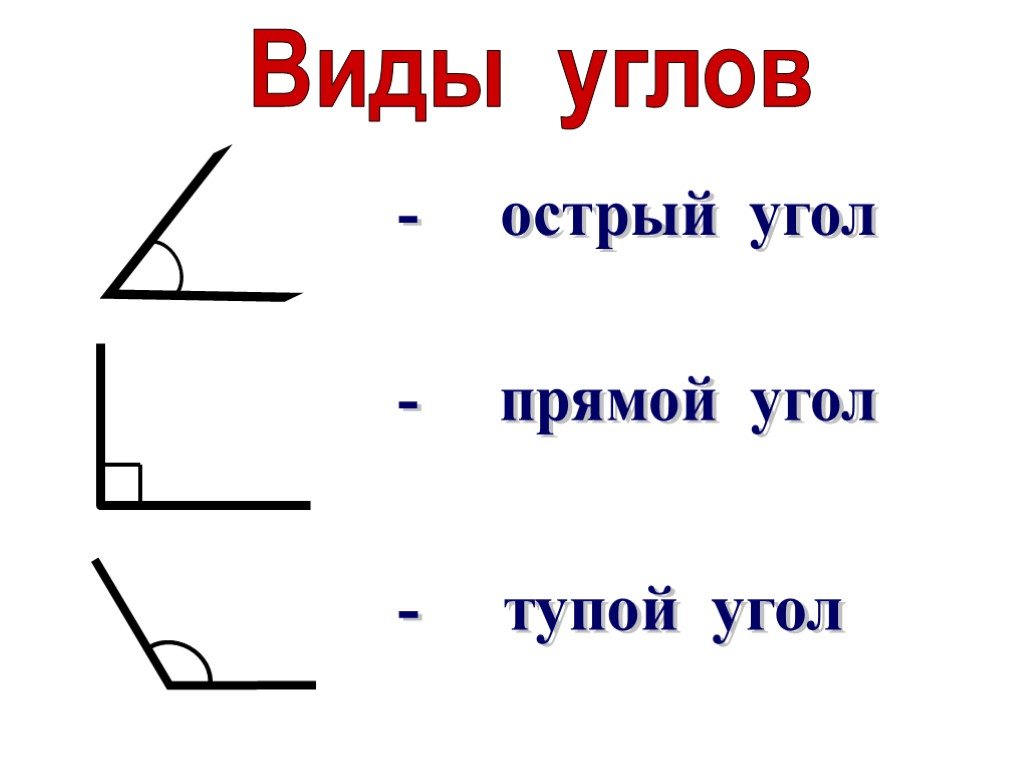
Записаться на бесплатный пробный урок
Практические вопросы по прямоугольным треугольникам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о прямоугольном треугольнике
Что такое прямоугольный треугольник в геометрии?
Треугольник, в котором одна из мер углов равна 90 градусов, называется прямоугольным треугольником или прямоугольным треугольником.
Какие существуют типы прямоугольных треугольников?
Треугольники классифицируются на основе измерения сторон и углов. Три типа прямоугольных треугольников упомянуты ниже.
- Равнобедренный прямоугольный треугольник — это треугольник, в котором углы равны 90º, 45º и 45º.
- Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90º, а два других острых угла имеют разную величину.
- Треугольник 30º — 60º — 90º — еще один интересный прямоугольный треугольник, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2:1.

Какова мера углов прямоугольного треугольника?
В прямоугольном треугольнике один из углов равен 90º. Два других угла острые. И все три угла прямоугольного треугольника в сумме дают 180°, как и любого другого треугольника.
Какая формула прямоугольного треугольника?
Формула, которая используется для прямоугольного треугольника, является теоремой Пифагора. Он гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон. Это означает, что (гипотенуза) 2 = (база) 2 + (высота) 2 .
Как найти площадь прямоугольного треугольника?
Площадь прямоугольного треугольника – это площадь, занимаемая треугольником, и равна половине произведения основания и высоты треугольника. Он двумерный и представлен в квадратных единицах. Формула, которая используется для нахождения площади прямоугольного треугольника: Площадь прямоугольного треугольника = 1/2 × основание × высота 9.0013
Может ли прямоугольный треугольник иметь две равные стороны?
Да, прямоугольный треугольник может иметь две равные стороны. Самая длинная сторона называется гипотенузой, а две другие стороны могут быть равны или не равны друг другу. Прямоугольный треугольник, у которого две стороны равны, называется равнобедренным прямоугольным треугольником.
Самая длинная сторона называется гипотенузой, а две другие стороны могут быть равны или не равны друг другу. Прямоугольный треугольник, у которого две стороны равны, называется равнобедренным прямоугольным треугольником.
Как найти недостающую сторону прямоугольного треугольника?
Недостающую сторону прямоугольного треугольника можно найти, если известна мера двух других сторон. Теорема Пифагора помогает найти значение недостающей стороны. По теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника. Например, если а, b и с — три стороны прямоугольного треугольника, где «а» — гипотенуза, то, согласно теореме, a 2 = б 2 + в 2 .
Как найти угол прямоугольного треугольника?
Расчет углов прямоугольного треугольника очень прост. Один из углов прямоугольного треугольника является прямым углом или 90 º . Теперь, если известен другой угол треугольника, то недостающий угол можно легко вычислить, используя свойство суммы углов, которое утверждает, что сумма углов треугольника всегда равна 180º.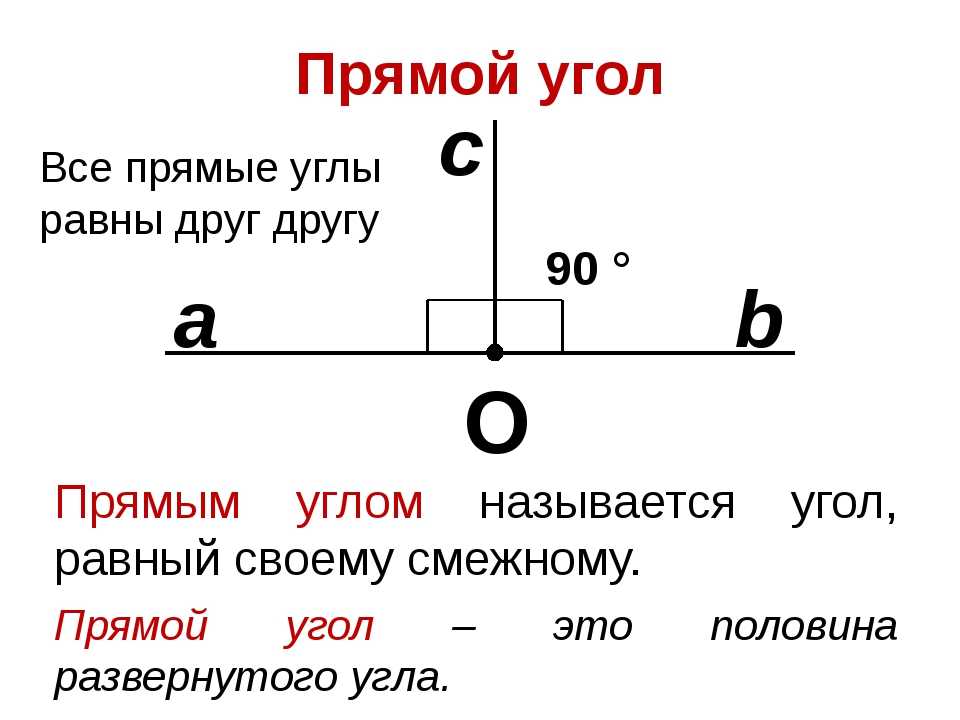
Как выглядит прямоугольный треугольник?
Прямоугольный треугольник выглядит как треугольник, две стороны которого образуют букву «L», а концы буквы «L» соединены линией, которая является гипотенузой и самой длинной стороной треугольника.
Из каких частей состоит прямоугольный треугольник?
Части прямоугольного треугольника можно описать следующим образом:
- В прямоугольном треугольнике один угол равен 90°, а два других угла являются острыми.
- Сторона, противоположная прямому углу, является наибольшей стороной и называется гипотенузой.
- Две другие стороны прямоугольного треугольника называются катетами и обозначаются как «основание» и «высота» треугольника. Высота также известна как высота этого треугольника.
Прямоугольный треугольник – формула, определение, свойства, факты
Треугольник, в котором один из внутренних углов равен 90°, называется прямоугольным треугольником. Самая длинная сторона прямоугольного треугольника, которая также является стороной, противоположной прямому углу, — это гипотенуза, а две стороны прямого угла — это высота и основание.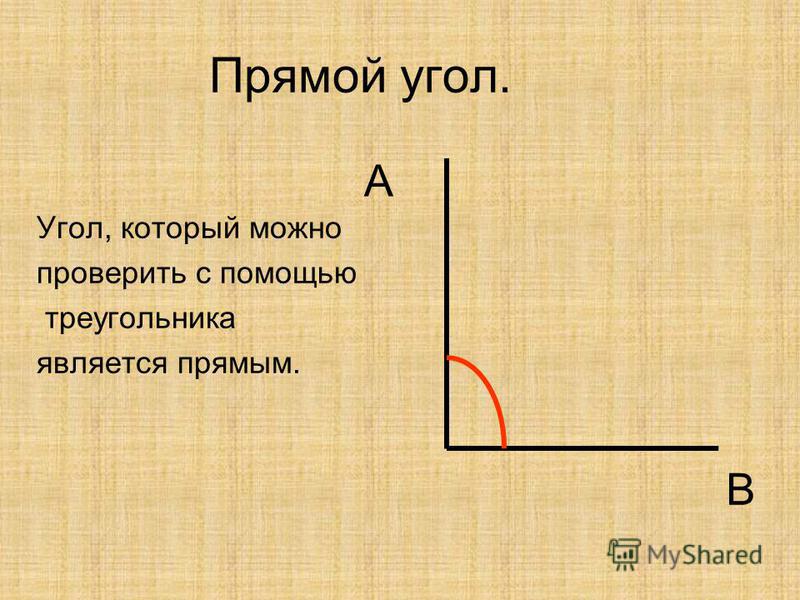 Вот как выглядит прямоугольный треугольник:
Вот как выглядит прямоугольный треугольник:
Полное пространство или территория, покрытая прямоугольным треугольником, известна как площадь прямоугольного треугольника. Он рассчитывается в квадратных единицах. Единицы m 2 , cm 2 , in 2 , yd 2 и другие обычно представляют площадь.
Особенности прямоугольного треугольника
- Прямой угол всегда является наибольшим углом в прямоугольном треугольнике.
- Гипотенуза, сторона, противоположная прямому углу, является самой длинной стороной.
- В прямоугольном треугольнике не может быть тупых углов.
Связанные игры
Типы прямоугольных треугольников
В широком смысле прямоугольные треугольники можно разделить на следующие категории: каждый. Он также известен как треугольник 45-90-45.
Это равнобедренный прямоугольный треугольник, стороны которого AB и AC равны, а ∠ B составляет 90°.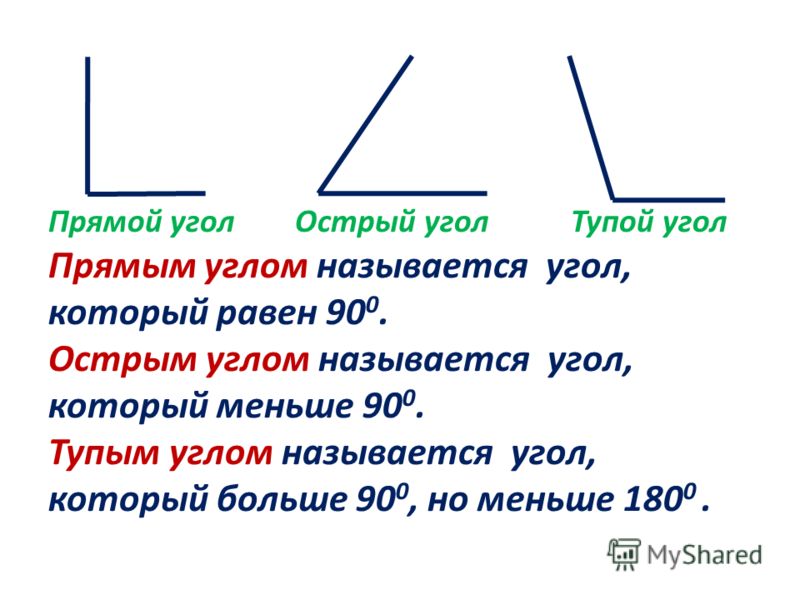 Здесь ∠ A и ∠ C измеряют по 45° каждый, потому что свойство гласит, что углы, противоположные равным сторонам, также равны.
Здесь ∠ A и ∠ C измеряют по 45° каждый, потому что свойство гласит, что углы, противоположные равным сторонам, также равны.
2. Разносторонний прямоугольный треугольник : В этом треугольнике один внутренний угол равен 90°, а два других имеют разные измерения. Например:
В прямоугольном треугольнике ABC ∠ A составляет 30°, ∠ B составляет 90°, а ∠ C составляет 60°. В этом треугольнике все три стороны будут разной длины и три угла будут разной величины.
Похожие рабочие листы
Формула прямоугольного треугольника
Теорема Пифагора
- Пифагор обнаружил, что квадрат гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника.
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника определяется как общая длина границы. Формула для периметра:
P (периметр) = a + b + c (сумма сторон треугольника)
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника определяется как площадь, занимаемая треугольником. Формула площади:
Формула площади:
Площадь = $\frac{1}{2}\times base\time height$
Решенные примеры
- Наибольшая сторона треугольника равна 10 см. Если высота треугольника 8 см, определите площадь по теореме Пифагора.
Решение:
Гипотенуза — самая длинная сторона прямоугольного треугольника.
Здесь гипотенуза ( H ) = 10 см, высота ( h ) = 8 см, а основание ( b ) неизвестно. по теореме Пифагора 00 = б 2 + 8 2
100 = б 2 + 64
B 2 = 36 CM 2
B = $ \ SQRT {36} $ = 6 CM
Область = $ \ FRAC {1) умножить на основание\умножить на высоту$
= $\frac{1}{2}\times 6\times 8 = 24$
Следовательно, площадь треугольника = 24 квадратных см.
- Соотношение сторон треугольника 3:4:5. Периметр 840 м. Найдите его площадь.

Решение :
Пусть стороны треугольника равны 3 x , 4 x и 5 x соответственно.
Мы знаем, что периметр = 840 м.
3 x + 4 x + 5 x = 840
12 x = 840
x = $10}{\frac 0 3
Итак, стороны
3 х = 3(70) = 210 м
4 х = 4(70) = 280 м
5 х = 5(70) 9010 м 9010 м 350 м — самая длинная сторона треугольника, это гипотенуза.
Итак, 210 м и 280 м — это основание и высота треугольника взаимозаменяемо.
Используя формулу площади прямоугольного треугольника, получаем
Площадь = $\frac{1}{2}\times base\times height = \frac{1}{2}\times 210\times 280 = 29,400$
Следовательно, площадь данного треугольника = 29,400 м 2
- Какова мера гипотенузы в прямоугольном треугольнике, высота которого равна 7 см, а основание равно 5 см?
Решение:
Высота перпендикуляра ( h ) = 7 см, основание ( b ) = 5 см и гипотенуза ( H ) = ? По теореме Пифагора 99 2 = 5 2 + 7 2
Н 2 = 25 + 49
Н 2 = 74
H = $\sqrt{74}$ см
Практические задачи
1
В прямоугольном треугольнике стороны a = 12 и b = 32, а периметр треугольника равен 58 см.
 Найдите с, третью сторону треугольника.
Найдите с, третью сторону треугольника.44 см
50 см
12 см
14 см
Правильный ответ: 14 см
58 = 12 + 32 + c, c = 14 см , АБ = 23 см, ВС = 14 см, СА = 13 см. Чему равен периметр треугольника? 92} = \sqrt{16 + 9} = \sqrt{25}$ = 5 см
Часто задаваемые вопросы
Может ли прямоугольный треугольник иметь две равные стороны?
Прямоугольный треугольник также может быть равнобедренным, что означает, что у него две стороны и два угла равны. Прямоугольный равнобедренный треугольник имеет угол 90° и два угла по 45°.
Могут ли 8 см, 15 см и 17 см составлять три стороны прямоугольного треугольника?
Мы можем проверить, образуют ли 8 см, 15 см и 17 см три стороны прямоугольного треугольника, используя теорему Пифагора.
H (гипотенуза) 2 = P (перпендикулярная высота) 2 + B (основание) 2
1289 = 225 + 64
289 = 289
Отсюда проверено, что 8 см, 15 см и 17 см могут составить три стороны прямоугольного треугольника.

 Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.
Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.