Пропорция онлайн калькулятор: Онлайн калькулятор: Пропорция

Содержание

Калькулятор сахарной браги для самогона, расчет пропорций онлайн «Домашний Заготовщик»

8 800 700-20-81

Перезвоните мне

Корзина

Загрузка…

8 800 700-20-81

Перезвоните мне

Войти

Процесс самогоноварения начинается с приготовления браги. Именно от нее
во многом зависит качество и выход напитка после перегонки. Важно правильно
рассчитать гидромодуль (пропорции браги для самогона из сахара). Чаще всего на 1
килограмм сахара-песка используют 4,5-5 литров воды. Это весьма приблизительные
пропорции. Подсчитать все точно поможет калькулятор. С его помощью вы узнаете
крепость продукта из указанного количества сахара, необходимый объем воды.
На калькуляторе самогонщика необходимо указать следующие параметры:
— количество сахара-песка в килограммах;
— объем сахарного раствора в литрах.
При выборе для самогона пропорций воды и сахара важно учитывать устойчивость
дрожжей к спирту. При достижении определенной крепости они перестают
сбраживать оставшийся сахарный раствор. В этом случае вы получите меньше
спирта, чем планировали, израсходуете лишний сахар-песок. Калькулятор
самогонщика онлайн брага помогает рассчитать оптимальные пропорции. Для
декстрозы необходимо выполнять расчеты самостоятельно. Она стоит дороже, чем
обычный сахар-песок, выход спирта меньше. При брожении в питательной среде из
декстрозы дрожжи выделяют меньше побочных продуктов, чем в сахарном растворе,
поэтому качество дистиллята получается выше.

Предварительный расчет для самогона дает возможность заранее узнать, какой результат будет получен в итоге. Правильный подбор пропорций сахарной бражки для самогона – залог успеха всего процесса самогоноварения. Ошибки на этом этапе чреваты тем, что все дальнейшие усилия не принесут результата, который планировался изначально. Делать расчет удобней всего на калькуляторе самогонщика.

Процесс брожения представляет собой развитие колонии дрожжей в питательной среде. Правильный расчет пропорций сахарного
самогона помогает самогонщику получать продукт высокого качества. Необходимо учитывать, что на процесс брожения сахарного
раствора оказывают влияние многие факторы, поэтому полученные на калькуляторе значения являются теоретическими. Калькулятор
выхода самогона поможет спланировать весь процесс, чтобы приблизиться к идеальному результату. Калькулятор рассчитает пропорции самогона из сахара моментально онлайн. Также он выполнит расчет выхода спирта сырца из сахарной бражки.

Широкий ассортимент

Собственное производство

Гарантия возврата денег

Рассрочка без переплаты на 6 месяцев

Быстрая доставка в любой город России

Z-тест для двух пропорций калькулятор

Рельефы Статистика

Инструкции: Этот калькулятор проводит z-тест для двух пропорций населения ($p_1$ и $p_2$), пожалуйста, выберите нулевые и альтернативные гипотезы, введите уровень значимости, размеры образцов, количество благоприятных случаев (или промежуточных пропорций) и результатыZ-тест будет отображаться для вас:

Ho: $p_1$ —Select— = ≥ ≤ $p_2$

Ha: $p_1$ —Select— ≠ < > $p_2$

Размер образца ($n_1$) =

Размер образца ($n_2$) =

Пропорция образца ($\hat p_1$) =

Пропорция образца ($\hat p_2$) =

Выгодные случаи ($X_1$) =

Выгодные случаи ($X_2$) =

Уровень значимости ($\alpha$) =

Подробнее о Z-тест на два пропорция Таким образом, вы можете лучше понять результаты, полученные этим решателем: Z-тест для двух пропорций — это тест гипотезы, который пытается претендовать на пропорции населения P

и П. _2. ОтказВ частности, мы заинтересованы в оценке того, разумно утверждать, что P _1. = P. _2. с использованием образца информации.Z-тест для двух пропорций имеет две не перекрывающиеся гипотезы, ноль и альтернативную гипотезу.

Каковы нулевые и альтернативные гипотезы для Z-теста на два пропорция?

Нулевая гипотеза — это утверждение о параметре популяции, который не указывает на эффект, а альтернативная гипотеза является дополнительной гипотезами нулевой гипотезы. Основными свойствами одного образца Z-теста для двух пропорций населения являются:

В зависимости от наших знаний о ситуации «нет эффекта», Z-тест может быть двусторонним, левым хвостом или правым хвостом

Основным принципом тестирования гипотезы является то, что нулевая гипотеза отклоняется, если полученная статистика тестирования достаточно маловероятна под предположением, что нулевая гипотеза правда

P-значение является вероятность получения образцов результатов как экстремальных или более экстремальных, чем полученные пример результатов, в соответствии с предположением, что нулевая гипотеза верна

В тестах гипотезы есть два типа ошибок. Ошибка типа I возникает, когда мы отклоним настоящую нулевую гипотезу, а ошибка II типа II возникает, когда мы не можем отклонить ложную нулевую гипотезу

Что такое формула Z-теста в этом случае?

Формула для Z-статистики для двух пропорций населения

\[z = \frac{\hat p_1 — \hat p_2}{\sqrt{\bar p(1-\bar p)(\frac{1}{n_1} + \frac{1}{n_2})}}\]

где $\bar p = \frac{X_1+X_2}{n_1+n_2}$ соответствует Объединенная пропорция (Обратите внимание, что в вышеупомянутом Z-тесте для пропорций формулы, мы попадаем в знаменатель что-то вроде нашего «лучшее предположение» о том, что пропорция населения от информации из двух образцов, предполагая, что нулевая гипотеза о равенстве пропорций верна).

Нулевая гипотеза отвергается, когда Z-статистика лежит в области отклонения, которая определяется уровнем значимости ($\alpha$) и типом хвоста (двуххвостые, левосторонние или правые).

Дело для одной пропорции населения

Если у вас есть только одна пропорция образца (так что вы тестируете на одну пропорцию населения), вы должны использовать наш Z-TEST для одного пропорции калькулятора , что конкретно обращается к такому случаю.

Базовый статистический пакет Тест гипотезы Статистический тест Статистические средства Solver. Z-тест Z-тест на два пропорция Z-тест для двух пропорций калькулятора

Калькулятор процентной доли

— Как рассчитать процентную долю?

‘ Калькулятор процентной доли’ – это онлайн-инструмент, помогающий рассчитать процентную долю.

Что такое калькулятор процентной доли?

«Калькулятор процентной доли» – это онлайн-инструмент, помогающий рассчитать процентную долю. Онлайн-калькулятор поможет вам рассчитать процентную долю за несколько секунд.

Калькулятор процентной пропорции

Как

Использовать калькулятор процентной доли?

Чтобы найти процентную долю, выполните следующие действия:

Шаг 1: Введите часть (A) и целое (B) в заданное поле ввода.
Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти процентную долю.
Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и найти процентное соотношение для различных значений.

Как найти процентную долю?

Процентная пропорция — это доля одного числа в пропорции к другому числу, выраженная в процентах. Его также можно принять как долю числа, равного другому числу. Другими словами, процентная доля дается как доля числа от другого числа.

Процент Доля числа = A / B × 100 , где A — первое число, а B — второе число

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

БЕСПЛАТНАЯ БЕСПЛАТНАЯ ИССЛЕДОВАНИЯ КЛАССА

Решанные примеры по калькулятору процентов.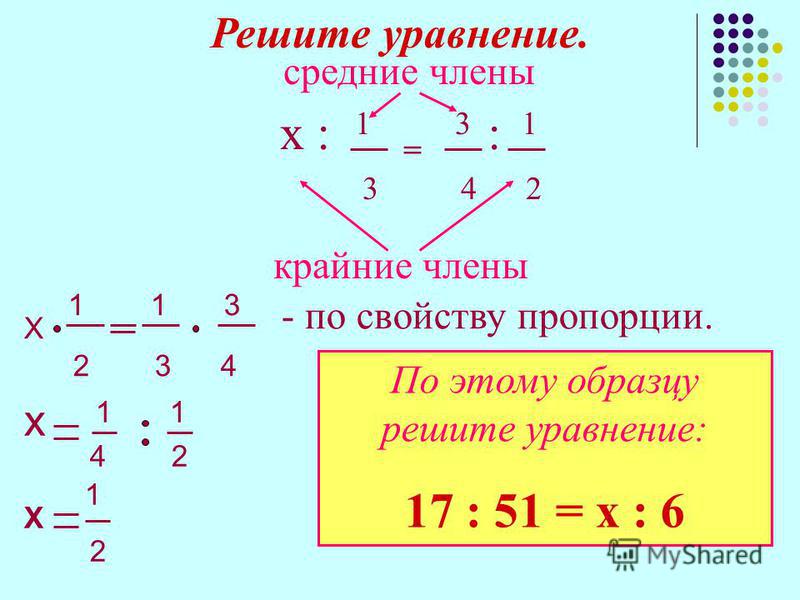 10 и В = 25
Процент Доля числа = A / B × 100
= 10 / 25 × 100
= 2/5 × 100
= 40%
Пример 2:
Найдите пропорцию , B = 30
Решение:
Дано, A = 27 и B = 30
Проценты Доля числа = A / B × 100
= 1 / 30 × 5 100
= 90%
Пример 3:
Найдите пропорцию в процентах, где A = 45 , B = 65
Решение:
DED, A = 45 и B = 65
процент доли числа = A /B × 100
= 45 /65 × 100
= 9/13 × 100
= 69,23 %
Точно так же вы можете попробовать калькулятор, чтобы найти калькулятор процентной пропорции, если,
1) A = 10, B = 30
2) A = 24, B = 50
☛ Похожие статьи: 4
Процентная доля
Проценты
☛ Математические калькуляторы:
Калькулятор пропорций | Как решить пропорции?
Создано Кацпером Павликом, доктором медицинских наук, и Юлией Жулавинской
Отредактировано Домиником Черниа, доктором философии, и Джеком Боуотером
Последнее обновление: 17 декабря 2022 г.
Содержание:
Что такое пропорция? – определение пропорции
Константа пропорциональности – значения прямо и обратно пропорциональны
Как решать пропорции – примеры пропорций
Золотое сечение
Закон кратных пропорций – пропорциональные отношения в химии
Определение прямо пропорционального налога
Калькулятор пропорций помогает вычислять одинаковые пропорции. Прежде чем мы сможем использовать калькулятор, важно понять, что такое пропорция и как решать пропорции вручную. Чтобы помочь вам понять эти темы, мы представляем вам определение пропорции и понятие константы пропорциональности. Прочитав этот текст, вы сможете сказать, являются ли два параметра прямо пропорциональными или обратно пропорциональными.
Наконец, мы поговорим о некоторых реальных примерах пропорций. Вы увидите, что пропорциональные отношения присутствуют повсюду в окружающем нас мире . Ученые используют закон кратных пропорций при проведении химических реакций, а бухгалтеры (или любой налогоплательщик) должны быть знакомы с определением пропорционального налога, чтобы знать, сколько денег они должны заплатить государству.
Что такое пропорция? – определение пропорции
Пропорция – это соотношение между двумя величинами. Показывает, какая часть одной части содержится в целом. Результат обычно отображается в виде дроби, но также может быть представлен двоеточием, десятичным числом или процентом. Если вы предпочитаете отображение в процентах, мы рекомендуем вам посетить наш процентный калькулятор, который также может быть лучшим выбором для решения пропорций со 100100100 в качестве знаменателя. Он по-прежнему соответствует определению пропорции, но также позволяет вам, например, рассчитать, какой процент торта на день рождения съел ваш дядя 😊.
Так же, как дробь состоит из двух частей, числителя и знаменателя , то же верно и для пропорции. Верхнее число пропорции является числителем, а нижняя часть пропорции — знаменателем. Чтобы проиллюстрировать это, давайте рассмотрим пример.
Предположим, что есть торт, разрезанный на 12 частей. 5 из 12 ломтиков были съедены (этим наглым дядей). Вы хотите знать долю оставшихся кусочков по сравнению со всем тортом. У вас осталось 12-5=712-5 = 712-5=7 ломтиков, поэтому пропорция 7/127/127/12. Если вы хотите переписать эту пропорцию, используя двоеточие, вы можете записать ее как 7:127:127:12. Обратите внимание, что этот калькулятор пропорций не будет представлять пропорцию в последней форме.
Каков процесс, если мы хотим упростить или масштабировать пропорцию до большей, но эквивалентной пропорции? Следующий раздел о том, как решать пропорции, объясняет этот процесс.
Константа пропорциональности – значения прямо и обратно пропорциональны
Константа пропорциональности связывает отношения или произведения двух величин. Иногда его называют коэффициентом вероятности. Мы можем записать его в виде уравнения. Если две переменные равны прямо пропорциональна , то формула для константы пропорциональности выглядит так: две переменные находятся в прямо пропорциональной зависимости. Если две переменные обратно пропорциональны , то формула коэффициента пропорциональности будет следующей:
c=x×yc = x \times yc=x×y
переменные находятся в обратно пропорциональной зависимости.
Поначалу это может показаться очень теоретической концепцией, но вы будете удивлены количеством реальных применений этих констант. Мы используем их так часто, что не осознаем, что, говоря математическим языком, они являются константами пропорциональности. Скорость (или скорость) может быть одним из самых известных примеров. Это отношение между расстоянием и временем. Мы можем записать это так:
v=stv = \frac{s}{t}v=ts
Где vvv — скорость, sss — расстояние, а ttt — время.
Знакомо, не правда ли? Да, это та же формула, что и для константы пропорциональности двух прямо пропорциональных переменных . Так как эта связь (по определению пропорции) постоянна, то если мы изменим одну переменную, то и вторая переменная тоже должна будет измениться. Таким образом, зная нашу скорость, мы также можем рассчитать расстояние, которое мы преодолеем за 1 минуту, 1 час, 1 день или любой другой период. По мере постепенного увеличения значения времени пропорционально увеличивается и пройденное расстояние.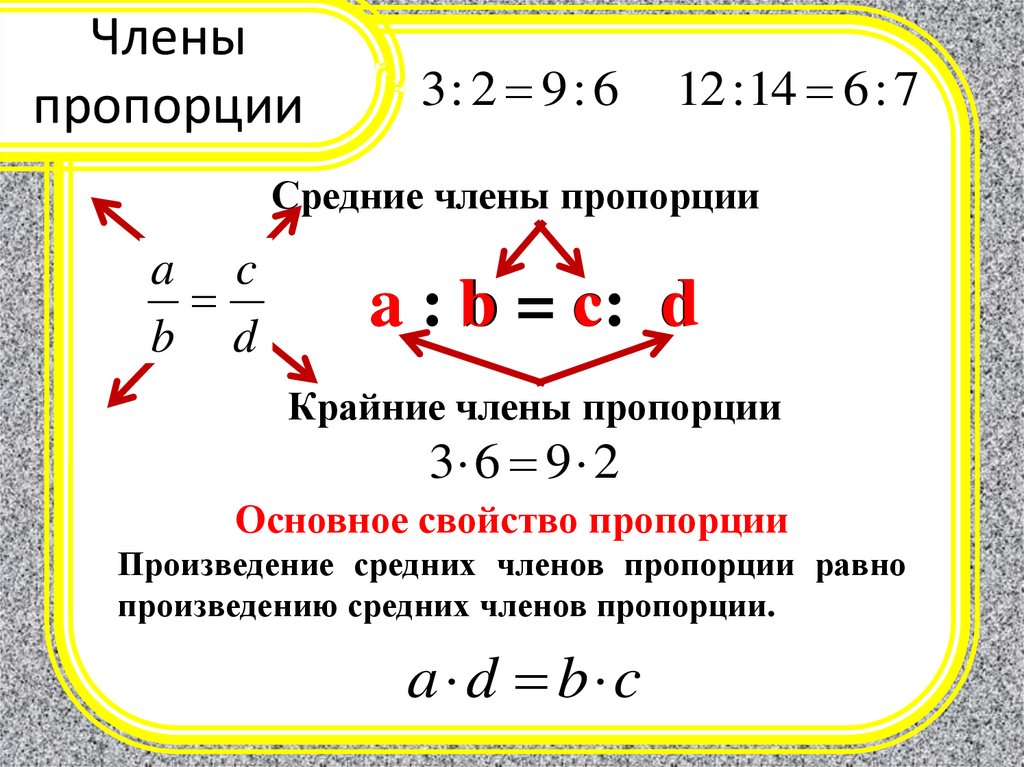 Наоборот, когда расстояние становится короче, значение времени также должно уменьшаться, чтобы поддерживать постоянное соотношение. Другими популярными примерами констант пропорциональности двух прямо пропорциональных переменных являются концентрация и плотность. В обоих этих примерах прямо пропорциональными переменными являются масса и объем.
Теперь поговорим о примере константы пропорциональности двух обратно пропорциональных величин. Продолжаем тему путешествий. На этот раз давайте посмотрим на формулу для расстояния:
s=v×ts = v \times ts=v×t
Это уравнение кажется более похожим на формулу константы пропорциональности двух обратно пропорциональные переменные , не так ли? Если расстояние (постоянное) останется прежним, то изменение скорости или времени вызовет изменение другой переменной. Поскольку речь идет об обратно пропорциональной зависимости, то увеличение скорости приводит к уменьшению времени в пути. Мы наблюдаем этот процесс в реальной жизни. Автомобиль, движущийся с более высокой скоростью, доедет до места назначения за более короткое время. В свою очередь, если мы хотим продлить время в пути (например, полюбоваться окрестностями или сэкономить на бензине), то скорость должна будет уменьшиться. Необходимо сохранить постоянное соотношение. В последних абзацах этого текста вы найдете несколько других реальных примеров пропорций и инструкции по их решению.
Как решать пропорции – примеры пропорций
Предположим, что у нас есть та же пропорция 7/127/127/12, но мы хотим масштабировать ее до большего эквивалентного отношения со знаменателем 969696. Для этого мы составить две равные пропорции и найти недостающую часть. Процесс решения пропорции выглядит следующим образом:
Установите обе дроби, пометив недостающую часть любой переменной по вашему выбору.
Поставьте знак равенства между двумя соотношениями. Обратите внимание, что соотношение и пропорция — это одно и то же.
Изолировать переменную с помощью перекрестного умножения, которое представляет собой умножение знаменателя одной пропорции на числитель другой и наоборот.
Решите для переменной.
Используйте калькулятор пропорций, чтобы проверить свой ответ. Теперь вы знаете все о решении пропорций.
Решая приведенный выше пример, получаем:
712=x9612x=96×712x=672x=56\frac{7}{12} = \frac{x}{96} \\[0.8em] 12x = 96 х 7 х [0,8 см] 12x = 672 \\[0,8см] х = 56 127=96x12x=96×712x=672x=56
Мы рекомендуем вам использовать калькулятор пропорций, если вы решаете пропорции с большими числами или с десятичными дробями.
С помощью пропорций можно регулировать количество ингредиентов в рецепте для большего количества гостей. Если вы хотите испечь блины, наш калькулятор рецептов блинов подскажет, что именно вам нужно приготовить на определенное количество человек.
Золотое сечение
В природе и строительстве существует особое соотношение, которое достигается, когда две величины имеют такое же отношение, как отношение их суммы к большей из двух величин. Это известно как золотое сечение , которое имеет значение примерно 1,618 . Мы знаем, что это звучит очень сложно, но вскоре все прояснится. Формула золотого сечения для двух величин aaa и bbb:
a+ba=ab\frac{a+b}{a} = \frac{a}{b}aa+b=ba
Калькулятор золотого сечения удобен для расчета этого отношения.
Золотое сечение можно увидеть в архитектуре и вообще в формах, таких как прямоугольник. Прямоугольник называется золотым, если при заданной ширине w=aw = aw=a и длине l=a+bl = a + bl=a+b отношение (a+b)/a=a/b(a+b )/a = a/b(a+b)/a=a/b дает значение приблизительно 1,618. Золотое сечение — это предел отношений последовательных чисел Фибоначчи и бесконечного десятичного числа. Таким образом, мы используем приблизительное значение 1,618. Калькулятор золотого прямоугольника рассчитает длину и ширину золотого прямоугольника.
В геометрии калькулятор пропорций пригодится при работе с подобными многоугольниками. По определению, два многоугольника называются подобными, если их стороны пропорциональны. Чаще всего это применяется с треугольниками. Закон синусов для треугольников основан на том, что существует пропорциональная связь между сторонами и углами треугольника.
Закон кратных пропорций – пропорциональные отношения в химии
Умение решать пропорции также может пригодиться при работе с химическими реакциями. Закон кратных пропорций — одно из фундаментальных правил стехиометрии, открытое британским химиком Джоном Дальтоном. Это методология расчета количества реагентов и продуктов химических реакций. Чтобы получить помощь в этом, ознакомьтесь с нашим калькулятором теоретической доходности. Полное заявление Далтона выглядит так:
Если два элемента образуют между собой более одного соединения, то отношения масс второго элемента, которые соединяются с фиксированной массой первого элемента, будут отношениями небольших целых чисел.
Говоря менее научным языком, если мы разделим массы атомов разных элементов, образующих одну частицу (например, CO₂ – углекислый газ), мы всегда получим постоянное отношение , характерное для этой частицы. Результат будет состоять очень часто из небольших чисел.
Покажем это на примере и рассчитаем соотношение для серной кислоты – H₂SO₄ :
Во-первых, мы должны подсчитать числа атомов определенных элементов, образующих серную кислоту. У нас есть 2 атома водорода H, 1 атом серы S и 4 атома кислорода O.
Во-вторых, нам нужно вычислить суммарную массу атомов каждого элемента. Один атом водорода весит 1 u (u обозначает атомную единицу массы), один атом кислорода весит 16 u, а один атом серы имеет массу 32 u.
Совместная масса атомов водорода: 2×1 u=2 u2 \times 1 \ \mathrm u = 2 \ \mathrm u2×1 u=2 u,
Общая масса кислорода в частице серной кислоты составляет: 4×16 u=64 u4 \times 16 \ \mathrm u = 64 \ \mathrm u4×16 u=64 u,
В этой частице всего один атом серы, поэтому вес серы равен 32 u32 \ \mathrm u32 u.
Последнее, что нужно сделать, это разделить все числа одно на другое. Единственное условие состоит в том, что мы должны сохранять все числа как целые числа. Мы не можем создавать дроби. Это будет выглядеть так:
H/O/S ⁣= ⁣2/64/32 ⁣= ⁣1/32/16\quad \mathrm H / \mathrm O / \mathrm S \! «=» 2/64/32\! «=» 1 / 32 / 16H/O/S=2/64/32=1/32/16
Вот и все! Мы получили соотношение малых чисел для частицы серной кислоты.
Благодаря этому знанию мы можем сказать, что если у нас есть 1 г (или любая другая единица массы) водорода, нам нужно добавить 16 г серы и 32 г кислорода, чтобы быть уверенным, что все атомы каждого элемента займут участие в реакции и что не будет никаких остатков.
У нас есть для вас задание! Проверьте (используя наш калькулятор пропорций), сколько граммов водорода и кислорода могут полностью прореагировать с 352 граммами серы, образуя серную кислоту (вы можете найти ответ в конце этого текста).
Есть и другие примеры пропорциональных отношений в химии. Молярность показывает соотношение между числом молей определенного растворенного вещества (растворенного вещества) и объемом раствора. Некоторых химиков-любителей может заинтересовать ABV (алкоголь по объему), представляющий отношение между объемом алкоголя и общим объемом напитка.
Определение прямого пропорционального налога
После беглого знакомства с миром химии пришло время посмотреть, сможем ли мы найти наши любимые пропорции в финансах. На самом деле, мы можем! Некоторые из налогов, которые мы платим, являются пропорциональными налогами. Это означает, что ставка налога является фиксированной , и каждый должен платить один и тот же процент от своего дохода (или любой другой стоимости, подлежащей пропорциональному налогообложению).
Давайте проиллюстрируем это на примере. Пропорциональная ставка налога составляет 15%. Человек X имеет доход в размере 15 000 долларов США, поэтому налог, который ему или ей придется заплатить в конце налогового года, будет равен:
15 долларов США, ⁣000×15%=2 доллара США, ⁣250\15 долларов США,\! 000 \умножить на 15\% = \$2,\!250$15,000×15%=2,250$
В свою очередь, человек Y зарабатывает 125,000$. Однако определение пропорционального налога требует, чтобы ставка была фиксированной, поэтому для расчета налога, который ему или ей придется заплатить, мы можем использовать аналогичную формулу:
$125, ⁣000×15%=$18, ⁣750\$125,\!000 \times 15\% = \$18,\!750$125,000×15%=$18,750
Хотя сумма налога, уплаченная лицом Y больше, чем налог лица X, это такая же часть их дохода в целом, а именно 15/100 или 15%.
Еще один вид налога (вероятно, самый популярный) — прогрессивный налог. Это похоже на пропорциональный налог, поскольку вы также должны платить определенный процент от своего дохода. Разница в том, что этот процент (или налоговая ставка) меняется с увеличением дохода. В прогрессивном налоге существуют определенные налоговые ставки для определенных диапазонов величины дохода. Например, люди с доходом менее 100 000 долларов могут платить 20% своего заработка, а люди с доходом более 100 000 долларов могут иметь ставку налога в размере 25%.
Ответ на вопрос: По закону кратных пропорций 352 грамма серы могут полностью прореагировать с 22 граммами водорода и 704 граммами кислорода с образованием серной кислоты.