Калькулятор расчета объёма жидкости в цистерне онлайн
Инструкция для калькулятора количества и объема жидкости в цистерне
Размеры вводите в миллиметрах:
D – диаметр емкости можно замерить рулеткой. Необходимо помнить что диаметр – это отрезок наибольшей длины, соединяющий две точки на окружности и проходящий через ее центр.
H – уровень жидкости замеряют, используя метршток, но если такого инструмента нет под рукой, воспользуйтесь обычным стержнем из проволоки или деревянной планкой подходящей длины. Соблюдая меры безопасности, опустите строго вертикально стержень в цистерну до дна, отметьте на нем уровень, достаньте и измерьте рулеткой. Также определить H можно, измерив, расстояние от верха цистерны до поверхности жидкости и отняв этот показатель от значения диаметра.
L – длина емкости.
Если необходим чертеж в бумажном виде, целесообразно отметить пункт «Черно-белый чертеж».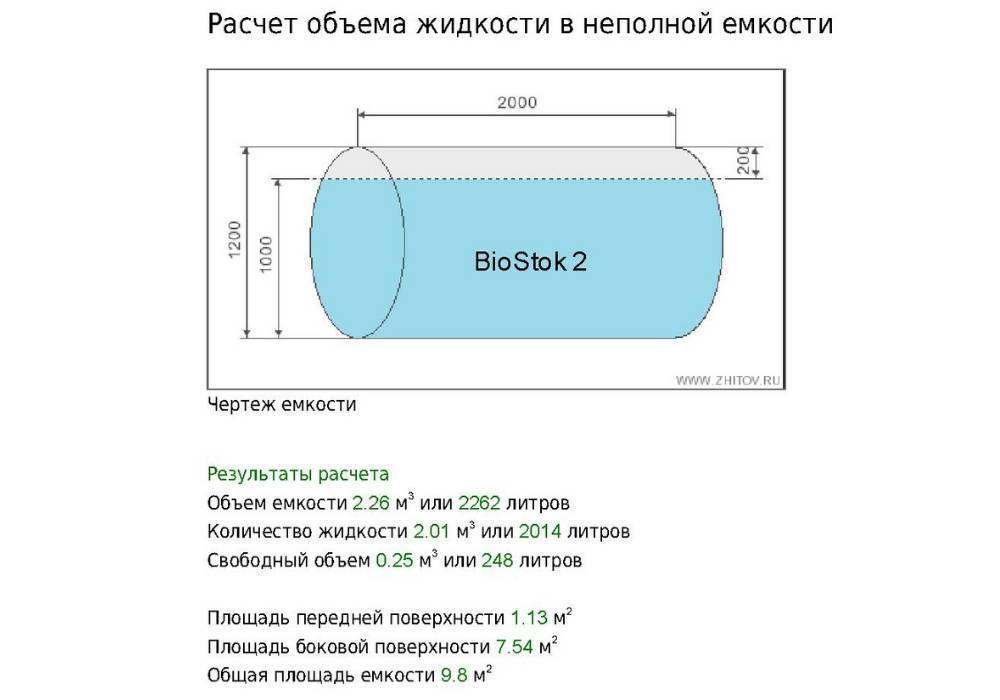
Нажмите «Рассчитать» и получите следующие данные:
Объём емкости – этот параметр характеризует полный объём цистерны, т.е. какое максимальное количество жидкости в кубических метрах или литрах может в нее поместиться.
Количество жидкости – сколько вещества находится в цистерне на данный момент.
Свободный объём позволяет оценить, сколько жидкости еще можно залить в емкость.
В результате, Вы получаете расчет не только объема цистерны, но и объема жидкости в неполной цистерне.
Изделия из металла следует периодически красить, тогда срок их службы значительно возрастет. Зная площадь передней поверхности, площадь боковой поверхности и общую площадь емкости легко оценить необходимое количество лакокрасочных материалов для обработки всей емкости или ее отдельных частей.
Объем трубы
Геометрия трубопроводов и емкостей цилиндрической формы зачастую ставит в тупик даже самых опытных строителей при попытке «на глаз» посчитать, сколько воды или любой другой жидкости находится внутри. Кроме того, расчет объема трубы нередко приходится выполнять в связи с вопросами заполнения систем отопления, канализации и водопроводных труб, где остаточное количество жидкости влияет на работоспособность систем.
Как можно посчитать объем воды внутри трубы
Вычислить объем воды в трубе можно несколькими способами:
- Использовать онлайн калькулятор или простейшую программку, набранную в Exele;
- Рассчитать значение вручную, используя тригонометрическую формулу из курса школьных задачек;
- Применить табличный вариант значений из справочника машиностроителя.
Чем проще метод расчета, тем меньше шансов допустить ошибку, даже если абсолютно уверены в правильности используемой методики.
Важно! Если полистать учебник тригонометрии, можно убедиться, что задачу, как рассчитать объем трубы, решают школьники уже не один десяток лет. Поэтому не стоит пытаться найти свое оригинальное решение и изобретать велосипед заново, просто воспользуйтесь методикой упрощенного расчета, составленной умным человеком.
Главное, перед тем как посчитать объем трубы, проверьте методику расчета на практике простейшим способом. Например, можно использовать небольшую цилиндрическую емкость или бак. Хорошим помощником может стать мерный стакан или цилиндрическая градуированная колба. Сравните рассчитанный и реальный объёмы воды в емкости.
Простейшие способы расчета объема заполнения трубы
Прежде всего, стоит определиться с исходными данными или параметрами трубы. Если речь идет об обычной цилиндрической трубе, то полный объем можно рассчитать простым арифметическим действием — умножить площадь сечения на длину трубы, V=S*L.
На практике вариантов расчета объема трубы в литрах или кубах может быть два:
- Полный внутренний объем трубопровода.
 Чаще всего такой случай возникает при проливке системы тепло или водоснабжения, когда необходимо рассчитать потребное количество реактива, исходя из объема воды, полностью заполняющего трубы;
Чаще всего такой случай возникает при проливке системы тепло или водоснабжения, когда необходимо рассчитать потребное количество реактива, исходя из объема воды, полностью заполняющего трубы; - Более сложный случай – частичное заполнение цилиндрического объема. Например, в случаях, когда имеется цилиндрическая цистерна или пластиковая емкость, установленная горизонтально, и вода заполняет лишь небольшую часть бака.
Измерения внутреннего объема трубопровода
Чтобы определить количество воды в трубе, измерим или возьмем из справочника внутренний диаметр трубопровода. Если искать справочные данные нет времени, можно измерить наружный диаметр и толщину стенки в миллиметрах. Далее вычитаем из наружного диаметра D удвоенную толщину стенки и получаем d— внутренний диаметр.
По формуле S=(3.14*d2)/4 рассчитываем площадь сечения внутреннего объема и умножаем на длину трубопровода V= S*L. Далее, чтобы получить объем в литрах, вычисленное значение необходимо разделить на 1000000.
Если расчет выполнялся для химической обработки или промывки трубопровода или теплообменника значительной длины, например, в несколько сот метров, то специалисты рекомендуют делать поправку на температуру. При высокой температуре металл расширяется, а значит, и увеличивается внутренний объем трубы.
Расчет для частичного заполнения трубы
Этот случай сложнее, и требует определенного понимания процесса. Первоначально необходимо определиться с тем, какой параметр реально можно измерить. Можно измерять высоту столба жидкости с помощью мерного шеста, или используя поплавковый уровнемер, определить расстояние от верхней стенки трубы до зеркала воды. Первый метод проще.
Чаще всего проблема нахождения объема воды, заполняющего емкость или трубу на относительно небольшом уровне, решается с помощью программного модуля. Его можно выбрать на сайте или сделать самому по приведенной ниже формуле и схеме.
Чтобы не возникало сомнений в правильности вычисления, один разочек посчитать объем можно вручную, для типового случая с мерным стаканом.
Если внимательно проанализировать приведенную методику, то можно увидеть, что в формуле используется тригонометрическая функция, но нет никаких других опорных данных, кроме высоты или уровня жидкости h и радиуса R. Чтобы не попасть впросак, следует понимать, что это радиус внутреннего пространства трубы. Поэтому величину R необходимо определить так: измерить по наружному диаметру, вычесть удвоенную толщину стенки и поделить на 2.
С помощью программки или сайта можно составить целую таблицу значений объема для различных уровней жидкости. Это будет полезным, если подобную задачу приходится решать довольно часто.
Для наиболее ленивых и смекалистых все подобные вычисления были неоднократно проделаны высококлассными инженерами и специалистами. Результаты расчетов сведены в таблицу и даже пересчитаны в относительные величины, чтобы сделать методику более универсальной.
Остается измерить высоту жидкости в трубе и подставить свое значение внутреннего диаметра.
Заключение
Разумеется, пользование тригонометрическими формулами или даже табличными методиками может показаться сложным. В этом случае придется слепо довериться сайту или онлайн-калькулятору. Подобные схемы упрощают жизнь, но за достоверность полученных результатов поручиться очень сложно.
Калькулятор расчета минимально необходимого диаметра водопроводной трубы
Если хозяин дома берется за самостоятельное проектирование системы водоснабжения, то ему предстоит решить множество различных задач. Одна из основных – это правильный подбор труб для прокладки магистралей от источника к дому и для внутренней разводки. Они выбираются по нескольким важным критериям, в зависимости от условий эксплуатации на конкретном участке. Но обязательным общим критерием является достаточность диаметра трубы для полноценной работы всего водопровода или его отдельной «ветки».
Согласитесь, мало толку от неправильно спланированного водопровода, если от недостаточного поступления воды из кранов льются слабые струйки, принять нормально душ в приобретенной кабинке – не выходит, стиральная или посудомоечная машина начинают сигнализировать кодами ошибок и т.п. Не особо комфортна бывает даже та ситуация, когда работа одного сантехнического прибора сказывается на возможностях другого. Например, кто-то моется в ванной, и поэтому на кухне практически ничего нельзя делать из-за слаого напора. А ведь таких точек в доме может быть и намного больше! Все эти неприятности, чаще всего – от неправильно подобранного диаметра трубы на определённом участке. И он просто не справляется с нужными объёмами подачи воды на конечные устройства.
Определиться с этим параметром поможет калькулятор расчета минимально необходимого диаметра водопроводной трубы. Ниже будет дано несколько полезных пояснений по работе с ним.
Перейти к расчётам
Пояснения по работе с калькуляторомРасчет – совсем несложен, базируется на известных физических и геометрических формулах и на рекомендациях по эксплуатации водопровода и сантехнических устройств, изложенных в СНИП.
Итак, необходимо найти диаметр D, который обеспечит прохождение через трубу за единицу времени требуемого количества воды.
Вспоминаем формулу площади круга (в нашем случае – это внутреннее сечение трубы)
S = π × D² / 4
S — площадь сечения трубы, м²
D — внутренний диаметр трубы, м;
π — не требующая особого представления константа, значение которой можно взять равным 3.14 – супер-точность нам не требуется.
Отсюда, диаметр равен:
D = √(4 × S / π)
Идем дальше. Наш водопровод с сечением S должен быть способен обеспечить определенный расход воды на точке потребления (одной или одновременно нескольких).
Наш водопровод с сечением S должен быть способен обеспечить определенный расход воды на точке потребления (одной или одновременно нескольких).
Количество воды, проходящее через трубу в единицу времени (а это и есть расход), определяется несложной формулой:
Q = S × V
Q — необходимый расход воды, м³/с;
V — скорость потока воды в трубе, м/с.
Преобразуем это выражение для определения площади сечения S…
S = Q / V
… и подставим в первую формулу. Тем самым – получим необходимое нам рабочее выражение.
D = √ (4 × Q / (π × V))
Так как в формуле присутствуют числовые константы, можно сделать с ними некоторые упрощения. В итоге перед нами готовая формула для дальнейшей работы.
D = 1,129 × √ (Q / V)
Теперь о том, откуда берутся исходные величины.
- Расход воды.
 Любой сантехнический прибор характеризуется свойственным ему расходом воды (литров в секунду), при котором не нарушается комфортность пользования или корректность работы устройства. Аналогично – и для бытовой техники, подключаемой непосредственно к водопроводным трубам (стиральных и посудомоечных машин).
Любой сантехнический прибор характеризуется свойственным ему расходом воды (литров в секунду), при котором не нарушается комфортность пользования или корректность работы устройства. Аналогично – и для бытовой техники, подключаемой непосредственно к водопроводным трубам (стиральных и посудомоечных машин).
Примерные значения таких расходов показаны в таблице ниже:
| Разновидности сантехнических приборов и бытовой техники, подключаемой к водопроводу. | Примерный нормальный расход (литров в секунду) |
|---|---|
| Смеситель умывальника | 0.1 |
| Сливной бачок унитаза | 0.1 |
| Биде | 0.08 |
| Смеситель на кухонной мойке | 0.15 |
| Посудомоечная машина | 0.2 |
| Смеситель с душем для ванны | 0.25 |
| Душевая кабинка обычная | 0.25 |
| Душевая кабинка или ванна (джакузи) с гидромассажем | 0. 3 3 |
| Стиральная машина-автомат | 0.3 |
| «Хозяйственный» кран ¾» (полив участка, мытье автомобиля, уборка и прочие надобности) | 0.3 |
Практика, да и расчеты показывают, что для любой точки, потребляющей до 0,15 л/с обычно бывает достаточно диаметра трубы в 15 мм (½»), до 0,25÷0,3 л/с – 20 мм (¾»). Но хорошо спланированная водопроводная система должна обеспечивать и одновременную работу нескольких сантехнических и бытовых приборов. То есть значение расхода может быть и значительно выше. Безусловно, вероятность того, что все они будут включены разом – очень невелика. Поэтому при подсчете суммарного расхода в формулу вводят вероятностный коэффициент, зависящий от общего количества подключённых на рассчитываемом участке точек потребления.
В нашем калькуляторе этот коэффициент тоже предусмотрен. Пользователю необходимо лишь указать, какие конкретно приборы и в каком количестве подключены в системе (не менее двух). Или на определённом ее участке, для которого проводится расчет – например, на одном из ответвлений коллектора.
Или на определённом ее участке, для которого проводится расчет – например, на одном из ответвлений коллектора.
Суммарный расход программа подсчитает самостоятельно.
- Скорость потока воды в трубе. В соответствии с положениями СНИП 2.04.01-85 «Внутренний водопровод и канализация зданий» скорость потока во внутренних водопроводных сетях ограничивается максимальным значением в 3 м/с. Однако, практика показывает, что для домашних систем с их преобладанием труб малого диаметра (до 1 дюйма) скорость потока желательно иметь поменьше. Дело в том, что с ее ростом резко увеличиваются показатели гидравлического сопротивления. И плюс к тому — на этом фоне водопровод частенько начинает чувствительно шуметь.
Считается, что для домашних условий оптимальными значениями скорости, при которых достигается «гармония» между производительностью трубы (расходом) и требуемым напором воды, будет диапазон примерно от 0,6 до 1,0 м/с.
Впрочем, это рекомендация, и никто не мешает просчитать и для других показателей скорости — как больше указанного «номинала», так и меньше его. В программе такая возможность предусмотрена.
В программе такая возможность предусмотрена.
Результат показывается в миллиметрах.
Надо сказать, что это, возможно, еще не конечный… Возможно, придётся вносить корректировки на потери напора.
Как проверить проектируемый участок водопровода на потери напора?
Если упустить этот момент, то может случиться, что напор воды на конечной точке окажется слабоват для нормальной работы устройств. Заранее проверить собственный проект поможет калькулятор расчета потерь напора в водопроводе.
Выбор диаметра трубы в зависимости от расхода воды онлайн калькулятор таблица
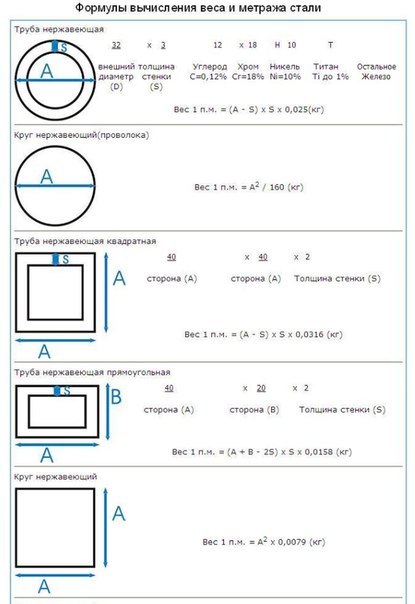
Таблица выбора диаметра трубы от расхода воды
| Диаметр, дюйм |
Диаметр, мм |
Расход воды м3/час |
| 1″ |
25. 4 4 |
1.8 |
| 32 |
3.3 | |
| 1 1/2″ |
38.1 |
5.1 |
| 2″ |
50.8 |
10.7 |
| 2 1/2″ | 63. 5 5 |
19.1 |
| 3″ |
76 |
30.4 |
| 3 1/2″ | 89 |
45.6 |
| 4″ |
102 |
|
| 4 1/2 | 114 |
86. 4 4 |
Расчет расхода воды в зависимости от диаметра трубы. Не целые числа вводите через точку (АА.АА)
Значения величин в этой таблице основаны на принятых в практике соответствиях диаметров труб расходам воды. Эти практические расчеты основаны на том требовании, что скорость воды в трубах не должна достигать шумового предела (приблизительно 2 метра в секунду для труб диаметром до 50 мм и 3 метра в секунду для труб диаметром до 114 мм), и обычно она оказывается в диапазоне 0.8-1.5 м/c для труб диаметром до 50 мм и до 2.5 метров в секунду для труб диаметром до 114 мм, в бетонном производстве трубы большего диаметра для подачи воды практически не используются. Поэтому вычисления по этой таблице допустимы только до диаметра 114 мм. Для труб большего диаметра данные мы не собирали и не анализировали.
Еще раз обращаем внимание — расчеты на данной странице можно вести только для труб диаметром до 114 мм. !!!
!!!
При выборе диаметра трубы нужно учесть непостоянный характер потребления!
К примеру : необходимо для производства 30 м3 бетона 4.5 тонн воды и 2 тонны для заправки миксеров, итого 6.5 тонн воды. Казалось бы, по таблице можно выбрать с запасом трубу диаметром 50 мм. с расходом 10.7 тонны воды в час. Это неправильный ответ. Вода для приготовления бетона будет потребляться не час, а 20-30 минут, остальное время — выгрузка бетона, технологические простои. Поэтому труба должна пропускать не 4.5, а 9-13.5 тонн воды для приготовления бетона. Ну и плюс 2 тонны для миксеров. Итого не 6.5, а 11-15.5 тонн воды. Нужно выбирать 53-ю или 57-ю трубу. Кстати, все вышесказанное относится и к выбору насосов.
Компания Тех Альянс не несет ответственности за любые последствия, наступившие при использовании результатов данных расчетов.
Объем трубы в литрах, рассчитать по диаметру и длине
Содержание:
- Рассчитать объем трубы в литрах, калькулятор
- Как рассчитать объем трубы в литрах
Объем трубы в литрах можно рассчитать с помощью онлайн калькулятора двумя способами:
- указав наружный диаметр в мм, длину трубы в метрах и толщину стенки в мм. Будет удобен для вычисления объема в литрах для тех труб, у которых указана толщина стенок в нанесенной на нее маркировке, например, полипропиленовые для пайки и/или для скрутки фитингом.
- указав внутренний диаметр в мм и длину трубы в метрах (погонные метры).
Делая расчет объема трубы в литрах, необходимо помнить о возможных погрешностях, например, повороты, неполная заполняемость некоторых участков труб и т. д.
д.
Рассчитать объем трубы в литрах, калькулятор
- Зная толщину стенки, диаметр и длину
- Зная диаметр и длину
Как рассчитать объем трубы в литрах?
Чтобы узнать внутренний диаметр трубы, зная наружный, необходимо толщину стенки ( b ) умножить на 2, результат вычесть из наружного диаметра ( D ).
Формула выглядит следующим образом: Внутренний диаметр трубы = D — ( b * 2 )
Также можно воспользоваться таблицами, например, трубы для пайки. В которой уже указаны толщина стенки и ее диаметры для PN10, PN20 и PN25.
Для расчета объема цилиндра применяют формулу: V = Пи * R² * h = Пи * ( d² / 4 ) * h, где:
- Пи — 3,1415926;
- R – радиус цилиндра;
- d – диаметр цилиндра, в нашем случае — внутренний диаметр трубы;
- h – высота цилиндра, в случае расчета объема трубы h заменяем на L — длину трубы.
Исходя из этого, формула для расчета объема трубы по известному, внутреннему диаметру примет вид:
V объем трубы = Пи * ( d² / 4 ) * L
Важно! Перед началом расчета с помощью формул, все размеры необходимо перевести в единую меру, т. е. — сантиметры или дециметры.
е. — сантиметры или дециметры.
Пример расчета объема трубы в литрах
D (наружный диаметр трубы) = 17 мм, b (толщина стенки) = 1,3 мм, L (длина трубы) = 10 м.
Внутренний диаметр равен, d = 17 — (1.3*2) = 14,4 мм
Для расчета объема трубы, переводим значения в см:
- L = 10 м = 1000 см;
- d = 14,4 мм = 1,44 см;
- V трубы по внут. диам. = 3.1415926 * (1.44²/4) * 1000 = 1628,55 см³
- 1 см³ = 0,001 литру
- 1 литр = 1000 см³
Следовательно, объем трубы: V в литрах = 1628,55 * 0,001 = 1,62855 литра
Онлайн калькулятор расчета объема бетона
Для точного определения времени выполнения работ по бетонированию и количества расходуемого материала следует провести расчеты, в этом поможет онлайн калькулятор расчета объема бетона.
Калькулятор объема бетона самостоятельно рассчитает для вас необходимое количество раствора, предоставив максимально точные цифры. Расход учитывается в кубических метрах.
Расход учитывается в кубических метрах.
Рассчитать объем бетона фундаментной плиты или стяжки
Калькулятор ниже производит расчет бетона на плитный фундамент в соответствии со строительными нормами и правилами. Для расчета плитного фундамента необходимо знать площадь и толщину плиты, т.к. плита – это обыкновенный прямоугольный параллелепипед.
Плитный фундамент представляет собой замкнутую железобетонную цельную монолитную плиту, которая укладывается под всю площадь дома, распределяя тем самым нагрузку по всей длине.
Введите свои данные в поля для расчёта:
Площадь = Длина * Ширина фундаментной плины
Для выполнения расчетов нужно вести длину и ширину помещения (площадь основания), толщину стяжки. Измерить прямоугольник можно по самой опалубке или взять цифры из чертежной документации.
Если количество воды при изготовлении смеси определяете “на глаз”, а песок может быть разного объема и плотности, калькулятор может дать погрешность 10-20 %.
Правильно посчитать кубатуру бетона в этом случае намного сложнее: длину конструкции, в которую входит периметр с внешней стороны и длину всех перегородок между комнатами, мы должны умножить на ее высоту и ширину (при условии, что лента фундамента имеет по всей длине одинаковое сечение).
Обязательно нужно учитывать глубину грунтовых вод, ландшафт, почву и прочие факторы при расчете высоты фундамента.
Столбчатый фундамент считается одним из самых простых в изготовлении и, кроме этого, достаточно экономным по затратам на стройматериалы.
Фундамент состоит из ростверка (верхней части свайного или столбчатого фундамента, распределяющей нагрузку от несущих элементов здания) и свай (вертикальных опорных элементов), поддерживающих горизонтальную часть конструкции над грунтом. Расчет объема бетона здесь сложнее, чем в предыдущих случаях.
Нужно заранее спланировать расход материалов при штукатурных работах, так как неожиданная остановка в работе может сказаться на качестве выполненной работы.
Калькулятор может давать погрешность от 3 до 10% объема из-за не точности производства земляных работ, усадки грунта (бетон тяжелее воды в 2.5 раза), а так же незначительные потери при разгрузке бетона.
Расход воды через трубу при заданном давлении
Содержание статьи
Основная задача расчёта объёма потребления воды в трубе по её сечению (диаметру) – это подобрать трубы так, чтобы водорасход не был слишком большой, а напор оставался хороший. При этом необходимо учесть:
- диаметры (ДУ внутреннего сечения),
- потери напора на рассчитываемом участке,
- скорость гидропотока,
- максимальное давление,
- влияние поворотов и затворов в системе,
- материал (характеристики стенок трубопровода) и длину и т.д..
Подбор диаметра трубы по расходу воды с помощью таблицы считается более простым, но менее точным способом, чем измерение и расчёт по давлению, скорости воды и прочим параметрам в трубопроводе, сделанный по месту.
Табличные стандартные данные и средние показатели по основным параметрам
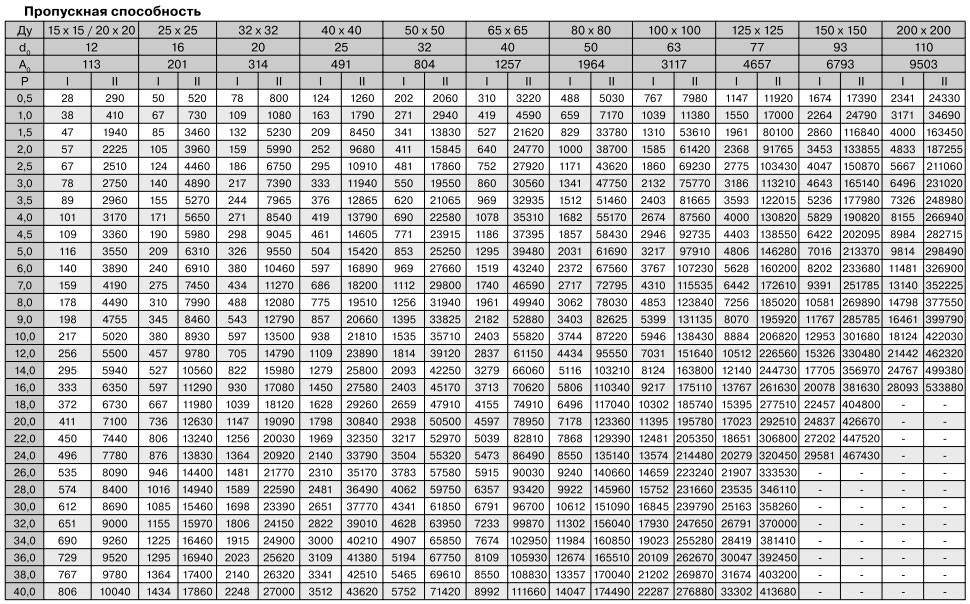
Для определения расчётного максимального расхода воды через трубу приводится таблица для 9 самых распространённых диаметров при различных показателях давления.
Среднее значение давления в большинстве стояках находится в интервале 1,5-2,5 атмосфер. Существующая зависимость от количества этажей (особенно заметная в высотных домах) регулируется путём разделения системы водообеспечения на несколько сегментов. Водонагнетение с помощью насосов влияет и на изменение скорости гидропотока. Кроме того, при обращении к таблицам в расчёте водопотребления учитывают не только число кранов, но и количество водонагревателей, ванн и др. источников.
Изменение характеристик проходимости крана с помощью регуляторов водорасхода, экономителей, аналогичных WaterSave (http://water-save.com/), в таблицах не фиксируются и при расчёте расхода воды на (по) трубе, как правило, не учитываются.
Способы вычисления зависимостей водорасхода и диаметра трубопровода
С помощью нижеприведённых формул можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода воды.
В данной формуле водорасхода:
- под q принимается расход в л/с,
- V – определяет скорость гидропотока в м/с,
- d – внутреннее сечение (диаметр в см).
Зная водорасход и d сечения, можно, применив обратные вычисления, установить скорость, или, зная расход и скорость – определить диаметр. В случае наличия дополнительного нагнетателя (например, в высотных зданиях), создаваемое им давление и скорость гидропотока указываются в паспорте прибора. Без дополнительного нагнетания скорость потока чаще всего варьируется в интервале 0,8-1,5 м/сек.
Для более точных вычислений принимают во внимание потери напора, используя формулу Дарси:
Для вычисления необходимо дополнительно установить:
- длину трубопровода (L),
- коэффициент потерь, который зависит от шероховатостей стенок трубопровода, турбулентности, кривизны и участков с запорной арматурой (λ),
- вязкость жидкости (ρ).

Зависимость между значением D трубопровода, скоростью гидропотока (V) и водорасходом (q) с учётом угла уклона (i) можно выразить в таблице, где две известные величины соединяются прямой линией, а значение искомой величины будет видно на пересечении шкалы и прямой.
Для технического обоснования также строят графики зависимости эксплуатационных и капитальных затрат с определением оптимального значения D, которое устанавливается в точке пересечения кривых эксплуатационных и капитальных затрат.
Расчёт расхода воды через трубу с учётом падения давления можно проводить с помощью онлайн-калькуляторов (например: http://allcalc.ru/node/498; https://www.calc.ru/gidravlicheskiy-raschet-truboprovoda.html). Для гидравлического расчёта, как и в формуле, нужно учесть коэффициент потерь, что предполагает выбор:
- способа расчёта сопротивления,
- материала и вида трубопроводных систем (сталь, чугун, асбоценмент, железобетон, пластмасса), где принимается во внимание, что, например, пластиковые поверхности менее шероховатые, чем стальные, и не подвергаются коррозии,
- внутреннего диаметры,
- длины участка,
- падения напора на каждый метр трубопровода.

В некоторых калькуляторах учитываются дополнительные характеристики трубопроводных систем, например:
- новые или не новые с битумным покрытием или без внутреннего защитного покрытия,
- с внешним пластиковым или полимерцементным покрытием,
- с внешним цементно-песчаным покрытием, нанесённым разными методами и др.
Читайте далее
Оставьте комментарий и вступите в дискуссию
Калькулятор объема трубы
Как определить объем трубы?
Цилиндр — это трехмерное твердое тело с конгруэнтными основаниями в паре параллельных плоскостей. Эти основания представляют собой конгруэнтные круги. Ось цилиндра — это отрезок прямой с концами в центрах оснований.
Высота или высота цилиндра, обозначаемая $ h $, — это перпендикулярное расстояние между его круглыми основаниями.
Далее мы будем рассматривать только правый цилиндр, т.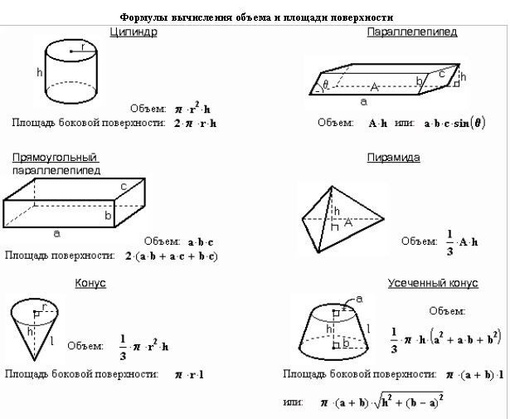 2) \ frac {\ pi} {4} \ times h $$
2) \ frac {\ pi} {4} \ times h $$
Трубы — Содержание воды — Вес и объем
| Размер трубы (внутренний диаметр) (дюйм) | Содержание воды | |||
|---|---|---|---|---|
| Объем | Вес (фунт / фут) | Объем / вес | ||
| (дюймы 3 / фут) | (галлоны / фут) | (литры / м, кг / м) | ||
| 1 / 4 | 0. 59 59 | 0,003 | 0,02 | 0,030 |
| 3/8 | 1,33 | 0,006 | 0,05 | 0,074 |
| 1/2 | 2,36 | 0,010 | 0,09 | 0,13 |
| 3/4 | 5,30 | 0,023 | 0,19 | 0,28 |
| 1 | 9,43 | 0,041 | 0,34 | 0,51 |
| 1 1/4 | 14.7 | 0,064 | 0,53 | 0,79 |
| 1 1/2 | 21,2 | 0,092 | 0,77 | 1,1 |
| 2 | 37,7 | 0,163 | 1,36 | 2,0 |
| 2 1/2 | 58,9 | 0,255 | 2,13 | 3,2 |
| 3 | 84,8 | 0,367 | 2,31 | 3,4 |
| 4 | 150.8 | 0,653 | 5,44 | 8,1 |
| 5 | 235,6 | 1,02 | 8,50 | 13 |
| 6 | 339,3 | 1,47 | 12,2 | 18 |
| 8 | 603,2 | 2,61 | 21,8 | 32 |
| 10 | 942,5 | 4,08 | 34,0 | 51 |
| 12 | 1357. 2 2 | 5,88 | 49,0 | 73 |
| 15 | 2120,6 | 9,18 | 76,5 | 114 |
- 1 фунт / фут = 1,49 кг / м
- 1 галлон ( США) / фут = 12,4 л / м
Обратите внимание, что для большинства труб номинальный размер не равен внутреннему диаметру. Для получения точных объемов — проверьте документацию на трубы или стандарт — и используйте калькулятор ниже.
Объемный вес для других жидкостей может быть рассчитан с учетом плотности.
Пример — содержание воды в трубе
Объем воды в трубе длиной 12 м и 2 « можно рассчитать как
(2,0 л / м) (12 м)
= 24 литра
Трубы — Калькулятор объема
Этот калькулятор можно использовать для расчета объема воды или других жидкостей в трубах. Калькулятор является универсальным и может использоваться для любых единиц, если единицы измерения согласованы. Если введено м результат м 3 / м и так далее.
Если введено м результат м 3 / м и так далее.
Внутренний диаметр трубы (м, мм, фут, дюйм …)
Используйте конвертер объема в левом столбце для других единиц.
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
Калькулятор объема конической ствола
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема трубки
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единица измерения объема в системе СИ — кубический метр, или м 3 . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер.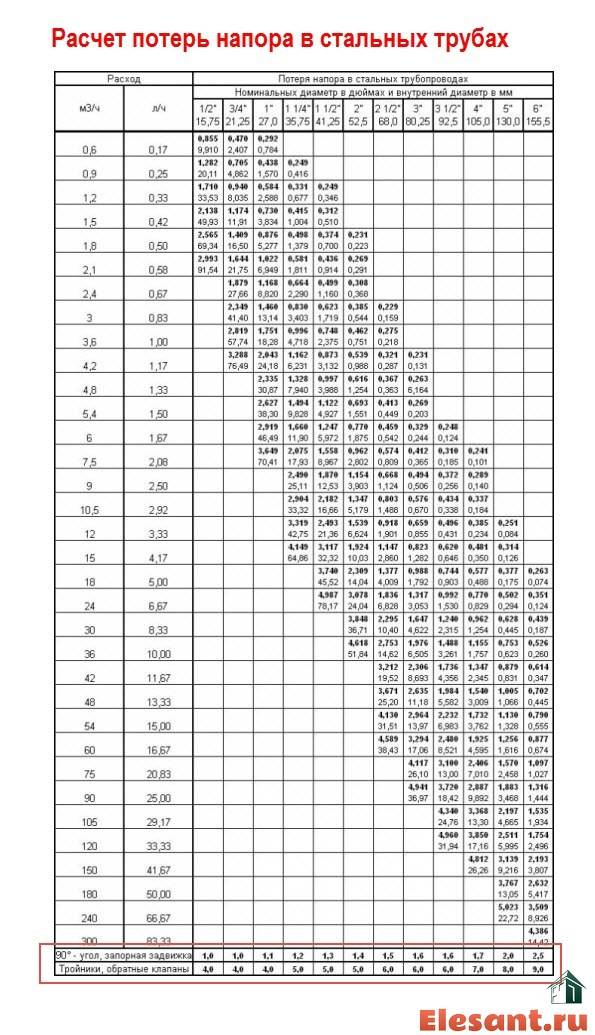 Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r . Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус формируется аналогично окружности набором отрезков прямой, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полукруглых линий, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
Математически конус формируется аналогично окружности набором отрезков прямой, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полукруглых линий, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, не зря потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем у сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.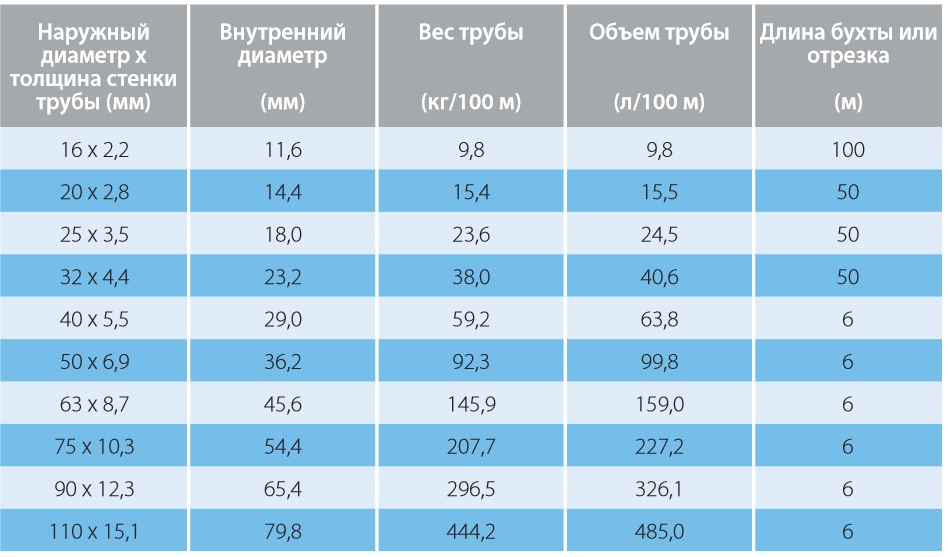 Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.
Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что он должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит замок из песка в своем доме и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в свою упаковку, рассчитан ниже:
Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на своем пути к самопознанию. Гималаи:
Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
где r, — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и ему нужно рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би есть усеченная пирамида с правым конусом, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10. 849 дюйм 3
849 дюйм 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки прямых, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипсоида. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1. 5 × 2 × 5 = 62,832 дюйма 3
5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямой. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
, где b — площадь основания, а h — высота
.Объем квадратной пирамиды:
, где a — длина края основания
EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра (объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
, где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы
EX: Beulah посвящен охране окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу через ручей. Он хочет облегчить доступ к своему дому и просит Беулу построить ему дорогу, следя за тем, чтобы ручей мог течь свободно, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые дамбы будут хорошей отправной точкой для прокладки трубы через ручей. Объем запатентованного бетона с низкой ударопрочностью, необходимый для строительства трубы с внешним диаметром 3 фута и внутренним диаметром 2.5 футов и длина 10 футов можно рассчитать следующим образом:
| объем = π × | × l0 = 21,6 фута 3 |
Единицы измерения общего объема
| Единица | кубических метров | миллилитров | ||
| миллилитров (кубических сантиметров) | 0,000001 | 1 | ||
| кубических дюймов | 0,00001639 | 16,39 | ||
| пинта | 0. 000473 000473 | 473 | ||
| кварта | 0,000946 | 946 | ||
| литр | 0,001 | 1,000 | ||
| галлон | 0,003785 | 3,785 | 900,365 0,03 0,68 | 0,03|
| кубический ярд | 0,764555 | 764,555 | ||
| кубический метр | 1 | 1,000,000 | ||
| кубический километр | 1,000,000,000 | 10 15 |
Расчет расхода 9 — Давление и диаметр Калькулятор расхода — давление и диаметр | Copely
Результаты
Щелкните вкладки ниже, чтобы просмотреть результаты.
Зависимость расхода жидкости от длины шланга Количество потока жидкости в зависимости от давления Зависимость расхода жидкости от диаметра ствола| Зависимость расхода жидкости от длины шланга | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Длина | 20.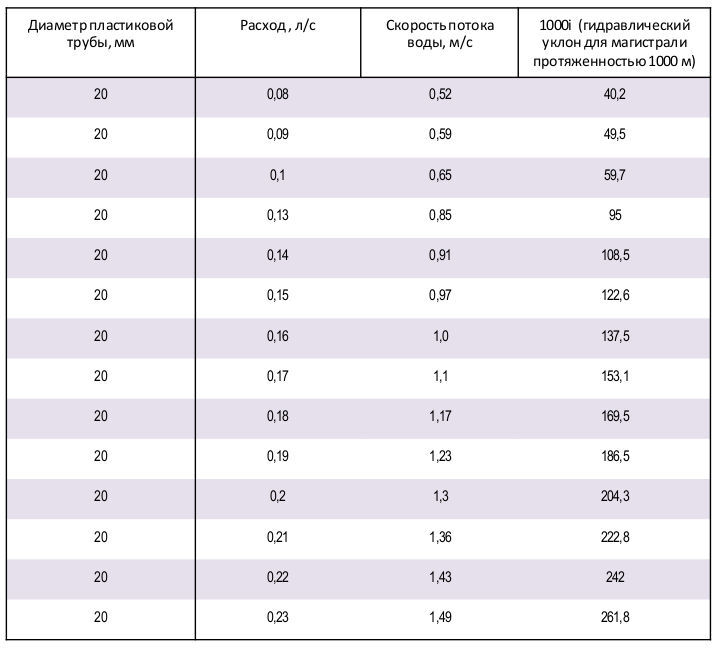 000 000 | 40,000 | 60,000 | 80,000 | 100 000 | 120,000 | 140.000 | 160,000 | 180,000 | 200,000 |
| Количество Расход жидкости (литры в минуту) | 95,273 | 68,458 | 56.202 | 48,807 | 43,727 | 39,961 | 37.026 | 34,656 | 32,689 | 31,023 |
| Диаметр отверстия (мм) | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
| Давление (бар) | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| Диаметр отверстия (дюймы) | 0.984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 |
Давление (фунт / кв. Дюйм) Дюйм) | 102,900 | 102,900 | 102,900 | 102,900 | 102,900 | 102,900 | 102.900 | 102,900 | 102,900 | 102,900 |
| Длина (фут) | 65,667 | 131,333 | 197.000 | 262,667 | 328,333 | 394 000 | 459,667 | 525,333 | 591 000 | 656,667 |
| Количество Расход жидкости (галлонов в минуту) | 20.960 | 15.061 | 12,364 | 10,738 | 9,620 | 8,791 | 8,146 | 7,624 | 7,192 | 6,825 |
| Коэффициент C | 20,105 | 20,105 | 20,105 | 20,105 | 20,105 | 20,105 | 20.105 | 20,105 | 20,105 | 20,105 |
| Скорость V (фут / сек) | 10.602 | 7,618 | 6.254 | 5,431 | 4,866 | 4,447 | 4,120 | 3,856 | 3,638 | 3,452 |
| Диаметр отверстия (фут) D | 0. 082021 082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 |
| Эквивалентная напорная жидкость, ч (фут) | 237,644 | 237,644 | 237,644 | 237,644 | 237.644 | 237,644 | 237,644 | 237,644 | 237,644 | 237,644 |
| Данные о зависимости расхода жидкости от давления | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Давление | 1,400 | 2,800 | 4.200 | 5,600 | 7.000 | 8.400 | 9,800 | 11.200 | 12.600 | 14 000 |
| Кол-во расход жидкости (л / мин) | 19,555 | 27,655 | 33,871 | 39,110 | 43,727 | 47.900 | 51,738 | 55,310 | 58.666 | 61,839 |
| Диаметр отверстия (мм) | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
| Длина | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Диаметр отверстия (дюйм) | 0. 984 984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 | 0,984 |
| Давление (фунт / кв. Дюйм) | 20,580 | 41.160 | 61,740 | 82,320 | 102,900 | 123.480 | 144.060 | 164.640 | 185,220 | 205,800 |
| Длина (фут) | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 |
| Кол-во расход жидкости (галлон / мин) | 4.302 | 6.084 | 7,452 | 8,604 | 9,620 | 10,538 | 11,382 | 12,168 | 12,906 | 13,605 |
| Коэффициент C | 20,105 | 20,105 | 20,105 | 20,105 | 20,105 | 20,105 | 20.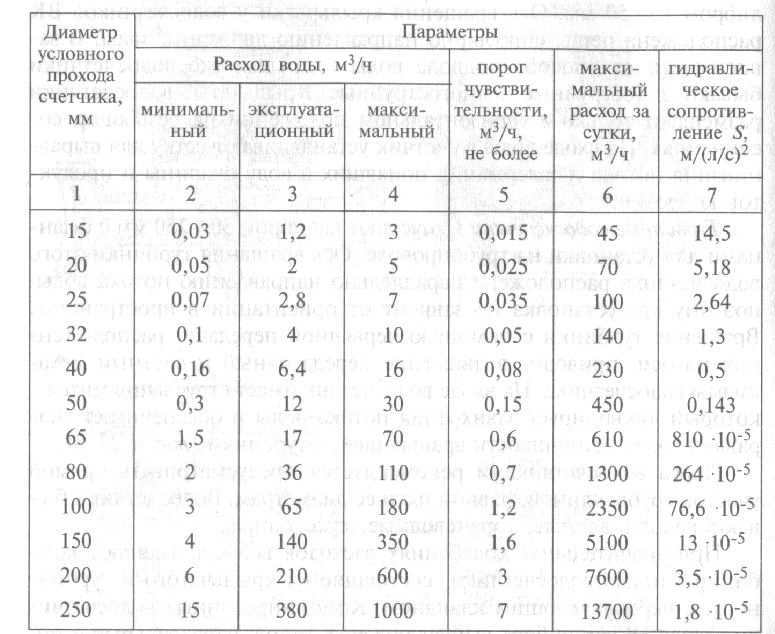 105 105 | 20,105 | 20,105 | 20,105 |
| Скорость V (фут / сек) | 2,176 | 3,077 | 3,769 | 4,352 | 4,866 | 5,330 | 5,757 | 6,155 | 6.528 | 6,881 |
| Диаметр отверстия (фут) D | 0.082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 | 0,082021 |
| Эквивалентная напорная жидкость, ч (фут) | 47,529 | 95,058 | 142,587 | 190.115 | 237.644 | 285,173 | 332,702 | 380,231 | 427,760 | 475,289 |
| Количество потока жидкости в зависимости от диаметра отверстия | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Диаметр отверстия | 5.000 | 10.000 | 15 000 | 20. 000 000 | 25.000 | 30,000 | 35,000 | 40,000 | 45,000 | 50,000 |
| Кол-во расход жидкости (л / мин) | 0,091 | 2,204 | 8,792 | 21,989 | 43,727 | 75,790 | 119,849 | 177,478 | 250,177 | 339.374 |
| Давление (бар) | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| Длина | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Диаметр отверстия (дюйм) | 0.197 | 0,394 | 0,591 | 0,787 | 0,984 | 1,181 | 1,378 | 1,575 | 1.772 | 1,969 |
| Давление (фунт / кв. Дюйм) | 102,900 | 102,900 | 102,900 | 102,900 | 102,900 | 102,900 | 102.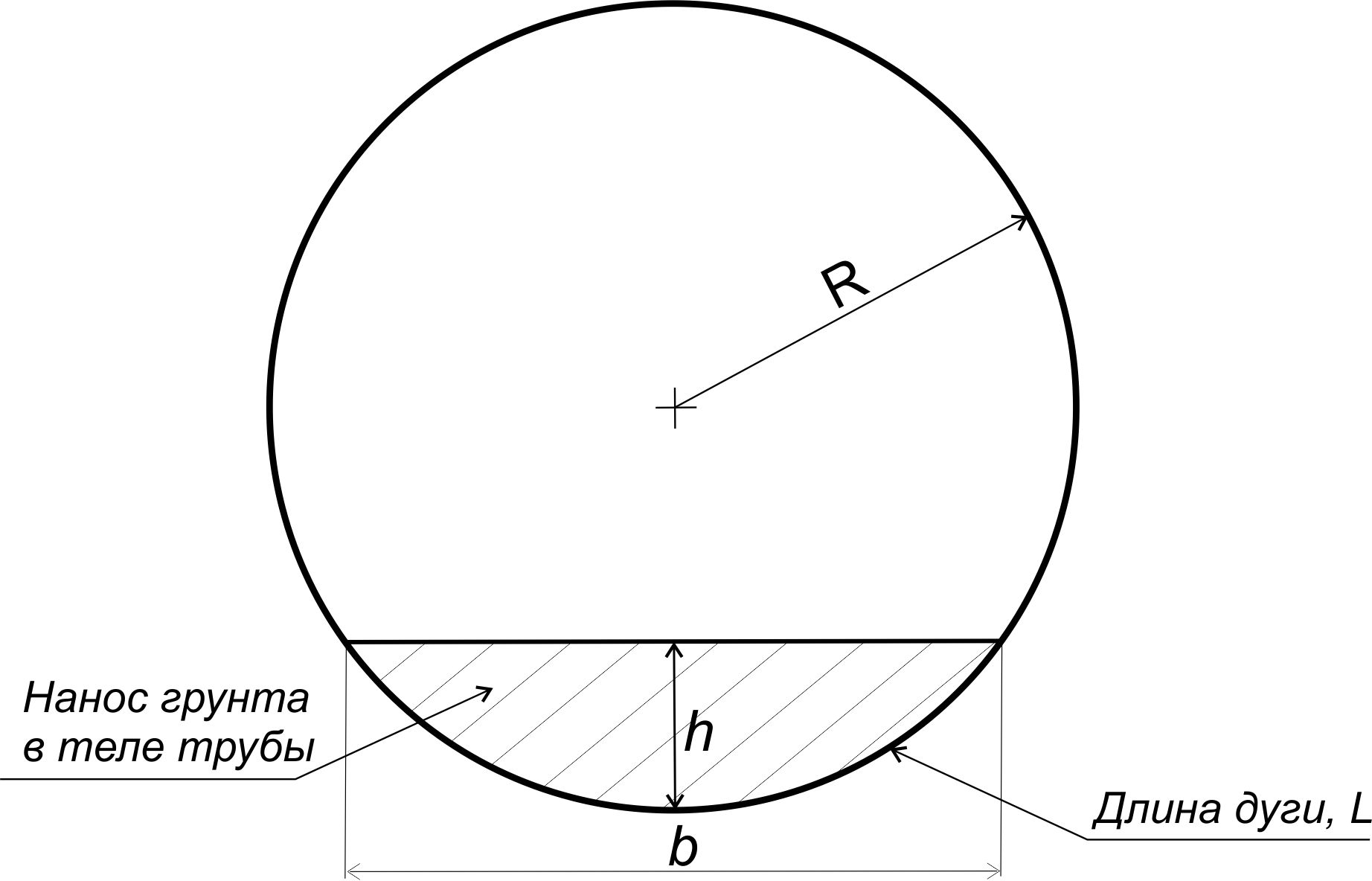 900 900 | 102,900 | 102,900 | 102,900 |
| Длина (фут) | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 | 328,333 |
| Кол-во расход жидкости (галлон / мин) | 0.020 | 0,485 | 1,934 | 4,838 | 9,620 | 16,674 | 26,367 | 39,045 | 55.039 | 74,662 |
| Коэффициент C | 2,314 | 9,976 | 14,458 | 17,638 | 20,105 | 22,120 | 23.824 | 25,300 | 26,602 | 27,767 |
| Скорость V (фут / сек) | 0,252 | 1,533 | 2,718 | 3,823 | 4,866 | 5,857 | 6.804 | 7,715 | 8,592 | 9,441 |
| Диаметр отверстия (фут) D | 0. 016 016 | 0,033 | 0,049 | 0,066 | 0,082 | 0,098 | 0,115 | 0,131 | 0,148 | 0,164 |
| Эквивалентная напорная жидкость, ч (фут) | 237,644 | 237,644 | 237,644 | 237,644 | 237,644 | 237.644 | 237,644 | 237,644 | 237,644 | 237,644 |
Расход жидкости в трубах
Количество жидкости, которое будет выпущено через шланг, зависит от давления, приложенного на подающем конце, длины шланга и диаметра отверстия. Характер поверхности отверстия, количество и форма изгибов на участке шланга также влияют на скорость потока.
Давление иногда указывается как «напор». Если напор указан в метрах водяного столба, каждый 1-метровый напор (3,28 фута) создает давление 0,1 бар (1,47 фунт / кв. Дюйм).
Все формулы для определения количества жидкости, которая будет протекать через шланг в данный момент времени, являются приблизительными. Приведенные выше графики построены на основе расчетов, предполагающих, что шланг находится в хорошем состоянии и проложен по прямой линии. В этом случае они будут точными с точностью до 10% от реальных полученных результатов.
Если набор условий, введенных в модель, дает отрицательные ответы, то очевидно, что необходимо соответствующим образом скорректировать переменные, пока не будет получен реалистичный результат.
Необходимо рассчитать падение давления жидкости, движущейся по трубе или трубе? Воспользуйтесь нашим калькулятором падения давления.
Вставить этот инструмент на свой веб-сайт
Скопируйте приведенный ниже код, чтобы встроить калькулятор скорости потока на свой веб-сайт.
Не пропустите последние новости
Подпишитесь на нашу эксклюзивную рассылку по электронной почте, чтобы получать последние новости и предложения от Copely.
Copely Developments Ltd будет использовать информацию, которую вы предоставляете в этой форме, чтобы время от времени связываться с вами
и рассказывать интересные истории, новые продукты и предстоящие события. Вы можете отписаться в любое время.
© 2021 Copely Developments Ltd — Турмастон-лейн, Лестер, LE4 9HU. — Входит в группу компаний COBA.
Как рассчитать поток жидкости через отверстие в трубе
Обновлено 14 декабря 2020 г.
Автор: J.Р. Камбак
Распространенная проблема труб — это коррозия. Со временем из-за коррозии в трубе может образоваться дыра, которая вызовет утечку. Расчет потока жидкости через отверстие может быть трудным из-за многих переменных, таких как скорость потока жидкости, давление в трубе и плотность жидкости, и это лишь некоторые из них, но не расстраивайтесь. Вы можете найти ответ, выполнив ряд простых шагов.
Шаг 1: Сбор измерений трубы
Получите измерения: диаметр (D) отверстия в трубе и высота (h) поверхности жидкости над отверстием.2
Результат будет в квадратных единицах длины.
Шаг 3: Найдите скорость жидкости
Используйте уравнение Бернулли, чтобы найти скорость жидкости (v), если оно еще не задано. Если давление жидкости в трубе постоянное (т. Е. Если поток устойчивый), жидкость выходит через отверстие в трубе со скоростью:
v = \ sqrt {2gh}
, где g — ускорение из-за гравитация, 9,8 м / с 2 .
Шаг 4: Найдите объемный расход жидкости (поток)
Умножьте площадь поперечного сечения отверстия на скорость жидкости, чтобы найти объемный расход жидкости (Q):
Q = Av
Объем жидкости, покидающей отверстие, в кубических метрах в секунду.3 \ text {/ s}
Поскольку 1 кубический метр = 61 024 кубических дюйма, Q = 52,9 дюйма 3 / с. Таким образом, 52,9 кубических дюйма воды покидает отверстие в трубе за секунду.
Расчет расхода для диафрагменного расходомера
Пока скорость жидкости достаточно дозвуковая ( V <мах 0,3), уравнение Бернулли для несжимаемой жидкости достаточно хорошо описывает поток. Применяя это уравнение к линии тока, движущейся вниз по оси горизонтальной трубы, получаем,где точка 1 находится выше по потоку от отверстия, а точка 2 немного позади отверстия.Рекомендуется располагать точку 1 на расстоянии одного диаметра трубы перед отверстием, а точку 2 — на половину диаметра трубы после отверстия. Поскольку давление в точке 1 будет выше, чем давление в точке 2 (для потока, движущегося от 1 к 2), разница давлений, как определено, будет положительной величиной.
Из непрерывности скорости можно заменить на площади поперечного сечения потока и объемный расход Q ,
Решение для объемного расхода Q дает,
Вышеприведенное уравнение применимо только к идеально ламинарным невязким потокам.Для реальных потоков (таких как вода или воздух) вязкость и турбулентность присутствуют и действуют для преобразования кинетической энергии потока в тепло. Чтобы учесть этот эффект, коэффициент расхода C d вводится в приведенное выше уравнение, чтобы незначительно уменьшить расход Q ,
Поскольку фактический профиль потока в точке 2 ниже по потоку от отверстия является довольно сложным, что делает эффективное значение A 2 неопределенным, выполняется следующая замена, вводящая коэффициент потока C f :
где A o — площадь отверстия.В результате объемный расход Q для реальных потоков определяется уравнением
Коэффициент расхода C f определен экспериментально и приведен в справочниках; для большинства отверстий он составляет от 0,6 до 0,9. Поскольку это зависит от диаметра отверстия и трубы (а также числа Рейнольдса), часто можно найти C f в таблице в зависимости от отношения диаметра отверстия к диаметру входа, иногда определяемого как b,
Массовый расход можно найти, умножив Q на плотность жидкости,
Калькулятор расхода— рассчитайте расход трубы
Использование калькулятора расхода
Этот калькулятор расхода в трубе рассчитывает объемный расход (расход , расход ) газа или жидкости, проходящих через круглую или прямоугольную трубу известных размеров с известной скоростью.Если вещество является жидкостью и известна его объемная плотность, калькулятор также выведет массовый расход (для расчета его для газов требуется дополнительная информация, в настоящее время он не поддерживается).
В зависимости от вашего выбора выходные данные выражаются в британских или метрических единицах измерения. Некоторые единицы вывода включают: м 3 / ч, м 3 / мин, м 3 / с, л / ч, л / мин, л / с, фут 3 / ч, фут 3 / мин, фут 3 / с, ярд 3 / час, ярд 3 / мин, ярд 3 / с, галлонов в час, галлонов в минуту.Единицы вывода для массового расхода включают: кг / ч, кг / мин, кг / с, тонны / ч, фунт / ч, фунт / мин, фунт / с, тонны / ч. Показатели вывода автоматически настраиваются для вашего удобства.
Формула расхода
Объемный расход потока жидкости или газа равен скорости потока, умноженной на его площадь поперечного сечения. Следовательно, формула для расхода ( Q ), также известная как «расход», выраженная через площадь проходного сечения ( A ) и его скорость ( v ), представляет собой так называемое уравнение расхода :
Результирующий Q — это объемный расход.В случае круглой трубы площадь поперечного сечения равна внутреннему диаметру, деленному на 2, умноженному на π, в то время как, если труба имеет прямоугольную форму, площадь поперечного сечения равна внутренней ширине, умноженной на внутреннюю высоту. Уравнение можно преобразовать простым способом, чтобы учесть площадь поперечного сечения или скорость.
Формула массового расхода
Массовый расход ṁ — это расход массы m через поверхность в единицу времени t, поэтому формула для массового расхода с учетом объемного расхода: ṁ = Q * ρ , где ρ (греческая строчная буква rho) — объемная плотность вещества.2 · 3,1416 ~ = 490,875 мм 2 . Мы можем преобразовать это в m 2 , разделив на 1000000 для более удобных результатов, получив 0,0004 m 2 . Используя приведенное выше уравнение расхода, мы заменяем значения для A и v и получаем Q = 0,0004 м 2 · 10 м / с) = 0,004 м 3 / с. Чтобы преобразовать это в 3 м / ч, нам нужно умножить на 3600, чтобы получить расход 17,6715 м 3 в час.
Если мы дополнительно знаем, что плотность воды составляет 1000 кг / м 3 , мы можем рассчитать массовый расход, равный 17.6715 м 3 / ч · 1000 кг / м 3 = 17671,5 кг / ч (= 17,6715 тонн в час, м 3 отменяется).
Пример 2: Прямоугольная труба имеет высоту 2 см и ширину 4 см, и газ проходит через нее со скоростью 15 м / с. Какая скорость разряда этой трубы? Сначала мы находим площадь поперечного сечения, которая просто равна 2 · 4 = 8 см 2 или 0,0008 м 2 . Чтобы найти расход Q, мы умножаем 0,0008 на 15, чтобы получить 0,012 кубических метров в секунду.Чтобы получить литры в секунду, нам просто нужно умножить на 1000, чтобы получить 12 л / с. Если мы хотим получить литры в час, мы можем дополнительно умножить на 3600, чтобы получить 43 200 литров в час.
Наш калькулятор особенно полезен, если входные единицы для расчета отличаются от желаемых выходных единиц, и в этом случае он выполнит эти преобразования единиц за вас.

 Чаще всего такой случай возникает при проливке системы тепло или водоснабжения, когда необходимо рассчитать потребное количество реактива, исходя из объема воды, полностью заполняющего трубы;
Чаще всего такой случай возникает при проливке системы тепло или водоснабжения, когда необходимо рассчитать потребное количество реактива, исходя из объема воды, полностью заполняющего трубы; Любой сантехнический прибор характеризуется свойственным ему расходом воды (литров в секунду), при котором не нарушается комфортность пользования или корректность работы устройства. Аналогично – и для бытовой техники, подключаемой непосредственно к водопроводным трубам (стиральных и посудомоечных машин).
Любой сантехнический прибор характеризуется свойственным ему расходом воды (литров в секунду), при котором не нарушается комфортность пользования или корректность работы устройства. Аналогично – и для бытовой техники, подключаемой непосредственно к водопроводным трубам (стиральных и посудомоечных машин).
