Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 67. деление на 3 — Математика — 2 класс
Математика 2 класс. Урок № 67
Деление на 3
Перечень вопросов, рассматриваемых в теме:
- Какое действие обратное умножению?
- Как найти неизвестный множитель?
- Как составить таблицу деления на 3 и таблицу, когда частное равно 3?
- Для чего необходимо знать деление на 3?
Глоссарий по теме:
Умножение – это сложение одинаковых слагаемых. Знак умножения — ‧, х.
Знак умножения — ‧, х.
Компоненты умножения: первый множитель, второй множитель.
Результат умножения – произведение.
Деление – действие обратное умножению.
Компоненты деления: делимое, делитель, частное.
Делимое – число, которое делят.
Делитель – число, на которое делят.
Частное – результат деления.
Обязательная литература и дополнительная литература:
- Моро М.И., Бантова М.А. и др. Математика 2 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 92
- М. И. Моро, С. И. Волкова. Для тех, кто любит математику 2 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение,2018. – с. 57
Теоретический материал для самостоятельного изучения
Рассмотрите равенство. 3 • 5 = 15, где 3 – первый множитель, 5 – второй множитель, 15 – произведение.
Действие деление обратное действию умножения. Если произведение разделить на один из множителей, то получится второй множитель. Поэтому составим записи на деление.
Поэтому составим записи на деление.
15 : 3 = 5
15 : 5 = 3
Перед вами таблица умножения числа 3.
3 • 2 = 6
3 • 3 = 9
3 • 4 = 12
3 • 5 = 15
3 • 6 = 18
3 • 7 = 21
3 • 8 = 24
3 • 9 = 27
Пользуясь данной таблицей, можно легко составить таблицу, где делитель равен 3.
6 : 3 = 2
9 : 3 = 3
12 : 3 = 4
15 : 3 = 5
18 : 3 = 6
21 : 3 = 7
24 : 3 = 8
27 : 3 = 9
И таблицу, где частное равно 3.
6 : 2 = 3
9 : 3 = 3
12 : 4 = 3
15 : 5 = 3
18 : 6 = 3
21 : 7 = 3
24 : 8 = 3
27 : 9 = 3
Мы составили таблицу деления на число 3 и таблицу, когда в частном получается 3. Достаточно знать хотя бы один из предложенных столбиков таблицы, можно быстро найти значение выражений.
Для чего необходимо знать деление на 3? Знание помогает при решении задач. Например, такой.
У Димы в пакете 12 конфет. Пакет порвался, и мальчик решил их разложить в 3 кармана поровну. Сколько конфет в одном кармане?
Сколько конфет в одном кармане?
12 : 3 = 4 (конф.)
В каждом кармане по 4 конфеты.
Вот еще одна задача.
Бабушка разлила 6 литров варенья в двухлитровые банки. Сколько банок с вареньем получилось у бабушки?
6 : 2 = 3 (б.)
У бабушки получилось 3 банки с вареньем.
Выполним несколько тренировочных заданий.
Рассмотрите рисунок. Составьте записи по рисунку.
5 • 3 = 15
15 : 5 = 3
15 : 3 = 5
Рассмотрите рисунок, составьте записи на умножение и деление.
Проверьте.
4 • 3 = 12 12 : 3 = 4 12 : 4 = 3
Решим задачу. Игрокам раздали 12 теннисных мячей, по 3 мяча каждому. Сколько игроков получили мячи?
Выполним рисунок.
Для решения выбираем действие деление, так как неизвестно количество игроков, получивших мячи.
Решение задачи:
12 : 3 = 4 (игрока).
Ответ: 4 игрока.
Решим еще одну задачу.
Раздали 12 теннисных мячей четырем игрокам поровну. Сколько мячей получил каждый игрок?
Сколько мячей получил каждый игрок?
Выполним рисунок. Каждый раз будем брать по 4 мяча (по числу игроков0 и раздавать игрокам по 1 мячу до тех пор, пока не останется ни одного мяча.
Решение задачи:
12 : 4 = 3 (мяча)
Ответ: по 3 мяча.
Вывод:
Ответим на вопросы, поставленные в начале урока.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Действие деление обратное действию умножения.
Если произведение разделить на один из множителей, то получится второй множитель.
Зная таблицу умножения числа 3 и взаимосвязи между компонентами действия умножения, можно составить таблицу деления на 3 и таблицу, когда в частном число 3.
Знание таблицы деления на 3 помогает быстро выполнять вычисления и решать задачи.
Выполним несколько тренировочных заданий.
1. Выполните вычисления.
3 • 5 18 : 3 27 : 9
2 • 3 21 : 3 6 : 2
Пользуясь таблицей умножения числа 3 и таблицей деления, найдем значение выражений.
3 • 5 = 15 18 : 3 = 6 27 : 9 = 3
2 • 3 = 6 21 : 3 = 7 6 : 2 = 3
2. Закончите записи, чтобы получились верные равенства.
3 • 8 = 243 • 5 = □4 • □ = 12
24 : 3 = □ 15 : □ = 3 12 : 3 = □
24 : 8 = □ 15 : □ = 5 □ : 4 = 3
Получим верные равенства
3 • 8 = 243 • 5 = 154 • 3 = 12
24 : 3 = 8 15 : 5 = 3 12 : 3 = 4
24 : 8 = 3 15 : 3 = 5 12 : 4 = 3
3. Решите задачу.
За 3 часа работы трактор расходует 21 литр топлива. Сколько литров топлива расходует трактор за 1 час?
21 : 3 = 7 (л)
Ответ: 7 литров за 1 час.
Деление дробей
Деление обыкновенных дробей
Чтобы разделить две дроби нужно выполнить следующие шаги:
- 1 Перевернуть вторую дробь(поменять числитель и знаменатель местами) и умножить полученные дроби .
 Следующие шаги, 2—4, в точности повторяют процесс умножения дробей.
Следующие шаги, 2—4, в точности повторяют процесс умножения дробей. - 2 Перемножить числители дробей между собой 5 × 4 = 20.
- 3 Перемножить знаменатели дробей между собой 8 × 3 = 24.
- 4 Сократим полученную дробь , в результате получим .
Деление обыкновенных дробей можно записать в виде:
При деление дробей не имеет значения, имеют ли они одинаковый знаменатель или разный.
Пример Выполните деление дробей
.
Чтобы проверить результат деления дробей, можно воспользоваться калькулятором дробей.
Пример Разделить дроби .
.
Деление дроби на число
Чтобы разделить дробь на число, нужно умножить знаменатель на числитель, а числитель оставить без изменения, затем сократить дробь.
Пример Разделим дробь на число
.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
4 класс. Моро. Учебник №2. Ответы к стр. 92
Моро. Учебник №2. Ответы к стр. 92
Числа от 1 до 1000
Итоговое повторение всего изученного
Арифметические действия
Умножение и деление
Ответы к стр. 92
1. В каком случае сложение можно заменить умножением? Покажи на примерах.
Умножением можно заменить сумму одинаковых слагаемых, например:
4 + 4 + 4 = 4 • 3 = 12
5 + 5 + 5 + 5 + 5 + 5 = 5 • 6 = 30
2. Какими знаками обозначаются умножение и деление и как называются выражения, в которых числа соединены знаком умножения? знаком деления?
Знак умножения: точка — •, знак деления: двоеточие — :.
25 • 4 — произведение, 60 : 5 — частное.
3. Покажи, как умножение можно заменить сложением.
7 • 3 38 • 4 156 • 2 9 • 6
7 • 3 = 7 + 7 + 7 = 21
38 • 4 = 38 + 38 + 38 + 38 = 152
156 • 2 = 156 + 156 = 312
9 • 6 = 9 + 9 + 9 + 9 + 9 + 9 = 54
4. Вставь знак >, < или = так, чтобы получилось верное равенство или неравенство.
Вставь знак >, < или = так, чтобы получилось верное равенство или неравенство.
37 • 4 + 5 Ο 37 • 5 68 • 7 Ο 68 • 7 + 68 7 • 9 Ο 7 • 10 – 7
37 • 4 + 5 < 37 • 5
68 • 7 < 68 • 7 + 68
7 • 9 = 7 • 10 – 7
5. Как называются при умножении и делении данные числа и число, которое получается в результате выполнения действия?
6 (первый множитель) • 5 (второй множитель) = 30 (произведение)
30 (делимое) : 6 (делитель) = 5 (частное)
6. Прочитай, используя различные словесные формулировки, следующие равенства:
18 • 3 = 54 128 : 4 = 32
18 • 3 = 54
1) 18 умножить на 3 равно 54.
2) Произведение 18 и 3 равно 54.
3) Первый множитель 18, второй 3, произведение 54.
4) Если 18 умножить на 3, то получится 54.
128 : 4 = 32
1) 128 разделить на 4 равно 54.
2) Частное 128 и 4 равно 32.
3) Делимое 128, делитель 4, частное 32.
4) Если 128 разделить на 4, то получится 32.
7. Составь и реши задачи на умножение и деление, используя слова: «Купили … вещей по цене … р.», «Сколько раз по … содержится в …?», «Сколько получится в каждой части, если … разделить на … равных частей?», «… больше в … раз», «… меньше в … раз», «Во сколько раз … больше, чем …?», «… в … раз меньше, чем …».
1) Купили 5 вещей по цене 30 р. Какова стоимость купленных вещей?
30 • 5 = 150 (р.)
О т в е т: стоимость 300 р.
2) Сколько раз по 5 содержится в 40?
40 : 5 = 8 (р.)
О т в е т: 8 раз.
3) Сколько получится в каждой части, если 50 разделить на 5 равных частей?
50 : 5 = 10
О т в е т: 10.
4) В первом шкафу было 20 книг, во втором в 3 раз больше. Сколько книг было во втором шкафу?
20 • 3 = 60 (к.)
О т в е т: 60 книг.
5) Грибники собрали 5 кг рыжиков, а белых грибов в 5 раз меньше. Сколько собрали белых грибов?
5 : 5 = 1 (кг)
О т в е т: 1 кг.
6) Во сколько раз 60 больше, чем 10?
60 : 10 = 6 (р.)
О т в е т: в 6 раз.
7) Задуманное число в 10 раз меньше, чем 300. Найдите задуманное число.
300 : 10 = 30
О т в е т: 30.
8. Что получится, если: 1) произведение двух чисел разделить на один из множителей; 2) умножить делитель на частное; 3) разделить делимое на частное?
1) Получится другой множитель.
2) Получится делимое.
3) Получится делитель.
9. 1) Объясни два способа проверки умножения и деления.
14 • 6 = 84 Проверка: I 98 : 7 = 14 Проверка:
84 : 6 = 14 I 14 • 7 = 98
84 : 14 = 6 I 98 : 14 = 7
2) Вычисли и сделай проверку.
356 • 8 45360: 9
1) Чтобы проверить результат умножения, нужно произведение разделить на один из множителей. Чтобы проверить деление, можно частное умножить на делитель или делимое разделить на частное.
2) 356 • 8 = 2848 Проверка:
2848 : 356 = 8
2848 : 8 = 356
45360 : 9 = 5040 Проверка:
5040 • 9 = 45360
45360 : 5040 = 9
ЗАДАНИЕ НА ПОЛЯХ
РЕБУС
9 • 7 = 63
9 • 3 = 27
9 • 8 = 72
8 • 3 = 24
(8 • 8 = 64)
7 • 3 = 21
6 • 5 = 30
4 • 7 = 28
ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс
4 класс. Моро. Учебник №2. Ответы к стр. 92
5 (100%) от 1 голосующихУмножение и деление двузначных чисел
Работа 1
1. Множитель 17, множитель 1. Найдите произведение.
2. Делимое 0, делитель 8. Чему равно частное.
3. Первый множитель 15, произведение 15. Чему равен второй множитель?
4. Во сколько раз 9 больше 1?
5. На сколько 9 больше 1?
6. Найдите произведение чисел 10 и10.
7. Найдите частное чисел 10 и 10.
8. Какое число надо разделить на 8, чтобы получить 1?
9. Какое число в 10 раз меньше 70?
10. На какое число нужно умножить 19, чтобы получить 19?
Работа 2
1. Множитель 21, множитель 0. Чему равно произведение?
2. Делимое 0, делитель 2. Чему равно частное?
Чему равно частное?
3. Множители 14 и 1. Чему равно произведение?
4. Во сколько раз 6 больше 1?
5. На сколько 6 больше 1?
6. Найдите произведение чисел 9 и 10.
7. Найдите частное чисел 9 и 9.
8. Какое число нужно разделить на 10, чтобы получить 1?
9. На какое число нужно умножить 12, чтобы получить 12?
10. Какое число в 10 раз меньше 50?
Работа 3
1. Первый множитель 12, второй – 4. Найдите произведение.
2. Число 13 увеличьте в 6 раз.
3. Множитель 5, произведение 90. Чему равен второй множитель?
4. Делимое 39, делитель 3. Чему равно частное?
5. Делимое 66, частное 6. Чему равен делитель?
6. На какое число нужно умножить 9, чтобы получить 81?
7. Какое число нужно умножить на 13, чтобы получить 65?
8. Какое число в 2 раза больше 34?
9. Во сколько раз 12 меньше 96?
10. Найдите частное чисел 64 и 4.
Работа 4
1. Число 17 увеличьте в 3 раза.
Число 17 увеличьте в 3 раза.
2. Множитель 16, множитель 4. Найдите произведение.
3. Какое число нужно умножить на 13, чтоб получить 65?
4. Найдите произведение чисел 14 и 3.
5. Какое число в 5 раз меньше 70?
6. Во сколько раз 72 больше 6?
7. На сколько 72 больше 6?
8. Делимое 51, частное 17. Чему равен делитель?
9. Найдите частное чисел 84 и 4.
10. В магазин привезли 8 корзин огурцов, по 12 кг в каждой. Сколько килограммов огурцов привезли в магазин?
Работа 5
1. Множитель 12, множитель 4. Найдите произведение.
2. Число 13 увеличьте в 6 раз.
3. Произведение 90, первый множитель 5. Найдите произведение.
4. Делимое 63, делитель 3. Чему равно частное?
5. На какое число нужно умножить 9, чтобы получить 81?
6. Найдите частное чисел 80 и 4.
7. Найдите частное чисел 51 и 3.
8. Какое число нужно разделить на 5, чтобы получить 14?
9. Какое число нужно умножить на 12, чтобы получить 36?
10. Найдите произведение чисел 20 и 5.
Найдите произведение чисел 20 и 5.
Математический диктант Умножение и деление 2 класс
Математический диктант Сложение и вычитание
2 класс
Шнякина Наталья Николаевна учитель начальных классов МБОУ СОШ ж.д.ст. БАМ
Математический диктант
1. Частное чисел 18 и 3 умножьте на 2
2. Произведение чисел 2 и 6 разделите на 3
3. Частное чисел 16 и 2 разделите на 4
4. Произведение чисел 2 и 9 разделите 3
5. Частное чисел 14 и 7 разделите на 2
6. 3 умножьте на 4 и разделите на 2
7. Произведение чисел 4 и 2 умножьте на 1
8. На сколько больше произведение чисел 4 и 5,
чем произведение чисел 2 и 9?
9. Уменьшите частное чисел 15 и 3 в 5 раз
10. Умножьте 2 на частное чисел 9 и 3
Умножьте 2 на частное чисел 9 и 3
8
1
12
2
1
6
4
6
2
6
Математический диктант
1. Найдите произведение чисел 7 и 2.
2. Найдите произведение чисел 8 и 2.
3. Увеличьте 6 в 2 раза.
4. Разделите 15 на 3.
5. Сколько будет: 18 разделить на 9?
6. Сколько будет: 5 умножить на 3?
7. Найдите частное чисел 16 и 4.
8. Делимое – это 12, делитель – 3.
Найдите частное чисел.
9. Сколько будет: 14 : 7 : 1?
10. Сколько будет: 9 умножить 2?
18
14
5
4
2
12
16
2
15
4
Математический диктант
1. Найдите произведение чисел 4 и 2.
2. Найдите произведение чисел 7 и 2.
3. Увеличьте 5 в 3 раза.
4. Разделите 16 на 4.
5. Сколько будет: 18 разделить на 3?
6. Сколько будет: 6 умножить на 2?
7. Найдите частное чисел 12 и 4.
8. Делимое – это 20, делитель – 5.
Найдите частное чисел.
9. Сколько будет: 20 : 10 : 2?
10. Сколько будет: 10 умножить 2?
20
8
4
4
1
15
14
6
12
3
Математический диктант
1. Найдите произведение чисел 40 и 2.
2. Найдите произведение чисел 20 и 2.
3. Увеличьте 10 в 3 раза.
4. Разделите 40 на 4.
5. Сколько будет: 80 разделить на 2?
6. Сколько будет: 30 умножить на 2?
7. Найдите частное чисел 60 и 3.
8. Делимое – это 100, делитель – 2.
Найдите частное чисел.
9. Сколько будет: 90 : 10 : 3?
10. Сколько будет: 10 умножить 2?
50
20
30
80
10
3
60
40
40
20
Учебник Моро 3 класс. 2 часть. Страница 105
2 часть. Страница 105
Страница 105
1. Объясни, почему верны равенства.
Равенства верны потому, что равны их левые и правые части.
2. Реши:
3. Закончи каждый вывод и приведи примеры:
Если произведение разделить на один из множителей, то получится другой множитель:
4 • 9 = 36, 36 : 4 = 9, 36 : 9 = 4.
Если делитель умножить на частное, то получится делимое:
48 : 8 = 6, 8 • 6 = 48.
Если делимое разделить на частное, то получится делитель:
63 : 7 = 9, 63 : 9 = 7.
4. Объясни, как выполнена проверка умножения и деления.
- 32 — первый множитель
- 3 — второй множитель
- 96 — произведение
Проверка: можно разделить произведение на первый множитель и получить второй, либо разделить произведение на второй множитель и получить первый.
- 75 — делимое
- 5 — делитель
- 15 — частное
Проверка: можно умножить частное на делитель и получить делимое, либо разделить делимое на частное и получить делитель.
5. 1) Закончи каждый вывод:
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
2) Объясни решение уравнений и проверку.
х • 24 = 72
- х — первый множитель, 24 — второй множитель, 72 — произведение;
- Чтобы найти первый множитель, надо произведение разделить на второй множитель: 72 : 24 = 3, значит х = 3
- Проверка: подставим найденное значение: 3 – 24 = 72
- 72 = 72, значит, уравнение решено верно.
х : 18 = 5
- х — делимое, 18 — делитель, 5 — частное
- Чтобы найти делимое, надо делитель умножить на частное: 18 • 5 = 90, значит х = 90;
- Проверка: подставим найденное значение: 90 : 18 = 5;
- 5 = 5, значит, уравнение решено верно.

51 : х = 17
- 51 — делимое, х — делитель, 17 — частное;
- Чтобы найти делитель, надо делимое разделить на частное: 51:17 = 3 ,значит х = 3
- Проверка: подставим найденное значение: 51:3=17
- 17 = 17, значит, уравнение решено верно.
3) Реши уравнения, не вычисляя.
х • 18 = 18
х = 1
х • 24 = 0
х = 0
36 : х = 1
х = 36
х : 1 = 17
х = 17
Головоломка:
7 • 8 = 56
8 • 3 = 24
3 • 7 = 21
Калькулятор простой факторизации
Пожалуйста, предоставьте целое число, чтобы найти его простые множители, а также дерево множителей.
Калькулятор Связанного Фактора | Калькулятор общего множителя
Что такое простое число?
Простые числа — это натуральные числа (положительные целые числа, которые иногда включают 0 в некоторых определениях), которые больше 1, которые не могут быть образованы путем умножения двух меньших чисел. Примером простого числа является 7, поскольку оно может быть образовано только путем умножения чисел 1 и 7.Другие примеры включают 2, 3, 5, 11 и т. Д.
Примером простого числа является 7, поскольку оно может быть образовано только путем умножения чисел 1 и 7.Другие примеры включают 2, 3, 5, 11 и т. Д.
Числа, которые могут быть образованы двумя другими натуральными числами, превышающими 1, называются составными числами. Примеры этого включают числа, например, 4, 6, 9 и т. Д.
Простые числа широко используются в теории чисел в связи с основной теоремой арифметики. Эта теорема утверждает, что натуральные числа больше 1 либо простые, либо могут быть разложены на множители как произведение простых чисел. Например, число 60 можно разложить на произведение простых чисел следующим образом:
60 = 5 × 3 × 2 × 2
Как видно из приведенного выше примера, в факторизации нет составных чисел.
Что такое факторизация на простые множители?
Факторизация на простые числа — это разложение составного числа на произведение простых чисел. Существует множество алгоритмов факторинга, некоторые из которых сложнее других.
Испытательный отдел:
Одним из методов нахождения простых множителей составного числа является пробное деление. Пробное разделение — один из самых базовых алгоритмов, хотя и очень утомительный. Он включает в себя проверку каждого целого числа путем деления рассматриваемого составного числа на целое число и определения того, может ли целое число делить число поровну и сколько раз.В качестве простого примера ниже приведено разложение 820 на простые множители с использованием пробного деления:
820 ÷ 2 = 410
410 ÷ 2 = 205
Поскольку 205 больше не делится на 2, проверьте следующие целые числа. 205 нельзя делить на 3 без остатка. 4 не является простым числом. Однако его можно разделить на 5:
.205 ÷ 5 = 41
Так как 41 — простое число, на этом пробное деление завершается. Таким образом:
820 = 41 × 5 × 2 × 2
Продукт также можно записывать как:
820 = 41 × 5 × 2 2
По сути, это метод «грубой силы» для определения простых множителей числа, и хотя 820 является простым примером, он может стать намного более утомительным очень быстро.
Разложение на простые числа:
Другой распространенный способ проведения факторизации на простые множители называется разложением на простые числа и может включать использование факторного дерева. Создание факторного дерева включает в себя разбиение составного числа на множители составного числа, пока все числа не станут простыми. В приведенном ниже примере простые множители находятся путем деления 820 на простой множитель 2 и последующего деления результата до тех пор, пока все множители не станут простыми. Пример ниже демонстрирует два способа создания факторного дерева с использованием числа 820:
.Таким образом, можно видеть, что факторизация числа 820 на простые множители в любом случае снова равна:
820 = 41 × 5 × 2 × 2
Хотя эти методы работают для меньших чисел (и есть много других алгоритмов), не существует известного алгоритма для гораздо больших чисел, и даже машинам может потребоваться много времени для вычисления простых разложений больших чисел; В 2009 году ученые завершили проект с использованием сотен машин для разложения 232-значного числа RSA-768, и на это потребовалось два года.
Разложение на простые числа общих чисел
Ниже приведены разложения на простые множители некоторых общих чисел.
Разложение на простые множители 2: простое число
Разложение на простые множители 3: простое число
Разложение на простые множители 4: 2 2
Разложение на простые множители 5: простое число
Разложение на простые множители 6: 2 × 3
Разложение на простые множители 7: простое число
Разложение на простые множители 8: 2 3
Разложение на простые множители 9: 3 2
Разложение на простые множители 10: 2 × 5
Разложение на простые множители 11: простое число
Разложение на простые множители 12: 2 2 × 3
Разложение на простые множители 13: простое число
Разложение на простые множители 14: 2 × 7
Разложение на простые множители 15: 3 × 5
Разложение на простые множители 16: 2 4
Разложение на простые множители 17: простое число
Разложение на простые множители 18: 2 × 3 2
Разложение на простые множители 19: простое число
Разложение на простые множители 20: 2 2 × 5
Разложение на простые множители 21: 3 × 7
Разложение на простые множители 22: 2 × 11
Разложение на простые множители 23: простое число
Разложение на простые множители 24: 2 3 × 3
Разложение на простые множители 25: 5 2
Разложение на простые множители 26: 2 × 13
Факторизация на простые числа 27: 3 3
Разложение на простые множители 28: 2 2 × 7
Разложение на простые множители 29: простое число
Разложение на простые множители 30: 2 × 3 × 5
Разложение на простые множители 31: простое число
Разложение на простые множители 32: 2 5
Разложение на простые множители 33: 3 × 11
Разложение на простые множители 34: 2 × 17
Разложение на простые множители 35: 5 × 7
Разложение на простые множители 36: 2 2 × 3 2
Разложение на простые множители 37: простое число
Разложение на простые множители 38: 2 × 19
Разложение на простые множители 39: 3 × 13
Разложение на простые множители 40: 2 3 × 5
Разложение на простые множители 41: простое число
Разложение на простые множители 42: 2 × 3 × 7
Разложение на простые множители 43: простое число
Разложение на простые множители 44: 2 2 × 11
Разложение на простые множители 45: 3 2 × 5
Разложение на простые множители 46: 2 × 23
Разложение на простые множители 47: простое число
Разложение на простые множители 48: 2 4 × 3
Разложение на простые множители 49: 7 2
Разложение на простые множители 50: 2 × 5 2
Разложение на простые множители 51: 3 × 17
Разложение на простые множители 52: 2 2 × 13
Разложение на простые множители 53: простое число
Разложение на простые множители 54: 2 × 3 3
Разложение на простые множители 55: 5 × 11
Разложение на простые множители 56: 2 3 × 7
Разложение на простые множители 57: 3 × 19
Разложение на простые множители 58: 2 × 29
Разложение на простые множители 59: простое число
Разложение на простые множители 60: 2 2 × 3 × 5
Разложение на простые множители 61: простое число
Разложение на простые множители 62: 2 × 31
Разложение на простые множители 63: 3 2 × 7
Разложение на простые множители 64: 2 6
Разложение на простые множители 65: 5 × 13
Разложение на простые множители 66: 2 × 3 × 11
Разложение на простые множители 67: простое число
Разложение на простые множители 68: 2 2 × 17
Разложение на простые множители 69: 3 × 23
Разложение на простые множители 70: 2 × 5 × 7
Разложение на простые множители 71: простое число
Разложение на простые множители 72: 2 3 × 3 2
Разложение на простые множители 73: простое число
Разложение на простые множители 74: 2 × 37
Разложение на простые множители 75: 3 × 5 2
Разложение на простые множители 76: 2 2 × 19
Разложение на простые множители 77: 7 × 11
Разложение на простые множители 78: 2 × 3 × 13
Разложение на простые множители 79: простое число
Разложение на простые множители 80: 2 4 × 5
Разложение на простые множители 81: 3 4
Разложение на простые множители 82: 2 × 41
Разложение на простые множители 83: простое число
Разложение на простые множители 84: 2 2 × 3 × 7
Разложение на простые множители 85: 5 × 17
Разложение на простые множители 86: 2 × 43
Разложение на простые множители 87: 3 × 29
Разложение на простые множители 88: 2 3 × 11
Разложение на простые множители 89: простое число
Разложение на простые множители 90: 2 × 3 2 × 5
Разложение на простые множители 91: 7 × 13
Разложение на простые множители 92: 2 2 × 23
Разложение на простые множители 93: 3 × 31
Разложение на простые множители 94: 2 × 47
Разложение на простые множители 95: 5 × 19
Разложение на простые множители 96: 2 5 × 3
Разложение на простые множители 97: простое число
Разложение на простые множители 98: 2 × 7 2
Разложение на простые множители 99: 3 2 × 11
Разложение на простые множители 100: 2 2 × 5 2
Разложение на простые множители 101: простое число
Разложение на простые множители 102: 2 × 3 × 17
Разложение на простые множители 103: простое число
Разложение на простые множители 104: 2 3 × 13
Разложение на простые множители 105: 3 × 5 × 7
Разложение на простые множители 106: 2 × 53
Разложение на простые множители 107: простое число
Разложение на простые множители 108: 2 2 × 3 3
Разложение на простые множители 109: простое число
Разложение на простые множители 110: 2 × 5 × 11
Разложение на простые множители 111: 3 × 37
Разложение на простые множители 112: 2 4 × 7
Разложение на простые множители 113: простое число
Разложение на простые множители 114: 2 × 3 × 19
Разложение на простые множители 115: 5 × 23
Разложение на простые множители 116: 2 2 × 29
Разложение на простые множители 117: 3 2 × 13
Разложение на простые множители 118: 2 × 59
Разложение на простые множители 119: 7 × 17
Разложение на простые множители 120: 2 3 × 3 × 5
Разложение на простые множители 121: 11 2
Разложение на простые множители 122: 2 × 61
Разложение на простые множители 123: 3 × 41
Разложение на простые множители 124: 2 2 × 31
Разложение на простые множители 125: 5 3
Разложение на простые множители 126: 2 × 3 2 × 7
Разложение на простые множители 127: простое число
Разложение на простые множители 128: 2 7
Разложение на простые множители 129: 3 × 43
Разложение на простые множители 130: 2 × 5 × 13
Разложение на простые множители 131: простое число
Разложение на простые множители 132: 2 2 × 3 × 11
Разложение на простые множители 133: 7 × 19
Разложение на простые множители 134: 2 × 67
Разложение на простые множители 135: 3 3 × 5
Разложение на простые множители 136: 2 3 × 17
Разложение на простые множители 137: простое число
Разложение на простые множители 138: 2 × 3 × 23
Разложение на простые множители 139: простое число
Разложение на простые множители 140: 2 2 × 5 × 7
Разложение на простые множители 141: 3 × 47
Разложение на простые множители 142: 2 × 71
Разложение на простые множители 143: 11 × 13
Разложение на простые множители 144: 2 4 × 3 2
Разложение на простые множители 145: 5 × 29
Разложение на простые множители 146: 2 × 73
Разложение на простые множители 147: 3 × 7 2
Разложение на простые множители 148: 2 2 × 37
Разложение на простые множители 149: простое число
Разложение на простые множители 150: 2 × 3 × 5 2
Разложение на простые множители 200: 2 3 × 5 2
Разложение на простые множители 300: 2 2 × 3 × 5 2
Разложение на простые множители 400: 2 4 × 5 2
Разложение на простые множители 500: 2 2 × 5 3
Разложение на простые множители 600: 2 3 × 3 × 5 2
Разложение на простые множители 700: 2 2 × 5 2 × 7
Разложение на простые множители 800: 2 5 × 5 2
Разложение на простые множители 900: 2 2 × 3 2 × 5 2
Разложение на простые множители 1000: 2 3 × 5 3
Калькулятор коэффициентаКоэффициент 1: 1
Коэффициенты 2: 1, 2
Факторы 3: 1, 3
Коэффициенты 4: 1, 2, 4
Коэффициенты 5: 1, 5
Факторы 6: 1, 2, 3, 6
Коэффициенты 7: 1, 7
Факторы 8: 1, 2, 4, 8
Коэффициенты 9: 1, 3, 9
Коэффициенты 10: 1, 2, 5, 10
Факторы 11: 1, 11
Факторы 12: 1, 2, 3, 4, 6, 12
Факторы 13: 1, 13
Факторы 14: 1, 2, 7, 14
Факторы 15: 1, 3, 5, 15
Коэффициенты 16: 1, 2, 4, 8, 16
Факторы 17: 1, 17
Факторы 18: 1, 2, 3, 6, 9, 18
Факторы 19: 1, 19
Факторы 20: 1, 2, 4, 5, 10, 20
Факторы 21: 1, 3, 7, 21
Коэффициенты 22: 1, 2, 11, 22
Факторы 23: 1, 23
Факторы 24: 1, 2, 3, 4, 6, 8, 12, 24
Факторы 25: 1, 5, 25
Факторы 26: 1, 2, 13, 26
Факторы 27: 1, 3, 9, 27
Факторы 28: 1, 2, 4, 7, 14, 28
Коэффициенты 29: 1, 29
Факторы 30: 1, 2, 3, 5, 6, 10, 15, 30
Факторы 31: 1, 31
Факторы 32: 1, 2, 4, 8, 16, 32
Коэффициенты 33: 1, 3, 11, 33
Коэффициенты 34: 1, 2, 17, 34
Факторы 35: 1, 5, 7, 35
Факторы 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Коэффициенты 37: 1, 37
Коэффициенты 38: 1, 2, 19, 38
Коэффициенты 39: 1, 3, 13, 39
Коэффициенты 40: 1, 2, 4, 5, 8, 10, 20, 40
Коэффициенты 41: 1, 41
Факторы 42: 1, 2, 3, 6, 7, 14, 21, 42
Коэффициенты 43: 1, 43
Коэффициенты 44: 1, 2, 4, 11, 22, 44
Факторы 45: 1, 3, 5, 9, 15, 45
Коэффициенты 46: 1, 2, 23, 46
Коэффициенты 47: 1, 47
Факторы 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Коэффициенты 49: 1, 7, 49
Коэффициенты 50: 1, 2, 5, 10, 25, 50
Коэффициенты 51: 1, 3, 17, 51
Факторы 52: 1, 2, 4, 13, 26, 52
Факторы 53: 1, 53
Коэффициенты 54: 1, 2, 3, 6, 9, 18, 27, 54
Коэффициенты 55: 1, 5, 11, 55
Факторы 56: 1, 2, 4, 7, 8, 14, 28, 56
Коэффициенты 57: 1, 3, 19, 57
Факторы 58: 1, 2, 29, 58
Коэффициенты 59: 1, 59
Коэффициенты 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Факторы 61: 1, 61
Факторы 62: 1, 2, 31, 62
Факторы 63: 1, 3, 7, 9, 21, 63
Факторы 64: 1, 2, 4, 8, 16, 32, 64
Факторы 65: 1, 5, 13, 65
Факторы 66: 1, 2, 3, 6, 11, 22, 33, 66
Коэффициенты 67: 1, 67
Факторы 68: 1, 2, 4, 17, 34, 68
Факторы 69: 1, 3, 23, 69
Коэффициенты 70: 1, 2, 5, 7, 10, 14, 35, 70
Коэффициенты 71: 1, 71
Факторы 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Коэффициенты 73: 1, 73
Коэффициенты 74: 1, 2, 37, 74
Факторы 75: 1, 3, 5, 15, 25, 75
Факторы 76: 1, 2, 4, 19, 38, 76
Факторы 77: 1, 7, 11, 77
Факторы 78: 1, 2, 3, 6, 13, 26, 39, 78
Факторы 79: 1, 79
Факторы 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Факторы 81: 1, 3, 9, 27, 81
Коэффициенты 82: 1, 2, 41, 82
Факторы 83: 1, 83
Факторы 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Факторы 85: 1, 5, 17, 85
Коэффициенты 86: 1, 2, 43, 86
Коэффициенты 87: 1, 3, 29, 87
Факторы 88: 1, 2, 4, 8, 11, 22, 44, 88
Факторы 89: 1, 89
Коэффициенты 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Коэффициенты 91: 1, 7, 13, 91
Коэффициенты 92: 1, 2, 4, 23, 46, 92
Коэффициенты 93: 1, 3, 31, 93
Коэффициенты 94: 1, 2, 47, 94
Коэффициенты 95: 1, 5, 19, 95
Факторы 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Коэффициенты 97: 1, 97
Факторы 98: 1, 2, 7, 14, 49, 98
Коэффициенты 99: 1, 3, 9, 11, 33, 99
Коэффициенты 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
Коэффициенты 104: 1, 2, 4, 8, 13, 26, 52, 104
Коэффициенты 105: 1, 3, 5, 7, 15, 21, 35, 105
Факторы 108: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108
Коэффициенты 110: 1, 2, 5, 10, 11, 22, 55, 110
Факторы 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112
Коэффициенты 117: 1, 3, 9, 13, 39, 117
Коэффициенты 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Коэффициенты 121: 1, 11, 121
Коэффициенты 125: 1, 5, 25, 125
Факторы 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126
Факторы 130: 1, 2, 5, 10, 13, 26, 65, 130
Факторы 132: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132
Факторы 135: 1, 3, 5, 9, 15, 27, 45, 135
Коэффициенты 140: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Факторы 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
Факторы 147: 1, 3, 7, 21, 49, 147
Коэффициенты 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Факторы 162: 1, 2, 3, 6, 9, 18, 27, 54, 81, 162
Факторы 169: 1, 13, 169
Коэффициенты 175: 1, 5, 7, 25, 35, 175
Коэффициенты 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
Факторы 189: 1, 3, 7, 9, 21, 27, 63, 189
Факторы 192: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192
Факторы 196: 1, 2, 4, 7, 14, 28, 49, 98, 196
Факторы 200: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200
Факторы 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
Факторы 216: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216
Факторы 225: 1, 3, 5, 9, 15, 25, 45, 75, 225
Коэффициенты 240: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240
Факторы 245: 1, 5, 7, 35, 49, 245
Факторы 250: 1, 2, 5, 10, 25, 50, 125, 250
Факторы 256: 1, 2, 4, 8, 16, 32, 64, 128, 256
Факторы 270: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270
Факторы 288: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288
Факторы 294: 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, 294
Факторы 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300
Факторы 343: 1, 7, 49, 343
Факторы 360: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 , 360
Факторы 375: 1, 3, 5, 15, 25, 75, 125, 375
Коэффициенты 400: 1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200, 400
Факторы 500: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500
Факторы 625: 1, 5, 25, 125, 625
Калькулятор факторинга
Использование калькулятора
Калькулятор факторинга находит факторы и пары факторов положительного или отрицательного числа. Введите целое число, чтобы найти его множители.
Введите целое число, чтобы найти его множители.
Для положительных целых чисел калькулятор будет отображать только положительные множители, потому что это обычно принятый ответ. Например, вы получаете 2 и 3 как пару факторов из 6. Если вам также нужны отрицательные факторы, вам нужно будет продублировать ответ самостоятельно и повторить все факторы как отрицательные, такие как -2 и -3, как еще одну пару факторов из 6. С другой стороны, этот калькулятор даст вам отрицательные множители для отрицательных целых чисел.Например, -2 и 3 И 2 и -3 являются парами факторов -6.
Факторы — это целые числа, которые умножаются для получения другого числа. Исходные числа являются множителями номера продукта. Если a x b = c, то a и b являются делителями c.
Допустим, вы хотите найти множители 16. Вы найдете все пары чисел, которые при умножении дают 16. Мы знаем, что 2 и 8 являются множителями 16, потому что 2 x 8 = 16. 4 — это множитель 16, потому что 4 х 4 = 16. Также 1 и 16 делятся на 16, потому что 1 x 16 = 16. Факторы 16 равны 1, 2, 4, 8, 16.
Также 1 и 16 делятся на 16, потому что 1 x 16 = 16. Факторы 16 равны 1, 2, 4, 8, 16.
Вы также можете думать о множителях в терминах деления: множители числа включают в себя все числа, которые делятся на это число без остатка. Рассмотрим число 10. Поскольку 10 делится на 2 и 5 без остатка, можно сделать вывод, что 2 и 5 делятся на 10.
В таблице ниже перечислены множители для 3, 18, 36 и 48. Важно отметить, что каждое целое число имеет как минимум два множителя: 1 и само число.Если число состоит только из двух факторов, это число является простым числом.
Примеры списков факторов
36
1, 2, 3, 4, 6, 9, 12, 18, 36
48
1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Как разложить числа на множители: факторизация
Калькулятор множителей учитывает числа пробным делением. Выполните следующие действия, чтобы использовать пробное деление для определения множителей числа.
Выполните следующие действия, чтобы использовать пробное деление для определения множителей числа.
- Найдите квадратный корень из целого числа n и округлите до ближайшего целого числа. Назовем этот номер s .
- Начните с числа 1 и найдите соответствующую пару факторов: n ÷ 1 = № . Итак, 1 и n — факторная пара, потому что деление дает целое число с нулевым остатком.
- Сделайте то же самое с числом 2 и продолжите проверку всех целых чисел ( n ÷ 2, n ÷ 3, n ÷ 4 … n ÷ s ) вверх на квадратный корень с округлением до с . Запишите пары факторов, в которых деление дает целые числа с нулевым остатком.
- Когда вы наберете номер n ÷ s , и вы записали все пары факторов, вы успешно разложили число № .

Пример факторизации с использованием пробного отдела
Факторы 18:
- Квадратный корень из 18 равен 4,2426, округленный до ближайшего целого числа 4 .
- Проверяя целочисленные значения от 1 до 4 для деления на 18 с остатком 0, мы получаем следующие пары факторов: (1 и 18), (2 и 9), (3 и 6). Множители 18: 1, 2, 3, 6, 9, 18.
Факторы отрицательных чисел
Вся приведенная выше информация и методы обычно применимы к факторизации отрицательных чисел.Просто обязательно следуйте правилам умножения и деления отрицательных чисел, чтобы найти все множители отрицательных чисел. Например, множители -6: (1, -6), (-1, 6), (2, -3), (-2, 3). См. Калькулятор решения математических уравнений и раздел Правила операций умножения.
Дополнительная литература
Являются ли отрицательные множители других чисел? на http://mathforum. org/library/drmath/view/63516.html
org/library/drmath/view/63516.html
Калькуляторы сопутствующего факторинга
Смотрите наши Калькулятор общих факторов, чтобы найти все факторы набора чисел и узнать, какие факторы являются общими.
Калькулятор наибольшего общего множителя находит наибольший общий делитель (НОД) или наибольший общий делитель (НОД) набора чисел.
Посмотреть Калькулятор наименьшего общего знаменателя, чтобы найти наименьший общий знаменатель для дробей, целых и смешанных чисел.
знаков после запятой: умножение и деление десятичных знаков
Урок 3: Умножение и деление десятичных знаков
/ en / decimals / сложение-и-вычитание-десятичные дроби / content /
Умножение на десятичные дроби
В разделе «Сложение и вычитание десятичных знаков» вы узнали, как складывать десятичные числа . Возможно, вам удастся вспомнить времена, когда вы добавляли десятичные дроби в реальной жизни. Например, вы идете в магазин и находите рубашку, которая вам действительно нравится. Ценник говорит, что он стоит 15,60 долларов. Вам так нравится рубашка, что вы решаете купить их пять.
Возможно, вам удастся вспомнить времена, когда вы добавляли десятичные дроби в реальной жизни. Например, вы идете в магазин и находите рубашку, которая вам действительно нравится. Ценник говорит, что он стоит 15,60 долларов. Вам так нравится рубашка, что вы решаете купить их пять.
Чтобы вычислить общую стоимость, вы можете добавить цен.
Добавление такого количества чисел может занять много времени. На уроке умножения мы узнали, что когда вы умножаете, вы увеличиваете число во много раз.Поскольку все цены на рубашки равны и , умножение может помочь вам решить эту проблему немного быстрее.
Когда вы умножаете десятичные числа, полезно поставить задачу так, чтобы вам было легче ее решать. шаг за шагом. .
Щелкните слайд-шоу ниже, чтобы узнать, как настроить задачу умножения с десятичными знаками.
Решение задач умножения с десятичными знаками
Умножение десятичных чисел во многом похоже на умножение больших чисел. Если большую проблему разделить на несколько более мелких, ее будет легче решить. Давайте посмотрим, как это работает, решив эту задачу: 2.3 x 4.
Если большую проблему разделить на несколько более мелких, ее будет легче решить. Давайте посмотрим, как это работает, решив эту задачу: 2.3 x 4.
Щелкните слайд-шоу, чтобы узнать, как умножать десятичные дроби.
Для решения нашей проблемы мы воспользуемся знакомым инструментом: таблицей умножения .
При умножении сложенных чисел начинайте с правой цифры на нижнем . Нижний номер состоит только из одной цифры: 4.
Умножим 4 на верхнее число 2.3. Поскольку в таблице умножения нет 2,3, нам придется умножать по одной цифре за раз.
Как обычно, будем решать проблему с справа налево . Итак, мы умножим 4 на цифру в правом верхнем углу . Здесь это 3.
Теперь пришло время решить 4 x 3. Мы можем использовать таблицу умножения .
4 x 3 равно 12, но нет места для записи обеих цифр под 4 и 3.

Помните, это означает, что мы должны будем носить с собой. Мы узнали о переносе чисел на уроке умножения больших чисел.
Правую цифру 2 запишем под чертой …
Запишем правую цифру 2 под чертой … затем перенесем левую цифру 1 , до следующий набор цифр в проблеме.
Теперь пора сделать следующий шаг. Умножим 4 x 2.
4 x 2 = 8.Но пока не будем писать 8 под чертой. Помните, есть еще один шаг.
Нам нужно убедиться, что мы добавили число, которое мы перенесли: 1.
Мы настроим нашу задачу сложения.
1 + 8 = 9.
Мы напишем 9 под строкой.
В нашей задаче мы умножили десятичное число: 2.3. Это означает, что наш ответ также должен быть десятичным числом.
Давайте разберемся, где поставить десятичную точку (.).

В задаче 2.3 имеет одну цифру после справа от десятичной точки.
Это означает, что в нашем ответе будет одна цифра после справа десятичной точки.
Разместим десятичную точку так, чтобы только одна цифра находилась справа от : 2.
Наша проблема решена. Итого 9,2. Мы знаем, что 2,3 х 4 = 9,2. Мы можем прочитать этот ответ как девять и две десятых .
Попробуем другую задачу. На этот раз мы умножим деньги: 3,05 доллара на 2.
Сначала мы умножим нижнее число 2 на цифру в правом верхнем углу. Это 5.
2 x 5 = 10.
Мы запишем 0 под линией …
Мы запишем 0 под линией … и перенесем 1. Поместим его над следующей цифрой.
Следующая цифра — 0.
Все, умноженное на ноль, равно нулю, поэтому мы знаем, что 2 x 0 = 0.

Помните, нам нужно убедиться, что мы добавили 1, что у нас есть.
0 + 1 = 1. Мы запишем 1 под строкой.
Наконец, мы умножим 2 и 3.
2 x 3 = 6, поэтому мы напишем 6 под чертой.
Пришло время поставить десятичную точку. Нам нужно, чтобы посчитал цифр до справа десятичной точки в нашей задаче.
3.05 содержит две цифры справа от десятичной точки.Это 0 и 5.
Это означает, что в нашем ответе должны быть две цифры справа от десятичной точки.
Мы поместим десятичную точку так, чтобы две цифры были справа: 1 и 0.
Наконец, мы напишем знак доллара ($) на слева от номера.
Мы решили проблему. 3,05 доллара США x 2 = 6,10 доллара США. Мы можем прочитать это как шесть долларов и десять центов .

Примечание : При определении места для десятичной точки в ответе подсчитайте общее количество цифр справа от каждой десятичной точки в вашей задаче. Например, если вы упрощаете 3,25 x 2,3, вы должны посчитать две цифры в 3,25 плюс одну цифру в 2,3. Следовательно, мы должны поместить десятичную точку в нашем ответе так, чтобы три цифры были справа (3,25 x 2,3 = 7,475).
Попробуй!
Попробуйте решить эти задачи умножения.Затем проверьте свой ответ, введя его в поле.
Десятичные дроби
Давайте посмотрим на другую ситуацию. Представим, что у вас есть забор, и вы хотите посадить перед ним 5 кустов. Ваш забор 20 футов в длину. Вы хотите распределить кусты поровну, поэтому вы знаете, что вам нужно разделить забор на 5 равных частей. Это означает, что вам нужно разделить 20 на 5.
В уроке о делении мы узнали, как настроить выражения деления. Для приведенной выше ситуации выражение будет выглядеть так:
В нашем выражении 20 — это целое число . Но что, если длина забора — это десятичное число ? Например, допустим, его длина составляет 20,75 футов. Хотите верьте, хотите нет, но деление десятичной дроби ничем не отличается.
Но что, если длина забора — это десятичное число ? Например, допустим, его длина составляет 20,75 футов. Хотите верьте, хотите нет, но деление десятичной дроби ничем не отличается.
Когда вы настраиваете выражение для деления десятичного числа, важно убедиться, что вы всегда делите на целое число . В нашем примере выше 20,75 делится на целое число 5. Деление на целое число упрощает управление длинным делением.
Щелкните слайд-шоу ниже, чтобы узнать, как настроить задачи деления с десятичными знаками.
Давайте настроим это выражение: 20.75 / 5.
На уроке деления мы узнали, что делить числа легче, если выражение написано немного иначе.
Как обычно, вместо записи чисел рядом с символом деления …
Как обычно, вместо того, чтобы писать числа рядом с символом деления … мы ‘ Я буду использовать разделительный кронштейн .

Число, которое мы делим, идет под разделительной скобкой. Это 20,75.
К левому разделительной скобки мы напишем число, на которое мы делим. В нашей задаче это 5.
Помните, что скобка деления также является знаком равно .
Частное , или ответ, написано над .
Приведем другое выражение.На этот раз , оба числа — десятичные числа: 80,1 / 4,2.
Сначала напишем скобку деления.
Далее запишем делимое число: 80.1.
Наконец, напишем число, на которое делим: 4.2.
Поскольку мы делим десятичное число на десятичное, нам нужно сделать еще один шаг.
Чтобы упростить деление, мы изменим число, на которое мы делим, на целое число .Значит, мы изменим 4.2.
Чтобы сделать 4,2 целым числом, нам нужно переместить десятичную точку так, чтобы она стояла после последней цифры в числе.

Это означает, что мы переместим его так, чтобы он стоял после 2.
Теперь все цифры находятся до слева от десятичной точки. Мы создали целый номер . 4.2 становится 42.
Целое число обычно записывается без десятичной точки после него…
Целое число обычно пишется без десятичной точки после нее … поэтому мы будем отбросить десятичную точку .
Видите, как мы это сделали? Мы переместили десятичную точку вправо , а затем удалили десятичную точку.
Поскольку мы переместили десятичную точку в одно число …
Поскольку мы переместили десятичную точку в одном числе … нам также необходимо переместить десятичную точку в другом числе: 80.1.
Итак, мы переместим эту десятичную точку на такое же количество раз .

80,1 становится 801.
801 — целое число, поэтому мы отбросим десятичную точку .
Теперь выражение деления — 801/42.
Перемещение десятичных знаков может быть непростым делом, поэтому важно сначала изменить число, которое вы делите на , на целое число .
Давайте попробуем еще раз с другим выражением: 0.4 / 0,02.
Сначала заменим 0,02 на целое число.
Мы переместим десятичную точку на один раз к вправо .
0,02 становится 0,2.
У нас все еще есть цифра справа от десятичной точки: 2. Это означает, что наша десятичная дробь еще не является целым числом.
Итак, мы переместим десятичную точку на вправо во второй раз.
0.2 становится 2. Все цифры теперь находятся слева от до десятичной точки.

, нули и десятичная точка больше не нужны. Мы бросим им .
Так как мы переместили первую десятичную точку два раза вправо …
Поскольку мы переместили первую десятичную точку два раза вправо … мы сделаем то же самое с вторая десятичная точка.
Мы переместим его на один раз в …
Мы переместим его на на один раз … затем мы добавим ноль …
Переместим его на на один раз … затем мы добавьте ноль … и затем переместим его на секунд раз.
0,4 становится 40.
Поскольку 40 — целое число, мы отбросим ноль и десятичную точку.
Выражение деления теперь 40/2. Наша проблема готова к решению.
Разделение десятичных чисел
В предыдущем слайд-шоу вы попрактиковались в настройке выражений деления с десятичными числами. Давайте подробнее рассмотрим, как разделить десятичную дробь. Разделение десятичного числа очень похоже на деление целого числа . В конце есть только один дополнительный шаг.
Давайте подробнее рассмотрим, как разделить десятичную дробь. Разделение десятичного числа очень похоже на деление целого числа . В конце есть только один дополнительный шаг.
Щелкните слайд-шоу, чтобы узнать, как делить десятичные дроби.
Для решения этой задачи воспользуемся длинным делением: 6.5 / 2.
На уроке, посвященном делению в столбик, мы узнали, что при решении задачи деления в столбик мы будем следовать шаблону , пока проблема не будет решена.
Начнем с левой цифры под скобкой деления. Это означает, что мы начнем с 6 …
Мы начнем с левой цифры под скобкой деления. Это означает, что мы начнем с 6 … и выясним, сколько раз его можно разделить на 2.
Мы воспользуемся таблицей умножения , чтобы помочь нам. Помните, если вам нужно повторить, как пользоваться таблицей умножения, вы можете вернуться к уроку умножения.
 Теперь пришло время решить 6/2.
Теперь пришло время решить 6/2.6/2 = 3.
Мы напишем 3 над 6.
Затем мы умножим на 3 и 2.
3 x 2 = 6.
Мы запишем 6 под 6.
Затем мы создадим нашу задачу вычитания .
6 — 6 = 0. Мы запишем 0 под линией.
Теперь мы опустим 5 и перепишем его рядом с 0.
05 означает то же самое, что и 5. 5 достаточно велико, чтобы его можно было разделить, поэтому мы выясним, сколько раз 5 можно разделить на 2.
В столбце 2 мы будем искать число, которое ближе всего к 5, но не больше 5. Это 4.
4 находится в строке 2. Это означает, что 2 переходит в 5 два раза .
Мы напишем 2 над 5.
Теперь пора умножить на 2 и 2.
2 x 2 = 4.
Напишем 4 под 5.
Теперь пришло время настроить нашу задачу вычитания .

5 — 4 = 1. Мы запишем 1 под строкой.
Поскольку наш ответ на задачу вычитания равен 1, мы посмотрим под скобкой , чтобы увидеть, есть ли еще одна цифра, которую мы можем опустить.
Нет больше цифр, которые нам нужно сбивать. На уроке деления в столбик мы узнали, что можем написать ноль рядом с числом под скобкой деления.
Итак, рядом с 6.5 напишем 0.
Теперь мы можем продолжить решение этой проблемы. Мы опустим 0 и перепишем его рядом с 1.
Давайте посмотрим, сколько раз 10 можно разделить на 2.
В столбце 2 мы поищем ближайшее число. до 10, но не более 10.В столбце 2 стоит цифра 10. Это именно то, что нам нужно!
10 находится в 5-м ряду. Это означает, что 2 входит в 10 пять раз.
Мы напишем 5 над 0.
Теперь пора умножить 5 и 2.
5 x 2 = 10.

Запишем 10 под 10.
Далее мы создадим задачу вычитания .
Теперь пора решать.10 — 10 = 0.
Так как ответ на задачу вычитания — 0 и больше нет цифр, которые нужно опускать, мы закончили деление. Нам нужно сделать только один последний шаг.
В этой задаче мы разделили десятичное число: 6.5. Это означает, что в нашем частном или ответе будет десятичная точка.
Мы просто запишем десятичную точку непосредственно над другой десятичной точкой. Видите, где мы его поместили между 3 и 2?
Мы решили проблему.Частное 3,25. Итак, 6,5 / 2 = 3,25. Мы можем прочитать это как три и двадцать пять сотых .
Попробуй!
Найдите частное для каждой из приведенных ниже задач на столбец. Проверьте свой ответ, введя его в поле.
/ en / decimals / преобразование десятичных дробей и дробей / содержание /
Расмус — Математика, Простые числа и делимость, Урок 1.
Расмус — Математика, Простые числа и делимость, Урок 1.- с 7. по 9. класс.| 2004 Rasmus ehf | Простые числа | Печать |
Prime числа и делимость
Урок 1.
Прайм число — это целое число больше 1, которое можно разделить только само по себе и 1.Наименьшие простые числа — 2, 3, 5, 7, 11, 13, 17, 19 и 23. Число 2 — единственное четное простое число. количество.
Пример:
| 7 = 1 7 | г. Число 7 имеет только два фактора: 1 и сам. |
| 11 = 1 11 | г. Число 11 имеет только два фактора: 1 и сам. |
композитный
числа: составное число имеет более двух факторов. Составные числа можно разбить на простые множители.
Составные числа можно разбить на простые множители.
Пример:
| 6 = 2 3 | 2 и 3 — простые числа. |
| 20 = 2 25 | 2 и 5 — простые числа. |
| 35 = 5 7 | 5 и 7 — простые числа. |
Prime факторы: Найдите простые множители 30.
| 30
= 2 35 простые множители 30 — это числа 2, 3 и 5. |
- Начните с наименьшего простого числа, которое коэффициент 30. Разделите на 2, чтобы получить коэффициент 15.
- Теперь используйте наименьшее простое число, которое фактор 15.Разделите на 3, чтобы получить множитель 5, который также является простым числом.
Вы
также можно найти простые множители целого числа, нарисовав множитель
дерево. | |
| 30 = 2 35 | |
Делимость
номеров:
Вы можете использовать
Сито Эратосфена в
найти простые числа.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все
четные числа делятся на 2. | Если сумма цифр номера делится на 3 , число делится на 3 . |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если
последние 2 цифры числа можно разделить на 4, число делится на
4. Пример: 1 12 4 = 28 и 12 4 = 3 | Если число заканчивается на 0 или 5, оно делится на 5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если
число можно разделить на 2 и 3, оно делится на 6.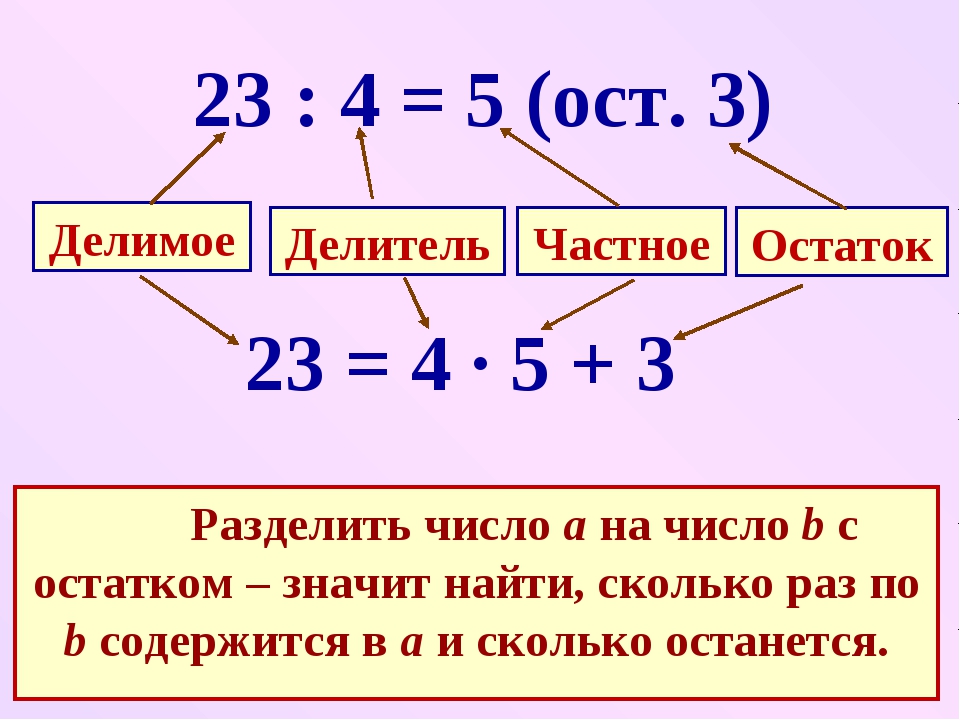 | Эти числа делятся на 7. |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эти
числа делятся на 8. | Если
сумму цифр номера можно разделить на 9
, число делится на 9
. Пример: 54 9 = 6 5 + 4 = 9 |
Первые 27 простых чисел показаны желтым цветом в таблице ниже.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вы можете
найдите эти простые числа, вычеркнув кратные 2, 3, 5 и 7
(кроме себя) на графике. |
Попрактикуйтесь в этих методах, а затем пройдите тест 1 на Prime
числа.
Пс. Не забудьте использовать контрольный список, чтобы отслеживать
твоя работа.
Что такое целые числа в математике
Коммутативность умножения
Для любых двух натуральных чисел a и b
a × b = b × a
Например, 2 × (-5) = -10.И (-5) × 2 = -10. Так что 2 × (-5) = (-5) × 2
Умножение на ноль
Для любого целого числа a , a × 0 = 0 × a = 0
Например, (–2) × 0 = 0; 0 × (- 5) = 0; 7 × 0 = 0
Примечание:
Если любое целое число умножить на ноль, произведение будет равно нулю.
Умножение на 1
Для любого целого числа a имеем a × 1 = 1 × a =
a
Например, (–2) × (–1) = 2; 5 × (–1) = –5; 6 × 1 = 6
Умножение трех целых чисел
Для любых трех целых чисел a, b и c,
(а × б) × с =
а × (б × в)
Если мы скажем, [(–4) × (–2)] × 5 = 8 × 5 = 40
И, (–4) × [(–2) × 5] = (–4) × (–10) = 40
Таким образом, [(–4) × (–2)] × 5 = (–4) × [(–2) × 5]
Распределительная собственность
Для любых целых чисел a, b и c,
а × (Ь + с)
= a × b + a × c
Например, (- 7) × [(–3) + (–2)] = (- 7) × (–5) = 35
И [(- 7) × (–3)] + [(- 7) × (–2)] = 21 + 14 = 35
Итак, (- 7) × [(–3) + (–2)] = [(- 7 ) × (–3)] + [(- 7) × (–2)]
Умножение и деление радикальных выражений
Умножение радикальных выражений
При умножении радикальных выражений на один и тот же индекс мы используем правило произведения для радикалов. Если a и b представляют положительные действительные числа,
Если a и b представляют положительные действительные числа,
Пример 1: Умножить: 2⋅6.
Решение: Эта задача является произведением двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножить: 93⋅63.
Решение: Эта проблема является продуктом кубических корней.Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами стоят коэффициенты.
Пример 3: Умножить: 23⋅52.
Решение: Используя правило произведения для радикалов и тот факт, что умножение является коммутативным, мы можем умножить коэффициенты и подкоренные выражения следующим образом.
Обычно первый шаг, связанный с применением коммутативного свойства, не показан.
Ответ: 106
Пример 4: Умножение: −2 5×3⋅3 25×23.
Решение:
Ответ: −30x
Используйте свойство распределенности при умножении рациональных выражений более чем на один член.
Пример 5: Умножить: 43 (23-36).
Решение: Примените свойство распределения и умножьте каждый член на 43.
Ответ: 24-362
Пример 6: Умножение: 4×23 (2×3−5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x − 10x⋅2×3
Процесс умножения радикальных выражений с несколькими членами — это тот же процесс, который используется при умножении многочленов. Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Пример 7: Умножение: (5 + 2) (5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножение: (3x − y) 2.
Решение:
Ответ: 9x − 6xy + y
Попробуй! Умножить: (23 + 52) (3−26).
Ответ: 6-122 + 56-203
Выражения (a + b) и (a − b) называются сопряженными. Множители (a + b) и (a − b) являются сопряжениями .. При умножении сопряжений сумма произведений внутреннего и внешнего членов дает 0.
Пример 9: Умножение: (2 + 5) (2−5).
Решение: Примените свойство распределения, а затем объедините одинаковые термины.
Ответ: −3
Важно отметить, что при умножении сопряженных радикальных выражений мы получаем рациональное выражение.Это верно в целом и часто используется при изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b мы имеем следующее свойство:
Деление радикальных выражений (рационализация знаменателя)
Чтобы разделить радикальные выражения с одинаковым индексом, мы используем правило частного для радикалов. Если a и b представляют собой неотрицательные числа, где b 0, то мы имеем
Пример 10: Деление: 8010.
Решение: В этом случае мы видим, что 10 и 80 имеют общие множители. Если мы применим правило частного для радикалов и запишем его как единый квадратный корень, мы сможем уменьшить дробное подкоренное выражение.
Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Решение:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Решение:
Ответ: 3b⋅a32
Когда делитель радикального выражения содержит радикал, обычно находят эквивалентное выражение, в котором знаменатель является рациональным числом. Нахождение такого эквивалентного выражения называется рационализацией знаменателя Процесс определения эквивалентного радикального выражения с рациональным знаменателем ..
Для этого умножьте дробь на единицу специальной формы, чтобы подкоренное выражение в знаменателе можно было записать со степенью, соответствующей индексу.После этого упростите и удалите радикал в знаменателе. Например,
Например,
Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой коэффициент.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без радикала в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Рационализируйте знаменатель: 123x.
Решение: Подкоренное выражение в знаменателе определяет факторы, которые необходимо использовать для его обоснования. В этом примере умножьте на 1 в форме 3x3x.
Ответ: 3x6x
Как правило, мы обнаруживаем необходимость уменьшить или отменить после рационализации знаменателя.
Пример 15: Рационализируйте знаменатель: 525ab.
Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b не отменяют в этом примере. Не отменяйте факторы внутри радикала с теми, которые находятся снаружи.
Ответ: 10abab
Попробуй! Рационализируем знаменатель: 4a3b.
Ответ: 23ab3b
До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одним и тем же корнем дает рациональный знаменатель. В общем, это верно, только когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не дает рационального объяснения. В этом случае, если мы умножим на 1 в форме x23x23, то мы можем записать подкоренное выражение в знаменателе как степень 3. Затем упрощение результата дает рационализированный знаменатель. Например,
Затем упрощение результата дает рационализированный знаменатель. Например,
Следовательно, чтобы рационализировать знаменатель радикальных выражений с одним радикальным членом в знаменателе, начните с факторизации подкоренного выражения знаменателя. Коэффициенты этого подкоренного выражения и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на корень n -й степени из множителей, что даст n -ю степенью всех множителей в подкоренном выражении знаменателя.
Пример 16: Рационализируйте знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один множитель 5. Следовательно, умножьте на 1 в форме 5353.
Ответ: 535
Пример 17: Рационализируйте знаменатель: 27a2b23.
Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Рационализируйте знаменатель: 1 4×35.
Решение: В этом примере мы умножим на 1 в форме 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена с квадратными корнями, мы можем рационализировать это с помощью очень специальной техники.Этот метод заключается в умножении числителя и знаменателя дроби на сопряжение знаменателя. Напомним, что умножение радикального выражения на его сопряжение дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13−2.
Решение: В этом примере сопряжение знаменателя равно 3 + 2. Следовательно, умножьте на 1 в виде (3 + 2) (3 + 2).
Ответ: 3 + 2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, исключаются путем умножения на сопряжение.Мы можем использовать свойство (a + b) (a − b) = a − b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62 + 6.
Решение: Умножьте на 1 в форме 2−62−6.
Ответ: −2 + 3
Пример 21: Рационализируйте знаменатель: x + yx − y.
Решение: В этом примере мы умножим на 1 в форме x − yx − y.
Ответ: x − 2xy + yx − y
Попробуй! Рационализируйте знаменатель: 35 + 525−3.
Ответ: 195 + 4511
Основные выводы
- Чтобы умножить два одночленных радикальных выражения, умножьте коэффициенты и умножьте подкоренные выражения.
 По возможности упростите результат.
По возможности упростите результат. - Примените свойство распределенности при умножении радикальных выражений на несколько членов.Затем упростите и объедините все похожие радикалы.
- Умножение двухчленного радикального выражения, содержащего квадратные корни, на его сопряжение, приводит к рациональному выражению.
- Принято писать радикальные выражения без радикалов в знаменателе. Процесс поиска такого эквивалентного выражения называется рационализацией знаменателя.
- Если выражение имеет один член в знаменателе, включающий радикал, то рационализируйте его, умножив числитель и знаменатель на корень n -й степени множителей подкоренного выражения, чтобы их степени равнялись индексу.
- Если радикальное выражение имеет в знаменателе два члена, включающих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на его сопряжение.
Тематические упражнения
Часть A: Умножение радикальных выражений
Умножить. ( Предположим, что все переменные неотрицательны. )
( Предположим, что все переменные неотрицательны. )
1. 3⋅5
2.7⋅3
3. 2⋅6
4. 5⋅15
5. 7⋅7
6. 12⋅12
7. 25⋅710
8. 315⋅26
9. (25) 2
10. (62) 2
11. 2x⋅2x
12. 5лет 5лет
13. 3a⋅12
14. 3a⋅2a
15. 42x⋅36x
16. 510–22 года
17.53⋅253
18. 43⋅23
19. 43⋅103
20. 183⋅63
21. (5 93) (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23⋅9a3
26. 7b3⋅49b23
27. 6×23⋅4×23
28. 12y3⋅9y23
29. 20x2y3⋅10x2y23
20x2y3⋅10x2y23
30.63xy3⋅12x4y23
31,5 (3-5)
32. 2 (3−2)
33,37 (27−3)
34,25 (6−310)
35. 6 (3−2)
36,15 (5 + 3)
37. х (х + ху)
38. у (ху + у)
39. 2ab (14a − 210b)
40. 6ab (52a − 3b)
41. (2−5) (3 + 7)
42. (3 + 2) (5-7)
43.(23−4) (36 + 1)
44. (5−26) (7−23)
45. (5−3) 2
46. (7−2) 2
47. (23 + 2) (23−2)
48. (2 + 37) (2−37)
49. (a − 2b) 2
50. (ab + 1) 2
51. Каковы периметр и площадь прямоугольника длиной 53 сантиметра и шириной 32 сантиметра?
52. Каковы периметр и площадь прямоугольника длиной 26 сантиметров и шириной 3 сантиметра?
53. Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?
54. Если основание треугольника составляет 63 метра, а высота — 36 метров, то какова площадь?
Часть B: Деление радикальных выражений
Разделить.
55. 753
56. 36010
57. 7275
58. 9098
59.90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16a5b232a2b23
64. 192a2b732a2b23
Рационализируйте знаменатель.
65,15
66,16
67. 23
68. 37
69. 5210
70. 356
71.3−53
72. 6−22
73. 17x
74. 13лет
75. a5ab
a5ab
76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25н3 25м2н3
85.327x2y5
86. 216xy25
87. ab9a3b5
88. abcab2c35
89. 310-3
90,26-2
91. 15 + 3
92. 17−2
93. 33 + 6
94. 55 + 15
95. 105-35
96. −224-32
97. 3 + 53−5
98. 10−210 + 2
99.23−3243 + 2
100. 65 + 225−2
101. x + yx − y
102. х − yx + y
103. a − ba + b
104. ab + 2ab − 2
105. x5−2x
x5−2x
106. 1x − y
Часть C: Обсуждение
107. Изучите и обсудите некоторые из причин, по которым рациональное использование знаменателя является обычной практикой.
108. Объясните своими словами, как рационализировать знаменатель.
ответов
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6a
15: 24×3
17: 5
19: 2 53
21:30 23
23: 16
25: 3a
27: 2x⋅3×3
29: 2xy⋅25×3
31: 35−5
33: 42-321
35: 32−23
37: x + xy
39: 2a7b − 4b5a
41: 6 + 14−15−35
43: 182 + 23−126−4
45: 8−215
47: 10
49: a − 22ab + 2b
51: Периметр: (103 + 62) см; площадь: 156 квадратных сантиметров
53: 18 квадратных метров
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2a
65: 55
67: 63
69: 104
71: 3−153
73: 7x7x
75: ab5b
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9ab32b
85: 9x3y45xy
87: 27a2b453
89: 310 + 9
91: 5-32
93: −1 + 2
95: −5-352
97: −4−15
99: 15−7623
101: x2 + 2xy + yx2 − y
103: a − 2ab + ba − b
105: 5x + 2×25−4x
.

 Следующие шаги, 2—4, в точности повторяют процесс умножения дробей.
Следующие шаги, 2—4, в точности повторяют процесс умножения дробей. Моро. Учебник №2. Ответы к стр. 92
Моро. Учебник №2. Ответы к стр. 92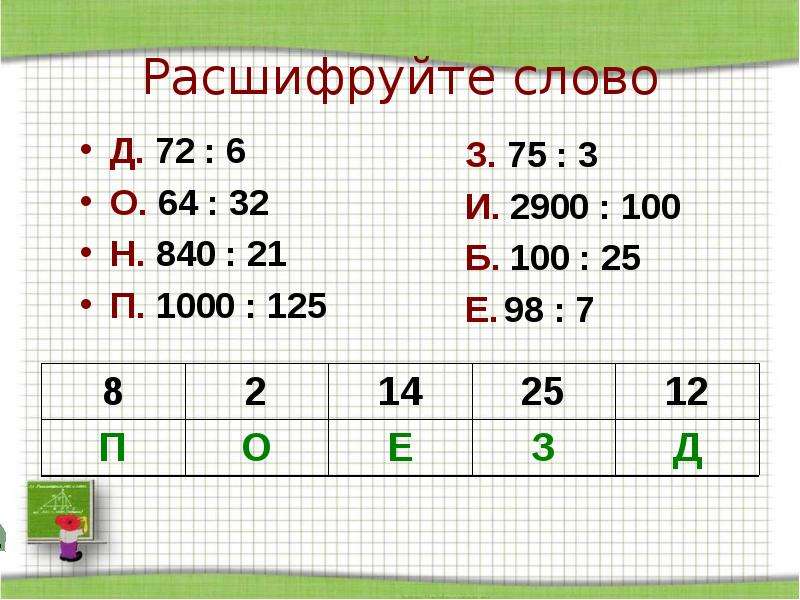 2 часть. Страница 105
2 часть. Страница 105









 Теперь пришло время решить 6/2.
Теперь пришло время решить 6/2.


 По возможности упростите результат.
По возможности упростите результат.