Порядок выполнения действий: правила, примеры.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
Определение 1В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.

- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1Условие: вычислите, сколько будет 7−3+6.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7−3+6=4+6=10
Ответ: 7−3+6=10.
Пример 2Условие: в каком порядке нужно выполнять вычисления в выражении 6:2·8:3?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3Условие: подсчитайте, сколько будет 17−5·6:3−2+4:2.
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
17−5·6:3−2+4:2=17−10−2+2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17−10−2+2=7−2+2=5+2=7
Ответ: 17−5·6:3−2+4:2=7.
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание Пример 4Условие: вычислите, сколько будет 5+(7−2·3)·(6−4):2.
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7−2·3=7−6=1
Считаем результат во вторых скобках.
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5+(7−2·3)·(6−4):2=5+1·2:2
Начнем с умножения и деления, потом выполним вычитание и получим:
5+1·2:2=5+2:2=5+1=6
На этом вычисления можно закончить.
Ответ: 5+(7−2·3)·(6−4):2=6.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).
Решение
У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ:

Ответ: 4+(3+1+4·(2+3))=28.
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4+(4+(4−6:2))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−6:2=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам: 4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6Условие: найдите, сколько будет (3+1)·2+62:3−7.
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+36:3−7.
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
(3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13
Ответ: (3+1)·2+62:3−7=13.
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Порядок арифметических действий, скобки | Формулы и расчеты онлайн
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Например,
\[ 4 — 2 + 1 = 3 \]
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
\[ (4 — 2) + 1 = 3 \]
\[ 4 — (2 + 1) = 1 \]
Пример 1:
\[ (2 + 4) · 5 = 6 · 5 = 30 \]
\[ 2 + (4 · 5) = 2 + 20 = 22 \]
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.
При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Пример 2:
\[ 2 · 5 — 3 · 3 \]
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1
Пример 3:
\[ 9 + 16 : 4 — 2 · (16 — 2 · 7 + 4) + 6 · (2 + 5) \]
Сначала выполняем действия в скобках:
16 — 2 · 7 + 4 = 16 — 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения,
которые сами уже содержат скобки. Тогда, кроме обычных (круглых),
применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками {}. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Пример 4:
\[ 5 + 2 · [14 — 3 · (8 — 6)] + 32 : (10 — 2 · 3) \]
Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4
действия в квадратных скобках дают:
14 — 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Пример 5:
\[ {100 — [35 — (30 — 20)]}· 2 \]
Порядок действий:
30 — 20 = 10
35 — 10 = 25
100 — 25 = 75
75 · 2 = 150
Порядок арифметических действий, скобки | стр. 19 |
|---|
Калькулятор онлайн по действиям. Порядок выполнения действий в выражениях без скобок и со скобками
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .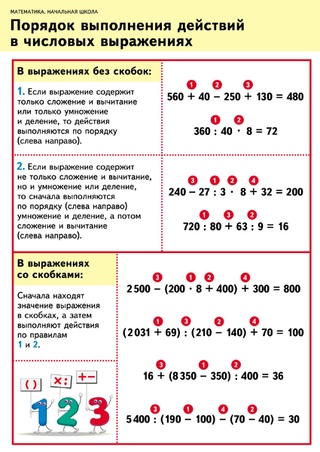
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо.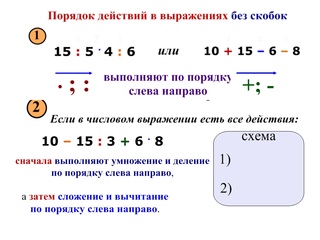 А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2
. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6
. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3)
. Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5
. Подставив найденное значение, получаем 3+1+4·5
. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.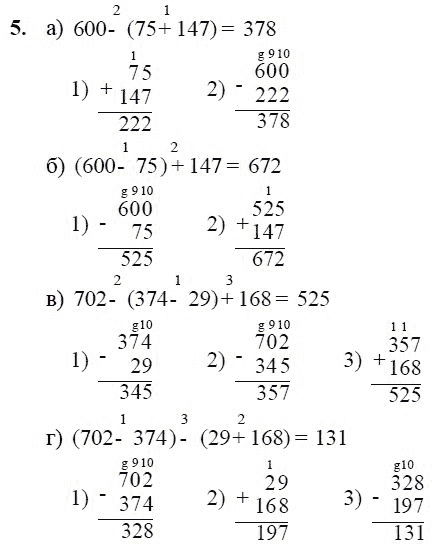
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Бесплатная программа ЛовиОтвет — функциональный калькулятор для решения примеров и уравнений. В программе Лови Ответ происходит автоматическое решение математических примеров и уравнений с выводом действий и этапов их решения.
Для чего нужна такая программа? Программа Лови Ответ — это своего рода математический решебник, который выводит ответ, с пошаговым решением выполненного задания.
Программа Лови Ответ будет интересна школьникам и их родителям. С помощью этой программы родители могут проверять домашние задания, которые выполнил учащийся. Также школьники и студенты могут решать примеры и уравнения при помощи этого математического калькулятора.
Взрослые, которые уже не помнят многого из школьного курса, а также учащиеся смогут при помощи данной программы, быстро решить математический пример любой степени сложности.
В программе ЛовиОтвет можно будет выполнять такие математические действия:
- Совершать действия с натуральными числами.
- Производить действия с дробями (десятичными, обыкновенными, смешанными).
- В программе можно будет упрощать выражения, производить действия с многочленами.
- Решать линейные и квадратные уравнения.
Примеры и уравнения будут решены в программе Лови Ответ пошагово, с последовательными действиями. Визуально, в окне программы, вы увидите решение примера или уравнения. Ответ и пошаговые действия для его решения, будут записаны на своеобразном тетрадном листе. Все этапы решения можно будет записывать в программе в столбик.
Все этапы решения можно будет записывать в программе в столбик.
Скачать программу ЛовиОтвет можно с официального сайта производителя. Программа доступна для работы на компьютерах с операционной системой Windows. Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone/iPod), для мобильных телефонов (java, java-mini).
Лови Ответ скачать
После загрузки, вам можно будет установить программу на свой компьютер.
Установка программы Лови Ответ
Запустите процесс установки программы LoviOtvet на своем компьютере.
При установке программы будьте внимательны! Снимите флажки в тех пунктах, где вам предложат установить дополнительные программы, для того, чтобы не устанавливать на свой компьютер постороннее программное обеспечение.
По завершению установки программы на компьютер, будет открыто главное окно программы ЛовиОтвет.
Обзор программы Лови Ответ
В верхней части окна программы расположены кнопки меню для управления программой.
С помощью кнопки меню «Правка» вы можете скопировать решение на свой компьютер, выбрав необходимый вариант копирования из контекстного меню. Из меню «Настройки» вы можете выбрать размер листа, клеток, очистить историю. Здесь вы можете изменить цвет отображения окна программы, передвинув в нужное место ползунок, по шкале цвета.
Под панелью меню расположено поле, в которое вводится задание.
В левой части окна расположены кнопки и переключатели для ввода данных. Здесь находится основная и дополнительная панель.
Дополнительную панель можно будет скрыть с помощью кнопки «Скрыть дополнительную панель». Отсюда, в случае необходимости, вы можете изменить размер листа и размер клеток в рабочей области.
Остальную часть окна программы занимает рабочая область, в которой будет отображено решение задания.
Для решения примера, с помощью соответствующих кнопок введите выражение, а затем нажмите на кнопку «Ответ». Решение можно будет выводить в нескольких вариантах: стандартное решение, обыкновенные дроби, решение «в столбик».
После клика по треугольнику в крайней правой части поля, в котором вводится пример или уравнение, откроется дополнительное поле, в котором будут отображена история расчетов. В этом поле можно будет очистить историю расчетов.
Подробнее о том, как пользоваться математическим калькулятором, можно будет прочитать на официальном сайте производителя программы ЛовиОтвет, на странице сайта «Как пользоваться».
Лови Ответ онлайн
Производитель запустил онлайн версию программы ЛовиОтвет, которая доступна по такому адресу: https://calc.loviotvet.ru/ .
По заявлению производителя, версия Лови Ответ онлайн менее функциональна, чем программа, которая устанавливается на компьютер или мобильное устройство. Но, все равно, онлайн калькулятор может быть полезен в некоторых случаях, для выполнения решения поставленных задач.
Выводы статьи
Бесплатная программа Лови Ответ — математический решебник и калькулятор, который помогает школьникам, студентам и родителям выполнять или проверять решение примеров и уравнений любой степени сложности.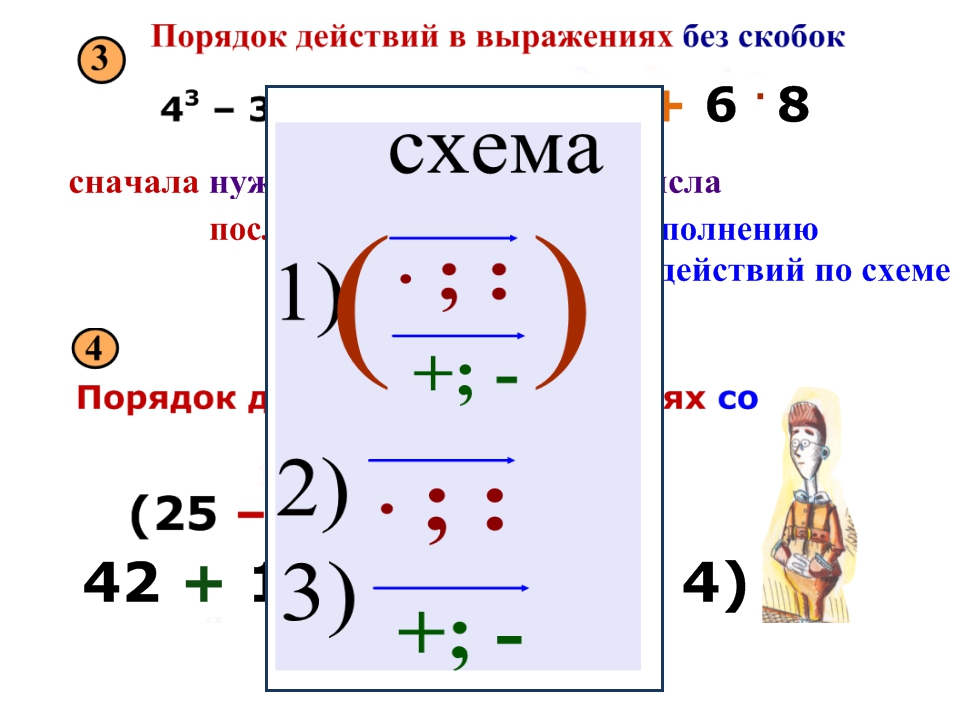
ЛовиОтвет — программа для решения примеров и уравнений (видео)
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
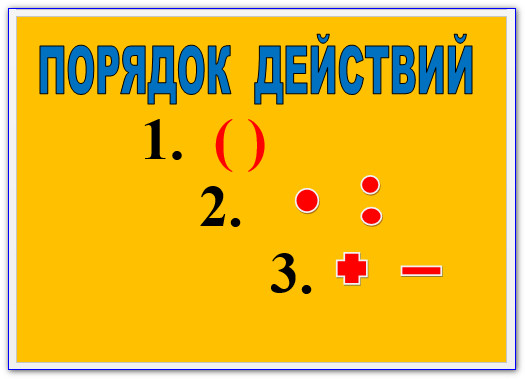
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Примеры с дробями – один из основных элементов математики. Существует много разных типов уравнений с дробями. Ниже приведена подробная инструкция по решению примеров такого типа.
Как решать примеры с дробями – общие правила
Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:
- Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель – число, находящееся в нижней части дроби, числитель – в верхней), нужно сложить их числители, а знаменатель оставить тем же.
- Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.

- Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
- Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
- Для того чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.
Как решать примеры с дробями – практика
Правило 1, пример 1:
Вычислить 3/4 +1/4.
Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.
Ответ: 3/4 + 1/4 = 4/4 = 1.
Правило 2, пример 1:
Вычислить: 3/4 – 1/4
Пользуясь правилом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Ответ: 3/4 – 1/4 = 2/4 = 1/2.
Правило 3, Пример 1
Вычислить: 3/4 + 1/6
Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
Ответ: 11/12
Правило 3, Пример 2:
Вычислить 3/4 – 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус. Получаем: 3*3-2*1/12 = 9-2/12 = 7/12.
Ответ: 7/12
Правило 4, Пример 1:
Вычислить: 3/4 * 1/4
Пользуясь четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3*1/4*4 = 3/16.
3*1/4*4 = 3/16.
Ответ: 3/16
Правило 4, Пример 2:
Вычислить 2/5 * 10/4.
Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.
2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1*1 = 1.
Ответ: 2/5 * 10/4 = 1
Правило 5, Пример 1:
Вычислить: 3/4: 5/6
Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Ответ: 9/10.
Как решать примеры с дробями – дробные уравнения
Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Рассмотрим пример:
Решить уравнение 15/3x+5 = 3
Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При решении таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).
Для этого существует ОДЗ (область допустимых значений).
Таким образом, 3x+5 ≠ 0.
Отсюда: 3x ≠ 5.
x ≠ 5/3
При x = 5/3 уравнение просто не имеет решения.
Указав ОДЗ, наилучшим способом решить данное уравнение будет избавиться от дробей. Для это сначала представим все не дробные значения в виде дроби, в данном случае число 3. Получим: 15/(3x+5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x+5)*1. Последовательность действий:
- Умножаем 15/(3x+5) на (3x+5)*1 = 15*(3x+5).
- Раскрываем скобки: 15*(3x+5) = 45x + 75.
- То же самое проделываем с правой частью уравнения: 3*(3x+5) = 9x + 15.
- Приравниваем левую и правую часть: 45x + 75 = 9x +15
- Переносим иксы влево, числа вправо: 36x = – 50
- Находим x: x = -50/36.
- Сокращаем: -50/36 = -25/18
Ответ: ОДЗ x ≠ 5/3 . x = -25/18.
Как решать примеры с дробями – дробные неравенства
Дробные неравенства по типу (3x-5)/(2-x)≥0 решаются при помощи числовой оси. Рассмотрим данный пример.
Рассмотрим данный пример.
Последовательность действий:
- Приравниваем числитель и знаменатель к нулю: 1. 3x-5=0 => 3x=5 => x=5/3
2. 2-x=0 => x=2 - Чертим числовую ось, расписывая на ней получившиеся значения.
- Под значение рисуем кружок. Кружок бывает двух типов – заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
- Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.
- Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3. (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.

- Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).
Ответ: x = Ø
Данный калькулятор пытается оценить сложность вычисления без калькулятора (на листочке) задач с использованием арифметических операций сложения, вычитания, умножения и деления.
Калькулятор определяет количество элементарных операций в примере, дает условную сложность выраженную в миллисекундах, требуемых для вычисления примера. Сложность складывается из суммы элементарных операций, помноженных на коэффициент сложности (время в миллисекундах, требуемое для выполнение операции). Расшифровка элементарных операций дается в таблице в нижней части калькулятора.
Результат вычисления
Количество элементарных операций
Сложность (время вычисления)
Расшифровка операций с указанием сложности.
++ сложность 200, увеличение на единицу, например, при умножении 2003000 — будет одно умножение 2 3 и 5 раз выполнится подсчет нулей
+ сложность 500, элементарное сложение например 5+4
— сложность 500, элементарное вычитание, например 3-2
* сложность 1000, элементарное умножение, например 2*2
/ сложность 1000, деление — операция деления сводится к последовательном выполнении операций умножения и вычитания, при этом мы прикидываем всякий раз какой множитель необходимо выбрать, чтобы произведение получилось чуть меньше или равно текущего делимого. Эта элементарная операция подсчитывается в данной колонке. Необходимые умножения и вычитания подсчитываются дополнительно.
Эта элементарная операция подсчитывается в данной колонке. Необходимые умножения и вычитания подсчитываются дополнительно.
0+ сложность 100, сложение с нулем — частный случай выделен отдельно, так как это более простая операция чем сложение.
0 сложность 100, подстановка нулей
°+ сложность 700, сложение с переносом единицы, например 16+7 — содержит две операции — элементарное сложение и перенос единицы в следующий разряд.
=0 сложность 200, сокращение — операции вычитания равных величин, например 100-100
°- сложность 600, заем единицы при вычитании, например при вычитании 11-9 будет выполнен один заем и одна операция вычитания.
** сложность 400, повторное умножение. часто случается, что при выполнении элементарных (и не только) операций умножения выполняются одни и те же операции. Например 2533 будет содержать два элементарных умножения и один повтор, мы просто можем переписать результат умножения 25 3 еще один раз.
*0 сложность 100, частный случай умножения на ноль
*1 сложность 200, частный случай умножения на единицу
°* сложность 700, перенос при умножении, например 234 — два элементарных умножения плюс один перенос (1) при умножении 3 4
+- сложность 300, смена знака
сложность 500, перестановка вычитаемых, выполняется если мы пытаемся вычесть из меньшего большее
. сложность 500, операций с плавающей точкой
Рассмотрим вычисление сложности на примере (4567+987-8354)*32/25:
Пример содержит все четыре арифметических операции.
Сначала выполняется сложение 4567+987=5554
Как видим, в этом примере имеется три элементарных сложения: 7+7, 6+8, 5+9, при выполнении каждого из которых осуществляется перенос единицы в старший разряд.
Затем вычитание 5554-8354=-2800
Так как из меньшего вычитается большее число, результат получается отрицательным, перед вычитанием выполняется перестановка операндов. Первые два разряда 5,4 сокращаются, затем при вычислении 3-5 осуществляется элементарное вычитание с займом единицы, затем просто вычитание 8-1-5=2.
Первые два разряда 5,4 сокращаются, затем при вычислении 3-5 осуществляется элементарное вычитание с займом единицы, затем просто вычитание 8-1-5=2.
Третьим действием выполняем умножение -2800*32=-89600
Так как первый множитель заканчивается нулями, выполняем подсчет их количества, чтобы в конце умножения приписать нули к результату. Затем умножаем 2832. При умножении на 3 8 и 28 выполняется перенос в след. разряд. 2 2 и 2*3 — просто элементарные умножения. Итого 4 элементарных умножения, 2 переноса, 2 подсчета.
Последнее действие — деление -89600/25=-3584
На каждом шаге деления осуществляется подбор множителя таким образом, чтобы произведение его на делитель было близко к числу, составляемому первыми разрядами текущего остатка от деления. Эта операция засчитывается как элементарное деление, после чего выполняется умножение и вычитание, сложность которых рассчитывается по аналогии с предыдущими шагами.
В частности при делении первых разрядов (86) на 25 выбираем множитель = 3. Далее производится умножение 25*3-75, далее вычитание 89-75=14.
Далее производится умножение 25*3-75, далее вычитание 89-75=14.
Итого при вычислении 89600/25 имеем: 4 деления и 4 вычитания, 8 произведений, 3 сокращения, два умножения с переносом, при умножении с переносом осуществляется одно сложение.
В конечном итоге в ходе вычисления всего примера произведено 52 элементарные операции — с учетом обозначенных весовых коэффициентов, общая сложность составляет 28500. Таким образом для решения данного примера понадобится примерно полминуты (28.5 секунды).
P.S. Все временные оценки и сам алгоритм вычисления сложности сделаны на основе субъективных предположений автора, комментарии и замечания приветствуются.
| Табличка на двери |
Проверка арифметических действий | Математика
Чтобы убедиться, что какое-нибудь арифметическое действие сделано без ошибки, его проверяют.
Проверкой называют совокупность арифметических приемов с целью убедиться, что данное арифметическое действие исполнено верно. Проверка также состоит из арифметических действий, выполненных в другом порядке.
Самый простой способ убедиться, что действие выполнено верно, состоит, конечно, в том, чтобы повторить его снова. Однако, замечено, что уверенность наша увеличивается, если мы убедимся другим путем в верности какого-нибудь результата, поэтому проверяют арифметические действия иначе.
Проверка основана на главных свойствах самих арифметических действий и на зависимости, существующей между данными и искомыми числами.
Основываясь на главных свойствах самих действий, мы можем каждое действие проверять тем же действием, только выполненным в другом порядке. Таким образом, сложение проверяется сложением, вычитание — вычитанием и т. д.
Проверка арифметических действий теми же действиями
Проверка сложения
Сумма не изменяется от перемены порядка слагаемых, следовательно, чтобы проверить сложение, нужно сложить слагаемые в другом порядке; если получится та же самая сумма, сложение сделано верно.
Сложение:
Проверка сложения:
сложение верно.
Обычно при проверке складываются слагаемые в обратном порядке, то есть снизу вверх.
Проверка вычитания
Вычитаемое равно уменьшаемому без разности, следовательно, чтобы проверить вычитание, нужно из уменьшаемого вычесть разность; если в остатке получится вычитаемое, вычитание сделано верно.
Вычитание:
Проверка вычитания:
Вычитание верно.
Проверка умножения
Произведение не изменяется от перемены порядка множителей, следовательно, чтобы проверить умножение, нужно переменить порядок множителей и снова выполнить умножение; если получим то же произведение, умножение выполнено верно.
Умножение:
Проверка умножения:
Умножение верно.
Проверка деления
При делении нацело делитель равен делимому, разделенному на частное, следовательно, чтобы проверить деление, в случае деления нацело, нужно делимое разделить на частное; если в частном получится делитель, деление сделано верно.
Деление верно.
Все онлайн калькуляторы для решения задач · Контрольная Работа РУ · Теперь вы можете задать любой вопрос!
Кусочно-заданная функция
Укажите кусочно-заданную функцию и перейдите к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построение графика и др.
Решение уравнений
Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике.
Решение пределов
Этот сервис позволяет найти предел функции. Также рассматривается подробное решение правилом Лопиталя.
Производная функции
Это сервис, где можно вычислить производную функции, частную производную функции, а также производную неявно заданной функции.
Разложение в ряд
Здесь можно выполнить разложение в ряд Тейлора, Фурье, найти сумму ряда.
Системы уравнений
Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.
Решение неравенств
Решает неравенство, а также изображает решённое неравенство на графике.
Решение интегралов
Это сервис, где можно вычислить определённые, неопредёленные интегралы, а также двойные, несобственные, кратные.
График функции
Это сервис построения графиков на плоскости и в пространстве. Приводится подробное решение на исследование функции.
Приводится подробное решение на исследование функции.
Решение систем неравенств
Вы можете попробовать решить любую систему неравенств с помощью данного калькулятора систем неравенств.
Порядок обжалования действий (бездействия) и решений государственных органов, органов местного самоуправления и их должностных лиц
Основания, условия и порядок обжалования решений и действий государственных органов, органов управления государственных внебюджетных фондов, органов местного самоуправления, подведомственных им учреждений и их должностных лиц
Решения и действия (бездействие) органов государственной власти, органов местного самоуправления, подведомственных им учреждений и должностных лиц могут быть обжалованы гражданами в досудебном (внесудебном) порядке и непосредственно в суд. Досудебный (внесудебный) порядок обжалования — обжалование решений и действий в вышестоящий орган, вышестоящему должностному лицу.
Вышестоящим органом Администрации Горнозаводского управленческого округа Свердловской области является Правительство Свердловской области. Адрес: 620031, г. Екатеринбург, пл. Октябрьская, д. 1. e-mail: [email protected]
Контакты для обращений граждан:
— в электронном виде через систему «Электронная приемная«.
— телефакс: (343) 362-15-13, (343) 371-76-42.
Обжалование действий (бездействия) должностных лиц осуществляется в соответствии с Федеральным законом от 02.05.2006 № 59-ФЗ «О порядке рассмотрения обращений граждан Российской Федерации». Основанием для процедуры внесудебного обжалования является жалоба заявителя. Жалоба должна содержать:
1) наименование органа, должностного лица решения и действия (бездействие) которых обжалуются;
2) фамилию, имя, отчество, сведения о месте жительства заявителя, а также номер (номера) контактного телефона, адрес (адреса) электронной почты (при наличии) и почтовый адрес, по которым должен быть направлен ответ заявителю;
3) сведения об обжалуемых решениях и действиях (бездействии) органа, должностного лица;
4) в случае необходимости в подтверждение своих доводов лицо, направляющее жалобу, может прилагать к письменной жалобе документы и материалы либо их копии.
Жалоба подается в письменном виде либо в электронной форме. Срок рассмотрения обращения гражданина составляет 30 дней (ст.12 Федерального закона № 59-ФЗ «О порядке рассмотрения обращений граждан Российской Федерации»). Решения и действия (или бездействие) органов государственной власти, органов местного самоуправления и должностных лиц могут быть обжалованы в суд. Судебная защита прав гарантируется Конституцией РФ. Заинтересованное лицо вправе в порядке, установленном законодательством о гражданском судопроизводстве, обратиться в суд за защитой нарушенных либо оспариваемых прав, свобод или законных интересов. К решениям, действиям (бездействию) органов государственной власти, органов местного самоуправления, должностных лиц, государственных или муниципальных служащих, оспариваемым в порядке гражданского судопроизводства, относятся коллегиальные и единоличные решения и действия (бездействие), в результате которых:
— нарушены права и свободы гражданина;
— созданы препятствия к осуществлению гражданином его прав и свобод;
— на гражданина незаконно возложена какая-либо обязанность или он незаконно привлечен к ответственности.
Гражданин вправе обратиться в суд с заявлением в течение трех месяцев со дня, когда ему стало известно о нарушении его прав и свобод. Заявление должно быть рассмотрено судом в течение 10 дней.
Порядок выполнения действий: правила, примеры.
Когда мы работаем с различными выражениями, включающими в себя цифры и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после.Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приводим нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
В третьей части мы приводим нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычислений простых выражений
Определение 1В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую — вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, необходимость умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали самые простые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1Условие: вычислите, сколько будет 7−3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в результате получаем десять. Вот запись всего решения:
Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в результате получаем десять. Вот запись всего решения:
7−3 + 6 = 4 + 6 = 10
Ответ: 7−3 + 6 = 10.
Пример 2Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого.У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем, что слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3Условие: подсчитайте, сколько будет 17−5 · 6: 3−2 + 4: 2.
Решение
Сначала определим верный порядок, поскольку у нас здесь есть все основные виды арифметических операций — сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому их выполняем в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. этого делим 4 на 2, После этого 2. Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому их выполняем в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. этого делим 4 на 2, После этого 2. Подставим найденные значения в исходное выражение:
17−5 · 6: 3−2 + 4: 2 = 17−10−2 + 2
Здесь уже нет ни деления, ни умножения, поэтому оставшиеся вычисления по порядку и получаем ответ:
17−10−2 + 2 = 7−2 + 2 = 5 + 2 = 7
Ответ: 17−5 · 6: 3−2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
Сформулируем нужное определение.
К действиям первой ступени вычитание и сложение, второй — умножение и деление.
Зная эти названия, мы можем записать данное ранее правило порядка действий так:
Определение 2В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий.В таком случае нужное правило можно записать так:
Определение 3Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Проиллюстрируем нашу мысль примером.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание Пример 4Условие: вычислите, сколько будет 5+ (7−2 · 3) · (6−4): 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2 · 3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7-2 · 3 = 7-6 = 1
Считаем результат во второй скобках.Там у нас всего одно действие: 6−4 = 2 .
Теперь нам нужно подставить полученные значения в первоначальное выражение:
5+ (7−2 · 3) · (6−4): 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычислении можно закончить.
Ответ: 5+ (7−2 · 3) · (6−4): 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие.Нам надо только применять правило выше по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5Условие: вычислите, сколько будет 4+ (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3), а именно с 2 + 3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5. Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 .Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4+ (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значений выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешнему.
Допустим, нам надо найти, сколько будет (4+ (4+ (4−6: 2)) — 1) −1.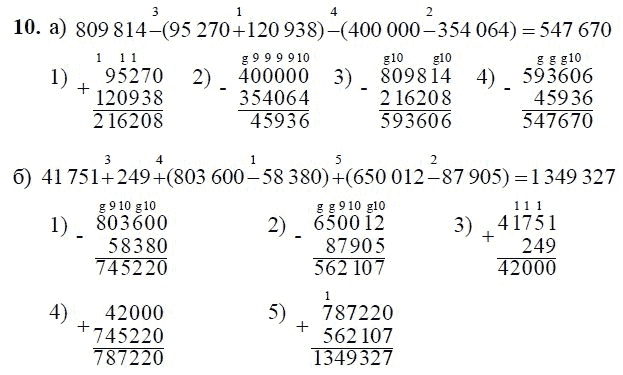 Начинаем с выражения во внутренних скобках. 4−6: 2 = 4−3 = 1, исходное выражение можно записать как (4+ (4 + 1) −1) −1.Снова обращаемся к внутренним скобкам: 4 + 1 = 5. Мы пришли к выражению (4 + 5−1) −1 . Считаем 4 + 5−1 = 8 и в итоге получаем разность 8-1, результатом чего будет 7.
Начинаем с выражения во внутренних скобках. 4−6: 2 = 4−3 = 1, исходное выражение можно записать как (4+ (4 + 1) −1) −1.Снова обращаемся к внутренним скобкам: 4 + 1 = 5. Мы пришли к выражению (4 + 5−1) −1 . Считаем 4 + 5−1 = 8 и в итоге получаем разность 8-1, результатом чего будет 7.
Порядок вычислений в выражениях со своими корнями, логарифмами иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем функции.После этого мы действовали по правилам. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6Условие: найдите, сколько будет (3 + 1) · 2 + 62: 3−7.
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62 = 36. Теперь подставим результат в выражении, после чего оно примет вид (3 + 1) · 2 + 36: 3−7.
Считаем: 62 = 36. Теперь подставим результат в выражении, после чего оно примет вид (3 + 1) · 2 + 36: 3−7.
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, следом — сложение и вычитание.
(3 + 1) · 2 + 36: 3−7 = 4 · 2 + 36: 3−7 = 8 + 12−7 = 13
Ответ: (3 + 1) · 2 + 62: 3−7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, сложные примеры подсчетов в случае выражений с корнями, степенью и др.Рекомендуем вам с ней ознакомиться.
Порядок арифметических действий, скобки | Формулы и расчеты онлайн
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Например,
\ [4–2 + 1 = 3 \]
Если действовать в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), используются скобками. Действия, заключенные в скобки, выполняются раньше другими. В нашем случае:
\ [(4–2) + 1 = 3 \]
\ [4 — (2 + 1) = 1 \]
Пример 1:
\ [(2 + 4) · 5 = 6 · 5 = 30 \]
\ [2 + (4 · 5) = 2 + 20 = 22 \]
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, произведены в том случае, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.
Они могут выполнять такие операции в таком виде:
- сначала выполняются действия, заключенные в скобки; при этом умножение и делаются делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем в порядке следования, но раньше сложения и вычитания.

Пример 2:
\ [2 · 5 — 3 · 3 \]
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1
Пример 3:
\ [9 + 16: 4 — 2 · (16 — 2 · 7 + 4) + 6 · (2 + 5) \]
Сначала выполняем действия в скобках:
16-2 · 7 + 4 = 16-14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16: 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43
Указания для порядка действий необходимо заключать в скобки такие выражения,
которые сами содержат скобки.Тогда, кроме обычных (круглых) ,
применяют скобки иной формы, например квадратные [] . Если в скобки нужно заключить выражение, имеющиеся уже круглые и квадратные скобки, использовать фигурными скобками {} . Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д .. Наконец, выполняются остающиеся действия.
Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д .. Наконец, выполняются остающиеся действия.
Пример 4:
\ [5 + 2 · [14 — 3 · (8 — 6)] + 32: (10 — 2 · 3) \]
Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4
действия в квадратных скобках дают:
14 — 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32: 4 = 5 + 16 + 8 = 29
Пример 5:
\ [{100 — [35 — (30-20)]} · 2 \]
Порядок действий:
30-20 = 10
35-10 = 25
100-25 = 75
75 · 2 = 150
Порядок арифметических действий, скобки | стр.19 |
|---|
Калькулятор онлайн по действиям. Порядок выполнения действий в выражениях без скобок и со скобками
И вычисление значений выражений действия выполняются в определенном порядке, иными словами, нужно порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаки плюс, минус, умножить и разделить.Дальше разъясним, какого порядка действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выраженных степенях, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем — сложение и вычитание.
Озвученное воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе не эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3 + 6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3 + 6 = 4 + 6 = 10 .
Ответ:
7−3 + 6 = 10 .
Пример.
Укажите порядок выполнения действий в выражении 6: 2 · 8: 3 .
Решение.
Чтобы ответить на вопрос, обратимся к правилам, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении есть лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5 · 6: 3−2 + 4: 2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5 · 6: 3 найденное значение 10 , а вместо 4: 2 — значение 2 , имеем 17−5 · 6: 3−2 + 4: 2 = 17−10−2 + 2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева выполнить оставшиеся действия: 17−10−2 + 2 = 7−2 + 2 = 5 + 2 = 7 .
Ответ:
17−5 · 6: 3−2 + 4: 2 = 7 .
Первые порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего это выглядело бы так:.
Для предыдущего это выглядело бы так:.
Этого же порядка выполнения действий — сначала умножение и деление, затем сложение и вычитание.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
Если выражение не содержит скобок, то по порядку слева сначала выполняются действия второй ступени (умножение и деление), — действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задает порядок выполнения действий в выражениях со скобками. , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева выполняется умножение и деление, затем — сложение и вычитание.
Итак, выражения в скобках как составные части выражения, и в них уже сохранен порядок действий.Рассмотрим решения примеров для большей ясности.
Пример.
Выполните действия 5+ (7−2 · 3) · (6−4): 2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2 · 3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2 · 3 = 7−6 = 1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие — вычитание, выполняем его 6−4 = 2 .
Подставляем полученные значения в исходное выражение: 5+ (7−2 · 3) · (6−4): 2 = 5 + 1 · 2: 2 .В полученном выражении сначала выполняем слева направо умножение и деление, затем — вычитание, получаем 5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6 . На этом все выполнены, мы придерживались такого порядка их выполнения: 5+ (7−2 · 3) · (6−4): 2 .
Запишем краткое решение: 5+ (7−2 · 3) · (6−4): 2 = 5 + 1 · 2: 2 = 5 + 1 = 6
.
Ответ:
5+ (7−2 · 3) · (6−4): 2 = 6 .
Бывает, что выражение содержит скобки в скобках. Этого следует исполнять озвученное правило выполнения действий в выражениях со скобками.Покажем решение пример.
Пример.
Выполните действия в выражении 4+ (3 + 1 + 4 · (2 + 3)) .
Решение.
Это выражение со скобками, что означает, что выполнение действий нужно начинать с выражением в скобках, то есть, с 3 + 1 + 4 · (2 + 3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2 + 3 = 5 . Подставив найденное значение, получаем 3 + 1 + 4 · 5 . В этом выражении сначала выполняем умножение, затем — сложение, имеем 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 .Исходное значение, после подстановки этого значения, принимает вид 4 + 24 , и остается лишь закончить выполнение действий: 4 + 24 = 28 .
Ответ:
4+ (3 + 1 + 4 · (2 + 3)) = 28 .
.
Например, пусть нам нужно выполнить действия в выражении (4+ (4+ (4−6: 2)) — 1) −1
. Сначала выполняем действия во внутренних скобках, так как 4−6: 2 = 4−3 = 1
, то после этого исходное выражение примет вид (4+ (4 + 1) −1) −1
.Опять выполняем действие во внутренних скобках, так как 4 + 1 = 5
, то приходим к следующему выражению (4 + 5−1) −1
. Опять выполняем действия в скобках: 4 + 5−1 = 8
, при этом приходим к разности 8−1
, которая равна 7
.
Сначала выполняем действия во внутренних скобках, так как 4−6: 2 = 4−3 = 1
, то после этого исходное выражение примет вид (4+ (4 + 1) −1) −1
.Опять выполняем действие во внутренних скобках, так как 4 + 1 = 5
, то приходим к следующему выражению (4 + 5−1) −1
. Опять выполняем действия в скобках: 4 + 5−1 = 8
, при этом приходим к разности 8−1
, которая равна 7
.
Бесплатная ЛовиОтвет — функциональный калькулятор для решения схем и решений. В программе Лови происходит автоматическое решение математических правил и выводов действий и этапов их решения.
Для чего нужна такая программа? Программа Лови Ответ — это своего рода математический решебник, который выводит ответ, с пошаговым решением выполненного задания.
Программа Лови Ответ будет интересна школьникам и их родителям. С помощью этой программы родители могут проверять домашние задания, которые выполнил учащийся. Также школьники и студенты могут выполнять примеры и уравнения при помощи этого математического калькулятора.
Взрослые, которые уже не помнят многого из школьного курса, учащиеся решить при помощи данной программы, быстро математический пример любой степени сложности.
В программе ЛовиОтвет можно будет выполнять такие математические действия:
- Совершать действия с натуральными числами.
- Производить действия с дробями (десятичными, обыкновенными, смешанными).
- В программе можно будет упрощать выражения, выполнять действия с многочленами.
- Решать линейные и квадратные уравнения.
Примеры и уравнения будут решены в программе Лови Ответ пошагово, с последовательными действиями. Визуально, в окне программы, вы увидите пример или уравнения. Ответ и пошаговые действия для его решения, будут записаны на своеобразном тетрадном листе.Все этапы решения можно будет записывать в программе в столбик.
Скачать программу ЛовиОтвет можно с официального сайта производителя. Программа доступна для работы на компьютерах с операционной системой Windows. Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone / iPod), для мобильных телефонов (java, java-mini).
Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone / iPod), для мобильных телефонов (java, java-mini).
Лови Ответ скачать
После загрузки вам можно будет установить программу на свой компьютер.
Установка программы Лови Ответ
Запустите процесс установки программы LoviOtvet на свой компьютер.
При установке программы будьте внимательны! Снимите флажки в тех пунктах, где вам предложат установить дополнительные программы, для того, чтобы не установить на свой компьютер постороннее программное обеспечение.
По завершению установки программы на компьютер, откроется окно главное программы ЛовиОтвет.
Обзор программы Лови Ответ
В верхней части окна программы расположены кнопки меню для управления программой части.
С помощью кнопки меню «Правка» вы можете скопировать на свой компьютер, выбрав необходимый вариант копирования из контекстного меню.Из меню «Настройки» вы можете выбрать размер листа, клеток, очистить историю.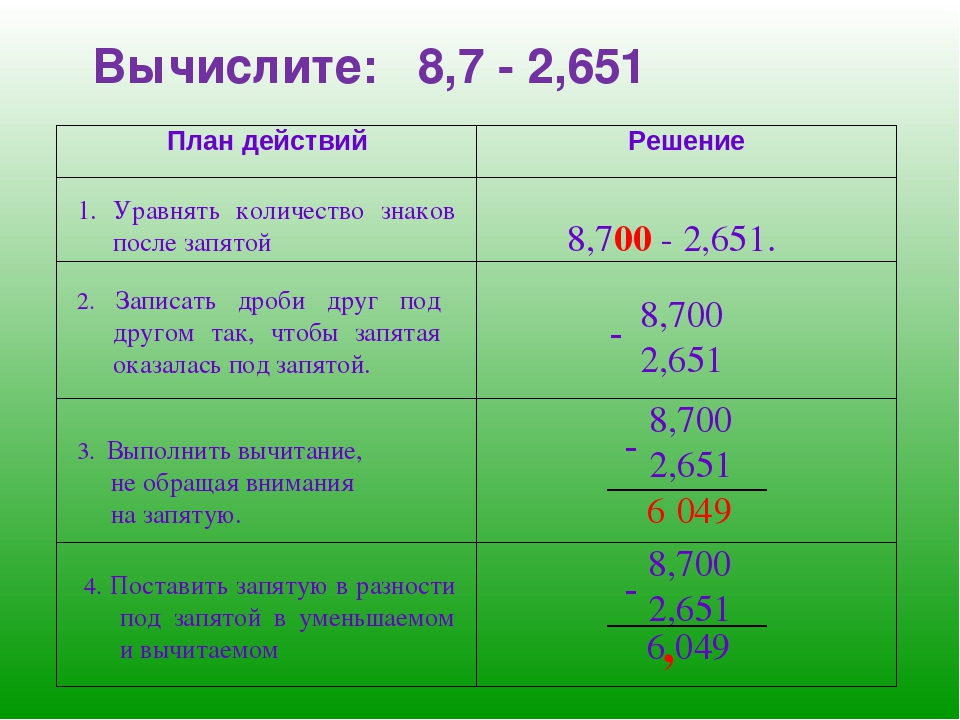 Здесь вы можете изменить цвет изображения окна программы, передвинув в нужное место ползунок, по шкале цвета.
Здесь вы можете изменить цвет изображения окна программы, передвинув в нужное место ползунок, по шкале цвета.
Под панелью меню расположено поле, которое вводится.
В левой части окна кнопки и переключатели для ввода данных. Здесь находится основная и дополнительная панель.
Дополнительную панель можно будет скрыть с помощью кнопки «Скрыть дополнительную панель».Можете отсюда, в случае необходимости, изменить размер листа и размер клеток в рабочей области.
Остальная часть окна программы занимает рабочую область, в которой будет отображено решение задания.
Для решения примера, с помощью соответствующих кнопок введите выражение, а затем нажмите кнопку «Ответ». Решение можно вывести в нескольких вариантах: стандартное решение, обыкновенные дроби, решение «в столбик».
После клика по треугольнику в крайней правой части поля, которое вводится пример или уравнение, откроется дополнительное поле, в котором будет отображена история расчетов. В этом поле можно будет очистить историю расчетов.
В этом поле можно будет очистить историю расчетов.
Подробнее о том, как пользоваться математическим калькулятором, можно будет прочитать на официальном сайте производителя ЛовиОтвет, на странице сайта «Как пользоваться».
Лови Ответ онлайн
Производитель запустил онлайн версию программы ЛовиОтвет, доступный по такому адресу: https://calc.loviotvet.ru/.
По заявлению производителя, версия Лови Ответ онлайн менее функциональна, чем программа, которая устанавливается на компьютер или мобильное устройство.Но, все равно, онлайн калькулятор может быть полезен в некоторых случаях, для выполнения решений поставленных задач.
Выводы статьи
Бесплатная программа Лови Ответ — математический решебник и калькулятор, который помогает школьникам, студентам и родителям выполнять или проверять решения примеров и уравнений любой степени сложности.
ЛовиОтвет — программа для решения примеров и соотношений (видео)
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы выполняем какие-либо постоянно действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся.Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3 + 4 и 8-3 + 4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражении слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражении без скобок входят только умножение и деление, то они действуют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис.2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в обозначении имеются только действия сложения и вычитания, но и умножения и деления?
.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются возможности сложения и вычитания, умножения и деления. Действуем по правиламу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18: 2-2 * 3 + 12: 3 = 9-6 порядке + 4 = 3 + 4 = 7
В каких действиях выполняются арифметические, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30 + 6 * (13-9) = 30 + 6 * 4 = 30 + 24 = 54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1.действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20-7) +15
32 + 9 * (19 — 16)
Будем действовать по правиламу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания.Установим порядок действий. Первым выполнить выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
Первым выполнить выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20-7) +15 = 43-13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилам первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19-16) = 32 + 9 * 3 = 32 + 27 = 59
В выражении 2 * 9-18: 3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания.Действуем по правиламу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2 * 9-18: 3 = 18-6 = 12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11-5) + 47 =
7 * 3 — (16 + 4) =
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание.В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложное, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37 + 9-6: 2 * 3 = 37 + 9-3 * 3 = 37 + 9-9 = 46-9 = 37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняется действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение.Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18: (11-5) + 47 = 18: 6 + 47 = 3 + 47 = 50
В этом выражении имеются также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7 * 3- (16 + 4) = 7 * 3-20 = 21-20 = 1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому можем изучить значение выражений, однако потренируемся применять это правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем направо слева направо умножение и деление, затем слева направо вычитание и сложение.
Во втором выражении имеются также скобки, значит, первое действие выполняем в скобках.После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилами выполнения действий в выражениях без скобок и со скобками.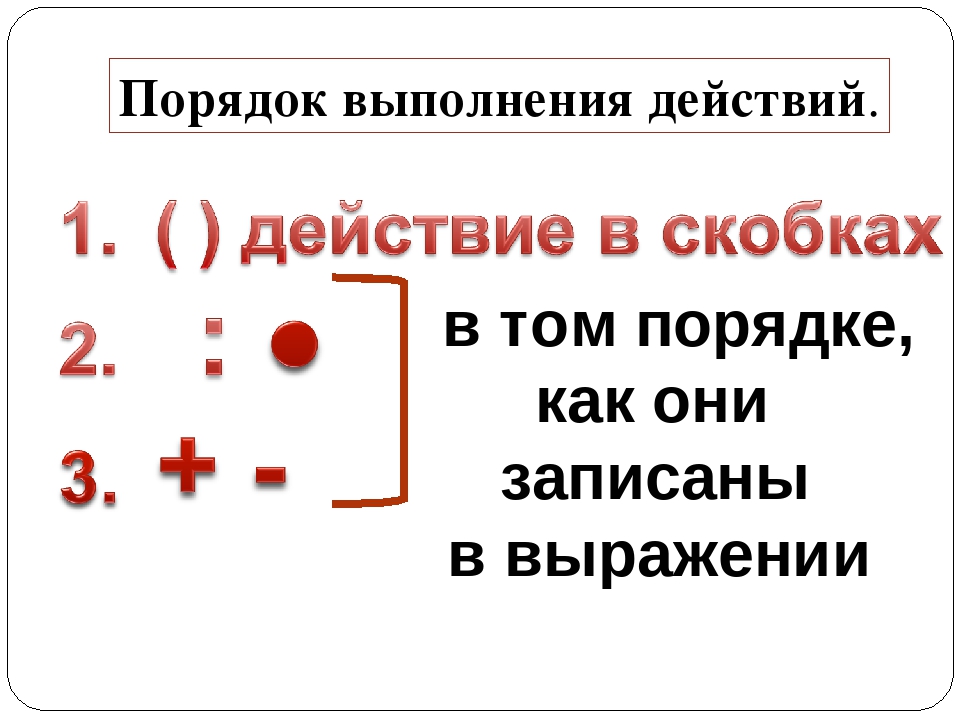
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М .: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др.Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М .: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М .: Просвещение, 2012. .
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М .: «Просвещение», 2011. .
- «Школа России»: Программы для начальной школы. — М .: «Просвещение», 2011. .
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М .: Просвещение, 2012. .
- В.Н. Рудницкая. Тесты. — М .: «Экзамен», 2012. .
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.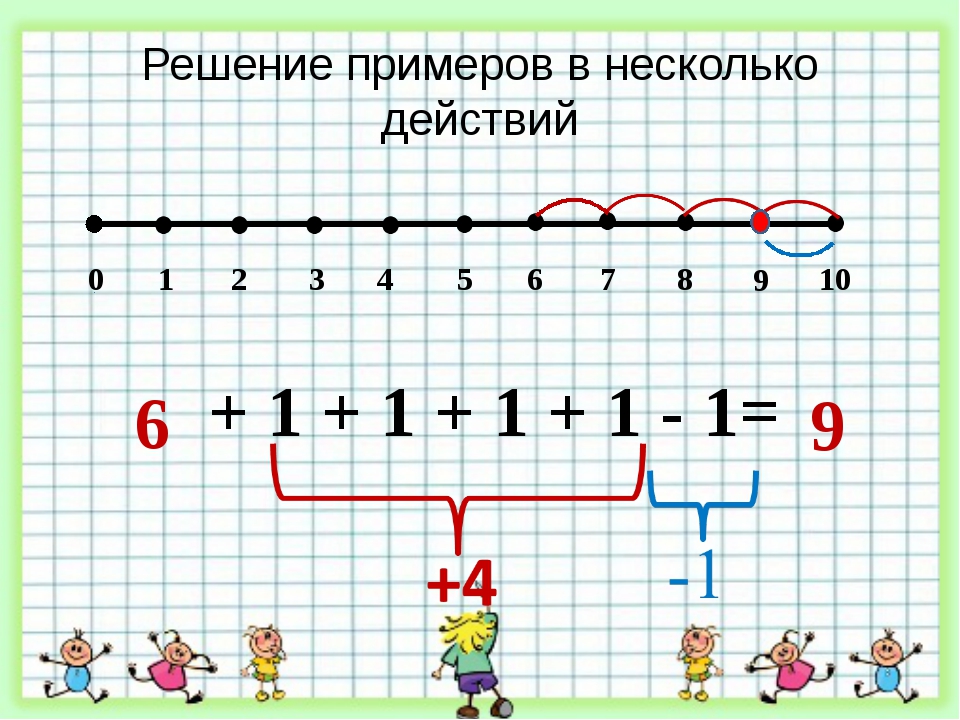
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление ;. 3. сложение; 4. вычитание; 5. сложение. Найдите значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Примеры с дробями — один из основных элементов математики. Существует много разных типов с дробями. Ниже приведена подробная инструкция по вариантам решения такого типа.
Как решать примеры с дробями — общие правила
Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:
- Для того, чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель — число, находящееся в нижней части, числитель — в верхней), нужно сложить их числители, а знаменатель оставить тем же.

- Чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.
- Для того, чтобы сложить или вычесть дробные выражения разными знаменателями, нужно найти наименьший общий знаменатель.
- Для того, чтобы найти дробное произведение, нужно перемножить числители и знаменатели, если есть возможность, сократить.
- Для того, чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.
Как примеры с дробями — практика
Правило 1, пример 1:
Вычислить 3/4 +1/4.
Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.
Ответ: 3/4 + 1/4 = 4/4 = 1.
Правило 2, пример 1:
Вычислить: 3/4 — 1/4
Пользуясь правиламиом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Ответ: 3/4 — 1/4 = 2/4 = 1/2.
Правило 3, Пример 1
Вычислить: 3/4 + 1/6
Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений пример. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким образом, таким числом является 12.Записываем в качестве в знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3 * 3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, умножаем 2 на 1, записываем в 2 * 1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3 * 3 + 2 * 1 = 11. 11/12.
Ответ: 11/12
Правило 3, Пример 2:
Вычислить 3/4 — 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус.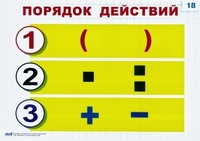 Получаем: 3 * 3-2 * 1/12 = 9-2 / 12 = 7/12.
Получаем: 3 * 3-2 * 1/12 = 9-2 / 12 = 7/12.
Ответ: 7/12
Правило 4, Пример 1:
Вычислить: 3/4 * 1/4
Используйте четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3 * 1/4 * 4 = 3/16.
Ответ: 16.03.
Правило 4, Пример 2:
Вычислить 2/5 * 10/4.
Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.
2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1 * 1 = 1.
Ответ: 2/5 * 10/4 = 1
Правило 5, Пример 1:
Вычислить: 3/4: 5/6
Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Ответ: 9/10.
Как решать примеры с дробями — дробные уравнения
Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Рассмотрим пример:
Решить уравнение 15 / 3x + 5 = 3
Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При использовании таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).
Таким образом, 3x + 5 0.
Отсюда: 3x 5.
x ≠ 5/3
При x = 5/3 уравнение просто не имеет решения.
Указав ОДЗ, наилучшим способом данное уравнение будет избавиться от дробей. Для этого сначала представим все не дробные значения в виде дроби, в данном числе 3. Получим: 15 / (3x + 5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x + 5) * 1. Последовательность действий:
- Умножаем 15 / (3x + 5) на (3x + 5) * 1 = 15 * (3x + 5).
- Раскрываем скобки: 15 * (3x + 5) = 45x + 75.
- То же самое проделываем с правой частью уравнения: 3 * (3x + 5) = 9x + 15.

- Приравниваем левую и правую часть: 45x + 75 = 9x +15
- Переносим иксы влево, числа вправо: 36x = — 50
- Находим x: x = -50/36.
- Сокращаем: -50/36 = -25/18
Ответ: ОДЗ x ≠ 5/3. х = -25/18.
Как решать примеры с дробями — дробные неравенства
Дробные неравенства по типу (3x-5) / (2-x) ≥0 решаются при помощи числовой оси. Рассмотрим данный пример.
Последовательность действий:
- Приравниваем числитель и знаменатель к нулю: 1.3x-5 = 0 => 3x = 5 => x = 5/3
2. 2-x = 0 => x = 2 - Чертим числовую ось, расписывая на получившиеся значения.
- Под значение рисуем кружок. Кружок бывает двух типов — заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
- Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.
- Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3.
 (3 * 3-5) / (2-3) = -4. значение отрицание, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.
(3 * 3-5) / (2-3) = -4. значение отрицание, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.
- Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).
Ответ: x = Ø
Данный калькулятор пытается оценить сложность вычислений без калькулятора (на листе) с использованием арифметических операций, вычитания, умножения и деления.
Калькулятор определяет количество элементов числа операций в примере, дает условную сложность выраженную в миллисекундах, требуемых для вычислений пример. Сложность складывается из суммы элементов операций, помноженных на коэффициент сложности (время в миллисекундах, необходимое для выполнения операции). Расшифровка элементов операций в таблице в нижней части калькулятора.
Расшифровка элементов операций в таблице в нижней части калькулятора.
Результат вычислений
Количество элементарных операций
Сложность (время вычислений)
Расшифровка операций с указанием сложности.
++ сложность 200, увеличение на единицу, например, при умножении 200 3000 — будет одно умножение 2 3 и 5 раз выполнится подсчет нулей
+ сложность 500, элементарное сложение например 5 + 4
— сложность 500, элементарное вычитание, например 3-2
* сложность 1000, элементарное умножение, например 2 * 2
/ сложность 1000, деление — операция деления сводится к последовательности операций умножения и вычитания, при этом мы прикидываем всякий раз какой множитель необходимо выбрать, чтобы произведение получилось чуть меньше или текущего делимого.Эта элементарная операция подсчитывается в данной колонке. Необходимые умножения и вычитания подсчитываются.
0+ сложность 100, сложность с нулем — частный случай выделен отдельно, так как это более простая операция чем сложение.
0 сложность 100, подстановка нулей
° + сложность 700, сложение с переносом единицы, например 16 + 7 — содержит две операции — элементарное сложение и перенос единицы в следующий разряд.
= 0 сложность 200, сокращение — операции вычитания равных величин, например 100-100
° — сложность 600, заем при вычитании, например, при вычитании 11-9 будет выполнен один заем и одна операция вычитания.
** сложность 400, повторное умножение. часто случается, что при выполнении операций умножения выполняются одни и те же операции. Например 25 33 будет содержать два элемента умножения и один повтор, мы просто можем переписать результат умножения 25 3 еще один раз.
* 0 сложность 100, частный случай умножения на ноль
* 1 сложность 200, частный случай умножения на единицу
° * сложность 700, перенос при умножении, например 23 4 — два элементарных умножения плюс один перенос (1) при умножении 3 4
+ — сложность 300, смена знака
сложность 500, перестановка вычитаемых, выполняется если мы пытаемся вычесть из меньшего большего
. сложность 500, операций с плавающей точкой
сложность 500, операций с плавающей точкой
Рассмотрение сложности на примере (4567 + 987-8354) * 32/25:
Пример содержит все четыре арифметических операции.
Произвести сложение 4567 + 987 = 5554
Как видим, в этом примере имеется три элементарных сложения: 7 + 7, 6 + 8, 5 + 9, при выполнении каждого из единиц в старший разряд.
Затем вычитание 5554-8354 = -2800
Так как из меньшего вычитается большее число, результат получается отрицательным, перед вычитанием выполняется перестановка операндов.Первые два разряда 5,4 сокращаются, затем при вычислении 3-5 осуществляется элементарное вычитание с займом единицы, затем просто вычитание 8-1-5 = 2.
Третьим выполняем умножение -2800 * 32 = -89600
Так как первый множитель заканчивается нулями, выполняем подсчет их количества, чтобы в конце умножения приписать нули к результату. Затем умножаем 28 32. При умножении на 3 8 и 2 8 выполняется перенос в след. разряд. 2 2 и 2 * 3 — элементарные умножения.Итого 4 элементарных умножения, 2 переноса, 2 подсчета.
разряд. 2 2 и 2 * 3 — элементарные умножения.Итого 4 элементарных умножения, 2 переноса, 2 подсчета.
Последнее действие — деление -89600 / 25 = -3584
На каждом шаге деления выполняется подборка таким образом, чтобы произведение его на делитель было близко к этому, составляющим первыми разрядами текущего остатка от деления. Эта операция засчитывается как элементарное деление, после чего выполняется умножение и вычитание, сложность рассчитывается по аналогии с предыдущими шагами.
В частности при делении первых разрядов (86) на 25 выбираем множитель = 3.Далее производится умножение 25 * 3-75, далее вычитание 89-75 = 14.
Итого при вычислении 89600/25 имеем: 4 деления и 4 вычитания, 8 произведений, 3 сокращения, два умножения с переносом, при умножении с переносом осуществляется одно сложение.
 Таким образом для решения данного примера используется примерно полминуты (28.5 секунды).
Таким образом для решения данного примера используется примерно полминуты (28.5 секунды).П.С. Все временные оценки и сам алгоритм вычисления сделаны на основе субъективных предположений автора, комментарии и замечания приветствуются.
| Табличка на двери |
1 + (4 + 8) = | 8 — (2 + 4) = | 3 + (6–5) = | 59 + 25 = |
82 + 14 = | 29 + 52 = | 18 + 47 = | 39 + 53 = |
37 + 53 = | 25 + 63 = | 87 + 17 = | 19 + 52 = |
2.Реши примеры правильно выполняя последовательность действий:
2.1. 36: 3 + 12 * (2 — 1): 3
2.2. 39 — (81: 9 + 48: 6) * 2
2.3. (7 + 5) * 2 — 48: 4
2.4. 18: 3 + (5 * 6): 2 — 4
3. Реши задачи, сперва составив правильно выражения, а за тем их решив:
3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше.Сколько упаковок порошка стало на складе?
3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?
3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?
ФИ _________________________________
21: 3 * 6 — (18 + 14): 8 = | 63: (81: 9) + (8 * 7-2): 6 = | 64: 2: 4+ 9 * 7-9 * 1 = |
37 * 2 + 180: 9 — 36: 12 = | 52 * 10-60: 15 * 1 = | 72: 4 +58: 2 = |
5 * 0: 25 + (72: 1 — 0): 9 = | 21: (3 * 7) — (7 * 0 + 1) * 1 = | 6: 6 + 0: 8-8: 8 = |
91: 7 + 80: 5 — 5: 5 = | 64: 4 — 3 * 5 +80: 2 = | (19 * 5 — 5): 30 = |
19 + 17 * 3 — 46 = | (39 + 29): 4 + 8 * 0 = | (60-5): 5 +80: 5 = |
54 — 26 + 38: 2 = | 63: (7 * 3) * 3 = | (160-70): 18 * 1 = |
200 — 80: 5 + 3 * 4 = | (29 + 25): (72: 8) = | 72:25 + 3 * 17 = |
80: 16 + 660: 6 = | 3 * 290 — 800 = | 950: 50 * 1-0 = |
(48: 3): 16 * 0 = | 90-6 * 6 + 29 = | 5 * (48-43) +15: 5 * 7 = |
54: 9 * 8 — 14: 7 * 4 = | 63: 7 * 4 + 70: 7 * 5 = | 24: 6 * 7-7 * 0 = |
21: 7 * 8 + 32: 8 * 4 = | 27: 3 * 5 + 26-18 * 4 = | 54: 6 * 7 — 0: 1 = |
45: 9 * 6 + 7 * 5 — 26 = | 28: 7 * 9 + 6 * (54-47) = | 6 * (9: 3) — 40: 5 = |
21 * 1 — 56: 7 — 8 = | 9 * (64: 8) — 18:18 | 3 * (14: 2) — 63: 9 = |
4 * 8 + 42: 6 * 5 = | 0 * 4 + 0: 5 + 8 * (48: 8) = | 56: 7 + 7 * 6 — 5 * 1 = |
31 * 3 — 17 — 80: 16 * 1 = | 57:19 * 32 — 11 * 7 = | 72-96: 8 +60: 15 * 13 = |
36 + 42: 3 + 23 + 27 * 0 = | 56:14 * 19 — 72: 18 = | (86-78: 13) * 4 = |
650-50 * 4 + 900: 100 = | 630: 9 + 120 * 5 + 40 = | 980 — (160 + 20): 30 = |
940 — (1680 — 1600) * 9 = | 29 * 2 + 26 — 37: 2 = | 72: 3 +280: (14 * 5) = |
300: (5 * 60) * (78: 13) = | 63+ 100: 4 — 8 * 0 = | 84: 7 + 70: 14 — 6: 6 = |
45: 15 — 180: 90 + 84: 7 = | 32 + 51 + 48: 6 * 5 = | 54: 6? 2 — 70: 14 = |
38: 2 — 48: 3 + 0 * 9 = | 30: 6 * 8-6 + 3 * 2 = | (95:19) * (68: 2) = |
(300 — 8 * 7) * 10 = | 1: 1 — 0 * 0 + 1 * 0 — 1 * 1 = | (80: 4 — 60:30) * 5 = |
2 * (120: 6 — 80: 20) = | 56: 4 + 96: 3- 0 * 7 = | 20+ 20: 4 — 1 * 5 = |
(18 + 14): 8 — (7 * 0 + 1) * 1 = | (8 * 7-2): 6 +63: (7 * 3) = | (50-5): 5 + 21: (3 * 7) = |
19 + 17 * 3-60: 15 * 1 = | 80: 5 + 3 * 5 +80: 2 = | 54: 9 * 8-64: 4 + 16 * 0 = |
72 * 10 — 64: 2: 4 = | 84 — 36 + 38: 2 | 91: 13 + 80: 5 — 5: 5 |
300 — 80: 5 + 6 * 4 = | 950: 190 * 1 + 14: 7 * 4 = | (39 + 29): 17 + 8 * 0 = |
(120–30): 18 * 1–72: 25 = | 210: 30 * 60-0: 1 = | 90-6 * 7 + 3 * 17 = |
240: 60 * 7-7 * 0 = | 60: 60 + 0: 80-80: 80 = | 720: 40 +580: 20 = |
9 * 7 — 9 * 1 + 5 * 0: 25 = | 21: 7 * 6 +32: 4 * 5 = | 80:16 +66: 6-63: (81: 9) = |
(19 * 5-5): 30 + 70: 7 = | 15: 5 * 7 + 63: 7 * 5 = | 54: 6 * 7 — (72: 1-0): 9 = |
3 * 290-600-5 * (48-43) = | (300-89 * 7) * 10 — 3? 2 = | (80: 4) + 30 * 2 + 180: 9 = |
30: 6 * 8-6 + 48: 3 + 0 * 9 = | (95:19) * (68:34) — 60: 30 * 5 = | 27: 3 * 5 — 48: 3 = |
3 * 290-800 + 950: 50 = | 80:16 +660: 6 * 1-0 = | 90-6 * 6 + 15: 5 * 7 = |
5 * (48-43) + (48: 3): 16 * 0 = | 280: (14 * 5) +630: 9 * 0 = | 300: (50 * 6) * (78: 6) = |
Если в примерах встретится вопросительный знак (?), Следует его заменить на знак * — умножение.
1. РЕШИ ВЫРАЖЕНИЯ:
35: 5 + 36: 4 — 3
26 + 6 х 8 — 45: 5 24: 6 + 18 — 2 х 6
9 х 6 — 3 х 6 + 19 — 27: 3
2. РЕШИ ВЫРАЖЕНИЯ:
48: 8 + 32 — 54: 6 + 7 х 4
17 + 24: 3 х 4 — 27: 3 х 2 6 х 4: 3 + 54: 6: 3 х 6 + 2 х 9
100 — 6 х 2: 3 х 9 — 39 + 7 х 4
3. РЕШИ ВЫРАЖЕНИЯ:
100 — 27: 3 х 6 + 7 х 4
2 х 4 + 24: 3 + 18 : 6 х 9 9 х 3-19 + 6 х 7-3 х 5
7 х 4 + 35: 7 х 5-16: 2: 4 х 3
4.РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 6: 3 + 6 х 8-17
5 х 8-4 х 7 + 13-11 24: 6 + 18: 2 + 20-12 + 6 х 7
21: 3 — 35: 7 + 9 х 3 + 9 х 5
5. РЕШИ ВЫРАЖЕНИЯ:
42: 7 х 3 + 2 + 24: 3 — 7 + 9 х 3
6 х 6 + 30: 5: 2 х 7 — 19 90 — 7 х 5 — 24: 3 х 5
6 х 5 — 12: 2 х 3 + 49
6. РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 7 + 54: 6: 3 х 5
50 — 45 : 5 х 3 + 16: 2 х 5 8 х 6 + 23-24: 4 х 3 + 17
48: 6 х 4 + 6 х 9-26 + 13
7.РЕШИ ВЫРАЖЕНИЯ:
42: 6 + (19 + 6): 5-6 х 2
60 — (13 + 22): 5-6 х 4 + 25 (27-19) х 4 + 18: 3 + (8 + 27): 5-17
(82-74): 2 х 7 + 7 х 4 — (63-27): 4
8. РЕШИ ВЫРАЖЕНИЯ:
90 — (40-24: 3): 4 х 6 + 3 х 5
3 х 4 + 9 х 6 — (27 + 9): 4 х 5
(50-23): 3 + 8 х 5-6 х 5 + (26 + 16): 6
(5 х 6 — 3 х 4 + 48: 6) + (82 — 78) х 7 — 13
54: 9 + (8 + 19): 3 — 32: 4 — 21: 7 + (42 — 14): 4 — ( 44 14): 5
9. РЕШИ ВЫРАЖЕНИЯ:
9 х 6 — 6 х 4: (33-25) х 7
3 х (12-8): 2 + 6 х 9-33 (5 х 9 — 25): 4 х 8 — 4 х 7 + 13
9 х (2 х 3) — 48: 8 х 3 + 7 х 6 — 34
10.РЕШИ ВЫРАЖЕНИЯ:
(8 х 6 — 36: 6): 6 х 3 + 5 х 9
7 х 6 + 9 х 4 — (2 х 7 + 54: 6 х 5) (76 — (27 + 9) + 8): 6 х 4
(7 х 4 + 33) — 3 х 6: 2
11. РЕШИ ВЫРАЖЕНИЯ:
(37 + 7 х 4-17): 6 + 7 х 5 + 33 + 9 х 3 — (85-67): 2 х 5
5 х 7 + (18 + 14): 4 — (26-8): 3 х 2-28: 4 + 27: 3 — (17 + 31): 6
12. РЕШИ ВЫРАЖЕНИЯ:
(58 — 31): 3 — 2 + (58 — 16): 6 + 8 х 5 — (60 — 42): 3 + 9 х 2
(9 х 7 + 56: 7 ) — (2 х 6-4) х 3 + 54: 9
13.РЕШИ ВЫРАЖЕНИЯ:
(8 х 5 + 28: 7) + 12: 2 — 6 х 5 + (13 — 5) х 4 + 5 х 4
(7 х 8 — 14: 7) + (7 х 4 + 12: 6) — 10: 5 + 63: 9
Тест «Порядок арифметических действий» (1 вариант)
1 (1б)
2 (1б)
3 (1б)
4 (3б)
5 (2б)
6 (2б)
7 (1б)
8 (1б)
9 (3б)
10 (3б)
11 (3б)
12 (3б)
110 — (60 +40): 10 х 8
а) 800 б) 8 в) 30
а) 3 4 6 5 2 1 4 5 6 3 2 1
3 4 6 5 1 2
5.В каком из выражений последнее действие умножение?
а) 1001: 13 х (318 +466): 22
в) 10000 — (5 х 9 + 56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025: 5 — (524-24: 6) х45
б) 5870 + (90-50 +30) х8-90
в) 5400: 60 х (3600: 90-90) х5
Выбери верный ответ:
9. 90 — (50-40: 5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5 + 6 — 4х4) х2
а) 100 б) 200 в) 60
11. (10000 + 10000: 100 +400): 100 +100
а) 106 б) 205 в) 0
12.150: (80 — 60: 2) х 3
а) 9 б) 45 в) 1
Тест «Порядок арифметических действий».
1 (1б)
2 (1б)
3 (1б)
4 (3б)
5 (2б)
6 (2б)
7 (1б)
8 (1б)
9 (3б)
10 (3б)
11 (3б)
12 (3б)
1. Какое действие в выражении сделаешь первым?
560 — (80 + 20): 10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант данного ответа:
а) 800 б) 490 в) 30
4.Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320: 8 х 7 + 9 х (240 — 60:15) в) 320: 8 х 7 + 9х (240 — 60:15)
3 4 6 5 2 1
б) 320: 8 х 7 + 9 х (240 — 60:15)
5. В каком из выражений последнее действие деление?
а) 1001: 13 х (318 +466): 22
б) 391 х37: 17 х (2248: 8 — 162)
в) 10000 — (5 х 9 + 56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025: 5 — (524 + 24 х6) х45
б) 5870 + (90-50 +30) х8-90
в) 5400: 60 х (3600: 90-90) х5
7.Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и:, затем + и — в) + и -, затем х и:
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б) х и :, затем + и — в) по порядку записи
Выбери верный ответ:
9. 120 — (50-10: 2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5 + 8 — 4х4) х2
а) 596 б) 1192 в) 60
11. (20 + 20000: 2000 +30): 20 +200
а) 106 б) 203 в) 0
12.160: (80 — 80: 2) х 3
а) 120 б) 0 в) 1
Проверка арифметических действий | Математика
Чтобы убедиться, что какое-нибудь арифметическое действие сделано без ошибок, его проверяют.
Проверкой представляет совокупность арифметических приемов с целью убедиться, что данное арифметическое действие исполнено верно. Проверка также состоит из арифметических действий, выполненных в другом порядке.
Самый простой способ убедиться, что действие выполнено верно, конечно, в том, чтобы повторить его снова.Однако, замечено, что уверенность наша увеличивается, если мы проверяемся другим путем в верности какого-нибудь результата, поэтому проверяем арифметические действия иначе.
Проверка на основные свойствах самих арифметических действий и зависимости существующей между данными и искомыми числами.
Основываясь на главных свойствах своих действий, мы можем выполнять действие тем же самым, только выполненным в другом порядке. Таким образом, сложение проверяется сложением, вычитание — вычитанием и т.д.
Проверка арифметических действий теми же действиями
Проверка сложения
Сумма не изменяется от перемены порядка слагаемых, следовательно, , чтобы проверить сложение, нужно сложить слагаемые в другом порядке; если получится та же самая сумма, сложение сделано верно .
Вложение:
Проверка сложения:
сложение верно.
Обычно при проверке складываются слагаемые в обратном порядке, то есть снизу вверх.
Проверка вычитания
Вычитаемое уменьшаемому без разности, следовательно, , чтобы проверить вычитание, нужно из требуемого вычесть разность; если в остатке получится вычитаемое, вычитание сделано верно .
Вычитание:
Проверка вычитания:
Вычитание верно.
Проверка умножения
Произведение не изменяется от перемены порядка множителей, следовательно, чтобы проверить, нужно переменить порядок множителей и снова умножить; если получим то же произведение, умножение выполнено верно .
Умножение:
Проверка умножения:
Умножение верно.
Проверка деления
При делении нацело делитель равенству делимому, разделенному на частное, следовательно, , чтобы деление, в случае деления нацело, нужно делимое разделить на частное; если в частном получится делитель, деление сделано верно .
Деление верно.
Все онлайн-калькуляторы для решения задач · Контрольная Работа РУ · Теперь вы можете задать любой вопрос!
Кусочно-заданная функция
Укажите кусочно-заданную функцию и выполните к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построению графика и др.
Решение вопросов
Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике.
Решение пределов
Этот сервис позволяет найти предел функции. Также подробное решение правилом Лопиталя.
Производственная функция
Это сервис, где можно вычислить производные функции, частные производные функции, а также производную не заданную функции.
Разложение в ряд
Здесь можно выполнить разложение в ряд Тейлора, Фурье, найти сумму ряда.
Системы уравнений
Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.
Решение неравенств
Решает неравенство, а также изображает решённое неравенство на графике.
Решение интегралов
Это сервис, где можно вычислить установленные, неопредёленные интегралы, а также двойные, несобственные, кратные.
График функции
Это сервис построения графиков на плоскости и в рекламе.Приводится подробное решение на исследование функции.
Решение систем неравенств
Вы можете попробовать решить любую систему неравенств с помощью данного калькулятора неравенств.
| Табличка на двери |



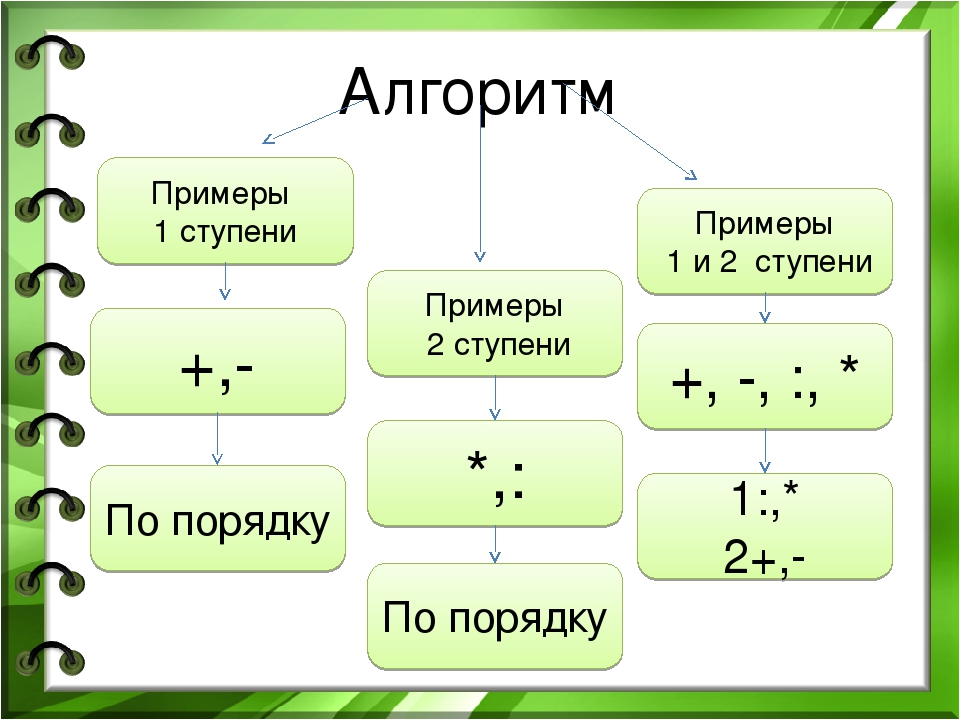




 действия, записанные в скобках;
действия, записанные в скобках; Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
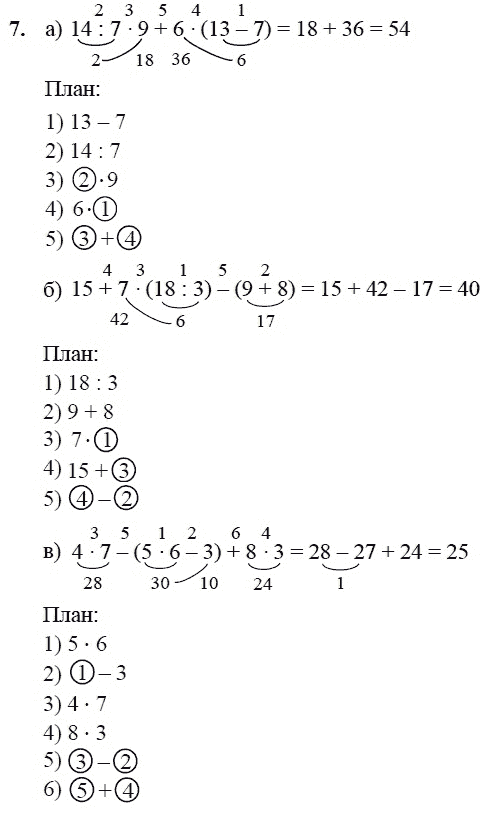
 За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. На языке Зенона это выглядит так:
На языке Зенона это выглядит так: Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

 Это не математическое действие.
Это не математическое действие.
 Какой еще туалет?
Какой еще туалет? Примеры со скобками (действия сложения и вычитания)
Примеры со скобками (действия сложения и вычитания) Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:


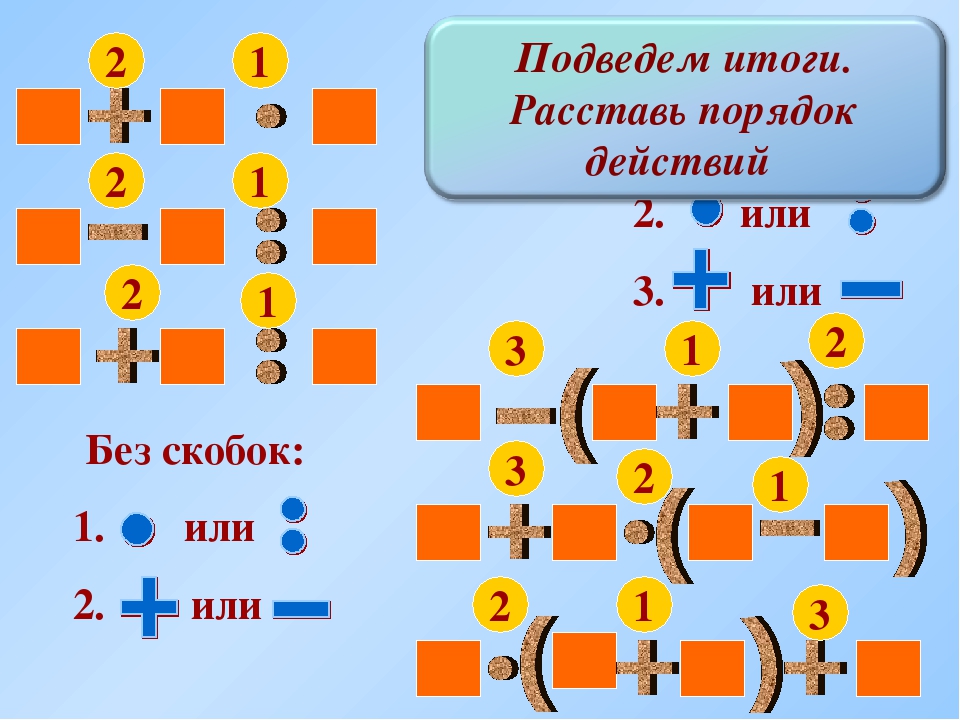 действия, записанные в скобках;
действия, записанные в скобках; Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.



 Найдите значение выражения.
Найдите значение выражения. Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?


 (3 * 3-5) / (2-3) = -4. значение отрицание, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.
(3 * 3-5) / (2-3) = -4. значение отрицание, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус. В третьей части мы приводим нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
В третьей части мы приводим нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в результате получаем десять.Вот запись всего решения:
Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в результате получаем десять.Вот запись всего решения: Первым делом нам надо разделить и умножить.Эти действия не имеют приоритета друг перед другом, поэтому их выполняем в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить.Эти действия не имеют приоритета друг перед другом, поэтому их выполняем в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение: Сформулируем нужное определение.
Сформулируем нужное определение. Проиллюстрируем нашу мысль примером.
Проиллюстрируем нашу мысль примером. Нам надо только применять правило выше по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Нам надо только применять правило выше по отношению ко всем выражениям в скобках. Возьмем такую задачу. Снова обращаемся к внутренним скобкам: 4 + 1 = 5. Мы пришли к выражению (4 + 5-1) — 1 . Считаем 4 + 5 — 1 = 8 и в результате получаем разность 8 — 1, результатом будет 7.
Снова обращаемся к внутренним скобкам: 4 + 1 = 5. Мы пришли к выражению (4 + 5-1) — 1 . Считаем 4 + 5 — 1 = 8 и в результате получаем разность 8 — 1, результатом будет 7.

 С точки зрения это выглядит, как физическое замедление времени до его полной остановки в момент, когда Ахиллес поравняется с моментом.Если время останавливается, Ахиллес уже не может перегнать черепаху.
С точки зрения это выглядит, как физическое замедление времени до его полной остановки в момент, когда Ахиллес поравняется с моментом.Если время останавливается, Ахиллес уже не может перегнать черепаху.
 На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.