Решить пример с корнями онлайн калькулятор: Инженерный калькулятор онлайн

дробный калькулятор с корнями

Вы искали дробный калькулятор с корнями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор дробей с корнями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробный калькулятор с корнями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как дробный калькулятор с корнями,калькулятор дробей с корнями,калькулятор дробей со степенями и корнями,калькулятор дробей со степенями онлайн с решением,калькулятор квадратов чисел,калькулятор корень уравнения,калькулятор онлайн корней уравнений,калькулятор онлайн с дробями и корнями онлайн калькулятор,калькулятор онлайн с дробями и с корнями калькулятор,калькулятор онлайн с корнями и дробями онлайн калькулятор,калькулятор радикалов,калькулятор с дробями и корнями и степенями,калькулятор с корнями дробный,калькулятор с корнями и дробями,калькулятор с корнями и дробями и степенями,калькулятор с корнями и дробями онлайн,калькулятор с корнями и степенями и дробями,калькулятор с корнями с решением,калькулятор с кубами и квадратами,калькулятор сокращения дробей с буквами и степенями онлайн,калькулятор степеней с дробями онлайн,калькулятор уравнений с корнями,найти значение выражения с дробями и степенями онлайн,онлайн калькулятор квадратов,онлайн калькулятор корней с решением,онлайн калькулятор корней уравнений,онлайн решение выражений с корнями,онлайн решение примеров с корнями,онлайн решить пример с корнями,решение выражений с корнями онлайн,решение примеров онлайн с корнями,решение примеров с корнями онлайн,решение примеров с корнями онлайн калькулятор с решением,решить выражение онлайн с корнями,решить выражение с корнями онлайн,решить онлайн пример с корнями,решить пример онлайн с корнями,сложение корней калькулятор,сократить дробь с корнями онлайн калькулятор.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и дробный калькулятор с корнями. Просто введите задачу в окошко и нажмите «решить» здесь (например, калькулятор дробей со степенями и корнями).

Где можно решить любую задачу по математике, а так же дробный калькулятор с корнями Онлайн?

Решить задачу дробный калькулятор с корнями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькуляторы | umath.ru

Популярные

График функции
Вычисление логарифма числа
Сокращение дробей
Приведение дробей к общему знаменателю
Разложение числа на простые множители
Калькулятор процентов
Возведение числа в степень
Вычисление корня из числа
Тригонометрические функции

Функции

График функции
Нахождение максимума и минимума функции
Нахождение точек локального экстремума функции
Разложение функции в ряд Тейлора, Маклорена

Пределы, производные, интегралы

Вычисление предела последовательности
Вычисление предела функции
Вычисление производной
Вычисление неопределённого интеграла
Вычисление определённого интеграла

Дроби, проценты

Сокращение арифметических дробей
Приведение дробей к общему знаменателю
Калькулятор дробей
Упрощение алгебраических дробей
Калькулятор процентов

Системы счисления

Перевод целых чисел из одной системы счисления в другую
Перевод дробных чисел из одной системы счисления в другую

Теория чисел

Разложение числа на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Функция Эйлера

Уравнения

Решение квадратного уравнения
Решение кубического уравнения
Упрощение математических выражений
Нахождение неизвестного члена пропорции

Матрицы

Сложение, вычитание матриц
Умножение матриц
Нахождение определителя матрицы

Корни, степени, логарифмы

Вычисление корня из числа
Возведение числа в степень
Вычисление логарифма числа

Комбинаторика и теория вероятностей

Вычисление факториала числа

Статистика

Вычисление медианы ряда чисел
Вычисление среднего арифметического и среднего геометрического чисел

Геометрия

Вычисление площади треугольника
Нахождение точки пересечения двух прямых
Уравнение прямой на плоскости по двум точкам
Уравнение прямой в пространстве по двум точкам

Тригонометрия

Вычисление синуса, косинуса, тангенса и котангенса

Калькулятор извлечения корня n-ой степени онлайн

Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.

Математическое обозначение

«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.

Квадратный корень

Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.

Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.

Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…

Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.

Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.

Кубический корень

Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:

1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…

Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.

Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.

Корень n-ной степени

Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.

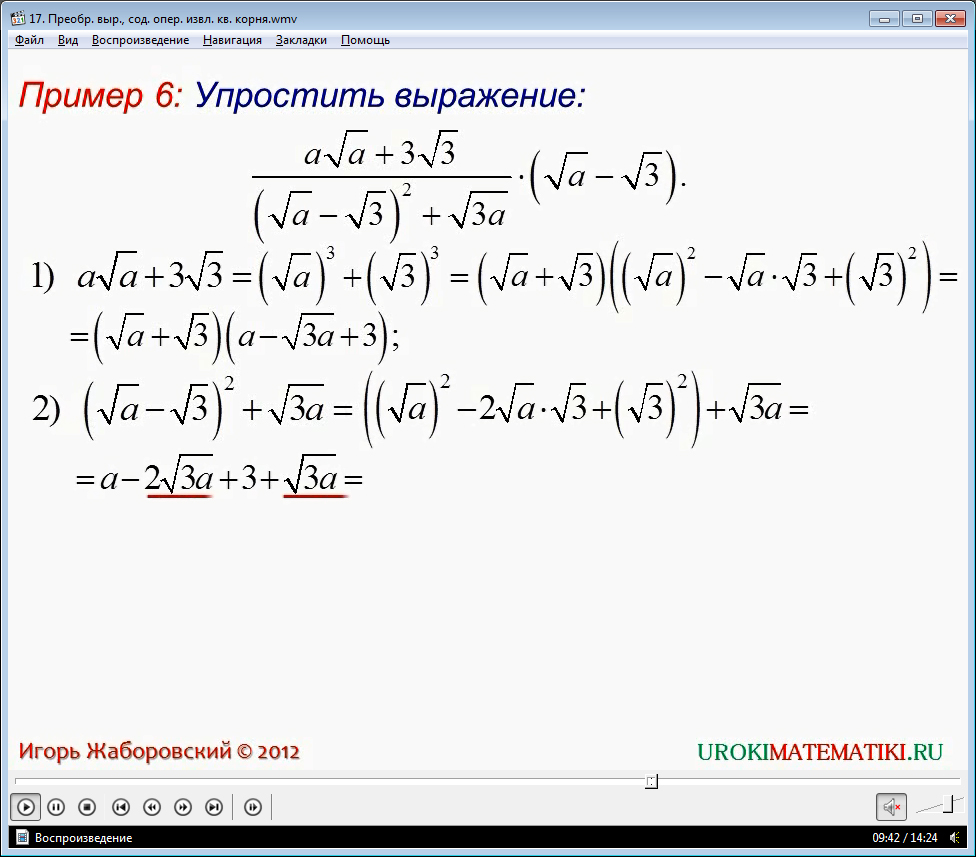
Рассмотрим пример

Диагональ квадрата

Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:

d = a × sqrt(2).

Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.

Заключение

Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.

Решение задач онлайн

Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.

Другие программы

Основы математики

Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.

Вы можете упростить, найти значение, объединять и умножать выражения.

Онлайн программа решения задач курса предварительной алгебры (геометрии)

Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.

Онлайн программа решения задач по алгебре

Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.
Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии — это правильный выбор.

Онлайн программа решения задач по тригонометрии

Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.

Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.

Онлайн программа решения задач курса предварительной алгебры

Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.

Онлайн программа решения задач курса высшей математики

Решение задач c определенными, неопределенными интегралами.

Онлайн программа решения статистических задач

Решайте задач с нахождением вероятности, комбинаторные задачи. Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез

Метод Горнера. Деление многочлена онлайн

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

Рассмотрим процедуру деления многочлена вида

 

на бином вида  

результат  деления  есть функция вида

Такой результат получается  только в  результате деления исходного  многочлена на бином без остатка.

В общем же случае говорится, что функцию   можно  представить в виде 

где r — это остаток от деления.

Коэффициенты функции   рассчитываются по рекуррентным формулам

 

Схема Горнера очень удобна своей простой и отсутствием функции деления.  Это позволяет решать с повышенной точностью подобные уравнения, а также решать целочисленные уравнения, без каких либо машинных(компьютерных) погрешностей.

Кстати!

Есть новый калькулятор который осуществляет деление многочлена на многочлен с остатком . Работает в том числе и в комплексном поле, кроме того, делящий многочлен может быть на самом деле многочленом(!), а не биномом, как в этой статье.

Кроме  этого, эта же схема позволяет решать задачу  определения значения функции при каком либо значении. «Фи!» — скажете Вы. «Это же элементарно, любой калькулятор это может».

 

да конечно, поставивив вместо неизвестного x необходимое значение мы получим нам нужный результат, но какой ценой?

Нам придется  возводить значения в степень, что несомненно внесет свою погрешность в расчеты.

Это  явно проявляется при работе в поле комплексных чисел, при делении многочлена на комплексный бином.

Нам проще воспользоватся теоремой Безу, которая гласит: Остаток r от деления многочлена на   на линейный двучлен  равен значению многочлена  при 

Бот созданный на этом сайте, позволяет Вам решать  поставленную задачу методом Горнера, не только для действительных чисел, но и для комплексных.

 Это расширяет возможности применения бота и позволяет более полно исследовать функцию.

Если делящий многочлен не является одночленом, то стоит воспользоватся калькулятором который делит произвольные многочлены друг на друга с вычислением остатка.Деление многочлена на многочлен.Division of complex polynomialsТеперь рассмотрим  примеры.

  разделить с остатком  

Пишем коэффициенты 2 0 -3 2 и через точку запятой -2. Надеюсь понятно почему пишем -2, а не+2 ?

Получаем ответ

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

 

Следующий пример  исходный полином тот же, но значение С будет комплексным например 1+i

Пишем коэффициенты 2 0 -3 2 и через точку запятой 1+i

Получаем

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

 

Таким образом мы можем писать любые значения, в том числе и комплексные,  в коэффицентах как делимого полинома так и делящего бинома

Удачных расчетов!

Калькулятор кубического корня онлайн — Расчет cube_root — производная — первообразная

Итоги:

Функция cube_root вычисляет в режиме онлайн кубический корень числа.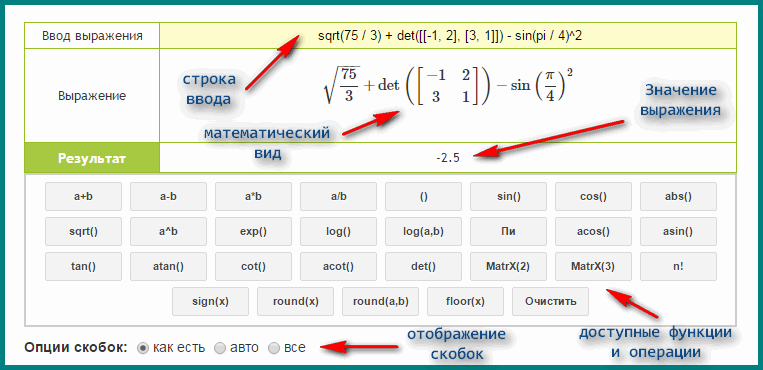

cube_root онлайн

---

Описание:

Кубический корень действительного числа x — это число в кубе, равное x.

Вычисление кубического корня

Онлайн вычисление кубического корня из числа

Функция позволяет онлайн вычислить

кубического корня числа.

Например, чтобы вычислить куб корень числа 27, вы должны ввести cube_root (`27`), после вычисления результата возвращается` 3`.

Например, чтобы выполнить вычисление кубического корня онлайн числа 8, введите cube_root (`8`), после вычисления возвращается значение 2.

Некоторые целые кубические корни

Кубический корень Функция для определения кубического корня числа, вот несколько примеров специальных кубических корней, которые дает онлайн-калькулятор.

1. , чтобы вычислить кубический корень из 8 , введите cube_root (`8`), результат 2.
2. , чтобы вычислить кубический корень из 27 , введите cube_root (`27`), результат — 3.
3. , чтобы вычислить кубический корень из 64 , введите cube_root (`64`), результат 4.
4. , чтобы вычислить кубический корень из 64 , введите cube_root (`125`), результат 5.4`.

   Пределы кубического корня

Пределы кубического корня существуют в `-oo` (минус бесконечность) и` + oo` (плюс бесконечность):
• Функция кубического корня имеет ограничение в `-oo`, которое равно` -oo`.
`lim_ (x -> — oo) root (3) (x) = — oo`
• Функция кубического корня имеет предел в` + oo`, который равен `+ oo`. 2)`

  ---

  Первообразный кубический корень:

  Калькулятор первообразных позволяет вычислить первообразную функции кубического корня.(4/3) `

  ---

  Предел кубического корня:

  Калькулятор пределов позволяет вычислять пределы функции кубического корня.

  Предел для cube_root (x) — limit_calculator (`» cube_root «(x)`)

  ---

  Графический корень куба:

  Графический калькулятор может построить функцию кубического корня в интервале ее определения.

  ---

  Расчет онлайн с cube_root (корень куба) Калькулятор дифференциальных уравнений

  — eMathHelp

  Калькулятор найдет решение данного ОДУ: первого порядка, второго порядка, n-го порядка, разделимое, линейное, точное, Бернулли, однородное или неоднородное.

  Также поддерживаются начальные условия.

  Показать инструкции

  • Как правило, знак умножения можно пропустить, поэтому «5x» эквивалентно «5 * x».3 (х).
  • Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
  • Если вы получили сообщение об ошибке, дважды проверьте свое выражение, добавьте круглые скобки и знаки умножения там, где это необходимо, и обратитесь к таблице ниже.
  • Все предложения и улучшения приветствуются. Пожалуйста, оставьте их в комментариях.

  В следующей таблице перечислены поддерживаемые операции и функции:

  9 0157 acsc (x)

  Тип	Get
  Константы
  e	e
  pi	`pi`
  i 901 901
  i 901 Операции
  a + b	a + b
  ab	ab
  a * b	`a * b`
  a ^ b, a ** b	` a ^ b`
  sqrt (x), x ^ (1/2)	`sqrt (x)`
  cbrt (x), x ^ (1/3)	`root (3 ) (x) `
  корень (x, n), x ^ (1 / n)	` root (n) (x) `
  x ^ (a / b)	` x ^ (a / b) `
  x ^ a ^ b	` x ^ (a ^ b) `
  abs (x)	` | x | `
  Функции
  e ^ x	`e ^ x`
  ln (x), журнал (x)	ln (x)
  ln (x) / ln (a)	`log_a (x)`
  Тригонометрические функции
  sin (x)	sin (x)
  cos (x)	cos (x)
  tan (x)	tan (x), tg (x)
  детская кроватка (x)	детская кроватка (x), ctg ( x)
  sec (x)	sec (x)
  csc (x)	csc (x), cosec (x)
  Обратные тригонометрические функции
  asin , arcsin (x), sin ^ -1 (x)	asin (x)
  acos (x), arccos (x), cos ^ -1 (x)	acos (x)
  атан (x), arctan (x), tan ^ -1 (x)	atan (x)
  acot (x), arccot ​​(x), cot ^ -1 (x)	acot (x)
  asec (x), arcsec (x), sec ^ -1 (x)	asec (x)
  acsc (x), arccsc (x), csc ^ -1 (x)
  Гиперболические функции
  sinh (x)	sinh (x)
  cosh (x)	cosh (x)
  tanh60 (x)
  coth (x)	coth (x)
  1 / cosh (x)	sech (x)
  1 / sinh (x)	csch (x)
  Обратные гиперболические функции
  asinh (x), arcsinh (x), sinh ^ -1 (x)	asinh (x)
  acosh (x), arccosh (x), cosh ^ — 1 (x)	acosh (x)
  atanh (x), arctanh (x), tanh ^ -1 (x)	atanh (x)
  acoth (x), arccoth (x) , детская кроватка ^ -1 (x)	acoth (x)
  acosh (1 / x)	asech (x)
  asinh (1 / x)	acsch (x)

  Если калькулятор что-то не вычислил или вы определили ошибку, запишите ее в комментарии ниже.

  Все предложения пишите в комментариях ниже.

  Калькулятор экспонент

  Использование калькулятора

  Этот калькулятор найдет показатель степени n в экспоненциальном уравнении x ⁿ = y, при этом x в n-й степени равен y. Введите x и y, и этот калькулятор найдет показатель степени n с помощью log (). Поскольку использование log () отрицательных чисел приводит к ошибкам вычислений, они не допускаются.n = \ log _ {} y \)

  По тождественности получаем:

  \ (n \ cdot \ log _ {} x = \ log _ {} y \)

  Делим обе стороны на бревно x:

  \ (n = \ dfrac {\ log _ {} y} {\ log _ {} x} \)

  Найти показатель числа

  Для уравнения 3 ⁿ = 81, где 3 называется основанием, а n называется показателем степени, найдите значение показателя n, используя логарифмы. n = \ log _ {} 81 \)

  По тождественности получаем:

  \ (n \ cdot \ log _ {} 3 = \ log _ {} 81 \)

  Делим обе стороны бревном 3:

  \ (n = \ dfrac {\ log _ {} 81} {\ log _ {} 3} \)

  Используя калькулятор, мы можем найти, что log 81 ≈ 1.9085 и log 3 ≈ 0,4771, тогда наше уравнение принимает вид:

  \ (n = \ dfrac {\ log _ {} 81} {\ log _ {} 3} \ приблизительно \ dfrac {1.9085} {0,4771} \ приблизительно 4 \)

  Проверяем наш ответ 3 ⁴ = 81 .

  Поскольку использование log () отрицательных чисел, 0 или 1 вызывает ошибки вычислений, мы предоставили некоторые ответы по определению, а не фактические вычисления.

  Калькулятор полиномиальных корней

  Список справки по математике — — Математическая справка Быстрый переход — Научный онлайн-калькулятор — Общая математика -Калькулятор фракцийКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощающие выраженияКалькулятор делителейКалькулятор факторингаКалькулятор наибольшего общего множителя (GCF) Калькулятор последнего общего множителя (LCM) Калькулятор простых чисел и средство проверкиПроверка идеального квадрата числа-валидатор — Алгебра и комбинаторики -уравнения SolverQuadratic Уравнение SolverSystem уравнений SolverCombinatoricsPermutationsPolynomialsPolynomials — Сложение и SubtractionPolynomials — Умножение и DivisionPolynomials — Дифференциация и IntegrationPolynomials — Паритет калькулятор (нечетный, четный, нет) Полиномы — Корень FinderPolynomials — Сформировать из RootsMatricesMatrix Calculator- определителя, обратная матрица CalculatorMatrix — Сложение, вычитание, умножение, исчисление, интегральный калькулятор, калькулятор определенного интеграла, калькулятор производной, числовая производная КалькуляторКалькулятор пределов Отклонение CalculatorVariance CalculatorKurtosis CalculatorSkewness Calculator- Описательная статистика Калькуляторы -Матрица Центральный момент CalculatorCorrelation Матрица CalculatorCovariance Матрица CalculatorMatrix Среднее геометрическое CalculatorMatrix гармоническое среднее CalculatorMatrix межквартильный Диапазон CalculatorMatrix Эксцесс CalculatorMatrix нецентральные Момент CalculatorMatrix Среднее CalculatorMatrix Максимальная CalculatorMatrix Минимальная CalculatorMatrix Медиана CalculatorMatrix Среднее отклонение CalculatorMatrix Среднее отклонение CalculatorMatrix Quantile Калькулятор Калькулятор перекоса квартиля матрицы КалькуляторыКалькуляторы распределения Вейбулла — Калькуляторы дискретных распределений — Калькуляторы биномиального распределенияКалькуляторы геометрического распределенияКалькуляторы распределения Пуассона Калькуляторы равномерного (дискретного) распределения

  Исчисление II — Корневой тест

  Онлайн-заметки Павла

  Ноты Быстрая навигация Скачать

  • Перейти к
  • Ноты
  • Проблемы с практикой
  • Проблемы с назначением
  • Показать / Скрыть
  • «> Показать все решения / шаги / и т. Д.
  • Скрыть все решения / шаги / и т. Д.
  • Разделы
  • Тест соотношения
  • Стратегия для серии
  • Разделы
  • Параметрические уравнения и полярные координаты
  • Векторы
  • Классы
  • Алгебра
  • Исчисление I
  • Исчисление II
  • Исчисление III
  • Дифференциальные уравнения
  • Дополнительно
  • Алгебра и триггерный обзор
  • Распространенные математические ошибки
  • Праймер для комплексных чисел
  • Как изучать математику
  • Шпаргалки и таблицы
  • Разное
  • Свяжитесь со мной
  • Справка и настройка MathJax
  • Мои студенты
  • Заметки Загрузки
  • Полная книга
  • Текущая Глава

  Калькулятор комплексных чисел

  Инструкции :: Все функции

  Инструкции

  Просто введите формулу в верхнее поле. Оператор степени / экспоненты / индекса () Круглые скобки

  Функции

  	sqrt	Квадратный корень
  	грех	синус
  	cos	косинус
  	желто-коричневый	касательная
  	asin	обратный синус (арксинус)
  	acos	обратный косинус (arccos)
  	атан	арктангенс (арктангенс)
  	sh	Гиперболический синус
  	куш	Гиперболический косинус
  	танх	Гиперболический тангенс
  	эксп.	e (константа Эйлера) в степени значения или выражения
  	пер.	Натуральный логарифм
  	круглый	округлить до ближайшего целого
  	этаж	Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и является целым числом.
  	потолок	Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и является целым числом.
  	вместе	конъюгат комплексного числа. Пример: con (2−3i) = 2 + 3i
  	и	действительная часть комплексного числа. Пример: re (2−3i) = 2
  	им.	мнимая часть комплексного числа.Пример: im (2−3i) = −3i

  Константы

  .