Деление многочленов столбиком онлайн
Примеры решенийРанг матрицыМетод КрамераУмножение матриц Определитель матрицы Метод обратной матрицы Обратная матрица Метод Гаусса онлайн LU разложение матрицы Производная онлайн
f(x)/g(x)=q(x)+r(x)/g(x).
Алгоритм деления в столбик применяется в частности при нахождении интегралов.
- Решение онлайн
- Видеоинструкция
Инструкция. Для получения решения в онлайн режиме необходимо ввести числитель и знаменатель.
При оформлении в качестве переменной использовать xtzupλПример деления в столбик.
№1.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 |
| -9x2-42 |
№2.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 -9x |
| -9x2-42 | |
| -9x2 + 27x | |
| -27x -42 |
№3.
| x3 -12x2-42 | x -3 |
| x3 -3x2 | x2 -9x -27 |
| -9x2-42 | |
| -9x2 + 27x | |
| -27x -42 | |
| -27x + 81 | |
| -123 |
Целая часть: x2 -9x -27
Остаток: -123
Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.
также и другие примеры решение столбиком.
Пример №1. Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x5+3x3-x2+4x+1, Q(x)=2x2-x+1
Пример №2. Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x4+6x3-2x2+x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x3(x-6)-2x(x-6)-12x+x-2 = -x3(x-6)-2x(x-6)-11(x-6)-66-2 = -x3(x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Умножение столбиком. Онлайн калькулятор | Математика
- Как умножать столбиком
- Калькулятор умножения столбиком
Как умножать столбиком
Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т.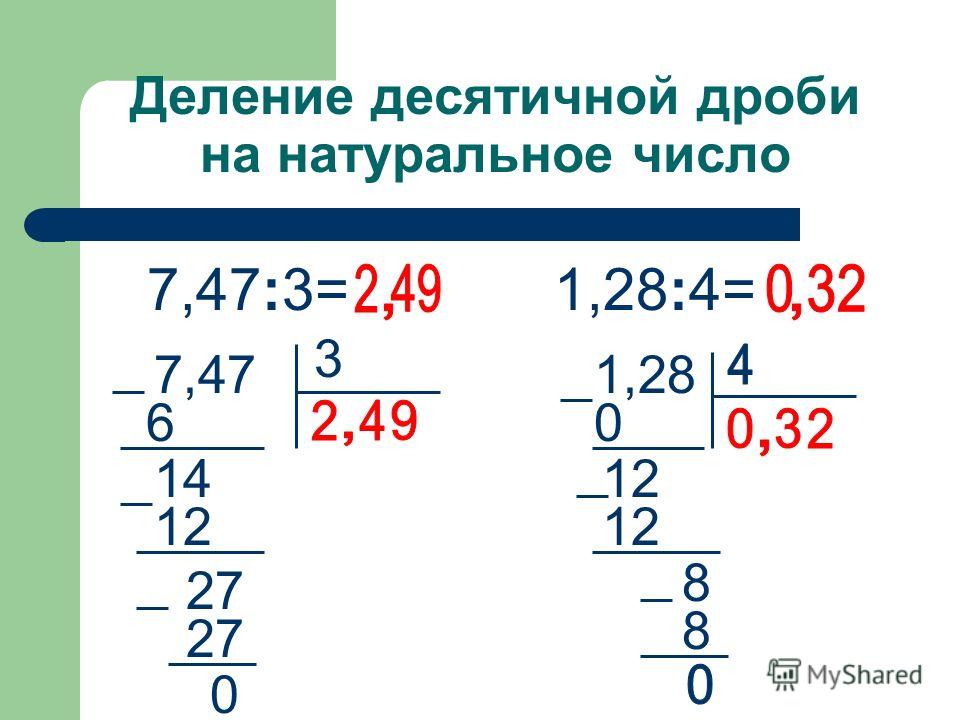 д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.
д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.
Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:
Умножить 846 на 5 — значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.
- 5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем. Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:
- 5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:
- 5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни.
 Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:
Умножить 3826 на 472 — значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.
2 раза по 3826 = 7652. Пишем полученное произведение под чертой:
Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением. Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.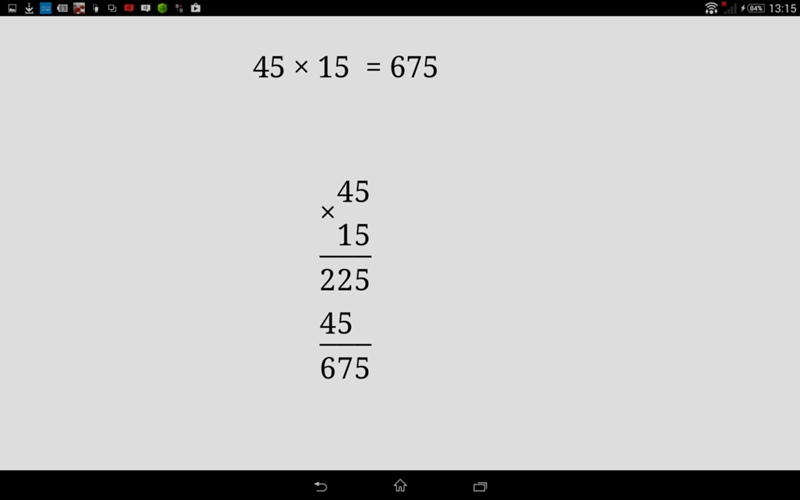
Умножаем 3826 на 7. Это будет второе частичное произведение (26782):
Умножаем множимое на 4. Это будет третье частичное произведение (15304):
Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):
Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:
Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.
Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:
И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.
Калькулятор умножения столбиком
Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку
Просто введите множимое и множитель и нажмите кнопку Вычислить
.
Вычисление определителя матрицы Пошаговое решение математических задач
Введите матрицу и нажмите кнопку Определитель.
Справка
| Матрица 5,3,7 2,4,9 3,6,4 |
Мы знаем, что не каждая система линейных уравнений имеет единственное решение. Иногда система из n уравнений с n переменными не имеет решения или бесконечное множество решений. В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать определить, имеет ли система уравнений единственное решение.
Каждой квадратной матрице A соответствует действительное число, называемое определителем А, пишется |А|.
Определитель матрицы 2 x 2 A,
определяется как
ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители
обозначаются вертикальными черточками.
ОЦЕНКА A 2 X 2
ОПРЕДЕЛИТЕЛЬ
Если
затем
ОПРЕДЕЛИТЕЛЬ А МАТРИЦА 3 X 3
Определитель матрицы 3 x 3 A,
определяется как
Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторизируя термины, данные выше, чтобы получить
Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.
Эти определители матриц 2 X 2 называются минорами элемента в матрица 3х3. Символ M ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые миноры из матрицы выше.
В матрице 4 x 4 миноры являются определителями матриц 3 x 3, а n x
Матрица n имеет миноры, которые являются определителями (n — 1) X (n — 1) матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или
столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце.
на + l или — 1, в зависимости от того, является ли сумма номеров строк и столбцов
числа четные или нечетные. Произведение минора на число + 1 или — l равно
называется кофактором .
КОФАКТОР Пусть M ij будет минором элемента au в матрице n x n . Кофактор иж , написано A ij , это:
Наконец, определитель матрицы n x n находится следующим образом.
ПОИСК ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его коэффициент.
сумма этих произведений дает значение определителя. Процесс формирования
эта сумма произведений называется расширением по данной строке или столбцу.
НАЙТИ
КОФАКТОР ЭЛЕМЕНТА
Для матрицы
найдите кофактор каждого из следующих элементов.
(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.
Кофактор равен (-1) 1+1 * (-6) = 1 * (-6) = -6.
(b) 3
Здесь i = 2 и j = 3.
Кофактор равен (-1) 2+3 * 10 = (-1) * 10 = -10.
(c) 8
Имеем i = 2 и j = l.
Кофактор равен (-1) 2+1 * (-8) = (-1) * (-8) = 8.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ 3 X 3
Вычисление
2 расширение
22 по второму столбцу.
Чтобы найти этот определитель, сначала найдите миноры каждого элемента во втором
столбец.
Теперь найдите кофактор каждого из этих миноров.
Определитель находится путем умножения каждого кофактора на соответствующий ему
элемент в матрице и нахождение суммы этих произведений.
ПРЕДОСТЕРЕЖЕНИЕ: Будьте очень внимательны и следите за всеми отрицательными знаками при
оценивающие детерминанты. Работайте осторожно, записывая каждый шаг, как в
Примеры. Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Работайте осторожно, записывая каждый шаг, как в
Примеры. Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Точно такой же ответ можно найти, используя любую строку или столбец матрицы.
Одна из причин, по которой в примере 3 использовался столбец 2, заключается в том, что он содержит элемент 0,
так что не особо надо было вычислять М 32 и А 32 выше. Быстро понимаешь, что нули могут быть очень полезны при работе с
детерминанты.
Вместо вычисления (-1) i+j для заданного элемента выполняется следующее
можно использовать шахматные доски для знаков:
Знаки чередуются для каждой строки и столбца, начиная с + в первом
строка, позиция первого столбца. Таким образом, эти массивы знаков могут быть воспроизведены как
нужный. Если мы разложим матрицу 3 X 3, например, вокруг строки 3, первый второстепенный
будет иметь связанный с ним знак +, второй второстепенный знак — и третий
минор + знак. Таким образом, эти массивы знаков могут быть расширены для определителей матриц 5 X 5, 6 X 6 и более крупных матриц.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ 4 X 4
Вычисление
Расширение по младшим по четвертой строке дает
Каждый из четырех определителей в Примере 4 должен быть оценен путем разложения
три несовершеннолетних, требующих большой работы, чтобы получить окончательное значение. Всегда ищите
строку или столбец с наибольшим количеством нулей, чтобы упростить работу. В следующем разделе мы
ввести несколько свойств, облегчающих вычисление определителей.
К счастью, определители больших матриц можно быстро вычислить.
легко с помощью компьютера или некоторых калькуляторов.
Использовать вычисляемые столбцы в таблице Excel
Excel
Импорт и анализ данных
Столы
Столы
Использовать вычисляемые столбцы в таблице Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Дополнительно. ..Меньше
..Меньше
Вычисляемые столбцы в таблицах Excel — отличный инструмент для эффективного ввода формул. Они позволяют вам ввести одну формулу в одну ячейку, а затем эта формула автоматически расширится до остальной части столбца сама по себе. Нет необходимости использовать команды «Заполнить» или «Копировать». Это может невероятно сэкономить время, особенно если у вас много строк. И то же самое происходит, когда вы меняете формулу; изменение также распространится на остальную часть вычисляемого столбца.
Примечание. Снимки экрана в этой статье были сделаны в Excel 2016. Если у вас другая версия, представление может немного отличаться, но, если не указано иное, функциональность такая же.
Создать вычисляемый столбец
Создать таблицу. Если вы не знакомы с таблицами Excel, вы можете узнать больше по ссылке: Обзор таблиц Excel.
Вставить новый столбец в таблицу. Вы можете сделать это, введя текст в столбце справа от таблицы, и Excel автоматически расширит таблицу за вас. В этом примере мы создали новый столбец, введя «Итого» в ячейку D1.
Советы:
Вы также можете добавить столбец таблицы с вкладки Домашняя страница . Просто щелкните стрелку для Вставить > Вставить столбцы таблицы слева .
Введите нужную формулу и нажмите Введите .
В этом случае мы ввели =sum( , затем выбрали столбцы Qtr 1 и Qtr 2 . В результате Excel построил формулу: =СУММ(Таблица1[@[Квартал 1]:[Квартал 2]]) . Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет =СУММ(B2:C2) , которую затем вам нужно будет скопировать или заполнить до остальных ячеек в столбце
В результате Excel построил формулу: =СУММ(Таблица1[@[Квартал 1]:[Квартал 2]]) . Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет =СУММ(B2:C2) , которую затем вам нужно будет скопировать или заполнить до остальных ячеек в столбце
. Дополнительные сведения о структурированных ссылках см. в разделе Использование структурированных ссылок с таблицами Excel.
Когда вы нажимаете Enter, формула автоматически заполняется всеми ячейками столбца — выше и ниже ячейки, в которую вы ввели формулу. Формула одинакова для каждой строки, но, поскольку это структурированная ссылка, Excel внутренне знает, какая строка какая.
Примечания:
org/ListItem»> При копировании или заполнении формулы во все ячейки пустого столбца таблицы также создается вычисляемый столбец.
Если ввести или переместить формулу в столбец таблицы, который уже содержит данные, вычисляемый столбец не создается автоматически. Однако кнопка Параметры автозамены отображается, чтобы предоставить вам возможность перезаписать данные, чтобы можно было создать вычисляемый столбец.
Если вы введете новую формулу, которая отличается от существующих формул в вычисляемом столбце, столбец будет автоматически обновлен новой формулой. Вы можете отменить обновление и сохранить только одну новую формулу из кнопки Параметры автозамены . Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.
Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.
Если вы ввели или скопировали формулу в ячейку пустого столбца и не хотите сохранять новый вычисляемый столбец, дважды щелкните Отменить . Вы также можете нажать Ctrl + Z дважды
Вычисляемый столбец может содержать ячейку с формулой, отличной от остальных. Это создает исключение, которое будет четко отмечено в таблице. Таким образом, непреднамеренные несоответствия могут быть легко обнаружены и устранены.
Примечание. Исключения вычисляемого столбца создаются при выполнении любого из следующих действий:
org/ListItem»> Введите данные, отличные от формулы, в ячейку вычисляемого столбца.
Введите формулу в ячейку вычисляемого столбца, а затем нажмите Отменить на панели быстрого доступа .
Введите новую формулу в вычисляемый столбец, который уже содержит одно или несколько исключений.
Скопируйте в вычисляемый столбец данные, которые не соответствуют формуле вычисляемого столбца.
Примечание. Если скопированные данные содержат формулу, эта формула перезапишет данные в вычисляемом столбце.
Удалить формулу из одной или нескольких ячеек вычисляемого столбца.
Примечание. Это исключение не отмечено.
Переместите или удалите ячейку в другой области рабочего листа, на которую ссылается одна из строк в вычисляемом столбце.
Уведомление об ошибке появится только в том случае, если у вас включена опция фоновой проверки ошибок. Если вы не видите ошибку, перейдите к File > Options 9.0032 > Формулы > убедитесь, что установлен флажок Включить фоновую проверку ошибок .
Если вы используете Excel 2007, нажмите кнопку Office , затем Параметры Excel > Формулы .
Если вы используете Mac, перейдите к Excel в строке меню, а затем нажмите Настройки > Формулы и списки > Ошибка проверки .
Параметр автоматического заполнения формул для создания вычисляемых столбцов в таблице Excel включен по умолчанию. Если вы не хотите, чтобы Excel создавал вычисляемые столбцы при вводе формул в столбцах таблицы, вы можете отключить параметр заполнения формул. Если вы не хотите отключать этот параметр, но не хотите всегда создавать вычисляемые столбцы во время работы с таблицей, вы можете запретить автоматическое создание вычисляемых столбцов.
Включение или выключение вычисляемых столбцов
org/ListItem»> На вкладке Файл щелкните Параметры .
Если вы используете Excel 2007, нажмите кнопку Office , затем Параметры Excel .
Нажмите Проверка .
В разделе Параметры автозамены щелкните Параметры автозамены .
Перейдите на вкладку Автоформат при вводе .
Под Автоматически по мере работы , установите или снимите флажок Заполнить формулы в таблицах для создания вычисляемых столбцов , чтобы включить или выключить эту опцию.
Совет: Вы также можете нажать кнопку Параметры автозамены , которая отображается в столбце таблицы после ввода формулы. Нажмите «Управление параметрами автозамены», а затем снимите флажок «Заполнить формулы в таблицах для создания вычисляемых столбцов», чтобы отключить этот параметр.
Если вы используете Mac, перейдите к Excel в главном меню, затем Настройки > Формулы и списки > Таблицы и фильтры > Автоматически заполнять формулы .
Остановить автоматическое создание вычисляемых столбцов
После ввода первой формулы в столбце таблицы нажмите отображаемую кнопку Параметры автозамены , а затем нажмите Остановить автоматическое создание вычисляемых столбцов .
Чтобы найти этот определитель, сначала найдите миноры каждого элемента во втором столбец.
Теперь найдите кофактор каждого из этих миноров.
 Работайте осторожно, записывая каждый шаг, как в
Примеры. Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Работайте осторожно, записывая каждый шаг, как в
Примеры. Пропуск шагов часто приводит к ошибкам в этих вычислениях.Вместо вычисления (-1) i+j для заданного элемента выполняется следующее можно использовать шахматные доски для знаков:
Вычисление
 ..Меньше
..Меньше Создать таблицу. Если вы не знакомы с таблицами Excel, вы можете узнать больше по ссылке: Обзор таблиц Excel.
Вставить новый столбец в таблицу. Вы можете сделать это, введя текст в столбце справа от таблицы, и Excel автоматически расширит таблицу за вас. В этом примере мы создали новый столбец, введя «Итого» в ячейку D1.
Советы:
Вы также можете добавить столбец таблицы с вкладки Домашняя страница . Просто щелкните стрелку для Вставить > Вставить столбцы таблицы слева .
Введите нужную формулу и нажмите Введите .
В этом случае мы ввели =sum( , затем выбрали столбцы Qtr 1 и Qtr 2 . В результате Excel построил формулу: =СУММ(Таблица1[@[Квартал 1]:[Квартал 2]]) . Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет =СУММ(B2:C2) , которую затем вам нужно будет скопировать или заполнить до остальных ячеек в столбце
В результате Excel построил формулу: =СУММ(Таблица1[@[Квартал 1]:[Квартал 2]]) . Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет =СУММ(B2:C2) , которую затем вам нужно будет скопировать или заполнить до остальных ячеек в столбце
Дополнительные сведения о структурированных ссылках см. в разделе Использование структурированных ссылок с таблицами Excel.
Когда вы нажимаете Enter, формула автоматически заполняется всеми ячейками столбца — выше и ниже ячейки, в которую вы ввели формулу. Формула одинакова для каждой строки, но, поскольку это структурированная ссылка, Excel внутренне знает, какая строка какая.
При копировании или заполнении формулы во все ячейки пустого столбца таблицы также создается вычисляемый столбец.
Если ввести или переместить формулу в столбец таблицы, который уже содержит данные, вычисляемый столбец не создается автоматически. Однако кнопка Параметры автозамены отображается, чтобы предоставить вам возможность перезаписать данные, чтобы можно было создать вычисляемый столбец.
Если вы введете новую формулу, которая отличается от существующих формул в вычисляемом столбце, столбец будет автоматически обновлен новой формулой. Вы можете отменить обновление и сохранить только одну новую формулу из кнопки Параметры автозамены . Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.
Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.
Если вы ввели или скопировали формулу в ячейку пустого столбца и не хотите сохранять новый вычисляемый столбец, дважды щелкните Отменить . Вы также можете нажать Ctrl + Z дважды
Введите данные, отличные от формулы, в ячейку вычисляемого столбца.
Введите формулу в ячейку вычисляемого столбца, а затем нажмите Отменить на панели быстрого доступа .
Введите новую формулу в вычисляемый столбец, который уже содержит одно или несколько исключений.
Скопируйте в вычисляемый столбец данные, которые не соответствуют формуле вычисляемого столбца.
Примечание. Если скопированные данные содержат формулу, эта формула перезапишет данные в вычисляемом столбце.
Удалить формулу из одной или нескольких ячеек вычисляемого столбца.
Примечание. Это исключение не отмечено.
Переместите или удалите ячейку в другой области рабочего листа, на которую ссылается одна из строк в вычисляемом столбце.
Если вы используете Excel 2007, нажмите кнопку Office , затем Параметры Excel > Формулы .
Если вы используете Mac, перейдите к Excel в строке меню, а затем нажмите Настройки > Формулы и списки > Ошибка проверки .
Включение или выключение вычисляемых столбцов
- org/ListItem»>
На вкладке Файл щелкните Параметры .
Если вы используете Excel 2007, нажмите кнопку Office , затем Параметры Excel .
Нажмите Проверка .
В разделе Параметры автозамены щелкните Параметры автозамены .
Перейдите на вкладку Автоформат при вводе .
Под Автоматически по мере работы , установите или снимите флажок Заполнить формулы в таблицах для создания вычисляемых столбцов , чтобы включить или выключить эту опцию.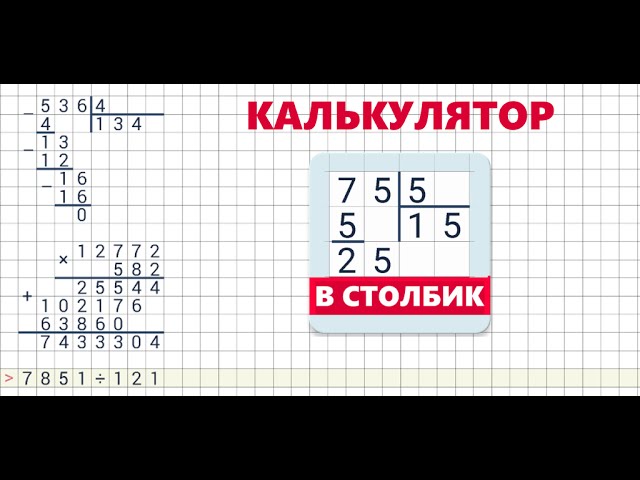
Совет: Вы также можете нажать кнопку Параметры автозамены , которая отображается в столбце таблицы после ввода формулы. Нажмите «Управление параметрами автозамены», а затем снимите флажок «Заполнить формулы в таблицах для создания вычисляемых столбцов», чтобы отключить этот параметр.
Если вы используете Mac, перейдите к Excel в главном меню, затем Настройки > Формулы и списки > Таблицы и фильтры > Автоматически заполнять формулы .
Остановить автоматическое создание вычисляемых столбцов
После ввода первой формулы в столбце таблицы нажмите отображаемую кнопку Параметры автозамены , а затем нажмите Остановить автоматическое создание вычисляемых столбцов .

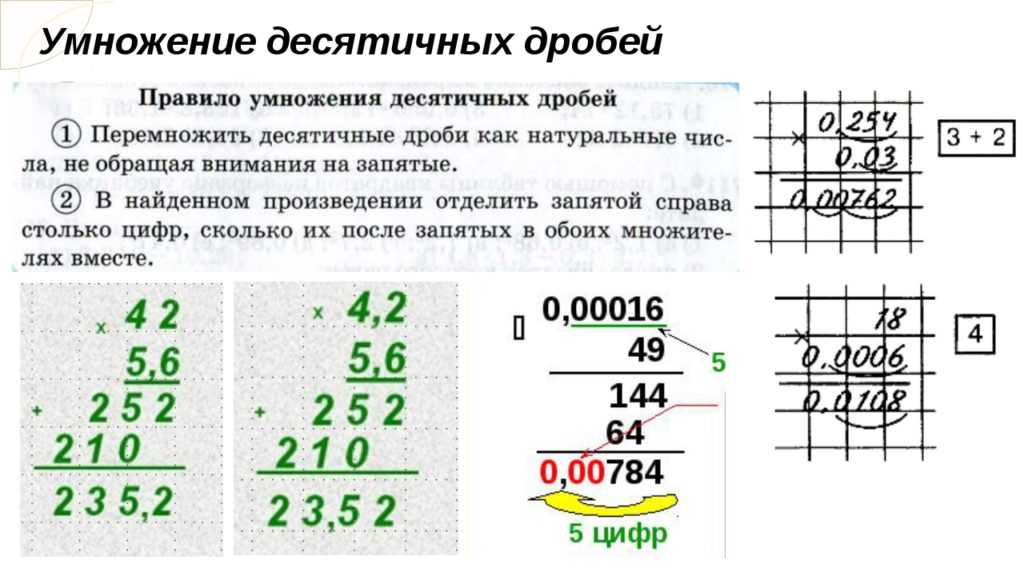 Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230: