Онлайн Тренажер ДРОБИ. Сложение, Вычитание, Умножение и Деление ⏳
Менталар представляет вам бесплатно онлайн тренажер Дроби.
Тренажер дроби для любого класса
Данный тренажер подходит для изучения и закрепления дробей в игре – начиная с 2 класса по изучению этой темы
3 класса , 4 класса, 5 класса, 6 класса дроби, 7 класса , 8 класса, 9 класса, 10 класса, 11 класса
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь будет состоять из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, является числителем . Второе число под линией – знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-то делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби – это обозначить линию, разделяющую каждое число, «вне». Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Упрощение дробей Тренажер
Первый метод – разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить. В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54.
- Снова разделите на 2, чтобы получить 6/27.
- Разделите на 3, чтобы получить 2/9
Добавление дробей Тренажер
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Дополнение: Пример 2
Допустим, вы хотите сложить дроби и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ – 3/6. Упростите это до ½.
Ответ – 3/6. Упростите это до ½.
Вычитание дробей по тренажеру
Вычитание дробей работает аналогичным образом:
- Шаг 1. Убедитесь, что знаменатели совпадают
- Шаг 2 – вычтите числители
- Шаг 3 – При необходимости упростите дробь
Вычитание: пример 1
Допустим, вас попросили потренироваться ¾ – ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ – be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей Тренажер
Умножение дробей относительно легко; вы просто перемножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
Деление дробей Тренажер
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и вы получите 3/2.
Может потребоваться дальнейшее уменьшение фракции для достижения сложной фракции.
Исследуй дальше Обратные Числа
Распространенные ошибки и на что следует обратить внимание. Тренажер
Давайте возьмем пример, сложив вместе ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Другие распространенные ошибки включают:
Оставляйте знаменатель неизменным во время вопросов, касающихся умножения или сложения.
Как неправильную дробь перевести в смешанное число. Тренажёр
Любую неправильную дробь можно превратить в смешанную. Для этого нужно выделить из нее целую часть.
Чтобы из неправильной дроби выделить целую часть, нужно:
разделить с остатком числитель на знаменатель;
частное без остатка будет целой частью;
остаток (если он есть) дает числитель дробной части, а знаменатель дробной части остается тем же, что и у неправильной дроби.
Тренажёр по этой теме поможет вам закрепить эту тему.
Как смешанное число перевести в неправильную дробь Тренажёр
Рассмотрим как любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Тренажёр и тест помогут вам закрепить эту тему.
Умножение и деление десятичных дробей Онлайн тренажер
Давайте проверим себя, как вы умеете умножать и делить десятичные дроби. Вспомните, как нужно умножать и делить дроби, а затем поработайте на нашем тренажёре. В нём всего 21 пример, но будьте внимательны!
Задания в тренажёре включают умножение и деление на 0,1; 0,01; 0,001; 0,0001 и т.д, а также умножение и деление десятичных дробей на 10, 100, 1000 и т.д. То есть мы учимся правильно переносить запятую.
Как умножать десятичные дроби на 10, 100, 1000, 10 000 и т. д?
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Например:
8,963 · 10 = 89,63
0,062 · 1000 = 0062 = 62 (нули перед числом не пишутся)
2,9 · 10000 = 2,9000 · 10000 = 29000
Как умножать десятичные дроби на 0,1; 0,01; 0,001 и т.д?
Умножить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).
Например:
54,3 · 0,1 = 54,3 : 10 = 5,43
0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001
Как делить десятичные дроби на 0,1; 0,01; 0,001 и т.д?
Разделить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что умножить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в делимом на столько знаков вправо, сколько нулей стоит в делителе перед единицей (ноль перед запятой тоже считаем).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
Например:
54,87 : 0,1 = 548,7
34,56 : 0,0001 = 34,5600 : 0,0001 = 345600
24 : 0,001 = 24,000 : 0,001 = 24000
Как делить десятичные дроби на 10, 100, 1000 и т.д?
Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.
При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.
Например:
374,5 : 100 = 3,745
5,021 : 1000 = 0005,021 : 1000 = 0,005021
0,1 : 100 = 000,1 : 100 = 0,001
В этом онлайн тренажере необходимо выбрать правильный ответ и нажать на него. В случае правильного ответа он загорится зеленым цветом, если ответ неверный — красным. В этом случае попробуйте найти правильный ответ, а затем нажмите кнопку «Дальше».
Онлайн тренажер по математике из раздела «Умножение и деление десятичных дробей»
Закрепляющие файлы для работы.
Менталар желает Вам легкой плодотворной усвояемой работы над собой.
Верьте в себя и у вас все получится!!!
Ваш сайт Менталар.
Сложение и вычитание дробей с одинаковыми знаменателями. — Kid-mama
Сложение и вычитание дробей с одинаковыми знаменателями.
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями.
- Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- С ответом
- С отметкой о просмотре
Сложение дробей — как складывать дроби 🤔
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дробей1. Дробь не имеет значения, при условии, если делитель равен нулю. 2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля. 3. Равными называются такие a/b и c/d, если: 4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. |
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.

Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.
Запишите вашего ребенка на бесплатный вводный урок математики в детскую школу Skysmart: порешаем задачки на интерактивной платформе, порисуем фигуры на онлайн-доске и покажем, что учиться можно с интересом и в удовольствие.
Правила на сложение (вычитание), умножение (деление) обыкновенных и десятичных дробей. 6 класс
Правила на сложение (вычитание), умножение (деление) обыкновенных и десятичных дробей. 6 класс
Подготовил: учитель математики Водопьянова Н. С.
1. Чтобы сложить (вычесть) десятичные дроби, нужно
1) уравнять в этих дробях количество знаков после запятой;
2) записать их друг под другом так, чтобы запятая была под запятой;
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) поставить в ответе запятую под запятой в данных дробях.
3,7 – 2,651 =
2. Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д. надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
0,065 100 =
2,9 1000 =
3. Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.
Если целая часть меньше делителя, то частное начинается с нуля.
19,2 : 8 = 2,88 : 4 =
4. Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
д. надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
8,765 : 100 =
2,9 10 =
5. Чтобы перемножить две десятичные дроби, надо:
1) выполнить умножение, не обращая внимание на запятые;
2) отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей
0,8 0,92 =
6. Чтобы разделить число на десятичную дробь, надо:
1) в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на натуральное число.
12,096 : 2,24 = 4,5 : 0,125 =
7. Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.
8. Чтобы умножить дробь на дробь, надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем, а второе знаменателем.
9. Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
10. Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
11. При сложении дробей с одинаковыми знаменателями числители складываются, а знаменатель оставляют тот же.
12. При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
13. Чтобы сложить или вычесть дроби с разными знаменателями, надо: 1) привести данные дроби к наименьшему общему знаменателю; 2) сложить ил вычесть полученные дроби.
Статистика Онлайн всего: 1 Гостей: 1 Пользователей: 0 В гостях у Президента России | Школьный помощник — это сервис, который поможет закрепить знания, полученные в школе, или наверстать пропущенный материал.
KID- MAMA — ваша домашняя школа. Здесь вы найдете онлайн игры и тренажеры, презентации, интерактивные модели, уроки, тесты, статьи, материалы для распечатывания, а также материалы и публикации, развивающие кругозор, смекалку, сообразительность и быструю интеллектуальную реакцию. Учиться с нами — интереснее и веселее!
| Календарь
Архив записей | ||||
Сложение и вычитание десятичных дробей
Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
- Записать числа в столбик таким образом, чтобы соответствующие разряды совпадали. Главный ориентир — десятичные точки. Они не являются отдельным разрядом, но должны стоять на одной вертикали;
- Сложить или вычесть полученные дроби столбиком — подобно тому, как мы складываем и вычитаем обычные числа.
 Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
Не забудьте «внедрить» десятичную точку между соответствующими разрядами; - Полученное число и будет ответом — больше ничего делать не надо.
Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.
Задача. Найдите значение выражений: 8,125 + 17,4; 3,5 + 121,048.
Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:
Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:
Как видите, ничего общего с тем, что должно получиться на самом деле.
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке». Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.
Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:
Задача. Найдите значение выражений: 7,34 + 18,5; 13 + 0,25;11,3 − 4,128; 5,21 − 11.
Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:
Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.
Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.
Смотрите также:
- Умножение и деление десятичных дробей
- Как представить обычную дробь в виде десятичной
- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)
- Задача 7 — геометрический смысл производной
- Метод узлов в задаче B5
- Задача B5: площадь сектора
Математические действия на английском языке
Наиболее употребительные простые дроби.Даже если ваша профессиональная деятельность никак не связана с точными науками, хотя бы основные математические действия на английском знать нужно. Они встречаются не только в специальной литературе, но и в фильмах, книгах, повседневной речи. В этой статье мы рассмотрим термины, связанные с арифметическими задачами, дробями, процентами. В конце я привожу озвученные карточки со основными словами на тему математики.
Обратите внимание, здесь рассматриваются только математические термины. Если вы ищете сведения о числительных, рекомендую эту статью: Числительные в английском языке.
Содержание:
Основные математические действия на английском: сложение, вычитание, умножение и деление
Наиболее употребительные математические термины относятся к арифметике. Обратите внимание, в русском языке у нас есть такие слова, как:
- Сложение, вычитание, деление, умножение – название действия.
- Складывать, вычитать, делить, умножать – глагол, обозначающий действие.
- Плюс, минус, разделить, умножить – название действия, которое мы используем в речи, когда читаем выражение, именно оно используется чаще всего.
В английском языке точно так же, поэтому представим арифметические действия в виде таблицы:
| Название действия (сущ.) | Название действия (глагол) | Используется в речи |
|---|---|---|
| Addition – сложение | Add – прибавлять | Plus – плюс |
| Subtraction – вычитание | Subtract – вычитать | Minus – минус |
| Multiplication – умножение | Multiply by – умножать на | Times – умножить |
| Division – деление | Divide by – делить на | Divided by – разделить |
| Equality – равенство | Equals to \ is equal to – равняться чему-то | Equals to \ is equal to \ is – равно |
Сама арифметическая задача (например, 2+2) называется problem (по-научному) или sum (разговорный вариант), решение или ответ – answer, а глагол “решать” – to solve (the problem).
Приведу примеры:
- 2+2=4 – Two plus two equals four.
- 7-2=5 – Seven minus two equals five.
Часто вместо equals или is equal to говорят просто is.
- 5×3=15 – Five times three is fifteen.
- 8÷4=2 – Eight divided by four is two.
Дроби на английском языке
Простые дроби – common fractions
Если у вас с математикой так же “прекрасно”, как у меня, напомню самое основное о дробях.
Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator). Напоминаю, числитель сверху, знаменатель снизу 🙂 Если число состоит из целого и дроби, например 1½, – это называется смешанная дробь или смешанное число (mixed numeral).
Числитель выражается количественным числительным, а знаменатель порядковым. Наиболее употребительные в речи дроби 1/2, 1/3, 1/4 в русском языке имеют не только “умные” называния “одна вторая”, “одна третья”, одна четвертая, но и простые: половина, треть, четверть. В английском точно так же.
- 1/2 – a half, one half.
- 1/3 – a third, one third.
- 1/4 – a quarter, one fourth.
- 1/5 – one fifth.
- 1/6 – one sixth.
- 2/3 – two thirds.
- 3/4 – three fourths.
- 1/8 – one eighth.
- 1/10 – a tenth.
- 1/100 – a hundredth.
- 1¼ – one and a quarter.
- 1½ – one and a half.
- 1¾ – one and three quarters.
Обратите внимание, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).
Существительное, которое определяется дробью, используется с предлогом of:
- 3/4 mile – Three fourths of a mile.

- 1/4 bottle – A quarter of a bottle.
Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:
- 2 ½ miles – Two and a half miles.
- 1¼ bottles – One and a quarter bottles.
Десятичные дроби – decimal fractions, decimals
В английском в десятичных дробях (decimals) целое от дроби отделяется точкой (point), а не запятой, как у нас.
Ноль перед точкой называется zero или (британский вариант) nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Лично я для простоты всегда говорю zero, потому что это слово проще выговорить и расслышать. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.
Целое число читается как обычное количественное числительное, например 45.1 – forty five point one. Но в дробной части каждая цифра читается отдельно тоже как количественное: 2.45 – two point four five (а не two point forty five).
Примеры:
- 0.1 – Point one, zero point one.
- 0.35 – Point three five, zero point three five.
- 1.25 – One point two five.
- 35.158 – Thirty five point one five eight.
- 15.05 – Fifteen point zero five.
Проценты в английском языке, трудности с числом глагола
Сотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.
- 1% – One percent.
- 10% – Ten percent.
- 17% – Seventeen percent.
Трудность может вызвать число глагола в выражениях с процентами. Например:
- Twenty percent of the students are/is present.
 – 20% студентов присутствуют.
– 20% студентов присутствуют. - The remaining twenty percent of the script has/have been rewritten. – Оставшиеся 20% сценария были переписаны.
В таких случаях глагол согласуется в числе с существительным после of:
- Twenty percent of the students are present (т. к. students – мн. число).
- The remaining twenty percent of the script has been rewritten (т. к. script – ед. число).
Возведение в степень в английском
Для обозначение степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Для 2-ой и 3-ей степени используются термины “в квадрате” (squared) и “в кубе” (cubed).
- 32 – Three squared, three to the second power.
- 33 – Three cubed, three to the third power.
- 104 – Ten to the fourth power, ten to the power of four.
- 3024 – Thirty to the power of twenty four.
Квадратный корень называется square root:
- √16 = 4 – The square root of sixteen is four.
- √25 = 5 – The square root of twenty five is five.
Математические выражения со скобками
Круглые скобки называются parentheses (ед. число parenthesis) или, проще, round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.
- (2+3)×4=24 – Two plus three quantity times four equals to twenty four.
- (3+5)2=64 Three plus five quantity squared is sixty four.
Карточки с английскими словами на тему “Математика”
Математические термины из этой статьи можно выучить с помощью карточек на Quizlet и PDF-карточек для распечатки.
| math (mathematics) | математика |
| do the math | считать (матем. действия) |
| problem (sum) | арифметическая задача |
| to solve | решать |
| answer | ответ |
| digit | цифра |
| number | число |
| odd number | нечетное число |
| even number | четное число |
| to add | прибавлять |
| to subtract | вычитать |
| to multiply by | умножать на |
| to divide by | делить на |
| to be equal to | равняться |
| plus | плюс |
| minus | минус |
| times | умножить |
| divided by | разделить |
| equals to | равно |
| common fractions | простые дроби |
| numerator | числитель |
| denominator | знаменатель |
| mixed number | смешанное число (дробь) |
| half | половина |
| quarter | четверть |
| decimals (decimal fractions) | десятичные дроби |
| point | точка (в дес. дробях) |
| percent | процент |
| to the power of five | в пятой степени |
| two squared | два в квадрате |
| two cubed | два в кубе |
| square root | квадратный корень |
| round brackets | круглые скобки |
| brackets | квадратные скобки |
| to round up the numbers | округлять числа |
Здравствуйте! Меня зовут Сергей Ним, я автор этого сайта, а также книг, курсов, видеоуроков по английскому языку.
Друзья! Меня часто спрашивают, но я не занимаюсь сейчас репетиторством. Если вам нужен репетитор, я рекомендую зайти на этот чудесный сайт. Здесь вы найдете учителей носителей и не носителей языка👅 для любых целей и на любой карман😄 Я сам прошел там более 100 уроков, рекомендую попробовать и вам!
Если вам нужен репетитор, я рекомендую зайти на этот чудесный сайт. Здесь вы найдете учителей носителей и не носителей языка👅 для любых целей и на любой карман😄 Я сам прошел там более 100 уроков, рекомендую попробовать и вам!
Складывающиеся дроби — положительные, полубесконечные
Сегодняшний пост немного отличается от обычного, но в некоторой степени связан с математикой, поэтому я решил, что все равно разместу его здесь. Недавно сложила карлика оригами Эрика Джойзела
Мой сложенный карлик
(здесь вы можете увидеть грубые инструкции Джойзела для гнома). Одна интересная особенность карлика, на которую указывает Джойзел в своих инструкциях, заключается в том, что карлик сложен из сетки 28 на 28. Как отмечает Джойзел, обычно в моделях оригами используются сетки, размеры которых равны степеням двойки — просто несколько раз сложите лист бумаги пополам, чтобы получить сетку 8 на 8 или сетку 32 на 32.Но 28 на 28 сложнее. Фактически, Джойзел советует вам использовать линейку для формирования сетки вместо того, чтобы вручную складывать 28-е. Но оказывается, что все-таки сбросить 28-е место не так уж и сложно. Вот о чем я пишу сегодня. Но прежде чем сразу перейти к фолдингу 28-го числа, мы начнем с немного более легкой темы.
Складывание квадрата в трети
Вот небольшая симпатичная последовательность складывания, чтобы сложить лист бумаги пополам. Сначала возьмите свой квадрат и сложите его пополам.Разверните, и у вас останется вертикальная складка, разрезающая квадрат пополам.
Далее сложите и разверните квадрат пополам по диагонали. Теперь сложите и разверните складку от правого нижнего угла до середины верхнего края. И теперь все готово! Две диагональные складки пересекают друг друга в точке на одной трети ширины бумаги!Почему это работает?
Вероятно, есть какой-то умный аргумент, который вы можете привести, используя евклидову геометрию и подобные треугольники и тому подобное, чтобы показать, что этот алгоритм действительно находит вам одну треть статьи. Но я думаю, что вместо этого проще использовать координатную геометрию. Давайте представим наш квадрат бумаги живущим на плоскости, так что его правый край — это ось $ y $, а нижний край — ось $ x $.
Но я думаю, что вместо этого проще использовать координатную геометрию. Давайте представим наш квадрат бумаги живущим на плоскости, так что его правый край — это ось $ y $, а нижний край — ось $ x $.
Обобщение на произвольные дроби
Тот простой факт, что $ 3 = 2 + 1 $ сыграл решающую роль в приведенном выше доказательстве.Сумма $ 2x $ в правой части и единственная $ x $ в левой части дают нам множитель $ 3x $. И эти 3 доллара стали знаменателем 1/3 доллара. Итак, что бы произошло, если бы наша правая сторона была $ -4x $ вместо $ -2x $?
\ [\ begin {выровнено} х + 1 & = -4x \\ 5x & = -1 \\ х & = -1/5 \ конец {выровнено} \]Тогда вместо того, чтобы найти точку $ 1/3 $ пути по странице, мы найдем точку $ 1/5 $ пути через страницу! В общем, если мы можем сложить линию с наклоном $ -n $, тогда мы можем сложить бумагу на сегменты шириной $ 1 / (n + 1) $.
А как сложить линию наклона $ -n $? Раньше мы складывали линию с наклоном $ -2 $, сначала складывая бумагу пополам, а затем складывая диагональ, разрезая одну из половинок пополам. Это создает линию наклона $ -2 $, потому что половина квадрата представляет собой прямоугольник $ 2: 1 $, а его диагональ имеет наклон $ -2 $. Точно так же мы можем использовать прямоугольник $ n: 1 $, чтобы сложить диагональ с уклоном $ -n $.
Таким образом, учитывая сгиб $ 1 / n $ на листе бумаги, мы можем найти $ 1 / (n + 1) $ следующим образом: Предположим, мы начинаем с квадрата, у которого есть складка $ 1 / n $ в поперечнике.
Далее сложите и разверните квадрат пополам по диагонали. Теперь сложите и разверните складку от правого нижнего угла к верхней части нашей начальной складки. И теперь все готово! Две диагональные складки пересекают друг друга в точке $ 1 / (n + 1) $ пути по бумаге!
И теперь все готово! Две диагональные складки пересекают друг друга в точке $ 1 / (n + 1) $ пути по бумаге!Складной 28-й
Эта процедура дает нам простой, хотя и утомительный метод складывания квадрата на 28 частей: сначала сложите его пополам, затем найдите $ 1/3 $, затем используйте $ 1/3 $, чтобы найти $ 1/4 $, затем используйте $ 1/4 $, чтобы найти $ 1/5 $ и так далее, пока мы, наконец, не найдем $ 1/27 $, чтобы найти $ 1/28 $.Конечно, это ужасная идея по нескольким причинам. Сгибание займет много времени, и на вашем квадрате останется бесчисленное количество лишних складок. Немного подумав, мы можем сложить 28-е место с гораздо меньшими усилиями и минимальными дополнительными складками.
$ 28 = 4 \ cdot 7 $. Сложить вещи на четверть просто: просто дважды сложите пополам. Таким образом, единственная сложная часть складывания 28-го — это складывание 7-го. $ 7 = 6 + 1 $, поэтому мы можем получить $ 1/7 $, сначала сбросив $ 1/6 $. А $ 1/6 $ — это всего лишь половина $ 1/3 $, которые мы уже знаем, как сбросить карты.Вот вся последовательность складывания:
Сначала возьмите свой квадрат и сложите его пополам. Разверните, и у вас останется вертикальная складка, разрезающая квадрат пополам.
Далее сложите и разверните квадрат пополам по диагонали. Вам нужно только сделать сильную складку в правом верхнем углу. Теперь сложите диагональ от правого нижнего угла к середине верхнего края. Сделайте защемление там, где эта складка пересекает другую диагональную складку. Как мы видели ранее, это пересечение составляет $ 1/3 $ по бумаге.Теперь согните правый край до только что сделанного пересечения, защемив верхнюю часть листа. Это создает защемление на бумаге размером $ 1/6 $. Теперь согните диагональ от правого нижнего угла к вершине только что сделанной щепотки за 1/6 $. Сожмите пальцы в том месте, где эта диагональ пересекается с исходной диагональю. Это пересечение составляет $ 1/7 $ по бумаге. Наконец, вы можете сложить правый край до пересечения $ 1/7 $, чтобы получить $ 1/14 $, и вы можете сложить правый край до складки $ 1/14 $, чтобы получить $ 1/28 $.Тогда все готово!
Наконец, вы можете сложить правый край до пересечения $ 1/7 $, чтобы получить $ 1/14 $, и вы можете сложить правый край до складки $ 1/14 $, чтобы получить $ 1/28 $.Тогда все готово!Как умножать дроби, складывая бумагу
Пример
¼ × ⅖
Сложите лист бумаги в 4 ряда (поскольку знаменатель первой дроби равен 4 ). Теперь сложите лист в 5 столбцов (поскольку знаменатель второй дроби равен 5 ).
Определите, на сколько частей вы разделили лист бумаги. Здесь 20 разделов, поэтому каждый раздел представляет ¹ / ₂₀
Обозначьте каждый из разделов с помощью / ₂₀
Оттенка в 1 строк (поскольку числитель первой дроби равен 1 ).Затем заштрихуйте 2 столбцов (поскольку числитель второй дроби равен 2 ).
$zd6jhbk-4=10.1.1.$6″> Наконец посчитайте перекрывающиеся участки. В этом примере 2 секций перекрываются из 20 частей в общей сложности. Это означает, что ответ — ² / ₂₀Ответ можно упростить до дроби, как / ₁₀
Изучение эквивалентных дробей с учащимися в Бостоне
На этой неделе мне посчастливилось еще раз посетить частную школу в Бостоне, Массачусетс.Мы работаем над 4-недельным изучением урока, где мы работаем вместе со школьными учителями над планированием уроков, наблюдением за уроками и оценкой уроков. В школе недавно была принята сингапурская математика, и учителя не знакомы с сингапурскими стратегиями. Это был очень полезный опыт для нас и учителей, поскольку мы говорили о проблемах в классе и о том, какие конкретные стратегии использовать для занятий.
Одной из важных областей, над которой мы работали, являются дроби — тема, в которой многие студенты испытывают трудности.Важнейшей концепцией дробей являются эквивалентные дроби. Заманчиво сразу погрузиться в математические процедуры, «предлагая» студентам умножить числитель и знаменатель на одно и то же число, чтобы найти эквивалентные дроби. Однако это лишит учащихся прекрасной возможности вывести свои собственные «правила» посредством индукции.
В нашем уроке мы начали урок со складывания бумаги, когда ученики должны были сложить длинную полосу бумаги пополам, затем на четверть, затем на восьмые и, наконец, на шестнадцатые.Студентам предлагается перенести свои результаты на модели стержней. Для вводного курса учащиеся сравнивают знаменатели и числители пар эквивалентных дробей, и им задают следующие вопросы:
- Что вы заметили?
- Есть узор?
- Есть ли правило?
Многие студенты быстро вводят свои собственные «правила» для эквивалентных дробей; некоторые из них неисправны, а некоторые выдержали испытание. Студенты знают, что им нужно рассуждать логически и быть готовыми защищать свои «правила» и убеждать остальных, что это работает! Это было увлекательное и содержательное обсуждение, поскольку мы приводим важные термины и понятия в дробях, таких как числитель, знаменатель, одно и то же целое, равное значение, одно и то же значение на числовой строке!
Студенты знают, что им нужно рассуждать логически и быть готовыми защищать свои «правила» и убеждать остальных, что это работает! Это было увлекательное и содержательное обсуждение, поскольку мы приводим важные термины и понятия в дробях, таких как числитель, знаменатель, одно и то же целое, равное значение, одно и то же значение на числовой строке!
Вот черновик от одного из студентов.
Исследование эквивалентных дробейВ качестве дополнения студентов попросили найти среднюю точку 3/8 и 4/8, например значение / балл, которое находится на полпути между 3/8 и 4/8. Это оказывается очень сложной задачей для многих студентов! Некоторые упомянули 3½ / 8, а некоторые — 3,5 / 8. Хотя это кажется логичным, это не соглашения, которые многие использовали бы, поэтому нам нужно найти альтернативы. Кому-то не потребовалось много времени, чтобы понять, что нам нужно изменить 3/8 на 6/16 и с 4/8 на 8/16, и при этом найти долю между 3/8 и 4/8 несложно! Это 16 июля!
Если вам нужны дополнительные ресурсы, отличным справочником является «Обучение овладению математикой: обучение дробям
», написанное доктором Дугласом Эджем и доктором Йипом Баном Харом.Он объясняет дроби очень концептуально, и ему легко следовать.Преподаете ли вы в классе эквивалентные дроби? С какими проблемами вы сталкиваетесь? Делитесь ими в комментариях ниже!
Дополнительные ресурсы фракций
Для получения дополнительных ресурсов фракций обратитесь к нашей главной странице фракций.
Использование складывания бумаги, дробных перегородок и числовых линий для развития понимания дробей для учащихся 5-8 классов
Как мой педагогический опыт, так и литература по этому исследованию убедительно свидетельствуют о том, что
фракции трудно преподавать и изучать по всему миру в целом, и в Намибии в частности.Одним из выявленных факторов было обучение дробям с упором на процедуры.
а не концептуальное понимание. Таким образом, этот исследовательский проект был разработан и
реализовал вмешательство, чтобы поэкспериментировать и предложить альтернативное обучение
подход дробей с использованием моделей. Целью этого исследования было: «Изучить использование
моделей для развития концептуального понимания учащимися 8-х классов и беглости выполнения процедур
с дробями ». Это расследование имело три основных направления.Во-первых, в исследовании изучались
характер концептуального понимания учащимися и беглость процедур с дробями до
педагогическое вмешательство посредством проведения предварительного тестирования и предварительного собеседования, а также
анализ ответов учащихся. Во-вторых, в исследовании изучались изменения в способностях учащихся
концептуальное понимание и беглость процедур с дробями после обучения
вмешательство посредством проведения послетестовых, пост-интервью и интервью по отзыву, а также
анализ ответов учащихся.В-третьих, в этом исследовании изучалось возможное влияние
обучающее вмешательство по изменениям в концептуальном понимании учащимися и процедурных
свободное владение дробями, анализируя видеоуроки и рабочие листы учащихся, и описывайте
их критическое взаимодействие.
Это исследование проводилось в многонациональной городской средней школе, расположенной в районе Ошикото.
Область, Намибия. Выборка состояла из 12 учащихся математики 8-х классов, возраст которых
колебался от 13 до 16 лет. Целенаправленный метод выборки использовался для выбора как
сайт исследования и участники.Это исследование оформлено как тематическое исследование и основано на
интерпретативная парадигма и качественное исследование.
Это исследование показало, что эти учащиеся продемонстрировали концептуальные и процедурные трудности в
их взаимодействие с моделями дробей и символами дробей перед обучением.
Концептуально исследование показало, что эти учащиеся читают дроби, используя неподходящие имена;
и учащиеся не определили целую единицу в моделях и, следовательно, определили фракции
представлены моделями дробей с использованием различных форм неподходящих символов дробей.Процедурно исследование показало, что эти учащиеся сравнивали и упорядочивали дроби
ненадлежащее использование размеров числителей и знаменателей по отдельности; и учащиеся
II
неправильно использовал метод наименьшего общего знаменателя для сложения дробей с
разные знаменатели.
Целью этого исследования было: «Изучить использование
моделей для развития концептуального понимания учащимися 8-х классов и беглости выполнения процедур
с дробями ». Это расследование имело три основных направления.Во-первых, в исследовании изучались
характер концептуального понимания учащимися и беглость процедур с дробями до
педагогическое вмешательство посредством проведения предварительного тестирования и предварительного собеседования, а также
анализ ответов учащихся. Во-вторых, в исследовании изучались изменения в способностях учащихся
концептуальное понимание и беглость процедур с дробями после обучения
вмешательство посредством проведения послетестовых, пост-интервью и интервью по отзыву, а также
анализ ответов учащихся.В-третьих, в этом исследовании изучалось возможное влияние
обучающее вмешательство по изменениям в концептуальном понимании учащимися и процедурных
свободное владение дробями, анализируя видеоуроки и рабочие листы учащихся, и описывайте
их критическое взаимодействие.
Это исследование проводилось в многонациональной городской средней школе, расположенной в районе Ошикото.
Область, Намибия. Выборка состояла из 12 учащихся математики 8-х классов, возраст которых
колебался от 13 до 16 лет. Целенаправленный метод выборки использовался для выбора как
сайт исследования и участники.Это исследование оформлено как тематическое исследование и основано на
интерпретативная парадигма и качественное исследование.
Это исследование показало, что эти учащиеся продемонстрировали концептуальные и процедурные трудности в
их взаимодействие с моделями дробей и символами дробей перед обучением.
Концептуально исследование показало, что эти учащиеся читают дроби, используя неподходящие имена;
и учащиеся не определили целую единицу в моделях и, следовательно, определили фракции
представлены моделями дробей с использованием различных форм неподходящих символов дробей.Процедурно исследование показало, что эти учащиеся сравнивали и упорядочивали дроби
ненадлежащее использование размеров числителей и знаменателей по отдельности; и учащиеся
II
неправильно использовал метод наименьшего общего знаменателя для сложения дробей с
разные знаменатели. Исследование также предложило концептуальные и процедурные изменения в концептуальных представлениях учащихся.
понимание дробей и свободное владение процедурами, и что вмешательство, казалось,
помогают учащимся лучше взаимодействовать с моделями дробей и символами дробей.Концептуально
результаты показали, что вмешательство с использованием моделей площадей и числовых линий, казалось,
эти учащиеся читают дроби с соответствующими именами; идентифицировать весь блок в
модели дробей и развитие чувства размера дробей по отношению к одной целой единице.
С процедурной точки зрения учащиеся сравнивали и упорядочивали дроби соответствующим образом, используя либо равные
дробные столбцы, равные числа строк, сравнительный анализ или правила сравнения и упорядочения
дроби с одинаковым числителем или знаменателем; и учащиеся использовали равные дробные столбцы,
визуально представить метод наименьшего общего знаменателя и признать, что только в равной степени
единицы размера можно пересчитать вместе.Это исследование выявило четыре фактора, которые могут повлиять на педагогическое вмешательство. Эти
Факторы, а именно: идентификация как символов дроби, так и соответствующих имен дробей, чтобы увидеть
дроби как относительные числа; подсказка для разбиения целых единиц фракционных моделей и
графически иллюстрирующие символы дроби для идентификации целой единицы в моделях дробей и
развить чувство размера дробей по отношению к одной целой единице; графически
иллюстрации символов дробей с использованием моделей для использования равных долей дроби и числовых линий,
бенчмаркинг и правила сравнения; и графически иллюстрирующие номиналы дробей
использование столбцов с равной дробью, чтобы понять, что вместе можно сосчитать только единицы одинакового размера.Это исследование убедительно свидетельствует о том, что эффективное использование моделей может способствовать развитию
концептуальное понимание учащимися и свободное владение процедурами дробей разными способами.
Исследование также предложило концептуальные и процедурные изменения в концептуальных представлениях учащихся.
понимание дробей и свободное владение процедурами, и что вмешательство, казалось,
помогают учащимся лучше взаимодействовать с моделями дробей и символами дробей.Концептуально
результаты показали, что вмешательство с использованием моделей площадей и числовых линий, казалось,
эти учащиеся читают дроби с соответствующими именами; идентифицировать весь блок в
модели дробей и развитие чувства размера дробей по отношению к одной целой единице.
С процедурной точки зрения учащиеся сравнивали и упорядочивали дроби соответствующим образом, используя либо равные
дробные столбцы, равные числа строк, сравнительный анализ или правила сравнения и упорядочения
дроби с одинаковым числителем или знаменателем; и учащиеся использовали равные дробные столбцы,
визуально представить метод наименьшего общего знаменателя и признать, что только в равной степени
единицы размера можно пересчитать вместе.Это исследование выявило четыре фактора, которые могут повлиять на педагогическое вмешательство. Эти
Факторы, а именно: идентификация как символов дроби, так и соответствующих имен дробей, чтобы увидеть
дроби как относительные числа; подсказка для разбиения целых единиц фракционных моделей и
графически иллюстрирующие символы дроби для идентификации целой единицы в моделях дробей и
развить чувство размера дробей по отношению к одной целой единице; графически
иллюстрации символов дробей с использованием моделей для использования равных долей дроби и числовых линий,
бенчмаркинг и правила сравнения; и графически иллюстрирующие номиналы дробей
использование столбцов с равной дробью, чтобы понять, что вместе можно сосчитать только единицы одинакового размера.Это исследование убедительно свидетельствует о том, что эффективное использование моделей может способствовать развитию
концептуальное понимание учащимися и свободное владение процедурами дробей разными способами.
Фракционные полосы — игровая площадка класса
На главную »Математика» Дробные полосы
Обзор
Распечатки
Интерактивный
Видео
Что такое дробные полоски?
Полоски фракций — это тонкие прямоугольные кусочки цветной бумаги, используемые для определения дробей. Дробные полоски могут быть разного цвета и длины, и их можно сложить, чтобы показать разные дробные части. Дробные части — это равные доли, составляющие целое. Например, для создания одного целого требуется четыре ¼ части.
Дробные полоски могут быть разного цвета и длины, и их можно сложить, чтобы показать разные дробные части. Дробные части — это равные доли, составляющие целое. Например, для создания одного целого требуется четыре ¼ части.
Полоски дроби полезны для определения дробей, отображения частей целого и распознавания эквивалентных дробей. При введении дробей лучше всего, чтобы учащиеся сами делали полоски дробей. Попросите учащихся разрезать плотную бумагу на полоски длиной 12 дюймов каждая.Затем попросите студентов сложить полоски пополам, трети, четвертые и шестые части. Поработайте со студентами, чтобы сравнить дроби на каждой полосе. Спросите студентов, сколько частей каждой фракции нужно сложить вместе, чтобы составить целое.
Почему мне следует использовать дробные полоски?
Полоски с дробями — отличный инструмент, на который можно положиться при обучении дробям. Дизайн полосок обеспечивает единообразие «целого» для учащихся. Когда учащиеся манипулируют частями одного и того же целого, эти полоски позволяют учащимся визуализировать и исследовать дробные отношения.
Полоски фракций идеально подходят для моделирования эквивалентных фракций. Эквивалентные дроби представляют собой одно и то же значение, даже если у них разные числители или знаменатели. Полоски позволяют учащимся увидеть, что половина представляет собой то же значение, что и две четверти, три шестых и пять десятых.
Учащиеся разовьют более глубокое понимание дробей, когда дроби отображаются различными способами и когда устанавливаются личные связи. Фракционные полоски облегчают это соединение, поскольку они могут легко отображать сценарии из реальной жизни, такие как равное использование шоколадного батончика или разделение футляра на равные части.
фракций — 20 готовых к работе ресурсов и мероприятий
фракции являются частью многих классов со второго по пятый класс. Эти 20 бесплатных игр с дробями , рабочие листы с дробями , мероприятия и ресурсы помогут упростить планирование уроков.
Существует ряд идей, которые вы можете адаптировать для деления дробей , эквивалентных дробей и даже упрощающих дробей .
1. Манипулятивные дроби. Вот отличный урок использования манипуляторов для определения дробных значений.Учащиеся создают образцы блоков для работы над определением числителя и знаменателя.
2. Виртуальные манипуляторы — Вытяните виртуальные манипуляторы дробей для решения с помощью готовых дробных столбцов. Также включает десятичные дроби и проценты.
3. Дробные классики — научите студентов двигаться и учиться, играя в классики. Студенты работают по упорядочиванию дробей и эквивалентных дробей .
Игры на дроби
4. Игра на дроби — это гонка на дроби! Студенты играют в эту игру с дробями, чтобы создавать группы дробей.Вам понравится, что уже включены три уровня сложности — мгновенная дифференциация!
5. Общие основные дроби — игра для первоклассников и второклассников, в которой все о разделении на части равного размера. Это также помогает укрепить идею о том, что части не обязательно должны совпадать, чтобы быть равными.
6. Контрольные дроби. Вот простое задание, которое учащиеся могут выполнять в совместных группах с помощью самодельных карточек дробей. Учащиеся сортируют, описывают и объясняют, почему они сортируют свои карточки по числам, «близким к контрольным».
7. Никаких подготовительных игр с дифференцированными дробями — Используя двусторонние счетчики, учащиеся создают свои собственные протоколы для работы над концептуализацией эквивалентных дробей . Идеально подходит для четвертого и пятого классов.
Стратегии решения
8. Дроби бабочки — Стратегия сложения или вычитания двух дробей, которая выглядит как крылья бабочки!
9. Плакаты со смешанными числами — Получите MAD с помощью этой стратегии — научите студентов умножать, складывать и затем делить, чтобы получить смешанные числа.
10. Упрощение дробей — стратегия, помогающая разбить процесс упрощения дробей . Обучайте, обводя и выделяя наиболее общий фактор, чтобы учащиеся могли повысить точность и показать свое мышление.
11. Стратегии дроби — вот три плаката, которые вы можете воссоздать в своем классе, чтобы проиллюстрировать, как учащиеся могут использовать числовую прямую, целую модель или модель площади для решения.
Визуализация дробей
12. Половинки и четверти — реальные примеры привязки диаграммы половинок и четвертей.Отлично подходит для начинающих студентов с того, что они уже знают о дробях.
13. Якорные диаграммы — четыре изображения якорных диаграмм, которые дадут вам идеи о том, как создавать полезные якорные диаграммы дробей в вашем классе.
14. Lego Land Fractions — С помощью Lego можно упростить визуализацию дробей для учащихся. Студенты могут «видеть» с помощью цветных блоков сравнение от части до целого.
15. Флипбук с дробями — это интерактивный флипбук или складной блокнот, который вы можете использовать при обучении тому, как выглядит каждая дробь, и способ сохранить его в математическом журнале.
Рабочие листы для дробей
16. Рабочие листы для дробных фигур — В этом рабочем листе для начальных дробей используются формы для усиления половин, четвертей и третей.
17. Зимняя тематическая практика дроби — Зимний тематический рабочий лист для второго класса, который работает над поиском дробей целых чисел 10-20.
18. Рабочий лист сравнения дробей — этот простой рабочий лист, который можно использовать с четвертым и пятым классами, поможет глубже мыслить, когда учащиеся работают над сравнением дробей.
Разделение на дроби
19. Игра на деление дробей — существует две версии, в одной используются блоки шаблонов, а в другой — игра в кости. Отличная альтернатива рабочим листам.
20. Видео о делении дробей — в этом видео учащиеся средней школы и запоминающийся стих рассказывают, как делить дроби.
Видео о делении дробей — в этом видео учащиеся средней школы и запоминающийся стих рассказывают, как делить дроби.
Спасибо талантливым учителям — у вас отличные ресурсы и идеи! Не стесняйтесь нажимать кнопку блога « I’m a Featured Teach Junkie », поскольку ваши творения определенно заслуживают внимания.{{high fives}}
More Fractions
Бумажные складные фракции. — Бесплатная онлайн-библиотека
Страница / Ссылка:
URL страницы: HTML-ссылка: Это создает другие формы, области которых мы можем обсудить, рассуждения (или вычисления). Например, сложив во всех углах ваш студенты обнаружат, что четыре «угловых треугольника» имеют той же площади, что и внутренний квадрат, потому что треугольники «накрыть» внутренний квадрат.Поскольку вместе четверо сложили треугольники и внутренний квадрат составляют исходный квадрат, площадь каждого (внутренний квадрат или сложенные треугольники) должны быть 25/2 = 12 1/2 квадратных единиц. Таким образом, площадь одного из сложенных треугольников равна 1/4 x 25/2 = 25/8 = 3. 1/8 квадратных единиц, а половина одного из этих сложенных треугольников равна 1/2 x 25/8 = 25/16 = 1 9/16 квадратных единиц. Кроме того, поскольку внутренний квадрат равен разделенный на четыре меньших квадрата, каждый меньший квадрат имеет площадь 1/4 x 25/2 = 25/8 = 3 1/8 квадратных единицы, как сложенный треугольник.Этот имеет смысл, потому что две половинки загнутого «уголка» треугольник подойдет, чтобы получился небольшой квадрат.Используя эту информацию и складывая или не складывая различные линии сгиба учащиеся могут создавать разные многоугольники и использовать рассуждения, чтобы найти свои районы. Если, как учитель, вы хотите, чтобы ваши ученики убедитесь, что формулы для нахождения площадей квадратов, прямоугольников, треугольники и трапеции согласуются с их рассуждениями, это может тоже быть назначенными (см. лист бумаги сгибаемых дробей).Примечание: это может делаться без формул и не прибегая к пифагорейским Теорема. Если используются формулы, в некоторых случаях необходимо будет полагаться на об использовании теоремы Пифагора. Студенты также могут обнаружить, что все фигуры можно разбить на самый маленький треугольник (площадью 25/16 квадратных единиц), что позволяет найти площадь всех форм по подсчет количества самых маленьких треугольников и умножение на 25/16 чтобы найти площадь сложенной формы.
Лист бумаги для складывания фракций
Указания: Сложите бумагу, чтобы получить каждый многоугольник ниже, и найдите
его площадь.


 Наш проект создан для дополнительных занятий по предметам школьной программы: русский язык, математика, геометрия, алгебра.
Наш проект создан для дополнительных занятий по предметам школьной программы: русский язык, математика, геометрия, алгебра.  Для закрепления материала — онлайн тренажер. Вопросы при каждой загрузке тренажера — разные.
Для закрепления материала — онлайн тренажер. Вопросы при каждой загрузке тренажера — разные. Не забудьте «внедрить» десятичную точку между соответствующими разрядами;
Не забудьте «внедрить» десятичную точку между соответствующими разрядами;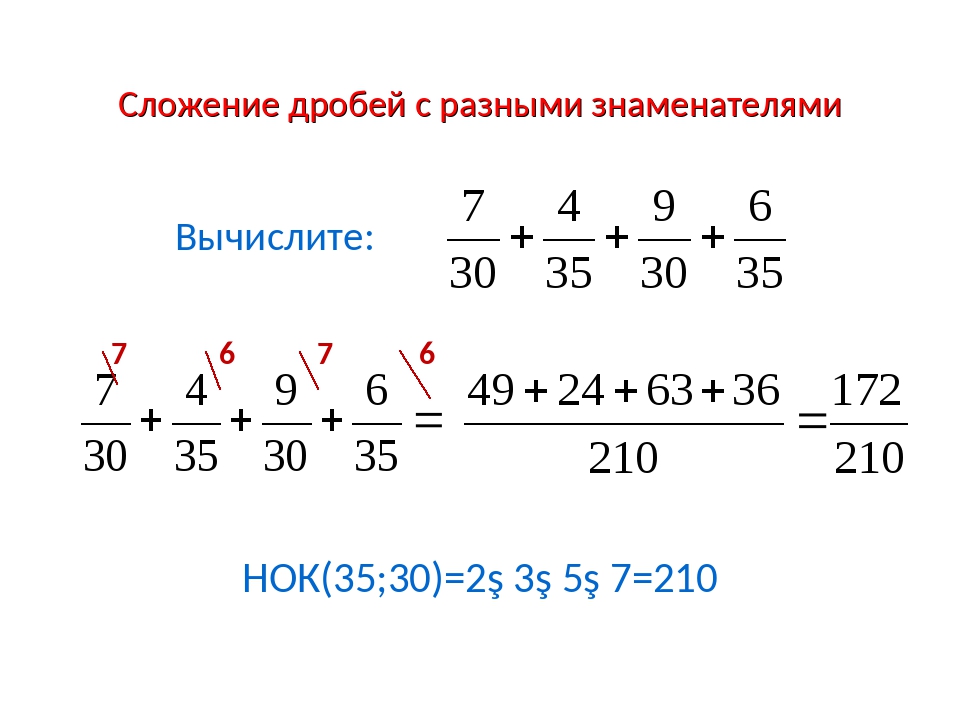
 – 20% студентов присутствуют.
– 20% студентов присутствуют.